关于maxwell v12中气隙磁密的计算

永磁无刷直流电机空载气隙磁场和绕组反电势的解析计算摘要：该文利用许-克变换构造了考虑齿槽效应的气隙相对比磁导函数，该气隙相对比磁导函数反映了齿槽效应对气隙磁场分布的影响，且这种影响的程度随气隙中的径向位置而变化。

在忽略铁心饱和的情况下，结合偏微分方程的解析算法，提出了一种考虑齿槽效应的永磁无刷直流电机空载气隙磁场分布和相绕组反电动势的解析计算方法。

计算结果与二维有限元计算结果对比，其计算波形和大小吻合很好。

证明此方法是正确的、可靠的，为永磁无刷直流电机优化设计和性能分析提供了基本分析手段。

关键词：永磁无刷电机；气隙磁场；反电势；解析计算1 引言对于永久磁钢表面安装的永磁电机，由于定子铁心开有若干槽，使气隙磁导并非均匀值，从而导致电机气隙磁场并非理想的梯形波，其中含有幅值较大的齿谐波，当电机旋转时会引起相绕组交链磁链的波动，使相绕组反电势出现波动，进而导致绕组相电流的脉动，引起电磁转矩的波动，最终引起电机的振动和噪声。

可见，要准确计算永磁电机的电磁转矩波动，首先应准确计算电机气隙内的磁场分布，从而可以准确计算出电机相绕组的反电动势变化波形和电机的电磁转矩波动，以确定有效的改进措施和控制策略。

而准确计算永磁电机气隙内磁场分布的关键是如何考虑齿槽结构对气隙磁场分布的影响。

在气隙磁场的求解方法中，有限元数值计算方法可以准确计算出气隙磁场的分布波形，具有通用性强、适用于各种媒质的特点。

但其前处理过程复杂、计算时间较长，对使用者有较高的技术要求，在电机优化设计中不便采用。

解析方法可以较准确地计算气隙磁场分布波形，同时可以观察到气隙磁场分布与结构尺寸之间的关系，具有很大的工程实用价值。

文献[1]、[2]利用解析方法对气隙磁场进行计算，求解出气隙磁场的分布波形，但文中忽略了齿槽的影响。

文献[3]讨论了永磁电机中定子斜槽（或转子斜极）、永磁体磁化方式、气隙长度、转子半径和永磁体极弧系数对气隙磁场分布的影响，给出计算气隙磁场分布的经验公式，由此计算出相绕组反电动势变化波形，可是文中忽略了齿槽的影响，公式的通用性也较差。

Ansoft Maxwell参数化-脚本化-多核运算-快捷教程RMxprt、Maxwell、Workbench和Simplorer基础培训教程一、Maxwell 2D部分1、多核运算在工具栏中点击选项，进入HPC编辑界面，将核心数设置为电脑总核心数，任务数设置为所需调用的核心数，在作业分配中勾选瞬态求解器，即可看到CPU占用率的上升。

2、气隙多层设置根据之前的仿真对比，为了获得更好的结果精度和计算时间，建议将气隙分为四层。

1）在气隙中，将Band默认设置为中间层，在Band和转子之间画一个圆面circle1，在Band和定子之间画圆面circle2.2）选择中circle1、circle2、Band右键分配网格，给定长度，最大长度建议使用默认值的1/10.3）划分初始网格：右键分析-应用网格。

查看网格：全选模型，右键绘制网格。

根据效果可以修改网格长度。

重画之前需将上次的网格初始化：右键分析-恢复初始网格。

3、求解1）设置模型运动设置-机械，给定转速，如果考虑机械瞬态可以勾选，设置转矩、转子转动惯量、阻尼。

模拟启动可以将转矩设置为负载转矩，转速设置为0rpm，即从0rpm启动直到额定工况。

有时设置机械项会出现错误：时间分解方法不支持机械瞬态。

一般重新设置，或者重新检查分析或者关闭多核运算即可)。

2）设置求解时间步长。

通常情况下，点击0.2秒后会达到稳定状态，根据需求设置求解时间和精度。

4、参数化自动求解参照《Ansoft12在工程电磁场中的应用》一书，第九章内容并结合自己的经验。

对于任意输入的数值，都可以将该数值变为字母参数（部分单词在软件中已经有特定定义，如时间、功率等）。

例如，计算不同负载。

1）将运动设置负载设置为负载转矩输入T，单位改为Nm。

2）在优化分析中，右键添加参数，出现如下图对话框，点击添加。

于为什么会出现这种情况，具体原因需要进一步排查。

3、在右侧添加变量T，并更改变化参数，可以在Table 中查看参数扫描变化范围。

—98—工装设计基于Maxwell 通过傅里叶变换获取谐波幅值的方法张艳明（河北电机股份有限公司，河北 石家庄 051430）摘 要：在永磁电机的设计中，有限元软件的应用避不可少。

当使用有限元软件设计永磁电机时，如何获取空载反电动势、气隙磁密的谐波幅值是一个麻烦的问题。

本文使用了传统的傅里叶分析结合Maxwell 的自定义输出的方法，可以实现替代软件自带的快速傅里叶分析，相比与软件自带的FFT 功能，我们可以定义空载反电动势或气隙磁密的某次谐波为优化目标，通过使用参数话扫描、单目标优化和多目标优化的方法来优化谐波。

本文以功率35kW、最高转速6000rpm 永磁同步电机为例，对其空载反电动势分别使用Maxwell 自带快速傅里叶变换与本方法求取谐波幅值，从而计算空载反电动势的各谐波含量，通过将计算结果进行对比，证明了该方法的正确性。

关键词：永磁电机； 空载反电动势； 傅里叶变换；谐波引言永磁同步电机相比于与感应电机，具有高效率、高功率因数、体积小和重量轻等特点，利于节能减排。

然而在设计阶段，永磁电机的磁场较感应电机更为复杂，磁路计算无法满足电气设计的精度要求，必须使用有限元仿真软件（Maxwell ）来完成设计和优化。

如何降低反电动势、气隙磁密的谐波含量是电机设计人员冥思苦想需要解决的问题，因为反电动势和气隙磁密的总谐波含量（THD ）越低，一般该设计的铁耗、转矩脉动、齿槽转矩、nvh 等性能都会越好。

但在Maxwell 中，虽然可以通过使用FFT report 功能可以查询谐波含量，但无法将谐波含量做为优化目标，无法使用参数化扫描和优化工具来快速优化该目标, 设计周期长。

为此，本文提出了一种使用傅里叶变换的理论公式，对反电动势进行傅里叶变换，求取关键阶次谐波含量，可以结合参数化扫描和优化工具快速完成永磁电机的优化设计。

1 空载反电动势空载反电动势E 0是永磁同步电机非常重要的参数。

E 0是由电动机中永磁体产生的空载气隙基波磁通在电枢绕组中感应产生，其值为其中E 0—— 空载反电动势；f —— 电源频率；K dp —— 绕组系数；N —— 每相匝数； ——空载气隙磁通2傅里叶变换的公式高等数学中，以周期T 为周期的函数f(x)在区间内[-T/2,T/2]上满足狄利克雷条件，即在区间[-T/2,T/2]上；1连续或只有有限个第一类间断点；2只有有限个极限点，那么在[-T/2,T/2]上就可以展成傅里叶级数。

17 直流电机在用户已经掌握RMxprt 的基本使用的基础上，我们将一些过程简化，以便介绍一些更高级的使用。

有关RMxprt 的详细介绍请参考第一部分的章节。

17.1基本原理无论是直流发电机还是直流电动机，转子上都嵌有绕组，称为电枢绕组。

电枢绕组通过电刷和直流电源相连，电刷与换向器滑动连接。

当转子旋转时，电枢绕组在磁场中旋转并产生反电势。

定子上有P 对主磁极，主磁极由磁极铁心和套在上面的励磁绕组构成。

励磁绕组有并联和串联之分，励磁绕组在气隙中产生N 极和S 极交替排列的定子磁场。

并励绕组可以分为他励和自励两种，他励励磁绕组是由独立的直流电源供电，自励励磁绕组是由电枢绕组供电。

并励励磁绕组与电枢绕组并联，串励励磁绕组与电枢绕组串联。

对于复励型励磁绕组，RMxprt 假定电枢绕组先与串励励磁绕组串联，然后再与并励励磁绕组并联。

电刷组件与换向片始终保持接触，直流电经电刷和换向片流入旋转的电枢绕组时，产生了一个转子磁场。

由于换向器的机械整流作用，电枢绕组产生的转子磁场始终与定子磁场垂直。

定、转子磁场相互作用产生电磁力矩。

电枢电流产生的磁场称为电枢反应磁场，电枢反应磁场会导致换向不良。

为了消除由于电枢反应带来的磁场畸变，改善换向，可以在两个临近的主磁极间安装换向磁极和换向绕组，并在主磁极下安装补偿绕组。

直流电机的反电势，是由并励励磁电流反电势(E f )和串励励磁电流反电势(E s )合成。

如下式所示：ωωa es f ef s f I C I C E E E +=+= (17.1)式中的C ef 和C es 分别表示并励和串励绕组的反电势系数，与磁场的饱和程度有关，单位为ohm.s/rad ；ω表示转子的机械角速度，单位为rad/s ；I f 和I a 分别为并励励磁电流和串励励磁电流。

电磁转矩方程如下，是由并联励磁电流产生的电磁转矩(T f )和串联励磁电流产生的电磁转矩(T s )合成。

2ats a f tf s f m I C I I C T T T +=+= (17.2)式中的C tf 和C ts 表示并励和串励绕组的转矩系数，数值上与C ef 和C ss 分别相等，单位为Nm/A 2。

15 开关磁阻电机本章我们将简化RMxprt 一些基本操作的介绍，以便介绍一些更高级的使用。

有关RMxprt 基本操作的详细介绍请参考第一部分的章节。

15.1基本理论开关磁阻电机的定子和转子均为凸极结构，通常定子的极对数大于转子的极对数。

定子磁极上有多相集中绕组，转子上无绕组。

当定子上某（些）绕组通电时，由于磁阻的差异，转子将受到力矩的作用，转子磁极向与定子磁极对齐（磁阻最小）的位置转动，以使定子绕组获得最大的磁链。

绕组的相数是定子极数与定、转子极数的最小公约数之比。

在开关磁阻电动机(SRM)中，定子和转子的极数不同，转子上设有位置传感器，定子电流严格地根据转子的位置换向。

转子的位置信号通过位置传感器获得。

定子绕组按顺序触发，一般情况下当一相绕组电流关断或快要关断时，下一相绕组被触发。

因此可以忽略两相绕组间的相互影响。

一相的电压方程为： t i i R u u S T d ),(d θψ++= (15.1)式中u T 表示晶体管或二极管的压降，R S 表示定子绕组电阻。

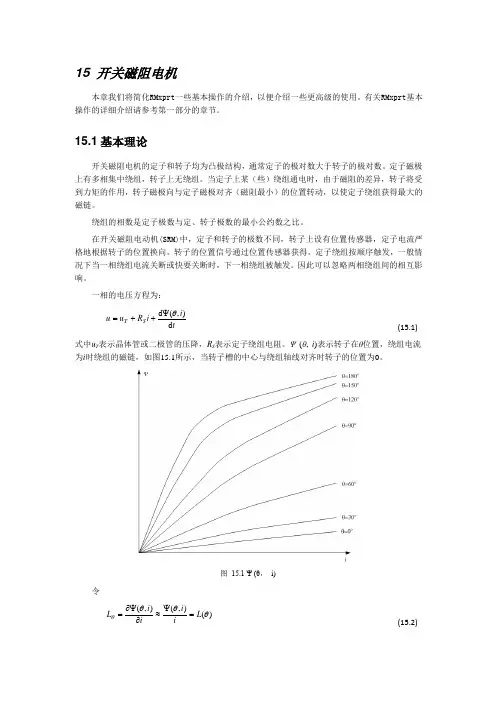
Ψ (θ, i )表示转子在θ位置，绕组电流为i 时绕组的磁链，如图15.1所示，当转子槽的中心与绕组轴线对齐时转子的位置为0。

图 15.1 Ψ (θ， i)令)(),(),(θθθθL i i i i L =ψ≈∂ψ∂= (15.2))(),(θθθθθG L i i 1G =∂∂≈∂ψ∂=(15.3)得出 i G i L i R u u e S T ωθ+++=p(15.4)式中ωe 表示转速，用电角度表示，微分算子为： t d dp = (15.5)瞬时电磁转矩t 2为：22Gi 21t = (15.6) 输入电功率可由电压和电流获得：⎰=T 1t ui T 1P 0d (15.7)输出的机械功率为：)(Fe t Cua fw 12P P P P P P +++-= (15.8) 式中P fw ，P Cua ，P t 和P Fe 分别表示摩擦和风损耗、电枢铜损耗、晶体管/二极管压降损耗和铁心损耗。

第54卷第3期2021年3月Vol.54.No.3Mae2021微电机MICROMOTORS直线电机不均匀气隙磁场解析计算方法刘思嘉，刘子锐(北京信息科技大学化学院，北京100192)摘要：直线感应电机运行时，其初级和次级之间可能因不平行而形成不均匀气隙，从而造成电机磁场分布变化。

对于这种不均匀气隙的电机磁场分布的计算，沿用 的基于均匀气隙的公式则会大。

为问题，首先基于电磁论，提出了一种不均匀气隙直线感应电机磁场的解析计算公式；其次线电机对解析公式进行；最后将解析公式计算结果与有限元方法计算得到的气隙磁场分布结果进行了对比％对比结果表明，这种 了气隙不均匀的解析磁场计算方法相气隙不均匀的计算，其平均小50%以上，为直线感应电机的设计和控制效果的提升提供了一种有益的％关键词：直线感应电机；不均匀气隙；磁析计算；有限元中图分类号：TM359.4文献标志码：A文章编号：1001-6848(2021)03-0041-05An Analytical Calculation Method of Flux Density for Uneven Air-gapLinear Induction MotorLIUSojoa，LIU Zoeu o(School of Automation,，Beijing Information of Science&Technology Unnersity，Beijing100192，China)Abstract:The linear induction motor(LIM)may lead to an uneven air-cap bWwwn its pamda and second-o/duang operation.This uneven air-cap will bring the vvriation of flux distribution in the LIM.The tradi­tional calculation method for electric machine flux will enhanco ewor when not consideang the uneven air­gap.Aiming to this problem，this paper firstly presented an analytic calculating metOod of the flux density based on MaxwWl's th—a，secondly provided a correction method consideang the uniqueness of LIM，final­ly compared Oie results with the results of th/inite element mwliod(FEM).The compaason Olustrates that the analytic method reduces the calculation wroe over50%Oian the calculation without consideang the une­ven air-cap.This method provides a useful afeanco for the future design and conOol of LIMs.Key wo—t:linear induction motor；uneven air-cap；analytical lux calculation；finite element methodo引言长期以来，直线感应电机(Linear Induction Mo-tvr，LIM)在轨道交得到大量关注，在国内外有大量的工程应用。

Maxwell使用要点2022-3-26一、安装不要采用中文文件夹。

二、Ma某well环境内建模1、在Ma某well环境内只能画直线、圆弧、圆等简单形状。

2、由线构造面（1）构成面域的多个线段须闭合，形成面域的边界闭合边界（2）如果该闭合边界的线段是由多个线段组成，则须线合并成一体，然后转换成面域。

合并成一体：选中所有线段ModelerBooleanUnite 转换成面域：选中所有线段ModelerSurfaceCoverLine由多个线段构成Unite成一体Cover成面域三、AutoCAD建模后导入Ma某well1、在AutoCAD建模时，定转子圆心应取（0,0）点。

如果模型不在（0,0）点，应采用带基点复制的方法，将模型的圆心移至（0,0）。

2、各个面域须自行封闭。

3、模型转换成面域。

建模时，须保证构成面域的边界是可靠连接的。

然后绘图面域，选择模型，按回车键，将所绘制的模型转换成面域。

转换成面域后，可以通过鼠标移动，删除、Undo，来检查模型的正确性。

4、输出.at格式模型文件文件输出，选择ACIS(某.at)文件类型，取合适的文件名，点击“保存”，框选要输出的模型，回车。

此时.at文件已经保存，可以在相应文件夹找到.at文件。

5、将.at模型导入Ma某wellModelerImport，找到已输出的.at文件，点击“打开”，则可输入有限元模型。

6、有限元模型可以一次性建模输入，也可以将各零件分别建模、转换.at、分别输入。

四、Ma某well前处理及求解设置1、选择模型的每一面域，修改其名称和颜色。

首先需正确对绕组分相2、将属于同一类的面域合并，以便施加励磁、材料，提高工作效率。

按住Ctrl键，选中需要合并的各个面域，ModelerBooleanUnite3、建立磁钢、冲片等材料。

（1）准备磁钢材料的Br、Hc，冲片材料的B-H曲线。

B-H曲线宜用记事本等编辑器，按要求的格式，输入磁化曲线数据，保存为.bh后缀名文件。

气隙储能计算公式气隙储能是在电磁学领域中一个比较专业的概念，咱们要弄清楚气隙储能计算公式，得先从一些基础的知识说起。

我记得有一次在实验室里，我和学生们一起研究一个电磁装置。

当时，大家都对其中的气隙部分充满了好奇。

那是一个小小的气隙，却藏着大大的能量秘密。

咱们先来说说气隙储能到底是啥。

简单来讲，气隙就像是一个能量的小仓库。

当电流通过电磁装置时，一部分能量就会存储在这个气隙里面。

这就好比你把钱存到银行里，气隙就是那个存钱的地方。

那气隙储能的计算公式是啥呢？一般来说，气隙储能的计算公式是：$W = \frac{1}{2}\mu_0 H^2 V$ 。

这里面的 $\mu_0$ 是真空磁导率，是个固定的值，就像咱们的身份证号码一样，不会变。

$H$ 是磁场强度，$V$ 是气隙的体积。

比如说，咱们有一个气隙，它的磁场强度是 100 安/米，体积是 0.01 立方米，真空磁导率约为4π×10⁻⁷亨利/米。

那咱们来算算这个气隙能存多少能量。

先把数值代入公式：$W = \frac{1}{2}× 4π×10⁻⁷ × 100^2 × 0.01$ 。

经过计算，就能得出这个气隙存储的能量啦。

在实际应用中，这个计算公式可重要啦。

就像工程师设计电机的时候，得算清楚气隙能存多少能量，才能保证电机正常工作，不会出问题。

再回到咱们开头说的那个实验室的事儿。

学生们一开始对这些公式和概念都有点迷糊，我就带着他们一步一步地推导，一步一步地计算。

看着他们从满脸疑惑到恍然大悟的表情，我心里那叫一个高兴。

气隙储能计算公式虽然看起来有点复杂，但只要咱们耐心去理解，多做几道题，多实践几次，就能把它掌握得妥妥的。

所以说，不管是在学习还是在实际工作中，遇到像气隙储能计算公式这样的难题，别害怕，别退缩，咱们一步步来，总能搞明白的！就像在黑暗中摸索，只要坚持，总会找到那盏明灯。