实验2分类预测模型-支持向量机

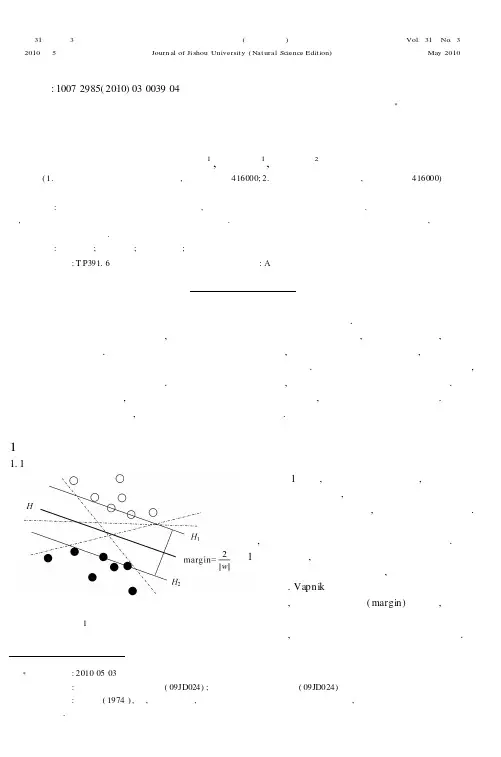
第31卷第3期吉首大学学报(自然科学版)Vol.31No .32010年5月Journ al of Ji shou Universit y (Nat ural Science Edit ion)May 2010文章编号:10072985(2010)03003904支持向量机下机器学习模型的分析*李海1,李春来1,侯德艳2(1.吉首大学数学与计算机科学学院,湖南吉首416000;2.湘西民族职业技术学院,湖南吉首416000)摘要:首先概述了支持向量机的发展与应用,指出其在机器学习领域有较大的发展前景.分析了支持向量机的基本算法,进而阐述了基于支持向量机的机器学习模型构造思路.给出了其应用于机器学习模型的核函数和训练算法,最后给出了学习模型的具体分类效果.关键词:机器学习;人工智能;支持向量机;模式识别中图分类号:T P391.6文献标志码:A学术界普遍认为支持向量机算法是继神经网络之后的一个新的研究方向.该项研究属于机器学习、模式识别和人工神经网络等多个学科,由于它与这些学科现有的理论和方法相比,有明显的优越性,因此有重大的潜在应用价值.支持向量机是根据结构风险最小化原则,尽量提高学习机的泛化能力,即由有限的训练样本得到的小的误差能够保证对独立的测试集仍保持小的误差.支持向量机算法是一个凸优化问题,因此局部最优解一定是全局最优解.这些特点是其他学习算法,如人工神经网络学习算法所不及的.虽然支持向量机发展时间很短,但是由于它的产生是基于统计学习理论的,因此具有坚实的理论基础.近几年涌现出的大量理论研究成果,更为其应用研究奠定了坚实基础.1支持向量机的学习理论1.1支持向量机的基本算法图1多种分类超平面示意图如图1所示,在线性可分的情况下,可以有多种选择去分类训练数据,但明显最黑的实线所代表的超平面具有更强的泛化性能,因此其分类效果更好.传统的分类方法会随机产生一个超平面并不断移动它,最终停留在使其分类错误率最小的位置上.如图1中的虚实线,这种处理方式造成的问题是训练样本可能会非常接近分类超平面,从而使得分类的推广性不强.Vapnik 提出的支持矢量机方法为了解决这一问题,引入了分类间隔(margin)的概念,从而使结构风险最小化问题变成了寻找一个既能满足分类精度要求,又有最大分类间隔的最优分类超平面.前*收稿日期:20100503基金项目湖南省教育厅重点项目(D );吉首大学校级课题资助(D )作者简介李海(),男,湖南益阳人,吉首大学数学与计算机科学学院实验师,主要从事计算机人工智能与算法研究:09J 02409J 024:1974.者能保证经验风险最小,而分类间隔最大则是为了使推广性的界的置信范围最小,从而使结构风险达到最小.[12]m 个训练样本(x 1,y 1),(x 2,y 2),,(x m ,y m )要求一个分类超平面,关键是求系数w 和b 由于支持向量机理论要求分离超平面具有良好的性质,即离超平面具有分类误差小、推广能力强的特点,这样分类超平面必须满足如下最优分类超平面的条件:y i [(w x i )+b ]!1i =1,2,,m,min w(w)=w 2.为了找到最优分类超平面,根据最优化理论,借助Lagrange 函数将原问题转化成求解标准型二次规划问题:max W()=#m i=1i -12#m i,j=1i j y i y j K (x i ,x j )s.t.#m i =1i y i =0,i !0i =1,2,,m.求最优超平面的关键在于求出i >0的以及b 0=12(K (w 0,x(1))+K(w 0,x(-1))).最优分类超平面为f (x)=sign{#i >0i y i K (x i ,x)-b 0}.通常i >0对应的样本点为支持向量.1.2支持向量机的机器学习基于数据的机器学习理论主要研究如何从一些观测数据中得出目前尚不能通过原理分析得到的规律,利用这些规律去分析客观对象,对未来数据或无法观测的数据进行预测.它的主要目的是根据给定的训练样本求出对某系统输入输出之间依赖关系的估计,使它能够对未知输出作出尽可能准确的模拟和预测.设未知系统的输入输出数据集为{(x 1,y 1),(x 2,y 2),,(x n ,y n )},且x 和y 之间通过系统存在某种依赖关系,即遵循某一联合概率P (x,y).机器学习问题就是根据n 个独立同分布的数据样本,在一组函数{f (x ,w)}中求一个最优的函数f (x,w 0)来对y 与x 之间的依赖关系进行估计,并使预测的期望风险最小:R e xp (w)=L(y,f (x,w))dP (x,y).2向量机下机器学习模型的思路图2二类SVM 分类问题及解决思路支持向量机SVM 算法主要的目标是找到一个超平面,使得它能够尽可能多地将2类数据集正确的分开,同时使分开的2类数据点距离分类面最远.针对训练样本集为线性、非线性2种情况分别讨论,并且将非线性分类问题转化为线性分类问题加以解决.图2给出了二类SVM 分类问题及解决思路的框图.已知n 个训练样本(x 1,y 1),(x 2,y 2),,(x n ,y n ),由数据样本向量x i %R n 和相应的数据样本的类别y i %Y(1,,c)组成.实现线性分类器就是要实现如下功能:训练出二元分类器(c =2的情况)的分类超平面,训练出最优化超平面.要实现零出错率的二元分类器(c =2的情况)就是要找到超平面f (x)=(!x )+b=0,这个超平面能够分离出2类数据集,第1类y =1,第2类y = 2.这个问题可以描述为(!x)+!,y =,(!x)+<,y =,(),其中!%R 是一个向量,%R 是一个标量如果能找到()式的解,那么这个训练数据集是线性可分的40吉首大学学报(自然科学版)第31卷b 01b 021n b .1.通过使用核函数,允许对非线性可分的数据集使用在线性特征空间中提取的方法.在非线性可分的情况下将向量x %R n 映射到一个高维的特征空间F 中,在这个高维特征空间中,线性的方法仍然能够使用.一个非线性数据映射可以定义为z =A T k(x)+b ,其中A(l &m)是一个矩阵参数,b %R m 是一个向量参数,向量k(x)=(k(x,x 1),,k(x,x l ))T 是核函数向量数据的核心,或者说是一个子集x %R n 是一个输入向量,z %R n 是经过映射的向量,是通过映射(x)将向量从特征空间F 映射为m 空间中的向量.[3]3支持向量机的核函数支持向量机的一个引人注目的特点是用满足Mer cer 条件的核函数代替向量间的内积运算来实现非线性变换,而不需要非线性的具体形式.研究人员根据这一思想改造经典的线性算法并构造出对应的基于核函数的非线性形式.支持向量机模型最重要的一个参数就是核函数.选择什么样的核函数,就意味着将训练样本映射到什么样的空间去进行线性划分.支持向量机算法的技巧在于不直接计算复杂的非线性变换,而是计算非线性变换的点积,即核函数,从而大大简化了计算.通过将核函数引入到一些学习算法,可以方便地将线性算法转换为非线性算法,笔者将其与支持向量机一起称为基于核函数的方法.在高维特征空间实际上只需要进行点积运算,可以用原空间中的函数实现得到,甚至没有必要知道变换的形式.根据泛函的有关理论,只要一种核函数K (x,x i )满足Mercer 条件,它就对应某一变换空间中的点积.因此,在最优分类面中采用适当的点积函数K (x,x i )就可以实现某一非线性变换后的线性分类,而计算复杂度却没有增加.张铃证明了核函数存在性定理,并提出了寻找核函数的算法.核函数存在性定理表明:给定1个训练样本集,就一定存在1个相应的函数,训练样本通过该函数映射到高维特征空间的相是线性可分的.[4]张铃进一步研究了支持向量机的支持向量集与核函数的关系,研究表明对非线性可分的情况,对一个特定的核函数,给定的样本集中的任意一个样本都可能成为一个支持向量.这意味着在1个支持向量机下观察到的特征在其他支持向量机下(其他核函数)并不能保持.因此,对解决具体问题来说,选择合适的核函数是很重要的.SVM 由训练样本集和核函数完全描述,因此采用不同的核函数就可以构造实现输入空间中不同类型的非线性决策面的学习机,导致不同的支持向量算法.文中主要应用到线性内核K (x i ,x j )=x i x j .4支持向量机的训练算法这里应用二类分类问题的支持向量机的训练算法序列最小优化(SMO)算法.SMO 方法是一种简单的算法,它能快速地解SVM 的二次规划问题.按照Osuna 的理论,在保证收敛的情况下,将SVM 的二次规划问题分解成一系列子问题来解决.和其他算法相比,SMO 方法在每一步选择一个最小的优化问题来解,对标准的SVM 优化问题来说,最小的优化问题就是只有2个拉格朗日乘子的优化问题.在每一步,SMO 方法选择2个拉格朗日乘子进行优化,然后更新SVM 以反映新的优化值.SMO 方法的优点在于,优化问题只有2个拉格朗日乘子,它用分析的方法即可解出,从而完全避免了复杂的数值解法;另外,它根本不需要巨大的矩阵存储,这样,即使是很大的SVM 学习问题,也可在PC 机上实现.SMO 方法包括2个步骤:一是用分析的方法解一个简单的优化问题,二是选择待优化的拉格朗日乘子的策略.SMO 解出只有2个乘子的问题后,在每一步更新拉格朗日乘子.为了加快收敛,SMO 用如下的策略选择拉格朗日乘子:对2个拉格朗日乘子分别采用不同的策略,第1个乘子的选择,在SMO 算法中通过外层的一个循环实现.外层循环在整个训练集上搜索,决定是否每一个样本都满足KKT 条件,如果有1个不满足KKT 条件,那么它就被选择进行优化.训练集中的样本都满足上述条件后,再检查训练集中的所有位于边界的样本来进行第个乘子的选择,SMO 选择是使目标函数值最小的乘子作为第个乘子进行优化如果这种方法失败,那么SMO 在所有的非边界样本上进行搜索,寻找能使目标函数值最小的乘子;若这种方法也失败,则在整个训练集上搜索,寻找使目标函数值最小的乘子41第3期李海,等:支持向量机下机器学习模型的分析22..5支持向量机的机器学习模型的实现装载数据后显示如图3所示.数据集线性可分的情况下,使用SMO 算法的分类结果如图4所示.图3支持向量机机器学习模型图4SMO 训练算法和线性核函数的分类6结语支持向量机是基于统计学习理论的新一代学习机器,具有很多吸引人的特点,它在函数表达能力、推广能力和学习效率上都要优于传统的人工神经网络,在实际应用中也解决了许多问题.鉴于支持向量机扎实的理论基础,并且和传统的降维方法相反,SVM 通过提高数据的维度将非线性分类问题转换成线性分类问题,较好地解决了传统算法中训练集误差最小而测试集误差仍较大的问题,算法的效率和精度都比较高.所以近年来该方法成为构造数据挖掘分类器的一项新型技术,在分类和回归模型中得到了很好的应用.参考文献:[1]VAPNIK V N.The Nat ur e of Statistical Lear ning [M].Ber lin:Spr inger,1995.[2]VAPNIK V N.Statistical Lear ning Theor y [M].New Nor k:John Wiley&Son,1998.[3]谭东宁,谭东汉.小样本机器学习理论:统计学习理论[J].南京理工大学学报:自然科学,2001(1):108112.[4]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000(1):3646.Analysis of Machine Learning Model Based on S upport Vector MachineLI H ai 1,LI Chun lai 1,H OU De yan 2(1.College of Mathematics and Computer Science,Jishou Univer sity,Jishou 416000,Hunan China;2.XiangxiVocational and Technical College for Nationalities,Jishou 416000,H unan China)Abstr act:The development of suppor t vector machines (SVM)is firstly summarized.Its application in machine learning has great pr ospects.T he basic SVM algorithm is analyzed,and the ideas of constructing machine learning based on SVM are presented.The kernel function and tr aining algor ithm of applying SVM in the machine learning model are put stly,the classifying effect of the learning model is shown.Key words:machine learning;artificial intelligence;support vector machine;pattern recognition(责任编辑向阳洁)42吉首大学学报(自然科学版)第31卷。

基于最小二乘支持向量机的短期负荷预测模型作者：张宁,许承权,薛小铃,郑宗华来源：《现代电子技术》2010年第18期摘要:支持向量机(SVM)是近年来发展起来的机器学习的新方法,它较好地解决了小样本、非线性、高维数、局部极小点等实际问题。

研究了支持向量机的拓展算法——最小二乘支持向量机(LSSVM),并将其应用于电力系统短期负荷时间序列预测。

通过实例并与神经网络模型预测结果相比较表明,LSSVM模型的预测精度要明显高于神经网络模型,验证了LSSVM模型可以很好地应用于短期负荷时间序列预测,并且具有较高的准确性与有效性,这为短期负荷预测提供了一个新的解决思路。

关键词:最小二乘支持向量机; 神经网络; 短期负荷预测;时间序列预测中图分类号:TN715-34文献标识码:A文章编号:1004-373X(2010)18-0131-03Short-term Load Forecasting Model Based on Least Square Support Vector MachineZHANG Ning1, XU Cheng-quan2, Xue Xiao-ling1, ZHENG Zong-hua1(1. Department of Physics & Electronic Information, Minjiang University, Fuzhou 350108, China;2. Department of Geograpgy, Minjiang University, Fuzhou 350108, China)Abstract: Support vector machine (SVM) is a novel machine learning method, which is powerful for solving the problems characterized by small samples, nonlinearity, high dimension, local minima, and other practical problems. The extension algorithm of the support vector mac hine-least squares support vector machine(LSSVM) is studied and applied to the time series forecasting of short-term load in power system. Compared with the predicting outcomings of the neural network model through some examples, the result shows that the forecast accuracy of LSSVM model is higher than that of neural network model, and verifies LSSVM model can apply effectively to short-term load forecasting. This provides a new resolution for short-term load forecasting .Keywords:least square support vector machine; neural network; short-term load prediction; time-sequence forcasting0 引言短期负荷预测是电力系统的重要工作之一。

《基于支持向量机的金融时间序列分析预测算法研究》篇一一、引言随着科技的发展，金融领域已经发生了深刻的变革。

特别是在金融市场预测和风险评估方面，如何准确地捕捉和分析金融时间序列数据成为了关键。

支持向量机（SVM）作为一种有效的机器学习算法，在金融时间序列分析预测中得到了广泛的应用。

本文旨在研究基于支持向量机的金融时间序列分析预测算法，以期为金融市场的预测和决策提供理论支持。

二、支持向量机概述支持向量机（SVM）是一种基于统计学习理论的机器学习方法，其核心思想是将数据映射到高维空间中，并通过最大化不同类别数据点之间的间隔来找到一个最佳分类超平面。

在金融时间序列分析中，SVM能够有效地捕捉到数据的非线性特征和动态变化，对未来的走势进行预测。

三、金融时间序列的特点金融时间序列数据具有复杂的非线性、波动性等特点。

与一般的数据相比，金融时间序列的变动具有很大的不确定性和难以预测性。

此外，金融市场受到政策、经济等多重因素的影响，导致金融时间序列数据的复杂性更加突出。

因此，对于金融时间序列的分析和预测需要采用更加先进的算法和技术。

四、基于支持向量机的金融时间序列分析预测算法针对金融时间序列的特点，本文提出了一种基于支持向量机的金融时间序列分析预测算法。

该算法主要包括以下几个步骤：1. 数据预处理：对原始的金融时间序列数据进行清洗和预处理，包括去除异常值、填充缺失值等操作。

2. 特征提取：根据金融时间序列的特点，提取出重要的特征信息，如价格、成交量等。

3. 模型构建：采用支持向量机算法构建分类或回归模型，对未来的走势进行预测。

4. 模型评估：通过交叉验证等方法对模型进行评估和优化，提高模型的预测精度和泛化能力。

五、实验与分析本文采用某股票市场的历史交易数据进行了实验和分析。

首先，对数据进行预处理和特征提取；然后，构建基于支持向量机的分类和回归模型；最后，对模型进行评估和优化。

实验结果表明，基于支持向量机的金融时间序列分析预测算法在股票市场走势的预测中具有较高的准确性和泛化能力。

基于贝叶斯网络和支持向量机的网络安全态势评估和预测方法研究网络安全一直都是人们关注的热点问题，这是因为随着计算机网络技术的不断发展，网络安全面临的威胁也随之增多。

为了保障网络安全，提高网络安全防御能力，学者们进行了大量的研究，提出了很多关于网络安全态势评估和预测的方法，而本文通过研究贝叶斯网络和支持向量机，提出一种新的网络安全态势评估和预测方法，以提升网络安全防御能力和保护网络安全。

一、贝叶斯网络1.1 贝叶斯网络概述贝叶斯网络是一种图模型，用于描述多个变量之间的依赖关系。

它是由有向无环图(DAG)和与每个节点相关联的概率表所组成的。

贝叶斯网络包含多个节点，每个节点表示一个变量，节点之间的有向边表示变量之间的依赖关系。

1.2 贝叶斯网络在网络安全中的应用贝叶斯网络已经在网络安全中得到了广泛的应用，它可以用来描述网络中的攻击路径、协议行为、恶意代码行为和用户行为，从而帮助网络管理员及时发现并解决网络安全问题。

例如，在入侵检测中，贝叶斯网络可以结合统计分析和机器学习的方法，通过对网络流量数据的分析，发现异常流量和攻击行为，从而提高网络攻击检测的准确性。

二、支持向量机2.1 支持向量机概述支持向量机(Support Vector Machine, SVM)是一种统计学习方法，属于有监督学习范畴。

它的主要思想是将特征空间映射到高维空间，从而在高维空间中找到最大间隔的超平面，用于区分不同的类别。

2.2 支持向量机在网络安全中的应用支持向量机已经广泛应用于网络安全领域，主要用来解决网络流量分类和入侵检测的问题。

通过对网络流量中的特征进行分析，构建分类模型，利用支持向量机的识别性能，实现对恶意流量的判别和隔离。

三、基于贝叶斯网络和支持向量机的网络安全态势评估和预测方法网络安全态势评估和预测主要是对网络中的威胁进行分析和预警，从而提前采取适当的措施保障网络安全。

本文通过分析贝叶斯网络和支持向量机的优缺点，提出了基于贝叶斯网络和支持向量机的网络安全态势评估和预测方法。

基于支持向量机的矿震危险性预测摘要：本文研究了基于支持向量机（SVM）的矿震危险性预测方法。

首先，它介绍了用于预测目标变量的SVM理论背景知识，并讨论了实验数据集特征选择过程。

其次，本文基于SVM对不同数据集进行了矿震危险性预测，并与传统的朴素贝叶斯（NB）分类器进行了比较。

最后，通过对实验结果的分析，我们发现，使用SVM预测结果比NBY更准确，有效地预测了矿震危险性。

关键词：支持向量机，矿震危险性，预测，朴素贝叶斯正文：矿震危险性预测是用来估计未来矿震活动性和破坏性的一种重要方法。

近年来，随着新技术和大数据技术的发展，如机器学习、人工智能和传感器技术，准确地预测矿震危险性变得更加重要。

在本文中，我们将探讨基于支持向量机（SVM）的矿震危险性预测方法。

首先，我们提供了关于SVM的理论背景知识，包括其基本原理、核函数和实现技术，用于预测矿震危险性的目标变量。

其次，我们讨论了实验数据集的特征选择过程，并使用对象关系图（ORG）模型对数据集进行了分析和可视化。

然后，我们基于SVM算法，将实验数据集分成训练集和测试集，并使用模型训练和评估来预测矿震危险性。

最后，基于SVM和朴素贝叶斯（NB）分类器的实验结果的分析表明，使用SVM模型对于矿震危险性的预测准确率更高。

本文中所提出的SVM-based预测方法有助于准确预测矿震危险性，为未来矿震预警提供了重要依据。

接下来，本文将展示准确预测矿震危险性的一些其他方法，例如神经网络（NN）、深度学习（DL）和关联规则挖掘（ARM）。

NN是使用人工神经元建立数学模型的算法，可用于从已知数据中学习和推理。

这种学习方法在分类、回归和其他特定任务上表现出色，对矿震危险性预测也有重要作用。

另一方面，DL算法利用多层神经网络，旨在从原始数据中识别模式，以及模拟真实世界中的函数映射。

随着这种算法的不断完善，它正在变得越来越有用，可以用于众多领域的机器学习应用，包括矿震危险性预测。

机器学习算法分类是否在⼈类监督下进⾏训练（监督，⽆监督和强化学习）在机器学习中，⽆监督学习就是聚类，事先不知道样本的类别，通过某种办法，把相似的样本放在⼀起归位⼀类；⽽监督型学习就是有训练样本，带有属性标签，也可以理解成样本有输⼊有输出。

所有的回归算法和分类算法都属于监督学习。

回归和分类的算法区别在于输出变量的类型，定量输出称为回归，或者说是连续变量预测；定性输出称为分类，或者说是离散变量预测。

分类KNN向量机SVC朴素贝叶斯决策树DecisionTreeClassifier随机森林RandomForestClassifier逻辑回归--》softmax回归回归线性回归--》岭回归 lasso回归向量机SVR决策树DecisionTreeRegressor随机森林回归RandomForestClassifier⼀. K-近邻算法（k-Nearest Neighbors，KNN）（分类）K-近邻是⼀种分类算法，其思路是：如果⼀个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的⼤多数属于某⼀个类别，则该样本也属于这个类别。

⼆．⽀持向量机SVM（可分类，可回归）在 SVM 中，选择⼀个超平⾯，它能最好地将输⼊变量空间划分为不同的类，要么是 0，要么是 1。

在 2 维情况下，可以将它看做⼀根线。

三．朴素贝叶斯（Naive Bayesian）（分类）计算参考：四. 线性回归算法 Linear Regression（回归）线性回归就是根据已知数据集求⼀线性函数，使其尽可能拟合数据，让损失函数最⼩，常⽤的线性回归最优法有最⼩⼆乘法和梯度下降法。

线性回归⼜分为两种类型，即简单线性回归（simple linear regression)，只有 1 个⾃变量；多变量回归（multiple regression)，⾄少两组以上⾃变量。

岭回归（也称为 Tikhonov 正则化）是线性回归的正则化版：在损失函数上直接加上⼀个正则项。

第1篇一、实验背景随着计算机科学、人工智能、大数据等领域的快速发展，智能计算技术逐渐成为当前研究的热点。

为了更好地掌握智能计算的基本原理和应用，我们进行了为期两周的智能计算实验。

本次实验旨在让学生通过实践操作，加深对智能计算理论知识的理解，提高解决实际问题的能力。

二、实验内容1. 实验环境本次实验所使用的软件平台为Python，主要利用NumPy、Pandas、Scikit-learn等库进行智能计算实验。

硬件环境为个人计算机，操作系统为Windows或Linux。

2. 实验步骤（1）数据预处理数据预处理是智能计算实验的第一步，主要包括数据清洗、数据集成、数据转换等。

通过NumPy和Pandas库对实验数据进行预处理，为后续的智能计算模型提供高质量的数据。

（2）特征工程特征工程是智能计算实验的关键环节，通过对原始数据进行降维、特征选择等操作，提高模型的预测性能。

本实验采用特征选择方法，利用Scikit-learn库实现。

（3）模型选择与训练根据实验需求，选择合适的智能计算模型进行训练。

本次实验主要涉及以下模型：1）线性回归模型：通过线性回归模型对实验数据进行预测，分析模型的拟合效果。

2）支持向量机（SVM）模型：利用SVM模型对实验数据进行分类，分析模型的分类性能。

3）决策树模型：采用决策树模型对实验数据进行预测，分析模型的预测性能。

4）神经网络模型：使用神经网络模型对实验数据进行分类，分析模型的分类性能。

（4）模型评估与优化对训练好的模型进行评估，根据评估结果对模型进行优化。

主要采用以下方法：1）交叉验证：利用交叉验证方法评估模型的泛化能力。

2）参数调整：通过调整模型参数，提高模型的预测性能。

3）特征选择：根据模型评估结果，重新进行特征选择，进一步提高模型的性能。

三、实验结果与分析1. 数据预处理经过数据清洗、数据集成、数据转换等操作，实验数据的质量得到了显著提高。

预处理后的数据满足后续智能计算模型的需求。

基于支持向量机的地区电网短期负荷预测模型研究摘要：支持向量机是一种针对分类和回归问题的统计学习理论，是一类基于结构风险最小化原则的新型机器学习算法。

其基本思想是通过用内积函数定义的非线性变换将输入空间变换到一个高维空间，在这个高维空间中寻求输入变量和输出变量之间的非线性关系的精确描述。

本文构造了基于支持向量机的地区电网短期负荷预测模型，该模型具有较好的泛化性和收敛性。

通过对实际电网负荷的预测仿真和测试，证实所提出的预测模型能获得满意的预测精度。

关键词：电力系统支持向量机短期负荷预测中图分类号：tm715 文献标识码：a 文章编号：1674-098x(2011)12(c)-0000-00电力系统短期负荷预测是电力系统调度部门的一项重要日常工作，是制订购电计划和安排运行方式的主要依据，其预测精度的高低直接影响到电力系统的安全性和经济性[1]。

在短期负荷预测研究的早期，时间序列法、回归分析法、灰色理论[2]等传统预测方法得到研究与应用，但由于电力负荷非线性强，使得这些方法难以模拟复杂多变的电力负荷，预测精度不理想。

近年来，随着智能技术的不断发展，专家系统、模糊逻辑、神经网络[3-4]等智能方法被广泛应用于电力系统的短期负荷预测中。

支持向量机(support vector machine svm )是一种针对分类和回归问题的统计学习理论，是一类基于结构风险最小化原则的新型机器学习算法。

其基本思想是通过用内积函数定义的非线性变换将输入空间变换到一个高维空间，在这个高维空间中寻求输入变量和输出变量之间的非线性关系的精确描述。

核心问题是寻找一种归纳原则以实现最小化风险泛函，得到最佳的推广能力[5]。

本文构造了基于svm的地区电网短期负荷预测模型，模型具有较好的泛化性和收敛性。

通过对实际电网负荷的预测仿真和测试，证实所提出的预测模型能获得满意的预测精度。

1 svm预测模型依据支持向量机理论，构造了svm子模型。