数字电子技术 (黄瑞祥 著) 浙江大学出版社 课后答案3
- 格式:pdf
- 大小:419.18 KB
- 文档页数:17

第1章 数字电路基础1.1 (1001010)2=1×26+1×23+1×21=(74)10(111001)2=1×25+1×24+1×23+1×20=(57)10 1.2 (54)10=(110110)2 (47)10=(101111)2 5427 13 6 3 1 01……MSB 10 1 1 0……LSB2 4723 11 5 2 1 01……MSB 01 1 1 1……LSB1.3 (58A)16 =(0101 1000 1010)2=1×210+1×28+1×27+1×23+1×21=1024+256+128+10=(1418)10或(58A)16=5×162+8×161+10×160=(1418)10 (CE)16 =(1100 1110)2=27+26+14=128+64+14=(206)10 =(0010 0000 0110)8421BCD 1.4 a 1.5 c 1.6 c 1.7 (×) 1.8 (×) 1.9 (√)1.10 ① 数字信号:在幅值上,时间上离散的(间断的、不连续的脉冲)信号. ② 数字电路:产生、处理、传输、变换数字信号的电路称为数字电路.③ 数字电路的特点:a )电路处于开关状态. 与二进制信号要求相一致,这两个状态分别用0和1两个数码表示;b )数字电路的精度要求不高,只要能区分出两种状态就可以;c )数字电路研究的问题是逻辑问题,一为逻辑分析,是确认给定逻辑电路的功能,二为逻辑设计,是找到满足功能要求的逻辑电路;d )研究数字电路的方法是逻辑分析方法,其主要工具是逻辑代数.有代数法和卡诺图法等;e )数字电路能进行逻辑运算、推理、判断,也能进行算术运算.算术运算也是通过逻辑运算实现的.1.11 ① 位置计数法:将表示数值的数码从左到右按顺序排列起来.它有三个要素a )基数R ,是指相邻位的进位关系,十进制R =10,即逢十进一,二进制R =2,即逢二进一.b )数码:表示数字的符号,十进制k i 从0~9共十个.二进制k i 是0和1,十六进制k i 从0~9~A~F 共十六个.c )位权:数码处于不同位置代表不同的位权,用R i表示.以小数点前从右到左为i 的位号分别为0、1、2、3…,小数点后从左到右i 的位号从–1,–2,–3…来确定R i.② 按权展开式是将任何进制数表示为十进制数值公式,是系数乘位权的集合,即(N )10=i i i k R ∞=-∞⨯∑. 1.12 ① (3027)10=3×103+2×101+7×100② (827)=8×102+2×101+7×100③ (1001)2=1×23+1×20④ (11101)2=1×24+1×23+1×22+1×20⑤ (273)16=2×162+7×161+3×160⑥ (4B5)16=4×162+11×161+5×1601.13 ① (6)10=(110)2② (13)=(1101)2 ③ (39)10=(100111)2 ④ (47)10=(101111)2 1.14 ① (1011)2=(11)10② (110101)2=(53)10③ (4A)16=4×161+10×160=(74)10④ (37)16 =3×161+7×160=(55)101.15 ① (1010 1101)2=(010 101 101)2=(255)8=(1010 1101)2=(AD)16② (100101011)2=(100 101 011)2=(453)8 =(0001 0010 1011)2=(12B)16 ③ ()2=(010 110 001 010)2=(2612)8 =(0101 1000 1010)2=(58A)16 1.16 ① (78)16=(0111 1000)2=(1111000)2 ② (EC)16=(1110 1100)2=(1110 1100)2 ③ (274)16=(0010 0111 0100)2=(1001110100)2注:从1.15~1.16均用分组方法,即二进制3位一组可表示1位八进制数;二进制4位一组可表示1位十六进制数.1.17 A =(1011010)2;B =(101111)2; C =(1010100)2;D =(110)2 (1)① A +B =(10001001)2② A –B =(101011)2 1011010 + 101111 100010011011010 – 101111 101011 ③ C ×D =(111111000)2④ C ÷D =(1110)2 1010100× 110 0000000 1010100 + 1010100 1111110001110 110 1010100 110 1001 110 0110110 0(2)A=(1011010)2=(90)10B=(101111)2=(47)10①A+B=(137)10=(10001001)2②A–B=(43)10=(101011)2C=(1010100)2=(84)10D=(110)2=(6)10③C×D=(504)10=(111111000)2这说明十进制四则运算的法则在二进制四则运算中也完全适用,对其它进制也一样.1.18 ① [0]8421BCD=(238)10② [10001]8421BCD=(7951)10③ [0]8421BCD=(640)101.19 ①逻辑函数:反映因果关系的二值逻辑表达式.原因(条件)为逻辑自变量,结果为逻辑因变量,它们都只有两种状态0和1,用以反映存在不存在,成立不成立,所以它们之间的关系称为(二值)逻辑函数.②与逻辑:表明所有的条件都具备结果才会发生这样的基本逻辑关系为“与”逻辑(逻辑乘).用式Y=A·B·C…表示.如学生成绩合格及不犯罪与能否毕业的关系即为与逻辑.③或逻辑关系:表明诸多条件中只要有1个以上具备结果就会发生,用Y=A+B+…表示.如去银行办理业务(储蓄),持存款证或持银行卡都可以办理.④非逻辑:是否定的因果关系,即条件具备结果就不能发生,用Y=A表示.如:征兵体检“有病”和“入伍”的关系就是非逻辑.“有病”存在,“入伍”就被否定了,有病不能入伍.1.21 由真值表可以写出最小项与或表达式.方法是将使函数Z为1的几种情况下输入变量的取值组合写成乘积项(变量取值为0写反变量因子,变量取值为1写原变量因子),然后将各乘积项相加,得Z=A B C+A B C+A BC+A B C+A B C1.23Z a=AB AB=A B+A B(摩根定理) =A⊕BZ b=B C AB+= (B⊕C)·AB=(BC+B C)AB=ABC1 1 1 0 1 1 1 1 1 11.24 见教材原文1.5节 1.25 a )Z a =m (0, 2, 3, 5, 6) =A B C +A B C +A BC +A B C +AB C =A C +B C +A B +A B Cb )Z b =m (0, 2, 7, 13, 15, 8, 10)=A B C D +A B C D +A BCD +A B C D +A B C D +AB C D +ABCD=B D +BCD +ABD1.26 (1)Z =A B +B +A B =A B +B =A +B (2)Z =A B C +A +B +C =A B C +A B C ++ =A B C +A B C =1(3)Z =AB ABC AB AB C +=++ =11AB AB C C +=+= (4)Z =A B CD +ABD +A C D=AD (B C +B +C ) =AD (C +B +C ) =AD ·1 =AD(5)Z =(A +B )(A CD +AD BC +)A B=(A +B )·A B ·(A CD +AD BC +) =0注:(A +B )A B =A A B +A B ·B =0(6)Z =AC (C D +A B )+BC (B AD CE ++)=0+BC ·(B +AD )·CE =BC (C +E )(B +AD ) =(BC E )(B +AD ) =BC E +BC E AD =BC E (7)Z =ABC +AC D +A C +CD=C (AB +A D +D )+A C =C (D +A )+A C =AC +CD +A C =A +CD(8)Z =A +B C +·(A +B +C )(A +B +C )=A +B C (A +B +C )(A +B +C ) ←展开=A +(A B C +B C )(A +B +C )←展开、吸收=A +B C(9)Z =B (A D +A D )+B (AD AD ABCE BC +++)=B (A D +A D )+B (A D +A D ) =A D +A D =A ⊕D(10)Z =AC +A C D +A B E F +B (D ⊕E )+BD E +B D E +BF=A (C +C D )+A B E F +BD E +B D E +BF =AC +AD +F (A B E +B )+B D E +BD E=AC +AD +A E F +BF +BD E +B D E1.27 求反函数Z 和对偶函数Z' (1)Z =AB +C (2)Z =(A +BC )C D Z =(A +B )·C Z =A ·(B +C )+C +DZ'=(A +B )·C Z' =A ·(B +C )+C +D(3)Z =()(+)A C A B AC BC ++ Z =(AC AB A C +++)·(B +C ) Z'=(AC AB A C +++)·(B +C )(4)Z =A D +AC +BCD +CZ =(A +D )·A C +·(B C D ++)·C Z'=(A +D )·A C +·(B C ++D )·C (5)Z =(AC +BD )ABC CD +Z =(A +C )·(B +D )+()()A B C C D +++ Z'=(A +C )·(B +D )+()()A B C C D +++ 1.28 用填卡诺图方法写最小项表达式 (1)F 1=A BC +AC +B C =m (1, 3, 5, 7)=ABC +A BC +A B C +ABC(2)F 2=A +B +CD =m (3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)=ABCD ABCD ABCD ABCD ABCD ABCD ++++++ABCD ABCD ABCD +++ABCD ABCD ABCD ABCD +++题1.28(1)F1卡诺图题1.28(2)F2卡诺图1.29 证明异或关系的正确性(1)A⊕0=A·0+A·0=A得证(2)A⊕1=A·1+A·1=A得证(3)A⊕A=A·A+A·A=0 得证(4)A⊕A=A·A+A·A=1 得证=A+A=1(5)(A⊕B)⊕C =(A⊕B)C+A B C⊕=ABC ABC ABC ABC+++=m(1, 2, 4, 7)A⊕(B⊕C) =A()⊕+⊕B C A B C=A(BC+BC)+A(B C+B C)=ABC ABC ABC ABC+++=m(1, 2, 4, 7)左式=右式,得证(6)右式AB⊕AC=AB·()()+=+++=+AC ABAC AB A C A B AC ABC ABC左式A(B⊕C)=A(B C+B C)=ABC ABC+得证(7)左式A⊕B=A B+AB=AB+AB=中式右式A⊕B⊕1=A⊕(B⊕1)=A⊕B=AB AB AB AB+=+=中式得证.1.30 用卡诺图法将函数化简为与或式.(1)Z ABC ABC ABC ABC=+++(2)1Z A B AB ABC BC=++++=题1.30(1)的卡诺图题1.30(2)的卡诺图(3)Z ABC AB AD C BD=++++填图后,可圈“0”得到Z=Z BCD再对Z取反,得到ZZ Z BCD B C D===++(4)Z(A、B、C)=m(0, 1, 2, 5, 6, 7)Z=AB AC BC++题1.30(3)的卡诺图题1.30(4)的卡诺图(5)Z(A、B、C、D)=m(0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 14)Z=B AC AD CD+++(6)Z(A、B、C、D)=m(0, 1, 2, 5, 8, 9, 10, 12, 14)Z=BC+BD+AD ACD+题1.30(5)的卡诺图题1.30(6)的卡诺图(7)Z=A C D ABCD ABCD++++,给定的约束条件为ABCD ABCD ABCD ABCD++++ 0ABCD ABCD+=Z=ACD ABCD ABCD++=ACD BCD AD++(8)Z=()CD A B ABC ACD⊕++给定的约束条件为AB+AC=0AC ACDZ=ABCD ABCD ABC ACD +++=BD ACD +题图1.30(7)的卡诺图题图1.30(8)的卡诺图(9)Z =m (0, 1, 2, 4)+d (3, 5, 6, 7)=1(10)Z =m (2, 3, 7, 8, 11, 14)+d (0, 5, 10, 15) Z =BD CD AC ++题图1.30(9)的卡诺图题图1.30(10)的卡诺图1.31 试用卡诺图法化简下列逻辑图 ① Z a =ABC ABC BC=ABC ABC BC ++ =ABC AC BC ++② Z b :按逻辑图逐级写函数式,最后得出Z b =A ⊕C +(A +B )()BC AC BD AD +=A ⊕C +(A +B )()()B C AC BD A D +++=A ⊕C +(A +B )ABCD ↓展开为与或式 =A ⊕C +(A +B )(A +B +C +D )=A ⊕C +AB +A C +AD +AB +B +BC +BD=A C +A C +AD +B 填入卡诺图 由卡诺图判断:Z b=AC+AC+AD+B该式已为最简与或式.题图1.31(a)的卡诺图题图1.31(b)的卡诺图1.32 化函数式为与非-与非式,并画出对应的逻辑图.(1)Z1 =AB+BC+AC=AB BC AC+++(2)Z2 =ABC AB BC AB=()++ABC AB BC AB=()++++ABC A B BC A BABC=1=ABC题图1.32(1)题图1.32(2)1.33 用最小项性质证明两个逻辑函数的与、或、异或运算可用卡诺图中对应的最小项分别进行与、或、异或运算来实现.解:命题所给出的结论是正确的.因为当输入变量的取值组合使某一最小项为1时,其他最小项均为0,若两函数相“与”,即Y=Y1·Y2,在对应最小项位置上Y1、Y2均为1时必然使Y为1;Y1Y2在该位置上有0,则0·0或1·0,Y必然为0,将所有对应最小项作乘运算就实现了Y=Y1·Y2运算.其他运算(或和异或)也是同样的道理.或运算是对应最小项相加;异或运算是对应最小项相异或.。

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。


第二章2.2 证明下列异或运算公式(1)A0A证明:左侧A0 A 0A得证(2)A1A证明:左侧 A 1 A 1A得证(3)A A0证明:左侧 A A A A得证(4)AA A证明:左侧 A A A AA得证(5)ABAB证明:右侧A B A BA B A BA B得证(6)(A B) C A (B C)证明:等式右侧 A (B C) A (BC BC)A(BC BC) A (BC BC)A(BC BC) A BC A BCA (B C)( B C)ABC A BCA (BB BC BC CC)ABC ABCABC ABC ABC ABC(A B AB)C (AB A B)C(A B)C (A B)C(将看成一个整体 (A B) ,用M来表示MC MCM C再替换 M ,则)(A B)C得证2.3 用逻辑代数法将下列逻辑函数式化简为最简与或表达式(1) L=AB(BC+A)解: L=AB(BC+A)=ABC+AB=AB(C+1)=AB(2)L=AB AB B解:L= AB AB B= AB (A1)B=AB B=AB B+A=A+B(3)L A ABC ABC BC BC解: L A ABC ABC BC BCA(1 BC ABC) C(B B)A C(4)L A B BD DCE AD解: L AB (A B)D DCEA B A BD DCEA B D DCEA B D (1CE)A B D(5)L( A B)AB A B AB解: L( A B)( A B)AB(A B)ABA B AB ABA B AB AB ABA (B B)B(A A )A B(6)L (A B C) (D E)(A B C DE )解: L(A B C) (D E)(A B C DE)(( A B C)(D E))(ABC DE )(A BC DE)(ABC DE )(0 DE( ABC ) ABCDE DE )DE2.4 已知函数L(A ,B,C)ABC ABC ABC 。
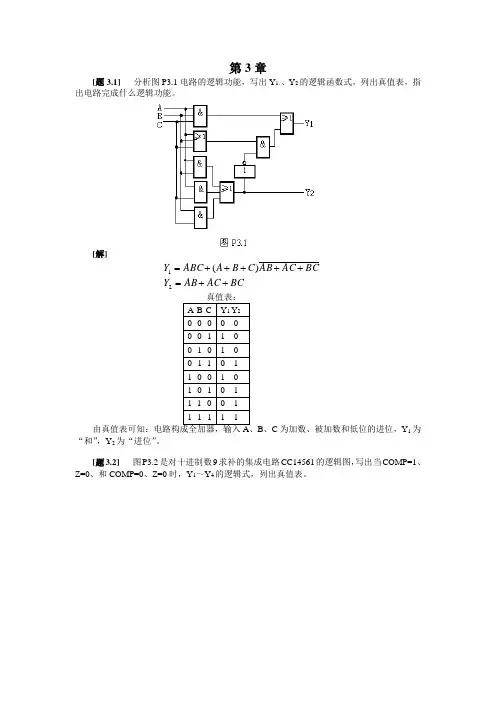
第3章[题3.1] 分析图P3.1电路的逻辑功能,写出Y 1、、Y 2的逻辑函数式,列出真值表,指出电路完成什么逻辑功能。
[解]BCAC AB Y BCAC AB C B A ABC Y ++=+++++=21)(B 、C 为加数、被加数和低位的进位,Y 1为“和”,Y 2为“进位”。
[题3.2] 图P3.2是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1、Z=0、和COMP=0、Z=0时,Y 1~Y 4的逻辑式,列出真值表。
[解](1)COMP=1、Z=0时,TG 1、TG 3、TG 5导通,TG 2、TG 4、TG 6关断。
3232211 , ,A A Y A Y A Y ⊕===, 4324A A A Y ++=(2)COMP=0、Z=0时,Y 1=A 1, Y 2=A 2, Y 3=A 3, Y 4=A 4。
COMP =0、Z=0的真值表从略。
[题3.3] 用与非门设计四变量的多数表决电路。
当输入变量A 、B 、C 、D 有3个或3个以上为1时输出为1,输入为其他状态时输出为0。
[解] 题3.3的真值表如表A3.3所示,逻辑图如图A3.3所示。
ABCD D ABC D C AB CD B A BCD A Y ++++= BCD ACD ABC ABC +++=B C D A C D A B D A B C ⋅⋅⋅=[题3.4] 有一水箱由大、小两台泵M L 和M S 供水,如图P3.4所示。
水箱中设置了3个水位检测元件A 、B 、C 。
水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作;水位低于C 点而高于B 点时M S 单独工作;水位低于B 点而高于A 点时M L 单独工作;水位低于A 点时M L 和M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路,要求电路尽量简单。
[解] 题3.4的真值表如表A3.4所示。


数字电子技术习题库一、填空题(每空1分,共20分)1. 有一数码10010011,作为自然二进制数时,它相当于十进制数( ),作为8421BCD 码时,它相当于十进制数( )。
2.三态门电路的输出有高电平、低电平和( )3种状态。
3.TTL 与非门多余的输入端应接( )。
4.TTL 集成JK 触发器正常工作时,其和端应接( )电平。
5. 已知某函数,该函数的反函数( )。
6. 如果对键盘上108个符号进行二进制编码,则至少要( )位二进制数码。
7. 典型的TTL 与非门电路使用的电路为电源电压为( )V ,其输出高电平为( )V ,输出低电平为( )V , CMOS 电路的电源电压为( ) V 。
8.74LS138是3线—8线译码器,译码为输出低电平有效,若输入为A 2A 1A 0 110时,输出 应为( )。
9.将一个包含有32768个基本存储单元的存储电路设计16位为一个字节的ROM 。
该ROM 有( )根地址线,有( )根数据读出线。
10. 两片中规模集成电路10进制计数器串联后,最大计数容量为( )位。
11. 下图所示电路中, Y 1=( );Y 3 =( )。
12. 某计数器的输出波形如图1所示,该计数器是( )进制计数器。
13.驱动共阳极七段数码管的译码器的输出电平为( )有效。
d R d S ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++=D C AB D C A B F F 01234567Y Y Y Y Y Y Y YABY 1 Y 2 Y 3二、单项选择题(本大题共15小题,每小题2分,共30分)(在每小题列出的四个备选项中只有一个是最符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
)1. 函数F(A,B,C) AB+BC+AC 的最小项表达式为( ) 。
A .F(A,B,C) ∑m (0,2,4) B. (A,B,C) ∑m (3,5,6,7) C .F(A,B,C) ∑m (0,2,3,4) D. F(A,B,C) ∑m (2,4,6,7)2.8线—3线优先编码器的输入为I 0—I 7 ,当优先级别最高的I 7有效时,其输出的值是( )。


第六章时序逻辑电路1.解:状态迁移图计数器的计数模为六。
2.(1)由所给方程画出逻辑图(2)该电路是异步电路,对异步电路的分析,主要注意每一级触发器的时钟。
对Q2、Q3而言,因为其J=K=1,每一时钟下降沿必翻转,即在Q1由1→0时,Q2翻转一次;同样,Q2由1→0时,Q3翻转一次。
为了判断电路的计数模,应先作出状态迁移表。
该电路为一个具有自启动能力的异步模九计数器(3) 由上述状态迁移表,可画出状态迁移图,如图所示。
2. 解 由波形图直接得状态迁移关系。
由此可看出该计数器是一个同步模六递减计数器。
由状态迁移表、作出卡诺图,从而求得各级触发器的特征方程,再与JK 触发器特征方程n nn Q K Q J Q+=+1相比较,即可得激励方程:nAn B nC A nAB nAC A n Cn A B nB n AC nAn A nB n A nB nC nA nB n Cn A nC nB nA n C Q Q Q C K Q K Q K J Q Q J Q Q J Q Q Q Q Q Q Q Q Q Q Q Q Q Q ========+=+=+++11111迁移表卡诺图 如选D 触发器,则激励方程为:n An B nC nAA n CnA nB n A B nC n A nC nB nA C nAn A n C nA nB n A n B nC n A nC n B n A n C Q Q Q C QD Q Q Q Q D Q Q Q Q Q D Q Q Q Q Q Q Q Q Q Q Q Q Q ==+=+==+=+=+++111由激励方程画出逻辑图。
D 触发器电路图。
最后还应检验自启动能力: 110→011; 111→110 显然该电路具有自启动能力。
3. 解:写出方程 激励方程:nnn Q Q D Q D 21211⊕==特征方程:nnn n n Q Q QQ Q 2112111⊕==++状态真值表状态迁移图该电路为同步四进制加法计数器。

习题八答案1. 试比较多谐振荡器、单稳态触发器、施密特触发器的工作特点,并说明每种电路的主要用途。
答:多谐振荡器是一种自激振荡电路,不需要外加输入信号,它没有稳定状态,只有两个暂稳态。
暂稳态间的相互转换完全靠电路本身电容的充电和放电自动完成。
改变外接R 、C 定时元件数值的大小,可调节振荡频率。
施密特触发器具有回差特性,它有两个稳定状态,有两个不同的触发电平。
施密特触发器可将任意波形变换成矩形脉冲,输出脉冲宽度取决于输入信号的波形和回差电压的大小。
单稳态触发器有一个稳定状态和一个暂稳态。
输入信号起到触发电路进入暂稳态的作用,其输出脉冲的宽度取决于电路本身 R 、C 定时元件的数值。
改变 R 、C 定时元件的数值可调节输出脉冲的宽度。
多谐振荡器是常用的矩形脉冲产生电路。
施密特触发器和单稳态触发器是两种常用的整形电路。
施密特触发器可用来进行整形、幅度鉴别、构成多谐振荡器等。
单稳态触发器常用于脉冲的延时、定时和整形等。
2.在图8.2所示555集成定时器中,输出电压uo 为高电平UOH、低电平UOL及保持原来状态不变的输入信号条件各是什么?假定UCO端已通过0.01μF 接地,u D 端悬空。
答:当1=R 时, TR U <3V CC ,则C 2输出低电平, 1=Q ,OH o U u =。
当1=R 时, TH U >32V CC ,TR U >3V CC ,则C 1输出低电平、C 2输出高电平,1=Q 、0=Q ,OL o U u =。
当1=R 时, TH U <32V CC,TR U >3V CC ,则C 1 C 2输出均为高电平,基本RS 触发器保持原来状态不变,因此o u 保持原来状态不变。
3.在图8.3所示多谐振荡器中,欲降低电路振荡频率,试说明下面列举的各种方法中,哪些是正确的,为什么?1) 加大R 1的阻值; 2) 加大R 2的阻值; 3) 减小C 的容量。
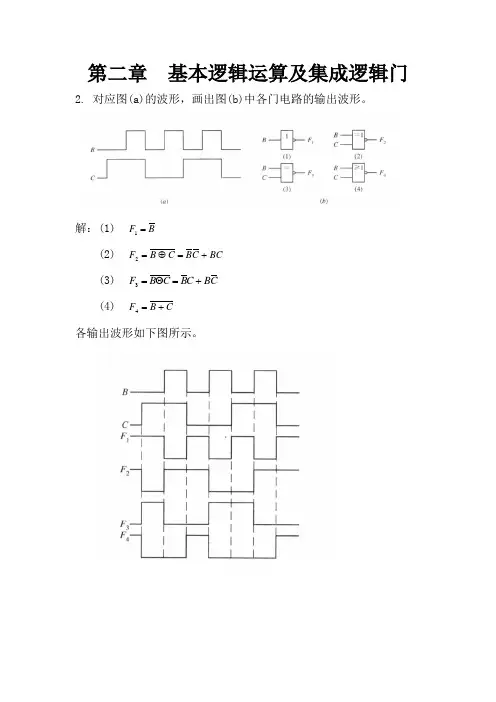
第二章基本逻辑运算及集成逻辑门2. 对应图(a)的波形,画出图(b)中各门电路的输出波形。
解:(1) BF=1(2) BC=⊕=F+CBCB2(3) C=ΘBF+=CBBC3(4) CB=F+4各输出波形如下图所示。
3. F 1和F 2的输出波形图如图所示:4.解: (a)不成立。
因为这两个门的输出端直接相连,当两者输出电平不同时,输出F 1不确定,甚至损坏器件。
(b)不成立。
因为其负载电阻只有150Ω,其输出高电平V R I U L OH OH 75.0150005.0max =⨯=∙=,不符合逻辑要求。
(c)不成立。
因为Ω<500S R ,该输入端相当于输入逻辑“0”, 103=∙∙=CD AB F 。
(d)成立。
为使该电路输出的U OH 能使负载门开启,其V U U ON OH 8.1min ==,故Ω===360005.08.1m in m in OH NOH L I U R ,本电路的R L =3Ω,,满足要求。
(e)不成立。
因为R S =3Ω>2Ω,该输入端相当于输入逻辑“1”,故015=++=CD AB F 。
5. 解 (a)无错。
因为R L =15Ω>R Lmin 。
(b)有错。
因为R L <R Lmin ,不能输出合格的U OH 。
(c)有错。
因为两个门输出端不能并接。
(d)有错。
因为输出端并接的三态门不可同时选通。
(e)无错。
因为这两个门的输入、输出端分别并接(这称作门的并联运用),所以两门的输入变量相同,输出电平也始终相同。
这样既不会损坏器件,也不会产生逻辑错误。
(f)有错。
因为电路中未接上拉电阻和直流电源。
(g)有错。
应把表达式改为C B A C B A F +=7。
(h)无错。
因为只有一个门选通,可正常工作。
6. 解 (1)(a) B B F C B A F C =∙====1,0111时;时,。
(b) B B F C B A F C =⊕==⊕==1,0122时;时,。
第1章习题参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16 (2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16 (4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000解:(1)10110001=177 (2)10101010=170(3)11110001=241 (4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255 (2)(3FF)16=1023(3)(AB)16=171 (4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25 (2)(1010.11)2=10.75(3)(1100. 101)2=12.625 (4)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。