彩色图像分割混合方法

rgb=cat(3,rgb_R,rgb_G,rgb_B);figure,imshow(rgb),title('RGB彩色图像');截图：（2）编写MATLAB程序，将一彩色图像从RGB空间转换为HIS空间，并观察其效果。

如例9.2所示。

程序：rgb=imread('LenaRGB.bmp');figure,imshow(rgb);rgb1=im2double(rgb);r=rgb1(:,:,1);g=rgb1(:,:,2);b=rgb1(:,:,3);I=(r+g+b)/3figure,imshow(I);tmp1=min(min(r,g),b);tmp2=r+g+b;tmp2(tmp2==0)=eps;S=1-3.*tmp1./tmp2;figure,imshow(S);tmp1=0.5*((r-g)+(r-b));tmp2=sqrt((r-g).^2+(r-b).*(g-b));theta=acos(tmp1./(tmp2+eps));H=theta;H(b>g)=2*pi-H(b>g);H=H/(2*pi);H(S==0)=0;figure,imshow(H);截图：（3）编写MATLAB程序，将一彩色图像在RGB空间进行彩色分割，并观察其效果。

如例9.11所示。

程序：rgb=imread('LenaRGB.bmp');figure,imshow(rgb);rgb1=im2double(rgb);r=rgb1(:,:,1);figure,imshow(r);g=rgb1(:,:,2);figure,imshow(g);b=rgb1(:,:,3);figure,imshow(b);r1=r;r1_u=mean(mean(r1(:)));[m,n]=size(r1);sd1=0.0;for i=1:mfor j=1:nsd1= sd1+(r1(i,j)-r1_u)*(r1(i,j)-r1_u);endendr1_d=sqrt(sd1/(m*n));r2=zeros(size(rgb1,1),size(rgb1,2));ind=find((r>r1_u-1.25*r1_d)&(r<r1_u+1.25*r1_d));r2(ind)=1;figure,imshow(r2);截图：（4）编写MATLAB程序，将一彩色图像在向量空间进行边缘检测，并观察其效果。

基于超像素的Grabcut彩色图像分割辛月兰【摘要】To overcome the disadvantage of time load for the image segmentation that set up the graph model in pixels,a Grabcut color image segmentation method which is based on the super pixels is proposed in this paper.Firstly,users can calibrate a rectangular box in the target zone manually,then split the'image into small areas of the similar color (super pixels) with the watershed algorithm two times.Set up the graph model using the super pixels as the graph nodes.In order to estimate the value of GMM,use the mean of the super pixels' color value to represent the all pixels in the same area.Finally,get the minimum value of the Gibbs energy with the minimum cut algorithm to achieve the optimal segmentation.Experimental results demonstrate that the new algorithm uses the little super pixels instead of the huge number of pixels.The algorithm achieves the excellent segmentation result in short runtime,speeds up the pace of segmentation,enhances the efficiency of the algorithm.%针对以像素为节点建立图模型进行图像分割耗时的特点,文中提出了一种基于超像素的Grabcut彩色图像分割方法.首先用户在目标所在区域手动标定一个矩形框;然后用两次分水岭算法将图像过分割成区域内颜色相似的小区域(超像素),用分割得到的超像素作为图的结点构建图模型;以每个超像素的颜色均值代表所在分块的全部像素点估计GMM(高斯混合模型)参数;最后用最小割算法求得吉布斯能量的最小值达到最优分割.实验结果表明,该算法以极少数超像素代替海量像素,在得到较好分割结果的同时,极大地缩短了运行时间,加快了分割速度,提高了效率.【期刊名称】《计算机技术与发展》【年(卷),期】2013(023)007【总页数】5页(P48-51,56)【关键词】分水岭;超像素;高斯混合模型;分割【作者】辛月兰【作者单位】陕西师范大学计算机科学学院,陕西西安710062;青海师范大学物理系,青海西宁810008【正文语种】中文【中图分类】TP310 引言图割理论在图像分割问题中得到了广泛的应用，并且已经取得了一些好的成果［1～6］。

多色调合成技巧：Photoshop中的通道分离方法Photoshop是一种功能强大的图像处理软件，它提供了许多工具和功能，可以帮助我们实现各种各样的效果。

在本教程中，我将介绍一种被称为“通道分离”的技巧，用于实现多色调合成。

通道分离方法可以将一张彩色图像分解为单独的红、绿、蓝通道，并将它们分别处理后再合成，以获得不同的色调效果。

首先，打开一张你想要进行多色调合成的彩色图像。

然后，点击菜单栏的“图像”选项，选择“模式”，再选择“RGB颜色”。

这样，图像会被转换为RGB模式，以便我们可以分离通道。

接下来，点击菜单栏的“窗口”选项，选择“通道”。

在通道面板中，你将看到红、绿、蓝三个通道的缩略图。

现在，我们将分别对这些通道进行处理，以实现不同的色调效果。

选择红色通道，然后按下Ctrl + A（或Command + A）。

这将选中整个通道。

接下来，按下Ctrl + C（或Command + C），将该通道复制到剪贴板。

然后，按下Ctrl + V（或Command + V），将它粘贴回图像中。

现在，你将看到图像只包含红色通道的内容。

在右上角的图层面板中，将红色通道的混合模式设置为“正常”。

然后，通过菜单栏的“过滤器”选项，选择“其他”再选择“高斯模糊”。

调整模糊半径，使图像变得模糊。

这样，你就可以获得一种柔和的红色色调效果。

接下来，重复以上步骤，将绿色和蓝色通道分别复制粘贴回图像中。

然后，分别调整它们的混合模式和模糊效果，以获得不同的绿色和蓝色色调效果。

在进行了通道分离和处理后，你可以通过将红、绿、蓝三个通道的颜色混合起来，再次合成图像。

首先，点击菜单栏的“窗口”选项，选择“图层”。

在图层面板中，你会看到三个图层，分别对应红、绿、蓝三个通道。

点击其中一个图层，然后按下Shift键，点击其他两个图层，将它们同时选中。

接下来，点击图层面板中的“图层”菜单，选择“新建组”。

这样，你就创建了一个包含所有通道图层的组。

图像分割阈值选取技术综述摘要图像分割是图像处理与计算机视觉领域低层次视觉中最为基础和重要的领域之一，它是对图像进行视觉分析和模式识别的基本前提．阈值法是一种传统的图像分割方法，因其实现简单、计算量小、性能较稳定而成为图像分割中最基本和应用最广泛的分割技术．已被应用于很多的领域。

本文是在阅读大量国内外相关文献的基础上，对阈值分割技术稍做总结，分三个大类综述阈值选取方法，然后对阈值化算法的评估做简要介绍。

关键词图像分割阈值选取全局阈值局部阈值直方图二值化1．引言所谓图像分割是指根据灰度、彩色、空间纹理、几何形状等特征把图像划分成若干个互不相交的区域，使得这些特征在同一区域内，表现出一致性或相似性，而在不同区域间表现出明显的不同[37]．简单的讲，就是在一幅图像中，把目标从背景中分离出来，以便于进一步处理。

图像分割是图像处理与计算机视觉领域低层次视觉中最为基础和重要的领域之一，它是对图像进行视觉分析和模式识别的基本前提．同时它也是一个经典难题，到目前为止既不存在一种通用的图像分割方法，也不存在一种判断是否分割成功的客观标准。

阈值法是一种传统的图像分割方法，因其实现简单、计算量小、性能较稳定而成为图像分割中最基本和应用最广泛的分割技术．已被应用于很多的领域，例如，在红外技术应用中，红外无损检测中红外热图像的分割，红外成像跟踪系统中目标的分割；在遥感应用中，合成孔径雷达图像中目标的分割等；在医学应用中，血液细胞图像的分割，磁共振图像的分割；在农业工程应用中，水果品质无损检测过程中水果图像与背景的分割。

在工业生产中，机器视觉运用于产品质量检测等等。

在这些应用中，分割是对图像进一步分析、识别的前提，分割的准确性将直接影响后续任务的有效性，其中阈值的选取是图像阈值分割方法中的关键技术。

2．阈值分割的基本概念图像阈值化分割是一种最常用，同时也是最简单的图像分割方法，它特别适用于目标和背景占据不同灰度级范围的图像[1]。

一种改进超像素融合的图像分割方法余洪山;张文豪;杨振耕;李松松;万琴;林安平【摘要】基于超像素的传统图像分割方法在边缘分割的一致性、计算效率和融合算法的自适应性等方面仍存在诸多问题.文章结合国内外相关研究进展,提出了一种新型超像素融合的图像分割方法.方法采用ERS超像素过分割算法,以强度、梯度直方图作为超像素特征,并采取EMD方法计算特征距离,通过混合Weibull模型获取融合自适应阈值,进而完成分割.算法时间复杂度降至为O(N),分割过程中不需要手动选取待分割区域,有效提高了算法的自适应性.实验结果表明本方法在分割边界准确度和处理效率方面优于现有方法.【期刊名称】《湖南大学学报（自然科学版）》【年(卷),期】2018(045)010【总页数】9页(P121-129)【关键词】超像素;区域融合;陆地移动距离;混合Weibull模型;图像分割【作者】余洪山;张文豪;杨振耕;李松松;万琴;林安平【作者单位】湖南大学电气与信息工程学院/机器人视觉感知与控制技术国家工程实验室,湖南长沙410082;湖南大学深圳研究院,广东深圳 518057;湖南大学电气与信息工程学院/机器人视觉感知与控制技术国家工程实验室,湖南长沙410082;湖南大学电气与信息工程学院/机器人视觉感知与控制技术国家工程实验室,湖南长沙410082;湖南大学深圳研究院,广东深圳 518057;湖南大学电气与信息工程学院/机器人视觉感知与控制技术国家工程实验室,湖南长沙410082;湖南大学电气与信息工程学院/机器人视觉感知与控制技术国家工程实验室,湖南长沙410082;湖南大学电气与信息工程学院/机器人视觉感知与控制技术国家工程实验室,湖南长沙410082【正文语种】中文【中图分类】TP273图像分割是利用颜色、纹理和灰度等特征将图像分割成一定数量的符合人类视觉感知分类的区域. 由于自然图像中场景的复杂性，加之人的视觉感知上的主观性，人们对图像场景理解不尽相同，因此图像分割一直是计算机视觉中的一个难点. 传统方法以像素为基本处理单元，使得算法时间消耗大、效率低. 超像素是指具有相似纹理、颜色和亮度等特征的相邻像素构成的图像块[1]，它利用像素之间特征的相似程度将像素分组，在很大程度上降低了后续图像处理任务的复杂度. 然而超像素分割会对图像产生过分割，并不能达到符合人的视觉感知的分割结果. 超像素算法多用于图像分割预处理，在后续图像处理中用超像素来代替像素，大大降低了时间的消耗.目前，基于超像素融合的图像分割研究开始获得越来越多的关注，典型方案有基于SLIC或Normalized cuts产生超像素过分割，然后提取超像素的特征(颜色、纹理和直方图等)，再基于一定的相似性度量标准计算相邻两个超像素的特征相似性距离. Hsu C Y等[2]提出了基于谱聚类的融合策略，该方法通过对SLIC 产生的超像素进行谱聚类取得了较高的效率，但其对于复杂场景的分割结果不够理想. Song X 等[3]采用了基于分层超像素的区域融合策略-MSRM(maximal similarity based region merging)[4]，针对前景对象很少的图像，该方法可以得到较好的分割结果，但需要人为给定前景对象所在的大致矩形区域. 当场景前景对象很多且分散时，该算法将很难处理，因此存在很大的局限性. Han B等[5]利用Normalized cuts[6]产生超像素，基于直方图的相似性度量计算相邻超像素间的非相似性距离来完成对图像的分割. 该方法虽然对相似的超像素进行了融合，但是融合比较保守导致分割结果过于细化，即在明显应该分割为一个对象的区域中存在没有融合的超像素边界. 综上所述，目前基于超像素融合的图像分割方案在边缘分割的一致性、特征相似性度量的可靠性、计算效率和融合算法的自适应性方面仍需进一步改善.针对上述问题，本文结合国内外相关研究进展，提出了一种改进超像素融合的图像分割方法. 主要改进如下：1)本文采用ERS(entropy rate superpixel)算法生成与真实边缘一致性更佳的超像素图像；2)选用稳定性好且计算简易的直方图特征(强度、颜色及方向直方图)，并采用陆地移动距离EMD(Earth Mover’s distance)计算超像素节点间相似性，以适应多种结构尺寸；3)采用Weibull 模型对相邻超像素的EMD 分布进行估计，获取融合处理的自适应阈值，从而提高了本文算法的鲁棒性. 本文算法时间复杂度为O(N)，处理过程中不需要手动选取待分割区域，分割结果的边界准确率和处理效率均具有明显的提高.1 改进的超像素融合图像分割方法如图1 所示，本文提出的超像素融合图像分割方法可划分为三部分：1)超像素过分割方法选择及图像预分割；2)以超像素节点为单位，求取强度、颜色以及方向(梯度)的特征直方图，基于特征相似性距离EMD模型，计算相邻节点各自特征直方图之间的相似性距离；3)建立Weibull 混合模型(Weibull mixture model)，对模型中的参数进行估计，确定节点特征相似性距离阈值γf ，并根据其进行超像素融合.1.1 基于超像素算法的图像预分割1.1.1 超像素算法选择目前，超像素算法主要分为两大类：基于图论的算法和基于梯度上升的算法.超像素的评价标准[7]主要包括：1)边缘贴合度；2)紧密度；3)计算效率等. 边缘贴合度指的是超像素边缘与真值边沿的吻合程度. 某些超像素方法虽然可以产生超像素，但是超像素的边缘可能穿过场景中物体的实际边缘. 紧密度反映了超像素形状是否规则以及边缘平滑程度. 常见的超像素算法性能比较[7]如表1 所示(使用公测数据集Berkeley dataset[8]中图片进行测试，其中边缘贴合度通过边界召回率boundary recall[7]反映)．图1 基于超像素融合的图像分割流程图Fig.1 Flow chart of image segmentation based on superpixel merging表1 几种超像素方法的性能特点Tab．1 Several superpixel algorithm performance characteristics算法边缘贴合度形状是否规整数量是否可控紧密度是否可控时间复杂度Ncuts0.68√√×O(N32)watersheds-×××O(Nlog (N))mean-shift-×××O(N2)Turbopixel0.61√√×O(N)SLIC0.82√√√O(N)ERS0.84×√√O(Nlog (N))超像素分割是为后续的分割服务的，所以超像素的边缘贴合度对后续的分割质量有着最直接的影响. 同时综合表格中时间复杂度、紧密度和数量是否可控等性能，本文采用的是边缘贴合度非常好的ERS(entropy rate superpixel)算法产生超像素.1.1.2 基于ERS的超像素计算和图模型构建ERS是由Liu等人[9]在2011年提出的一种基于图的聚类算法，该算法采用了一种新型的目标函数，并通过在图拓扑结构中最大化目标函数产生超像素. ERS算法构造的目标函数如表达式(1)所示：(1)式中，A表示图拓扑结构中的边集，λ是可调节的权重因子，H(A)代表随机游走熵率项，B(A)代表平衡项. H(A)项的定义为：(2)式(2)中，pi,j代表随机游走的转移概率，μi为随机游走的固定分布，H(A)构造的目的是为了生成紧密度较好的超像素，而构造平衡项则是为了约束超像素的尺寸．B(A)项的构造为：(3)式(3)中，ΖA是聚类分布，表示聚类分布的概率[10].用ERS算法对原始图像进行超像素过分割后，整幅图像由许多超像素构成. 超像素构成的“图”模型如图2所示，其中图结构由节点和边组成，即G=(V,E)，节点V 不再是图像中所有的像素集合，而由超像素构成，E是由连接相邻两个节点(超像素)的边构成的集合.图2 超像素“图”结构Fig.2 Superpixel “graph” structure1.2 特征提取与相似性度量1.2.1 超像素节点特征提取在二维彩色图像中，颜色、强度以及方向梯度是三种常用且易提取的直方图特征. 超像素是一定范围内像素点的集合，因此本文选取强度直方图、颜色直方图和方向直方图特征作为超像素节点特征.强度直方图是一个1维256区间的直方图，颜色直方图是由色调(hue)和饱和度(saturation)(HSV颜色空间中)构成的76*76(颜色位数为8位)的2维直方图，梯度直方图是用方向梯度(即垂直方向梯度与水平方向梯度的反正切)构成的1 维的360 区间的直方图，这个特征与HOG 特征类似. 为便于计算处理，算法将所有的特征直方图归一化处理.1.2.2 基于EMD的相似性度量1)EMD度量标准为了计算上述特征直方图相似性从而为超像素融合提供判断依据，本文采用EMD作为相似性度量标准. EMD是一种在某种区域两个概率分布距离的度量，即被熟知的Wasserstein度量标准. 如果两个分布被看作在区域上两种不同方式堆积一定数量的山堆，那么EMD是把一堆变成另一堆所需要移动单位小块最小的距离之和. EMD定义如表达式(4)[10]：(4)其中fij需要满足的约束条件：fij≥0(5)∑jfij≤pi(6)∑ifij≤qj(7)其中P和Q为两种给定的分布，P为m个特征量xi和其权重pi的集合，Q为n 个特征量yi和其权重qi的集合，P和Q分别记作P={(x1,p1),…,(xm,pm)}和Q={(y1,q1),…,(yn,qn)}. 在计算这两个分布EMD前，需先定义好P、Q中任意特征量Pi和Qi之间的距离dij(该距离称为ground distance，两个分布之间EMD 依赖于分布中特征量之间的ground distance). 当这两个特征量是向量时，dij是欧式距离，当这两个特征量是概率分布时则dij是相对熵(Kullback-Leibler divergence). 约束条件(5)是对方向性进行约束. (6)和(7)是对两个分布的量进行约束. 当P和Q归一化后有相同的总量时，EMD等同于两个分布之间的Mallows距离[11].EMD相比其它分布距离计算方法有着明显的优势[10]：EMD适用于计算两个直方图之间的距离，并且它能够处理变化尺寸的结构，有着更大的紧凑性和灵活性；如果两个分布有相等的总量，EMD则是一种真实的度量.2)相似性度量对于任意相邻的超像素对(节点)va和vb，提取其以强度(1维)、颜色(2维，HSV空间中色调和饱和度)和方向(1维)直方图为特征的4维特征直方图，再将其归一化处理，以此作为计算va、vb间EMD的参数. va、vb的特征相似性距离如式(8)[11]所示：(8)其中dn表示第n对相邻节点va和vb的特征相似性，且dn∈[0,1]，如果dn为0，则两个相邻节点特征完全一样，如果为1，则意味着相邻两个节点完全不相似.为常量，是以上述相邻节点的4维特征直方图为参数所能求得的最大可能的EMD，从而使得式(8)中dn的值在0到1之间. 其中，强度变化的最大可能为黑色到白色，色调(hue)变化的最大可能为0°到360°，饱和度(saturation)变化的最大可能为0%到100%，梯度方向变化的最大可能为水平梯度到垂直梯度.基于上述处理后，图像对应的图构建G=(V,E)基本完成，其中 V由超像素构成的集合，E为连接相邻两个节点(超像素)的边构成的集合，边权重由其连接的两个超像素之间的EMD确定，作为这两个超像素的相似性度量. 如图3所示．图3 “图”的权重示意图Fig.3 Schematic diagram of the weight of the graph1.3 自适应融合不同场景图像的最佳融合阈值不尽相同，如采用手动设置阈值，则需要多次更改阈值方能得到较好的分割结果. 为了确定本文超像素融合所需的自适应相似性阈值，首先需要得知边缘权重的分布模型，尚无证据表明相邻节点间的EMD服从均匀分布或者正态分布. 由于被比较的两个直方图特征向量分布是相关且非同分布的，根据文献[12]，这两个特征向量之间的Lp范数距离服从Weibull分布. 另外Chen-Ping Yu等人[13]的工作也对其进行了佐证. 因此，本文采用Weibull模型对相邻超像素的EMD分布进行估计，以获得自适应阈值，用于对不同场景图像的融合分割处理，从而提高了算法的鲁棒性.1.3.1 Weibull混合模型及参数估计Weibull是概率统计中常用的分布模型. 采用两个Weibull分布混合后对所有相邻超像素对的特征距离(EMD)X建立模型. 其混合模型完整形式如公式(9)所示：(9)其中θ=(ε1,φ1,μ1,ε2,φ2,μ2,π) 是待确定的模型参数.ε、φ、μ和π分别是尺度、形状、位置和混合参数.为了得到M2(Χ;θ) 中的参数，需要对M2(Χ;θ)进行参数估计，本文采用最大似然估计. 最大似然估计是基于观测样本的似然函数最大化来对参数进行估计的，M2(Χ;θ)的似然函数取对数后如下：lnM2(X;θ)=(10)该似然函数很复杂，并且存在位置参数μ1和μ2，因此，本文采用Nelder-Mead 方法[14-15]，它作为一种不含导数的优化方法，通过使(10)的负对数似然函数最小化来实现对参数的估计.为了得到相似性阈值γf，本文采用一个单一Weibull分布来拟合由两个Weibull 分布构成的混合Weibull模型，用AIC(Akaike Information Criterion)[16]信息准则来防止拟合混合Weibull模型过程中出现的过拟合. 相似性阈值γf由表达式(11)决定：(11)当混合模型更好的时候，γf的取值为max (x,η)，此时γf是混合的两个部分的交点，通过搜索向量Xf 的值可以以线性时间得到该方程的解. 当单一的Weibull更好时，即AIC(M2)>AIC(M1) 时，γf通过计算M1的逆累计分布函数得到，其中τ是给定的一个百分数，τ∈[0,1].1.3.2 超像素融合处理对于图像对应的图结构G=(V,E)，若相邻节点之间边的权重大于γf时，则认为该边连接的两个超像素差异较大，分属不同对象，该边继续保留，反之，则对两个超像素进行融合.超像素融合过程示意图如图4 所示，图中相似性阈值为0.6，即当连接相邻两个超像素(节点)的边的权值小于0.6 时，则认为这两个相邻超像素属于同一对象物体，可以对这两个超像素进行融合，形成一个更大的区域(如图4中实线连接的超像素节点)，反之，如果连接相邻超像素的边缘权值大于0.6，则认为该相邻超像素对不相似，属于不同的对象物体，继续保留分割边界(如图4 中的虚线形成的边界).2 实验结果与分析为验证本文方法的有效性和先进性，本文采用两个常用公测数据集BSD(Berkeley Segmentation Dataset)[8]以及SUN Dataset[17]的图像进行实验对比分析. 实验平台配置如下：PC主频为2.0 GHz，RAM为4 G，软件环境为MATLABR2014a.图4 超像素融合过程示意图Fig.4 Schematic of the superpixel merging process2.1 实验结果图5为本文方法得到的实验结果. 从图中可以看出：本文方法分割结果边界与场景真实边界具有良好的一致性，对于复杂的场景，如第二行图像所示，同样能得到与人的视觉感知相一致的结果．图5 实验结果Fig.5 Results of the experiment2.2 Weibull模型的有效性分析为了验证本文算法加入Weibull模型的有效性，本文另通过手动选取相似性阈值γf ，对不同场景图像进行超像素融合实验. 实验结果(超像素融合后的均值填充效果图)如图6所示.图6中最右侧为与真实场景最一致的融合效果图. 由实验结果可知，要得到良好的融合效果，必须手动调节多次阈值直至结果满意为止. 而且，对于不同场景的图像，其最佳相似性阈值不尽相同.加入Weibull模型后，最佳相似性阈值可由Weibull分布估计求得. 与上述手动调节阈值相比，具有更好的灵活性，避免了繁琐的调节阈值的步骤，可方便应用于不同的场景图像，极大地提高了算法的鲁棒性.2.3 分割结果直观效果对比为了验证本文算法的分割效果，本文选取了2种常用的基于超像素融合的分割算法并与其进行了对比，分别为DBSCN算法[18]对SLIC超像素融合的分割方法(SLIC-DBSCN)，基于原型对象(proto-object)的分割方法[12](PO).图6 手动选取阈值融合实验结果Fig.6 Merging results of selecting the threshold value manually不同算法的实验结果对比如图7所示，其中(a)为原始图像，(b)、(c)和 (d)分别为SLIC-DBSCN算法、PO算法以及本文算法的分割结果. 超像素数目均设定为600. 由图7中分割结果的对比可得，在产生相同超像素个数的情况下，本文方法得到的分割结果在保持边界的性能上优于SLIC-DBSCN算法和PO方法，分割结果视觉效果上更符合人的视觉感知.图8为图7的局部细节放大对比. 进一步从分割细节上进行了对比说明.图7 不同算法的实验结果对比Fig.7 Comparison of experimental results from different algorithm图8 局部细节放大对比图Fig.8 Partial details of the enlarged comparison chart2.4 分割结果性能量化对比为了对实验结果进行量化评价，本文采用了3种量化指标：1)PRI(Probabilistic Rand Index)[19]，它统计了实验的分割结果的边界标记像素与真实分割结果保持一致的数目，即分割结果的边缘准确度；2)VOI(Variation of Information)[20]，该指标针对两个类之间的信息的不同进行了距离度量；3)BDE(Boundary Displacement Error)[21]，该指标表示分割结果与真值之间的区域边界的平均位移.从以上指标可以得出，PRI越高，VOI，BDE越小，则分割结果的性能越好. 本文分割方法与Normalized cut(Ncut)[6]，Mean Shift[22]，Ultrametric Contour Maps(UCM)[23]，Segmentation by Aggregating Superpixels (SAS)[24]，SLIC-DBSCN算法以及PO算法的量化比较如表2所示，其中文献[6]、[22]、[23]、[24]的性能量化数据来自于文献[2]，实验数据集采用BSD.表2 本文方法与其他算法分割结果的性能评估Tab．2 The performance evaluation of this paper and ot her algorithm segmentation’s results方法PRIVOIBDENcuts[6]0.724 22.906 117.15Meanshift[22]0.795 81.972514.41UCM[23]0.811.68N/ASAS[24]0.831 91.684 911.29SLIC-DBSCN0.784 61.927 813.72PO0.846 31.582 511.21本文方法0.853 71.519 110.98本文采用BSD数据集做了40组分割实验，并对三种不同分割算法的时间分别计算平均值，实验图像尺寸481×321，在设置不同超像素数目N的情况下，三种方法平均消耗时间如表3所示．表3 不同N时算法的平均时间消耗Tab．3 Average time consumption of algorithm for different N s方法N=500N=800N=1 000SLIC-DBSCN18.826.238.5PO10.415.323.6本文方法10.716.124.5由表看出，本文算法具有较高的时间效率，相较于SLIC-DBSCN算法具有明显的优势，与PO算法相差无几. 随着超像素的数目增多，时间消耗亦随之增加，虽然N越大，超像素对边缘的贴合度越好，但是并不是对任何图像都将超像素的数目N设置的越大越好，对于图像尺寸较小时，如BSD数据集的尺寸为481×321，N 设置600即可获得很好的分割结果.3 结论本文在图像预处理阶段(超像素分割)采用了ERS算法，通过产生数目更少的超像素便可达到更好的边缘保持性能，这一点对后续的分割至关重要.此外，本文的算法充分运用了统计学，距离度量采用EMD ，通过 Weibull分布建立EMD统计模型．因此，该方法的实验结果具有很高的边缘准确性. 本文采用AIC信息准则确定自适应阈值，无需手动调节，从而提高了超像素聚类的鲁棒性，使得该算法能够适应复杂场景的分割. 在时间消耗上，本文的分割方法首先采用ERS超像素过分割，使得后续的融合都是基于超像素级的. 另外，本文的分割方法两次利用了“图”的结构(ERS为第一次利用“图”结构，然后基于超像素过分割的结果第二次建立“图”的结构)，这使得我们的算法具有很好的存储效率.与其他经典的传统分割算法([22]，[23]，[24])以及基于超像素融合的分割方法([2]，[12]，[18]等)的实验结果进行对比，本文对图像的分割结果性能优于其他方法，特别是在图像场景比较复杂的情况下，本文的分割结果对物体的边界保持得非常好.在对超像素融合后，将各个区域进行均值赋色，最后生成的分割图像的视觉效果和人类视觉的感知一致.参考文献【相关文献】[1] MALIK J. Learning a classification model for segmentation[J]. Proc Iccv, 2003,1(1):10-17．[2] HSU C Y, DING J J. Efficient image segmentation algorithm using SLIC superpixels and boundary-focused region merging[C]// Communications and SignalProcessing． Melmaruvathur: IEEE, 2014:1-5.[3] SONG X, ZHOU L, LI Z, et al. Interactive image segmentation based on hierarchical superpixels initialization and region merging[C]// International Congress on Image and Signal Processing． Dalian: IEEE, 2015: 410-414.[4] NING J, ZHANG L, ZHANG D, et al. Interactive image segmentation by maximal similarity based region merging[J]. Pattern Recognition, 2010, 43(2): 445-456.[5] HAN B, YAN J. A novel segmentation approach for color images with progressive superpixel merging[C]// International Conference on Computer Science and Network Technology． Changchun: IEEE, 2013: 433-437.[6] SHI J, MALIK J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905.[7] ACHANTA R, SHAJI A, SMITH K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282.[8] MARTIN D, FOWLKES C, TAL D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]// International Conference on Computer Vision．Vancouver: IEEE, 2001, 2:416-423.[9] LIU M Y, TUZEL O, RAMALINGAM S, et al. Entropy rate superpixel segmentation[C]// Computer Vision and Pattern Recognition．Colorado : IEEE, 2011: 2097-2104.[10] RUBNER Y, TOMASI C, GUIBAS L J. A metric for distributions with applications to image databases[C]// International Conference on Computer Vision． Bombay: IEEE Computer Society, 1998:59.[11] LEVINA E, BICKEL P. The earth mover's distance is the mallows distance: Someinsights from statistics[C]// Eighth IEEE International Conference on Computer Vision． Vancouver: IEEE, 2001, 2: 251-256.[12] BURGHOUTS G J, SMEULDERS A W M, GEUSEBROEK J M. The distribution family of similarity distances[C]// Conference on Neural Information Processing Systems.Vancouver: DBLP, 2009:201-208.[13] YU C P, HUA W Y, SAMARAS D, et al. Modeling clutter perception using parametric proto-object partitioning[C]// International Conference on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc， 2013:118-126.[14] NELDER J A, MEAD R. A simplex method for function minimization[J]. The Computer Journal, 1965, 7(4): 308-313.[15] LAGARIAS J C, REEDS J A, WRIGHT M H, et al. Convergence properties of the Nelder-Mead simplex method in low dimensions[J]. SIAM Journal on Optimization, 1998, 9(1): 112-147.[16] LUMLEY T, SCOTT A. AIC and BIC for modeling with complex survey data[J]. Journal of Survey Statistics and Methodology, 2015, 3(1): 1-18.[17] XIAO J, HAYS J, EHINGER K A, et al. Sun database: Large-scale scene recognition from abbey to zoo[C]// Computer Vision and Pattern Recognition. San Francisco: IEEE,2010:3485-3492.[18] ESTER M. A density-based algorithm for discovering clusters in large spatial Databases with Noise [C]// International Conference on Knowledge Discovery and Data Mining. Portland: AAAI Press, 1996:226-231.[19] UNNIKRISHNAN R, PANTOFARU C, HEBERT M. Toward objective evaluation of image segmentation algorithms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(6):929.[20] MEIL M. Comparing clusterings: an axiomatic view[C]//Proceedings of the 22nd International Conference on Machine Learning. Bonn: DBLP, 2005: 577-584.[21] FREIXENET J, X, RABA D, et al. Yet another survey on image segmentation: region and boundary information integration[J]. Lecture Notes in Computer Science, 2002, 2352:21-25.[22] COMANICIU D, MEER P. Mean shift: A robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619.[23] ARBELAEZ P, MAIRE M, FOWLKES C, et al. From contours to regions: An empirical evaluation[C]//Computer Vision and Pattern Recognition. Miami: IEEE, 2009: 2294-2301.[24] LI Z, WU X M, CHANG S F. Segmentation using superpixels: A bipartite graph partitioning approach[C]// Computer Vision and Pattern Recognition. Rhode Island: IEEE, 2012:789-796．。

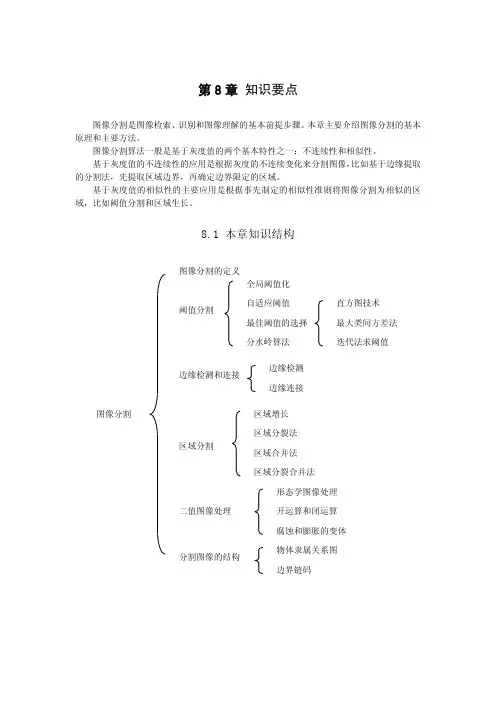
第8章 知识要点图像分割是图像检索、识别和图像理解的基本前提步骤。

本章主要介绍图像分割的基本原理和主要方法。

图像分割算法一般是基于灰度值的两个基本特性之一：不连续性和相似性。

基于灰度值的不连续性的应用是根据灰度的不连续变化来分割图像，比如基于边缘提取的分割法，先提取区域边界，再确定边界限定的区域。

基于灰度值的相似性的主要应用是根据事先制定的相似性准则将图像分割为相似的区域，比如阈值分割和区域生长。

8.1 本章知识结构8.2 知识要点1. 图像分割在对图像的研究和应用中，人们往往仅对图像中的某些部分感兴趣。

这些部分常称为目标或前景（其它部分称为背景），它们一般对应图像中特定的、具有独特性质的区域。

为了检索、辨识和分析目标，需要将它们分离提取出来，在此基础上才有可能对目标进一步利用。

图像分割就是指把图像分成各具特性的区域并提取出感兴趣目标的技术和过程。

图像分割是由图像处理过渡到图像分析的关键步骤。

一方面，它是目标表达的基础，对特征测量有重要的影响；另一方面，因为图像分割及其基于分割的目标表达、特征提取和参数测量等，能将原始图像转化为更抽象更紧凑的形式，所以使得更高层的图像分析和理解成为可能。

图像分割的应用非常广泛，几乎出现在有关图像处理的所有领域中，并涉及各种类型的图像。

图像分割在基于内容的图像检索和压缩、工业自动化、在线产品检验、遥感图像、医学图像、保安监视、军事、体育、农业工程等方面都有广泛的应用。

例如：在基于内容的图像检索和面向对象的图像压缩中，将图像分割成不同的对象区域等；在遥感图像中，合成孔径雷达图像中目标的分割，遥感云图中不同云系和背景分布的分割等；在医学应用中，脑部图像分割成灰质、白质、脑脊髓等脑组织和其它脑组织区域等；在交通图像分析中，把车辆目标从背景中分割出来等。

在各种图像应用中，只要需要对图像目标进行提取、测量等，就都离不开图像分割。

图像分割的准确性将直接影响后续任务的有效性，因此图像分割具有十分重要的意义。

基于高斯混合模型的图像分割方法图像分割是数字图像处理的一种基础技术，其主要目的是将一幅图像分成若干个子区域，每个子区域具有明显的特征，如颜色、亮度等。

在许多领域中都有着广泛的应用，如医学影像、计算机视觉、机器人等。

本文将介绍一种基于高斯混合模型的图像分割方法。

1. 高斯混合模型介绍高斯混合模型是一种常用的概率模型，可以用来描述多个高斯分布组成的混合分布。

其数学表述如下：$$p(x) = \sum_{k=1}^K\alpha_k\phi(x;\mu_k,\Sigma_k)$$其中，$x$ 是样本数据，$K$ 是高斯分布的个数，$\alpha_k$ 是第 $k$ 个高斯分布的权重系数，$\mu_k$ 和 $\Sigma_k$ 是第 $k$ 个高斯分布的均值向量和协方差矩阵，$\phi(x;\mu_k,\Sigma_k)$ 是第 $k$ 个高斯分布在 $x$ 处的密度函数。

高斯混合模型可以表示多种不同的数据分布，因此在图像分割中也有着广泛的应用。

2. 基于高斯混合模型的图像分割方法基于高斯混合模型的图像分割方法主要包括以下步骤：2.1 数据预处理首先对输入的图像进行预处理，如灰度化、降噪等。

这一步骤的主要目的是去除图像中的噪声和冗余信息，以便后续处理。

2.2 高斯混合模型建模将预处理后的图像数据作为样本数据，建立高斯混合模型。

根据经验或者实验结果，确定高斯分布的个数 $K$，然后利用 EM 算法对模型进行拟合，得到每个高斯分布的均值向量和协方差矩阵，以及对应的权重系数。

2.3 标签赋值将图像像素的灰度值作为输入样本，利用高斯混合模型计算出每个像素点属于每个高斯分布的概率。

然后根据加权最大概率准则，为每个像素点赋予一个标签，表示该像素点属于哪个高斯分布对应的区域。

2.4 区域合并根据相邻像素点的标签，将相邻像素点合并为一个区域。

合并的条件可以根据实际情况进行设置，如像素点灰度值差异较小、像素点位置相邻等。