2009年三明市普通高中毕业班质量检查

A．B．C．D．．下列事件是必然事件的是（A．打开电视机，正在播电视剧B．小明坚持体育锻炼，今后会成为奥运冠军C．买一张电影票，座位号正好是偶数D．13个同学中，至少有2．九年级（1）班名同学在某次“分钟仰卧起坐”的测试中，成绩如下（单位：次），39，46，，39，这组数据的众数、中位数分别是（分．请将答案填入答题卡．．．的相应位置）900，则这个多边形的边数是．30，AB=5个白球，它们除了颜色外都相同．随机从中个点．……的相应位置．作图或添辅助（第18题备用图））请你写出小明设计的三种测量方法中AB的长度：图①AB= ，图②AB= ，图③AB= ；（6分））请你再设计一种不同于以上三种的测量方法,画出示意图（不要求写画法），用字母标注需测量的边或角,并写出AB的长度．（4分）（本题满分10分）2009年4月1日《三明日报》发布了“2008年三明市国民经济和社会发展统计公报”90，AB为把产品打入国际市场，某企业决定从下面两个投资方案中选择一个进行投资生产．方＜a＜8），每件产品销售件；方案二：生产乙产品，每件产品成本为8件．另外，年销售x件乙产品．．．与相应生产件数x（x为正整数））如果你是企业决策者，为了获得最大收益，你会选择哪个投资方案？（4分）按顺时针方向旋转，角的两边090α<≤）． 分） 5分）∴不等式组的解集为33x -<≤． ···方法3：（2） 81 （每空2分））补全条形统计图正确（2分） ）设今明两年林业产值的年平均增长率为x ． 根据题意，得250(1)60.5x += ··································解得：10.1x ==10% ，2 2.1x =-（不合题意，舍去）答：今明两年林业产值的年平均增长率为10%AB=22a b + AB=22c a - AB=c AB=ac b90．ABE的外接圆相切．························ 6分 ······················ 7分 ······················ 8分 DN CD ，CMN S CM CD ∆，，············································· 11分 ······················ 12分 DN CD ，CMN S CM CD ∆， ∴DN 3 ···························· 9分 ，且AC ⊥······················ 10分重合，点P 与D 重合．··························· 8分 ··························· 9分 45， AC= BC ························· 10分 045α<≤时，ACQ =∠ACP +∠PCQ =∠························· 11分 4590α<<时，同理可得。

2009年三明市初中生学业质量检测地理试题（满分100分；考试时间60分钟）★友情提示：所有答案都必须填、涂在答题卡相应的位置上，答在本试卷上一律无效一、单项选择题（下列各题中，只有一个正确选项，请将正确选项涂在答题卡上，每题2分，共40分）1.下列四地中，位于西半球的是（）A．.0º、15ºW B．30ºN、165ºE C．0º、45ºE D．30ºS、150ºE 2、在比例尺1∶5000000的地图上，量得两地间的距离为3厘米，两地间的实地距离为A．1．5千米B．15千米C．150千米D．1500千米3．下列地理现象中，由地球自转造成的是（）Ａ．福建省冬季白昼时间比夏季白昼时间短Ｂ．当北京夜幕降临时，伦敦还是艳阳高照Ｃ．北京天安门广场升旗时刻每天都不同Ｄ．在地球寒带有极昼和极夜现象4．没有阳光直射，也没有极昼极夜现象的是（）A．北温带和南温带B．热带和南温带C．热带和北温带D．北寒带和南寒带5、有关亚洲地形地势的说法，正确的是（）A．中部高，四周低 B．以高原为主 C．四周高，中部低 D．以平原为主6．下列天气状况与人们的户外活动对应妥当的是（）A．沙尘漫天——在操场打篮球B．台风将至——捕鱼船队起航C．久雨初晴——带儿童日光浴D．雷雨大风——在大树下避雨7．黄土高原地区的典型民居是（）A．竹楼B．冰屋C．窑洞D．四合院8．下列省级行政单位与其行政中心匹配正确的是（）A．云南—贵阳B．浙江—南昌C．吉林—沈阳D．湖南—长沙9．关于我国人口的叙述，正确的是（）A．2000年我国总人口为15.36亿，是世界上人口最多的国家B．我国城镇人口比重大，农村人口比重小C．我国人口的突出特点是人口基数大，人口增长快D．我国人口约占世界人口总数的10％10．下列四幅图中，反映青藏地区气候特征的是（）11．我国民族分布的特点是（）A．大杂居，小聚居B．大聚居，小杂居C．汉族只分布在东部地区D．少数民族都分布在山区12、关于我国气候的叙述，正确的是（）A．我国的气候类型单一，对农作物、森林牧草的生长十分有利B．雨热同期是我国气候资源的一大优势C．与世界同纬度地区相比，我国的年较差和降水的年际变化都比较小D．我国是世界上季风气候最典型的国家，灾害性天气十分罕见13．我国长度最长、流域面积最广、水量最大的河流是（）A．珠江B．长江C．黄河D．黑龙江14．治理黄河的关键是（）A．加固黄河下游大堤B．加强中游地区水土保持工作C、在上游修建水库D．开挖河道15、我国四大牧区在自然条件方面共同的特征是（）A．都有广阔的天然草场B．都处在干旱地区C．降水都比较多D．草场都处在高寒地区16、煤炭是我们第一大能源，我国煤炭产量最多的省级行政区是（）A．福建B．广东C．云南D．山西17、下列我国南北铁路干线中，位于最东的铁路干线是（）A．京九线B．京广线C．京沪线D．宝成线18、被誉为“购物天堂”的城市是（）A、西安B、香港C、昆明D、三明19、台湾工业的主要特点是（）A．以钢铁、机械产业为主B．以旅游、博彩业为主C．以制造加工业为主D．以农产品加工业为主20、三明市最大的河流是（）A．尤溪B．金溪C．沙溪D．建溪二．非选择题（共60分，请将答案填在答题卡上）21．读“世界轮廓图”，写出图中字母和数字所代表的地理事物（8分）A 洲，B 洲，C 洲。

2014年厦门市高中毕业班适应性考试语文参考答案一、古代诗文阅读（27分）（一）默写常见的名句名篇（6分）1．（1）渐车帷裳（2）秋风萧瑟（3）吾未见其明也（4）杳不知其所之也（5）羽扇纶巾（6）略无慕艳意（二）文言文阅读（15分）2．B（审：明白）3．C（①是对獐子是否可驯养感到怀疑，③是王仲凫认为侯子不了解他的两条狗，⑥是獐子被咬死后有人认为没有凶犬獐子也会有灾难。

）4．D（意在告诫人们对于邪恶之人不可丧失警惕。

）5．（1）我依照（这个办法）安抚它们，难道它们能再去伤害（獐子）吗？（“因”“安”“岂……哉”各1分，句意不通顺酌情扣分。

）（2）王仲凫很不高兴，把狗咬死獐子的情况告诉了侯子。

（“语”“以”“状”各1分，句意不通顺酌情扣分）（三）古代诗歌阅读（6分）6．（1）（2分）示例一：“起”字写傍晚时钟声响起，以声衬静写出环境的静寂（1分），反衬诗人内心的不平静（1分）。

示例二：“连”字写眼前雨势连绵、苍茫暗淡之景（1分），烘托了诗人内心的伤感（1分）。

（意思对即可）(2)以问句起写“我”独自西行，以问句收写孤鸟南归，首尾呼应（1分）；鸟儿的南归和诗人西行相比照（1分），含蓄表达了对亲故的思念之情（1分），以及前途未卜的茫然和生命孤寂与无助（1分）。

（意思对即可）二、文学名著、文化经典阅读（16分）（一）文学名著阅读(10分)7．B E（B项，杜竹斋亏了两万元左右，而不是“赚了五千元”；杜竹斋抽出资本的原因主要是顾虑巨额资本的风险，而不是“嫌获利太少”；E项，女茶房在法庭上一口咬定一切罪行都是马斯洛娃独自干的，而不是“马斯洛娃和男茶房合伙谋财害命”；马斯洛娃当庭“什么话也没说”，“只抬头望望人，就垂下眼睛哭泣”，而不是“激烈申辩，语带嘲讽”。

）8．（5分）（1）第一问：张鲁图谋攻取西川。

（1分）第二问：【情节要点】①张松本想把西川地图献给曹操；②因被曹操冷遇，携图离去；③归川途中，受到刘备盛情款待；④张松便将地图献给刘备。

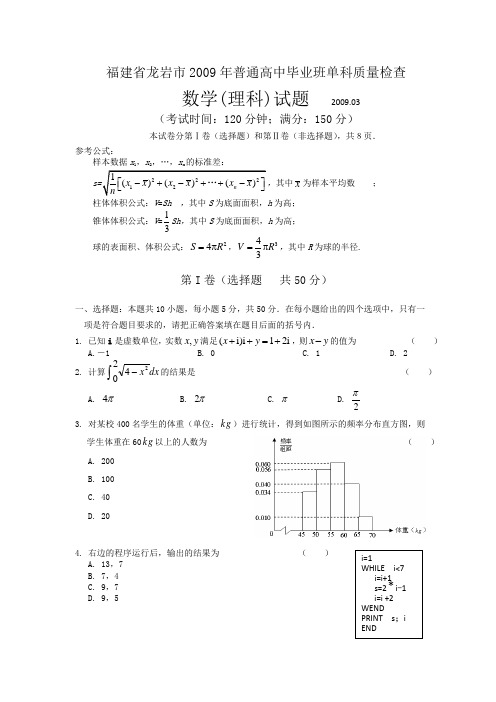
福建省龙岩市2009年普通高中毕业班单科质量检查 数学(理科)试题 2009.03（考试时间：120分钟；满分：150分）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），共８页．参考公式：样本数据x 1，x 2，…，x n 的标准差：其中x 为样本平均数 ；柱体体积公式：V =Sh ，其中S 为底面面积，h 为高；锥体体积公式：V =31Sh ，其中S 为底面面积，h 为高； 球的表面积、体积公式：24S R =π，343V R =π，其中R 为球的半径.第I 卷（选择题 共50分）一、选择题：本题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一 项是符合题目要求的，请把正确答案填在题目后面的括号内．1. 已知i 是虚数单位，实数y x ,满足(i)i 12i x y ++=+，则y x -的值为 （ ） A.－1 B. 0 C. 1 D. 22. 计算dx x 2402-⎰的结果是 （ ）A. π4B. π2C. πD.2π 3. 对某校400名学生的体重（单位：kg ）进行统计，得到如图所示的频率分布直方图，则 学生体重在60kg 以上的人数为 （ ） A. 200 B. 100 C. 40 D. 204. 右边的程序运行后，输出的结果为 （ ） A. 13，7 B. 7，4 C. 9，7 D. 9，55. 已知椭圆)0(12222>>=+b a b y a x 的焦点分别为1F 、2F ，4=b ，离心率为53．过1F 的直线交椭圆于A 、B 两点，则2ABF ∆的周长为 （ ）A. 10B. 12C. 16D. 206. 已知函数1cos 22sin )(2-+=x x x f ，将)(x f 的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，再将所得图象向右平移4π个单位，得到函数)(x g y =的图象，则)(x g 的解 析式为（ ） A. x sin 2 B. x cos 2C. )434sin(2π-x D. x 4cos 2. 7. 下列说法正确的是（ ）A. 函数)62sin(2π-=x y 的图象的一条对称轴是直线12π=xB. 若命题P ：“存在R x ∈，012>--x x ”，则命题P 的否定：“任意R x ∈，012≤--x x ”C. 若0≠x ，则21≥+xxD. “1=a ”是“直线0=-ay x 与直线0=+ay x 互相垂直”的充要条件 8. 设m 、n 是两条不同直线，α、β、γ是三个不同平面，给出下列四个命题：①若α⊥m ，α//n ，则n m ⊥ ②若βα//，γβ//，α⊥m ，则γ⊥m ③若α//m ，β//m ，则βα// ④若γα⊥，γβ⊥，则βα//其中正确命题的序号是（ ） A. ①和② B. ②和③C. ③和④D. ①和④9. 对任意两个正整数m 、n 定义某种运算○+：()()m n m n m n m n mn+⎧⊕=⎨⎩与奇偶性相同与奇偶性不同，则集合P (,|20,,a b a b a b ⊕=∈＝｛）N *｝中元素的个数为（ ） A. 21B. 22C. 23D. 2410. 把正整数按一定的规则排成了如图所示的三角形数表．设ij a （i ，j ∈N *）是位于这个三角形数表中从上往下数第i 行、从左往右数第j 个数，如42a ＝8． 若ij a ＝2009，则i 与j 的和为（ ） A. 105 B. 106 C. 107D. 108第Ⅱ卷（非选择题 共100分）二、填空题：本大题共5小题，每小题４分，共20分，请把正确答案填在后面横线上． 11. 袋中有3个黑球，1个红球．从中任取2个，取到一个黑球得0分，取到一个红球得2分，则所得分数ξ的数学期望=ξE .12. 已知二项式62）（xa x +的展开式中的常数项为15，则实数a 为 . 13. 设向量a ,b 满足| a －b |=2，| a |=2，且a －b 与a 的夹角为3π，则| b |= .14. 已知函数)(x f 是定义在R 上的奇函数，当x ≥0时，)1(log )(2+=x x f . 若2)(-<m f ，则实数m 的取值范围是 .15. 对任意正整数n ，定义n 的双阶乘!!n 如下：当n 为偶数时，!!(2)n n n =-(4)n -642⨯⨯⨯⨯； 当n 为奇数时，135)4)(2(!!⨯⨯⨯⨯--= n n n n .现有四个命题：①（2009！！）·（2008！！）=2009！； ② 2008·2008！！=2009！！－ 2008！！； ③ 2009！！的个位数字为5；④（a +b ）!! = a !!+b !!（a 、b ∈ N *）其中所有正确命题的序号是 .三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤． 16.（本小题满分13分）已知),2(ππα∈，且262cos2sin=+αα. （Ⅰ）求αcos 的值；（Ⅱ）若53)sin(-=-βα，),2(ππβ∈，求cos β的值.17.（本小题满分13分）如图，在体积为1的三棱柱111C B A ABC -中，侧棱⊥1AA 底面ABC ，AB AC ⊥，11==AA AC ，P 为线段AB 上的动点.（Ⅰ）求证：P C CA 11⊥；（Ⅱ）当AP 为何值时，二面角111A PB C --的 大小为4π？APBA 1C 1B 1C18. (本小题满分13分)近段时间我国北方严重缺水, 某城市曾一度取消洗车行业. 时间久了，车容影响了市容市 貌. 今年该市决定引进一种高科技产品污水净化器，允许洗车行开始营业，规定洗车行必须购买这种污水净化器，使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元，全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆，预计今后每年汽车数量将增加2000辆.洗车行A 经过测算，如果全市的汽车总量是x ，那么一年内在该洗车行洗车的平均辆次是x 41，该洗车行每年的其他费用是20000元. 问： 洗车行A 从今年开始至少经过多少年才能收回购买净化器的成本？ （注：洗车行A 买一台污水净化器就能满足洗车净水需求）19.（本小题满分13分）已知抛物线C:)0(22>=p px y 上横坐标为4的点到焦点的距离为5. （Ⅰ）求抛物线C 的方程；（Ⅱ）设),(11y x A ，),(22y x B 是抛物线C 上任意两点，且a y y =-||21（0>a ，且a 为常数）. 过弦AB 的中点M 作垂直于y 轴的直线交抛物线于点D ，连结AD 、BD 得到ABD ∆，求证：ABD ∆的面积为定值；（Ⅲ）在（Ⅱ）的条件下，分别过弦AD 、BD 的中点作垂直于y轴的直线依次交抛物线于点E 、F ，连结AE 、DE 和BF 、 DF ，得到ADE ∆和BDF ∆，并按此方法继续下去. 若设ABD S a ∆=1, ,2BDF ADE S S a ∆∆+=，n a 是第n 次操作时得到的12-n 个三角形面积的和，记n n a a a S +++= 21，求证：243a S n <.O20.（本小题满分14分）设函数1()(2)ln 2f x a x ax x=-++（a ∈R ）. （Ⅰ）当0=a 时，求)(x f 的极值；（Ⅱ）当0≠a 时，求)(x f 的单调区间；（Ⅲ）当2=a 时，对于任意正整数n ，在区间⎥⎦⎤⎢⎣⎡++n n 16,21上总存在m +4个数12,,a a 31234,,,,,,,m m m m m a a a a a a ++++使得<+++)()()(21m a f a f a f 1()m f a ++234()()()m m m f a f a f a +++++成立，试问：正整数m 是否有最大值？若有求其最大值；否则，说明理由.21. 本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题记分． （1）（本小题满分7分）选修4－2：矩阵与变换已知矩阵P=⎪⎪⎭⎫⎝⎛020a ，Q=⎪⎪⎭⎫⎝⎛010b ，若矩阵PQ 对应的变换把直线04:1=+-y x l 变为直线04:2=++y x l ，求a 、b 的值.（2）（本小题满分7分）选修4－4：坐标系与参数方程已知直线l 的极坐标方程是01sin cos =-+θρθρ．以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，椭圆Ｃ的参数方程是⎩⎨⎧==θθsin ,cos 2y x （θ为参数），求直线l 和椭圆Ｃ相交所成弦的弦长． （3）（本小题满分7分）选修4－5：不等式选讲已知实数c b a 、、满足12=++c b a ，1222=++c b a ，求证：213c -≤≤.2009年龙岩市普通高中毕业班单科质量检查数学(理科)试题参考答案及评分标准说明：一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则.二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分. 三、解答右端所注分数，表示考生正确做到这一步应得的累加分数.四、只给整数分数，选择题和填空题不给中间分.一、选择题：本题考查基本知识和基本运算，每小题5分，满分50分. 1. B 2. C 3. B 4.C 5.D 6.A 7. B 8. A 9. C 10. C 二、填空题：本题考查基本知识和基本运算，每小题4分，满分20分. 11. 112. 1±13. 214. (,3)-∞-15. ①③三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.16. 本题主要考查三角函数的倍角公式、两角和公式等基本知识，考查学生的运算求解能力. 满分13分.解：（Ⅰ）因为sin cos22αα+=两边同时平方得 1sin 2α=. ………………………………………（4分） 又2παπ<<，所以cos 2α=-. ………………………………………（6分） （Ⅱ）因为2παπ<<，2πβπ<<，所以2ππβ-<-<-，得22ππαβ-<-<.又3sin()5αβ-=-,知4cos()5αβ-=. …………………（9分）cos cos[()]cos cos()sin sin()βααβααβααβ=--=-+-413()525=+⨯-=………………………………………（13分）17. 本题主要考查线线位置关系，二面角的求法等基本知识，考查空间想像能力，运算求解能力和推理论证能力. 满分13分. 解：（Ⅰ）证明：连结1AC ，侧棱1AA ⊥底面ABC ，1AA AB ∴⊥，又AB AC ⊥.AB ∴⊥平面11A ACC .又1CA ⊂平面11A ACC ，1AB CA ∴⊥ . ………（3分） 11AC AA ==，∴四边形11A ACC 为正方形，11AC CA ∴⊥. 1AC AB A =， 1CA ∴⊥平面1AC B .又1C P ⊂平面1AC B ，11CA C P ∴⊥. …………（6分） （Ⅱ）1111111,,C A AA C A A B ⊥⊥1111AA A B A =.∴11C A ⊥平面11ABB A .又11111112ABC A B C V AB -=⨯⨯⨯=， 2AB ∴=. 如图，以1A 为原点，建立空间直角坐标系1A -xyz ，设AP=x ，则 1(0,0,0)A 、1(0,2,0)B 、1(0,0,1)C 、(1,,0)P x .知面11A PB 的一个法向量为11(0,0,1)A C =，……（9分） 设面11C PB 的一个法向量为(,,)n a b c =，1(1,2,0)B P x =- ，11C B (0,2,1)=- .由1110n B P n C B ⎧⋅=⎪⎨⋅=⎪⎩ 得(2)020a x b b c +-=⎧⎨-=⎩令1,2,2b c a x ===-则， (2,1,2)n x ∴=-………（11分）依题意：1111cos4||(2n AC n AC π⋅==⋅=2解得12x =，22x =2AP ∴=时，二面角111C PB A --的大小为4π. …………（13分） yCBA 1Az xC 1B 1PCB 118．本题主要考查数列与不等式等基本知识，考查运用数学知识分析问题与解决问题的能力，考查应用意识. 满分13分.解：设第一年（今年）的汽车总量为1a ，第n 年的汽车总量为n a ，则180000a = 282000a =，…80000(1)2000n a n =+-⋅.数列{}n a 构成的首项为80000，公差为2000的等差数列，12(1)8000020002n n n n S a a a n -=++⋅⋅⋅+=+⋅. ………………………（4分） 若洗车行A 从今年开始经过n 年可以收回购买净化设备的成本. 则（(1)8000020002n n n -+⋅）184⋅⋅-20000n ≥900000，………………………（8分） 整理得，2694500,n n +-≥ (6)(75)0,n n -+≥因为0n >，所以 6n ≥.答：至少要经过6年才能收回成本. …………………………………………（13分）19．本题主要考查直线与抛物线的位置关系、等比数列求和等基本知识，考查运算求解能力和分析问题、解决问题的能力. 满分13分 解：（Ⅰ）依题意得：452p+=，解得2p =. 所以抛物线方程为24y x = . ………………………………………………（3分） （Ⅱ）若12x x =，即直线AB 垂直于x 轴，不防设12y y >，由12,y y a -=又由抛物线对称性可得：12ay =.又2114y x =，得 2116a x = ，故S △ABD =332a . …………………………（4分）若12x x ≠，设直线AB 方程：y kx b =+，由方程组2,4,y kx b y x =+⎧⎨=⎩消去x 得：2440ky y b -+=.（※）依题意可知：0k ≠. 由已知得124y y k +=，124b y y k=. ……………………………………（5分） 由12y y a -=，得221212()4y y y y a +-=，即221616b a k k-=，整理得221616kb a k -=. 所以2216(1)a k kb =- . …………………………………………（6分）AB 中点222(,)bk M k k-，所以点212(,)D k k， 依题意知12211122ABD bkS DM y y a k -=-=⨯⨯. 又因为方程（※）中判别式16160kb =->，得10kb ->.所以2112ABD bkS a k -=⨯⨯ ，又22116a k bk -=， 所以23121632ABDa a Sa =⨯⨯=. 又a 为常数，故ABDS的面积为定值. …………………………………（9分）（Ⅲ）依题意得：31,32a a =3323()()242,4,3232a a a a =⨯=⨯…，311()2232n n n a a --⨯=. 故332n a S =⨯111416⎡+++⎢⎣…2212n -⎤+⎥⎦311()413214n a -=⋅- 311()244n a ⎡⎤=-⎢⎥⎣⎦＜324a . ………………………………（13分） 注：本题第（Ⅱ）问另解，参照本标准给分；第（Ⅲ）问若用定积分证明，同样给分. 20. 本题主要考查函数的单调性、极值、最值、不等式等基本知识，考查运用导数研究函数性质的方法，考查分类与整合及化归与转化等数学思想. 满分14分.解：（Ⅰ）依题意，知()f x 的定义域为(0,)+∞.当0a =时，1()2ln f x x x =+ ，222121()x f x x x x -'=-=. 令()0f x '=，解得12x =. 当102x <<时，()0f x '<；当12x >时，()0f x '> . 又1()22ln 22f =-，所以()f x 的极小值为22ln 2-，无极大值 . …………………………（3分）（Ⅱ）221()2a f x a x x-'=-+ 222(2)1ax a x x +--= .令()0f x '=，解得1211,2x x a =-=. …………………………（4分）若0a >，令()0f x '<，得102x <<；令()0f x '>，得12x > . 若0a <，①当2a <-时，112a -<， 令()0f x '<，得10x a <<-或12x >；令()0f x '>，得112x a -<<.②当2a =-时，22(21)()0x f x x -'=-≤. ③当20a -<<时，得112a ->，令()0f x '<，得102x <<或1x a >-；令()0f x '>，得112x a<<-.综上所述，当0a >时，()f x 的递减区间为1(0,)2，递增区间为1(,)2+∞. 当2a <-时，()f x 的递减区间为11(0,),(,)2a -+∞；递增区间为11(,)2a -. 当2a =-时，()f x 递减区间为(0,)+∞.当20a -<<时，()f x 的递减区间为11(0,),(,)2a -+∞，递增区间为11(,)2a-. …………………………（9分）（Ⅲ）当2a =时，1()4f x x x=+，由222141()4x f x x x -'=-+=，知11,62x n n ⎡⎤∈++⎢⎥⎣⎦时，()0f x '≥ . 1()()42f x f ==min ，1()(6)f x f n n =++max .依题意得：11()4(6)2mf f n n <++ 对一切正整数成立. ……………（11分）令16k n n=++ ，则8k ≥（当且仅当1n =时取等号）.又()f k 在区间1[6,)n n +++∞单调递增，得min 1()328f k =，故1328m <，又m 为正整数，得32m ≤，当32m =时，存在123212a a a ==⋅⋅⋅==，12348m m m m a a a a ++++====，对所有n 满足条件.所以，正整数m 的最大值为32. …………………………………（14分）21. （1）本题主要考查矩阵乘法与变换等基本知识，考查运算求解能力，考查函数与方程思想. 满分7分.解：PQ ＝020120000b a b a ⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭， PQ 矩阵表示的变换T ：(,)(,)P x y P x y '''满足条件 '20'0x b x y a y ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.所以'2,',x bx y ay =⎧⎨=⎩ ………………………（3分）直线40x y -+=任取点(),x y ，则点()2,bx ay 在直线40x y ++=上，故240bx ay ++=，又40x y -+=，得21,1,b a =⎧⎨=-⎩所以1,1.2a b =-⎧⎪⎨=⎪⎩ ………………………………………（7分）（2）本题主要考查直线极坐标方程和椭圆参数方程等基本知识，考查运算求解能力，考查化归与转化思想. 满分7分.解：由题意知直线和椭圆方程可化为：10x y +-=， ①2214x y +=． ② …………………………（２分）①②联立，消去y 得：2580x x -=，解得10x =，285x =． 设直线与椭圆交于A 、B 两点，则12AB x =-5=．故所求的弦长为5． …………………………（７分）（3）本题主要考查不等式证明等基本知识，考查化归与转化思想. 满分7分.解：因为22221,1a b c a b c ++=++=， 所以22221,1a b c a b c +=-+=-． 由柯西不等式：22222(12)()(2)a b a b ++≥+ ， …………………………（3分）225(1)(1)c c -≥-，整理得，2320c c --≤，解得21 3c-≤≤．∴213c-≤≤．…………………………（7分）。

2009年福建省宁德市普通高中毕业班质量检查数学（理科）试卷本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，本卷满分150分，考试时间120分钟。

注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上。

2．考生作答时，将答案答在答题卡上。

请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效。

3．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳酸笔书写，字体工整、笔迹清楚。

4．做选考题时，考生按照题目要求作答，并用2B 铅笔在答案题卡上把所选题目对应的题号涂黑。

5．保持答题卡卡面的清楚，不折叠、不破损，考试结束后，将本试卷和答题卡一并交回。

参考公式： 锥体的体积公式：13V Sh =，其中S 为底面面积，h 为高； 球的表面积、体积公式：24S r π=，343V r π=，其中r 为球的半径。

第I 卷（选择题 共50分）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合2{|40},{|(2)0},A x x B x x x =-<=->则A B I =A ．{|20}x x -<<B ．{|02}x x <<C ．{|0}x x <D ．R2．i 为虚数单位，则复数1i z i=+在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3．在等比数列{}n a 中，若141,8a a ==，则该数列的前6项和为A ．56B ．63C ．127D ．2554．已知一个算法的程序框图如图所示，当输出的结果为0时，输入的x 的值为A ．—1或1B ．—2或0C ．—2或1D ．—1或05．若抛物线22y px =的焦点与双曲线22163x y -=的 右焦点重合，则p 的值为 A ．3 B ．6 C ．3 D ．236．设a 为直线l 的方向向量，n 为平面α的法向量，则0a n ⋅=是//l α的A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分也非必要条件7．右图是一个多面体的三视图，则其全面积为A ．3B ．36+C ．36+D ．34+r8．设函数()sin()(0,0)2f x x πωϕωϕ=+><<的部分图象 如图所示，直线6x π=是它的一条对称轴，则函数()f x 的解析式为A ．()sin()3f x x π=+B ．()sin(2)6f x x π=- C ．()sin(4)3f x x π=+ D ．()sin(2)6f x x π=+ 9．函数()f x 是定义域为R 的奇函数，且0x >时，()21x f x x =--，则函数()f x 的零点个数是A ．1B ．2C ．3D ．4 10．已知四边形OABC 是边长为1的正方形，3OD OA =u u u r u u u r ，点P 为BCD ∆内（含边界）的动点，设(,)OP xOC yOD x y R =+∈u u u r u u u r u u u r ，则x y +的最大值等于A ．1B ．2C ．3D ．43第Ⅱ卷（非选择题 共100分）二、填空题：本大题共5小题，每小题4分，共20分，把答案填写在答题卡的相应位置。

2009年福建省龙岩市普通高中毕业班单科质量检查数学试卷（文科）参考公式：样本数据x 1，x 2， …，x n 的标准差：其中x 为样本平均数； 柱体体积公式：V =Sh ， 其中S 为底面面积，h 为高；锥体体积公式：V =31Sh ，其中S 为底面面积，h 为高； 球的表面积、体积公式：24S R =π，343V R =π，其中R 为球的半径．第I 卷（选择题 共60分）一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案填在题目的括号内。

1．已知i 是虚数单位，实数y x ,满足(i)i 12i x y ++=+，则y x -的值为 （ ）A ．－1B ．0C ．1D ．22．为了求函数22)(x x f x-=的一个零点，某同学利用计算器，得到自变量x 和函数值)(x f 的部分对应值（精确到0．01）如下表所示：则函数f （x ）的一个零点所在的区间是（ ）A ．（0．6，1．0）B ．（1．4，1．8）C ．（1．8，2．2）D ．（2．6，3．0）3．下图所示的几何体（下底面是正六边形），其侧视图正确的是（ ）A ．B ．C ．D ．4．已知函数⎩⎨⎧≤>=),0(2),0(log )(2x x x x f x 若21)(=a f ，则a 的值为（ ）A ．1-B ．2C ．1-或21D ．1-或25．对某校400名学生的体重（单位：kg ）进行统计，得到如图所示的频率分布直方图，则学生体重在60kg 以上的人数为（ ）A ．200B ．100C ．40D ．206．已知椭圆)0(12222>>=+b a b y a x 的焦点分别为1F 、2F ，4=b ，椭圆的离心率为53，过1F 的直线交椭圆于A 、B 两点，则2ABF ∆的周长为 （ ）A ．10B ．12C ．16D ．20 7．下图的程序运行后，输出的结果为（ ）A ．13，7B ．7，4C ．9，7D ．9，58．已知函数1cos 22sin )(2-+=x x x f ，将函数)(x f y =的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数)(x g y =的图象，则)(x g 的解析式为 （ ）A ．)8sin(2π+x B ．)4sin(2π+xC ．)44sin(2π+xD ．x 4cos 2 9．下列说法正确的是（ ）A ．若0≠x ，则21≥+x xB ．函数)62sin(2π-=x y 的图象的一条对称轴是直线12π=xC ．1=a 是直线0=-ay x 与直线0=+ay x 互相垂直的充要条件D ．若命题P ：“存在R x ∈，012>--x x ”，则命题P 的否定：“任意R x ∈，012≤--x x10．设m 、n 是两条不同直线，α、β、γ是三个不同平面，给出下列四个命题： ①若α⊥m ，α//n ，则n m ⊥ ②若βα//，γβ//，α⊥m ，则γ⊥m③若α//m ，β//m ，则βα//④若γα⊥，γβ⊥，则βα//其中正确命题的序号是 （ ）A ．①和②B ．②和③C ．③和④D ．①和④11．对任意两个正整数m 、n 定义某种运算○+：()()m n m n m n mn m n +⎧⊕=⎨⎩与奇偶性相同与奇偶性不同，则集合*P (,|8,,N a b a b a b ⊕=∈＝｛）｝中元素的个数为（ ）A ．5B ．7C ．9D ．1112．若变量x 、y 满足条件10,40,1,x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩则y xx y +的取值范围是（ ）A ．[]2,+∞B ．102,3⎡⎤⎢⎥⎣⎦C ．3410,153⎡⎤⎢⎥⎣⎦ D ．5,33⎡⎤⎢⎥⎣⎦第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题４分，共16分．请把正确答案填在后面横线上． 13．圆03222=-+-y x x 的圆心到直线033=-+y x 的距离为 ．14．设向量)3,2(=，b (1,2)=，若向量λa + b 与向量c (4,1)=-垂直，则λ＝ ．15．已知函数()f x 为R 上的奇函数，当0x ≥时，()(1)f x x x =+．若()2f a =-，则实数a = ．16．对任意正整数n ，定义n 的阶乘!n 如下：123)2)(1(!⨯⨯⨯⨯--= n n n n ．例如4！=4×3×2×1． 现有四个命题： ①2！×3！= 6！；② 2009！的个位数字为0； ③（a +b ）!=a !+b !（a ，b ∈ N *）；④n ·n ！=（n +1）！- n ！（n ∈N *）．其中所有正确命题的序号是 ．三、解答题：本大题共６小题，共74分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）已知),2(ππα∈，且sincos223αα+=． （Ⅰ）求αcos 的值；（Ⅱ）若53)sin(-=+βα，)2,0(πβ∈，求βsin 的值．18．（本小题满分12分）晚会上，主持人前面放着A 、B 两个箱子，每箱均装有3个完全相同的球，各箱的三个球分别标有号码1，2，3。

2009年三明市初中毕业暨高级中等学校招生统一考试数学试卷参考答案及评分标准说明：以下各题除本卷提供的解法外，其他解法本标准不一一例举，评卷时可参考评分标准，按相应给分段评分．用计算器计算的部分，列式后可直接得到结果．一、选择题（每小题4分，共40分）1． B 2． C 3． B 4．A 5．D 6．A 7．C 8．D 9．B 10．C二、填空题（每小题4分，共24分）11． 12． 2(2)a x - 13． 7 14． 10 15． 1416． 21n n -+ 三、解答题（共86分）17．（1）解法一：原式=2(3)(3)(3)(3)9a a a a a a ++-÷+-- ································································· 3分 =2(3)(3)(3)(3)a a a a a a +-⋅+- ································································ 5分 =2a a··························································································· 7分 =2 ································································································· 8分解法二：原式=（1133a a +-+）⋅29a a - ····························································· 2分 =1(3)(3)3a a a a +-⋅-+1(3)(3)3a a a a +-⋅+ ··········································· 4分 =33a a a a +-+ ···················································································· 6分 =2a a····························································································· 7分 =2 ································································································· 8分（2）解：解不等式①，得 3x >-， ··········································································· 3分 解不等式②，得 3x ≤， ············································································· 6分 不等式①、②的解集在数轴上表示如下：·············································· 7分 ∴不等式组的解集为33x -<≤． ··································································· 8分18．解：（1）①tan a α⋅ ② 2c ③ b （每空2分）（2）示意图正确2分，AB 表示正确2分．（注：本题方法多种，下面列出3种供参考）方法1：方法2： 方法3：19．解：（1） 221 （2） 81 （每空2分）（3）补全条形统计图正确（2分）（4）设今明两年林业产值的年平均增长率为x ．根据题意，得250(1)60.5x += ······························································································ 2分解得：10.1x ==10% ，2 2.1x =-（不合题意，舍去） ······························· 3分答：今明两年林业产值的年平均增长率为10%． ········································ 4分AB=c AB=acb20．（1）证法一：∵∠B =90°， ∴AE 是△ABE 外接圆的直径． ··· …1分 取AE 的中点O ，则O 为圆心，连接OB 、OD ． ················ 2分∵AB =AD ，∠BAO =∠DAO ，AO =AO ， ∴△AOB ≌△AOD ． ················································ 4分∴OD =OB ． ··········································································· 5分 ∴点D 在△ABE 的外接圆上． ············································· 6分证法二：∵∠B =90°，∴AE 是△ABE 外接圆的直径． ········································ 1分 ∵AB =AD ，∠BAE =∠DAE ，AE =AE ，∴△ABE ≌△ADE ． ··············································································· 3分 ∴∠ADE =∠B =90°． ················································································· 4分取AE 的中点O ， 则O 为圆心，连接OD ，则OD =12AE ． ∴点D 在△ABE 的外接圆上． ·································································· 6分（2）证法一：直线CD 与△ABE 的外接圆相切． ·························································· 7分理由：∵AB ∥CD ， ∠B =90°． ∴∠C =90°． ····················································· 8分 ∴∠CED +∠CDE =90°． ·········································································· 9分 又∵OE =OD ， ∴∠ODE =∠OED ． ································································· 10分 又∠AED =∠CED ， ∴∠ODE =∠DEC ．∴ODC ∠=∠CDE +∠ODE =∠CDE +∠CED =90°． ················································ 11分 ∴CD 与△ABE 的外接圆相切． ·························································· 12分 证法二： 直线CD 与△ABE 的外接圆相切． ························································ 7分 理由：∵AB ∥CD ， ∠B =90°． ∴∠C =90°． ··························································· 8分 又∵OE =OD ， ∴∠ODE =∠OED ． ···················································· 9分 又∠AED =∠CED ，∴∠ODE =∠DEC ． ······················································· 10分 ∴OD ∥BC ．∴90ODC ∠= ． ··············································································· 11分 ∴CD 与△ABE 的外接圆相切． ······································································ 12分21．解：（1）1(10)y a x =- （1δx δ200，x 为正整数） ········································ 2分22100.05y x x =- （1δx δ120，x 为正整数） ······················································ 4分（2）①∵3＜a ＜8， ∴10-a ＞0，即1y 随x 的增大而增大 ， ··································· 5分∴当x =200时，1y 最大值=（10-a ）×200=2000-200a （万美元） ···················· 6分 ②220.05(100)500y x =--+ ··································································· 7分∵-0.05＜0， ∴x =100时， 2y 最大值=500（万美元） ··································· 8分（3）由2000-200a ＞500，得a ＜7.5，∴当3＜a ＜7.5时，选择方案一； ········································································ 9分 由2000200500a -=，得 7.5a =，∴当a =7.5时，选择方案一或方案二均可； ························································ 10分 由2000200500a -<，得 7.5a >，∴当7.5＜a ＜8时，选择方案二． ······································································ 12分 22．（1）证法一：连接BD ，则BD 过点O ．∵AD ∥BC ， ∴∠OBM =∠ODN ． ···················· 1分又OB =OD ， ∠BOM =∠DON ， ······················ 2分∴△OBM ≌△ODN ． ····························· 3分∴BM =DN ． ···························· 4分证法二：∵矩形ABCD 是中心对称图形，点O 是对称中心．···································································································· 1分∴B 、D 和M 、N 关于O 点中心对称． ····························· 3分∴BM =DN ． ···································································· 4分（2）证法一：∵矩形ABCD ，∴AD ∥BC ，AD =BC ．又BM =DN ， ∴AN =CM ． ························ 5分∴四边形AMCN 是平行四边形． ························· 6分由翻折得，AM =CM ， ························ 7分∴四边形AMCN 是菱形． ························· 8分证法二：由翻折得，AN =NC ，AM =MC ，∠AMN =∠CMN ． ······················································· 5分∵AD ∥BC ， ∴∠ANM =∠CMN ．∴∠AMN =∠ANM ． ∴AM =AN ． ··································································· 6分 ∴AM =MC =CN =NA ． ··············································································· 7分 ∴四边形AMCN 是菱形． ········································································· 8分（3）解法一：∵12CDN S DN CD ∆= ，12CMN S CM CD ∆= ，又CDN S ∆：CMN S ∆=1︰3，∴DN ︰CM =1︰3 ············································· 9分设DN =k ，则CN =CM =3k ．过N 作NG ⊥MC 于点G ，则CG =DN =k ，MG =CM -CG =2k ． ························ 10分NG =∴MN == ································································ 11分∴DN MN == ··························································· 12分 解法二：∵12CDN S DN CD ∆= ，12CMN S CM CD ∆= ， 又CDN S ∆：CMN S ∆=1︰3， ∴DN ︰CM =1︰3 ·················································· 9分连接AC ，则AC 过点O ，且AC ⊥MN ．设DN =k ，则CN =AN =CM =3k ，AD =4 k ．CD == ··················································· 10分OC =12AC =∴MN=2ON = ··················································· 11分 ∴DN MN ==． ···························································································· 12分 23．解：（1）根据题意，得 10,22550.2b c b c ⎧-++=⎪⎪⎨⎪-++=⎪⎩ ······························································· 1分 解得3,5.2b c =⎧⎪⎨=-⎪⎩ ············································ 2分 ∴215322y x x =-+- ······················································· 3分 =21(3)22x --+ ∴顶点C 的坐标为（3，2）． ·············································································· 4分（2）①∵CD =DB =AD =2，CD ⊥AB ，∴∠DCB =∠CBD =45°． ············································· 5分ⅰ）若CQ =CP ，则∠PCD =12∠PCQ =22.5°． ∴当α=22.5°时，△CPQ 是等腰三角形． ·············· 6分ⅱ）若CQ =PQ ，则∠CPQ =∠PCQ =45°，此时点Q 与D 重合，点P 与A 重合．∴当α=45°时，△CPQ 是等腰三角形． ············································ 7分ⅲ）若PC =PQ ， ∠PCQ =∠PQC =45°，此时点Q 与B 重合，点P 与D 重合．∴α=0°，不合题意． ············································ 8分 ∴当α=22.5°或45°时，△CPQ 是等腰三角形． ················································· 9分 ②连接AC ，∵AD =CD =2，CD ⊥AB ，∴∠ACD =∠CAD =45 ， AC= BC=················································ 10分 ⅰ）当045α< ≤时，∵∠ACQ =∠ACP +∠PCQ =∠ACP +45°．∠BPC =∠ACP +∠CAD =∠ACP +45°．∴∠ACQ =∠BPC ． ··························································· 11分 又∵∠CAQ =∠PBC =45°，∴△ACQ ∽△BPC ． ∴AQ AC BC BP=． ∴AQ·BP =AC·BC=×=8 ·············································································· 12分ⅱ）当4590α<< 时，同理可得AQ·BP =AC·BC =8 ············································ 13分。

2009年三明市初中毕业暨高级中等学校招生统一考试语文试题（满分：150分；考试时间：6月20日上午8：30—10：30）友情提示：1.本试卷6页。

2.考生将自己的姓名、准考证号及所有答案均填写在答题卡上。

3.答题要求见答题卡上的“注意事项”。

一、语基（20分）（一）古诗文积累（10分）1.上下句默写。

（2分）（1）学而不思则罔，。

（《论语》）（2），奉命于危难之间。

（诸葛亮《出师表》）2.将晏殊《浣溪沙》一词默写完整。

（4分）浣溪沙晏殊，。

夕阳西下几时回？，。

小园香径独徘徊。

3.根据提示，默写诗句。

（4分）（1）初中毕业前夕，同学们互相激励，用李白《行路难》中的“，”来表达坚定的信念和对未来的憧憬。

（2）诗人心中激荡着保家卫国、建功立业的强烈愿望：辛弃疾表示“，赢得生前身后名”,李贺坦言“报君黄金台上意，”。

（二）阅读下面语段，完成4~6题。

（10分）在改革开放和现代化建设实践中，一批推动三明经济发展、代表三明地方形象的“名片”yùn育而生，它们是三明的文化符号和金字招牌。

这次脱颖而出的“三明十大名片”，极具代表性。

文明城这张名片是三明市20多年来精神文明创建活动成果的结晶；毛泽东词《如梦令·元旦》这张名片见证了三明革命老区人民为中国革命作出的巨大贡献；三钢这张名片凝．聚着几代炼钢人的心血、汗水、智慧与骄傲；绿色三明这张名片抒写了生态家园美景，（1）了林业改革的辉煌成就；泰宁世界地质公园这张名片（2）了山区人敢于走向世界的胆识与气魄；沙县小吃这张名片（3）着当代农民工的创业梦想与光荣；海峡两岸林博会这张名片使三明在海西建设中的地位和作用更加（4）；还有石壁客家祖地、闽学大师（杨时·罗从彦·朱熹）等名片，反映了三明这个地方的历史底yùn和文化积淀．。

这一张张名片沉甸甸、金闪闪，都是值得代代相传的宝贵财富。

（摘自《让“三明十大名片”闪金光》，有改动）4．根据拼音写汉字或给加点字注音。

时文短评（人教版高三教案设计）周爱菊【教学目标】知识目标：1、了解09高考新增题型—-时文短评的特点与类型2、把握概括与短评的一般要求能力目标：1、掌握一句话概括的主要写法与答题规范2、掌握短评的主要写法与答题规范【教学重、难点】掌握短评的主要写法与答题步骤【教学方法】多媒体课件、讨论法、分析法【教学课时】一课时【课前准备】1、印发课堂要做的练习给学生2、上课前播放歌曲——化学版的《青花瓷》。

【教学过程】一、导入新课同学们，刚刚大家所听的歌曲是广东的一位化学教师为方便学生记忆而改版的《青花瓷》,大家对他这种做法有什么看法吗？（学生回答后展示《新民晚报》2009、08、08上刊登的一些学生和老师对这件事发表的评论）像这种对最近发生的新闻或现象进行评论就是我们今天要讲的《时文评论》。

课件投影：时文：时效性比较强的网络、报刊文摘。

（捕捉社会热点）短评：“短”是指它篇幅短小，“评"评说，文体上属于议论文的范畴。

二、介绍09年高考对时文短评的要求及其题型这道题是09年1月份的省质检才出现的新题型，它的题型设置一般是：提供两则简短时文（1）用一句话概括以上材料的内容。

--准确捕捉基本信息（2)对材料所阐述的内容（现象、观点)有何看法?请阐述。

-—做出自己的评判今天我们主要就是针对这两种题型来学习时文短评主要的写法和答题规范.现在我们先来学习第一道题——一句话概括.三、一句话概括1、师生一起做示例：《09龙岩质检卷》材料一中国科技大学计算机系的贫困生小方在入学的第二个月，意外发现自己的就餐卡上多了一笔钱。

原来，科大采用“校园一卡通”网络技术，对学生的就餐情况进行监控,若学生在食堂月均用餐60次以上,消费总额却在150元以下者，则无需申请,其就餐卡上就会多出一笔由学校“隐形”提供的补助。

材料二“这房子能住吗？"“饭能吃吗？”2月10日，30多名小学生寒假期间在老师的带领下慰问贫困生，当他们走进一名叫关鹤琳的学生家时,发出了这样的感叹。