8-邻域边界跟踪算法

像素8邻域的英文The English term for 像素8邻域 is "8-pixel neighborhood". It refers to the neighboring pixels surrounding a central pixel in an image. In digital image processing, the 8-pixel neighborhood is commonly used for various operations such as edge detection, noise reduction, and image segmentation.When we talk about the 8-pixel neighborhood, we are referring to the eight adjacent pixels that surround a central pixel in a 2D image. These eight pixels are located to the north, south, east, west, and at the four diagonal directions from the central pixel. The concept of the 8-pixel neighborhood is widely used in image processing algorithms to analyze the local features and patternswithin an image.In image processing, the 8-pixel neighborhood is often used in tasks such as image enhancement, feature extraction, and object recognition. For example, in edge detection algorithms, the gradients of intensity values between the central pixel and its 8-pixel neighbors are calculated to identify the edges and boundaries within the image.Similarly, in image segmentation, the 8-pixel neighborhoodis used to group pixels with similar attributes together to form distinct regions within the image.The 8-pixel neighborhood is also important in thecontext of image filtering and noise reduction. By considering the intensity values of the neighboring pixels, various filtering techniques can be applied to remove noise and enhance the overall quality of the image. For example, the median filter, which replaces the central pixel withthe median intensity value of its 8-pixel neighborhood, is commonly used for noise reduction in digital images.在数字图像处理中，像素8邻域通常用于各种操作，如边缘检测、噪声减少和图像分割。

数字图像课后习题答案第一章1、说明图象数字化与图象空间分辨率之间的关系答。

数字图像的分辨率是数字图像数字化精度的衡量指标之一。

图像的空间分辨率是在图像采样过程中选择和产生的，图像的空间分辨率用来衡量数字图像对模拟图像空间坐标数字化的精度。

一般来说，采样间隔越大，所得图像像素数越少，空间分辨率低，质量差，严重时出现像素呈块状的国际棋盘效应。

采样间隔越小，所得图像像素数越多，空间分辨率高，图像质量好，但数据大。

2、说明图象数字化与图象灰度分辨率之间的关系。

答。

图像的灰度分辨率是图像量化过程中选择和产生的，灰度分辨率是指对应同一模拟图像的高度分布进行量化操作所采用的不同量化级数。

量化等级越多，所得图像层次越丰富，灰度分辨率越高，图像质量好，但数据量大。

量化等级越少，图像层次越丰富，灰度分辨率低，会出现假轮廓现象，图像质量变差，但数据量小。

3、看图说明伪彩色图象采集卡的工作原理，并说明LUT的原理和作用。

答。

伪彩色图像采集卡的工作原理是，视频信号输入经过视频信号的A/D变换后，经帧存储器后进行计算机处理，输出显示，然后径伪彩色查询表LUT，实现为彩色输出功能，最后按D/A以控制彩色监视器的电子枪强度，形成彩色。

LUT的作用是具有为彩色查询表功能的LUT的作用是输出为彩色。

第二章1、如何快速计算DCT，对奇异点如何处理？答。

DCT的快速算法将N点的序列延拓成2N点序列，用FFT求2N点序列的离散傅里叶变换，由此得N点的DCT.对于奇异点的单独定义。

用奇异值分解的DCT的数字图像水印法来处理。

第三章1、试述直方图均衡化的增强原理。

答。

对原始图像中的像素灰度作某种映射变换，使变换后的图像灰度的概率密度是均匀分布的，即变换后的图像是一副灰度级均匀分布的图像。

设归一化的灰度变量r,s；T(r)为单调递增函数，保证灰度级从黑到白的次序不变；有0≤T(r)≤1，确保映射后的像素灰度在允许的范围内S的概率密度函数为分布函数的f(s)=p(R)d(r)导数,左右两边求导,结果图像的直方图为均匀的,P(s)=1,两边积分,变换函数为r的累积直方图函数时，能达到直方图均衡化的目的,对于数字图像，用频率代替概率.2试述规定化直方图增强原理；答。

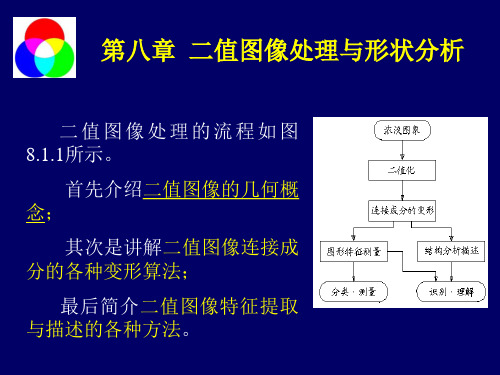
数字图像处理知识点总结第二章：数字图像处理的基本概念2.3 图像数字化数字化是将一幅画面转化成计算机能处理的数字图像的过程。

包括：采样和量化。

2.3.1、2.3.2采样与量化1.采样：将空间上连续的图像变换成离散点。

（采样间隔、采样孔径）2.量化：采样后的图像被分割成空间上离散的像素，但是灰度是连续的，量化就是将像素灰度转换成离散的整数值。

一幅数字图像中不同灰度值的个数称为灰度级。

二值图像是灰度级只有两级的。

（通常是0和1）存储一幅大小为M×N、灰度级数为G的图像所需的存储空间：（bit）2.3.3像素数、量化参数与数字化所得到的数字图像间的关系1.一般来说，采样间隔越大，所得图像像素数越少，空间分辨率低，质量差，严重时会出现国际棋盘效应。

采样间隔越小，所的图像像素数越多，空间分辨率高，图像质量好，但是数据量大。

2.量化等级越多，图像层次越丰富，灰度分辨率高，图像质量好，但数据量大。

量化等级越少，图像层次欠丰富，灰度分辨率低，会出现假轮廓，质量变差，但数据量小。

2.4 图像灰度直方图2.4.1定义灰度直方图是反映一幅图像中各灰度级像素出现的频率，反映灰度分布情况。

2.4.2性质（1）只能反映灰度分布，丢失像素位置信息（2）一幅图像对应唯一灰度直方图，反之不一定。

（3）一幅图像分成多个区域，多个区域的直方图之和是原图像的直方图。

2.4.3应用（1）判断图像量化是否恰当（2）确定图像二值化的阈值（3）物体部分灰度值比其他部分灰度值大的时候可以统计图像中物体面积。

（4）计算图像信息量（熵）2.5图像处理算法的形式2.5.1基本功能形式（1）单幅->单幅（2）多幅->单幅（3）多幅/单幅->数字或符号2.5.2图像处理的几种具体算法形式（1）局部处理（邻域，如4-邻域，8-邻域）（移动平均平滑法、空间域锐化等）（2）迭代处理反复对图像进行某种运算直到满足给定条件。

（3）跟踪处理选择满足适当条件的像素作为起始像素，检查输入图像和已得到的输出结果，求出下一步应该处理的像素。

由雅可比的终止条件修正的 Moore 邻点跟踪算法1. 简介雅可比的终止条件修正的 Moore 邻点跟踪算法（Modified Moore’s Neighbor Tracing Algorithm based on Jacobian Termination Condition）是一种用于图像处理和计算机视觉中的边缘跟踪算法。

该算法基于雅可比矩阵的终止条件修正，能够在图像中准确地跟踪边缘，并提取出边缘的几何特征。

边缘跟踪是图像处理中的一个重要任务，它可以用于目标检测、图像分割、形状识别等应用。

Moore 邻点跟踪算法是最经典的边缘跟踪算法之一，但在某些情况下存在跟踪终止的问题。

为了解决这个问题，本算法引入了雅可比矩阵的终止条件修正，使得跟踪结果更加准确可靠。

本文将详细介绍由雅可比的终止条件修正的 Moore 邻点跟踪算法的原理、步骤和实现细节，并给出一个简单的示例来说明算法的应用。

2. 算法原理雅可比的终止条件修正的 Moore 邻点跟踪算法基于 Moore 邻点跟踪算法，并在其基础上引入了雅可比矩阵的计算和终止条件的修正。

算法的主要原理如下：1.初始化：选取图像中的一个像素作为起始点。

2.计算雅可比矩阵：在当前点位置处计算图像的梯度，并根据梯度计算雅可比矩阵。

3.终止条件判断：根据雅可比矩阵的特征值判断是否终止跟踪。

如果特征值的绝对值小于设定的阈值，则终止跟踪；否则，继续下一步。

4.跟踪下一个点：根据雅可比矩阵的特征向量选择下一个跟踪的点，并更新当前点位置为选定的点。

5.重复步骤2-4，直到终止条件满足。

通过引入雅可比矩阵的终止条件修正，该算法能够在跟踪过程中更加准确地判断是否终止跟踪，避免了 Moore 邻点跟踪算法中可能出现的跟踪终止问题。

3. 算法步骤基于上述原理，由雅可比的终止条件修正的 Moore 邻点跟踪算法的步骤如下：1.初始化：选择一个起始点作为当前点。

2.计算雅可比矩阵：在当前点位置处计算图像的梯度，并根据梯度计算雅可比矩阵。