2020版高考数学空间直角坐标系习题理(含解析)

专题13 坐标系与参数方程【知识要点】1．极坐标系的概念，极坐标系中点的表示．在平面内取一个定点O ，O 点出发的一条射线Ox ，一个长度单位及计算角度的正方向(通常取逆时针方向)，合称为一个极坐标系．O 称为极点，Ox 称为极轴．设M 是平面内任意一点，极点O 与点M 的距离｜OM |叫做点M 的极径，记作ρ ；以极轴Ox 为始边，射线OM 为终边的角xOM 叫做点M 的极角，记作θ ，有序数对(ρ ，θ )叫做点M 的极坐标．一般情况下，约定ρ ≥0．2．极坐标系与直角坐标系的互化．直角坐标化极坐标：x ＝ρ cos θ ，y ＝ρ sin θ ； 极坐标化直角坐标：， 3．参数方程的概念设在平面上取定一个直角坐标系xOy ，把坐标x ，y 表示为第三个变量t 的函数……①，如果对于t 的每一个值(a ≤t ≤b )，①式所确定的点M (x ，y )都在一条曲线上；而这条曲线上任意一点M (x ，y )，都可由t 的某个值通过①式得到，则称①式为该曲线的参数方程，其中t 称为参数．4．参数方程与普通方程的互化把参数方程化为普通方程，需要根据其结构特征，选取适当的消参方法．常见的消参方法有：代入消元法；加减消参法；平方和(差)消参法；乘法消参法等．把曲线C 的普通方程F (x ，y )＝0化为参数方程的关键：一是适当选取参数；二是确保互化前后方程的等价性．要注意方程中的参数的变化范围． 5．直线、圆、椭圆的参数方程．(1)经过一定点P 0(x 0，y 0)，倾斜角为α 的直线l 的参数方程为(t 为参数)；(2)直线参数方程的一般形式为(t 为参数)；222y x +=ρ).0(tan =/=x xyθ⎩⎨⎧==)()(t g y t f x b t a ≤≤⎩⎨⎧+=+=ααsin ,cos 00t y y t x x ⎩⎨⎧+=+=bt y y at x x 00,(3)圆的参数方程为(θ 为参数)；(4)椭圆的参数方程为(θ 为参数)．【复习要求】1．理解坐标系的作用．2．能在极坐标系中用极坐标表示点的位置，理解在极坐标系和平面直角坐标系中表示点的位置的区别，能进行极坐标和直角坐标的互化．3．了解参数方程．4．能选择适当的参数写出直线、圆和圆锥曲线的参数方程，并会简单的应用． 【例题分析】例1 (1)判断点是否在曲线上． (2)点P 的直角坐标为，则点P 的极坐标为______．(限定0＜θ ≤2π)(3)点P 的极坐标为，则点P 的直角坐标为______．解：(1)因为，所以点是在曲线上． (2)根据ρ 2＝x 2＋y 2，， 得ρ ＝2，，又点P 在第四象限，，所以，所以点P 的极坐标为 (3)根据x ＝ρ cos θ ，y ＝ρ sin θ ，得， 所以点P 的直角坐标为 例2 (1)圆ρ ＝2(cos θ ＋sin θ )的半径为______．⎩⎨⎧+=+=θθsin ,cos 00r y y r x x )0(12222>>=+b a b y a x ⎩⎨⎧==θθsin ,cos b y a x )35π,23(-2cos θρ=)3,1(-)4π,3(-2365πcos2cos-==θ)35π,23(-2cos θρ=)0(tan =/=x xy θ3tan -=θ2π23π≤<θ35π=θ).3π5,2(223,223-==y x ).223,223(-(2)直线与圆ρ ＝2sin θ 交与A ，B 两点，则|AB |＝______． 解：(1)由ρ ＝2(cos θ ＋sin θ )，得ρ 2＝2ρ (cos θ ＋sin θ )， 所以，x 2＋y 2＝2x ＋2y ，即(x －1)2＋(y －1)2＝2， 所以圆ρ ＝2(cos θ ＋sin θ )的半径为． (2)将直线与圆ρ ＝2sin θ 化为直角坐标方程，得 由得，即， 由ρ ＝2sin θ ，变形为ρ 2＝2ρ sin θ ，得x 2＋y 2＝2y ，即x 2＋(y －1)2＝1， 因为圆的半径为1，圆心到直线的距离为， 所以评述：(1)应熟练运用直角坐标与极坐标互化的方法解决有关极坐标的问题；(2)由直角坐标化极坐标时要注意点位于哪一个象限才能确定θ 的大小，如例1(2)，否则，极坐标不唯一； (3)例2也可以用极坐标有关知识直接解决．这需要知道一些直线与圆的极坐标方程的知识．如： ①过极点，倾斜角为α 的直线：θ ＝α (ρ ∈R )或写成θ ＝α 及θ ＝α ＋π． ②过A (a ，α)垂直于极轴的直线：ρ cos θ ＝a cos α ． ③以极点O 为圆心，a 为半径的圆(a ＞0)：ρ ＝a ．④若O (0，0)，A (2a ，0)，以OA 为直径的圆：ρ ＝2a cos θ ． ⑤若O (0，0)，A (2a ，)，以OA 为直径的圆：ρ ＝2a sin θ ． 对于例2(2)，可以利用结论①⑤，作出直线与圆，通过解三角形的方法求|AB ｜，当然也可以用极坐标方程直接解ρ ，根据ρ 的几何意义求｜AB ｜．例3 圆O 1和圆O 2的极坐标方程分别为ρ ＝4cos θ ，ρ ＝－4sin θ ． (1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程； (2)求经过圆O 1和圆O 2交点的直线的直角坐标方程．)(3πR ∈=ρθ2)(3πR ∈=ρθ3π=θxy=3πtan x y 3=21311=+=d .3)21(12||2=-=AB 2π解：(1)由ρ ＝4cos θ 得ρ 2＝4ρ cos θ ，根据x ＝ρ cos θ ，y ＝ρ sin θ ，所以x 2＋y 2＝4x ． 即x 2＋y 2－4x ＝0为圆O 1的直角坐标方程，同理x 2＋y 2＋4y ＝0为圆O 2的直角坐标方程．(2)由解得 即圆O 1和圆O 2交于点(0，0)和(2，－2)．过交点的直线的直角坐标方程为y ＝－x ．例4(1)曲线的参数方程是(t 为参数，t ≠0)，它的普通方程是________． (2)在平面直角坐标系xOy 中，直线l 的参数方程为 (参数t ∈R )，圆C 的参数方程为(参数θ ∈[0，2π])，则圆C 的圆心坐标为______，圆心到直线l 的距离为______． 解：(1)由得，带入y ＝1－t 2，得 注意到，所以已知参数的普通方程为 (2)直线l 的普通方程为x ＋y －6＝0，圆C 的普通方程为x 2＋(y －2)2＝4， 所以圆心坐标为(0，2)，圆心到直线l 的距离评述：(1)应熟练运用将参数方程化为普通方程的方法解决有关参数方程的问题；(2)在将参数方程化为普通方程的过程中应注意消参带来的范围变化问题．如例4(1)，若参数方程为(t 为参数，t ＞0)，则其普通方程为 例5 求椭圆的内接矩形的最大面积．解：设内接矩形在第一象限内的顶点为P (a cos θ ，b sin θ )，P 点在两轴上的投影分别为A 、B ，则有S 内接矩形＝4S 矩形OAPB ＝4·a cos θ ·b sin θ ＝2ab sin2θ ． 因为，所以2θ ∈(0，π)，S 内接矩形的最大值为2ab ． ⎪⎩⎪⎨⎧=++=-+,04,042222y y x x y x ⎩⎨⎧==;0,011y x ⎩⎨⎧-==.2,222y x ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-=21,11t y t x ⎩⎨⎧-=+=t y t x 3,3⎩⎨⎧+==2sin 2,cos 2θθy x t x 11-=x t -=11,)1()2()11(122--=--=x x x x y 111=/-=t x ⋅--=2)1()2(x x x y .222|620|=-+=d ⎪⎪⎩⎪⎪⎨⎧-=-=21,11t y t x ).1()1()2(2<--=x x x x y 12222=+by a x )2π,0(∈θ评述：圆锥曲线参数方程主要应用于利用参数方程设圆锥曲线上的点，从而讨论最值等有关问题．椭圆的参数方程为 (θ 为参数)．抛物线y 2＝2px (p ＞0)的参数方程为.例6 圆M 的参数方程为x 2＋y 2－4Rx cos α －4Ry sin α ＋3R 2＝0(R ＞0)． (1)求该圆的圆心坐标以及圆M 的半径；(2)当R 固定，α 变化时，求圆心M 的轨迹，并证明此时不论α 取什么值，所有的圆M 都外切于一个定圆． 解：(1)依题意得圆M 的方程为(x －2R cos α )2＋(y －2R sin α )2＝R 2， 故圆心的坐标为M (2R cos α ，2R sin α )，半径为R ．(2)当α 变化时，圆心M 的轨迹方程为 (α 为参数)，两式平方相加得x 2＋y 2＝4R 2，所以圆心M 的轨迹是圆心在原点，半径为2R 的圆．由于所以所有的圆M 都和定圆x 2＋y 2＝R 2外切，和定圆x 2＋y 2＝9R 2内切．例7 过P (5，－3)，倾斜角为α ，且的直线交圆x 2＋y 2＝25于P 1、P 2两点．(1)求|PP 1|·|PP 2｜的值；(2)求弦P 1P 2的中点M 的坐标．解：(1)由已知得所以已知直线的参数方程为…………………①(t 为参数)代入圆的方程化简，得…………………② ②的两个解t 1、t 2就是P 1、P 2对应的参数，由参数的几何意义及韦达定理知)0,0(12222>>=+b a b y a x ⎩⎨⎧==θθtan sec b y a x ⎩⎨⎧==pty ptx 222⎩⎨⎧==,sin 2,cos 2ααR y R x ,32)sin 2()cos 2(22R R R R R -==+αα,2)sin 2()cos 2(22R R R R R +==+αα53cos -=α53cos -=α,54sin =α⎪⎪⎩⎪⎪⎨⎧+-=-=,543,535t y t x .095542=+-t t｜PP 1|·｜PP 2|＝|t 1|·|t 2|＝9．(2)设M (x ，y )为P 1P 2的中点，则点M 对应的参数，代入参数方程， 得 所以 评述：根据直线的参数方程的标准式中t 的几何意义，有如下常用结论： ①直线与圆锥曲线相交，交点对应的参数分别为t 1，t 2，则弦长l ＝|t 1－t 2｜； ②定点M 0是弦M 1M 2的中点t 1＋t 2＝0；③设弦M 1M 2的中点为M ，则点M 对应的参数值，(由此可求得|M 2M |及中点坐标)． 习题13一、选择题 1．极坐标的直角坐标为 (A)(1，)(B)(－，－1)(C)(－1，－)(D)(－1，)2．椭圆(θ 为参数)的焦距等于( )(A) (B)2 (C) (D)3．已知某条曲线的参数方程为(0≤t ≤5)，则该曲线是( )(A)线段 (B)圆弧 (C)双曲线的一支 (D)射线4．若是极坐标系中的一点，则四点中与P 重合的点有( )(A)1个(B)2个(C)3个(D)4个527221=+=t t t ,2533,2544==y x M PP PP ,9||||21=⋅).2533,2544(⇒221t t t M +=)34π(2,3333⎩⎨⎧==θθsin 5,cos 2y x 212129292⎪⎩⎪⎨⎧-=+=1,2322t y t x )3π,2(--P 、、、)3π5,2()3π8,2()3π2,2(-M R Q )3π5π2,2(-k N )(Z ∈k5．在极坐标系中，若等边△ABC 的两个顶点是，那么顶点C 的坐标可能是( ) (A) (B) (C)(D)(3，π)二、选择题6．过极点，倾斜角是的直线的极坐标方程为____________． 7．点M 的直角坐标(3，－3)化为极坐标是____________． 8．直线(t 为参数)过定点____________．9．曲线(t 为参数)与y 轴的交点坐标是____________．10．参数方程(θ 为参数)表示的曲线的普通方程是____________．三、解答题11．求过点，并且和极轴垂直的直线的极坐标方程．12．在椭圆上求一点，使点M 到直线的距离最小，并求出最小距离．13．设圆C 是以C (4，0)为圆心，半径等于4的圆．(1)求圆C 的极坐标方程；(2)从极点O 作圆C 的弦ON ，求ON 的中点M 的轨迹方程．)4π5,2()4π,2(B A 、)4π3,4()43π,32()π,32(6π⎩⎨⎧+-=+=t y at x 41,3⎩⎨⎧=+-=t y t x ,12⎩⎨⎧+==θθθcos sin ,2sin y x )4π,3(14922=+y x 021032=-+y x14．已知点M (2，1)和双曲线，求以M 为中点的双曲线右支的弦AB 所在直线l 的方程．专题13 坐标系与参数方程参考答案习题13一、选择题1．C 2．B 3．A 4．C 5．B 二、填空题 6．； 7．； 8．(3，－1)； 9．(0，1)，(0，－1)； 三、解答题 11． 12．解：由题设知椭圆参数方程为(θ 为参数)．设M 的坐标(3cos θ ，2sin θ )由点到直线距离 即d 的最小值为，此时．所以M 的坐标为13．解：(1)设P (ρ ，θ )为圆C 上任意一点，圆C 交极轴于另一点A ．由已知|OA |＝8，在Rt △ABC 中，|OP |＝|OA ｜cos θ ，即ρ ＝8cos θ ，这就是圆C 的方程．1222=-y x )(6πR ∈=ρθ)47π,23(⋅=223cos θρ⎩⎨⎧==θθsin 2,cos 3y x ,13|210)4πsin(26|13|210sin 6cos 6|-+=-+=θθθd 261344π=θ).2,223((2)连结CM ，因为M 是ON 的中点，所以CM ⊥ON ，故M 在以OC 为直径的圆上． 由r ＝|OC |＝4，得动点M 的轨迹方程是ρ ＝4cos θ ．14．解：设AB 的方程为(t 为参数)，代入双曲线方程，得(2cos 2α －sin 2α )t 2＋(8cos α －2sin α )t ＋5＝0，由于M 为AB 的中点，则t 1＋t 2＝0，则tan α ＝4，从而AB 的方程为：4x －y －7＝0．⎩⎨⎧+=+=ααsin 1,cos 2t y t x。

9.7 空间向量在空间几何体的运用（一）一．设直线l ，m 的方向向量分别为a ，b ，平面α，β的法向量分别为1n ，2n ，则有如下结论：二．点面距已知AB 为平面α的一条斜线段(A 在平面α内)，n 为平面α的法向量，则B 到平面α的距离为|||cos ,|||||||||AB d AB AB AB AB ⋅===<>n n n ||||AB ⋅n n ．注：空间中其他距离问题一般都可以转化为点面距问题．考向一 利用空间向量证明平行【例1】在正方体ABCD ­A 1B 1C 1D 1中，M ，N 分别是CC 1，B 1C 1的中点．求证：MN ∥平面A 1BD ． 【答案】见解析【解析】法一 如图，以D 为原点，DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，设正方体的棱长为1，则D (0,0,0)，A 1(1,0,1)，B (1,1,0)，M ⎝ ⎛⎭⎪⎫0，1，12，N ⎝ ⎛⎭⎪⎫12，1，1，于是DA 1→＝(1,0,1)，DB →＝(1,1,0)，MN →＝⎝ ⎛⎭⎪⎫12，0，12.设平面A 1BD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ⊥DA 1→，n ⊥DB →，即⎩⎪⎨⎪⎧n ·DA 1→＝x ＋z ＝0，n ·DB →＝x ＋y ＝0，取x ＝1，则y ＝－1，z ＝－1，∴平面A 1BD 的一个法向量为n ＝(1，－1，－1)．又MN →·n ＝⎝ ⎛⎭⎪⎫12，0，12·(1，－1，－1)＝0，∴MN →⊥n .∴MN ∥平面A 1BD ．法二 MN →＝C 1N →－C 1M →＝12C 1B 1→－12C 1C →＝12(D 1A 1→－D 1D →)＝12DA 1→，∴MN →∥DA 1→，∴MN ∥平面A 1BD ．法三 MN →＝C 1N →－C 1M →＝12C 1B 1→－12C 1C →＝12DA →－12A 1A →＝12()DB →＋BA →－12()A 1B →＋BA →＝12DB →－12A 1B →. 即MN →可用A 1B →与DB →线性表示，故MN →与A 1B →，DB →是共面向量，故MN ∥平面A 1BD ． 【拓展】1.(变条件)本例中条件不变，试证明平面A 1BD ∥平面CB 1D 1.[证明] 由例题解析知，C (0,1,0)，D 1(0,0,1)，B 1(1,1,1)， 则CD 1→＝(0，－1,1)，D 1B 1→＝(1,1,0)， 设平面CB 1D 1的法向量为m ＝(x 1，μ1，z 1)，则⎩⎪⎨⎪⎧m ⊥CD 1→m ⊥D 1B 1→，即⎩⎪⎨⎪⎧m ·CD 1→＝－y 1＋z 1＝0，m ·D 1B 1→＝x 1＋y 1＝0，令y 1＝1，可得平面CB 1D 1的一个法向量为m ＝(－1,1,1)， 又平面A 1BD 的一个法向量为n ＝(1，－1，－1)． 所以m ＝－n ，所以m ∥n ，故平面A 1BD ∥平面CB 1D 1. 2．(变条件)若本例换为：在如图3­2­4所示的多面体中，EF ⊥平面AEB ，AE ⊥EB ，AD ∥EF ，EF ∥BC ，BC ＝2AD ＝4，EF ＝3，AE ＝BE ＝2，G 是BC 的中点，求证：AB ∥平面DEG .图3­2­4[证明] ∵EF ⊥平面AEB ，AE ⊂平面AEB ，BE ⊂平面AEB ， ∴EF ⊥AE ，EF ⊥BE .又∵AE ⊥EB ，∴EB ，EF ，EA 两两垂直．以点E 为坐标原点，EB ，EF ，EA 分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系．由已知得，A (0,0,2)，B (2,0,0)，C (2,4,0)，F (0,3,0)，D (0,2,2)，G (2，2,0)，∴ED →＝(0,2,2)，EG →＝(2,2,0)，AB →＝(2,0，－2)．设平面DEG 的法向量为n ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧ED →·n ＝0，EG →·n ＝0，即⎩⎪⎨⎪⎧2y ＋2z ＝0，2x ＋2y ＝0，令y ＝1，得z ＝－1，x ＝－1，则n ＝(－1,1，－1)， ∴AB →·n ＝－2＋0＋2＝0，即AB →⊥n . ∵AB ⊄平面DEG ， ∴AB ∥平面DEG .考向二 垂直、【例2】如图1，在四棱锥S ABCD -中，底面ABCD 是正方形，AS ⊥底面ABCD ，且A S A B =，E 是SC 的中点．求证：（1）直线AD ⊥平面SAB ； （2）平面BDE ⊥平面ABCD ．图1 图2【答案】见解析【解析】如图2，以A 为原点， AB ，AD ，AS 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系Axyz ，设2AS AB ==，则(0,0,0)A ，(0,2,0)D ，(2,2,0)C ，(2,0,0)B ，(0,0,2)S ，(1,1,1)E 易得(0,0,2)AS =，(2,0,0)AB =设平面SAB 的法向量为(,,)x y z =n ，则AS AB ⎧⎪⎨⎪⎩⊥⊥n n ，即2020AS z AB x ⎧⋅==⎪⎨⋅==⎪⎩n n取1y =，可得平面SAB 的一个法向量为(0,1,0)=n又(0,2,0)AD =，所以2AD =n ，所以AD ∥n ，所以直线AD ⊥平面SAB 方法1：如图2，连接AC 交BD 于点O ，连接OE ，则点O 的坐标为(1,1,0) 易得(0,0,1)OE =，(0,0,2)AS =，显然2AS OE =，故AS OE ∥，所以AS OE ∥ 又AS ⊥底面ABCD ，所以OE ⊥底面ABCD 又OE ⊂平面BDE ，所以平面BDE ⊥平面ABCD 方法2：易得(1,1,1)BE =-，(2,2,0)BD =-设平面BDE 的法向量为(,,)x y z =m ，则BE BD ⎧⎪⎨⎪⎩⊥⊥m m ，即0220BE x y z BD x y ⎧⋅=-++=⎪⎨⋅=-+=⎪⎩m m取1x =，得1y =，0z =，所以平面1A BD 的一个法向量为(1,1,0)=mAS ⊥底面ABCD ，可得(0,0,2)AS =是平面ABCD 的一个法向量因为(0,0,2)(1,1,0)0AS ⋅=⋅=m ，所以AS ⊥m ，所以平面BDE ⊥平面ABCD【举一反三】1.如图所示，正三棱柱ABC ­A 1B 1C 1的所有棱长都为2，D 为CC 1的中点，求证：AB 1⊥平面A 1BD ．【答案】见解析【解析】法一：如图所示，取BC 的中点O ，连接AO .因为△ABC 为正三角形，所以AO ⊥BC ．因为在正三棱柱ABC ­A 1B 1C 1中，平面ABC ⊥平面BCC 1B 1，所以AO ⊥平面BCC 1B 1.取B 1C 1的中点O 1，以O 为原点，以OB →，OO 1→，OA →分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系， 则B (1,0,0)，D (－1,1,0)，A 1(0,2，3)，A (0,0，3)，B 1(1,2,0)． 所以AB 1→＝(1,2，－3)，BA 1→＝(－1,2，3)，BD →＝(－2,1,0)． 因为AB 1→·BA 1→＝1×(－1)＋2×2＋(－3)×3＝0.AB 1→·BD →＝1×(－2)＋2×1＋(－3)×0＝0.所以AB 1→⊥BA 1→，AB 1→⊥BD →，即AB 1⊥BA 1，AB 1⊥BD ． 又因为BA 1∩BD ＝B ，所以AB 1⊥平面A 1BD ． 法二：建系同方法一．设平面A 1BD 的法向量为n ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧n ⊥BA 1→n ⊥BD→，即⎩⎪⎨⎪⎧n ·BA 1→＝－x ＋2y ＋3z ＝0，n ·BD →＝－2x ＋y ＝0，令x ＝1得平面A 1BD 的一个法向量为n ＝(1,2，－3)， 又AB 1→＝(1,2，－3)，所以n ＝AB 1→，即AB 1→∥n . 所以AB 1⊥平面A 1BD ．考向三 利用空间向量解决平行与垂直关系中的探索性问题【例3】如图，三棱柱ABC －A 1B 1C 1中，AA 1⊥平面ABC ，BC ⊥AC ，BC ＝AC ＝AA 1＝2，D 为AC 的中点．(1)求证：AB 1∥平面BDC 1；(2)设AB 1的中点为G ，问：在矩形BCC 1B 1内是否存在点H ，使得GH ⊥平面BDC 1.若存在，求出点H 的位置，若不存在，说明理由． 【答案】见解析【解析】(1)证明：连接B 1C ，设B 1C ∩BC 1＝M ，连接MD ，在△AB 1C 中，M 为B 1C 中点，D 为AC 中点， ∴DM ∥AB 1，又∵AB 1不在平面BDC 1内，DM 在平面BDC 1内， ∴AB 1∥平面BDC 1.(2)以C 1为坐标原点，C 1A 1→为x 轴，C 1C →为y 轴，C 1B 1→为z 轴建立空间直角坐标系． 依题意，得C 1(0,0,0)，D (1,2,0)，B (0,2,2)，G (1,1,1)，假设存在H (0，m ，n )， GH →＝(－1，m －1，n －1)，C 1D →＝(1,2,0)，DB →＝(－1,0,2)，由GH ⊥平面BC 1D ，得GH →⊥C 1D →⇒(－1，m －1，n －1)·(1,2,0)＝0⇒m ＝32.同理，由GH →⊥DB →得n ＝12，即在矩形BCC 1B 1内存在点H ，使得GH ⊥平面BDC 1.此时点H 到B 1C 1的距离为32，到C 1C 的距离为12.【举一反三】1.如图所示，在四棱锥P －ABCD 中，底面ABCD 是正方形，侧面PAD ⊥底面ABCD ，E ，F 分别为PA ，BD 中点，PA ＝PD ＝AD ＝2.(1)求证：EF ∥平面PBC ；(2)在棱PC 上是否存在一点G ，使GF ⊥平面EDF ？若存在，指出点G 的位置；若不存在，说明理由．【答案】见解析【解析】(1)证明：如图所示，连接AC .因为底面ABCD 是正方形，AC 与BD 互相平分．F 是BD 中点，所以F 是AC 中点．在△PAC 中，E 是PA 中点，F 是AC 中点，所以EF ∥PC . 又因为EF ⊄平面PBC ，PC ⊂平面PBC ，所以EF ∥平面PBC . (2)取AD 中点O ，连接PO .在△PAD 中，PA ＝PD ，所以PO ⊥AD .因为平面PAD ⊥底面ABCD ，且平面PAD ∩平面ABCD ＝AD ，所以PO ⊥平面ABCD . 因为OF ⊂平面ABCD ，所以PO ⊥OF . 又因为F 是AC 中点，所以OF ⊥AD .以O 为原点，OA ，OF ，OP 分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系．因为PA ＝PD ＝AD ＝2，所以OP ＝3，则C (－1,2,0)，D (－1,0,0)，P (0,0，3)，E ⎝ ⎛⎭⎪⎫12，0，32，F (0,1,0)．于是DE →＝⎝ ⎛⎭⎪⎫32，0，32，DF →＝(1,1,0)．设平面EFD 的法向量n ＝(x 0，y 0，z 0)．因为⎩⎪⎨⎪⎧n ·DF →＝0，n ·DE →＝0，所以⎩⎪⎨⎪⎧x 0＋y 0＝0，32x 0＋32z 0＝0，即⎩⎨⎧y 0＝－x 0，z 0＝－3x 0.令x 0＝1，则n ＝(1，－1，－3)．假设在棱PC 上存在一点G ，使GF ⊥平面EDF . 设G (x 1，y 1，z 1)，则FG →＝(x 1，y 1－1，z 1)． 因为EDF 的一个法向量n ＝(1，－1，－3)． 因为GF ⊥平面EDF ，所以FG →＝λn .于是⎩⎨⎧x 1＝λ，y 1－1＝－λ，z 1＝－3λ，即⎩⎨⎧x 1＝λ，y 1＝1－λ，z 1＝－3λ.又因为点G 在棱PC 上，所以GC →与PC →共线．因为PC →＝(－1,2，－3)，CG →＝(x 1＋1，y 1－2，z 1)， 所以x 1＋1－1＝y 1－22＝z 1－3， 即1＋λ－1＝－λ－12＝－3λ－3，无解．故在棱PC 上不存在一点G ，使GF ⊥平面EDF . 考向四 点面距【例4】如图，已知正方体1111ABCD A B C D -的棱长为3a ，求平面11AB D 与平面1BDC 之间的距离．．【解析】由正方体的性质，易得平面11AB D ∥平面1BDC ， 则两平面间的距离可转化为点B 到平面11AB D 的距离．如图，以D 为坐标原点，DA ，DC ，1DD 所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，【举一反三】1．在我国古代数学名著《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑（bie nao ）.已知在鳖臑P ABC -中，PA ⊥平面ABC ，2PA AB BC ===，M 为PC 的中点，则点P 到平面MAB 的距离为_____．【解析】以B 为坐标原点，BA,BC 所在直线分别为x 轴，y 轴建立空间直角坐标系，如图，则()()()()0,0,0,2,0,0,2,0,2,0,2,0B A P C ,由M 为PC 的中点可得()1,1,1M ;()()1,1,1,2,0,0BM BA ==, ()2,0,2BP =.设(),,x y z =n 为平面ABM 的一个法向量，则00n BA n BM ⎧⋅=⎨⋅=⎩,即200x x y z =⎧⎨++=⎩，令1z =-，可得()0,1,1=-n ，点P 到平面MAB 的距离为BP d ⋅==n n.1．在棱长为1的正方体ABCD -A 1B 1C 1D 1中，点A 关于平面BDC 1对称点为M ，则M 到平面A 1B 1C 1D 1的距离为（ ）A ．32B ．54C ．43D ．53【答案】D【解析】以D 为原点，DA ，DC ，DD 1所在直线分别为x ，y ，z 轴，建立空间直角坐标系，D （0，0，0），B （1，1，0），C 1（0，1，1），A （1，0，0），A 1（1，0，1），DB =（1，1，0），1DC =（0，1，1）， 设平面BDC 1的法向量n =（x ，y ，z ），则100n DB x y n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取x=1，得n =（1，-1，1），∴平面BDC 1的方程为x-y+z=0，过点A （1，0，0）且垂直于平面BDC 1的直线方程为： （x-1）=-y=z ，令（x-1）=-y=z=t ，得x=t+1，y=-t ，z=t ，代入平面方程x-y+z=0，得t+1+t+t=0，解得t=13- ，∴过点A （1，0，0）且垂直于平面BDC 1的直线方程与平面BDC 1的交点为211333⎛⎫ ⎪⎝⎭，，-∴点A 关于平面BDC 1对称点M 122333⎛⎫ ⎪⎝⎭，，-， 1225333A M ⎛⎫=- ⎪⎝⎭，，-，平面A 1B 1C 1D 1的法向量m =（0，0，1），∴M 到平面A 1B 1C 1D 1的距离为d=15=3m A M m⋅故选：D ． 2．在棱长为2的正方体1111ABCD A B C D -中，E ，F 分别为棱1AA 、1BB 的中点，M 为棱11A B 上的一点，且1(02)A M λλ=<<，设点N 为ME 的中点，则点N 到平面1D EF 的距离为（ ）AB．2C．3λ D【答案】D【解析】以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系， 则M （2，λ，2），D 1（0，0，2），E （2，0，1），F （2，2，1），1ED ＝（﹣2，0，1），EF ＝（0，2，0）1sin()cos 22C C π+==＝（0，λ，1）， 设平面D 1EF 的法向量n ＝（x ，y ，z ），则1·20·20n ED x z n EF y ⎧=-+=⎨==⎩，取x ＝1，得n ＝（1，0，2），∴点M 到平面D 1EF 的距离为：d＝5EM n n==N 为EM 中点，所以N ，选D ．3．如图：正三棱柱111ABC A B C -的底面边长为3，D 是CB 延长线上一点，且BD BC =，二面角1B AD B --的大小为60︒；（1）求点1C 到平面1B AD 的距离；（2）若P 是线段AD 上的一点 ，且12DP A A =，在线段1DC 上是否存在一点Q ，使直线//PQ 平面1ABC ？若存在，请指出这一点的位置；若不存在，请说明理由．【答案】（1）4； （2）存在,当113C Q QD =时，1//PQ AC 知//PQ 平面1ABC . 【解析】（1）设E 为AD 的中点，则BE AD ⊥，在正三棱柱111ABC A B C -中，1BB ⊥平面ABC ,而AD ⊂平面ABC ，所以1BB AD ⊥，而1BB EB B =,因此AD ⊥平面1BB E ，而1B E ⊂平面1BB E ，所以有1B E AD ⊥1BEB ∴∠为二面角1B AD B --的平面角，如下图所示：160BEB ∴∠=︒120ABD ∠=︒，32BE =,11tan BB BEB BE ∴∠==侧棱11AA BB ==；111111C ADB A C DB A BB C V V V ---==11273328⎛=⨯= ⎝⎭又AD =11AB B D ==知1112ADB S AD B E ∆=⋅=∴点1C 到平面1ADB 的距离2738d =⨯=（2）由（1）可知AD =1AA =，12DP AA =，13AP PD ∴=，当113C Q QD =时，有1//PQ AC 成立，而 1AC ⊂平面1ABC ，所以 //PQ 平面1ABC ，故存在，当113C Q QD =时，符合题意。

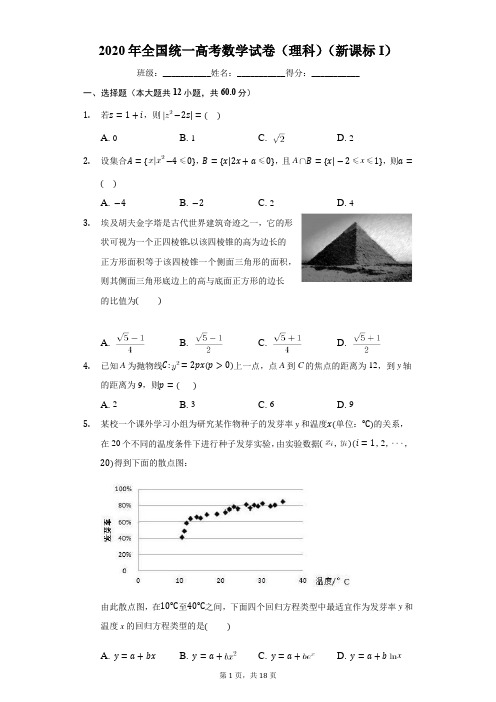
2020年全国统一高考数学试卷（理科）（新课标I）班级：___________姓名：___________得分：___________一、选择题（本大题共12小题，共60.0分）1.若z=1+i，则−2z|=()A. 0B. 1C.D. 22.设集合A={−40}，B={x|2x+a0}，且A B={x|−2x1}，则a=()A. −4B. −2C. 2D. 43.埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为()A. B. C. D.4.已知A为抛物线C:=2px(p>0)上一点，点A到C的焦点的距离为12，到y轴的距离为9，则p=()A. 2B. 3C. 6D. 95.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位：℃)的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据(，)(i=1，2，，20)得到下面的散点图：由此散点图，在10℃至40℃之间，下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是()A. y=a+bxB. y=a+C. y=a+D. y=a+b x6.函数f(x)=−的图像在点(1,f(1))处的切线方程为()A. y=−2x−1B. y=−2x+1C. y=2x−3D. y=2x+17.设函数f(x)=(x+)在[−，]的图像大致如下图，则f(x)的最小正周期为()A. B. C. D.8.(x+y2)(x+y)5的展开式中x3y3的系数为()xA. 5B. 10C. 15D. 209.已知(0,)，且3cos2α−8cosα=5，则=()A. B. C. D.10.已知A，B，C为球O的球面上的三个点，为ABC的外接圆，若的面积为4，AB=BC=AC=，则球O的表面积为()A. 64B. 48C. 36D. 3211.已知M:+−2x−2y−2=0，直线l:2x+y+2=0，P为l上的动点，过点P作M的切线PA，PB，且切点为A，B，当|PM||AB|最小时，直线AB的方程为()A. 2x−y−1=0B. 2x+y−1=0C. 2x−y+1=0D. 2x+y+1=012.若2a+log2a=4b+2log4b，则()A. a>2bB. a<2bC. a>D. a<二、填空题（本大题共4小题，共20.0分）13.若x，y满足约束条件则z=x+7y的最大值为__________．14.设，为单位向量，且||=1，则||=__________．15.已知F为双曲线C:−=1(a>0,b>0)的右焦点，A为C的右顶点，B为C上的点且BF垂直于x轴.若AB的斜率为3，则C的离心率为__________．16.如图，在三棱锥P−ABC的平面展开图中，AC=1，AB=AD=，AB AC，AB AD，CAE=，则FCB=__________．三、解答题（本大题共7小题，共80.0分）17.设{}是公比不为1的等比数列，为，的等差中项．(1)求{}的公比;(2)若=1，求数列{}的前n项和．18.如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底面直径，AE=AD．ABC是底面的内接正三角形，P为DO上一点，PO=DO．(1)证明：PA平面PBC;(2)求二面角B−PC−E的余弦值．19.甲、乙、丙三位同学进行羽毛球比赛，预定赛制如下：累计负两场者被淘汰;比赛前抽签决定首次比赛的两个人，另一人轮空;每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人淘汰;当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束．经抽签，甲、乙首先比赛，丙轮空.设每场比赛双方获胜的概率都为．(1)求甲连胜四场的概率;(2)求需要进行第五场比赛的概率;(3)求丙最终获胜的概率．20.已知A，B分别为椭圆E:+=1(a>1)的左、右顶点，G为E的上顶点，=8，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D，(1)求E的方程;(2)证明：直线CD过定点．21.已知函数f(x)=+−x．(1)当a=1时，讨论f(x)的单调性;(2)当x0时，f(x)+1，求a的取值范围．22.[选修4−4:坐标系与参数方程]在直角坐标系xOy中，曲线的参数方程为(t为参数).以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线的极坐标方程为4−16+3=0．(1)当k=1时，是什么曲线?(2)当k=4时，求与的公共点的直角坐标．23.[选修4−4:坐标系与参数方程]已知函数f(x)=|3x+1|−2|x−1|．(1)画出y=f(x)的图像;(2)求不等式f(x)>f(x+1)的解集．答案和解析1. D解：由z =1+i 得z 2=2i ，2z =2+2i ，|z 2−2z |=|2i −(2+2i)|=2．2. B解：由已知可得A ={x|−2⩽x ⩽2}，B ={x|x ⩽−a2}， 又因为A ∩B ={x|−2⩽x ⩽1}， 所以−a2=1，从而a =−2,3. C解：如图，设正四棱锥的高为h ，底面边长为a,侧面三角形底边上的高为ℎ′， 则由题意可得{ℎ2=12aℎ′ℎ2=(ℎ′)2−(a2)2,故(ℎ′)2−(a2)2=12aℎ′，化简可得4(ℎ′a )2−2(ℎ′a )−1=0,解得ℎ′a=1±√54．负值舍去可得ℎ′a=1+√544.C解：设点A的坐标为(x,y)，由点A到y轴的距离为9，可得x=9,由点A到点C的焦点的距离为12，可得x+p2=12解得p=6．5.D解：用光滑的曲线把图中各点连接起来，由图象的走向判断，此函数应该是对数函数类型的，故应该选用的函数模型为y=a+bln x．6.B解：先求函数的导函数f′(x)=4x3−6x2，则由函数的几何意义可知在点(1,f(1))的切线斜率为k=f′(1)=−2．又因为f(1)=−1，则切线方程为y−(−1)=−2(x−1)，则y=−2x+1．7.C解：由图可知f(−4π9)=cos(−4π9w+π6)=0，所以−4π9w+π6=π2+kπ(k∈Z),化简可得w=−3+9k4(k∈Z)，又因为T<2π<2T，即2π|w|<2π<4π|w|，所以1<|ω|<2，当且仅当k=−1时1<|ω|<2，所以w=32，所以最小正周期T=2π|w|=4π3．8.C解：(x+y)5的展开式通项为C5r x5−r y r，r=0，1，2，3，4，5，则(x+y2x )(x+y)5的展开式有xC5r x5−r y r，y2xC5r x5−r y r，取r=3和r=1时可得10x3y3，5x3y3，合并后系数为15，9.A解：∵3cos2α−8cosα=5，∴3(2cos2α−1)−8cosα=5，即3cos2α−4cosα−4=0，(3cosα+2)(cosα−2)=0，α∈(0,π)，即cosα=−23，又α∈(0,π)，sinα>0，∴sinα=√1−cos2α=√53，10.A解：由圆O1的面积为4π=πr2，故圆O1的半径ρ=2，∵AB=BC=AC=OO1，则三角形ABC是正三角形，=2r=4，得AB=OO1=2√3，由正弦定理：ABsin60∘由R2=r2+OO12，得球O的半径R=4，表面积为4πR2=64π，11.D解：圆M方程化为：(x−1)2+(y−1)2=4，圆心M(1,1)，半径r=2，根据切线的性质及圆的对称性可知，则|PM|⋅|AB|=4S△PAM=2|PA|⋅|AM|，要使其值最小，只需|PA|最小，即|PM|最小，此时，=√5，|PA|=√|PM|2−|AM|2=1，∴|PM|=√5(x−1)，联立l的方程解得P(−1,0)，过点M且垂直于l的方程为y−1=12以P为圆心，|PA|为半径的圆的方程为(x+1)2+y2=1，即x2+y2+2x=0，结合圆M的方程两式相减可得直线AB的方程为2x+y+1=0，12.B解：根据指数及对数的运算性质，4b+2log4b=22b+log2b，∵log2(2b)=log2b+1>log2b，∴22b+log2(2b)>22b+log2b=2a+log2a，根据函数f(x)=2x+log2x是定义域上的增函数，由f(2b)>f(a)，得a<2b，13.1解：根据约束条件画出可行域为：由z=x+7y得y=−17x+17z，平移直线y=−17x，要使z最大，则y=−17x+17z在y轴上的截距最大，由图可知经过点A(1,0)时截距最大，此时z=1，14.√3解：|a⃗+b⃗ |2=a⃗2+b⃗ 2+2a⃗⋅b⃗ =2+2a⃗⋅b⃗ =1，a⃗⋅b⃗ =−12，|a⃗−b⃗ |2=a⃗2+b⃗ 2−2a⃗⋅b⃗ =2−2a⃗⋅b⃗ =3，∴|a⃗−b⃗ |=√3．15.2解：由题意可知，B在双曲线C的右支上，且在x轴上方，∵BF垂直于x轴，把x=c代入x2a2−y2b2=1，得y=b2a，∴B点坐标为(c,b2a)，又A点坐标为(a,0)，∴k AB=b2a−0c−a=3，化简得b2=3ac−3a2=c2−a2，即2a2−3ac+c2=0，解得c=2a或c=a(舍)，故e=ca=2．16.−14解：由已知得BD=√2AB=√6，∵D、E、F重合于一点，∴AE=AD=√3，BF=BD=√6，∴△ACE中，由余弦定理得，∴CE=CF=1，BC²=AC²+AB²，BC=2，∴在△BCF中，由余弦定理得．17.解：⑴设等比数列{a n}的公比为q(q≠1)，由题意知：2a1=a2+a3，即2a1=a1q+a1q2，所以q2+q−2=0，解得q=−2．(2)若a1=1，则a n=(−2)n−1，所以数列{na n}的前n项和为T n=1+2×(−2)+3×(−2)2+⋯+n(−2)n−1，则−2T n=−2+2×(−2)2+3×(−2)3+⋯+n(−2)n，两式相减得3T n=1+(−2)+(−2)2+(−2)3+(−2)n−1−n(−2)n=1−(−2)n1−(−2)−n(−2)n=1−(3n+1)(−2)n3，所以T n=1−(3n+1)(−2)n9．18.(1)证明：不妨设⊙O的半径为1，则AO=OB=OC=1，AE=AD=2，AB=BC=CA=√3，DO=√DA2−OA2=√3，PO=√66DO=√22，PA=PB=PC=√PO2+AO2=√62，在△PAC中，PA2+PC2=AC2，故PA⊥PC，同理可得PA⊥PB，PB∩PC=P，PB，PC⊂平面PBC，∴PA ⊥平面PBC ．(2)解：以OE ，OD 所在直线分别为y ，z 轴，圆锥底面内垂直于OE 的直线为x 轴，建立如图所示的空间直角坐标系O −xyz ，则有B (√32,12,0),C (−√32,12,0),P (0,0,√22),E (0,1,0)， BC ⃗⃗⃗⃗⃗ =(−√3,0,0),CE ⃗⃗⃗⃗⃗ =(√32,12,0),CP ⃗⃗⃗⃗⃗ =(√32,−12,√22)， 设平面PBC 的法向量为n 1⃗⃗⃗⃗ =(x 1,y 1,z 1)，则{BC ⃗⃗⃗⃗⃗ ⋅n ⃗ =0CP ⃗⃗⃗⃗⃗ ⋅n ⃗ =0，解得n 1⃗⃗⃗⃗ =(0,√2,1)， 同理可得平面PCE 的法向量n 2⃗⃗⃗⃗ =(√2,−√6,−2√3)， 由图形可知二面角B −PC −E 为锐角，则cosθ=|n 1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗ |n 1⃗⃗⃗⃗⃗ |⋅|n 2⃗⃗⃗⃗⃗ ||=2√55， 故二面角B −PC −E 的余弦值为2√55．19. 解：(1)甲连胜四场只能是前四场全胜，则P =(12)4=116．(2)设甲输掉一场比赛为事件A ，乙输掉一场比赛为事件B ，丙输掉一场比赛为事件C ， 四场比赛能结束为事件N ，则P(N)=P(ABAB)+P(ACAC)+P(BABA)+P(BCBC)=116×4=14所以需要进行第五场比赛的概率为P =1−P(N)=1−14=34(3) 丙获胜的概率为：P =P (ABAB )+P(BABA)+P(ABACB)+P(BABCA)+P(ABCAB)+P(ABCBA) +P(BACAB)+P(BACBA)+P(ACABB)+P(ACBAB)+P(BCABA)+P(BCBAA) =(12)4×2+(12)5×10=716．20. 解：由题意A (−a,0),B (a,0),G (0,1),AG ⃗⃗⃗⃗⃗ =(a,1),GB ⃗⃗⃗⃗⃗ =(a,−1), AG ⃗⃗⃗⃗⃗ ⋅GB ⃗⃗⃗⃗⃗ =a 2−1=8⇒a 2=9⇒a =3， ∴椭圆E 的方程为x 29+y 2=1．(2)由(1)知A (−3,0),B (3,0),P (6,m )，则直线PA 的方程为y =m 9(x +3)，联立{y =m 9(x +3)x 29+y 2=1⇒(9+m 2)x 2+6m 2x +9m 2−81=0,由韦达定理−3x C =9m 2−819+m 2⇒x C =−3m 2+279+m 2，代入直线PA 的方程y =m 9(x +3)得，y C =6m9+m 2，即C (−3m 2+279+m 2,6m9+m 2)，直线PB的方程为y=m3(x−3)，联立{y=m3(x−3)x29+y2=1⇒(1+m2)x2−6m2x+9m2−9=0,由韦达定理3x D=9m2−91+m2⇒x D=3m2−31+m2，代入直线PA的方程y=m3(x−3)得，y D=−2m1+m2，即D(3m2−31+m2,−2m1+m2)，∴直线CD的斜率k CD=6m9+m2−−2m1+m2−3m2+279+m2−3m2−31+m2=4m3(3−m2)，∴直线CD的方程为y−−2m1+m2=4m3(3−m2)(x−3m2−31+m2)，整理得y=4m3(3−m2)(x−32)，∴直线CD过定点(32,0)．21.解：(1)当a=1时，f(x)=e x+x2−x，f′(x)=e x+2x−1，记g(x)=f′(x)，因为g′(x)=e x+2>0，所以g(x)=f′(x)=e x+2x−1在R上单调递增，又f′(0)=0，得当x>0时f′(x)>0，即f(x)=e x+x2−x在(0,+∞)上单调递增；当x<0时f′(x)<0，即f(x)=e x+x2−x在(−∞,0)上单调递减．所以f(x)=e x+x2−x在(−∞,0)上单调递减，在(0,+∞)上单调递增．(2)①当x=0时，a∈R；②当x>0时，f(x)≥12x3+1即a≥12x3+x+1−e xx2，令ℎ(x)=12x3+x+1−e xx2，ℎ′(x)=(2−x)(e x−12x2−x−1)x3记m(x)=e x−12x2−x−1，m′(x)=e x−x−1令q(x)=e x−x−1，因为x>0，所以q′(x)=e x−1>0，所以m′(x)=q(x)=e x−x−1在(0,+∞)上单调递增，即m′(x)=e x−x−1> m′(0)=0所以m(x)=e x−12x2−x−1在(0,+∞)上单调递增，即m(x)=e x−12x2−x−1>m(0)=0，故当x∈(0,2)时，ℎ′(x)>0，ℎ(x)=12x3+x+1−e xx2在(0,2)上单调递增；当x∈(2,+∞)时，ℎ′(x)<0，ℎ(x)=12x3+x+1−e xx2在(2,+∞)上单调递减；所以[ℎ(x)]max=ℎ(2)=7−e24，所以a≥7−e24，综上可知，实数a的取值范围是[7−e24,+∞)．22.解：(1)当k=1时，曲线C1的参数方程为{x=costy=sint，化为直角坐标方程为x2+y2=1，表示以原点为圆心，半径为1的圆．(2)k=4时，曲线C1的参数方程为{x=cos 4ty=sin4t，化为直角坐标方程为√x+√y=1，曲线C2化为直角坐标方程为4x−16y+3=0，联立{√x+√y=14x−16y+3=0，解得{x=14y=14,所以曲线C1与曲线C2的公共点的直角坐标为(14,14 )．23.解：(1)函数f(x)=|3x+1|−2|x−1|=，图像如图所示：(2)函数f(x+1)的图像即为将f(x)的图像向左平移一个单位所得，如图，联立y=−x−3和y=5x+4解得交点横坐标为x=−，原不等式的解集为．。

2020 年普通高等学校招生全国统一考试数学（海南）一、选择题（本题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，只有一项符合题目要求的）1. 设集合A ={2，3，5，7}，B ={1，2，3，5，8}，则A B =（ ）A. {1，3，5，7}B. {2，3}C. {2，3，5}D. {1，2，3，5，7，8} 【答案】C【解析】【分析】根据集合交集的运算可直接得到结果.【详解】因为A ={2，3，5，7}，B ={1，2，3，5，8}，所以{}2,3,5A B =故选：C【点睛】本题考查的是集合交集的运算，较简单.2. (12)(2)i i ++=（ ）A. 45i +B. 5iC. -5iD. 23i + 【答案】B【解析】【分析】直接计算出答案即可.【详解】2(12)(2)2425i i i i i i ++=+++=故选：B【点睛】本题考查的是复数的计算，较简单.3. 在ABC 中，D 是AB 边上的中点，则CB =（ ）A. 2CD CA +B. 2CD CA -C. 2CD CA -D. 2CD CA +【答案】C【解析】【分析】根据向量的加减法运算法则算出即可. 【详解】()222CB CA AB CA AD CA CD CA CD CA -=+=+=+-=故选：C【点睛】本题考查的是向量的加减法，较简单.4. 日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为（ ）A. 20°B. 40°C. 50°D. 90°【答案】B【解析】【分析】画出过球心和晷针所确定的平面截地球和晷面的截面图，根据面面平行的性质定理和线面垂直的定义判定有关截线的关系，根据点A 处的纬度，计算出晷针与点A 处的水平面所成角.【详解】画出截面图如下图所示，其中CD 是赤道所在平面的截线；l 是点A 处的水平面的截线，依题意可知OA l ⊥；AB 是晷针所在直线.m 是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直， 根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与点A 处的水平面所成角为40BAE ∠=︒.故选：B【点睛】本小题主要考查中国古代数学文化，考查球体有关计算，涉及平面平行，线面垂直的性质，属于中档题.5. 某中学的学生积极参加体育锻炼，其中有96%的学生喜欢足球或游泳，60%的学生喜欢足球，82%的学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是（ ）A. 62%B. 56%C. 46%D. 42%【答案】C【解析】【分析】 记“该中学学生喜欢足球”为事件A ，“该中学学生喜欢游泳”为事件B ，则“该中学学生喜欢足球或游泳”为事件A B +，“该中学学生既喜欢足球又喜欢游泳”为事件A B ⋅，然后根据积事件的概率公式()P A B ⋅=()()()P A P B P A B +-+可得结果.【详解】记“该中学学生喜欢足球”事件A ，“该中学学生喜欢游泳”为事件B ，则“该中学学生喜欢足球或游泳”为事件A B +，“该中学学生既喜欢足球又喜欢游泳”为事件A B ⋅，则()0.6P A =，()0.82P B =，()0.96P A B +=，所以()P A B ⋅=()()()P A P B P A B +-+0.60.820.960.46=+-=所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为46%.故选：C【点睛】本题考查了积事件的概率公式，属于基础题.6. 要安排3名学生到2个乡村做志愿者，每名学生只能选择去一个村，每个村里至少有一名志愿者，则不同的安排方法共有（ ）A. 2种B. 3种C. 6种D. 8种【答案】C【解析】【分析】首先将3名学生分成两个组，然后将2组学生安排到2个村即可.【详解】第一步，将3名学生分成两个组，有12323C C =种分法第二步，将2组学生安排到2个村，有222A =种安排方法所以，不同的安排方法共有326⨯=种故选：C【点睛】解答本类问题时一般采取先组后排的策略.7. 已知函数2()lg(45)f x x x =--在(,)a +∞上单调递增，则a 的取值范围是（ ）A. (2,)+∞B. [2,)+∞C. (5,)+∞D. [5,)+∞【答案】D【解析】【分析】首先求出()f x 的定义域，然后求出2()lg(45)f x x x =--的单调递增区间即可.【详解】由2450x x -->得5x >或1x <-所以()f x 的定义域为(),1(5,)-∞-⋃+∞因为245y x x =--在(5,)+∞上单调递增所以2()lg(45)f x x x =--在(5,)+∞上单调递增所以5a ≥故选：D【点睛】在求函数的单调区间时一定要先求函数的定义域.8. 若定义在R 的奇函数f (x )在(,0)-∞单调递减，且f (2)=0，则满足(10)xf x -≥的x 的取值范围是（）A. [)1,1][3,-+∞B. 3,1][,[01]--C. [1,0][1,)-⋃+∞D. [1,0][1,3]-⋃【答案】D【解析】【分析】首先根据函数奇偶性与单调性，得到函数()f x 在相应区间上的符号，再根据两个数的乘积大于等于零，分类转化为对应自变量不等式，最后求并集得结果.【详解】因为定义在R 上的奇函数()f x 在(,0)-∞上单调递减，且(2)0f =，所以()f x 在(0,)+∞上也是单调递减，且(2)0f -=，(0)0f =，所以当(,2)(0,2)x ∈-∞-⋃时，()0f x >，当(2,0)(2,)x ∈-+∞时，()0f x <，所以由(10)xf x -≥可得： 0210x x <⎧⎨-≤-≤⎩或0012x x >⎧⎨≤-≤⎩或0x = 解得10x -≤≤或13x ≤≤，所以满足(10)xf x -≥的x 的取值范围是[1,0][1,3]-⋃，故选：D.【点睛】本题考查利用函数奇偶性与单调性解抽象函数不等式，考查分类讨论思想方法，属中档题.二、选择题（本题共 4 小题，每小题 5 分，共 20 分．在每小题给出的选项中，有多项符合题目要求．全部选对的得 5 分，有选错的得 0 分，部分选对的得 3 分）9. 我国新冠肺炎疫情进入常态化，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图，下列说法正确的是（ ）A. 这11天复工指数和复产指数均逐日增加;B. 这11天期间，复产指数增量大于复工指数的增量;C. 第3天至第11天复工复产指数均超过80%;D. 第9天至第11天复产指数增量大于复工指数的增量;【答案】CD【解析】【分析】注意到折线图中有递减部分，可判定A 错误；注意考查第1天和第11天的复工复产指数的差的大小，可判定B 错误；根据图象，结合复工复产指数的意义和增量的意义可以判定CD 正确.【详解】由图可知，第1天到第2天复工指数减少，第7天到第8天复工指数减少，第10天到第11复工指数减少，第8天到第9天复产指数减少，故A 错误；由图可知，第一天的复产指标与复工指标的差大于第11天的复产指标与复工指标的差，所以这11天期间，复产指数增量小于复工指数的增量，故B 错误;由图可知，第3天至第11天复工复产指数均超过80%，故C 正确;由图可知，第9天至第11天复产指数增量大于复工指数的增量，故D 正确;【点睛】本题考查折线图表示的函数的认知与理解，考查理解能力，识图能力，推理能力，难点在于指数增量的理解与观测，属中档题.10. 已知曲线22:1C mx ny +=.（ ）A. 若m >n >0，则C 是椭圆，其焦点在y 轴上B. 若m =n >0，则CC. 若mn <0，则C是双曲线，其渐近线方程为y = D. 若m =0，n >0，则C 是两条直线【答案】ACD【解析】【分析】结合选项进行逐项分析求解，0m n >>时表示椭圆，0m n =>时表示圆，0mn <时表示双曲线，0,0m n =>时表示两条直线【详解】对于A ，若0m n >>，则221mx ny +=可化为22111x y m n+=， 因为0m n >>，所以11m n<， 即曲线C 表示焦点在y 轴上的椭圆，故A 正确；对于B ，若0m n =>，则221mx ny +=可化为221x y n +=， 此时曲线C表示圆心在原点，半径为n n的圆，故B 不正确； 对于C ，若0mn <，则221mx ny +=可化为22111x y m n+=， 此时曲线C 表示双曲线，由220mx ny +=可得m y x n=±-，故C 正确； 对于D ，若0,0m n =>，则221mx ny +=可化为21y n=， n y =±，此时曲线C 表示平行于x 轴的两条直线，故D 正确； 故选：ACD.【点睛】本题主要考查曲线方程的特征，熟知常见曲线方程之间的区别是求解的关键，侧重考查数学运算的核心素养.11. 下图是函数y = sin(ωx +φ)的部分图像，则sin(ωx +φ)= （ ）A. πsin(3x +） B. πsin(2)3x - C. πcos(26x +） D. 5πcos(2)6x - 【答案】BC【解析】【分析】 首先利用周期确定ω的值，然后确定ϕ的值即可确定函数的解析式，最后利用诱导公式可得正确结果.【详解】由函数图像可知：22362T πππ=-=，则222T ππωπ===，所以不选A, 当2536212x πππ+==时，1y =-∴()5322122k k Z ππϕπ⨯+=+∈， 解得：()223k k ϕππ=+∈Z ， 即函数的解析式为：2sin 22sin 2cos 2sin 236263y x k x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=++=++=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 而5cos 2cos(2)66x x ππ⎛⎫+=-- ⎪⎝⎭ 故选：BC.【点睛】已知f (x )＝Asin (ωx ＋φ)(A ＞0，ω＞0)的部分图象求其解析式时，A 比较容易看图得出，困难的是求待定系数ω和φ，常用如下两种方法：(1)由ω＝2Tπ即可求出ω；确定φ时，若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0，则令ωx 0＋φ＝0(或ωx 0＋φ＝π)，即可求出φ.(2)代入点的坐标，利用一些已知点(最高点、最低点或“零点”)坐标代入解析式，再结合图形解出ω和φ，若对A ，ω的符号或对φ的范围有要求，则可用诱导公式变换使其符合要求.12. 已知a >0，b >0，且a +b =1，则（ ） A. 2212a b +≥ B. 122a b -> C. 22log log 2a b +≥-D. ≤【答案】ABD【解析】【分析】 根据1a b +=，结合基本不等式及二次函数知识进行求解.详解】对于A ，()222221221a b a a a a +=+-=-+21211222a ⎛⎫⎪⎭+ ⎝≥-=， 当且仅当12a b ==时，等号成立，故A 正确；对于B ，211a b a -=->-，所以11222a b -->=，故B 正确； 对于C ，2222221log log log log log 224a b a b ab +⎛⎫+=≤==- ⎪⎝⎭， 当且仅当12a b ==时，等号成立，故C 不正确； 对于D ，因为()21212a b ab a b +=+≤++=，所以2a b +≤，当且仅当12a b ==时，等号成立，故D 正确； 故选：ABD 【点睛】本题主要考查不等式的性质，综合了基本不等式，指数函数及对数函数的单调性，侧重考查数学运算的核心素养.三、填空题（本题共 4 小题，每小题 5 分，共 20 分）13. 已知正方体ABCD -A 1B 1C 1D 1的棱长为2，M 、N 分别为BB 1、AB 的中点，则三棱锥A -NMD 1的体积为____________【答案】13【解析】【分析】利用11A NMD D AMN V V --=计算即可.【详解】因为正方体ABCD -A 1B 1C 1D 1的棱长为2，M 、N 分别为BB 1、AB 的中点所以11111112323A NMD D AMN V V --==⨯⨯⨯⨯= 故答案为：13【点睛】在求解三棱锥的体积时，要注意观察图形的特点，看把哪个当成顶点好计算一些.14. 3C ：y 2=4x 的焦点，且与C 交于A ，B 两点，则AB =________．【答案】163 【解析】 【分析】 先根据抛物线的方程求得抛物线焦点坐标，利用点斜式得直线方程，与抛物线方程联立消去y 并整理得到关于x 的二次方程，接下来可以利用弦长公式或者利用抛物线定义将焦点弦长转化求得结果.【详解】∵抛物线的方程为24y x =，∴抛物线的焦点F 坐标为(1,0)F ，又∵直线AB 过焦点F 且斜率为3，∴直线AB 的方程为：3(1)y x =-代入抛物线方程消去y 并化简得231030x x -+=，解法一：解得121,33x x == 所以212116||1||13|3|33AB k x x =+-=+⋅-= 解法二：10036640∆=-=>设1122(,),(,)A x y B x y ，则12103x x +=, 过,A B 分别作准线1x =-的垂线，设垂足分别为,C D 如图所示.12||||||||||11AB AF BF AC BD x x =+=+=+++1216+2=3x x =+故答案为：163【点睛】本题考查抛物线焦点弦长，涉及利用抛物线的定义进行转化，弦长公式，属基础题.15. 将数列{2n –1}与{3n –2}的公共项从小到大排列得到数列{a n }，则{a n }的前n 项和为________．【答案】232n n -【解析】 【分析】首先判断出数列{}21n -与{}32n -项的特征，从而判断出两个数列公共项所构成新数列的首项以及公差，利用等差数列的求和公式求得结果.【详解】因为数列{}21n -是以1为首项，以2为公差的等差数列， 数列{}32n -是以1首项，以3为公差的等差数列，所以这两个数列的公共项所构成的新数列{}n a 是以1为首项，以6为公差的等差数列， 所以{}n a 的前n 项和为2(1)16322n n n n n -⋅+⋅=-， 故答案为：232n n -.【点睛】该题考查的是有关数列的问题，涉及到的知识点有两个等差数列的公共项构成新数列的特征，等差数列求和公式，属于简单题目.16. 某中学开展劳动实习，学生加工制作零件，零件的截面如图所示．O 为圆孔及轮廓圆弧AB 所在圆的圆心，A 是圆弧AB 与直线AG 的切点，B 是圆弧AB 与直线BC 的切点，四边形DEFG 为矩形，BC ⊥DG ，垂足为C ，tan ∠ODC =35，//BH DG ，EF =12 cm ，DE=2 cm ，A 到直线DE 和EF 的距离均为7 cm ，圆孔半径为1 cm ，则图中阴影部分的面积为________cm 2．【答案】542π+ 【解析】 【分析】利用3tan 5ODC ∠=求出圆弧AB 所在圆的半径，结合扇形的面积公式求出扇形AOB 的面积，求出直角OAH △的面积，阴影部分的面积可通过两者的面积之和减去半个单位圆的面积求得.【详解】设==OB OA r ，由题意7AM AN ==，12EF =，所以5NF =，因为5AP =,所以45AGP ︒∠=， 因为//BH DG ，所以45AHO ︒∠=，因为AG 与圆弧AB 相切于A 点，所以OA AG ⊥， 即OAH △为等腰直角三角形； 在直角OQD △中，25OQ r =，27DQ =， 因为3tan 5OQ ODC DQ ∠==，所以32522125=， 解得22r =等腰直角OAH △的面积为11222242S =⨯=； 扇形AOB 的面积(221322324S ππ=⨯⨯=，所以阴影部分的面积为1215422S S ππ+-=+. 故答案为：542π+. 【点睛】本题主要考查三角函数在实际中应用，把阴影部分合理分割是求解的关键，以劳动实习为背景，体现了五育并举的育人方针.四、解答题（本题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤．）17.在①ac =sin 3c A =，③=c 这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c 的值；若问题中的三角形不存在，说明理由．问题：是否存在ABC ，它的内角,,A B C 的对边分别为,,a b c ，且sin 3sin A B ，6C π=，________?注：如果选择多个条件分别解答，按第一个解答计分． 【答案】详见解析 【解析】 【分析】解法一：由题意结合所给的条件，利用正弦定理角化边，得到a ,b 的比例关系，根据比例关系，设出长度长度，由余弦定理得到c 的长度，根据选择的条件进行分析判断和求解.解法二：利用诱导公式和两角和的三角函数公式求得tanA 的值，得到角,,A B C 的值，然后根据选择的条件进行分析判断和求解. 【详解】解法一： 由sin 3sin AB可得：ab=不妨设(),0a b m m =>，则：2222222cos 32c a b ab C m m m m =+-=+-⨯=，即c m =选择条件①的解析：据此可得：2ac m =⨯==1m ∴=，此时1c m ==. 选择条件②的解析： 据此可得：222222231cos 222b c a m m m A bc m +-+-===-， 则：sin A ==，此时：sin 32c A m =⨯=，则：c m ==选择条件③的解析： 可得1c mb m==，c b =， 与条件=c 矛盾，则问题中的三角形不存在. 解法二：∵(),,6sinA C B A C ππ===-+,∴()6sinA A C A π⎛⎫=+=+⎪⎝⎭, ()1??22sinA A C =+= ，∴sinA =,∴tanA =23A π=,∴6B C π==,若选①，ac =,∵a ==2=若选②，3csinA =,则32=,c =;若选③,与条件=c 矛盾.【点睛】在处理三角形中的边角关系时，一般全部化为角的关系，或全部化为边的关系．题中若出现边的一次式一般采用到正弦定理，出现边的二次式一般采用到余弦定理．应用正、余弦定理时，注意公式变式的应用．解决三角形问题时，注意角的限制范围．18. 已知公比大于1的等比数列{}n a 满足24320,8a a a +==． （1）求{}n a 的通项公式；（2）求112231(1)n n n a a a a a a -+-+⋯+-.【答案】（1）2nn a =；（2）2382(1)55n n +-- 【解析】 【分析】(1)由题意得到关于首项、公比的方程组，求解方程组得到首项、公比的值即可确定数列的通项公式； (2)首先求得数列(){}111n n n a a -+-的通项公式，然后结合等比数列前n 项和公式求解其前n 项和即可.【详解】(1) 设等比数列{}n a 的公比为q (q >1)，则32411231208a a a q a q a a q ⎧+=+=⎨==⎩， 整理可得：22520q q -+=，11,2,2q q a >==，数列的通项公式为：1222n nn a -=⋅=.(2)由于：()()()1121111122112n n n n n n n n a a --++-+=-⨯⨯=--，故：112231(1)n n n a a a a a a -+-+⋯+-35791212222(1)2n n -+=-+-+⋯+-⋅()()3223221282(1)5512n n n +⎡⎤--⎢⎥⎣⎦==----. 【点睛】等比数列基本量的求解是等比数列中的一类基本问题，解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用，等差数列与等比数列求和公式是数列求和的基础.19. 为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的PM2.5和2SO 浓度（单位：3μg/m ），得下表：（1）估计事件“该市一天空气中PM2.5浓度不超过75，且2SO 浓度不超过150”的概率； （2）根据所给数据，完成下面的22⨯列联表：（3）根据（2）中的列联表，判断是否有99%的把握认为该市一天空气中PM2.5浓度与2SO 浓度有关？附：2 2()()()()()n ad bcKa b c d a c b d-=++++，【答案】（1）0.64；（2）答案见解析；（3）有.【解析】【分析】（1）根据表格中数据以及古典概型的概率公式可求得结果；（2）根据表格中数据可得22⨯列联表；（3）计算出2K，结合临界值表可得结论.【详解】（1）由表格可知，该市100天中，空气中的 2.5PM浓度不超过75，且2SO浓度不超过150的天数有32618864+++=天，所以该市一天中，空气中的 2.5PM浓度不超过75，且2SO浓度不超过150的概率为640.64100=；（2）由所给数据，可得22⨯列联表为：2SO2.5PM[]0,150(]150,475合计[]0,7564 16 80(]75,11510 10 20合计74 26 100（3）根据22⨯列联表中的数据可得222()100(64101610)()()()()80207426n ad bcKa b c d a c b d-⨯⨯-⨯==++++⨯⨯⨯36007.4844 6.635481=≈>，因为根据临界值表可知，有99%的把握认为该市一天空气中 2.5PM 浓度与2SO 浓度有关.【点睛】本题考查了古典概型的概率公式，考查了完善22⨯列联表，考查了独立性检验，属于中档题. 20. 如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面P AD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，QB 2，求PB 与平面QCD 所成角的正弦值． 【答案】（1）证明见解析；（26. 【解析】 【分析】（1）利用线面平行的判定定理以及性质定理，证得//AD l ，利用线面垂直的判定定理证得AD ⊥平面PDC ，从而得到l ⊥平面PDC ；（2）根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Q m ，之后求得平面QCD 的法向量以及向量PB 的坐标，求得cos ,n PB <>，即可得到直线PB 与平面QCD 所成角的正弦值. 【详解】（1）证明：在正方形ABCD 中，//AD BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ， 所以//AD 平面PBC ，又因为AD ⊂平面PAD ，平面PAD 平面PBC l =，所以//AD l ，因为在四棱锥P ABCD -中，底面ABCD 是正方形，所以,,AD DC l DC ⊥∴⊥ 且PD ⊥平面ABCD ，所以,,AD PD l PD ⊥∴⊥ 因为CDPD D =所以l ⊥平面PDC ；（2）如图建立空间直角坐标系D xyz -，因为1PD AD ==，则有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ， 设(,0,1)Q m ，则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-， 因为QB 2222(1)(01)(10)21m m -+-+-=⇒=设平面QCD 的法向量为(,,)n x y z =，则00DC n DQ n ⎧⋅=⎨⋅=⎩，即00y x z =⎧⎨+=⎩，令1x =，则1z =-，所以平面QCD 的一个法向量为(1,0,1)n =-，则2222226cos ,2310(1)111n PB n PB n PB⋅<>====⨯++-⋅++ 根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线与平面所成角的正弦值等于6|cos ,|n PB <>=所以直线PB 与平面QCD 6【点睛】该题考查的是有关立体几何的问题，涉及到的知识点有线面平行的判定和性质，线面垂直的判定和性质，利用空间向量求线面角，利用基本不等式求最值，属于中档题目.21. 已知椭圆C ：22221(0)x y a b a b+=>>过点M （2，3）,点A 为其左顶点，且AM 的斜率为12 ，（1）求C 的方程；（2）点N 为椭圆上任意一点，求△AMN 的面积的最大值.【答案】（1）2211612x y +=；（2）18. 【解析】 【分析】(1)由题意分别求得a ,b 的值即可确定椭圆方程；(2)首先利用几何关系找到三角形面积最大时点N 的位置，然后联立直线方程与椭圆方程，结合判别式确定点N 到直线AM 的距离即可求得三角形面积的最大值. 【详解】(1)由题意可知直线AM 的方程为：13(2)2y x -=-，即24-=-x y . 当y =0时，解得4x =-，所以a =4，椭圆()2222:10x y C a b a b+=>>过点M (2，3)，可得249116b +=， 解得b 2=12.所以C 的方程：2211612x y +=.(2)设与直线AM 平行的直线方程为：2x y m -=，如图所示，当直线与椭圆相切时，与AM 距离比较远的直线与椭圆的切点为N ，此时△AMN 的面积取得最大值.联立直线方程2x y m -=与椭圆方程2211612x y +=，可得：()2232448m y y ++=，化简可得：2216123480y my m ++-=，所以()221444163480m m ∆=-⨯-=，即m 2=64，解得m =±8， 与AM 距离比较远的直线方程：28x y -=， 直线AM 方程为：24-=-x y ，点N 到直线AM 的距离即两平行线之间的距离，利用平行线之间的距离公式可得：d ==，由两点之间距离公式可得||AM ==所以△AMN的面积的最大值：1182⨯=. 【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．22. 已知函数1()e ln ln x f x a x a -=-+．（1）当a e =时，求曲线y =f （x ）在点（1，f （1））处的切线与两坐标轴围成的三角形的面积； （2）若f （x ）≥1，求a 的取值范围． 【答案】（1）21e -（2）[1,)+∞ 【解析】【分析】（1）先求导数，再根据导数几何意义得切线斜率，根据点斜式得切线方程，求出与坐标轴交点坐标，最后根据三角形面积公式得结果；（2）解法一：利用导数研究，得到函数()f x 得导函数()’f x 的单调递增，当a=1时由()’10f =得()()11min f x f ==,符合题意；当a>1时，可证1()(1)0f f a ''<，从而()'f x 存在零点00x >，使得01001()0x f x ae x -'=-=，得到min ()f x ，利用零点的条件，结合指数对数的运算化简后，利用基本不等式可以证得()1x ≥恒成立；当01a <<时，研究()f 1.即可得到不符合题意.综合可得a 的取值范围. 解法二：利用指数对数的运算可将()111lna x lnx f x elna x e lnx +-≥++-≥+转化为,令()xg x e x =+,上述不等式等价于()()1g lna x g lnx +-≥,注意到()g x 的单调性，进一步等价转化为1lna lnx x ≥-+，令()1h x lnx x =-+,利用导数求得()max h x ，进而根据不等式恒成立的意义得到关于a 的对数不等式，解得a 的取值范围.【详解】（1）()ln 1x f x e x =-+，1()x f x e x'∴=-，(1)1k f e '∴==-. (1)1f e =+，∴切点坐标为(1,1+e ),∴函数f(x)在点(1,f (1)处的切线方程为1(1)(1)y e e x --=--,即()12y e x =-+,∴切线与坐标轴交点坐标分别为2(0,2),(,0)1e --, ∴所求三角形面积为1222||=211e e -⨯⨯--; （2）解法一：1()ln ln xf x ae x a -=-+,11()x f x ae x-'∴=-，且0a >. 设()()g x f x =',则121()0,x g x ae x -'=+> ∴g(x )在(0,)+∞上单调递增，即()f x '在(0,)+∞上单调递增，当1a =时，()01f '=,∴()()11min f x f ==,∴()1f x ≥成立.当1a >时，11a < ，111a e -<∴，111()(1)(1)(1)0a f f a e a a-''∴=--<, ∴存在唯一00x >，使得01001()0x f x ae x -'=-=，且当0(0,)x x ∈时()0f x '<，当0(,)x x ∈+∞时()0f x '>，0101x ae x -∴=，00ln 1ln a x x ∴+-=-， 因此01min 00()()ln ln x f x f x ae x a -==-+001ln 1ln 2ln 12ln 1a x a a a x =++-+≥-+=+>1, ∴()1,f x >∴()1f x ≥恒成立；当01a <<时， (1)ln 1,f a a a =+<<∴(1)1,()1f f x <≥不是恒成立.综上所述，实数a 的取值范围是[1,+∞).解法二：()111x lna x f x ae lnx lna e lnx lna -+-=-+=-+≥等价于11lna x lnx e lna x lnx x e lnx +-++-≥+=+,令()xg x e x =+,上述不等式等价于()()1g lna x g lnx +-≥, 显然()g x 为单调增函数，∴又等价于1lna x lnx +-≥，即1lna lnx x ≥-+，令()1h x lnx x =-+,则()111x h x x x-=-=' 在()0,1上h’(x)>0,h(x)单调递增；在(1,+∞)上h’(x)<0,h(x)单调递减，∴()()10max h x h ==,01lna a ≥≥，即，∴a 的取值范围是[1,+∞).【点睛】本题考查导数几何意义、利用导数研究不等式恒成立问题，考查综合分析求解能力，分类讨论思想和等价转化思想，属较难试题.。

考点测试47 空间向量及其应用高考概览本考点是高考必考知识点，考查题型为选择、填空题、解答题，中等难度考纲研读1．了解空间直角坐标系，会用空间直角坐标表示点的位置 2．会简单应用空间两点间的距离公式3．了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示4．掌握空间向量的线性运算及其坐标表示5．掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线与垂直一、基础小题1．空间四边形ABCD 中，已知M ，G 分别为BC ，CD 的中点，则向量AB→＋12(BD→＋BC →)＝( ) A ．AG→ B ．CG → C ．BC → D ．12BC → 答案 A解析 如图所示，12(BD →＋BC →)＝BG→，AB →＋BG →＝AG →．故选A ．2．分别以棱长为1的正方体ABCD －A 1B 1C 1D 1的棱AB ，AD ，AA 1所在的直线为x ，y ，z 轴，建立空间直角坐标系，则四边形AA 1B 1B 的对角线的交点的坐标为( )A ．0，12，12B ．12，0，12 C ．12，12，0 D ．12，12，12 答案 B解析 设所求交点为O ，在空间直角坐标系中，点A 1(0，0，1)，B (1，0，0)，则AB →＝(1，0，0)，AA 1→＝(0，0，1)，故AO →＝12，0，12，即对角线的交点坐标为12，0，12，故选B ．3．若向量a ＝(2，－2，－2)，b ＝(2，0，4)，则a 与b 的夹角的余弦值为( ) A ．48585 B ．6985 C ．－1515 D ．0 答案 C解析 cos 〈a ，b 〉＝a ·b |a ||b |＝2×2－823×25＝－1515．4．设一地球仪的球心为空间直角坐标系的原点O ，球面上的两个点A ，B 的坐标分别为A (1，2，2)，B (2，－2，1)，则|AB |等于( )A ．18B ．12C ．3 2D ．23 答案 C解析 |AB |＝(1－2)2＋(2＋2)2＋(2－1)2＝32．5．在空间四边形ABCD 中，AB →·CD →＋AC →·DB →＋AD →·BC→＝( )A ．－1B ．0C ．1D ．不确定 答案 B 解析如图，设a ＝DA →，b ＝DB →，c ＝DC →，则AB →·CD →＋AC →·DB →＋AD →·BC →＝(b －a )·(－c )＋(c －a )·b ＋(－a )·(c －b )＝－b ·c ＋a ·c ＋c ·b －a ·b －a ·c ＋a ·b ＝0．6．在正方体ABCD －A 1B 1C 1D 1中，给出以下向量表达式：①(A 1D 1→－A 1A →)－AB →；②(BC →＋BB 1→)－D 1C 1→；③(AD →－AB →)－2DD 1→；④(B 1D 1→＋A 1A →)＋DD 1→． 其中能够化简为向量BD 1→的是( )A ．①②B ．②③C ．③④D ．①④ 答案 A解析 ①(A 1D 1→－A 1A →)－AB →＝AD 1→－AB →＝BD 1→； ②(BC →＋BB 1→)－D 1C 1→＝BC 1→－D 1C 1→＝BD 1→； ③(AD →－AB →)－2DD 1→＝BD →－2DD 1→≠BD 1→； ④(B 1D 1→＋A 1A →)＋DD 1→＝B 1D →＋DD 1→＝B 1D 1→≠BD 1→．综上，①②符合题意．故选A ．7．在空间直角坐标系中，已知△ABC 的顶点坐标分别为A (1，－1，2)，B (5，－6，2)，C (1，3，－1)，则边AC 上的高BD ＝( )A ．5B ．41C ．4D ．25 答案 A解析 设AD→＝λAC →，AC →＝(0，4，－3)，则AD →＝(0，4λ，－3λ)，AB →＝(4，－5，0)，BD →＝(－4，4λ＋5，－3λ)．由AC →·BD→＝0，得λ＝－45，所以BD →＝－4，95，125，所以|BD→|＝5．故选A ．8．已知空间向量a ，b ，满足|a |＝|b |＝1，且a ，b 的夹角为π3，O 为空间直角坐标系的原点，点A ，B 满足OA →＝2a ＋b ，OB →＝3a －b ，则△OAB 的面积为________．答案534解析 由已知OA →＝2a ＋b ，OB →＝3a －b ，得|OA→|＝ (2a ＋b )2＝ 7，|OB→|＝(3a －b )2＝7．∴cos ∠BOA ＝OA →·OB →|OA →||OB →|＝1114，∴sin ∠BOA ＝5314．∴S △OAB ＝12|OA →||OB →|sin ∠BOA ＝534． 二、高考小题9．(2014·广东高考)已知向量a ＝(1，0，－1)，则下列向量中与a 成60°夹角的是( )A ．(－1，1，0)B ．(1，－1，0)C ．(0，－1，1)D ．(－1，0，1) 答案 B解析 经检验，选项B 中向量(1，－1，0)与向量a ＝(1，0，－1)的夹角的余弦值为12，即它们的夹角为60°．故选B ．10．(2015·浙江高考)已知e 1，e 2是空间单位向量，e 1·e 2＝12．若空间向量b 满足b ·e 1＝2，b ·e 2＝52，且对于任意x ，y ∈R ，|b －(x e 1＋y e 2)|≥|b －(x 0e 1＋y 0e 2)|＝1(x 0，y 0∈R )，则x 0＝________，y 0＝________，|b |＝________．答案 1 2 22解析 ∵e 1，e 2是单位向量，e 1·e 2＝12，∴cos 〈e 1，e 2〉＝12，又∵0°≤〈e 1，e 2〉≤180°，∴〈e 1，e 2〉＝60°．不妨把e 1，e 2放到空间直角坐标系Oxyz 的平面xOy 中，设e 1＝(1，0，0)，则e 2＝⎝ ⎛⎭⎪⎫12，32，0，再设OB →＝b ＝(m ，n ，r )，由b ·e 1＝2，b ·e 2＝52，得m ＝2，n ＝3，则b ＝(2，3，r )．而x e 1＋y e 2是平面xOy 上任一向量，由|b －(x e 1＋y e 2)|≥1知点B (2，3，r )到平面xOy 的距离为1，故可得r ＝1，则b ＝(2，3，1)，∴|b |＝22．又由|b －(x e 1＋y e 2)|≥|b －(x 0e 1＋y 0e 2)|＝1知x 0e 1＋y 0e 2＝(2，3，0)，解得x 0＝1，y 0＝2．三、模拟小题11．(2018·山东临沂模拟)若直线l 的方向向量为a ＝(1，0，2)，平面α的法向量为n ＝(－2，0，－4)，则( )A ．l ∥αB ．l ⊥αC ．l ⊂αD ．l 与α斜交 答案 B解析 ∵a ＝(1，0，2)，n ＝(－2，0，－4)，即n ＝－2a ，故a ∥n ，∴l ⊥α． 12．(2018·河南安阳联考)设平面α的一个法向量为n 1＝(1，2，－2)，平面β的一个法向量为n 2＝(－2，－4，k )，若α∥β，则k ＝( )A ．2B ．－4C ．－2D ．4 答案 D解析 ∵α∥β，∴n 1∥n 2，由题意可得－21＝－42＝k－2，∴k ＝4．13．(2018·河北衡水月考)正方体ABCD －A 1B 1C 1D 1中，点E 为上底面A 1C 1的中心．若向量A E →＝AA 1→＋xAB →＋yAD →，则实数x ，y 的值分别为( ) A ．x ＝1，y ＝1 B ．x ＝1，y ＝12 C ．x ＝12，y ＝12 D ．x ＝12，y ＝1 答案 C14．(2018·合肥质检)长方体ABCD －A 1B 1C 1D 1中，AB ＝1，BC ＝2，AA 1＝3，点M 是BC 的中点，点P ∈AC 1，Q ∈MD ，则PQ 长度的最小值为( )A ．1B ．43C ．233 D ．2 答案 C解析 根据题意建立如图所示的空间直角坐标系， 设P (x 0，2x 0，3－3x 0)， Q (x 1，2－x 1，3)，x 0， x 1∈[0，1]，所以 PQ ＝(x 0－x 1)2＋(2x 0＋x 1－2)2＋(3－3x 0－3)2 ＝2⎝⎛⎭⎪⎫x 1＋x 0－222＋272⎝ ⎛⎭⎪⎫x 0－292＋43， 当且仅当x 0＝29，x 1＝89时，PQ 取得最小值， 即PQ min ＝43＝233．15．(2018·贵阳模拟)如图，在直三棱柱ABC －A 1B 1C 1中，∠ACB ＝90°，2AC ＝AA 1＝BC ＝2．若二面角B 1－DC －C 1的大小为60°，则AD 的长为( )A ． 2B ．3C ．2D ．22 答案 A解析 如图，以C 为坐标原点，CA ，CB ，CC 1所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，则C (0，0，0)，A (1，0，0)，B 1(0，2，2)，C 1(0，0，2)设AD ＝a ，则D 点坐标为(1，0，a )，CD →＝(1，0，a )，CB 1→＝(0，2，2)，设平面B 1CD 的一个法向量为m ＝(x ，y ，z )．则⎩⎪⎨⎪⎧m ·CB 1→＝0，m ·CD →＝0⇒⎩⎨⎧2y ＋2z ＝0，x ＋az ＝0.令z ＝－1，得m ＝(a ，1，－1)，又平面C 1DC 的一个法向量为n ＝(0，1，0)，则由cos60°＝m ·n|m ||n |，得1a 2＋2＝12，即a ＝2，故AD ＝2． 16．(2018·北京海淀区一模)正方体ABCD －A 1B 1C 1D 1的棱长为1，若动点P 在线段BD 1上运动，则DC →·AP →的取值范围是________．答案 [0，1] 解析以DA 所在的直线为x 轴，DC 所在的直线为y 轴，DD 1所在的直线为z 轴，建立空间直角坐标系Dxyz ．则D (0，0，0)，C (0，1，0)，A (1，0，0)，B (1，1，0)，D 1(0，0，1)． ∴DC →＝(0，1，0)，BD 1→＝(－1，－1，1)． ∵点P 在线段BD 1上运动，∴设BP →＝λBD 1→＝(－λ，－λ，λ)，且0≤λ≤1．∴AP→＝AB →＋BP →＝DC →＋BP →＝(－λ，1－λ，λ)． ∴DC →·AP →＝1－λ∈[0，1]．一、高考大题1．(2018·全国卷Ⅲ)如图，边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；(2)当三棱锥M －ABC 体积最大时，求面MAB 与面MCD 所成二面角的正弦值．解 (1)证明：由题设知，平面CMD ⊥平面ABCD ，交线为CD ． 因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ． 因为M 为CD 上异于C ，D 的点，且DC 为直径， 所以DM ⊥CM ．又BC ∩CM ＝C ，所以DM ⊥平面BMC ． 而DM ⊂平面AMD ，故平面AMD ⊥平面BMC ．(2)以D 为坐标原点，DA →的方向为x 轴正方向，建立如图所示的空间直角坐标系Dxyz ．当三棱锥M －ABC 体积最大时，M 为CD 的中点．由题设得D (0，0，0)，A (2，0，0)，B (2，2，0)，C (0，2，0)，M (0，1，1)， AM→＝(－2，1，1)，AB →＝(0，2，0)，DA →＝(2，0，0)． 设n ＝(x ，y ，z )是平面MAB 的法向量，则 ⎩⎪⎨⎪⎧n ·AM →＝0，n ·AB →＝0，即⎩⎨⎧－2x ＋y ＋z ＝0，2y ＝0. 可取n ＝(1，0，2)．DA→是平面MCD 的法向量，因此， cos 〈n ，DA →〉＝n ·DA →|n ||DA →|＝55，sin 〈n ，DA→〉＝255，所以面MAB 与面MCD 所成二面角的正弦值是255．2．(2018·全国卷Ⅱ)如图，在三棱锥P －ABC 中，AB ＝BC ＝22，P A ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且二面角M －P A －C 为30°，求PC 与平面P AM 所成角的正弦值．解 (1)证明：因为P A ＝PC ＝AC ＝4，O 为AC 的中点，所以OP ⊥AC ，且OP ＝23．连接OB ．因为AB ＝BC ＝22AC ，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2．由OP 2＋OB 2＝PB 2，知OP ⊥OB ．由OP ⊥OB ，OP ⊥AC ，AC ∩OB ＝O ，知PO ⊥平面ABC ．(2)如图，以O 为坐标原点，OB →的方向为x 轴正方向，建立如图所示的空间直角坐标系Oxyz ．由已知得O (0，0，0)，B (2，0，0)，A (0，－2，0)，C (0，2，0)，P (0，0，23)，则AP →＝(0，2，23)，取平面P AC 的法向量OB →＝(2，0，0)．设M (a ，2－a ，0)(0<a ≤2)，则AM →＝(a ，4－a ，0)．设平面P AM 的法向量为n ＝(x ，y ，z )． 由AP →·n ＝0，AM →·n ＝0得⎩⎨⎧2y ＋23z ＝0，ax ＋(4－a )y ＝0，可取n ＝(3(a －4)，3a ，－a )， 所以cos 〈OB→，n 〉＝23(a －4)23(a －4)2＋3a 2＋a 2．由已知得|cos 〈OB→，n 〉|＝32．所以23|a －4|23(a －4)2＋3a 2＋a2＝32． 解得a ＝－4(舍去)，a ＝43． 所以n ＝⎝⎛⎭⎪⎫－833，433，－43． 又PC →＝(0，2，－23)，所以cos 〈PC →，n 〉＝34． 所以PC 与平面P AM 所成角的正弦值为34．3．(2017·全国卷Ⅰ)如图，在四棱锥P －ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°．(1)证明：平面P AB ⊥平面P AD ；(2)若P A ＝PD ＝AB ＝DC ，∠APD ＝90°，求二面角A －PB －C 的余弦值． 解 (1)证明：由已知∠BAP ＝∠CDP ＝90°，得 AB ⊥AP ，CD ⊥PD ．因为AB ∥CD ，所以AB ⊥PD ． 又AP ∩DP ＝P ，所以AB ⊥平面P AD ．因为AB ⊂平面P AB ，所以平面P AB ⊥平面P AD ． (2)在平面P AD 内作PF ⊥AD ，垂足为点F ．由(1)可知，AB ⊥平面P AD ，故AB ⊥PF ，可得PF ⊥平面ABCD ．以F 为坐标原点，F A →的方向为x 轴正方向，|AB →|为单位长度建立如图所示的空间直角坐标系Fxyz ．由(1)及已知可得A 22，0，0，P 0，0，22，B 22，1，0，C －22，1，0，所以PC →＝－22，1，－22，CB →＝(2，0，0)，P A →＝22，0，－22，AB →＝(0，1，0)．设n ＝(x 1，y 1，z 1)是平面PCB 的一个法向量，则 ⎩⎪⎨⎪⎧n ·PC →＝0，n ·CB →＝0，即⎩⎨⎧－22x 1＋y 1－22z 1＝0，2x 1＝0.所以可取n ＝(0，－1，－2)．设m ＝(x 2，y 2，z 2)是平面P AB 的一个法向量，则 ⎩⎪⎨⎪⎧m ·P A →＝0，m ·AB →＝0，即⎩⎨⎧22x 2－22z 2＝0，y 2＝0.所以可取m ＝(1，0，1)，则cos 〈n ，m 〉＝n ·m |n ||m |＝－23×2＝－33．由图可知，二面角A －PB －C 为钝角， 所以二面角A －PB －C 的余弦值为－33．二、模拟大题4．(2018·齐鲁名校调研)如图，五边形ABSCD中，四边形ABCD为长方形，三角形SBC为边长为2的正三角形，将三角形SBC沿BC折起，使得点S在平面ABCD上的射影恰好在AD上．(1)当AB＝2时，证明：平面SAB⊥平面SCD；(2)若AB＝1，求平面SCD与平面SBC所成二面角的余弦值的绝对值．解(1)证明：过点S作SO⊥AD，垂足为O，依题意得SO⊥平面ABCD，∴SO⊥AB，SO⊥CD，又AB⊥AD，SO∩AD＝O，∴AB⊥平面SAD，AB⊥SA，AB⊥SD．在△SAB中，利用勾股定理得SA＝SB2－AB2＝4－2＝2，同理可得SD＝2．在△SAD中，AD＝2，SA＝SD＝2，∴SA2＋SD2＝AD2，即SA⊥SD．∵AB∩SA＝A，∴SD⊥平面SAB，又SD⊂平面SCD，∴平面SAB⊥平面SCD．(2)连接BO，CO，∵SB＝SC，SO⊥平面ABCD，∴Rt△SOB≌Rt△SOC，∴BO＝CO，又四边形ABCD为长方形，∴Rt△AOB≌Rt△DOC，∴OA＝OD．取BC的中点为E，连接OE，得OE∥AB，连接SE，易得SE＝3，其中OE＝1，OA＝OD＝1，OS＝3－12＝2．易知OS ，OE ，AD 互相垂直，不妨以OA →，OE →，OS →所在方向分别为x ，y ，z轴的正方向建立空间直角坐标系．则B (1，1，0)，C (－1，1，0)，D (－1，0，0)，S (0，0，2)， ∴DC→＝(0，1，0)，SC →＝(－1，1，－2)，BC →＝(－2，0，0)， 设m ＝(x 1，y 1，z 1)是平面SCD 的法向量， 则有⎩⎪⎨⎪⎧m ·DC →＝0，m ·SC →＝0，即⎩⎨⎧y 1＝0，－x 1＋y 1－2z 1＝0，令z 1＝1，得m ＝(－2，0，1)． 设n ＝(x 2，y 2，z 2)是平面SBC 的法向量， 则有⎩⎪⎨⎪⎧n ·BC →＝0，n ·SC →＝0，即⎩⎨⎧－2x 2＝0，－x 2＋y 2－2z 2＝0，令z 2＝1，得n ＝(0，2，1)， 则|cos 〈m ，n 〉|＝|m ·n ||m ||n |＝13×3＝13． ∴平面SCD 与平面SBC 所成二面角的余弦值的绝对值为13．5．(2018·太原五中阶段测验)如图，在四棱锥P －ABCD 中，四边形ABCD 是菱形，对角线AC 与BD 的交点为O ，PD ＝PB ＝AB ＝2，P A ＝6，∠BCD ＝60°．(1)证明：PO ⊥平面ABCD ；(2)在棱CD 上是否存在点M ，使平面ABP 与平面MBP 所成锐二面角的余弦值为55？若存在，请指出M 点的位置；若不存在，请说明理由．解 (1)证明：∵PD ＝PB ，且O 为BD 的中点， ∴PO ⊥BD ．在菱形ABCD 中，∵∠BCD ＝60°，AB ＝2， ∴OA ＝3，OB ＝1． 又PB ＝2，∴PO ＝3．∵P A ＝6，∴P A 2＝PO 2＋OA 2，∴PO ⊥OA ． ∵BD ∩AO ＝O ，∴PO ⊥平面ABCD ．(2)以O 为原点，OA ，OB ，OP 所在直线分别为x ，y ，z 轴建立如图所示的空间直角坐标系，则A (3，0，0)，B (0，1，0)，C (－3，0，0)，D (0，－1，0)，P (0，0，3)． ∴AB →＝(－3，1，0)，BP →＝(0，－1，3)，BC →＝(－3，－1，0)，CD →＝(3，－1，0)，设平面ABP 的法向量为n 1， 由⎩⎪⎨⎪⎧n 1·AB →＝0，n 1·BP →＝0，得平面ABP 的一个法向量为n 1＝(1，3，1)， 设CM→＝λCD →， 则BM→＝BC →＋CM →＝BC →＋λCD → ＝(3(λ－1)，－(λ＋1)，0)． 设平面BPM 的法向量为n 2， 由⎩⎪⎨⎪⎧n 2·BP →＝0，n 2·BM →＝0，得平面BPM 的一个法向量为 n 2＝(λ＋1，3(λ－1)，λ－1)． 由|cos 〈n 1，n 2〉|＝|5λ－3|5·(λ＋1)2＋4(λ－1)2＝55，得5λ2－6λ＋1＝0，∴λ＝1或λ＝15．即当点M 与点D 重合或|CM→|＝15|CD →|时，平面ABP 与平面MBP 所成锐二面角的余弦值为55．6．(2018·江西重点盟校联考)如图，正三棱柱ABC －A 1B 1C 1的所有棱长均为2，D 为棱BB 1(不包括端点)上一动点，E 是AB 的中点．(1)若AD ⊥A 1C ，求BD 的长；(2)当D 在棱BB 1(不包括端点)上运动时，求平面ADC 1与平面ABC 的夹角的余弦值的取值范围．解 (1)由AC ＝BC ，AE ＝BE ，知CE ⊥AB ，又平面ABC ⊥平面ABB 1A 1，平面ABC ∩平面ABB 1A 1＝AB ，CE ⊂平面ABC ，所以CE ⊥平面ABB 1A 1． 而AD ⊂平面ABB 1A 1，所以AD ⊥CE ，又AD ⊥A 1C ，A 1C ∩CE ＝C ，所以AD ⊥平面A 1CE ， 因为A 1E ⊂平面A 1CE ，所以AD ⊥A 1E ． 易知此时D 为BB 1的中点，故BD ＝1．(2)以点E 为原点，EB 所在直线为x 轴，EC 所在直线为y 轴，过E 作垂直于平面ABC 的垂线为z 轴，建立如图所示的空间直角坐标系，设BD ＝t ，0<t <2，则A (－1，0，0)，D (1，0，t )，C 1(0，3，2)，AD →＝(2，0，t )，AC 1→＝(1，3，2)， 设平面ADC 1的法向量为n ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧n ·AD→＝2x ＋tz ＝0，n ·AC 1→＝x ＋3y ＋2z ＝0，取x ＝1，得n ＝1，43t －13，－2t ， 而平面ABC 的一个法向量为m ＝(0，0，1)， 设平面ADC 1与平面ABC 的夹角为θ，θ为锐角， 所以cos θ＝|m ·n ||m ||n |＝2t1＋43t －132＋4t 2＝3t 2－2t ＋7＝3(t －1)2＋6．由于t ∈(0，2)，故cos θ∈217，22，21 7，2 2．即平面ADC1与平面ABC的夹角的余弦值的取值范围为。

§13.1 坐标系与参数方程第1课时 坐标系1．平面直角坐标系设点P (x ，y )是平面直角坐标系中的任意一点，在变换φ：⎩⎪⎨⎪⎧x ′＝λ·x ，λ>0，y ′＝μ·y ，μ>0的作用下，点P (x ，y )对应到点P ′(x ′，y ′)，称φ为平面直角坐标系中的坐标伸缩变换，简称伸缩变换． 2．极坐标系(1)极坐标与极坐标系的概念在平面内取一个定点O ，自点O 引一条射线Ox ，同时确定一个长度单位和计算角度的正方向(通常取逆时针方向)，这样就建立了一个极坐标系．点O 称为极点，射线Ox 称为极轴．平面内任一点M 的位置可以由线段OM 的长度ρ和从射线Ox 到射线OM 的角度θ来刻画(如图所示)．这两个数组成的有序数对(ρ，θ)称为点M 的极坐标．ρ称为点M 的极径，θ称为点M 的极角．一般认为ρ≥0.当极角θ的取值范围是[0,2π)时，平面上的点(除去极点)就与极坐标(ρ，θ)(ρ≠0)建立一一对应的关系．我们设定，极点的极坐标中，极径ρ＝0，极角θ可取任意角．(2)极坐标与直角坐标的互化设M 为平面内的一点，它的直角坐标为(x ，y )，极坐标为(ρ，θ)．由图可知下面关系式成立：⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ或⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x(x ≠0)，这就是极坐标与直角坐标的互化公式．3．常见曲线的极坐标方程概念方法微思考1．平面直角坐标系内的点与坐标能建立一一对应关系，在极坐标系中点与坐标也能建立一一对应关系吗？提示 不能，极径需和极角结合才能唯一确定一个点．2．由极坐标的意义可判断平面上点的极坐标唯一吗？提示 平面上的点的极坐标不是唯一的，如果限定ρ取正值，θ∈[0,2π)，平面上的点(除去极点)与极坐标(ρ，θ)(ρ≠0)建立一一对应关系．题组一 思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)若点P 的直角坐标为(1，－3)，则点P 的一个极坐标是⎝⎛⎭⎫2，－π3.( √ ) (2)在极坐标系中，曲线的极坐标方程不是唯一的．( √ ) (3)极坐标方程θ＝π(ρ≥0)表示的曲线是一条直线．( × ) 题组二 教材改编2．若以直角坐标系的原点为极点，x 轴的正半轴为极轴建立极坐标系，则线段y ＝1－x (0≤x ≤1)的极坐标方程为( ) A ．ρ＝1cos θ＋sin θ，0≤θ≤π2B ．ρ＝1cos θ＋sin θ，0≤θ≤π4C ．ρ＝cos θ＋sin θ，0≤θ≤π2D ．ρ＝cos θ＋sin θ，0≤θ≤π4答案 A解析 ∵y ＝1－x (0≤x ≤1)， ∴ρsin θ＝1－ρcos θ(0≤ρcos θ≤1)； ∴ρ＝1sin θ＋cos θ⎝⎛⎭⎫0≤θ≤π2. 3．在极坐标系中，圆ρ＝－2sin θ的圆心的极坐标是( ) A.⎝⎛⎭⎫1，π2 B.⎝⎛⎭⎫1，－π2 C ．(1,0) D ．(1，π) 答案 B解析 方法一 由ρ＝－2sin θ，得ρ2＝－2ρsin θ，化成直角坐标方程为x 2＋y 2＝－2y ，化成标准方程为x 2＋(y ＋1)2＝1，圆心坐标为(0，－1)，其对应的极坐标为⎝⎛⎭⎫1，－π2. 方法二 由ρ＝－2sin θ＝2cos ⎝⎛⎭⎫θ＋π2，知圆心的极坐标为⎝⎛⎭⎫1，－π2，故选B.题组三 易错自纠4．在极坐标系中，已知点P ⎝⎛⎭⎫2，π6，则过点P 且平行于极轴的直线方程是( ) A ．ρsin θ＝1 B ．ρsin θ＝ 3 C ．ρcos θ＝1 D ．ρcos θ＝ 3答案 A解析 先将极坐标化成直角坐标表示，P ⎝⎛⎭⎫2，π6转化为直角坐标为x ＝ρcos θ＝2cos π6＝3，y ＝ρsin θ＝2sin π6＝1，即(3，1)，过点(3，1)且平行于x 轴的直线为y ＝1，再化为极坐标为ρsin θ＝1.5．在直角坐标系xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系．若曲线C 的极坐标方程为ρ＝2sin θ，则曲线C 的直角坐标方程为 ． 答案 x 2＋y 2－2y ＝0解析 由ρ＝2sin θ，得ρ2＝2ρsin θ，所以曲线C 的直角坐标方程为x 2＋y 2－2y ＝0. 6．在以O 为极点的极坐标系中，圆ρ＝4sin θ和直线ρsin θ＝a 相交于A ，B 两点．当△AOB 是等边三角形时，求a 的值．解 由ρ＝4sin θ可得圆的直角坐标方程为x 2＋y 2＝4y ， 即x 2＋(y －2)2＝4.由ρsin θ＝a 可得直线的直角坐标方程为y ＝a (a >0)．设圆的圆心为O ′，y ＝a 与x 2＋(y －2)2＝4的两交点A ，B 与O 构成等边三角形，如图所示．由对称性知∠O ′OB ＝30°，OD ＝a . 在Rt △DOB 中，易求DB ＝33a ， ∴B 点的坐标为⎝⎛⎭⎫33a ，a .又∵B 在x 2＋y 2－4y ＝0上，∴⎝⎛⎭⎫33a 2＋a 2－4a ＝0， 即43a 2－4a ＝0，解得a ＝0(舍去)或a ＝3.所以a ＝3.题型一极坐标与直角坐标的互化1．(1)化圆的直角坐标方程x2＋y2＝r2(r>0)为极坐标方程；(2)化曲线的极坐标方程ρ＝8sin θ为直角坐标方程．解(1)将x＝ρcos θ，y＝ρsin θ代入x2＋y2＝r2(r>0)，得ρ2cos2θ＋ρ2sin2θ＝r2，即ρ＝r. 所以以极点为圆心，r为半径的圆的极坐标方程为ρ＝r(0≤θ<2π)．(2)方法一把ρ＝x2＋y2，sin θ＝yρ代入ρ＝8sin θ，得x2＋y2＝8·yx2＋y2，化简得x2＋y2－8y＝0，即x2＋(y－4)2＝16.方法二方程ρ＝8sin θ两边同时乘ρ，得ρ2＝8ρsin θ，因为ρ2＝x2＋y2，ρsin θ＝y，所以x2＋y2－8y＝0，即x2＋(y－4)2＝16.2．在极坐标系中，已知曲线C1：ρcos θ－3ρsin θ－1＝0，C2：ρ＝2cos θ.(1)求曲线C1，C2的直角坐标方程，并判断两曲线的形状；(2)若曲线C1，C2交于A，B两点，求两交点间的距离．解(1)∵C1：ρcos θ－3ρsin θ－1＝0，∴x－3y－1＝0表示一条直线．由C2：ρ＝2cos θ，得ρ2＝2ρcos θ，∴x2＋y2＝2x，即(x－1)2＋y2＝1.∴C2是圆心为(1,0)，半径为1的圆．(2)由(1)知，点(1,0)在直线x－3y－1＝0上，∴直线C1过圆C2的圆心．因此两交点A，B的连线是圆C2的直径．∴两交点A，B间的距离|AB|＝2r＝2.思维升华(1)极坐标与直角坐标互化的前提条件：①极点与原点重合；②极轴与x轴的正半轴重合；③取相同的单位长度．(2)直角坐标方程化为极坐标方程比较容易，只要运用公式x ＝ρcos θ及y ＝ρsin θ直接代入并化简即可；而极坐标方程化为直角坐标方程则相对困难一些，解决此类问题常通过变形，构造形如ρcos θ，ρsin θ，ρ2的形式，进行整体代换． 题型二 求曲线的极坐标方程例1 将圆x 2＋y 2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得到曲线C . (1)求曲线C 的标准方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与直线l 垂直的直线的极坐标方程．解 (1)设(x 1，y 1)为圆上的点，在已知变换下变为曲线C 上的点(x ，y )，依题意，得⎩⎪⎨⎪⎧x ＝x 1，y ＝2y 1.由x 21＋y 21＝1，得x 2＋⎝⎛⎭⎫y 22＝1， 即曲线C 的标准方程为x 2＋y 24＝1.(2)由⎩⎪⎨⎪⎧x 2＋y 24＝1，2x ＋y －2＝0，解得⎩⎪⎨⎪⎧ x ＝1，y ＝0或⎩⎪⎨⎪⎧x ＝0，y ＝2.不妨设P 1(1,0)，P 2(0,2)，则线段P 1P 2的中点坐标为⎝⎛⎭⎫12，1，所求直线的斜率为k ＝12， 于是所求直线的方程为y －1＝12⎝⎛⎭⎫x －12， 化为极坐标方程，并整理得2ρcos θ－4ρsin θ＝－3， 故所求直线的极坐标方程为ρ＝34sin θ－2cos θ.思维升华 求曲线的极坐标方程的步骤(1)建立适当的极坐标系，设P (ρ，θ)是曲线上任意一点．(2)由曲线上的点所适合的条件，列出曲线上任意一点的极径ρ和极角θ之间的关系式． (3)将列出的关系式进行整理、化简，得出曲线的极坐标方程．跟踪训练1 已知极坐标系的极点为直角坐标系xOy 的原点，极轴为x 轴的正半轴，两种坐标系中的长度单位相同，圆C 的直角坐标方程为x 2＋y 2＋2x －2y ＝0，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t ，y ＝t(t 为参数)，射线OM 的极坐标方程为θ＝3π4.(1)求圆C 和直线l 的极坐标方程；(2)已知射线OM 与圆C 的交点为O ，P ，与直线l 的交点为Q ，求线段PQ 的长． 解 (1)∵ρ2＝x 2＋y 2，x ＝ρcos θ，y ＝ρsin θ， 圆C 的直角坐标方程为x 2＋y 2＋2x －2y ＝0， ∴ρ2＋2ρcos θ－2ρsin θ＝0，∴圆C 的极坐标方程为ρ＝22sin ⎝⎛⎭⎫θ－π4. 又直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t ，y ＝t (t 为参数)，消去t 后得y ＝x ＋1，∴直线l 的极坐标方程为sin θ－cos θ＝1ρ.(2)当θ＝3π4时，|OP |＝22sin ⎝⎛⎭⎫3π4－π4＝22， ∴点P 的极坐标为⎝⎛⎭⎫22，3π4，|OQ |＝122＋22＝22， ∴点Q 的极坐标为⎝⎛⎭⎫22，3π4，故线段PQ 的长为322. 题型三 极坐标方程的应用例2 在平面直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋cos α，y ＝2＋sin α(α为参数)，直线C 2的直角坐标方程为y ＝3x .以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系． (1)求曲线C 1和直线C 2的极坐标方程；(2)若直线C 2与曲线C 1交于A ，B 两点，求1|OA |＋1|OB |.解 (1)由曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋cos α，y ＝2＋sin α(α为参数)，得曲线C 1的普通方程为(x －2)2＋(y －2)2＝1，则C 1的极坐标方程为ρ2－4ρcos θ－4ρsin θ＋7＝0， 由于直线C 2过原点，且倾斜角为π3，故其极坐标方程为θ＝π3(ρ∈R )．(2)由⎩⎪⎨⎪⎧ρ2－4ρcos θ－4ρsin θ＋7＝0，θ＝π3，得ρ2－(23＋2)ρ＋7＝0，设A ，B 对应的极径分别为ρ1，ρ2，则ρ1＋ρ2＝23＋2，ρ1ρ2＝7， ∴1|OA |＋1|OB |＝|OA |＋|OB ||OA |·|OB |＝ρ1＋ρ2ρ1ρ2＝23＋27. 思维升华 极坐标应用中的注意事项(1)极坐标与直角坐标互化的前提条件：①极点与原点重合；②极轴与x 轴正半轴重合；③取相同的长度单位．(2)若把直角坐标化为极坐标求极角θ时，应注意判断点P 所在的象限(即角θ的终边的位置)，以便正确地求出角θ.利用两种坐标的互化，可以把不熟悉的问题转化为熟悉的问题． (3)由极坐标的意义可知平面上点的极坐标不是唯一的，如果限定ρ取正值，θ∈[0,2π)，平面上的点(除去极点)与极坐标(ρ，θ)(ρ≠0)建立一一对应关系．跟踪训练2 (2017·全国Ⅱ)在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρcos θ＝4.(1)M 为曲线C 1上的动点，点P 在线段OM 上，且满足|OM |·|OP |＝16，求点P 的轨迹C 2的直角坐标方程；(2)设点A 的极坐标为⎝⎛⎭⎫2，π3，点B 在曲线C 2上，求△OAB 面积的最大值． 解 (1)设点P 的极坐标为(ρ，θ)(ρ>0)，点M 的极坐标为(ρ1，θ)(ρ1>0)．由题意知|OP |＝ρ，|OM |＝ρ1＝4cos θ.由|OM |·|OP |＝16，得C 2的极坐标方程ρ＝4cos θ(ρ>0)． 因此C 2的直角坐标方程为(x －2)2＋y 2＝4(x ≠0)． (2)设点B 的极坐标为(ρB ，α)(ρB >0)． 由题设知|OA |＝2，ρB ＝4cos α，于是△OAB 的面积S ＝12|OA |·ρB ·sin ∠AOB＝4cos α·⎪⎪⎪⎪sin ⎝⎛⎭⎫α－π3 ＝2⎪⎪⎪⎪sin ⎝⎛⎭⎫2α－π3－32≤2＋ 3.当α＝－π12时，S 取得最大值2＋ 3.所以△OAB 面积的最大值为2＋ 3.1．在以直角坐标系中的原点O 为极点，x 轴正半轴为极轴的极坐标系中，已知曲线的极坐标方程为ρ＝21－sin θ.(1)将曲线的极坐标方程化为直角坐标方程；(2)过极点O 作直线l 交曲线于点P ，Q ，若|OP |＝3|OQ |，求直线l 的极坐标方程． 解 (1)ρ＝21－sin θ可化为ρ－ρsin θ＝2，∵ρ＝x 2＋y 2，ρsin θ＝y ，∴曲线的直角坐标方程为x 2＝4y ＋4. (2)设直线l 的极坐标方程为θ＝θ0(ρ∈R )， 根据题意21－sin θ0＝3·21－sin (θ0＋π)，解得θ0＝π6或θ0＝5π6，∴直线l 的极坐标方程为θ＝π6(ρ∈R )或θ＝5π6(ρ∈R )．2．已知曲线C 1的参数方程为⎩⎨⎧x ＝t ＋1t ，y ＝t －1t(t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ＝4cos θ. (1)求曲线C 1的极坐标方程和曲线C 2的直角坐标方程；(2)若射线θ＝π6分别与曲线C 1，C 2交于A ，B 两点(异于极点)，求|AB |的值．解(1)由⎩⎨⎧x ＝t ＋1t，y ＝t －1t⇒⎩⎪⎨⎪⎧x ＋y 2＝t ，x －y 2＝1t ，两式相乘得x 2－y 2＝4.因为⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，所以曲线C 1的极坐标方程为ρ2cos 2θ－ρ2sin 2θ＝4， 即ρ2cos 2θ＝4，因为ρ＝4cos θ，所以ρ2＝4ρcos θ， 则曲线C 2的直角坐标方程为x 2＋y 2－4x ＝0.(2)联立⎩⎪⎨⎪⎧ρ2cos 2θ＝4，θ＝π6，得ρA ＝22，联立⎩⎪⎨⎪⎧ρ＝4cos θ，θ＝π6，得ρB ＝23，故|AB |＝|ρB －ρA |＝23－2 2.3．极坐标系与直角坐标系xOy 有相同的长度单位，以坐标原点O 为极点，以x 轴正半轴为极轴．已知曲线C 1的极坐标方程为ρ＝22sin ⎝⎛⎭⎫θ＋π4，曲线C 2的极坐标方程为ρsin θ＝a (a >0)，射线θ＝φ，θ＝φ＋π4，θ＝φ－π4，θ＝φ＋π2与曲线C 1分别交异于极点O 的四点A ，B ，C ，D . (1)若曲线C 1关于曲线C 2对称，求a 的值，并把曲线C 1和C 2化成直角坐标方程；(2)求|OA |·|OC |＋|OB |·|OD |的值．解 (1)C 1：ρ2＝22ρ⎝⎛⎭⎫22sin θ＋22cos θ＝2ρsin θ＋2ρcos θ， 化为直角坐标方程为(x －1)2＋(y －1)2＝2.把C 2的方程化为直角坐标方程为y ＝a ，因为曲线C 1关于曲线C 2对称，故直线y ＝a 经过圆心(1,1)，解得a ＝1，故C 2的直角坐标方程为y ＝1. (2)由题意可得，|OA |＝22sin ⎝⎛⎭⎫φ＋π4， |OB |＝22sin ⎝⎛⎭⎫φ＋π2＝22cos φ，|OC |＝22sin φ， |OD |＝22cos ⎝⎛⎭⎫φ＋π4， 所以|OA |·|OC |＋|OB |·|OD |＝8sin ⎝⎛⎭⎫φ＋π4sin φ＋8cos ⎝⎛⎭⎫φ＋π4cos φ ＝8cos π4＝8×22＝4 2. 4．在直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝2＋2cos α，y ＝2sin α(α为参数)，以O 为极点，x 轴的正半轴为极轴建立极坐标系，直线的极坐标方程为ρ(sin θ＋3cos θ)＝ 3.(1)求C 的极坐标方程；(2)射线OM ：θ＝θ1⎝⎛⎭⎫π6≤θ1≤π3与圆C 的交点为O ，P ，与直线l 的交点为Q ，求|OP |·|OQ |的取值范围．解 (1)圆C 的普通方程是(x －2)2＋y 2＝4，又x ＝ρcos θ，y ＝ρsin θ，所以圆C 的极坐标方程为ρ＝4cos θ.(2)设P (ρ1，θ1)，则有ρ1＝4cos θ1，设Q (ρ2，θ1)，且直线l 的极坐标方程是ρ(sin θ＋3cos θ)＝3，则有ρ2＝3sin θ1＋3cos θ1， 所以|OP ||OQ |＝ρ1ρ2＝43cos θ1sin θ1＋3cos θ1＝433＋tan θ1⎝⎛⎭⎫π6≤θ1≤π3， 所以2≤|OP ||OQ |≤3.即|OP ||OQ |的取值范围是[2,3]．5.如图，在直角坐标系xOy 中，曲线C 1：⎩⎨⎧x ＝2＋7cos α，y ＝7sin α(α为参数)．以O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ＝8cos θ，直线l 的极坐标方程为θ＝π3(ρ∈R )．(1)求曲线C 1的极坐标方程与直线l 的直角坐标方程；(2)若直线l 与C 1，C 2在第一象限分别交于A ，B 两点，P 为C 2上的动点，求△P AB 面积的最大值．解 (1)依题意得，曲线C 1的普通方程为(x －2)2＋y 2＝7， 曲线C 1的极坐标方程为ρ2－4ρcos θ－3＝0， 直线l 的直角坐标方程为y ＝3x .(2)曲线C 2的直角坐标方程为(x －4)2＋y 2＝16，设A ⎝⎛⎭⎫ρ1，π3，B ⎝⎛⎭⎫ρ2，π3，则ρ21－4ρ1cos π3－3＝0，即ρ21－2ρ1－3＝0，得ρ1＝3或ρ1＝－1(舍)， ρ2＝8cos π3＝4，则|AB |＝|ρ2－ρ1|＝1， C 2(4,0)到l 的距离为d ＝|43|4＝23，以AB 为底边的△P AB 的高的最大值为4＋23， 则△P AB 的面积的最大值为12×1×(4＋23)＝2＋ 3. 6．在平面直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ(a >b >0，φ为参数)，在以O 为极点，x 轴的正半轴为极轴的极坐标系中，曲线C 2是圆心在极轴上，且经过极点的圆．已知曲线C 1上的点M ⎝⎛⎭⎫1，22对应的参数φ＝π4，射线θ＝π3与曲线C 2交于点D ⎝⎛⎭⎫1，π3. (1)求曲线C 1，C 2的直角坐标方程；(2)若点A ，B 为曲线C 1上的两个点且OA ⊥OB ，求1|OA |2＋1|OB |2的值． 解 (1)将M ⎝⎛⎭⎫1，22及对应的参数φ＝π4，代入⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ， 得⎩⎨⎧ 1＝a cos π4，22＝b sin π4，即⎩⎪⎨⎪⎧a ＝2，b ＝1， 所以曲线C 1的方程为⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ，φ为参数， 所以曲线C 1的直角坐标方程为x 22＋y 2＝1. 设圆C 2的半径为R ，由题意，圆C 2的极坐标方程为ρ＝2R cos θ(或(x －R )2＋y 2＝R 2)，将点D ⎝⎛⎭⎫1，π3代入ρ＝2R cos θ，得1＝2R cos π3， 即R ＝1，所以曲线C 2的极坐标方程为ρ＝2cos θ，所以曲线C 2的直角坐标方程为(x －1)2＋y 2＝1.(2)设A (ρ1，θ)，B ⎝⎛⎭⎫ρ2，θ＋π2在曲线C 1上，所以ρ21cos 2θ2＋ρ21sin 2θ＝1，ρ22sin 2θ2＋ρ22cos 2θ＝1， 所以1|OA |2＋1|OB |2＝1ρ21＋1ρ22＝⎝⎛⎭⎫cos 2θ2＋sin 2θ＋⎝⎛⎭⎫sin 2θ2＋cos 2θ＝32.。

2020年高考理科数学试题解析（课标Ⅰ）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页，第Ⅱ卷3至4页。

全卷满分150分。

考试时间120分钟。

注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷3至5页。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。

3. 全部答案在答题卡上完成，答在本试题上无效。

4. 考试结束，将本试题和答题卡一并交回。

第Ⅰ卷一、 选择题共12小题。

每小题5分，共60分。

在每个小题给出的四个选项中，只有一项是符合题目要求的一项。

1、已知集合A=｛x |x 2－2x ＞0｝，B=｛x |－5＜x ＜5｝，则 ( ) A 、A∩B=∅ B 、A ∪B=R C 、B ⊆A D 、A ⊆B【命题意图】本题主要考查一元二次不等式解法、集合运算及集合间关系，是容易题. 【解析】A=(-∞,0)∪(2,+∞), ∴A ∪B=R,故选B.2、若复数z 满足 (3－4i)z ＝|4＋3i |，则z 的虚部为 ( ) A 、－4（B ）－45（C ）4（D ）45【命题意图】本题主要考查复数的概念、运算及复数模的计算，是容易题.【解析】由题知z =|43|34i i +-=4)(34)(34)i i i +-+=3455i +，故z 的虚部为45，故选D.3、为了解某地区的中小学生视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，在下面的抽样方法中，最合理的抽样方法是 ( )A 、简单随机抽样B 、按性别分层抽样C 、按学段分层抽样D 、系统抽样 【命题意图】本题主要考查分层抽样方法，是容易题.【解析】因该地区小学、初中、高中三个学段学生的视力情况有较大差异，故最合理的抽样方法是按学段分层抽样，故选C.4、已知双曲线C ：22221x y a b-=（0,0a b >>C 的渐近线方程为A .14y x =±B .13y x =±C .12y x =± D .y x =±【命题意图】本题主要考查双曲线的几何性质，是简单题.【解析】由题知，2c a =，即54=22c a =222a b a +，∴22b a =14，∴b a =12±，∴C 的渐近线方程为12y x =±，故选C . 5、运行如下程序框图，如果输入的[1,3]t ∈-，则输出s 属于A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5]【命题意图】本题主要考查程序框图及分段函数值域求法，是简单题.【解析】有题意知，当[1,1)t ∈-时，3s t =[3,3)∈-，当[1,3]t ∈时，24s t t =-[3,4]∈， ∴输出s 属于[-3,4]，故选A .6、如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为 ( )A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 3【命题意图】本题主要考查球的截面圆性质、球的体积公式，是容易题.【解析】设球的半径为R ，则由题知球被正方体上面截得圆的半径为4，球心到截面圆的距离为R-2，则222(2)4R R =-+，解得R=5，∴球的体积为3453π⨯=500π33cm ，故选A. 7、设等差数列{a n }的前n 项和为S n ，1m S -＝－2，m S ＝0，1m S +＝3，则m ＝ ( ) A 、3 B 、4 C 、5 D 、6【命题意图】本题主要考查等差数列的前n 项和公式及通项公式，考查方程思想，是容易题. 【解析】有题意知m S =1()2m m a a +=0，∴1a =－m a =－（m S -1m S -）=－2， 1m a += 1m S +-m S =3，∴公差d =1m a +-m a =1，∴3=1m a +=－2m +，∴m =5，故选C.8、某几何体的三视图如图所示，则该几何体的体积为 A .168π+ B .88π+ C .1616π+ D .816π+【命题意图】本题主要考查简单组合体的三视图及简单组合体体积公式，是中档题.【解析】由三视图知，该几何体为放到的半个圆柱底面半径为2高为4，上边放一个长为4宽为2高为2长方体，故其体积为21244222π⨯⨯+⨯⨯ =168π+，故选A . 9、设m 为正整数，2()mx y +展开式的二项式系数的最大值为a ，21()m x y ++展开式的二项式系数的最大值为b ，若13a =7b ，则m ＝ ( ) A 、5 B 、6 C 、7 D 、8【命题意图】本题主要考查二项式系数最大值及组合数公式，考查方程思想，是容易题. 【解析】由题知a =2mm C ，b =121m m C ++，∴132mm C =7121m m C ++，即13(2)!!!m m m ⨯=7(21)!(1)!!m m m ⨯++， 解得m =6，故选B.10、已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的右焦点为F (3,0)，过点F 的直线交椭圆于A 、B 两点。

课时作业48 利用向量求空间角1．在正方体ABCD-A1B1C1D1中，点E为BB1的中点，则平面A1ED与平面ABCD所成的锐二面角的余弦值为( B )A.1 2B.23C.33D.22解析：以A为原点，AB，AD，AA1所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系A-xyz，设棱长为1，则A1(0,0,1)，E⎝⎛⎭⎪⎫1，0，12，D(0,1,0)，∴A1D→＝(0,1，－1)，A1E→＝⎝⎛⎭⎪⎫1，0，－12，设平面A1ED的一个法向量为n1＝(1，y，z)．则有⎩⎪⎨⎪⎧A1D→·n1＝0，A1E→·n1＝0，即⎩⎪⎨⎪⎧y－z＝0，1－12z＝0，∴⎩⎪⎨⎪⎧y＝2，z＝2，∴n1＝(1,2,2)．∵平面ABCD的一个法向量为n2＝(0,0,1)，∴cos〈n1，n2〉＝23×1＝23，即所成的锐二面角的余弦值为23.2．(2019·大同模拟)设正方体ABCD-A1B1C1D1的棱长为2，则点D1到平面A1BD的距离是( D )A.32B.22C.223 D.233解析：如图，以点D 为坐标原点，DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴，建立坐标系，则D (0,0,0)，D 1(0,0,2)，A 1(2,0,2)，B (2,2,0)，D 1A 1→＝(2,0,0)，DB →＝(2,2,0)，DA 1→＝(2,0,2)，设平面A 1BD 的一个法向量n ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧n ·DA 1→＝0，n ·DB →＝0，∴⎩⎪⎨⎪⎧2x ＋2z ＝0，2x ＋2y ＝0，令z ＝1，得n ＝(－1,1,1)．∴D 1到平面A 1BD 的距离d ＝|D 1A 1→·n ||n |＝23＝233. 3．(2018·全国卷Ⅰ)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为( A )A.334 B.233C.324D.32解析：由正方体的性质及题意可得，正方体共顶点的三条棱所在直线与平面α所成的角均相等．如图，正方体ABCD -A 1B 1C 1D 1中，易知棱AB ，AD ，AA 1所在直线与平面A 1BD 所成的角均相等，所以α∥平面A 1BD ，当平面α趋近点A 时，截面图形的面积趋近于0；当平面α经过正方体的中心O 时，截面图形为正六边形，其边长为22，截面图形的面积为6×34×⎝ ⎛⎭⎪⎫222＝334；当平面α趋近于C 1时，截面图形的面积趋近于0，所以截面图形面积的最大值为334，故选A.4．已知三棱锥P -ABC 的所有顶点都在表面积为16π的球O 的球面上，AC 为球O 的直径．当三棱锥P -ABC 的体积最大时，二面角P -AB -C 的大小为θ，则sin θ等于( C )A.23B.53C.63D.73解析：如图，设球O 的半径为R ，由4πR 2＝16π，得R ＝2， 设点P 到平面ABC 的距离为d ， 则0＜d ≤2，因为AC 为球的直径， 所以AB 2＋BC 2＝AC 2＝16，则V 三棱锥P -ABC ＝16AB ·BC ·d ≤16·AB 2＋BC 22·2＝83，当且仅当AB ＝BC ＝22，d ＝2时，V 三棱锥P -ABC 取得最大值， 此时平面PAC ⊥平面ABC ，连接PO ，因为PO ⊥AC ，平面PAC ∩平面ABC ＝AC ，PO ⊂平面PAC ，所以PO ⊥平面ABC ，过点P 作PD ⊥AB 于D ， 连接OD ，因为AB ⊥PO ，AB ⊥PD ，PO ∩PD ＝P ， 所以AB ⊥平面POD ，则AB ⊥OD ， 所以∠PDO 为二面角P -AB -C 的平面角， 因为OD ＝12BC＝2，所以PD ＝PO 2＋OD 2＝6，则sin θ＝sin ∠PDO ＝PO PD ＝63，故选C. 5．如图所示，在正方体ABCD -A 1B 1C 1D 1中，E ，F 分别是正方形A 1B 1C 1D 1和正方形ADD 1A 1的中心，则EF 和CD 所成的角的大小是 45° .解析：以D 为原点，分别以DA 、DC 、DD 1所在直线为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系D -xyz ，设正方体的棱长为1，则D (0,0,0)，C (0,1,0)，E ⎝ ⎛⎭⎪⎫12，12，1，F ⎝ ⎛⎭⎪⎫12，0，12，EF →＝⎝ ⎛⎭⎪⎫0，－12，－12，DC →＝(0,1,0)， ∴cos 〈EF →，DC →〉＝EF →·DC→|EF →||DC →|＝－22，∴〈EF →，DC →〉＝135°，∴异面直线EF 和CD 所成的角的大小是45°.6．如图，四边形ABCD 和ADPQ 均为正方形，它们所在的平面互相垂直，动点M 在线段PQ上，E，F分别为AB，BC的中点．设异面直线EM与AF所成的角为θ，则cosθ的最大值为25.解析：建立空间直角坐标系如图所示．设AB＝1，则AF→＝⎝⎛⎭⎪⎫1，12，0，E⎝⎛⎭⎪⎫12，0，0.设M(0，y,1)(0≤y≤1)，则EM→＝⎝⎛⎭⎪⎫－12，y，1.∵θ∈⎝⎛⎦⎥⎤0，π2，∴cosθ＝|AF→·EM→||AF→||EM→|＝⎪⎪⎪⎪⎪⎪－12＋12y1＋14·14＋y2＋1＝21－y5·4y2＋5.则⎣⎢⎡⎦⎥⎤21－y4y2＋52＝1－8y＋14y2＋5.令8y＋1＝t，1≤t≤9，则8y＋14y2＋5＝16t＋81t－2≥15，当且仅当t ＝1时取等号． ∴cos θ＝21－y5·4y 2＋5≤15×25＝25，当且仅当y ＝0时取等号． 7．如图，四棱锥P -ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．(1)证明：PB ∥平面AEC ；(2)设二面角D -AE -C 为60°，AP ＝1，AD ＝3，求三棱锥E -ACD 的体积． 解：(1)证明：连接BD 交AC 于点O ，连接EO . 因为ABCD 为矩形，所以O 为BD 的中点． 又E 为PD 的中点，所以EO ∥PB .又因为EO ⊂平面AEC ，PB ⊄平面AEC ，所以PB ∥平面AEC .(2)因为PA ⊥平面ABCD ，ABCD 为矩形，所以AB ，AD ，AP 两两垂直．如图，以A 为坐标原点，AB →的方向为x 轴的正方向，|AP →|为单位长，建立空间直角坐标系A -xyz ，则D (0，3，0)，E ⎝ ⎛⎭⎪⎫0，32，12，AE →＝⎝ ⎛⎭⎪⎫0，32，12.设B (m,0,0)(m ＞0)，则C (m ，3，0)，AC →＝(m ，3，0)． 设n 1＝(x ，y ，z )为平面ACE 的法向量，则⎩⎪⎨⎪⎧n 1·AC →＝0，n 1·AE →＝0，即⎩⎪⎨⎪⎧mx ＋3y ＝0，32y ＋12z ＝0，可取n 1＝⎝⎛⎭⎪⎫3m ，－1，3. 又n 2＝(1,0,0)为平面DAE 的法向量， 由题设得|cos 〈n 1，n 2〉|＝12，即33＋4m 2＝12，解得m ＝32. 因为E 为PD 的中点， 所以三棱锥E -ACD 的高为12.三棱锥E -ACD 的体积V ＝13×12×3×32×12＝38.8．(2019·江西六校联考)在如图所示的几何体中，四边形ABCD 为平行四边形，∠ABD ＝90°，EB ⊥平面ABCD ，EF ∥AB ，AB ＝2，EB ＝3，EF ＝1，BC ＝13，且M 是BD 的中点．(1)求证：EM ∥平面ADF ；(2)求二面角A -FD -B 的余弦值的大小． 解：(1)证法一：取AD 的中点N ，连接MN ，NF .在△DAB 中，M 是BD 的中点，N 是AD 的中点，所以MN ∥AB ，MN ＝12AB ，又因为EF ∥AB ，EF ＝12AB ，所以MN ∥EF 且MN ＝EF .所以四边形MNFE 为平行四边形，所以EM ∥FN ， 又因为FN ⊂平面ADF ，EM ⊄平面ADF ，故EM ∥平面ADF . 证法二：因为EB ⊥平面ABD ，AB ⊥BD ，故以B 为原点，建立如图所示的空间直角坐标系B -xyz .由已知可得EM →＝⎝ ⎛⎭⎪⎫32，0，－3，AD →＝(3，－2,0)，AF →＝(0，－1，3)， 设平面ADF 的法向量是n ＝(x ，y ，z )． 由⎩⎪⎨⎪⎧n ·AD →＝0，n ·AF →＝0得⎩⎨⎧3x －2y ＝0，－y ＋3z ＝0，令y ＝3，则n ＝(2,3，3)．又因为EM →·n ＝0，所以EM →⊥n ， 又EM ⊄平面ADF ，故EM ∥平面ADF .(2)由(1)中证法二可知平面ADF 的一个法向量是n ＝(2,3，3)． 易得平面BFD 的一个法向量是m ＝(0，－3，1)．所以cos 〈m ，n 〉＝m ·n |m |·|n |＝－34，又二面角A -FD -B 为锐角， 故二面角A -FD -B 的余弦值大小为34. 9．(2019·河南郑州一模)如图所示，在四棱锥P -ABCD 中，PA ⊥平面ABCD ，△DAB ≌△DCB ，E 为线段BD 上的一点，且EB ＝ED ＝EC ＝BC ，连接CE 并延长交AD 于F .(1)若G 为PD 的中点，求证：平面PAD ⊥平面CGF ；(2)若BC ＝2，PA ＝3，求平面BCP 与平面DCP 所成锐二面角的余弦值． 解：(1)证明：在△BCD 中，EB ＝ED ＝EC ＝BC ，故∠BCD ＝π2，∠CBE ＝∠CEB ＝π3，连接AE ，∵△DAB ≌△DCB ，∴△EAB ≌△ECB ，从而有∠FED ＝∠BEC ＝∠AEB ＝π3，AE ＝CE ＝DE .∴∠AEF ＝∠FED ＝π3.故EF ⊥AD ，AF ＝FD . 又PG ＝GD ，∴FG ∥PA .又PA ⊥平面ABCD ，故GF ⊥平面ABCD ， ∴GF ⊥AD ，又GF ∩EF ＝F ，故AD ⊥平面CFG . 又AD ⊂平面PAD ， ∴平面PAD ⊥平面CGF .(2)以点A 为坐标原点建立如图所示的空间直角坐标系，则A (0,0,0)，B (2,0,0)，C (3，3，0)，D (0，23，0)，P (0,0,3)． 故BC →＝(1，3，0)，CP →＝(－3，－3，3)，CD →＝(－3，3，0)． 设平面BCP 的一个法向量为n 1＝(1，y 1，z 1)，则⎩⎨⎧ 1＋3y 1＝0，－3－3y 1＋3z 1＝0，解得⎩⎪⎨⎪⎧y 1＝－33，z 1＝23，即n 1＝⎝⎛⎭⎪⎫1，－33，23. 设平面DCP 的一个法向量为n 2＝(1，y 2，z 2)，则⎩⎨⎧－3＋3y 2＝0，－3－3y 2＋3z 2＝0，解得⎩⎨⎧y 2＝3，z 2＝2，即n 2＝(1，3，2)．从而平面BCP 与平面DCP所成锐二面角的余弦值为|n 1·n 2||n 1||n 2|＝43169×8＝24. 10．(2017·全国卷Ⅱ)如图，四棱锥P -ABCD 中，侧面PAD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°，E 是PD 的中点．(1)证明：直线CE ∥平面PAB ；(2)点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45°，求二面角M -AB -D 的余弦值． 解：(1)取PA 的中点F ，连接EF ，BF . 因为E 是PD 的中点， 所以EF ∥AD ，EF ＝12AD .由∠BAD ＝∠ABC ＝90°得BC ∥AD ， 又BC ＝12AD ，所以EF 綊BC ，四边形BCEF 是平行四边形，CE ∥BF ，又BF ⊂平面PAB ，CE ⊄平面PAB ，故CE ∥平面PAB .(2)由已知得BA ⊥AD ，以A 为坐标原点，AB →的方向为x 轴正方向，|AB →|为单位长，建立如图所示的空间直角坐标系A -xyz ，则A (0,0,0)，B (1,0,0)，C (1,1,0)，P (0,1，3)，PC →＝(1,0，－3)，AB →＝(1,0,0)．设M (x ，y ，z )(0＜x ＜1)，则BM →＝(x －1，y ，z )，PM →＝(x ，y－1，z －3)．因为BM 与底面ABCD 所成的角为45°， 而n ＝(0,0,1)是底面ABCD 的法向量，所以|cos 〈BM →，n 〉|＝sin 45°，|z |x －12＋y 2＋z2＝22， 即(x －1)2＋y 2－z 2＝0.①又M 在棱PC 上，设PM →＝λPC →， 则x ＝λ，y ＝1，z ＝3－3λ.②由①②解得⎩⎪⎨⎪⎧x ＝1＋22，y ＝1，z ＝－62(舍去)，或⎩⎪⎨⎪⎧x ＝1－22，y ＝1，z ＝62.所以M ⎝ ⎛⎭⎪⎫1－22，1，62，从而AM →＝⎝⎛⎭⎪⎫1－22，1，62. 设m ＝(x 0，y 0，z 0)是平面ABM 的法向量， 则⎩⎪⎨⎪⎧m ·AM →＝0，m ·AB →＝0，即⎩⎨⎧2－2x 0＋2y 0＋6z 0＝0，x 0＝0，所以可取m ＝(0，－6，2)．于是cos 〈m ，n 〉＝m·n |m ||n |＝105.易知所求二面角为锐角． 因此二面角M -AB -D 的余弦值为105.11．如图，在四棱锥P -ABCD 中，AD ∥BC ，∠ADC ＝∠PAB ＝90°，BC ＝CD ＝12AD ，E 为棱AD 的中点，异面直线PA 与CD 所成的角为90°.(1)在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；(2)若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值．解：(1)在梯形ABCD中，AB与CD不平行．如图，延长AB，DC，相交于点M(M∈平面PAB)，点M即为所求的一个点．理由如下：由已知，BC∥ED，且BC＝ED.所以四边形BCDE是平行四边形，从而CM∥EB.又EB⊂平面PBE，CM⊄平面PBE，所以CM∥平面PBE.(说明：延长AP至点N，使得AP＝PN，则所找的点可以是直线MN上任意一点)(2)解法一：由已知，CD⊥PA，CD⊥AD，PA∩AD＝A，所以CD⊥平面PAD.从而CD⊥PD.所以∠PDA是二面角P-CD-A的平面角．所以∠PDA＝45°.设BC＝1，则在Rt△PAD中，PA＝AD＝2.过点A作AH⊥CE，交CE的延长线于点H，连接PH.易知PA⊥平面ABCD，又CE⊂平面ABCD，从而PA⊥CE.于是CE⊥平面PAH.所以平面PCE⊥平面PAH.过A作AQ⊥PH于Q，则AQ⊥平面PCE.所以∠APH是PA与平面PCE所成的角．在Rt△AEH中，∠AEH＝45°，AE＝1，所以AH＝22. 在Rt △PAH 中，PH ＝PA 2＋AH 2＝322，所以sin ∠APH ＝AH PH ＝13.解法二：由已知，CD ⊥PA ，CD ⊥AD ，PA ∩AD ＝A ， 所以CD ⊥平面PAD . 于是CD ⊥PD .从而∠PDA 是二面角P -CD -A 的平面角． 所以∠PDA ＝45°.由PA ⊥AB ，可得PA ⊥平面ABCD . 设BC ＝1，则在Rt △PAD 中，PA ＝AD ＝2.作Ay ⊥AD ，以A 为原点，以AD →，AP →的方向分别为x 轴、z 轴的正方向，建立如图所示的空间直角坐标系A -xyz ，则A (0,0,0)，P (0,0,2)，C (2,1,0)，E (1,0,0)，所以PE →＝(1,0，－2)，EC →＝(1,1,0)，AP →＝(0,0,2)． 设平面PCE 的法向量n ＝(x ，y ，z )， 由⎩⎪⎨⎪⎧n ·PE →＝0，n ·EC →＝0，得⎩⎪⎨⎪⎧x －2z ＝0，x ＋y ＝0，设x ＝2，解得n ＝(2，－2,1)． 设直线PA 与平面PCE 所成角为α，则sin α＝|n ·AP →||n |·|AP →|＝22×22＋－22＋12＝13. 所以直线PA 与平面PCE 所成角的正弦值为13.12．(2019·江西南昌二中月考)如图，在等腰梯形ABCD中，∠ABC＝60°，CD＝2，AB ＝4，点E为AB的中点，现将该梯形中的三角形EBC沿线段EC折起，形成四棱锥B-AECD.(1)在四棱锥B-AECD中，求证：AD⊥BD；(2)若平面BEC与平面AECD所成二面角的平面角为120°，求直线AE与平面ABD所成角的正弦值．解：(1)证明：由三角形BEC沿线段EC折起前，∠ABC＝60°，CD＝2，AB＝4，点E为AB的中点，得三角形BEC沿线段EC折起后，四边形AECD为菱形，边长为2，∠DAE＝60°，如图，取EC的中点F，连接DF，BF，DE，∵△BEC和△DEC均为正三角形，∴EC⊥BF，EC⊥DF, 又BF∩DF＝F，∴EC⊥平面BFD，∵AD∥EC，∴AD⊥平面BFD，∵BD⊂平面BFD，∴AD⊥BD.(2)以F为坐标原点，建立如图的空间直角坐标系，由EC ⊥平面BFD ，知z 轴在平面BFD 内， ∵BF ⊥EC ，DF ⊥EC ，∴∠BFD 为平面BEC 与平面AECD 所成二面角的平面角， ∴∠BFD ＝120°，∴∠BFz ＝30°， 又∵BF ＝3，∴点B 的横坐标为－32，点B 的竖坐标为32. 因D (3，0,0)，E (0,1,0)，A (3，2,0)，B ⎝ ⎛⎭⎪⎫－32，0，32， 故AE →＝(－3，－1,0)，BD →＝⎝⎛⎭⎪⎫332，0，－32，AD →＝(0，－2，0)．设平面ABD 的法向量为n ＝(x ，y ，z )，∴⎩⎪⎨⎪⎧BD →·n ＝⎝ ⎛⎭⎪⎫332，0，－32·x ，y ，z ＝0，AD →·n ＝0，－2，0·x ，y ，z ＝0，得⎩⎪⎨⎪⎧332x －32z ＝0，－2y ＝0，令x ＝1，得y ＝0，z ＝3，∴平面ABD 的一个法向量为n ＝(1,0，3)，∴cos 〈AE →，n 〉＝AE →·n|AE →||n |＝－3，－1，0·1，0，32×2＝－34，∵直线AE 与平面ABD 所成角为锐角， ∴直线AE 与平面ABD 所成角的正弦值为34.。

绝密★启用前2020年普通高等学校招生全国统一考试课标1理科数学2020年全国1高考数学与2020全国1高考数学难度方面相对持平，在选择题和填空题方面难度有所提升，解答题方面难度有所减缓.在保持稳定的基础上，进行适度创新，尤其是选择填空压轴题.试卷内容上体现新课程理念，贴近中学数学教学，坚持对基础性的考查，同时加大了综合性、应用性和创新性的考查，如理科第2、3、10、11、12、16、19题，文科第2、4、9、12、19题.1.体现新课标理念，重视对传统核心考点考查的同时，增加了对数学文化的考查，如理科第2题，文科第4题以中国古代的太极图为背景，考查几何概型.2.关注通性通法.试卷淡化了特殊的技巧，全面考查通性通法，体现了以知识为载体，以方法为依托，以能力考查为目的的命题要求.3.考查了数学思想、数学能力、数学的科学与人文价值，体现了知识与能力并重、科学与人文兼顾的精神.如理科第6、10、13、15题，文科第5、12、13、16题对数形结合思想的考查；理科第11，文科第9题对函数与方程思想的考查；理科第12、16题对数学的科学与人文价值的考查.4.体现了创新性，如理科第19题，文科第19题立意新、情景新、设问新，增强了学生数学应用意识和创新能力.命题趋势：（1）函数与导数知识：以函数性质为基础，考查函数与不等式综合知识，如理科第5题，；以基本初等函数为背景考查构造新函数解决比较大小问题，如理科第11题；对含参单调性以及零点问题的考查，如理科21题，比较常规.（2）三角函数与解三角形知识：对三角函数图像与性质的考查，如理科第9题；；对解三角形问题的考查，如理科第17题.重视对基础知识与运算能力的考查.（3）数列知识：对数列性质的考查，如理科第4题；突出了数列与现实生活的联系，考查学生分析问题的能力，如理科第12题，难点较大.整体考查比较平稳，没有出现偏、怪的数列相关考点.（4）立体几何知识：对立体几何图形的认识与考查，如理科第7题，试题难度不大，比较常规；对简单几何体的体积知识的考查，如理科第16题，用到函数知识进行解决，体现了综合性，难度较大，立体几何解答题的考查较常规，如理科对二面角的考查.（5）解析几何知识：对圆锥曲线综合知识的考查，如理科第15题，难度偏大；解答题考查较为常规，考查直线与圆锥曲线的位置关系，难度中等，重视对学生运算能力的考查.【试卷解析】一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A ={x |x <1}，B ={x |31x <}，则 A ．{|0}A B x x =<I B ．A B =R U C ．{|1}A B x x =>UD ．A B =∅I【答案】A2．如图，正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是A ．14 B ．π8 C ．12D ．π4【答案】B 【解析】试题分析：设正方形边长为a ，则圆的半径为2a ，则正方形的面积为2a ，圆的面积为24a π.由图形的对称性可知，太极图中黑白部分面积相等，即各占圆面积的一半.由几何概型概率的计算公式得，此点取自黑色部分的概率是221248a a ππ⋅=，选B. 秒杀解析：由题意可知，此点取自黑色部分的概率即为黑色部分面积占整个面积的比例，由图可知其概率1142p <<，故选B.【考点】几何概型【名师点睛】对于几何概型的计算，首先确定事件类型为几何概型并确定其几何区域（长度、面积、体积或时间），其次计算基本事件区域的几何度量和事件A 区域的几何度量，最后计算()P A . 3．设有下面四个命题1p ：若复数z 满足1z ∈R ，则z ∈R ；2p ：若复数z 满足2z ∈R ，则z ∈R ；3p ：若复数12,z z 满足12z z ∈R ，则12z z =；4p ：若复数z ∈R ，则z ∈R .其中的真命题为 A.13,p pB ．14,p pC ．23,p pD ．24,p p【答案】B4．记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为A ．1B ．2C ．4D ．8【答案】C 【解析】试题分析：设公差为d ，45111342724a a a d a d a d +=+++=+=，611656615482S a d a d ⨯=+=+=，联立112724,61548a d a d +=⎧⎨+=⎩解得4d =，故选C.秒杀解析：因为166346()3()482a a S a a +==+=，即3416a a +=，则4534()()24168a a a a +-+=-=，即5328a a d -==，解得4d =，故选C. 【考点】等差数列的基本量求解【名师点睛】求解等差数列基本量问题时，要多多使用等差数列的性质，如{}n a 为等差数列，若m n p q +=+，则m n p q a a a a +=+.5．函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是 A ．[2,2]-B ．[1,1]-C ．[0,4]D ．[1,3]【答案】D6．621(1)(1)x x++展开式中2x 的系数为 A ．15B ．20C ．30D ．35【答案】C 【解析】试题分析：因为6662211(1)(1)1(1)(1)x x x x x++=⋅++⋅+，则6(1)x +展开式中含2x 的项为2226115C x x ⋅=，621(1)x x⋅+展开式中含2x 的项为44262115C x x x ⋅=，故2x 前系数为151530+=，选C. 【考点】二项式定理【名师点睛】对于两个二项式乘积的问题，第一个二项式中的每项乘以第二个二项式的每项，分析好2x 的项共有几项，进行加和.这类问题的易错点主要是未能分析清楚构成这一项的具体情况，尤其是两个二项式展开式中的r 不同.7．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12 C．14 D．16【答案】B8．右面程序框图是为了求出满足3n−2n>1000的最小偶数n，那么在和两个空白框中，可以分别填入A．A>1 000和n=n+1B．A>1 000和n=n+2C．A≤1 000和n=n+1D．A≤1 000和n=n+2【答案】D9．已知曲线C1：y=cos x，C2：y=sin (2x+2π3)，则下面结论正确的是A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2C．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2D．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2 【答案】D 【解析】试题分析：因为12,C C 函数名不同，所以先将2C 利用诱导公式转化成与1C 相同的函数名，则222:sin(2)cos(2)cos(2)3326C y x x x ππππ=+=+-=+，则由1C 上各点的横坐标缩短到原来的12倍变为sin 2y x =，再将曲线向左平移12π个单位得到2C ，故选D. 【考点】三角函数图像变换.【名师点睛】对于三角函数图像变换问题，首先要将不同名函数转换成同名函数，利用诱导公式，需要重点记住sin cos(),cos sin()22ππαααα=-=+；另外，在进行图像变换时，提倡先平移后伸缩，而先伸缩后平移在考试中经常出现，无论哪种变换，记住每一个变换总是对变量x 而言.10．已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为 A ．16B ．14C ．12D ．10【答案】A2222||sin cos()2p pDE παα==-，所以22222211||||4()cos sin cos sin p p AB DE αααα+=+=+ 2222222211sin cos 4()(cos sin )4(2)4(22)16cos sin cos sin αααααααα=++=++≥⋅+=11．设x 、y 、z 为正数，且235x y z ==，则A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z【答案】D12．几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推.求满足如下条件的最小整数N ：N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是 A ．440B ．330C ．220D ．110【答案】A【解析】试题分析：由题意得，数列如下：11,1,2,1,2,4,1,2,4,,2k -LL L则该数列的前(1)122k k k ++++=L 项和为 1(1)1(12)(122)222k k k k S k ++⎛⎫=+++++++=-- ⎪⎝⎭L L 要使(1)1002k k +>，有14k ≥，此时122k k ++<，所以2k +是之后的等比数列11,2,,2k +L 的部分和，即1212221t t k -+=+++=-L ，所以2314tk =-≥，则5t ≥，此时52329k =-=， 对应满足的最小条件为293054402N ⨯=+=，故选A. 【考点】等差数列、等比数列的求和.【名师点睛】本题非常巧妙的将实际问题和数列融合在一起，首先需要读懂题目所表达的具体含义，以及观察所给定数列的特征，进而判断出该数列的通项和求和.另外，本题的难点在于数列里面套数列，第一个数列的和又作为下一个数列的通项，而且最后几项并不能放在一个数列中，需要进行判断. 二、填空题：本题共4小题，每小题5分，共20分.13．已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2 b |= . 【答案】2314．设x，y满足约束条件2121x yx yx y+≤⎧⎪+≥-⎨⎪-≤⎩，则32z x y=-的最小值为.【答案】5-15．已知双曲线C：22221x ya b-=（a>0，b>0）的右顶点为A，以A为圆心，b为半径作圆A，圆A与双曲线C 的一条渐近线交于M、N两点.若∠MAN=60°，则C的离心率为________.23【考点】双曲线的简单性质.【名师点睛】双曲线渐近线是其独有的性质，所以有关渐近线问题受到出题者的青睐.做好这一类问题要抓住以下重点：①求解渐近线，直接把双曲线后面的1换成0即可；②双曲线的焦点到渐近线的距离是b；③双曲线的顶点到渐近线的距离是abc.16．如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为_______.【答案】415【考点】简单几何体的体积【名师点睛】对于三棱锥最值问题，肯定需要用到函数的思想进行解决，本题解决的关键是设好未知量，利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决，当变量是高次时需要用到求导得方式进行解决.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分. 17．（12分）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求△ABC 的周长.【考点】三角函数及其变换.【名师点睛】在处理解三角形问题时，要注意抓住题目所给的条件，当题设中给定三角形的面积，可以使用面积公式建立等式，再将所有边的关系转化为角的关系，有时需将角的关系转化为边的关系；解三角形问题常见的一种考题是“已知一条边的长度和它所对的角，求面积或周长的取值范围”或者“已知一条边的长度和它所对的角，再有另外一个条件，求面积或周长的值”，这类问题通法思路是：全部转化为角的关系，建立函数关系式，如sin()y A x b ωϕ=++，从而求出范围，或利用余弦定理以及基本不等式求范围；求具体的值直接利用余弦定理和给定条件即可. 18.（12分）如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o .（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠=o ，求二面角A -PB -C 的余弦值.则3cos ,||||3⋅==-<>n m n m n m ， 所以二面角A PB C --的余弦值为33-. 【考点】面面垂直的证明，二面角平面角的求解【名师点睛】高考对空间向量与立体几何的考查主要体现在以下几个方面：①求异面直线所成的角，关键是转化为两直线的方向向量的夹角；②求直线与平面所成的角，关键是转化直线的方向向量和平面的法向量的夹角；③求二面角，关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键. 19．（12分）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm ）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布2(,)N μσ．（1）假设生产状态正常，记X 表示一天内抽取的16个零件中其尺寸在(3,3)μσμσ-+之外的零件数，求(1)P X ≥及X 的数学期望；（2）一天内抽检零件中，如果出现了尺寸在(3,3)μσμσ-+之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．（ⅰ）试说明上述监控生产过程方法的合理性； （ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：9.95 10.12 9.969.96 10.01 9.92 9.98 10.04 10.269.9110.1310.029.2210.0410.059.95经计算得16119.9716i i x x ===∑，161622221111()(16)0.2121616i ii i s x x x x ===-=-≈∑∑，其中i x 为抽取的第i 个零件的尺寸，1,2,,16i =⋅⋅⋅．用样本平均数x 作为μ的估计值ˆμ，用样本标准差s 作为σ的估计值ˆσ，利用估计值判断是否需对当天的生产过程进行检查？剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据，用剩下的数据估计μ和σ（精确到0.01）． 附：若随机变量Z 服从正态分布2(,)N μσ，则(33)0.997 4P Z μσμσ-<<+=，160.997 40.959 2=，0.0080.09≈．试题解析：（1）抽取的一个零件的尺寸在(3,3)μσμσ-+之内的概率为0.9974，从而零件的尺寸在(3,3)μσμσ-+之外的概率为0.0026，故~(16,0.0026)X B .因此(1)1(0)10.99740.0408P X P X ≥=-==-=.X 的数学期望为160.00260.0416EX =⨯=.20.（12分）已知椭圆C ：2222=1x y a b+（a >b >0），四点P 1（1,1），P 2（0,1），P 3（–1，32），P 4（1，32）中恰有三点在椭圆C 上. （1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点.若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点.（2）设直线P 2A 与直线P 2B 的斜率分别为k 1，k 2，如果l 与x 轴垂直，设l ：x =t ，由题设知0t ≠，且||2t <，可得A ，B 的坐标分别为（t ，24t -，（t ，24t -）. 则221242421t t k k ---++==-，得2t =，不符合题设. 从而可设l ：y kx m =+（1m ≠）.将y kx m =+代入2214x y +=得222(41)8440k x kmx m +++-=由题设可知22=16(41)0k m ∆-+>.设A （x 1，y 1），B （x 2，y 2），则x 1+x 2=2841kmk -+，x 1x 2=224441m k -+.而12121211y y k k x x --+=+121211kx m kx m x x +-+-=+ 1212122(1)()kx x m x x x x +-+=.由题设121k k +=-，故1212(21)(1)()0k x x m x x ++-+=.即222448(21)(1)04141m kmk m k k --+⋅+-⋅=++.解得12m k +=-. 当且仅当1m >-时，0∆>，欲使l ：12m y x m +=-+，即11(2)2m y x ++=--， 所以l 过定点（2，1-）【考点】椭圆的标准方程，直线与圆锥曲线的位置关系.【名师点睛】椭圆的对称性是椭圆的一个重要性质，判断点是否在椭圆上，可以通过这一方法进行判断；证明直线过定点的关键是设出直线方程，通过一定关系转化，找出两个参数之间的关系式，从而可以判断过定点情况.另外，在设直线方程之前，若题设中为告知，则一定要讨论直线斜率不存在和存在情况，接着通法是联立方程组，求判别式、韦达定理，根据题设关系进行化简. 21.（12分）已知函数2()(2)x xf x ae a e x =+--.（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分. 22．[选修4―4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩（θ为参数），直线l 的参数方程为4,1,x a t t y t =+⎧⎨=-⎩（为参数）. （1）若a =−1，求C 与l 的交点坐标；（2）若C 上的点到l 17 a.【解析】试题分析：（1）先将曲线C 和直线l 化成普通方程，然后联立求出交点坐标；（2）直线l 的普通方程为440x y a +--=，设C 上的点(3cos ,sin )θθ，l 的距离为17d =.对a 进行讨23．[选修4—5：不等式选讲]（10分）已知函数f （x ）=–x 2+ax +4，g (x )=│x +1│+│x –1│.（1）当a =1时，求不等式f （x ）≥g （x ）的解集；（2）若不等式f （x ）≥g （x ）的解集包含[–1，1]，求a 的取值范围.【解析】试题分析：（1）将1a =代入，不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤，对x 按1x <-，11x -≤≤，1x >讨论，得出最值的解集；（2）当[1,1]x ∈-时，()2g x =.若()()f x g x ≥的解集包含[1,1]-，。

专练67 高考大题专练(七) 坐标系与参数方程1．[2022·贵阳市五校联考]以直角坐标系的原点O 为极点，x 轴的非负半轴为极轴建立极坐标系．已知曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝3t ，y ＝2t 2＋1(t 为参数)，直线l 的极坐标方程为ρsin (θ－π6)＝－ 3.(1)已知点M(6，a)在曲线C 上，求a 的值；(2)设点P 为曲线C 上一点，求点P 到直线l 距离的最小值．2．[2022·全国甲卷(理)，22]在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t 6y ＝t (t为参数)，曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋s 6y ＝－s(s 为参数). (1)写出C 1的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 3的极坐标方程为2cos θ－sin θ＝0，求C 3与C 1交点的直角坐标，及C 3与C 2交点的直角坐标．3．[2022·安阳模拟]在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧x ＝2cos θ，y ＝sin θ(θ为参数)，直线l 过点M(1，0)且倾斜角为α.(1)求出直线l 的参数方程和曲线C 的普通方程； (2)若直线l 与曲线C 交于A ，B 两点，且|MA|·|MB||||MA|－|MB|＝33，求cos α的值．4.[2021·全国甲卷]在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ＝22cos θ.(1)将C 的极坐标方程化为直角坐标方程；(2)设点A 的直角坐标为(1，0)，M 为C 上的动点，点P 满足AP →＝2AM →，写出P 的轨迹C 1的参数方程，并判断C 与C 1是否有公共点．5．[2022·石嘴山模拟]在平面直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝1＋cos α，y ＝sin α(α为参数)，以坐标原点O 为极点，x 轴非负半轴为极轴建立极坐标系，点A 为曲线C 1上的动点，点B 在线段OA 的延长线上且满足|OA|·|OB|＝8，点B 的轨迹为C 2.(1)求曲线C 1，C 2的极坐标方程；(2)设点M 的极坐标为(2，3π2)，求△ABM 面积的最小值．6．[2022·全国乙卷(理)，22]在直角坐标系xOy 中，曲线C 的参数方程为⎩⎨⎧x ＝3cos 2t ，y ＝2sin t(t 为参数)，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，已知直线l 的极坐标方程为ρsin (θ＋π3)＋m ＝0.(1)写出l 的直角坐标方程；(2)若l 与C 有公共点，求m 的取值范围．专练67 高考大题专练(七) 坐标系与参数方程1．解析：(1)∵点M 在曲线C 上，∴6＝3t ，∴t＝2，∴a＝y ＝2×22＋1＝9. (2)∵直线l 的极坐标方程为ρsin (θ－π6)＝－3，∴直线l 的直角坐标方程为x －3y －23＝0. ∵点P 在曲线C 上，∴设P(3t ，2t 2＋1)， 则点P 到直线l 的距离为d ＝|3t －23t 2－33|2，当t ＝34时，d min ＝21316. 2．解析：(1)C 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t 6，y ＝t ．消去参数t ，得C 1的普通方程为y 2＝6x －2(y≥0). (2)曲线C 3的极坐标方程为2cos θ－sin θ＝0， 两边同乘ρ，得2ρcos θ－ρsin θ＝0， 则C 3的直角坐标方程为y ＝2x.联立得方程组⎩⎪⎨⎪⎧y 2＝6x －2（y≥0），y ＝2x ，解得⎩⎪⎨⎪⎧x ＝12，y ＝1或⎩⎪⎨⎪⎧x ＝1，y ＝2.将曲线C 2的参数方程中的参数s 消去，得y 2＝－6x －2(y≤0).联立得方程组⎩⎪⎨⎪⎧y 2＝－6x －2（y≤0），y ＝2x ，解得⎩⎪⎨⎪⎧x ＝－12，y ＝－1或⎩⎪⎨⎪⎧x ＝－1，y ＝－2.所以C 3与C 1交点的直角坐标为⎝ ⎛⎭⎪⎫12，1和()1，2，C 3与C 2交点的直角坐标为⎝ ⎛⎭⎪⎫－12，－1和(－1，－2).3．解析：(1)曲线C 的参数方程⎩⎨⎧x ＝2cos θ，y ＝sin θ(θ为参数)，转换为普通方程为x 22＋y2＝1；直线l 过点M(1，0)且倾斜角为α，则参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos α，y ＝t sin α(t 为参数).(2)把直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋t cos α，y ＝t sin α(t 为参数)代入x 22＋y 2＝1.得到(1＋sin 2α)t 2＋2t cos α－1＝0， 所以t 1＋t 2＝－2cos α1＋sin 2α， t 1t 2＝－11＋sin 2α(t 1和t 2分别为A 和B 对应的参数)， t 1t 2<0，则t 1，t 2异号，||MA|－|MB||＝||t 1|－|t 2||＝|t 1＋t 2|， 由|MA|·|MB|||MA|－|MB||＝33，整理得|t 1＋t 2|＝⎪⎪⎪⎪⎪⎪－2cos α1＋sin 2α＝3|t 1t 2|＝31＋sin 2α， 解得cos α＝±32. 4．解析：(1)根据ρ＝22cos θ，得ρ2＝22ρcos θ， 因为x 2＋y 2＝ρ2，x ＝ρcos θ，所以x 2＋y 2＝22x ，所以C 的直角坐标方程为(x －2)2＋y 2＝2. (2)设P(x ，y)，M(x′，y′)，则AP →＝(x －1，y)，AM →＝(x′－1，y′).因为AP →＝2AM →，所以⎩⎨⎧x －1＝2（x′－1）y ＝2y′，即⎩⎪⎨⎪⎧x′＝x －12＋1y′＝y 2，因为M 为C 上的动点，所以(x －12＋1－2)2＋(y 2)2＝2，即(x －3＋2)2＋y 2＝4.所以P 的轨迹C 1的参数方程为⎩⎨⎧x ＝3－2＋2cos α，y ＝2sin α(其中α为参数，α∈[0，2π)).所以|CC 1|＝3－22，⊙C 1的半径r 1＝2，又⊙C 的半径r ＝2，所以|CC 1|<r 1－r ， 所以C 与C 1没有公共点．5．解析：(1)由曲线C 1的参数方程⎩⎪⎨⎪⎧x ＝1＋cos α，y ＝sin α(α为参数)，消去参数，可得普通方程为(x －1)2＋y 2＝1，即x 2＋y 2－2x ＝0， 又由x ＝ρcos θ，y ＝ρsin θ，代入可得曲线C 1的极坐标方程为ρ＝2cos θ，设点B 的极坐标为(ρ，θ)，A 点的极坐标为(ρ0，θ0)， 则|OB|＝ρ，|OA|＝ρ0，ρ0＝2cos θ0，θ＝θ0， 因为|OA|·|OB|＝8， 所以ρ·ρ0＝8，即8ρ＝2cos θ，即ρcos θ＝4， 所以曲线C 2的极坐标方程为ρcos θ＝4. (2)由题意，可得|OM|＝2，则S △ABM ＝S △OBM －S △OAM ＝12|OM|·|x B －x A |＝12×2×|4－2cos 2θ|＝|4－2cos 2θ|，即S △ABM ＝4－2cos 2θ，当cos 2θ＝1时，可得S △ABM 的最小值为2. 6．解析：(1)由ρsin (θ＋π3)＋m ＝0，得12ρsin θ＋32ρcos θ＋m ＝0. ∵ρcos θ＝x ，ρsin θ＝y ， ∴l 的直角坐标方程为32x ＋12y ＋m ＝0.(2)(方法一)把x ＝3cos 2t ，y ＝2sin t 代入32x ＋12y ＋m ＝0，得m ＝－32cos 2t －sin t ＝－32＋3sin 2t －sin t ＝3(sin t －16)2－1912.∵sin t∈[－1，1]，∴当sin t ＝16时，m 取得最小值－1912；当sin t ＝－1时，m 取得最大值52.∴m 的取值范围是[－1912，52].(方法二)x ＝3cos 2t ＝3(1－2sin 2t)＝3[1－2(y 2)2]＝3－32y 2.∵y＝2sin t ，sin t∈[－1，1]，∴y∈[－2，2]. 联立得方程组⎩⎪⎨⎪⎧x ＝3－32y 2，3x ＋y ＋2m ＝0.消去x 并整理，得3y 2－2y －4m －6＝0， 即4m ＝3y 2－2y －6＝3(y －13)2－193(－2≤y≤2).∴－193≤4m≤10，∴－1912≤m≤52.∴m 的取值范围是[－1912，52].。