MATLAB中的阈值获取和阈值去噪

MATLAB中的信号降噪与滤波方法概述：信号降噪和滤波是信号处理领域中的重要任务之一。

随着技术的发展，信号的采集和传输变得越来越容易，但同时也引入了噪声。

信号降噪和滤波方法可以用来抑制这些噪声，并提高信号质量。

在MATLAB中，有丰富的信号降噪和滤波函数和工具箱，为用户提供了便捷的信号处理工具。

1. 信号降噪方法1.1 均值滤波均值滤波是最简单和常用的信号降噪方法之一。

它通过计算信号中每个数据点周围一定邻域的均值来去除噪声。

MATLAB提供了函数`smoothdata`来实现均值滤波，用户可以根据自己的需求设定滤波窗口的大小。

1.2 中值滤波中值滤波也是一种常用的信号降噪方法，它通过将信号中每个数据点周围一定邻域的数据进行排序，然后选取中间值作为滤波结果。

MATLAB提供了函数`medfilt1`来实现中值滤波，用户可以指定滤波窗口的大小。

1.3 小波变换小波变换是一种多尺度分析方法，它可以将信号分解为不同尺度的频率成分。

小波变换在信号降噪中的应用非常广泛。

MATLAB提供了相关函数`wdenoise`来实现小波降噪，用户可以根据信号特点选择合适的小波基和降噪参数。

1.4 高斯滤波高斯滤波是一种线性、平滑的滤波方法，它通过卷积信号与一个高斯核函数来实现滤波。

MATLAB提供了函数`imgaussfilt`和`imgaussfilt2`来实现一维和二维高斯滤波。

2. 信号滤波方法2.1 低通滤波低通滤波器可以通过去除信号中高于一定频率的成分来实现滤波效果。

MATLAB中有多种低通滤波器的设计方法，比如巴特沃斯滤波器、切比雪夫滤波器等。

用户可以使用函数`butter`和`cheby1`来设计低通滤波器，并使用函数`filter`来应用滤波器。

2.2 高通滤波高通滤波器可以通过去除信号中低于一定频率的成分来实现滤波效果。

MATLAB中也提供了多种高通滤波器的设计方法，用户可以使用函数`butter`和`cheby1`来设计高通滤波器，并使用函数`filter`来应用滤波器。

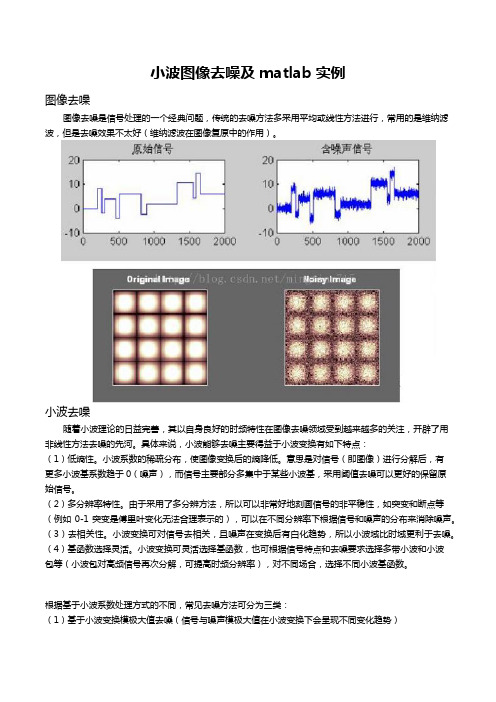
小波图像去噪及matlab实例图像去噪图像去噪是信号处理的一个经典问题，传统的去噪方法多采用平均或线性方法进行，常用的是维纳滤波，但是去噪效果不太好（维纳滤波在图像复原中的作用）。

小波去噪随着小波理论的日益完善，其以自身良好的时频特性在图像去噪领域受到越来越多的关注，开辟了用非线性方法去噪的先河。

具体来说，小波能够去噪主要得益于小波变换有如下特点：（1）低熵性。

小波系数的稀疏分布，使图像变换后的熵降低。

意思是对信号（即图像）进行分解后，有更多小波基系数趋于0（噪声），而信号主要部分多集中于某些小波基，采用阈值去噪可以更好的保留原始信号。

（2）多分辨率特性。

由于采用了多分辨方法，所以可以非常好地刻画信号的非平稳性，如突变和断点等（例如0-1突变是傅里叶变化无法合理表示的），可以在不同分辨率下根据信号和噪声的分布来消除噪声。

（3）去相关性。

小波变换可对信号去相关，且噪声在变换后有白化趋势，所以小波域比时域更利于去噪。

（4）基函数选择灵活。

小波变换可灵活选择基函数，也可根据信号特点和去噪要求选择多带小波和小波包等（小波包对高频信号再次分解，可提高时频分辨率），对不同场合，选择不同小波基函数。

根据基于小波系数处理方式的不同，常见去噪方法可分为三类：（1）基于小波变换模极大值去噪（信号与噪声模极大值在小波变换下会呈现不同变化趋势）（2）基于相邻尺度小波系数相关性去噪（噪声在小波变换的各尺度间无明显相关性，信号则相反）（3）基于小波变换阈值去噪小波阈值去噪是一种简单而实用的方法，应用广泛，因此重点介绍。

阈值函数选择阈值处理函数分为软阈值和硬阈值，设w是小波系数的大小，wλ是施加阈值后小波系数大小，λ为阈值。

（1）硬阈值当小波系数的绝对值小于给定阈值时，令其为0，而大于阈值时，保持其不变，即：（2）软阈值当小波系数的绝对值小于给定阈值时，令其为0，大于阈值时，令其都减去阈值，即：如下图，分别是原始信号，硬阈值处理结果，软阈值处理结果。

基于MATLAB语音信号处理去噪毕业设计论文语音信号在实际应用中通常不可避免地受到噪音的干扰，这使得语音信号的处理变得困难。

因此，在语音信号处理领域，去噪技术一直是一个热门的研究方向。

本文将介绍一种基于MATLAB的语音信号处理去噪方法的毕业设计论文。

本文的主要内容分为以下几个部分。

首先，介绍语音信号处理的背景和意义。

在现实生活中，由于外界环境和设备的限制，语音信号往往会受到各种噪音的污染，如背景噪音、电磁干扰等。

因此，开发一种有效的语音信号处理去噪方法具有重要的实际意义。

其次，介绍基于MATLAB的语音信号处理去噪方法。

本文将采用小波降噪方法对语音信号进行去噪处理。

首先，对输入的语音信号进行小波变换，将信号转换到小波域。

然后，通过对小波系数进行阈值处理，将噪声系数置零，从而实现去噪效果。

最后，通过逆小波变换将信号转换回时域，并输出去噪后的语音信号。

接下来，介绍实验设计和结果分析。

本文将使用MATLAB软件进行实验设计，并选取一组含有不同噪声干扰的语音信号进行测试。

通过对不同噪声信号进行处理，比较不同参数设置下的去噪效果，评估提出方法的性能。

最后，总结全文并展望未来的研究方向。

通过本次研究，我们可以看到基于MATLAB的语音信号处理去噪方法在去除噪音方面具有较好的效果，并具有很大的应用潜力。

然而，该方法仍然有改进的空间。

未来的研究可以在算法优化、参数选择和应用场景等方面进行深入研究，进一步提高语音信号处理去噪的效果和性能。

总的来说，本文介绍了一种基于MATLAB的语音信号处理去噪方法的毕业设计论文。

通过对实验结果的分析和对未来研究方向的展望，本文为从事语音信号处理领域的研究人员提供了一定的参考和启示。

图像去噪是数字图像处理中的重要环节与步骤。

去噪效果的好坏直接影响到后续的图像处理工作如图像分割、边缘检测等。

图像信号在产生、传输过程中都可能会受到噪声的污染，一般数字图像系统中的常见噪声主要有：高斯噪声（主要由阻性元器件内部产生）、椒盐噪声（主要是图像切割引起的黑图像上的白点噪声或光电转换过程中产生的泊松噪声）等；目前比较经典的图像去噪算法主要有以下三种：均值滤波算法：也称线性滤波，主要思想为邻域平均法，即用几个像素灰度的平均值来代替每个像素的灰度。

有效抑制加性噪声，但容易引起图像模糊，可以对其进行改进，主要避开对景物边缘的平滑处理。

中值滤波：基于排序统计理论的一种能有效抑制噪声的非线性平滑滤波信号处理技术。

中值滤波的特点即是首先确定一个以某个像素为中心点的邻域，一般为方形邻域，也可以为圆形、十字形等等，然后将邻域中各像素的灰度值排序，取其中间值作为中心像素灰度的新值，这里领域被称为窗口，当窗口移动时，利用中值滤波可以对图像进行平滑处理。

其算法简单，时间复杂度低，但其对点、线与尖顶多的图像不宜采用中值滤波。

很容易自适应化。

Wiener维纳滤波：使原始图像与其恢复图像之间的均方误差最小的复原方法，是一种自适应滤波器，根据局部方差来调整滤波器效果。

对于去除高斯噪声效果明显。

实验一：均值滤波对高斯噪声的效果代码I=imread('C:\Documents and Settings\Administrator\桌面\1.gif');%读取图像J=imnoise(I,'gaussian',0,0.005);%加入均值为0，方差为0.005的高斯噪声subplot(2,3,1);imshow(I);title('原始图像');subplot(2,3,2); imshow(J);title('加入高斯噪声之后的图像');%采用MATLAB中的函数filter2对受噪声干扰的图像进行均值滤波K1=filter2(fspecial('average',3),J)/255; %模板尺寸为3K2=filter2(fspecial('average',5),J)/255;% 模板尺寸为5K3=filter2(fspecial('average',7),J)/255; %模板尺寸为7K4= filter2(fspecial('average',9),J)/255; %模板尺寸为9 subplot(2,3,3);imshow(K1);title('改进后的图像1');subplot(2,3,4); imshow(K2);title('改进后的图像2');subplot(2,3,5);imshow(K3);title('改进后的图像3');subplot(2,3,6);imshow(K4);title('改进后的图像4');PS：filter2用法fspecial函数用于创建预定义的滤波算子，其语法格式为：h = fspecial(type)h = fspecial(type,parameters)参数type制定算子类型，parameters指定相应的参数，具体格式为：type='average'，为均值滤波，参数为n，代表模版尺寸，用向量表示，默认值为[3,3]。

matlab阈值分割Matlab阈值分割是一种图像处理技术，它可以将一幅图像分为几个不同的部分。

它使用一个阈值来区分不同的图像像素，并将像素分组到相应的部分中。

Matlab阈值分割的原理是：从图像中计算一个阈值T，如果像素值大于T，则将其分配到第一部分，如果像素值小于等于T，则将其分配到第二部分。

Matlab阈值分割通常使用两种方法：绝对值分割和相对值分割。

绝对值分割是一种普遍使用的阈值分割技术，它将像素的灰度值作为T的参考，并以此来划分像素。

在这种情况下，阈值T必须手动设置，因此，如果要进行阈值分割，需要让用户输入一个阈值，然后根据用户输入的阈值进行分割。

另一种常用的Matlab阈值分割是相对值分割。

它使用图像中像素灰度值的相对大小作为阈值T，并以此来划分像素。

相对值分割可以很好地处理复杂的图像，因为它可以根据图像的特征自动计算一个合适的阈值。

Matlab阈值分割可以用来识别图像中的特定对象，例如，可以使用Matlab阈值分割来识别图像中的人脸、地面、植被等。

此外，它还可以用来检测图像中的异常像素，例如，可以使用Matlab阈值分割来检测图像中的噪声、瑕疵或其他异常像素。

Matlab阈值分割也可以用来实现图像分割，即将一幅图像分割成不同的部分，例如，可以使用Matlab阈值分割将图像分割成天空、海洋、山脉和沙漠等不同的部分。

此外，Matlab阈值分割还可以用来实现图像去噪，即将图像中的噪声去除，以获得更清晰的图像。

另外，Matlab阈值分割也可以用来实现图像压缩，即将图像中的像素压缩到更小的大小，以节省存储空间。

总之，Matlab阈值分割是一种有用的图像处理技术，可以用来实现图像分割、去噪和压缩等多种功能。

它可以使用绝对值分割和相对值分割来实现不同的功能，因此，它可以满足不同用途的需求。

小波去噪的matlab程序-回复如何使用Matlab进行小波去噪。

小波去噪是数值信号处理中常用的一种方法，它可以有效地去除信号中的噪声，保留有用的信号部分。

Matlab是一个强大的数值计算和数据可视化工具，也提供了丰富的信号处理工具箱，其中包括小波去噪算法。

本文将介绍如何使用Matlab进行小波去噪，以帮助读者更好地理解和应用这一方法。

首先，我们需要定义被噪声污染的信号。

在Matlab中，可以通过生成具有噪声的信号来模拟实际应用。

以下是一段生成具有高斯白噪声的正弦信号的代码：fs = 1000; 采样频率T = 1/fs; 采样间隔L = 1000; 信号长度t = (0:L-1)*T; 时间向量f = 50; 正弦信号频率A = 0.7; 正弦信号幅度x = A*sin(2*pi*f*t); 生成正弦信号添加高斯白噪声mu = 0; 噪声均值sigma = 0.5; 噪声标准差n = sigma*randn(size(t)); 生成高斯白噪声x_noisy = x + n; 带噪声的信号上述代码中，我们生成了一个频率为50 Hz的正弦信号，并添加了均值为0、标准差为0.5的高斯白噪声。

生成的带噪声的信号存储在变量`x_noisy`中。

接下来，我们需要选择一种小波基函数以分析信号，并选择合适的小波系数阈值来进行去噪。

Matlab提供了多种小波基函数和小波系数阈值选择方法，如Daubechies小波基函数和固定阈值法、SureShrink方法等。

以下是一段使用Daubechies小波基函数和可视化小波系数阈值选择结果的代码：执行小波变换[c, l] = wavedec(x_noisy, 5, 'db4'); 小波分解可视化小波系数figure;subplot(2,1,1);plot(x_noisy);title('原始信号');subplot(2,1,2);plot(c);title('小波系数');小波系数阈值选择thr = wthrmngr('dw1ddenoLVL','penalhi',c,l); 阈值选择sorh = 's'; 阈值类型，s代表软阈值，h代表硬阈值keepapp = 1; 保留近似系数X = wdencmp('gbl',c,l,'db4',5,thr,sorh,keepapp); 小波去噪可视化去噪结果figure;subplot(2,1,1);plot(x_noisy);title('带噪声的信号');subplot(2,1,2);plot(X);title('去噪后的信号');上述代码中，我们使用了Daubechies小波基函数对信号进行了5级小波分解，并可视化了小波系数。

小波去噪是信号处理中常用的一种方法，在MATLAB中也有相应的函数可以实现小波去噪。

下面我们将介绍MATLAB中对1维数据进行小波去噪的具体过程。

1. 准备原始数据我们需要准备一维的原始数据，可以是来自传感器采集的数据，也可以是从文件中读取的数据。

在MATLAB中，可以使用load函数或者从其它数据源导入数据。

2. 选择小波基和分解层数在进行小波去噪之前，需要选择适合的小波基和分解层数。

MATLAB 中提供了丰富的小波基选择，包括Daubechies小波、Symlet小波、Coiflet小波等。

根据信号的特点和需要去除的噪声类型，选择合适的小波基和分解层数。

3. 进行小波分解使用MATLAB中的wavedec函数对原始数据进行小波分解。

该函数的调用形式为[C, L] = wavedec(X, N, wname)，其中X为原始数据，N为分解层数，wname为小波基名称。

函数返回小波系数C和长度向量L。

4. 去除小波系数中的噪声根据小波分解得到的小波系数，可以利用MATLAB中的过滤函数对小波系数进行去噪。

常用的去噪方法包括阈值去噪、软硬阈值去噪等。

这些方法可以有效地去除信号中的噪声成分，得到干净的信号。

5. 重构信号经过去噪处理后，可以使用MATLAB中的waverec函数对去噪后的小波系数进行重构，得到去噪后的信号。

该函数的调用形式为X = waverec(C, L, wname)，其中C为去噪后的小波系数，L为长度向量，wname为小波基名称。

6. 可视化和分析可以利用MATLAB中丰富的绘图函数对去噪前后的信号进行可视化比较，以及对去噪效果进行分析。

通过比较原始信号和去噪后的信号，可以直观地了解去噪效果，并进行进一步的分析和处理。

通过以上步骤，我们可以在MATLAB中对一维数据进行小波去噪处理，去除信号中的噪声成分，得到干净的信号。

小波去噪是一种简单而有效的信号处理方法，在实际应用中具有广泛的应用前景。

matlab11种数字信号滤波去噪算法Matlab是一种强大的数学软件，广泛应用于信号处理领域。

在数字信号处理中，滤波去噪是一个重要的任务，可以提高信号的质量和准确性。

本文将介绍Matlab中的11种数字信号滤波去噪算法。

1. 均值滤波：该算法通过计算信号中一定窗口内的像素平均值来去除噪声。

它适用于高斯噪声和椒盐噪声的去除。

2. 中值滤波：该算法通过计算信号中一定窗口内的像素中值来去除噪声。

它适用于椒盐噪声的去除。

3. 高斯滤波：该算法通过对信号进行高斯模糊来去除噪声。

它适用于高斯噪声的去除。

4. 维纳滤波：该算法通过最小均方误差准则来估计信号的真实值，并去除噪声。

它适用于高斯噪声的去除。

5. 自适应滤波：该算法通过根据信号的局部特性来调整滤波器的参数，从而去除噪声。

它适用于非线性噪声的去除。

6. 小波去噪：该算法通过将信号分解为不同频率的小波系数，并对系数进行阈值处理来去除噪声。

它适用于各种类型的噪声的去除。

7. Kalman滤波：该算法通过对信号进行状态估计和观测更新来去除噪声。

它适用于线性系统的去噪。

8. 粒子滤波：该算法通过使用一组粒子来估计信号的状态，并通过重采样来去除噪声。

它适用于非线性系统的去噪。

9. 线性预测滤波：该算法通过使用线性预测模型来估计信号的未来值，并去除噪声。

它适用于平稳信号的去噪。

10. 自适应线性组合滤波：该算法通过对信号进行线性组合来估计信号的真实值，并去除噪声。

它适用于各种类型的噪声的去除。

11. 稀疏表示滤波：该算法通过使用稀疏表示模型来估计信号的真实值，并去除噪声。

它适用于各种类型的噪声的去除。

以上是Matlab中的11种数字信号滤波去噪算法。

每种算法都有其适用的场景和优缺点，根据具体的信号和噪声类型选择合适的算法进行去噪处理。

Matlab提供了丰富的函数和工具箱，可以方便地实现这些算法，并对信号进行滤波去噪。

通过合理选择和组合这些算法，可以有效提高信号的质量和准确性，为后续的信号处理任务提供更好的基础。