(完整word版)复习总结
- 格式:doc
- 大小:68.01 KB
- 文档页数:3
高中数学 必修1知识点 第一章 集合与函数概念【1.1.1】集合的含义与表示(1)集合的概念集合中的元素具有确定性、互异性和无序性. (2)常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.(3)集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. (4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. (5)集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系(6)子集、真子集、集合相等(7)已知集合A 有(1)n n ≥个元素,则它有2n 个子集,它有21n -个真子集,它有21n -个非空子集,它有22n-非空真子集.【1.1.3】集合的基本运算(8)交集、并集、补集B{x A A = ∅=∅ B A ⊆ B B ⊆ B{x A A = A ∅= B A ⊇ B B ⊇{|x x ()U A =∅ð ()U A U =ð【补充知识】含绝对值的不等式与一元二次不等式的解法(1)含绝对值的不等式的解法(2)一元二次不等式的解法0)〖1.2〗函数及其表示()()()U U A B A B =痧?()()()U U A B A B =痧?【1.2.1】函数的概念(1)函数的概念①设A 、B 是两个非空的数集,如果按照某种对应法则f,对于集合A 中任何一个数x ,在集合B中都有唯一确定的数()f x 和它对应,那么这样的对应(包括集合A ,B 以及A 到B 的对应法则f )叫做集合A 到B 的一个函数,记作:f A B →.②函数的三要素:定义域、值域和对应法则.③只有定义域相同,且对应法则也相同的两个函数才是同一函数. (2)区间的概念及表示法①设,a b 是两个实数,且a b <,满足a x b ≤≤的实数x 的集合叫做闭区间,记做[,]a b ;满足a xb <<的实数x 的集合叫做开区间,记做(,)a b ;满足a x b ≤<,或a x b <≤的实数x 的集合叫做半开半闭区间,分别记做[,)a b ,(,]a b ;满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞. 注意:对于集合{|}x a x b <<与区间(,)a b ,前者a 可以大于或等于b ,而后者必须a b <.(3)求函数的定义域时,一般遵循以下原则:①()f x 是整式时,定义域是全体实数.②()f x 是分式函数时,定义域是使分母不为零的一切实数.③()f x 是偶次根式时,定义域是使被开方式为非负值时的实数的集合.④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1. ⑤tan y x =中,()2x k k Z ππ≠+∈.⑥零(负)指数幂的底数不能为零. ⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集.⑧对于求复合函数定义域问题,一般步骤是:若已知()f x 的定义域为[,]a b ,其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出.⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论. ⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义. (4)求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,只是提问的角度不同.求函数值域与最值的常用方法:①观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值.②配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的值域或最值. ③判别式法:若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=,则在()0a y ≠时,由于,x y 为实数,故必须有2()4()()0b y a y c y ∆=-⋅≥,从而确定函数的值域或最值.④不等式法:利用基本不等式确定函数的值域或最值.⑤换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题.⑥反函数法:利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值. ⑦数形结合法:利用函数图象或几何方法确定函数的值域或最值. ⑧函数的单调性法.【1.2.2】函数的表示法(5)函数的表示方法表示函数的方法,常用的有解析法、列表法、图象法三种.解析法:就是用数学表达式表示两个变量之间的对应关系.列表法:就是列出表格来表示两个变量之间的对应关系.图象法:就是用图象表示两个变量之间的对应关系. (6)映射的概念①设A 、B 是两个集合,如果按照某种对应法则f,对于集合A 中任何一个元素,在集合B 中都有唯一的元素和它对应,那么这样的对应(包括集合A ,B 以及A 到B 的对应法则f )叫做集合A 到B 的映射,记作:f A B →.②给定一个集合A 到集合B 的映射,且,a A b B ∈∈.如果元素a 和元素b 对应,那么我们把元素b 叫做元素a 的象,元素a 叫做元素b 的原象.〖1.3〗函数的基本性质【1.3.1】单调性与最大(小)值(1)函数的单调性①定义及判定方法yxo②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数. ③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为减,()u g x =为减,则[()]y f g x =为增;若()y f u =为增,()ug x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则[()]y f g x =为减.(2)打“√”函数()(0)af x x a x=+>的图象与性质()f x 分别在(,-∞、)+∞上为增函数,分别在[0)、上为减函数.(3)最大(小)值定义 ①一般地,设函数()y f x =的定义域为I,如果存在实数M 满足:(1)对于任意的x I ∈,都有()f x M≤;(2)存在0x I ∈,使得0()f x M=.那么,我们称M 是函数()f x 的最大值,记作max ()f x M=.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y 轴两侧相对称的区间增减性相同,偶函数在y 轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.〖补充知识〗函数的图象(1)作图利用描点法作图:①确定函数的定义域; ②化解函数解析式; ③讨论函数的性质(奇偶性、单调性); ④画出函数的图象. 利用基本函数图象的变换作图:要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象. ①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴()()y f x y f x =−−−→=--原点1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象,并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去(2)识图对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系. (3)用图函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具.要重视数形结合解题的思想方法.第二章 基本初等函数(Ⅰ) 〖2.1〗指数函数【2.1.1】指数与指数幂的运算(1)根式的概念①如果,,,1nxa a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 表示;当n 是偶数时,正数a 的正的n n 次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a=;当n为奇数时,a=;当n为偶数时,(0)|| (0)a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)rr r ab a b a b r R =>>∈【2.1.2】指数函数及其性质(4)指数函数〖2.2〗对数函数 【2.2.1】对数与对数运算(1)对数的定义 ①若(0,1)xaN a a =>≠且,则x 叫做以a 为底N 的对数,记作log a xN =,其中a 叫做底数,N 叫做真数.②负数和零没有对数. ③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>.(2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…).(4)对数的运算性质 如果0,1,0,0aa M N >≠>>,那么①加法:log log log ()aa a M N MN += ②减法:log log log a a aM M N N-=③数乘:log log ()n aa n M M n R =∈ ④log a N a N =⑤loglog (0,)bn a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b N N b b a =>≠且【2.2.2】对数函数及其性质(5)对数函数(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()xy ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y f x -=.(7)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=;③将1()xf y -=改写成1()y f x -=,并注明反函数的定义域.(8)反函数的性质 ①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数.〖2.3〗幂函数(1)幂函数的定义 一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数.一、二象限(图象关于y 轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.②过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1). ③单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当qpα=(其中,p q 互质,p 和q Z ∈),若p 为奇数q 为奇数时,则q py x=是奇函数,若p 为奇数q 为偶数时,则q py x=是偶函数,若p 为偶数q 为奇数时,则qpy x=是非奇非偶函数.⑤图象特征:幂函数,(0,)y x x α=∈+∞,当1α>时,若01x <<,其图象在直线y x =下方,若1x >,其图象在直线y x =上方,当1α<时,若01x <<,其图象在直线y x =上方,若1x >,其图象在直线y x =下方.〖补充知识〗二次函数(1)二次函数解析式的三种形式 ①一般式:2()(0)f x ax bx c a =++≠②顶点式:2()()(0)f x a x h k a =-+≠③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式. ③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便.(3)二次函数图象的性质 ①二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--. ②当0a>时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2b a -+∞上递增,当2bx a=-时,2min 4()4ac b f x a-=;当0a <时,抛物线开口向下,函数在(,]2b a -∞-上递增,在[,)2ba-+∞上递减,当2bx a=-时,2max 4()4ac b f x a -=.③二次函数2()(0)f x ax bx c a =++≠当240b ac ∆=->时,图象与x轴有两个交点11221212(,0),(,0),||||||M x M x M M x x a =-=. (4)一元二次方程20(0)axbx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布. 设一元二次方程20(0)axbx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=-③判别式:∆ ④端点函数值符号. ①k <x 1≤x 2 ⇔②x 1≤x 2<k ⇔③x1<k <x 2 ⇔ af (k )<0④k 1<x 1≤x 2<k 2 ⇔⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔ f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1<x 1<k 2≤p 1<x 2<p 2 ⇔ 此结论可直接由⑤推出. (5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (Ⅰ)当0a>时(开口向上)①若2b p a -<,则()m f p = ②若2b p q a ≤-≤,则()2b m f a =- ③若2b q a->,则()m f q =02a )q ()f pxxx(Ⅱ)当0a <时(开口向下) ①若2b p a -<,则()M f p = ②若2b p q a ≤-≤,则()2b M f a =- ③若2b q a->,则()M f q =①若02b x a -≤,则()m f q = ②02b x a->,则()m f p =.第三章 函数的应用一、方程的根与函数的零点 1、函数零点的概念:对于函数))((D x x f y ∈=,把使0)(=x f 成立的实数x 叫做函数))((D x x f y ∈=的零点。

第三单元知识小结一、字词盘点1.字(1)难读的字挪(nuó) 徊(huái) 蚁(yǐ) 绽(zhàn)(2)难写的字藏:容易少写下面“臧”字左边的三笔。
蒸:容易少写最下面的“灬”。
揉:左窄右宽,右上是“矛”,不是“予”。
偎:左窄右宽,“畏”字左下不要多写“丿”。
(3)多音字旋{xu án (旋转)xu àn (旋风) 薄{b ó(薄雾)b áo (薄饼)b ò(薄荷)挨{ái (挨打)āi (挨近) 吭{k ēng (吭气)ℎáng (引吭高歌)2.词(1)必须掌握的词空虚 叹息 徘徊 蚁穴 翻箱倒柜 念叨停顿 晃动 碰倒 原谅 惆怅 休止 时光惊惶 亲吻 依偎 挽回 消逝(2)近义词聪明~聪慧 确乎~的确 旋转~转动觉察~察觉遮挽~挽留叹息~叹气徘徊~踌躇蒸融~融化盼望~渴望昏暗~阴暗答应~同意明媚~明朗简单~简易吓唬~惊吓焦急~着急兴奋~高兴原谅~饶恕耽搁~耽误缥缈~虚无急遽~急剧孤独~孤单惆怅~忧郁(3)反义词去➝来谢➝开聪明➝愚蠢空虚➝充实枯➝青散➝聚旋转➝静止徘徊➝果断盼望➝渴望昏暗➝明亮答应➝拒绝明媚➝昏暗简单➝复杂焦急➝冷静兴奋➝平静原谅➝埋怨缥缈➝真实急遽➝缓慢孤单➝热闹惆怅➝兴奋(4)词语归类①ABB式词语:头涔涔泪潸潸赤裸裸类似的词语:笑哈哈笑眯眯笑嘻嘻笑盈盈绿油油黑洞洞蓝湛湛红彤彤白花花②AABB式词语:念念叨叨空空落落类似的词语:高高兴兴快快乐乐安安全全整整齐齐安安静静干干净净舒舒服服③ABAB式词语:咔嚓咔嚓类似的词语:研究研究练习练习活动活动锻炼锻炼思考思考表扬表扬分析分析④ABCB式词语:一动不动类似的词语:应有尽有出尔反尔将心比心倚老卖老人云亦云毅然决然心服口服⑤含有数字的成语:千门万户一动不动类似的词语:一心一意三心二意六神无主九死一生九牛一毛五光十色五湖四海⑥由两个动宾结构组成的词语:翻箱倒柜类似的词语:翻山越岭跋山涉水含辛茹苦忍辱负重开天辟地咬文嚼字装腔作势⑦量词一滴水滴一块方砖一个蚁穴一本电影画报一派荒凉⑧动词拨弄蚁穴翻看画报闭上眼睛⑨修饰词悄悄地挪移逃去如飞的日子游丝样的痕迹绽开的泡沫无可挽回地消逝漫长而急遽的变化孤独而惆怅的黄昏又大又重的洗衣盆二、佳句积累1.比喻句在默默里算着,八千多日子已经从我手中溜去,像针尖上一滴水滴在大海里,我的日子滴在时间的流里,没有声音,也没有影子。

高中生物知识点总结1、生命系统的结构层次依次为:细胞→组织→器官→系统→个体→种群→群落→生态系统细胞是生物体结构和功能的基本单位;地球上最基本的生命系统是细胞2、光学显微镜的操作步骤:对光→低倍物镜观察→移动视野中央(偏哪移哪)→高倍物镜观察:①只能调节细准焦螺旋;②调节大光圈、凹面镜3、原核细胞与真核细胞根本区别为:有无核膜为界限的细胞核①原核细胞:无核膜,无染色体,如大肠杆菌等细菌、蓝藻②真核细胞:有核膜,有染色体,如酵母菌,各种动物注:病毒无细胞结构,但有DNA或RNA4、蓝藻是原核生物,自养生物5、真核细胞与原核细胞统一性体现在二者均有细胞膜和细胞质6、细胞学说建立者是施莱登和施旺,细胞学说建立揭示了细胞的统一性和生物体结构的统一性。
细胞学说建立过程,是一个在科学探究中开拓、继承、修正和发展的过程,充满耐人寻味的曲折7、组成细胞(生物界)和无机自然界的化学元素种类大体相同,含量不同8、组成细胞的元素①大量无素:C、H、O、N、P、S、K、Ca、Mg②微量无素:Fe、Mn、B、Zn、Mo、Cu③主要元素:C、H、O、N、P、S④基本元素:C⑤细胞干重中,含量最多元素为C,鲜重中含最最多元素为O9、生物(如沙漠中仙人掌)鲜重中,含量最多化合物为水,干重中含量最多的化合物为蛋白质。
10、(1)还原糖(葡萄糖、果糖、麦芽糖)可与斐林试剂反应生成砖红色沉淀;脂肪可苏丹III染成橘黄色(或被苏丹IV染成红色);淀粉(多糖)遇碘变蓝色;蛋白质与双缩脲试剂产生紫色反应。
(2)还原糖鉴定材料不能选用甘蔗(3)斐林试剂必须现配现用(与双缩脲试剂不同,双缩脲试剂先加A液,再加B液)11、蛋白质的基本组成单位是氨基酸,氨基酸结构通式为NH2—C—COOH,各种氨基酸的区别在于R基的不同。
12、两个氨基酸脱水缩合形成二肽,连接两个氨基酸分子的化学键(—NH—CO—)叫肽键。
13、脱水缩合中,脱去水分子数=形成的肽键数=氨基酸数—肽链条数14、蛋白质多样性原因:构成蛋白质的氨基酸种类、数目、排列顺序千变万化,多肽链盘曲折叠方式千差万别。

九年级数学二次函数常考题型常考知识点总结:1、二次函数的看法:一般地,形如y ax2bx c 〔 a ,b,c 是常数,a 0〕的函数,叫做二次函数。
注:和一元二次方程近似,二次项系数 a 0 ,而b,c能够为零.二次函数的定义域是全体实数.2、二次函数 y ax2bx c的结构特点:⑴ 等号左侧是函数,右侧是关于自变量x 的二次式, x 的最高次数是2.⑵ a ,b ,c 是常数, a 是二次项系数, b 是一次项系数,c是常数项3、 y a x h2k 的性质:a 的符号张口方向极点坐标对称轴性质a0向上h,k X=h x h 时, y 随x的增大而增大;x h 时, y 随x 的增大而减小;x h 时, y 有最小值 k .a0向下h,k X=h x h 时, y 随x的增大而减小;x h 时, y 随x 的增大而增大;x h 时, y 有最大值 k .4、二次函数 y ax2bx c的性质:〔 1〕当a0时,抛物线张口向上,对称轴为xb ,极点坐标为 b ,4ac b2;当 x b时, y2a 2 a4a2a随 x 的增大而减小;当xb时, y 随x的增大而增大;当x b时, y 有最小值4ac b2.2a2a4a〔 2〕当a0时,抛物线张口向下,对称轴为xb ,极点坐标为 b ,4ac b2;当 x b时, y2a 2 a4a2a随 x 的增大而增大;当xb时, y 随x的增大而减小;当x b时, y 有最大值4ac b2。
2a2a4a5、二次函数剖析式确实定:依照条件确定二次函数剖析式,平时利用待定系数法.用待定系数法求二次函数的剖析式必定依照题目的特点,选择合适的形式,才能使解题简略.一般来说,有以下几种情况:(1〕抛物线上三点的坐标,一般采纳一般式;(2〕抛物线极点或对称轴或最大〔小〕值,一般采纳极点式;(3〕抛物线与 x 轴的两个交点的横坐标,一般采纳两根式;6、二次函数、二次三项式和一元二次方程之间的内在联系〔 a 0 时〕:0抛物线与x 轴有二次三项式的值可正、一元二次方程有两个不相等实根两个交点可零、可负0抛物线与x 轴只二次三项式的值为非负一元二次方程有两个相等的实数根有一个交点0抛物线与x 轴无二次三项式的值恒为正一元二次方程无实数根 .交点题型 :依照图像,判断 a 、 b 、c 的关系问题。

选择题1.大规模可编程器件主要有FPGA、CPLD 两类,下列对FPGA 结构与工作原理的描述中,正确的是(C)。
A.FPGA 全称为复杂可编程逻辑器件;B.FPGA 是基于乘积项结构的可编程逻辑器件;C.基于SRAM 的FPGA 器件,在每次上电后必须进行一次配置;D.在Altera 公司生产的器件中,MAX7000 系列属FPGA 结构。
2.不完整的IF语句,其综合结果可实现(A)A. 时序逻辑电路B.组合逻辑电C. 双向电路D. 三态控制电路3.综合是EDA设计流程的关键步骤,在下面对综合的描述中,(D)是错误的。
A.综合就是把抽象设计层次中的一种表示转化成另一种表示的过程;B.综合就是将电路的高级语言转化成低级的,可与FPGA / CPLD的基本结构相映射的网表文件;C.为实现系统的速度、面积、性能的要求,需要对综合加以约束,称为综合约束;D.综合可理解为一种映射过程,并且这种映射关系是唯一的,即综合结果是唯一的。
4.大规模可编程器件主要有FPGA、CPLD两类,下列对FPGA结构与工作原理的描述中,正确的是( C )。
A.FPGA全称为复杂可编程逻辑器件;B.FPGA是基于乘积项结构的可编程逻辑器件;C.基于SRAM的FPGA器件,在每次上电后必须进行一次配置;D.在Altera公司生产的器件中,MAX7000系列属FPGA结构。
5.以下关于状态机的描述中正确的是(B)A.Moore型状态机其输出是当前状态和所有输入的函数B.与Moore型状态机相比,Mealy型的输出变化要领先一个时钟周期C.Mealy型状态机其输出是当前状态的函数D.以上都不对6.目前应用最广泛的硬件描述语言是(B)。
A. VHDLB. Verilog HDLC. 汇编语言D. C语言7.一模块的I/O 端口说明:“input [7:0] a;”,则关于该端口说法正确的是( A )。
A. 输入端口,位宽为8B. 输出端口,位宽为8C. 输入端口,位宽为7D. 输出端口,位宽为78.基于EDA 软件的FPGA / CPLD 设计流程为:原理图/HDL 文本输入→综合→___ __→→适配→编程下载→硬件测试。

勾股定理全章知识点总结大全一•基础知识点:1:勾股定理直角三角形两直角边a、b的平方和等于斜边c的平方。
(即:a2+b2= c2)要点诠释:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1 )已知直角三角形的两边求第三边(在ABC中,C 90,贝廿 c V a2~b , b 7c2~a2, a 7c2~b2)(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边(3 )利用勾股定理可以证明线段平方关系的问题2:勾股定理的逆定理如果三角形的三边长:a、b、c,则有关系a2+b2 =c2,那么这个三角形是直角三角形。
要点诠释:勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时应注意:(1 )首先确定最大边,不妨设最长边长为:c ;(2)验证c2与a2+b2是否具有相等关系,若c2 =a2+b2,则厶ABC是以/C为直角的直角三角形(若c2>a2+b2,则△ AB(是以/C为钝角的钝角三角形;若c2<a2+b2,则△ AB(为锐角三角形)。
(定理中a,b,c及a2 b2 c2只是一种表现形式,不可认为是唯一的,如若三角形三边长a , b,c满足a2 c2 b2,那么以a,b,c为三边的三角形是直角三角形,但是b为斜边)3:勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,都与直角三角形有关。
4:互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
--WORD 格式--专业资料--可编辑---Bb C5:勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙, 面积不会改变②根据同一种图形的面积不同的表示方法,列出等 式,推导出勾股定理 常见方法如下:方法二: 四个直角三角形的面积与小正方形面积的和等于大正 方形的面积.四个直角三角形的面积与小正方形面积的 和口^为 S 4 1ab c22ab c 22大正方形面积为S (a b)2a 22ab b 2所以 a 2b 2c 2方法三:S弟形?a b) (a b),S 梯形 2S ADE S ABE 2 ?ab,化间得^证6:勾股数① 能够构成直角三角形的三边长的三个正整方法一:4SS正方形EFGHS正方形ABCD,4 £ab (b a)2 c2,化简可证.baabbaDbA a数称为勾股数,即a2 b2 c2中,a,b,c为正整数时,称a,b,c为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5 ;6,8,10 : 5,12,13 : 7,24,25 等③用含字母的代数式表示n组勾股数:n2 1,2n,n2 1(n 2,n为正整数);2n 1,2n2 2n,2 n2 2n 1 (n ^为正整数)m2 n2,2mn,m2 n2(m n, m n 为正整数)二、规律方法指导1 •勾股定理的证明实际采用的是图形面积与代数恒等式的关系相互转化证明的。

第一章绪论一、什么是生理学?生理学是生物科学中的一个分支,是一门实验性科学,它以生物机体的功能为研究对象。
生理学的任务就是研究这些生理功能的发生机制、条件、机体的内外环境中各种变化对这些功能的影响以及生理功能变化的规律。
二、内环境与稳态的概念(1)内环境的概念内环境指细胞直接生存并与之进行物质交换的环境,主要由组织液和血浆组成。
(2)稳态内环境理化性质维持相对恒定的状态,称为稳态,它是一种动态平衡。
细胞的正常代谢活动需要稳态,而代谢活动本身又经常破坏稳态,生命活动正是在稳态不断破坏和不断恢复的过程中维持和进行的。
三、人体生理功能三大调节方式?各有何特点?1.神经调节指通过神经系统的活动,对生物体各组织、器官、系统所进行的调节。
特点是准确、迅速、持续时间短暂。
2、体液调节体内产生的一些化学物质(激素、代谢产物)通过体液途径(血液、组织液、淋巴液)对机体某些系统、器官、组织或细胞的功能起到调节作用。
特点是作用缓慢、持久而弥散。
3.自身调节组织和细胞在不依赖于神经和体液调节的情况下,自身对刺激发生的适应性反应过程。
特点是调节幅度小。
四、什么是反射?反射指生物体在中枢神经系统参与下对刺激产生的规律性反应。
五、正、负反馈的概念.负反馈凡是反馈信息与控制信息的作用性质相反的反馈,称为负反馈,起纠正、减弱控制信息的作用。
正反馈凡是反馈信息与控制信息的作用性质相同的反馈,称为正反馈,起加强控制信息的作用。
第二章细胞的基本功能一、细胞膜的跨膜物质转运形式有哪些?各有何特点?细胞膜对物质转运形式有单纯扩散、易化扩散、主动转运和人胞、出胞。
从能量的角度来看,单纯扩散与易化扩散时,物质是顺电—化学梯度通过细胞膜的,不耗能,属于被动转运。
主动转运是指物质逆电化学梯度通过细胞膜的耗能的转运过程。
这里,电—化学梯度包括电学梯度(电位差)和化学梯度(浓度差)两层含义。
1、细胞膜转运物质的方式及其各自的特点归纳如下:表2-1 细胞膜转运物质的方式及特点转运方式单纯扩散主动转运载体运输通道转运出胞入胞转运物质小分子脂溶性小分子非脂溶性小分子非脂溶性小分子非脂溶性大分子团块大分子团块转运特点顺浓度差顺电位差不耗能逆浓度差逆电位差利用生物泵耗能①结构特异性②饱和现象③竞争性抑制顺浓度差顺电位差不耗能①化学门控通道②电压门控通道③机械门控通道顺浓度差顺电位差不耗能耗能耗能二、细胞的生物电现象1.兴奋性的概念1) 兴奋性:活细胞或组织对外界刺激具有发生反应的能力或特性称为兴奋性。

初中物理知识点总结(大全)第一章声现象知识归纳1 . 声音的发生:由物体的振动而产生。
振动停止,发声也停止。
2.声音的传播:声音靠介质传播。
真空不能传声。
通常我们听到的声音是靠空气传来的。
3.声速:在空气中传播速度是:340米/秒。
声音在固体传播比液体快,而在液体传播又比空气体快。
4.利用回声可测距离:S=1/2vt5.乐音的三个特征:音调、响度、音色。
(1)音调:是指声音的高低,它与发声体的频率有关系。
(2)响度:是指声音的大小,跟发声体的振幅、声源与听者的距离有关系。
6.减弱噪声的途径:(1)在声源处减弱;(2)在传播过程中减弱;(3)在人耳处减弱。
7.可听声:频率在20Hz~20000Hz之间的声波:超声波:频率高于20000Hz的声波;次声波:频率低于20Hz 的声波。
8.超声波特点:方向性好、穿透能力强、声能较集中。
具体应用有:声呐、B超、超声波速度测定器、超声波清洗器、超声波焊接器等。
9.次声波的特点:可以传播很远,很容易绕过障碍物,而且无孔不入。
一定强度的次声波对人体会造成危害,甚至毁坏机械建筑等。
它主要产生于自然界中的火山爆发、海啸地震等,另外人类制造的火箭发射、飞机飞行、火车汽车的奔驰、核爆炸等也能产生次声波。
第二章物态变化知识归纳1. 温度:是指物体的冷热程度。
测量的工具是温度计, 温度计是根据液体的热胀冷缩的原理制成的。
2. 摄氏温度(℃):单位是摄氏度。
1摄氏度的规定:把冰水混合物温度规定为0度,把一标准大气压下沸水的温度规定为100度,在0度和100度之间分成100等分,每一等分为1℃。
3.常见的温度计有(1)实验室用温度计;(2)体温计;(3)寒暑表。
体温计:测量范围是35℃至42℃,每一小格是0.1℃。
4. 温度计使用:(1)使用前应观察它的量程和最小刻度值;(2)使用时温度计玻璃泡要全部浸入被测液体中,不要碰到容器底或容器壁;(3)待温度计示数稳定后再读数;(4)读数时玻璃泡要继续留在被测液体中,视线与温度计中液柱的上表面相平。
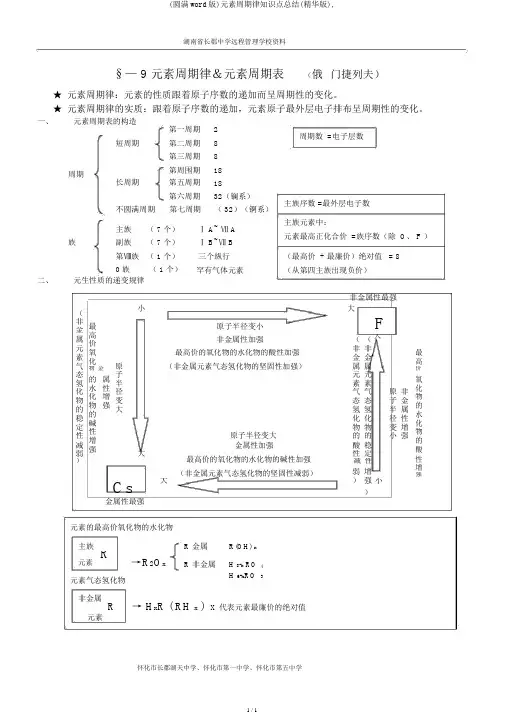
(圆满word 版)元素周期律知识点总结(精华版),1 / 1湖南省长郡中学远程管理学校资料§— 9 元素周期律&元素周期表(俄 门捷列夫)★ 元素周期律:元素的性质跟着原子序数的递加而呈周期性的变化。
★ 元素周期律的实质:跟着原子序数的递加,元素原子最外层电子排布呈周期性的变化。
一、元素周期表的构造第一周期 2周期数 =电子层数短周期第二周期 8第三周期 8周期第周围期 18长周期第五周期 18第六周期 32(镧系)主族序数 =最外层电子数不圆满周期 第七周期( 32)(锕系)主族( 7 个) Ⅰ A~ Ⅶ A 主族元素中:元素最高正化合价 =族序数(除 O 、 F )族副族( 7 个)Ⅰ B~Ⅶ B第Ⅷ族 ( 1 个)三个纵行 (最高价 + 最廉价)绝对值 = 80 族 ( 1 个)罕有气体元素(从第四主族出现负价)二、元生性质的递变规律非金属性最强(小大F非 最原子半径变小金高属非金属性加强( ( 大价元非 非氧 最高价的氧化物的水化物的酸性加强最素金 金 化高气 原 (非金属元素气态氢化物的坚固性加强)属 属物 金 价态 的 属 子元 元 氧氢 半素 素水 性化化 径气 气 原 非化 增物物 变态 态 子 金物 强的的 大氢 氢 半 属的水稳化 化 径 性碱化定物 物 变 增 性 原子半径变大物 性的 的 小 强增的减 金属性加强酸 稳 强酸弱大性 定最高价的氧化物的水化物的碱性加强性)减 性(非金属元素气态氢化物的坚固性减弱)弱 增增Cs强) 强大小)金属性最强元素的最高价氧化物的水化物主族R 金属 R(OH) x元素R→R 2O xR 非金属H 8-x RO 4 元素气态氢化物H 6-x RO3非金属→ H x R ( RH x ) X 代表元素最廉价的绝对值R元素怀化市长郡湖天中学、怀化市第一中学、怀化市第五中学。

第一章概论1。
数据结构描述的是按照一定逻辑关系组织起来的待处理数据元素的表示及相关操作,涉及数据的逻辑结构、存储结构和运算2。
数据的逻辑结构是从具体问题抽象出来的数学模型,反映了事物的组成结构及事物之间的逻辑关系可以用一组数据(结点集合K)以及这些数据之间的一组二元关系(关系集合R)来表示:(K, R)结点集K是由有限个结点组成的集合,每一个结点代表一个数据或一组有明确结构的数据关系集R是定义在集合K上的一组关系,其中每个关系r(r∈R)都是K×K上的二元关系3.数据类型a。
基本数据类型整数类型(integer)、实数类型(real)、布尔类型(boolean)、字符类型(char)、指针类型(pointer)b。
复合数据类型复合类型是由基本数据类型组合而成的数据类型;复合数据类型本身,又可参与定义结构更为复杂的结点类型4.数据结构的分类:线性结构(一对一)、树型结构(一对多)、图结构(多对多)5。
四种基本存储映射方法:顺序、链接、索引、散列6。
算法的特性:通用性、有效性、确定性、有穷性7.算法分析:目的是从解决同一个问题的不同算法中选择比较适合的一种,或者对原始算法进行改造、加工、使其优化8.渐进算法分析a.大Ο分析法:上限,表明最坏情况b.Ω分析法:下限,表明最好情况c.Θ分析法:当上限和下限相同时,表明平均情况第二章线性表1.线性结构的基本特征a.集合中必存在唯一的一个“第一元素”b。
集合中必存在唯一的一个“最后元素"c.除最后元素之外,均有唯一的后继d。
除第一元素之外,均有唯一的前驱2.线性结构的基本特点:均匀性、有序性3。
顺序表a.主要特性:元素的类型相同;元素顺序地存储在连续存储空间中,每一个元素唯一的索引值;使用常数作为向量长度b。
线性表中任意元素的存储位置:Loc(ki)= Loc(k0)+ i * L(设每个元素需占用L个存储单元)c. 线性表的优缺点:优点:逻辑结构与存储结构一致;属于随机存取方式,即查找每个元素所花时间基本一样缺点:空间难以扩充d.检索:ASL=【Ο(1)】e。

高一生物必修一复习提纲第一章走进细胞第一节从生物圈到细胞1.细胞是生物体结构和功能的基本单位.生命活动是建立在细胞的基础上的.●无细胞结构的病毒必需寄生在活细胞中才能生存.●单细胞生物(如:草履虫),单个细胞即能完成整个的生物体全部生命活动.●多细胞生物的个体,以人为例,起源于一个单细胞:受精卵,经过细胞的不断分裂与分化,形成一个多细胞共同维系的生物个体.2.细胞是最基本的生命系统. 最大的生命系统是:生物圈。
生命系统结构层次:细胞组织器官系统个体种群群落生态系统生物圈第二节细胞的多样性与统一性一.细胞的多样性与统一性1.细胞的统一性: 细胞膜,细胞质,细胞质中都有核糖体.主要遗传物质都是DNA.2.细胞的多样性: 大小,细胞核,细胞质中的细胞器,包含的生物类群等均不同.根据细胞内有无以核膜为界限的细胞核,把细胞分为真核细胞和原核细胞两大类.这两类细胞分别构成了两大类生物:原核生物和真核生物.●常见的细菌有: 乳酸菌,大肠杆菌,根瘤菌,霍乱杆菌,炭疽杆菌.●常见的蓝藻有: 颤藻,发菜,念珠藻,蓝球藻.●常见的真菌有: 酵母菌.二:细胞学说建立(德科学家:施旺,施莱登) 细胞学说说明细胞的统一性和生物体结构的统一性。
1、细胞是一个有机体,一切动植物都由细胞发育而来,并由细胞和细胞产物所组成。
2、细胞是一个相对独立的单位,既有它自己的生命,又对与其他细胞共同组成的整体的生命起作用。
3、新细胞可以从老细胞中产生。
第二章: 组成细胞的分子.第一节: 组成细胞的元素与化合物一: 元素组成细胞的主要元素是: C H O N P S 基本元素是: C H O N 最基本元素: C组成细胞的元素常见的有20多种,根据含量的不同分为: 大量元素和微量元素.大量元素: C H O N P S K Ca Mg 微量元素: Fe Mn Zn Cu B Mo生物与无机自然界的统一性与差异性. 元素种类基本相同,元素含量大不相同.占细胞鲜重最大的元素是: O 占细胞干重最大的元素: C二:组成细胞的化合物:无机化合物:水,无机盐细胞中含量最大的化合物或无机化合物: 水有机化合物:糖类,脂质,蛋白质,核酸.细胞中含量最大的有机化合物或细胞中干重含量最大的化合物:蛋白质。
小学数学知识归纳总结(打印版)基本概念第一章数和数的运算(一)整数1、整数的意义自然数和0都是整数。
2、自然数我们在数物体的时候,用来表示物体个数的1,2,3……叫做自然数。
一个物体也没有,用0表示。
0也是自然数。
3、计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
其中“一”是计数的基本单位。
10个1是10,10个10是100……每相邻两个计数单位之间的进率都是10.这样的计数法叫做十进制计数法。
4、数位计数单位按照一定的顺序排列起来,它们所占的位置叫做数位.5、整数的读法:从高位到低位,一级一级地读。
读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万"字.每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零.6、整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
7、一个较大的多位数,为了读写方便,常常把它改写成用“万"或“亿"作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
⑴准确数:在实际生活中,为了计数的简便,可以把一个较大的数改写成以万或亿为单位的数。
改写后的数是原数的准确数。
例如把 1254300000 改写成以万做单位的数是 125430 万;改写成以亿做单位的数 12。
543 亿。
⑵近似数:根据实际需要,我们还可以把一个较大的数,省略某一位后面的尾数,用一个近似数来表示。
例如: 1302490015 省略亿后面的尾数是 13 亿。
⑶四舍五入法:求近似数,看尾数最高位上的数是几,比5小就舍去,是5或大于5舍去尾数向前一位进1。
这种求近似数的方法就叫做四舍五入法。
8、整数大小的比较:位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大那个数就大。
以此类推。
1、小数的意义把整数1平均分成10份、100份、1000份……得到的十分之几、百分之几、千分之几……可以用小数表示。
二次函数知识点总结和题型总结一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:①a ≠ 0 ②最高次数为2 ③代数式一定是整式2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵a b c,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.例题:例1、已知函数y=(m -1)x m2 +1+5x -3是二次函数,求m 的值。
练习、若函数y=(m 2+2m -7)x 2+4x+5是关于x 的二次函数,则m 的取值范围 为 。
二、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。
c的性)2h的性4.()2y a x h k=-+的性质:二次函数的对称轴、顶点、最值如果解顶点式-则最值果解析般式y=ax2+bx+c则最值为4ac-b24a)1.抛物线y=2x2+4x+m2-m经过坐标原点,则m的值为。
2.抛物y=x 2+bx+c 线的顶点坐标为(1,3),则b = ,c = . 3.抛物线y =x 2+3x 的顶点在( )A.第一象限B.第二象限C.第三象限D.第四象限4.若抛物线y =ax 2-6x 经过点(2,0),则抛物线顶点到坐标原点的距离为( )5.若直线y =ax +b 不经过二、四象限,则抛物线y =ax 2+bx +c( ) A.开口向上,对称轴是y 轴 B.开口向下,对称轴是y 轴 C.开口向下,对称轴平行于y 轴 D.开口向上,对称轴平行于y 轴6.已知二次函数y=mx 2+(m -1)x+m -1有最小值为0,则m = 。
三、二次函数图象的平移 1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2) 函数y=ax 2+bx+c 的图象和性质例题:1.抛物线y=x 2+4x+9的对称轴是 。
专题一定语从句一、关系代词引导的定语从句1、that 指人或物在从句中作主语,宾语或表语which 指物在从句中作主语,宾语或表语(作宾语时可以省略)who 指人在从句中作主语,宾语或表语whom 指人在从句中作宾语whose 指人或物在从句中作定语as 指人或物在从句中作主语,宾语或表语but 指人或物在从句中作主语,宾语或表语注意:指物时,whose+名词=the+名词+of which 或of which+the+名词2、as 的用法(1)常用于下列结构:such…as;so…as;the same…as; as…as注意:the same…as 表示同一类,不同一个the same…that 表示同一个(2)as与which的区别a、位置不同as可放在主句后,主句前或主句中间;which只能放在主句后。
b、as起连接作用,表达说话人的观点、看法,并指出主句内容的根据或出处,意为“正如,正像”。
Which相当于并列句,可以用and this来代替,意为“这一点,这件事’”。
注意:as常用于下列结构:as we know/ as is known to all, as we all can see, as has been said before/above,as might be excepted, as is often the case, 一般不能用which代替as。
C、在从句中作主语时,which既可作系动词be的主语也可作实义动词的主语,而as只可作系动词be的主语。
3、but用作关系代词,相当于who/that…not例:In China there is no one but knows Lei Feng.二、只用that不用which的情况1、.先行词为all , much,everything, nothing , something ,anything,nothing, none,the one 等不定代词时2、先行词被only,any, few, little, no , all,just , very ,right等修饰时。
人教版小学数学知识点归纳第一章数和数的运算一概念(一)整数1、整数的意义自然数和0都是整数。
2 、自然数我们在数物体的时候,用来表示物体个数的1,2,3……叫做自然数.一个物体也没有,用0表示。
0也是自然数。
3、计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法。
4 、数位计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
5、数的整除整数a除以整数b(b ≠0),除得的商是整数而没有余数,我们就说a能被b整除,或者说b能整除a 。
例如15÷3=5,所以15能被3整除,3能整除15。
如果数a能被数b(b ≠0)整除,a就叫做b的倍数,b就叫做a的因数.倍数和约数是相互依存的。
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
个位上是0、2、4、6、8的数,都能被2整除,例如:202、480、304,都能被2整除。
个位上是0或5的数,都能被5整除,例如:5、30、405都能被5整除。
.一个数的各位上的数的和能被3整除,这个数就能被3整除,例如:12、108、204都能被3整除。
能被2整除的数叫做偶数,不能被2整除的数叫做奇数。
0也是偶数.自然数按能否被2 整除的特征可分为奇数和偶数.一个数,如果只有1和它本身两个因数,这样的数叫做质数,100以内的质数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53 、59、61、67、71、73、79、83、89、97。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数,例如4、6、8、9、12都是合数。
1不是质数也不是合数,自然数除了1外,不是质数就是合数。
如果把自然数按其因数的个数的不同分类,可分为质数、合数和1。
每个合数都可以写成几个质数相乘的形式。
一、基本概念
1. 高分子化合物
2. 结构单元、重复单元、单体单元
3. 均缩聚、混缩聚、共缩聚
4. 均聚物、共聚物、共混物
5. 平均官能度
6. 凝胶点
7. 、
8. 分子量的多分散性
9. 分子量分布、分子量分布指数
10. 线形结构大分子、体型结构大分子
11. 碳链聚合物、杂链聚合物
12. 线形缩聚、体型缩聚
13. 平衡缩聚、非平衡缩聚
14. 反应程度、转化率
15. 摩尔系数、过量百分数
16. 歧化终止
17. 偶和终止
18. 动力学链长
19. 诱导期
20. 自由基寿命
21. 聚合上限温度
22. 自加速效应
23. 引发效率
24. 笼蔽效应
25. 诱导分解
26. 阻聚
27. 缓聚
28. 活性聚合物
29. 遥爪聚合物
30. 配位聚合
31. 插入聚合
32. 络合聚合
33. 定向聚合
34. 有规立构聚合和立构选择聚合
35. 立构规整度
36. 基团转移聚合
37. 原子转移自由基聚合
38. Ziegler-Natta聚合
39. 光学异构、几何异构和构象异构
40. 竞聚率
41. 种子聚合
42. 临界胶束浓度
43. 乳化
44. 胶束
45. 增溶作用
46. 临近基团效应
47. 扩链、交联
48. 解聚、老化
49. 光稳定剂
50. 与低分子化合物相比,高分子化合物有什么特征?
51. 乙二酰氯与乙二胺、己二胺中的哪一个反应能得到高聚物而不是环状物。
52. 为什么在缩聚反应中不用转化率而用反应程度描述反应过程?
53. 在自由基聚合反应中,调节分子量的措施有哪些?试以氯乙烯悬浮聚合、苯乙烯本
体聚合、醋酸乙烯溶液聚合和丁二烯乳液聚合中分子量调节方法为例来阐述和讨
论。
54. 工业上用自由基聚合生产的大品种有哪些?简述它们常用的聚合方法和聚合条件。
55. 悬浮聚合法生产聚氯乙烯时,为什么采用高活性和中活性引发剂并用的引发体系?
56. 在尼龙-6和尼龙-66生产中为什么要加入醋酸或己二酸控制分子量?在涤纶树脂生
产中为什么不加入分子量控制剂?
57. 比较硝基苯、苯醌、DPPH、FeCl3和氧的阻聚常数和阻聚效果。
58. 试从单体、引发剂、聚合方法及反应的特点等方面对自由基、阴离子和阳离子聚合
反应进行比较。
59. 比较逐步聚合、自由基聚合、阴离子聚合的
① 转化率和时间的关系
② 聚合物相对分子质量与时间的关系
60. 聚乙烯有几种分类方法?这几种聚乙烯在结构和性能上有何不同?它们分别是由
何种聚合方法生产的?
61. 简述Natta的双金属机理和Cossee-Arlman的单金属机理的基本论点、不同点和各
自的不足之处。
62. 无规、交替、嵌段、接枝共聚物的结构有何差异?在这些共聚物名称中,对前后单
体的位置有何规定?
63. 试讨论二元共聚物组成微分方程的适用范围。
64. 为什么要对共聚物的组成进行控制?在工业上有哪几种控制方法?它们各针对何
种聚合体系?各举一例加以说明。
65. 温度、溶剂对自由基共聚的竞聚率有何影响?竞聚率在共聚过程中有无变化?对离
子共聚的竞聚率又如何影响?
66. 在自由基共聚合反应中,苯乙烯的相对活性远大于醋酸乙烯。当醋酸乙烯均聚时如
果加入少量苯乙烯,则醋酸乙烯难以聚合。试解释发生这一现象的原因。
67. 试述Q、e概念,如何根据Q、e值来判断单体间的共聚行为。
68. 简述乳液聚合的机理。单体、引发剂和乳化剂所在的场所。引发、增长和终止情况
的场所。胶束、乳胶粒和单体液滴的变化。
69. 悬浮聚合时,常需不断搅拌,并加入分散剂。试分析它们对悬浮稳定性的贡献。分
散剂有哪几类?它们的作用机理有何不同?
70. 聚合物化学反应有哪些特征?与低分子化学反应有什么不同?
71. 根据反应发生前后聚合度和官能团的变化情况,可将聚合物化学反应可分为哪几种
类型?
72. 聚合物降解有几种类型?热降解有几种情况?评价聚合物的热稳定性的指标是什
么?
73. 简述下列聚合物的合成方法。① ABS树脂、② HIPS树脂、③ SBS热塑性弹性
体、④ 端羧基和端羟基聚苯乙烯
74. 引起高分子材料老化的主要因素有哪些?解释2,6-二叔丁基对甲酚的抗氧机理和2-
羟基二苯甲酮的光稳定作用机理。
75. а-甲基苯乙烯、聚甲醛、聚乙烯、聚氯乙烯进行热降解反应,分别得到何种产物
二、反应方程式(会根据中文名写出结构式或根据结构式写出中文名,了解主要特性和用途)
1. α-甲基苯乙烯
2. 偏二氰基乙烯
3. α-氰基丙烯酸甲酯
4. 双酚A+环氧氯丙烷
5. 对苯二甲酸+丁二醇
6. 聚丙烯酸甲酯
7. 聚醋酸乙烯
8. 聚己二酰己二胺
9. 聚己内酰胺
10. 聚丙烯腈
11. 聚甲基丙烯腈
12. 聚酰亚胺
13. 聚苯醚
14. 聚醚砜
15. 聚醚醚酮
16. 丁苯橡胶
17. 涤纶
18. 聚甲醛
19. 聚氧化乙烯
20. CH2CCH3COOCH3(1)(2)(3)(6)CH2CHOHnnNH CH2 6NHOC CH2 8COnCH2C CH3 2=CHCH2nNH CH2 5COnCCH3CH3OCOOn
21. CH2CCH3COOCH3(1)(2)(4)(5)(6)CH2CHOHnnNH CH2 6NHOC CH2 8COn2C CH3 2=CHCH2nNH CH2 5COnCCH3CH3OCOOn
22. CH2CCH3COOCH3(1)(2)(3)(5)(6)CH2CHOHnnNH CH2 6NHOC CH2 8COnCH2C CH3 2=CHCH2nNH CH2 5COnCCH3CH3OCOOn
23. CH2CCH3COOCH3(1)(2)(3)(4)(5)(6)CH2CHOHnnNH CH2 6NHOC CH2 8COnCH2C CH3 2=CHCH2nNH CH2 5COnCCH3CH3OCOOn
24. CH2CCH3COOCH3(1)(2)(3)(4)(5)(6)CH2CHOHnnNH CH2 6NHOC CH2 8COnCH2C CH3 2=CHCH2nNH CH2 5COnCCH3CH3OCOOn
25. CH2CCH3COOCH3(1)(2)(3)(4)(5)(6)CH2CHOHnnNH CH2 6NHOC CH2 8COnCH2C CH3 2=CHCH2nNH CHCOnCCH3CH3OCOOn
26. 要合成分子链中含有以下特征基团的聚合物,应选用哪类单体,并通过何种反应聚
合而成?① -NH-CO-、② -NH-CO-O-、③ -NH-CO-HN-、④ -OCH2CH2-
27. 氯乙烯以偶氮二异庚腈为引发剂聚合时的各个基元反应
28. 试用方程式表示高压聚乙烯中短支链的产生
29. 醋酸乙烯和醋酸烯丙基分别以AIBN在CH3OH中引发聚合。试写出形成的相应聚合
物的结构
30. 4-甲基-1-戊烯和3-乙基-1-戊烯在较低温度下的聚合反应机理
31. 用阴离子聚合方法合成四种不同端基(—OH、—COOH、—SH、—NH2)的聚丁烯
遥爪聚合物的反应过程
32. 聚乙烯的氯化
33. 1,4-聚异戊二烯的氯化
34. 聚乙烯的氯磺化
35. SBS加氢
36. 下列聚合物用哪类交联剂或固化剂进行交联,用方程式表示:① 乙二醇和马来酸
酐合成的聚酯、② 聚乙烯、③ 氯磺化聚乙烯、④ 环氧树脂、⑤ 顺丁橡胶、
⑥ 线型酚醛树脂、⑦ 聚二甲基硅氧烷