小波分析在心电信号去噪中的应用(内附Matlab去噪源代码)

心电信号滤波处理matlab报告一、需求分析。

心电信号是用于检测人体心脏功能的信号。

在记录和处理心电信号时，由于各种原因，会有各种不同的噪声和干扰信号，这些都会影响到分析心电信号的正确性和准确性。

为了处理这些噪声和干扰信号，需要对心电信号进行滤波。

在本文中，我们将使用MATLAB对心电信号进行滤波处理。

二、滤波处理方法。

主要有以下两种方法：1、数字滤波器法。

数字滤波器法是通过数字滤波器对信号进行处理。

数字滤波器是由数字电路组成的，可以对信号进行模拟处理。

数字滤波器法可以根据所需的滤波器特性，尤其是通带特性、截止频率等滤波参数设计数字滤波器。

2、小波变换法。

小波变换法是将信号分解成多个频带，每个频带的特征都不一样。

这样，可以对不同频率的信号进行不同的处理，从而达到更好的滤波效果。

小波变换法常用于去除心电信号中的基音干扰。

三、matlab代码实现。

接下来，将使用MATLAB对ECG信号（心电信号）进行滤波处理。

1、读取ECG信号。

首先，需要加载ecg.mat，这是一个包含心电信号的MATLAB数据文件。

load ecg;。

plot(ecg); 。

2、数字滤波器处理。

接下来，我们将使用数字滤波器对信号进行处理，以去除高频噪声。

例如，我们可以使用高通滤波器，相当于在信号中去除低频成分。

设计高通滤波器：fcuts = [50 60];。

mags = [0 1];。

devs = [0.005 0.005];。

[n, Wn] = buttord(fcuts/(Fs/2), mags, devs);。

[b, a] = butter(n, Wn, 'high');。

对信号进行滤波处理：ecg1 = filter(b,a,ecg);。

然后可以将处理后的信号与原始信号进行比较，以查看滤波后的效果。

plot(ecg1); % 滤波后的信号。

hold on;。

plot(ecg); % 原始信号。

3、小波变换处理。

matlab 小波阈值去噪-回复Matlab小波阈值去噪是一种常用的信号处理技术，可以有效地去除信号中的噪声，提高信号的质量和可靠性。

本文将介绍小波阈值去噪的基本原理、步骤和实际应用。

第一部分：小波变换的基本原理小波分析是一种基于时间-频率局部化的信号分析方法。

它通过使用一组特定的基函数（即小波函数），将信号分解成不同频率和时间的组合，从而提供了更丰富的信号信息。

小波变换包括两个主要步骤：分解（Decomposition）和重建（Reconstruction）。

在分解阶段，信号被分解成一系列的低频和高频分量，每个分量对应不同尺度和频率的信息。

在重建阶段，通过合并这些分量，可以还原出原始信号。

第二部分：小波阈值去噪的基本原理小波阈值去噪是基于小波变换的一种方法，它的基本原理是对信号的小波系数进行阈值处理。

由于噪声通常具有较高的频率成分和较小的幅度，而信号则具有较低的频率成分和较大的幅度，因此可以通过设定一个合适的阈值，将小于该阈值的小波系数置为零，然后进行逆变换，以实现去噪的效果。

第三部分：小波阈值去噪的步骤小波阈值去噪的具体步骤如下：步骤一：选择合适的小波函数根据信号的特性，选择适合的小波函数。

常用的小波函数有Daubechies小波、Symlet小波和Haar小波等。

步骤二：进行小波分解将待处理的信号进行小波分解，得到各个尺度的小波系数。

步骤三：确定阈值根据经验或统计方法，确定一个适当的阈值。

常用的阈值选择方法有固定阈值和自适应阈值。

固定阈值方法中，常用的有绝对阈值和相对阈值。

绝对阈值方法认为小于某个固定阈值的小波系数都是噪声，可以直接置零。

相对阈值方法则是基于信号的统计特性，将小波系数除以标准差，并乘以一个系数作为阈值。

自适应阈值方法中，常用的有Soft Thresholding和Hard Thresholding。

Soft Thresholding将小于阈值的小波系数进行缩放；Hard Thresholding则是将小于阈值的小波系数直接置零。

4.6 小波去噪举例[4,6]4.6.1 MATLAB中用wnoise函数测试去噪算法％ waveletnoise.msqrt_snr=3;init=231434;[x,xn]=wnoise(3,11,sqrt_snr,init); % WNOISE generate noisy wavelet test data.% X= WNOISE(FUN,N) returns values of the test function given by FUN, on a % 2^N sample of [0,1].% [X,XN] = WNOISE(FUN,N,SQRT_SNR) returns values of the test function% given by FUN and rescaled such that std(x) = SQRT_SNR (standard% deviation). The returned vector XN contains the same test vector X corrupted% by an additive Gaussian white noise N(0,1).% Then XN has a signal-to-noise ratio of (SQRT_SNR^2).% [X,XN] = WNOISE(FUN,N,SQRT_SNR,INIT) returns previous vectors X % and XN, but the generator seed is set to INI value.subplot(3,2,1),plot(x)title('original test function')subplot(3,2,2),plot(xn)title('noised function')% 产生一个长为2**11点，包含高斯白噪声的正弦信号，噪声的的标准％偏差为3。

小波阈值滤波matlab代码小波阈值滤波是一种常用的信号处理方法，用于去除信号中的噪声。

在Matlab中，可以使用Wavelet Toolbox来实现小波阈值滤波。

以下是一个简单的小波阈值滤波的Matlab代码示例：```matlab% 加载信号load('signal.mat'); % 假设信号保存在signal.mat文件中 % 设置小波基和阈值wavelet = 'db4'; % 选择小波基level = 5; % 小波变换的层数threshold = 0.1; % 阈值% 对信号进行小波变换[c, l] = wavedec(signal, level, wavelet);% 计算阈值sigma = median(abs(c)) / 0.6745; % 用中值绝对偏差估计信号的标准差threshold = sigma * sqrt(2 * log(length(signal))); % 使用经验公式计算阈值% 应用阈值c_hat = wthresh(c, 's', threshold); % 确保小于阈值的系数被置为0% 重构信号signal_hat = waverec(c_hat, l, wavelet);% 绘制原始信号和滤波后的信号figure;subplot(2,1,1);plot(signal);title('原始信号');subplot(2,1,2);plot(signal_hat);title('滤波后的信号');```该代码首先加载了一个信号，然后设置了小波基和阈值。

接下来，通过使用`wavedec`函数对信号进行小波变换，得到小波系数和长度。

然后，通过计算阈值，使用`wthresh`函数对小波系数进行阈值处理，将小于阈值的系数置为0。

最后，通过使用`waverec`函数对处理后的小波系数进行重构，得到滤波后的信号。

小波去噪是信号处理中常用的一种方法，在MATLAB中也有相应的函数可以实现小波去噪。

下面我们将介绍MATLAB中对1维数据进行小波去噪的具体过程。

1. 准备原始数据我们需要准备一维的原始数据，可以是来自传感器采集的数据，也可以是从文件中读取的数据。

在MATLAB中，可以使用load函数或者从其它数据源导入数据。

2. 选择小波基和分解层数在进行小波去噪之前，需要选择适合的小波基和分解层数。

MATLAB 中提供了丰富的小波基选择，包括Daubechies小波、Symlet小波、Coiflet小波等。

根据信号的特点和需要去除的噪声类型，选择合适的小波基和分解层数。

3. 进行小波分解使用MATLAB中的wavedec函数对原始数据进行小波分解。

该函数的调用形式为[C, L] = wavedec(X, N, wname)，其中X为原始数据，N为分解层数，wname为小波基名称。

函数返回小波系数C和长度向量L。

4. 去除小波系数中的噪声根据小波分解得到的小波系数，可以利用MATLAB中的过滤函数对小波系数进行去噪。

常用的去噪方法包括阈值去噪、软硬阈值去噪等。

这些方法可以有效地去除信号中的噪声成分，得到干净的信号。

5. 重构信号经过去噪处理后，可以使用MATLAB中的waverec函数对去噪后的小波系数进行重构，得到去噪后的信号。

该函数的调用形式为X = waverec(C, L, wname)，其中C为去噪后的小波系数，L为长度向量，wname为小波基名称。

6. 可视化和分析可以利用MATLAB中丰富的绘图函数对去噪前后的信号进行可视化比较，以及对去噪效果进行分析。

通过比较原始信号和去噪后的信号，可以直观地了解去噪效果，并进行进一步的分析和处理。

通过以上步骤，我们可以在MATLAB中对一维数据进行小波去噪处理，去除信号中的噪声成分，得到干净的信号。

小波去噪是一种简单而有效的信号处理方法，在实际应用中具有广泛的应用前景。

小波去噪
［xd,cxd,lxd]=wden（x，tptr,sorh，scal,n,'wname’）
式中：
输入参数x 为需要去噪的信号;
1.tptr ：阈值选择标准.
1）无偏似然估计（rigrsure）原则.它是一种基于史坦无偏似然估计（二次方程）原理的自适应阈值选择.对于一个给定的阈值t，得到它的似然估计，再将似然t 最小化，就得到了所选的阈值，它是一种软件阈值估计器.
2）固定阈值（sqtwolog）原则.固定阈值thr2 的计算公式为：thr 2log（n) 2 = （6）式中，n 为信号x(k）的长度。

3)启发式阈值（heursure) 原则。

它是rigrsure原则和sqtwolog 原则的折中。

如果信噪比很小，按rigrsure 原则处理的信号噪声较大,这时采用sqtwolog原则.
4）极值阈值（minimaxi）原则。

它采用极大极小原理选择阈值，产生一个最小均方误差的极值,而不是没有误差.
2.sorh ：阈值函数选择方式，即软阈值（s) 或硬阈值(h）。

3.scal :阈值处理随噪声水平的变化，scal=one 表示不随噪声水平变化,scal=sln 表示根据第一层小波分解的噪声水平估计进行调整，scal=mln 表示根据每一层小波分解的噪声水平估计进行调整.
4.n 和wname 表示利用名为wname 的小波对信号进行n 层分解。

输出去噪后的数据xd 及xd 的附加小波分解结构［cxd,lxd］。

常见的几种小波：haar，db，sym，coif，bior。

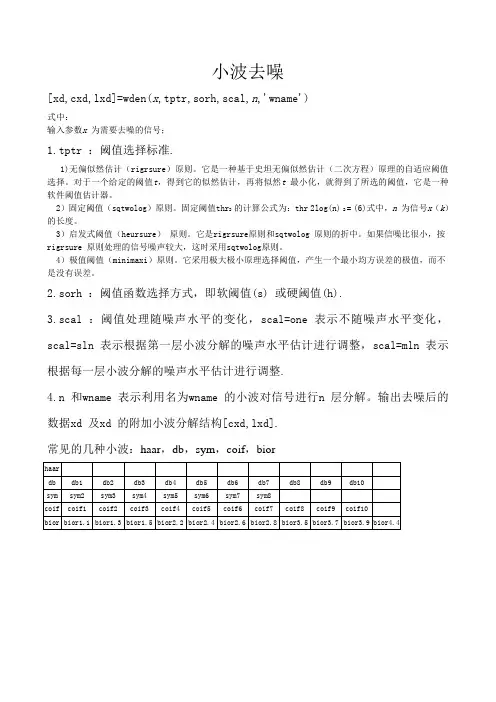
小波去噪[xd,cxd,lxd]=wden(x,tptr,sorh,scal,n,'wname')式中：输入参数x 为需要去噪的信号；1.tptr ：阈值选择标准.1)无偏似然估计（rigrsure）原则。

它是一种基于史坦无偏似然估计（二次方程）原理的自适应阈值选择。

对于一个给定的阈值t，得到它的似然估计，再将似然t 最小化，就得到了所选的阈值，它是一种软件阈值估计器。

2）固定阈值（sqtwolog）原则。

固定阈值thr2 的计算公式为：thr 2log(n) 2 = (6)式中，n 为信号x（k）的长度。

3）启发式阈值（heursure）原则。

它是rigrsure原则和sqtwolog 原则的折中。

如果信噪比很小，按rigrsure 原则处理的信号噪声较大，这时采用sqtwolog原则。

4）极值阈值（minimaxi）原则。

它采用极大极小原理选择阈值，产生一个最小均方误差的极值，而不是没有误差。

2.sorh ：阈值函数选择方式，即软阈值(s) 或硬阈值(h).3.scal ：阈值处理随噪声水平的变化，scal=one 表示不随噪声水平变化，scal=sln 表示根据第一层小波分解的噪声水平估计进行调整，scal=mln 表示根据每一层小波分解的噪声水平估计进行调整.4.n 和wname 表示利用名为wname 的小波对信号进行n 层分解。

输出去噪后的数据xd 及xd 的附加小波分解结构[cxd,lxd].常见的几种小波：haar，db，sym，coif，bior用MATLAB对一语音信号进行小波分解，分别用强阈值，软阈值，默认阈植进行消噪处理。

复制内容到剪贴板代码:%装载采集的信号leleccum.matload leleccum;%=============================%将信号中第2000到第3450个采样点赋给sindx=2000:3450;s=leleccum(indx);%=============================%画出原始信号subplot(2,2,1);plot(s);title('原始信号');%=============================%用db1小波对原始信号进行3层分解并提取系数[c,l]=wavedec(s,3,'db1');a3=appcoef(c,l,'db1',3);d3=detcoef(c,l,3);d2=detcoef(c,l,2);d1=detcoef(c,l,1);%=============================%对信号进行强制性消噪处理并图示结果dd3=zeros(1,length(d3));dd2=zeros(1,length(d2));dd1=zeros(1,length(d1));c1=[a3 dd3 dd2 dd1];s1=waverec(c1,l,'db1');subplot(2,2,2);plot(s1);grid;title('强制消噪后的信号');%=============================%用默认阈值对信号进行消噪处理并图示结果%用ddencmp函数获得信号的默认阈值[thr,sorh,keepapp]=ddencmp('den','wv',s);s2=wdencmp('gbl',c,l,'db1',3,thr,sorh,keepapp); subplot(2,2,3);plot(s2);grid;title('默认阈值消噪后的信号');%=============================%用给定的软阈值进行消噪处理sosoftd2=wthresh(d2,'s',1.823);softd3=wthresh(d3,'s',2.768);c2=[a3 softd3 softd2 softd1];s3=waverec(c2,l,'db1');subplot(2,2,4);plot(s3);grid;title('给定软阈值消噪后的信号');ftd1=wthresh(d1,'s',1.465);。

小波变换图像降噪的matlab代码求小波变换图像降噪的matlab代码load wbarb; % 装载原始图像subplot(221); % 新建窗口image(X); % 显示图像colormap(map); % 设置色彩索引图title('原始图像'); % 设置图像标题axis square; % 设置显示比例,生成含噪图像并图示init=2055615866; % 初始值randn('seed',init); % 随机值XX=X+8*randn(size(X)); % 添加随机噪声subplot(222); % 新建窗口image(XX); % 显示图像colormap(map); % 设置色彩索引图title('含噪图像'); % 设置图像标题axis square; %用小波函数coif2 对图像XX 进行2 层分解[c,l]=wavedec2(XX,2,'coif2'); % 分解n=[1,2]; % 设置尺度向量p=[10.28,24.08]; % 设置阈值向量,对高频小波系数进行阈值处理%nc=wthcoef2('h',c,l,n,p,'s');%nc=wthcoef2('v',c,l,n,p,'s');nc=wthcoef2('d',c,l,n,p,'s');X1=waverec2(nc,l,'coif2'); % 图像的二维小波重构subplot(223); % 新建窗口image(X1); % 显示图像colormap(map); %设置色彩索引图title('第一次消噪后的图像'); % 设置图像标题axis square; % 设置显示比例,再次对高频小波系数进行阈值处理%mc=wthcoef2('h',nc,l,n,p,'s');mc=wthcoef2('v',nc,l,n,p,'s');mc=wthcoef2('d',nc,l,n,p,'s');X2=waverec2(mc,l,'coif2'); % 图像的二维小波重构subplot(224); % 新建窗口image(X2); % 显示图像colormap(map); % 设置色彩索引图title('第二次消噪后的图像'); % 设置图像标题axis square; % 设置显示比例。

matlab小波降噪方式Matlab小波降噪方式小波降噪是一种常见的信号处理方法，可以有效地从噪声中恢复出原始信号。

在Matlab中，有多种小波降噪方式可以选择，本文将介绍其中几种常用的方法。

一、小波变换简介小波变换是一种时间-频率分析方法，可以将信号分解成不同尺度的小波函数。

通过小波变换，可以将信号的时域特征和频域特征结合起来，更好地描述信号的局部特性。

二、小波降噪原理小波降噪的基本原理是通过将信号在小波域进行分解，根据小波系数的幅值和相位信息，对信号进行去噪处理。

具体而言，小波降噪方法将信号分解成多个尺度的小波系数，然后根据小波系数的幅值和相位信息对信号进行处理，最后再将处理后的小波系数进行逆变换得到降噪后的信号。

三、小波降噪方法1. 阈值去噪法阈值去噪法是小波降噪中最常用的方法之一。

该方法通过设置阈值，将小波系数中幅值小于阈值的系数置零，从而实现去噪效果。

常用的阈值选择方法有固定阈值、基于软硬阈值的方法等。

2. 基于小波包变换的降噪法小波包变换是小波变换的一种扩展形式，可以对信号进行更细致的分解和重构。

基于小波包变换的降噪法可以在小波域中选择最佳小波包基函数，对信号进行更精细的降噪处理。

3. 基于模态分解的小波降噪法模态分解是一种将信号分解成若干个本征模态函数的方法，它可以有效地提取信号的局部特性。

基于模态分解的小波降噪法将信号进行模态分解，然后对每个本征模态函数进行小波降噪处理，最后将处理后的本征模态函数进行重构。

四、Matlab中的小波降噪函数在Matlab中，有多个工具箱和函数可以实现小波降噪。

其中，wavelet toolbox是Matlab中最常用的小波分析工具箱，提供了丰富的小波变换和小波降噪函数。

1. wdenoise函数wdenoise函数是Matlab中最基本的小波降噪函数，可以实现简单的阈值去噪。

该函数的基本语法为：y = wdenoise(x,'DenoisingMethod',method,'Wavelet',wavename) 2. wpdencmp函数wpdencmp函数是基于小波包变换的小波降噪函数，可以实现更精细的降噪处理。

小波去噪matlab程序
本文介绍了一种使用小波去噪图像的matlab程序，主要步骤如下：
（1）首先从图像获取原始数据，并转换为灰度图像；
（2）接下来进行小波变换，将灰度图片转换为小波系数矩阵；
（3）引入一种基于稀疏性表示的噪声检测剔除技术，从小波系数矩阵中提取出噪声数据；
（4）最后，用剔除噪声后的小波系数矩阵进行逆小波变换，可以得到去噪后的图像数据，这就是小波去噪后的图像。

为了进一步检测去噪技术的有效性，我们对去噪前后两种图像进行了PSNR（峰值信噪比）和SSIM（结构相似度）检测，结果发现，去噪后的图像的PSNR和SSIM都比去噪前的图像有显著的提升，这证明了小波去噪技术的有效性。

总之，本文介绍了一种基于小波去噪的图像处理方法，其所提供的解决方案可以很好地提高图像质量。

因此，小波去噪技术可以在实际应用中发挥重要作用。

提纲内容：1概要1.3labview简介及小波工具箱VI。

及labview的VI滤波显示。

、1.2matlab简介及小波工具箱，wavemenu 及GUI的设计1.1小波变换在信号去噪应用的原理及方法。

1.1.1小波变换在心电去噪的应用。

1.1.2不同小波在心电去噪的效果比较，选取coif4进行去噪。

使用coif4进行噪声模拟去噪（基线漂移，肌电干扰，工频干扰）。

Matlab心电去噪程序实现。

包括不同小波基的去噪对比，最终选择。

及基于coif4进行去噪的不同阈值的选择对滤波效果的影响，最终得出结论：默认阈值的效果比较好。

前言人体的心电信号是一种非平稳、非线性微弱的电信号，常规心电信号的幅值在mV级，频率为0.05~100Hz。

采集心电信号时，由于受到仪器、人体和环境的影响，采集到的电信号常伴有噪声，信噪比较低。

噪声类型主要有三种：1.肌电干扰。

肌电干扰是由于采集心电时，人体的活动或紧张所引起的。

其频率在5~2000Hz之间。

2.工频干扰。

它是由于供电网络及其他电器设备产生的空间电磁干扰，频率在50~60之间。

3.基线漂移。

基线漂移是由于测量电极移动、人体呼吸等引起的低频干扰，频率一般小于1Hz。

小波变换是一个时间和频率的局域变换，能有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度的分析，具有多分辨率的特点，被誉为是“数学显微镜”。

小波变换在诸如信号检测、特征提取、故障诊断与定位、数据压缩等方面成为有力的工具。

本文主要讨论在labview和matlab混合编程环境下，小波变换在处理心电信号噪声方面的应用。

通过比较不同小波基对心电的去噪结果得出结论：使用coif4进行4层小波去噪效果最好。

并且对比默认阈值处理、强制去噪和给定阈值去噪的结果发现：默认阈值去噪结果良好。

LabVIEW语言是由美国NI公司推出的一种非常优秀的面向对象的图形化编程语言。

LabVIEW是实验室虚拟仪器集成环境（Laboratory Virtual Instrument Engineering Workbench）的简称，它是一个开放型的开发环境，使用图标代替文本代码创建应用程序，拥有大量与其它应用程序通信的VI库，大大简化了过程控制和测试软件的开发。