计量经济学习题“粮食产量影响因素”

中国粮食产量影响因素分析摘要：粮食是人类最基本的生活消费品，粮食问题是关系到国家的国计民生的头等问题。

众所周知，农业是国民经济发展的基础，粮食是基础的基础，因此粮食生产是关系到一个国家发展与生产的一个关键的主题。

建国以来我国的粮食产量出现了多次的变动，给消费者和生产者带来了很大的影响，所以了解影响粮食生产因素很重要。

通过计量经济学方法创建我国粮食生产函数，我们会发现粮食播种、化肥施用量、受灾面积是影响粮食生产的三大因素，其中粮食播种面积的影响最大。

【关键词】粮食产量；影响因素；回归分析一、引言众所周知，粮食是我们人类生命得以延续的最基础的物质条件，没有粮食这个重要基础，人类将无法继续生存。

回顾我国粮食的生产情况，我们会发现，随着技术水平的提高，社会的发展，从整体来讲我国粮食产量呈上升的趋势。

二、中国粮食生产现状分析在改革开放（1978年）之前我国粮食产量非常缓慢增长，一直都在30000万吨以下。

改革开放后，我国粮食产量从30000万吨一路疯狂走高，粮食生产得到飞速发展，但波动也更频繁复杂。

在1997年总产量首次跨上50000万吨的大难关，达到了50453万吨，增长率为8.13%。

但在2004年开始出现了几年的连续减产的现象，曾一路降到43069万吨的局面，一下子退回到十几年前的水平，让人更加担忧。

从2004年以来的5年里，我国粮食产量连续10年增产。

在2013年粮食产量达到60193.8万吨。

改革开放以来粮食产量一直是我国最关心的问题，我国逐步改革统购统销的体制，减少定购数量，提高粮食收购价格，使粮食生产实现高速增长。

我国粮食产量从30000万吨开始一路走高。

1980—2010年这30年，我国粮食生产得到快速发展。

1978年我国农村实行改革和粮食价格提高，极大地调动了农民的积极性。

1978年中国粮食产量首次突破30000万吨，增长了7．8％。

1979年粮食产量继续增长8.9％，主要是由于国家大幅度提高粮食收购价格，粮食统购价提高20％，超购部分加价50％，从而促进粮食产量飞速增长。

粮食生产试题及答案解析一、单项选择题（每题2分，共10分）1. 我国粮食作物的主要类型是：A. 玉米B. 小麦C. 水稻D. 大豆答案：B2. 以下哪个因素对粮食生产影响最大？A. 气候B. 土壤C. 种子D. 灌溉答案：A3. 我国粮食生产的主要区域是：A. 东北地区B. 西南地区C. 华北地区D. 华南地区答案：A4. 粮食作物的种植季节通常是：A. 春季B. 夏季C. 秋季D. 冬季答案：A5. 粮食作物的主要营养成分是：A. 蛋白质B. 脂肪C. 碳水化合物D. 维生素答案：C二、多项选择题（每题3分，共15分）1. 以下哪些因素会影响粮食产量？A. 种植技术B. 气候变化C. 病虫害D. 土壤肥力答案：ABCD2. 我国粮食生产的主要挑战包括：A. 土地资源有限B. 气候变化C. 人口增长D. 农业技术落后答案：ABC3. 粮食作物的种植需要考虑的因素有：A. 土壤条件B. 气候条件C. 种植成本D. 市场需求答案：ABCD4. 粮食作物的收获后处理包括：A. 脱粒B. 干燥C. 储存D. 加工答案：ABCD5. 粮食作物的种植方式有：A. 直播B. 移栽C. 育苗D. 杂交答案：ABC三、判断题（每题2分，共10分）1. 粮食作物的种植密度越大，产量越高。

（错误）2. 粮食作物的种植需要充足的阳光和水分。

（正确）3. 粮食作物的种植不需要考虑土壤的酸碱度。

（错误）4. 粮食作物的种植过程中，病虫害的防治非常重要。

（正确）5. 粮食作物的种植只依赖于自然条件，不需要人为干预。

（错误）四、简答题（每题5分，共20分）1. 请简述粮食作物种植的主要步骤。

答案：粮食作物种植的主要步骤包括选种、整地、播种、田间管理、病虫害防治、收获和后处理等。

2. 粮食作物种植中，如何提高产量？答案：提高粮食作物产量的方法包括选用优良品种、合理密植、科学施肥、病虫害防治、适时灌溉和收获等。

3. 粮食作物的储存需要注意哪些因素？答案：粮食作物储存时需要注意温度、湿度、通风、防虫和防霉等因素，以保证粮食的质量和安全。

影响我国粮食产量因素的计量经济学分析作者：颜慧贤夏佳蕊朱立峰来源：《商情》2015年第37期【摘要】“国以民为本，民以食为天，食以粮为重”，因而粮食生产问题是关系国计民生的重要问题。

我国作为人口最多的国家对农业的依赖程度更高，粮食产量对国家稳定、国民经济发展的意义也更为重要。

本文从影响粮食产量的因素出发，以国家统计年鉴中1997-2011共15年的数据为依据，运用Eviews3.0统计软件，综合运用计量经济学、经济学、统计学的方法对粮食产量的影响因素建立回归模型，最终得出粮食播种面积、化肥施用量、成灾面积这三个因素是影响粮食产量的主要因素的结论。

最后对如何增加粮食产量提供一些参考性建议。

【关键词】粮食产量，影响因素，回归分析一、模型的建立（一）理论分析。

我国是一个人口大国同时又是一个农业相对落后的国家而粮食又是人类赖以生存的基础，所以提高粮食生产能力是我国不容忽视的重大问题。

粮食产量的影响因素众多，其中投入产出、自然环境因素最为显著，根据实际情况选取可能的影响因素因素探讨粮食生产的投入产出关系最终将这种关系用数学表达式表示出来，最后通过确定的函数模型对粮食生产提出可行性建议。

（二）模型设定1.确定模型所包含的变量。

为了对影响粮食总产量的因素进行深入分析，在众多影响粮食总产量的因素中以粮食总产量为被解释变量Y；粮食总播种面积、农业机械总动力、有效灌溉面积、化肥施用量、受灾面积、成灾面积为解释变量X.2.样本数据的搜集与整理。

通过查阅2011年统计年鉴，搜集整理了1997年到2011年的粮食总产量以及6个可能影响因素的数据。

见下表：表1是设定模型所用的时间序列数据。

其中，粮食总产量为因变量Y；粮食总播种面积为X1、农业机械总动力为X2、有效灌溉面积为X3、化肥施用量为X4、受灾面积为X5、成灾面积为X6。

二、模型参数的估计模型为：Y=β0+β1X1+β2X2+β3X3+β4X4+β5X5+β6X6+μ μ为随机扰动项利用计量经济学的基本方法--最小二乘法（OLS）对所摘样本数据进行模型的从参数估计，结果如下：（图中各变量名称均为首字母）Y=-79529.88+0.478599X1-0.521481X2+0.775946X3+15.70729X4-0.092737X5-0.011504X6为初步所得模型。

学校代码专业代码计量经济学实验报告报告题目：我国影响粮食产量的可量化因素实证分析姓名：学号：班级：专业：学院：指导教师：完成时间：我国影响粮食产量的可量化因素实证分析摘要：粮食是人类生存之本，经济发展之基。

本文采用回归分析的方法对1985年-2014年影响我国粮食产量变化的主要可量化因素进行分析，建立了以粮食产量为因变量，以粮食作物播种面积、农用化肥施用量、有效灌溉面积、农业机械总动力、受灾面积、农产品生产价格指数六项因素为自变量的多元线性回归模型，并检验模型的正确性做出相关修正。

在此基础上对提高粮食产量，促进农业发展提出可供参考的建议。

关键词：粮食产量 可量化因素 回归分析一、引言粮食安全、能源安全和金融安全并称为世界经济三大安全。

而作为拥有十四亿人口的人口大国，粮食问题也一直是政府和社会各界所关心的战略问题。

粮食作为人类生存最基本的消费品，而一个国家的粮食问题关系到本国国民经济的运行。

在研究粮食问题时，本国的粮食生产安全是至关重要的。

建国以来，我国粮食产量多次波动，一方面制约了宏观经济的发展，另一方面给粮食生产者和消费者的生活带来极大的不利影响。

通过查看近30年的数据可以发现，我国粮食产量在总趋势上呈上升趋势。

而本文则希望通过分析六项可量化因素，研究各项因素对粮食产量增加的影响程度，并对进一步提高我国粮食产量做出建议。

二、理论模型构建为了研究我国粮食年总产量，选择“粮食产量”作为被解释变量。

根据对影响我国粮食产量的主要因素粮食作物播种面积、农用化肥施用量、有效灌溉面积、农业机械总动力、受灾面积、农产品生产价格指数6项可量化因素作为解释变量。

由此，建立计量经济模型如下：i i X X X X X X C Y μββββββ+++++++=655443322110三、描述性分析（一）总量分析为了得出影响我国粮食产量的因素，我从粮食作物播种面积、农用化肥施用量、有效灌溉面积、农业机械总动力、受灾面积、农产品生产价格指数等方面进行考虑。

三是优化农业基础设施，完善水利灌溉，推广节 水灌溉技术，提高防洪能力。
四是促进农业生产机械化，提高农业生产效率。
参考文献：
[1]焦宇航.影响我国粮食产量因素的计量分析[J].魅力中国,2014(4):303.
DOI：10.16675/14- 1065/f.2019.04.013
/ 理论探索 /
· 31 ·
基于计量经济学分析我国粮食产量的影响因素
□ 刘嘉欢，高 明
（河北农业大学 河北 沧州 061100）
摘 要：粮食问题关系民生，是各国普遍关注的问题。中国人口基数大、增长速度快，保障粮食安全对促进社会和谐
最小二乘估计结果显示，可决系数调整后的 R2=0.979 235，表明粮食产量变化的 97.92％可以由
选取的 6 个因素共同变化来解释，模型拟合程度较 好。5％的显著性水平下，F=236.784 5＞2.51，通过 F 检验，方程整体显著程度好。
但是从斜率项 t 检验值来看，X3、X5、X6 的 t 检验 值小于临界值，3 个因素对被解释变量影响不显著。
操作 Eviews6.0 软件制作各解释变量间的相关系 数表，初步判断出 X1 和 X5、X3 和 X6 之间存在较大相 关性，判断模型存在多重共线性。通过逐步回归进一 步检验与修正，逐步回归中，剔除了解释变量 X5、X6， 解决了多重共线性问题，修正后回归结果为： Y 0.060 206X2+
0.080 092X3+0.835 401X4 t=(0.256 543) (17.922 93) (- 3.601 084)
(2.246 206) (2.055 802) R2=0.983 234 AdjustedR2=0.980 654 F=381.183 9 3. 2. 3 计量经济学检验

基于计量经济模型河北省粮食产量影响因素分析杨雨芳，赵慧峰（河北农业大学 经济贸易学院，河北 保定 071000）[摘要]农业是国民经济的基础产业，粮食是人类赖以生存和发展的必需品，保证粮食安全是一个永恒课题。

选取河北省2001～2016年16年的数据，运用线性回归方法建立了影响粮食产量的计量经济模型，并借助E-views8.0软件对模型进行OLS等分析检验。

结果表明，影响河北省粮食产量因素的二大因素是化肥施用量和粮食作物播种面积，其中影响最大的是化肥施用量。

最后，提出增加粮食产量必须合理施用化肥，保持粮食作物播种面积，增加资本和技术投入，加大对各种自然灾害防御的对策建议。

[关键词]河北省粮食产量；化肥施用量；粮食作物播种面积；回归分析 影响因素[中图分类号]F224；F326.11 [文献标识码]A1　引言近年来，河北省粮食产量不断增加，但影响粮食产量的因素如自然灾害、环境波动、人地矛盾等，依旧不可忽视。

为确保粮食安全，国家实施了一系列保护农业的政策，河北省也应利用国家政策，大力发展农业经济。

影响粮食产量的因素很多，为有效促进粮食增产，必须分析众多因素中，影响较大的几个因素，并针对河北省农业发展现状，提出对策建议。

本文依据河北省粮食产量的现状，确定出影响粮食产量的5大因素，运用E-views8.0软件处理相关数据得出结论，并通过分析结论，提出促进河北省粮食增产的可行性建议。

2变量的选取影响河北省粮食产量的因素很多，通过资料查询和文献参考，得出影响粮食产量的因素有：粮食播种面积、受灾面积、有效灌溉面积、化肥施用量、农业劳动力。

本文运用2001～2016年的数据来说明这些因素对粮食产量的影响。

各变量描述性如表1所示。

[收稿日期]2018-10-25[作者简介]杨雨芳（1990—），女，河北邯郸人，河北农业大学硕士研究生。

[通讯作者]赵慧峰（1964—），女，河北保定人，教授，博士生导师，研究方向；农业经济理论与政策和农村金融。

2012学年第一学期科目金融计量经济学导论任课教师班级组员中国粮食生产与相关投入的分析【摘要】“民以食为天”。

粮食是宝中之宝，世界上任何国家都注重粮食生产，我们中国也不例外，以7%的土地养活了世界22%的人口，取得举世瞩目的成果。

粮食是人类最基本的生活消费品，一个国家的粮食问题是关系到本国的国计民生的头等大事。

人们都知道，农业是国民经济发展的基础，粮食是基础的基础，因此粮食生产是关系到一个国家生产与发展的一个永恒的主题。

建国以来我国的粮食产量出现了多次的波动，给消费者和生产者带来了很不利的影响，所以了解影响粮食生产因素很重要。

本文根据粮食产量的历史和现状，从计量经济的角度分析影响我国粮食产量的因素。

运用线性回归方法建立了影响粮食产量的计量经济模型,并对模型进行分析和评价。

结果我们会发现粮食播种面积、农化肥施用量、成灾面积是影响粮食生产的三大因素，其中农化肥施用量的影响最大。

【关键词】粮食产量、播种面积、化肥施用量、成灾面积、农业机械总动力、农业劳动力一、摘要简介研究主题：以过国内数据为例，研究影响我国粮食生产的因素，初步考虑相关因素可能有：粮食产量（Y）、农化肥施用量（x1）、粮食播种面积（x2）、成灾面积（x3）、农业机械总动力（x4）、农业劳动力（x5）数据类型：年统计数数据频度：年起止时间：1983-2010年样本大小：28主要研究方法：线性回归小组成员：二、模型的提出影响粮食生产的因素很多，有劳动力、物质投入、土地、生产方式、技术进步、生产结构、制度因素、气候变化和自然灾害等等因素都影响着粮食产量。

为了基本涵盖这些基本因素，本文选择了以农业化肥施用量、粮食播种面积、成灾面积、农业机械总动力等为解释变量，以粮食产量为被解释变量。

对于这些影响因素，我找到了1983到2010年的关于这些因素的数据，借此来分析中国粮食产量的影响因素和它们是如何来影响粮食产量的，以下是对所找的数据做的一些说明：1、粮食产量。

粮食产量影响因素的计量分析本文作者(任蕊黄裕吉婕),请您在阅读本文时尊重作者版权。

摘要粮食生产是关系国计民生的战略物资。

本文以改革开放以来的相关数据为依托,对影响我国粮食生产的主要因素进行了相关分析和回归分析,并得出结论。

揭示了粮食产量变化的原因,并对如何提高我国粮食生产提出了建议。

关键词粮食产量影响因素计量分析一、问题的提出我国是一个农业大国,人口众多,粮食问题是一个关系国计民生的重要问题,粮食产量的高低将直接影响国民经济其它部门的发展水平,关系国家的长治久安。

因此,研究影响粮食产量的主要因素,有利于揭示粮食增产的规律,对指导粮食增产有重要的意义。

1978年以来我国的粮食产量多次出现了波动,这不仅制约了国民经济的发展, 而且给粮食生产者和消费者都带来了极为不利的影响。

所以分析和认识近几十年来的中国粮食产量的影响因素至关重要,我们认识从图中可以认识到我国粮食产量从总趋势来看是增长的,然而对总趋势作进一步分析,发现1978 年至今, 粮食产量的总趋势是增长的, 但这增长是在波动中的增长, 这其中的原因可以从粮食产量的影响因素中得到说明,本文将就影响粮食产量的具体因素作计量分析。

二、模型设定影响粮食生产的因素很多, 有劳动力、物质投入、土地、生产方式、产业结构, 技术进步、制度因素等。

为了基本涵盖这些因素, 在影响粮产量的因素中我选取了农业机械总动力、有效灌溉面积、化肥施用量、粮食播种面积、成灾面积5个因素作为研究粮食产量的模型中的解释变量,以粮食产量作为被解释变量, 模型使用时间序列数据(1978—2008 年), 资料来源于中国统计年鉴。

综上, 我们建立模型如下:三、模型的估计与调整(一)做最小二乘估计。

利用eviews软件对被释变量Y与各个解释变量做多元回归分析,该模型样本回归估计式:T =(-2.889)(1.0498)(1.505)(-15.761)(6.881)(-3.573)R2 = 0.970608F = 165.1161DW = 0.950479统计推断检验:可决系数R2=0.9706接近1,认为该模型的拟合程度可以接受;且F=165.1161>F0.05(5,26),故认为粮食生产与上述解释变量间总体线性关系显著。

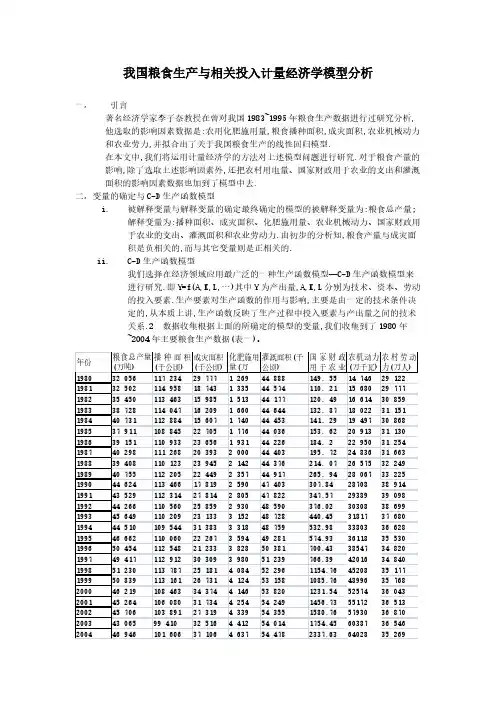
我国粮食生产与相关投入计量经济学模型分析一，引言著名经济学家李子奈教授在曾对我国1983~1995年粮食生产数据进行过研究分析,他选取的影响因素数据是:农用化肥施用量,粮食播种面积,成灾面积,农业机械动力和农业劳力,并拟合出了关于我国粮食生产的线性回归模型.在本文中,我们将运用计量经济学的方法对上述模型问题进行研究.对于粮食产量的影响,除了选取上述影响因素外,还把农村用电量、国家财政用于农业的支出和灌溉面积的影响因素数据也加到了模型中去.二，变量的确定与C-D生产函数模型i.被解释变量与解释变量的确定最终确定的模型的被解释变量为:粮食总产量;解释变量为:播种面积、成灾面积、化肥施用量、农业机械动力、国家财政用于农业的支出、灌溉面积和农业劳动力.由初步的分析知,粮食产量与成灾面积是负相关的,而与其它变量则是正相关的.ii.C-D生产函数模型我们选择在经济领域应用最广泛的一种生产函数模型—C-D生产函数模型来进行研究.即Y=f(A,K,L,…)其中Y为产出量,A,K,L分别为技术、资本、劳动的投入要素.生产要素对生产函数的作用与影响,主要是由一定的技术条件决定的,从本质上讲,生产函数反映了生产过程中投入要素与产出量之间的技术关系.2　数据收集根据上面的所确定的模型的变量,我们收集到了1980年~2004年主要粮食生产数据(表一)。

iii.模型的估计设定:粮食总产量为Y播种面积为X1成灾面积为X2,化肥施用量为X3,灌溉面积为X4,国家财政用于农业资金为X5,农机动力为X6,农村劳动力为X7.由C-D生产函数模型,得模型形式如下:Y t=AX it biεt(i=1,2,…,7)(1)两边取对数并进行变换,得:log Y t =b0+b i logX it+μt　(i=1,2,…,7)(2)其中b0=logA,μt=logεt.运用Eviews软件对模型(2)进行OLS估计,我们得到估计结果Dependent Variable: LOG(Y)Method: Least SquaresDate: 06/10/09 Time: 03:55Sample: 1980 2004Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C 3.375895 5.5021110.6135640.5476LOG(X1)0.9587450.279512 3.4300650.0032LOG(X2)-0.1037040.040353-2.5699500.0199LOG(X3)0.4948670.104450 4.7378190.0002LOG(X4)-0.5649730.462026-1.2228180.2381LOG(X5)-0.0143810.074375-0.1933540.8490LOG(X6)0.0183880.1192590.1541820.8793LOG(X7)-0.0694990.137533-0.5053240.6198 R-squared0.963763Mean dependent10.66170varAdjusted R-squared0.948842S.D. dependent var0.127561S.E. of regression0.028852Akaike info criterion-3.998937Sum squared resid0.014151Schwarz criterion-3.608897Log likelihood57.98671F-statistic64.59068Durbin-Watson stat 1.245744Prob(F-statistic)0.000000从表2可以看出,回归估计的判决系数R2很高,方程很显著,但是8个参数的t检验值中，却只有两个略微显著.显然,出现了严重的多重共线性。

对我国粮食产量影响因素的计量分析摘要：本文主要对我国粮食产量的变动进行多因素分析，选取1988年—2007年20年的数据，建立以粮食产量为被解释变量，以农业化肥施用量、粮食播种面积、成灾面积、农业机械总动力和第一产业从业人口为解释变量的多元线性回归模型，利用模型对粮食产量情况进行多元线性回归分析，建立粮食生产函数。

最后，就有关如何根据实际情况促进农业发展，确保我国粮食增产、增收提出一点建议。

关键词：粮食产量；多元线性回归分析；粮食生产函数；农业发展1.引言粮食问题是我国面临的大问题,不光是国人，很多外国人也关注这个问题。

1994年美国学者布朗发表《谁来养活中国》一文,震动了中国和世界。

我国是世界上人口最多的国家，但人均耕地面积远远少于世界平均水平，如何在有限的土地上养活这么多的人口，解决粮食问题无疑是重中之重。

从历史数据来看，我国粮食总产量在1998年达到高峰，为5.12亿吨,此后，粮食生产呈现持续下滑的局面, 一直持续到2003年。

2003年以后，中央加大了对“三农”的关注力度，每年出台的中央1号文件都是针对解决“三农”问题的。

由于中央对农业生产的高度重视，以及连续出台的多项惠农政策，极大地调动了农民的生产积极性。

从2004 年开始，粮食生产止住了连续年的下滑, 粮食总产量达4.69亿吨, 比2003年增加了0.38亿吨，增产8.8%,实现了1998年以来的首次增产。

2005年在2004年的基础之上又达新高,总产量达到了48402万吨。

2006年更是达到了49804万吨 ,实现了连续三年的大丰收。

2007年我国的粮食产量再创新高 ,突破5亿吨大关，但我国粮食生产仍存在着许多问题。

2.样本数据与变量的选取根据理论和经验分析，影响粮食生产的主要因素有农业化肥施用量、粮食播种面积、成灾面积、农业机械总动力和农业劳动力，其中，成灾面积的符号为负，其余均应为正。

为此，本文收集了我国自1988年至2007年，粮食产量、农业化肥施用量、粮食播种面积、成灾面积、农业机械总动力和第一产业从业人口的相关数据。

粮食单产影响因素的计量分析发布日期：2005/9/29 来源：[网友投稿] 浏览：[1505] 评论：[0] 字体：大中小粮食单产影响因素的计量分析谢彦明[1]高淑桃（四川农业大学经济管理学院，四川雅安，625014）摘要：我国粮食产量主要取决于粮食单产水平而非粮食播种面积。

本文应用多元线性回归分析了包括化肥投入、灌溉、耕地成灾面积、机械动力在内的影响我国粮食单产水平四个因素，应用势分析的方法刻画了上述因素的时间序列趋势图。

在此基础上，探讨了不同阶段不同因素对粮食单产水平增长的贡献，并提出了相应的对策建议。

关键词：粮食安全粮食单产综合生产能力势效系数一、提高粮食单产水平的必要性粮食安全是指一个国家满足粮食需求以及抵御可能出现的各种不测事件的能力，其决定性因素是粮食生产及消费的能力和水平，同时和国家经济发展水平及外贸状况有着密切的联系。

它关系到一国的国计民生，面对我国粮食产量的持续下滑，2004年和2005年中央连续出台了两个一号文件，明确提出提高我国农业综合生产能力，确保粮食安全的问题。

粮食产量是粮食安全问题的一个重要方面，可以说粮食产量是确保粮食安全的根基，而粮食单产水平又直接关系到粮食的总产量水平。

我国粮食总产量历年波动幅度与粮食单产历年波动幅度的时间序列呈现出高度的相关性，每一周期年限以及波峰、波谷完全对应，相关系数在0.01的显著水平下达0.908，可见我国的粮食总产量高低主图一：我国粮食总产量与单产水平波动时间序列趋势图注：粮食单产与粮食总产量波动幅度计算公式：粮食单产波动幅度=本年粮食单产/上年粮食单产100-100（单位:公斤/公顷）；粮食总产量波动幅度=本年粮食总产量/上年粮食总产量100-100（单位:万吨）要是由粮食单产水平决定的。

经济发展要求释放出一定数量的耕地用于建设、退耕还林等用地，通过大幅增加粮食的耕种面积来增加粮食产量已经不再现实，1998年至2002年间，我国耕地面积减少6390.37万亩，年均减少1278.07万亩，而减少的耕地主要用于粮食生产，粮食播种面积由1979年119263千公顷下降到2004年的106350千公顷。

影响全国农业生产总值因素分析一、问题的提出农业发展显然是关系民生的大问题，国家也很着力于此。

大力发展现代农业。

现代农业是与传统农业相对应的农业形态，是以广泛应用现代科学技术、普遍使用现代生产工具、全面实行现代经营管理为本质特征和主要标志的发达农业。

发展现代农业总的要求是：加快农业科技进步，加强农业设施建设，调整农业生产结构，转变农业增长方式，提高农业综合生产能力。

只有大力增强农业科技创新和转化能力，尽快取得一批具有自主知识产权的重大农业科技成果，加强农业技术推广和服务，深入实施农业科技入户工程，积极推进重要农时、重点作物、关键环节和粮食主产区的机械化作业，才能突破农业发展面临的资源瓶颈制约，提高农业的综合素质和整体效益。

只有切实加强农田水利基本建设，改造中低产田，加快兽医管理体制改革和动物疫病防控体系建设，推进农产品加工、储运、流通设施建设，才能提高农业抗御自然灾害的能力和转化增值的能力。

只有加大优势农产品区域布局规划的实施力度，不断优化农产品结构和提高农产品质量安全水平，大力发展畜牧和水产养殖业，积极发展农村二、三产业特别是农产品加工业，加快推进农村劳动力有序转移，才能适应人民生活水平提高对农产品多样化和优质化的需求，不断拓宽农民增收渠道。

农业自古以来就是我国的支柱产业，是我国国民经济的基础。

我国的经济结构能否顺利调整，国民经济能否发展得更快一些、更好一些，在很大程度上取决于农业基础是否稳固。

只有加强农业基础，确保农产品供给，才能顺利推进工业化和城镇化；只有加强农业基础，依靠科技进步，开拓农村市场，才能支撑国民经济的快速增长；只有加强农业基础建设，使农业发展、农民富裕、农村稳定，才能保持整个社会的长期稳定与可持续发展。

但我国又是一个生产力比较落后的国家，只有研究农业产值主要受哪些因素影响，才能有对策的投入，将基础产业发展上去。

选此模型的目的就在于分析决定农业产值的主要影响因素，以及各营下各因素的影响程度，从而对生产提出建设性意见。

我国粮食产量的影响因素分析摘要：本文针对我国是一个农业大国的基本国情，选取我国1978-2011年的相关数据，对我国粮食产量的影响因素的分析、检验，并对各因素的影响程度的大小进行比较，最终建立合适的回归模型，对其做统计和经济意义上的分析，并根据结果提出建议。

关键词：农业粮食产量有效灌溉面积受灾面积一、问题的提出我国是传统意义上的农业大国，农业生产一直在我国经济发展中占据着重要的地位。

建国后，在经历人民公社运动、大跃进以及文革的浩劫后，农业发展严重滞后，无法满足人民的需要。

1978年改革开放也首先在农村地区开展，实行家庭生产承包责任制，农业有了快速的发展。

随着科技的不断进步，粮食产量也不断上升。

可是农村人口和耕地面积的不断减少也制约着粮食产量的进一步增加。

到底是哪些因素制约着粮食产量呢？针对这个问题，本文选取了我国1978年到2011年的相关数据，通过建立回归模型，对各种影响因素进行分析。

并且在通过分析知道影响粮食产量的因素后，提出了提高粮食产量的有效途径。

二、数据收集本文选取了1978年至2011年的34组数据，从数据个数来看完全满足多元回归模型的设定需要。

选取1978年以后的数据主要是因为1978年之前，由于人民公社化运动期间农业数据的浮夸形象，以及文革期间农业生产的停滞等非正常社会现象会影响模型的分析，故从1978年我国改革开放之后开始选取数据。

1978年-2011年我国粮食生产与相关投入的数据表年份粮食产量(万吨) 农业机械总动力(万千瓦)有效灌溉面积(千公顷)农用化肥施用折纯量(万吨)粮食作物播种面积(千公顷)受灾面积(千公顷)Y X1 X2 X3 X4 X5 1978 30476.50 11749.90 44965.00 884.00 120587.20 50807 1979 33211.50 13379.50 45003.13 1086.30 119262.70 39367 1980 32055.50 14745.75 44888.07 1269.40 117234.27 50025 1981 32502.00 15680.10 44573.80 1334.90 114957.67 39786 1982 35450.00 16614.21 44176.87 1513.40 113462.40 33133 1983 38727.50 18021.90 44644.07 1659.80 114047.20 347131984 40730.50 19497.22 44453.00 1739.80 112883.93 31887 1985 37910.80 20912.55 44035.93 1775.80 108845.13 44365 1986 39151.20 22950.00 44225.80 1930.60 110932.60 471351987 40297.70 24836.0044403.00 1999.30 111267.77420861988 39408.10 26575.00 44375.91 2141.50 110122.60 50874 1989 40754.90 28067.00 44917.20 2357.10 112204.67 46991 1990 44624.30 28707.70 47403.07 2590.30 113465.87 38474 1991 43529.30 29388.60 47822.07 2805.10 112313.60 55472 1992 44265.80 30308.40 48590.10 2930.20 110559.70 51332 1993 45648.80 31816.60 48727.90 3151.80 110508.70 48827 1994 44510.10 33802.50 48759.10 3317.90 109543.70 55046 1995 46661.80 36118.05 49281.60 3593.70 110060.40 45824 1996 50453.50 38546.90 50381.60 3827.90 112547.92 46991 1997 49417.10 42015.60 51238.50 3980.70 112912.10 53427 1998 51229.53 45207.71 52295.60 4083.69 113787.40 50145 1999 50838.58 48996.12 53158.41 4124.32 113160.98 49980 2000 46217.52 52573.61 53820.33 4146.41 108462.54 54688 2001 45263.67 55172.10 54249.39 4253.76 106080.03 52215 2002 45705.75 57929.85 54354.85 4339.39 103890.83 46946 2003 43069.53 60386.54 54014.23 4411.56 99410.37 54506 2004 46946.95 64027.91 54478.42 4636.58 101606.03 37106 2005 48402.19 68397.85 55029.34 4766.22 104278.38 38818 2006 49804.23 72522.12 55750.50 4927.69 104957.70 41091 2007 50160.28 76589.56 56518.34 5107.83 105638.36 48992 2008 52870.92 82190.41 58471.68 5239.02 106792.65 39990 2009 53082.08 87496.10 59261.45 5404.35 108985.75 47214 2010 54647.71 92780.48 60347.70 5561.68 109876.09 37426 2011 57120.85 97734.66 61681.56 5704.24 110573.02 32471三、模型设定1、分别做被解释变量（Y）与解释变量（X1、X2、X3、X4、X5）的散点图，结果如下:由散点图可知，解释变量与别解释变量间的线性关系并不明确，故对原方程两边同时取对数，建立新的回归方程3、为了方便计算，对变量进行重新定义，在eviews对话框中输入genr y=log(y)genr x1=log(x1)genr x2=log(x2)genr x3=log(x3)genr x4=log(x4)genr x5=log(x5)建立新的回归模型，结果如下图由上图可知新的多元回归模型为54321128441.0461565.1401626.0603457.0078124.0408078.2X X X X X Y -++-+-=四、模型的检验与调整（一）经济意义检验由经济分析可知，粮食产量（Y ）与农业机械总动力（X1）、有效灌溉面积（X2）、农用化肥施用折纯量（X3）、粮食作物播种面积（X4）应成正相关关系，与受灾面积（X5）应成负相关关系。

计量经济学(论文) 题目:专业: 统计学姓名:学号:指导教师:数学与统计学院2011年11月17日重庆粮食产量研究[摘要] 本文根据《中国农业信息网》的相关统计数据在建立计量经济学模型的基础上，分析探讨了重庆粮食总产量的影响因素，进行了统计分析和经济意义分析，并提出了一些政策建议。

[关键词] 因素分析参数检验粮食总产量引言粮食是人类生存最基本的生活消费品，一个国家的粮食问题是关系到本国的国计民生的头等大事。

我们知道，农业是国民经济发展的基础，粮食是基础的基础，因此粮食生产是关系到一个国家生存与发展的一个永恒的主题。

建国以来我国的粮食产量多次出现了波动，这不仅制约了国民经济的发展，而且给粮食生产者和消费者都带来了极为不利的影响。

分析近几十年来的重庆粮食产量并从中发现一些规律，有助于我们认识重庆粮食产量的现状。

重庆粮食产业现状：从改革开放到重庆直辖，重庆粮食无论是从总产量的增长速度来考察，还是以单位面积产量的增长速度来分析，都取得了长足的发展。

重庆粮食通过1978-1997年的快速发展，在粮食播种面积由4766万亩下降到4323万亩的情况下,粮食总产由1978年的814.7万吨,增加到1997年的1185万吨，人均粮食占有量达到389公斤，在人均耕地不足全国的2/3的情况下，人均粮食占有量接近全国平均水平，不仅彻底扭转了长期口粮缺乏的局面，总体上还表现出自给有余。

到1997年，本地消费已呈现相对饱和状态，粮食市场还出现了一定程度的“卖难”，粮食生产的首要目的，维持基本生存，满足消费需求的历史使命已基本完成。

此时粮食生产的品质构成难以适应消费需求的矛盾开始显现，于是对主要粮食产品生产进行结构调整成了当务之急。

通过近些年来各级政府和农业部门在粮油结构调整方面的艰苦努力，主动调减粮食特别是低质低效粮食播种面积，保持粮食总产量相对稳定，粮食的品种结构和品质结构发生了很大变化。

粮食为全市农业产业结构的调整也提供了有力的支撑。

昆明学院2015届数理统计论文设计（论文）题目楚雄农业产值的影响因素分析姓名 xxxxx学号 xxxxxxxxx所属系数学系专业年级数学与应用数学2011级数学<3>班指导教师 xxxxxx截止日期：2013年12月摘要本文是根据楚雄州农业的现状，想从计量经济学的角度来验证一下是否存在政府对农业投入不足、以及农村中存在大量的剩余劳动力。

根据经济学原理，在模型中引入了三个变量：政府财政对农业的投入、农民自己的投入以及农业的从业人员。

从而用经济学中柯布-道格拉斯生产理论初步确定函数+α+=，再用数理统计Eviews软件分析了历年来政府财政LgYβLgLLgKLgA对农业的投入、农民自己的投入以及农业的从业人员做相关分析，从所做的散点图可知它们之间有线性相关性，接着做了线性方程的拟定做了序列的相关性检验。

从所做的回归结果看，楚雄州农村中确实存在正文6.2处问题，根据模型的回归结果得到了一些结论，同时也给出了政策建议。

关键词：农业产出投资居民的投入农业从业人员人数AbstractThis paper is the present situation of the current conditions are based on agriculture, from the perspective of econometrics to investigate whether there was a government agricultural input is insufficient, and there are a large number of rural surplus labor force. According to the principle of economics, the introduction of the three variables in the model: government financial support to agriculture, farmers and the agricultural own investment professionals. To use economics in the theory of cobb-douglas production function, identified as to use Eviews software analysis of mathematical statistics over the years the government fiscal spending on agriculture, farmers and the agricultural own investment professionals to do correlation analysis, from the scatter image, has a linear correlation between them, and then do a linear equation to formulate a series of correlation test. From the regression results ?keywords: The number of agricultural workers into agricultural production investment residents目录第一章、研究目的和意义 (4)2.1理论依据 (5)2.2、给定变量 (5)第三章、模型设定 (6)3.1、根据经济学理论模型设定 (6)3.2、模型拟定 (6)第四章、参数估计 (8)将原始模型简化为： (8)第五章、检验及修正 (9)5.1．经济意义检验 (9)5.2．统计推断检验 (9)5.3．计量经济学检验 (9)5.3.1多重共线性检验 (9)5.3.2修正：采用逐步回归法对其进行补救。

《计量经济学》课程论文我国粮食总产量影响因素分析姓名：吴双专业：国际经济与贸易（双语）学号：40502051指导教师：周游日期：2007年12月Ⅰ．问题的提出目前，我国70%人口为农村人口，农业生产的发展直接关系广大农民生活的提高，直接关系到国家经济建设目标的实现．本文将对影响我国粮食产量的诸多因素（包括农业机械总动力、化肥施用量、土地灌溉面积、单位面积劳动力投入量）进行分析，并从中分离出主要影响因素．Ⅱ．模型的设定将“我国粮食总产量”设为因变量，“农业机械总动力”“化肥施用量”“土地灌溉面积”“单位面积劳动力投入量”设为自变量，设定了以下计量经济学模型：其中Y=农业总产值(亿元)X1＝农业机械总动力（万吨） X2＝化肥施用量（万吨） X3＝土地灌溉面积（千公顷）X4＝单位面积劳动力投入量（人/公顷）Ⅲ．参数估计iX X X X C Y μββββ+++++=44332211根据1980年到2003年数据进行OLS回归估计，结果如下：表１OLS回归估计结果Dependent Variable: YMethod: Least SquaresDate: 12/17/07 Time: 16:01Sample: 1980 2003Included observations: 24Variable Coefficient Std. Error t-Statistic Prob.X1 -0.160331 0.091224 -1.757556 0.0949X2 8.851661 1.618620 5.468648 0.0000X3 -0.684407 0.510325 -1.341120 0.1957X4 12503.62 6791.248 1.841138 0.0813C 28655.33 28599.93 1.001937 0.3290R-squared 0.879097 Mean dependent var 42846.86 Adjusted R-squared 0.853644 S.D. dependent var 5316.370 S.E. of regression 2033.858 Akaike info criterion 18.25631 Sum squared resid 78595000 Schwarz criterion 18.50174 Log likelihood -214.0757 F-statistic 34.53773 Durbin-Watson stat 1.374316 Prob(F-statistic) 0.000000Y = 28655.33－0.160331X1+ 8.851661X2－0.684407X3+ 12503.62X4se(28599.93) (0.091224) (1.618620) (0.510325) (6791.248) t (1.001937) (-1.757556) (5.468648) (-1.341120) (1.841138)2R=0.879097 F = 34.53773Ⅳ．模型的检验及修正１．多重共线性由OLS 回归结果（表一）可看见，该模型2R =0.879097，2R =0.853644可决系数较高．但是当ａ= 0.05时，086.2)20()424()(025.0025.02==-=-∂t t k n t ，不仅X1、X3、X4系数的t 检验不显著，而且X1、X3系数的符号与预期的相反，这表明很可能存在严重的多重共线性． 计算各解释变量的相关系数，如下：多重共线性．利用逐步回归修正的方法解决多重共线性问题．分别做Ｙ对X1、X2、X3、X4的一元回归，结果如下：其中加入X2的方程2R 最大，以X2为基础，顺次加入其他变量逐步回归，结果如表４所示：新加入X3后虽然2R 略有改进，但X3参数为负数不合理，应予剔除．所以结果中应选择保留X2、X4，再加入其他变量逐步回归．新加入X3后虽然2R 略有改进，但X1参数为负数不合理，应予剔除．X3情况与X1相同，所以应予剔除．最后修正多重共线性影响的回归结果为：表６ 修正多重共线性影响的OLS 回归结果Dependent Variable: Y Method: Least Squares Date: 12/17/07 Time: 21:18 Sample: 1980 2003 Included observations: 24Variable Coefficient Std. Error t-Statistic Prob. X2 4.556762 0.459774 9.910879 0.0000 X4 19955.83 7065.872 2.824256 0.0102 C-13221.1015571.88-0.8490370.4054R-squared 0.824198 Mean dependent var 42846.86 Adjusted R-squared 0.807455 S.D. dependent var 5316.370 S.E. of regression 2332.818 Akaike info criterion 18.46401 Sum squared resid 1.14E+08 Schwarz criterion 18.61127 Log likelihood -218.5681 F-statistic 49.22643 Durbin-Watson stat 0.740395 Prob(F-statistic)0.000000(15571.88) (0.459774) (7065.872)t (-0.849037) (9.910879) (2.824256)2R =0.824198 2R = 0.807455 F = 49.22643２． 异方差利用Eviews 软件生成残差平方序列22)(resid e i =，绘制e i 2对X2和X4的散点如下：4283.199********.41.13221XX Y ++-=由上图可以看出，模型很可能存在异方差，但是是否确实存在还应通过更进一步的检验，下面将通过White检验法检验模型是否存在异方差．利用Eviews软件对模型进行White检验，结果如下表：Test Equation:Dependent Variable: RESID^2 Method: Least Squares Date: 12/17/07 Time: 16:19 Sample: 1980 2003 Included observations: 24Variable Coefficient Std. Error t-Statistic Prob. C 1.03E+09 1.02E+09 1.008926 0.3264 X2 84679.11 58380.25 1.450475 0.1641 X2^2 -0.453075 2.700281 -0.167788 0.8686 X2*X4 -37895.63 23260.25 -1.629201 0.1206 X4 -1.02E+09 9.60E+08 -1.062682 0.3020 X4^22.52E+082.25E+081.1179000.2783R-squared 0.530659 Mean dependent var 4761785. Adjusted R-squared 0.400286 S.D. dependent var 5800114. S.E. of regression 4491677. Akaike info criterion 33.68567 Sum squared resid 3.63E+14 Schwarz criterion 33.98018 Log likelihood -398.2280 F-statistic 4.070329 Durbin-Watson stat 2.210344 Prob(F-statistic)0.011990从表７中可以看出73581.122=nR ，在05.0=α下查2χ分布表得临界值0705.11)5(205.0=χ．73581.122=nR ＞0705.11)5(205.0=χ，所以模型存在异方差．利用加权最小二乘法修正异方差，选取权数21e w =，其中22)(resid e =．修正结果如下：表８ 最小二乘法修正异方差结果Dependent Variable: Y Method: Least Squares Date: 12/17/07 Time: 21:51 Sample: 1980 2003 Included observations: 24 Weighting series: W1Variable Coefficient Std. Error t-Statistic Prob. X2 4.651806 0.144925 32.09800 0.0000 X4 14592.19 2372.459 6.150660 0.0000 C -1774.1535157.215 -0.3440140.7343Weighted StatisticsR-squared 0.999833 Mean dependent var 42310.64 Adjusted R-squared 0.999818 S.D. dependent var 65888.75 S.E. of regression 889.9166 Akaike info criterion 16.53660 Sum squared resid 16630983 Schwarz criterion 16.68386 Log likelihood -195.4392 F-statistic 590.2806 Durbin-Watson stat1.749898 Prob(F-statistic) 0.000000Unweighted StatisticsR-squared 0.816751 Mean dependent var 42846.86 Adjusted R-squared 0.799299 S.D. dependent var 5316.370 S.E. of regression 2381.717 Sum squared resid 1.19E+08Durbin-Watson stat 0.6966834219.14592651806.4153.1774X X Y ++-=(5157.215)(0.144925) (2372.459)t (-0.344014) (32.09800) (6.150660)2R =0.999833 2R = 0.999818 F = 590.2806 再对修正结果进行White 检验如下：表９ White 检验结果（二）White Heteroskedasticity Test:F-statistic 0.980433 Probability 0.456336 Obs*R-squared5.137153 Probability0.399372Test Equation:Dependent Variable: STD_RESID^2 Method: Least Squares Date: 12/17/07 Time: 21:57 Sample: 1980 2003 Included observations: 24Variable Coefficient Std. Error t-Statistic Prob. C -1.68E+08 2.73E+08 -0.613038 0.5475 X2 8780.798 15671.48 0.560304 0.5822 X2^2 0.134301 0.724858 0.185279 0.8551 X2*X4 -4700.165 6243.935 -0.752757 0.4613 X41.43E+082.58E+080.5535490.5867X4^2-29383155 60467904 -0.485930 0.6329R-squared 0.214048 Mean dependent var 692957.6 Adjusted R-squared -0.004272 S.D. dependent var 1203170. S.E. of regression 1205737. Akaike info criterion 31.05540 Sum squared resid 2.62E+13 Schwarz criterion 31.34991 Log likelihood -366.6648 F-statistic 0.980433 Durbin-Watson stat 2.740051 Prob(F-statistic)0.456336此时 5.1371532=nR ＜0705.11)5(205.0=χ，说明异方差已消除．并且参数的t 检验均通过，可决系数大幅提高，Ｆ检验也显著．３．自相关对样本量为２４、两个解释变量的模型，在５％显著水平下查DW 统计表可知，188.1=L d ，546.1=U d ．由表８知，模型中DW 为1.749898，而L d ＜DW ＜4－U d ，说明不存在自相关．由于能力有限，本文不再对时间序列平稳性做检验．所以最终的粮食总产量影响因素模型为4219.14592651806.4153.1774X X Y ++-=se (5157.215) (0.144925) (2372.459) t (-0.344014) (32.09800) (6.150660)2R =0.999833 2R = 0.999818 F = 590.2806模型经济意义为，在假定其他变量不变的情况下，每年化肥施用量每加１万吨，粮食总产量将增加4.651806万吨；单位面积劳动力投入量每增加１人／公顷，粮食总产量将增加14592.19万吨．结果与理论分析和经验判断基本一致．Ⅴ．对模型的经济解释从模型可以看出化肥的施用量与单位面积劳动力投入量是影响农业产值增长的最显著因素．说明我国目前农业生产中，农民自己对农业的投入所产生的效益最大。