实用回归分析(1-3)

数据分析方法：回归分析实用指南引言数据分析在当今社会中扮演着至关重要的角色。

通过收集、整理和分析数据，我们可以获得有关特定问题或现象的深入洞察。

回归分析是一种常用的统计分析方法，可以帮助我们理解变量之间的关系，并预测未来的趋势。

本文将为您介绍回归分析的概念、应用和常见方法，希望能够为您在实际应用中提供一些有用的指导。

什么是回归分析？回归分析是一种用于研究变量之间关系的统计方法。

它通过建立一个数学模型来描述自变量（独立变量）与因变量（依赖变量）之间的关系。

回归分析可以帮助我们理解变量之间的关联性，从而探索隐藏在数据背后的规律。

回归分析的应用领域回归分析在各个领域都有广泛的应用，以下是一些常见的应用领域：1. 经济学在经济学中，回归分析被用来研究各种经济变量之间的关系，如GDP与投资、通货膨胀与失业率等。

通过回归分析，经济学家可以预测未来的经济趋势，为政府和企业提供决策支持。

2. 市场营销在市场营销领域，回归分析被广泛应用于市场调研和销售预测。

通过分析市场数据和消费者行为，市场营销人员可以确定哪些因素对产品销售额产生积极影响，并相应地调整营销策略。

3. 医学研究医学研究中也常用回归分析来探索疾病与生活方式、遗传因素等之间的关系。

通过回归分析，医生和研究人员可以找到影响疾病发生和发展的风险因素，从而提供更有效的预防和治疗方法。

4. 社会科学回归分析在社会科学研究中也是一个重要的工具。

通过回归分析，社会科学家可以研究教育、犯罪、就业等不同社会现象之间的关系，从而为社会政策制定提供依据。

简单线性回归分析在回归分析中，最简单的一种形式是简单线性回归分析。

在简单线性回归中，我们只考虑一个自变量和一个因变量之间的关系。

1. 模型表达式简单线性回归模型的表达式为：Y=β0+β1X+ɛ其中，Y是因变量，X是自变量，β0和β1是回归系数，ɛ是误差项。

2. 回归系数解释回归系数β0和β1分别表示截距和斜率。

截距β0表示当自变量X为0时，因变量Y 的预测值。

回归分析实例范文回归分析是一种统计方法，用于研究两个或多个变量之间的关系。

它可以帮助我们了解变量之间的相关性，以及一个变量对另一个变量的影响程度。

以下是一个回归分析的实例，以说明如何运用回归分析来探索变量之间的关系。

假设我们有两个变量：广告费用（x）和销售额（y）。

我们对其中一产品进行了市场调研，收集了一些数据，如下所示：广告费用（万元），销售额（万元）-----------，-----------4，1002，508，2006，15010，250我们的目标是确定广告费用与销售额之间的关系，以及预测未来的销售额。

首先，我们可以通过绘制散点图来观察两个变量之间的关系。

从散点图中可以看出，广告费用与销售额之间存在着正相关关系，即广告费用越高，销售额也越高。

接下来，我们可以使用回归分析来量化这种关系。

在回归分析中，我们假设存在一个线性关系，即销售额（y）与广告费用（x）之间的关系可以用一条直线来表示。

我们希望找到一条最佳拟合线，使得该直线尽可能地通过数据点。

通过回归分析，我们可以得到以下回归方程，用于预测销售额：y=β0+β1*x其中，β0表示截距，β1表示斜率。

回归分析还可以计算出拟合优度（R²），来评估模型的拟合程度。

R²的取值范围为0到1，越接近1表示模型的拟合程度越好。

现在，我们来计算回归方程和拟合优度。

首先，我们需要计算β1和β0。

β1可以通过以下公式来计算：β1 = ∑((xi - x平均)*(yi - y平均)) / ∑((xi - x平均)²)β0可以通过以下公式计算：β0=y平均-β1*x平均其中，x平均和y平均分别表示广告费用和销售额的平均值。

计算得到β1≈20计算得到β0≈5因此，回归方程为：y=5+20*x接下来，我们计算拟合优度（R²）。

拟合优度可以通过以下公式计算：R²=SSR/SSTO其中，SSR（回归平方和）表示拟合线解释的总方差SSR = ∑((yi - y预测)²)SSTO（总平方和）表示实际观测值和实际平均值之间的总方差，可以通过以下公式计算：SSTO = ∑((yi - y平均)²)计算得到SSR≈850计算得到SSTO≈1166.67因此，拟合优度（R²）为：R²=850/1166.67≈0.73拟合优度为0.73，说明回归模型可以解释销售额的73%的变异性。

回归分析方法及其应用实例环境与规划学院2012级地理科学2014年11月回归分析方法及其应用实例摘要：回归分析方法，就是研究要素之间具体数量关系的一种强有力的工具，运用这种方法能够建立反应地理要素之间具体数量关系的数学模型，即回归模型。

本文首先给出回归分析方法的主要内容及解决问题的一般步骤，简单的介绍了回归分析建模的一般过程，进而引出了基本的一元线性回归分析方法的数学模型。

其次，叙述了多元线性回归理论模型，列举了多元线性回归模型应遵从的假定条件，探讨了多元线性回归模型中未知参数的估计方法及其参数的检验问题。

最后通过具体的案例来总结了多元回归分析的应用。

关键词：多元线性回归模型；模型检验；SPSS；实例应用。

引言：用回归分析建模的一般过程：（1）画散点图（2）设定模型（3）最小二乘估计模型中的参数并写出回归方程（4）拟合优度的测量（5）回归参数的显著性检验及其置信区间（6）残差分析(回归分析的前提假定)（7）预测（点、区间）在利用回归分析解决问题时，首先要建立模型，即函数关系式，其自变量称为回归变量，因变量称为应变量或响应变量。

如果模型中只含有一个回归变量，称为一元回归模型，否则称为多元回归模型（实际中所见到的大都是线性回归模型，非线性的一般可以化为线性的来处理）。

一、一元线性回归模型有一元线性回归模型（统计模型）如下：Y t =β0+β1 x t + u t上式表示变量y t和x t之间的真实关系。

其中yt称被解释变量（因变量），xt称解释变量（自变量），ut称随机误差项，β0称常数项，β1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t) =β0+ β1 x t,（2）随机部分，u t(包含了所有没有考虑在内的影响因素对因变量的影响，越小越好)二、多元线性回归模型2.1 当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元线性回归。

设可预测的随机变量为y，它受到k个非随机因素X1，X2，X3``````X k 和不可预测的随机因素ε的影响。

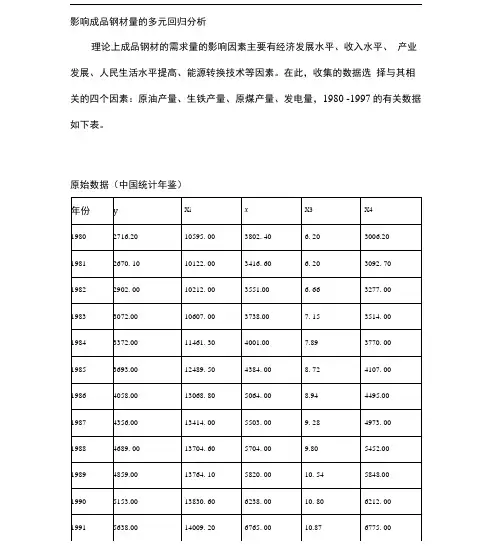
影响成品钢材量的多元回归分析理论上成品钢材的需求量的影响因素主要有经济发展水平、收入水平、产业发展、人民生活水平提高、能源转换技术等因素。

在此，收集的数据选择与其相关的四个因素：原油产量、生铁产量、原煤产量、发电量，1980 -1997的有关数据如下表。

原始数据（中国统计年鉴）将中国成品钢材的需求量设为y,作为被解释变量，而原油产量生铁产 量X2、原煤产量対、发电量X4作为解释变量，通过建立这些经济变量的线性 模型来研究影响成品钢材需求量的原因。

模型的设定二参数估计设因变量y 与自变量Xi 、X2、X3、X4的一般线性回归模型为0 + iXi2X2 3X34X4是随机变量，通常满足o ； Var ()=a.因变量：成品钢材（万吨）再用SPSS做回归线性，根据系数表得岀回归方程为:$ 170. 287 0. 041% 0. 554X2 17. 818x3 0. 389x t再做回归预测，得出如下截图:¥XI k2 x3 [)(4 PREJ RES 12716. 203802. 40 e. so 3006. 20 2e?S. 0S76G -182.837662G70. 1010122. 0C 3416. 60 G. 20 3092. 70 2736. 53110 -60. 431102902. 0010212. 00 3651.00 6. 66 3277. 00 2072,91514 29 19ZaG3072. 0010607. 00 3738. 00 7J5 3514.00 3043. 62443 28 375573372. 0011461. 30 4001.00 A89 3770. 00 3240. 51684 131. 484163693 0012489,50 4384. 00 3 72 4107.00 3526,63541 1B6. 3&459 4056. 0013068. 0C 50B4. 00 8.94 4495 00 4C2£. 56ei9 31 433814356. 0013414. 00 5503. 00 9.28 4973. 00 A4 35.52677 -79. 526774689. 0013704. 6C 5704. 00 9.80 5452. 00 4712.05819 ■ 23.058194059. 00137E4 W 582C. 00 10 54 5346. 00 4914.91371 -55.613715153. 0013630. 60 623B. CD IQ. BO 621200 5250.70360 -127.703S05638. 0014009. 20 5765. 00 1187 6775. 00 5733. 194656E97 0Q14209. 70 7599. 03 11. 16 7539 00 6623. 64790 173. 3K21D 771E. 0014623 00 9739. 00 11 51 8395. 00 7474. 00431 241.196608482 0014608, 20 3741,00 12. 40 0281. 00 S3 56.43425 126. 656769979. 8015004. 94 10529. 27 1361 10070. 30 9051. 44M -81. 64200933S. 0215733. 39 107Z2. 50 13. 97 10013. 10 9421. 11147 -63. 091479978. 931607J 14 11511. 41 1373 11355.63 10059. 53741 -80. 60741 16225 86 12044. 54 1367 12334. 69 10P27. 33875 ■17453. 00 12445. 96 14. 54 13457. 00 11323. 07164故当原油产量为16225. 86万吨，生铁产量为12044. 54万吨，原煤产量为13. 87万吨以及发电量为12334. 89亿千瓦时时，成品钢材量预测值为10727. 33875万吨；当原油产量为17453万吨，生铁产量为12445. 96万吨，原煤产量为14. 54万吨以及发电量为13457亿千瓦时时，成品钢材量预测值为10727. 33875万吨。

回归分析是一种统计学方法，用于探索和解释变量之间的关系。

它可以帮助研究者理解变量如何相互影响，从而预测未来的趋势或结果。

在进行回归分析之前，需要先了解一些基本概念和步骤。

第一步：收集数据进行回归分析的第一步是收集相关数据。

这些数据可以是实验数据，调查结果，或者是已有的历史数据。

确保数据的准确性和完整性对于回归分析的结果至关重要。

第二步：确定变量在回归分析中，通常会有两种变量：自变量和因变量。

自变量是用来预测因变量的变量，而因变量则是被预测的变量。

在选择自变量时，需要考虑其与因变量的相关性，避免选择无关的变量。

第三步：建立模型建立回归模型是回归分析的核心步骤。

最常见的回归模型是线性回归模型，它假设自变量与因变量之间存在线性关系。

除了线性回归模型外，还有多项式回归模型、对数回归模型等。

选择合适的模型需要根据实际情况和数据特点进行判断。

第四步：拟合模型一旦确定了回归模型，就需要利用数据对模型进行拟合。

拟合模型的过程是通过最小化残差，来确定模型的参数估计值。

残差是观测值与模型预测值之间的差异，拟合模型的目标是使残差尽可能小。

第五步：评估模型评估模型的好坏是回归分析中的关键步骤。

常用的评估方法包括R方值、残差分析、假设检验等。

R方值是用来衡量模型对观测数据的拟合程度，值越接近于1表示模型拟合得越好。

残差分析可以帮助检验模型的假设是否成立，假设检验则可以用来检验模型的显著性。

第六步：预测结果一旦建立了合适的回归模型，并对模型进行了评估，就可以利用模型进行预测。

预测结果可以帮助研究者了解自变量对因变量的影响程度，从而进行合理的决策。

需要注意的是，回归分析只能用来观察变量之间的相关关系，并不能说明因果关系。

在进行回归分析时，需要注意变量选择、模型建立、模型评估等步骤，以确保分析结果的准确性和可靠性。

总之，回归分析是一种强大的工具，可以帮助研究者理解变量之间的关系，并进行预测和决策。

通过深入了解回归分析的基本步骤和方法，可以更好地应用这一方法来解决实际问题。