统计学_贾俊平_第4版_课后答案
- 格式:doc
- 大小:2.85 MB
- 文档页数:87

贾平凹统计学第四版第八章课后答案8.01 已知某炼铁厂的含碳量服从正态分布N(4.55, 0.108),现在测定了9炉铁水,其平均含碳量为4.484。
如果估计方差没有变化,可否认为现在生产的铁水平均含碳量为4.55 (a=0.05) 。
H0: = 4.55H1: 1 4.55= 0.05 n = 9临界值(s): -1.96,1.96 在-1.96~1.96之间接受;否则拒绝检验统计量: =(4.484-4.55)/(0.33/3 )= -0.6 -0.6∈(-1.96,1.96) 决策:在 = 0.05的水平上接受H0结论: 有证据表明现在生产的铁水平均含碳量为4.558.02 一种元件,要求其使用寿命不得低于700小时。
现从一批这种元件中随机抽取36件,测得其平均寿命为680小时。
已知该元件寿命服从正态分布,s=60小时,试在显著性水平a=0.05下确定这批元件是否合格。
H0: <700H1: ≥700= 0.05 n = 36临界值(s):1.645 <1.645接受;否则拒绝检验统计量: =(680-700)/(60/6)=-2 -2<1.645决策:在 = 0.05的水平上接受H0结论: 有证据表明元件不合格8.03 某地区小麦的一般生产水平为亩产250公斤,其标准差为30公斤。
现用一种化肥进行试验,从25个小区抽样结果,平均产量为270公斤。
问这种化肥是否使小麦明显增产?(a=0.05) H0: ≤250 H1: >250= 0.05 n = 25临界值(s):1.645 <1.645接受;否则拒绝检验统计量: =(270-250)/(30/5)=3.33 3.33>1.645决策:在 = 0.05的水平上拒绝H0结论: 有证据表明这种化肥使小麦明显增产8.04 糖厂用自动打包机打包,每包标准重量是100公斤。
每天开工后需要检验一次打包机工作是否正常。
某日开工后测得9包重量如下:99.3 98.7 100.5 101.2 98.3 99.7 99.5 102.1 100.5已知包重服从正态分布,试检验该日打包机工作是否正常?(a=0.05)H0: =100H1: ≠100= 0.05 n = 9 s=1.21 =99.98临界值(s): -2.31,2.31 在-2.31~2.231之间接受;否则拒绝检验统计量: =(99.98-100)/(1.21/3)=0.50 0.50∈(-2.31,2.31)决策:在 = 0.05的水平上接受H0结论: 有证据表明试检验该日打包机工作正常8.05 某种大量生产的袋装食品,按规定不得少于250克。
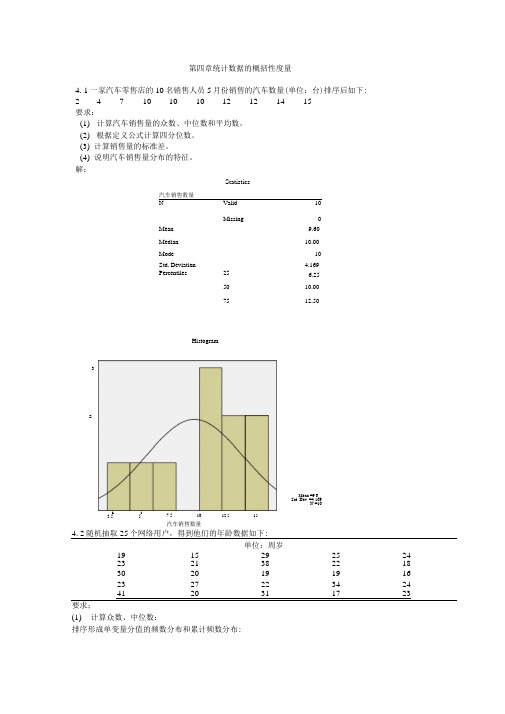
第四章统计数据的概括性度量4. 1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下: 2 4 7 10 10 10 12 12 14 15要求:(1) 计算汽车销售量的众数、中位数和平均数。
(2) 根据定义公式计算四分位数。
(3) 计算销售量的标准差。
(4) 说明汽车销售量分布的特征。
解:汽车销售数量StatisticsNValid 10Missing0 Mean9.60Median10.00Mode10Std. Deviation4.169 Percentiles25 6.255010.007512.504. 2随机抽取25个网络用户,得到他们的年龄数据如下:单位:周岁19 15 29 25 24 23 21 38 22 18 30 20 19 19 16 23 27 22 34 24 41 20 31 17 23要求;(1) 计算众数、中位数:排序形成单变量分值的频数分布和累计频数分布:LI2.557.5 10汽车销售数量12.5 15Mean =9.6Std. Dev. =4.169N =10Histogram32网络用尸的年龄FrequencyPercent Cumulative FrequencyCumulative PercentValid15 14.0 14.016 1 4.0 2 8.0 17 1 4.0 3 12.0 18 1 4.0 4 16.0 19 3 12.0 7 28.0 20 2 8.0 9 36.0 21 1 4.0 10 40.0 22 2 8.0 12 48.0 233 12.0 15 60.0 24 2 8.0 17 68.0 25 1 4.0 18 72.0 27 1 4.0 19 76.0 29 1 4.0 20 80.0 30 1 4.0 21 84.0 31 1 4.0 22 88.0 34 1 4.0 23 92.0 38 1 4.0 24 96.0 41 1 4.0 25100.0Total25100.0从频数看出,众数 Mo 有两个:19、23;从累计频数看,中位数 Me=23。

附录:教材各章习题答案第1章统计与统计数据1.1(1)数值型数据;(2)分类数据;(3)数值型数据;(4)顺序数据;(5)分类数据。
1.2(1)总体是“该城市所有的职工家庭”,样本是“抽取的2000个职工家庭”;(2)城市所有职工家庭的年人均收入,抽取的“2000个家庭计算出的年人均收入。
1.3(1)所有IT从业者;(2)数值型变量;(3)分类变量;(4)观察数据。
1.4(1)总体是“所有的网上购物者”;(2)分类变量;(3)所有的网上购物者的月平均花费;(4)统计量;(5)推断统计方法。
1.5(略)。
1.6(略)。
第2章数据的图表展示2.1(1)属于顺序数据。
(2)频数分布表如下服务质量等级评价的频数分布(3)条形图(略)(4)帕累托图(略)。
2.2(1)频数分布表如下40个企业按产品销售收入分组表(2)某管理局下属40个企分组表2.3频数分布表如下某百货公司日商品销售额分组表直方图(略)。
2.4茎叶图如下箱线图(略)。
2.5(1)排序略。
(2)频数分布表如下100只灯泡使用寿命非频数分布(3)直方图(略)。
(4)茎叶图如下2.6(1)频数分布表如下(2)直方图(略)。
(3)食品重量的分布基本上是对称的。
2.7(1)频数分布表如下(2)直方图(略)。
2.8(1)属于数值型数据。
(2)分组结果如下(3)直方图(略)。
2.9(1)直方图(略)。
(2)自学考试人员年龄的分布为右偏。
2.10(1)茎叶图如下(2)A班考试成绩的分布比较集中,且平均分数较高;B班考试成绩的分布比A班分散,且平均成绩较A班低。
2.11(略)。
2.12(略)。
2.13(略)。
2.14(略)。
2.15箱线图如下:(特征请读者自己分析)第3章 数据的概括性度量 3.1(1)100=M ;10=e M ;6.9=x 。
(2)5.5=L Q ;12=U Q 。
(3)2.4=s 。
(4)左偏分布。
3.2(1)190=M ;23=e M 。

请举出统计应用的几个例子:1、用统计识别作者:对于存在争议的论文,通过统计量推出作者2、用统计量得到一个重要发现:在不同海域鳗鱼脊椎骨数量变化不大,推断所有各个不同海域内的鳗鱼是由海洋中某公共场所繁殖的3、挑战者航天飞机失事预测请举出应用统计的几个领域:1、在企业发展战略中的应用2、在产品质量管理中的应用3、在市场研究中的应用④在财务分析中的应用⑤在经济预测中的应用你怎么理解统计的研究内容:1、统计学研究的基本内容包括统计对象、统计方法和统计规律。
2、统计对象就是统计研究的课题,称谓统计总体。
3、统计研究方法主要有大量观察法、数量分析法、抽样推断法、实验法等。
④统计规律就是通过大量观察和综合分析所揭示的用数量指标反映的客观现象的本质特征和发展规律。
举例说明分类变量、顺序变量和数值变量:分类变量:表现为不同类别的变量称为分类变量,如“性别”表现为“男”或“女”,“企业所属的行业”表现为“制造业”、“零售业”、“旅游业”等,“学生所在的学院”可能是“商学院”、“法学院”等顺序变量:如果类别有一定的顺序,这样的分类变量称为顺序变量,如考试成绩按等级分为优、良、中、及格、不及格,一个人对事物的态度分为赞成、中立、反对。
这里的“考试成绩等级”、“态度”等就是顺序变量。
数值变量:可以用数字记录其观察结果,这样的变量称为数值变量,如“企业销售额”、“生活费支出”、“掷一枚骰子出现的点数”。
定性数据和定量数据的图示方法各有哪些:1、定性数据的图示:条形图、帕累托图、饼图、环形图2、定量数据的图示:a、分组数据看分布:直方图b、未分组数据看分布:茎叶图、箱线图、垂线图、误差图c、两个变量间的关系:散点图d、比较多个样本的相似性:雷达图和轮廓图直方图与条形图有何区别:1、条形图中的每一个矩形表示一个类别,其宽度没有意义,而直方图的宽度则表示各组的组距。
2、由于分组数据具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开排列。

第十一章一元线性回归练习题答案二.填空题 1. 不能;因为该相关系数为样本计算出的相关系数,它的大小受样本数据波动的影响,它是否显著尚需检验;t 检验;2.图1;不能;因为图1反映的是线性相关关系,图2反映的是非线性性相关关系,相关系数只能反映线性相关变量间的相关性的强弱,不能反映非线性相关性的强弱。
三.计算题1.(1) SSR 的自由度是1,SSE 的自由度是18。
(2)2418/6080220/1/==-=SSE SSR F(3)判定系数%14.57140802===SST SSR R 在y 的总变差中,由57.14%的变差是由于x 的变动说引起的。
(4)7559.05714.02-=-=-=R r相关系数为-0.7559。
(5)线性关系显著和:线性关系不显著和y x y x H 10H :因为414.424=>=αF F,所以拒绝原假设,x 与y 之间的线性关系显著。
2.(1)方差分析表df SS MS F Significance F回归分析 1 425 425 85 0.017 残差 15 75 5 - - 总计16500---(2)判定系数%8585.05004252====SST SSR R表明在维护费用的变差中,有85%的变差可由使用年限来解释。
(3)9220.085.02===R r二者相关系数为0.9220,属于高度相关(4)x y248.1388.6ˆ+= 分布;显著。
的自由度为t n r n r t 2);12||2---=回归系数为1.248,表示每增加一个单位的产量,该行业的生产费用将平均增长1.248个单位。
(5)线性关系显著性检验:线性关系显著:生产费用和产量之间性关系不显著生产费用和产量之间线10:H H因为Significance F=0.017<05.0=α,所以线性关系显著。
(6)348.3120248.1388.6248.1388.6ˆ==⨯++=x y当产量为10时,生产费用为31.348万元。

贾俊平第四版统计学- 第八章假设检验练习答案第八章假设检验练习答案•选择题1. 第一类错误,第二类错误,一,2. 第一类,第二类,原假设,不拒绝3.(1)H。
:220,H i:220(2)第一类错误是指新方法不能降低成本但被采用,导致成本上升;第二类错误是指新方法能够降低成本,但没有采用。
4.失学儿童中女孩所占的比例(或男孩所占的比例*);H。
:3,H1:43(或H 0:4* 1, Hz P(1).n三•计算题1.解:H°: 4.55, H1 4.55总体服从正态分布,总体含碳量的标准差b =0.108,n=9,检验统计量为z X 0 4.484 4.55 d------ 0 1.833 /、n 0.108/ .9不拒绝原假设结论:在显著性水平a =0.05下,样本提供的证据不足以推翻“现在生产的铁水平均含碳量为4.55”的说法。
2. H0: 6.7,H1: 6.7n=200>30大样本,总体标准差未知,X 7.25, s 2.5a=0.05,双侧检验,临界值为Z o.o25 1.96,因为z>-1.96,未落入拒绝域检验统计量为z 需需 3-11=0.01,右侧检验,临界值为Z o.oi 2.33。
因为z=3.11>Z o.oi ,落入拒绝域,所以拒绝原假设。
结论:在显著性水平a =0.01下,认为“如今每个家庭每天看电视的平均时间比十年前增加了3. 解:H 0: 60, H 1: 60n=7<30小样本,总体标准差未知,经计算 x 65, s 11.34域,所以不拒绝原假设。
结论:在显著性水平a =0.01下,样本提供的证据还不足以推翻“促销活动无效” 的说法。
4. H 0: 30%,H 1: 30%n 0 400* 0.3 120 5,且 n (10) 400* 0.7 280 5,大样本,经计算样本比例为 P=100/400=0.25 p0 0.25 0.30 检验统计量为z r 1 0 1 2.1820*(1 0) 0.30*0.70x n \ 400 =0.05,双侧检验,临界值为Z 0.025 1.96。
统计学(第四版)贾俊平 第五章 参数估计 练习题答案5.1(答案精确到小数点后两位)(1)已知:n=49,15σ=,样本均值的标准误差X σ==(2)已知:置信水平:2195%, 1.96Z αα-==,估计误差E=2151.96 4.207Z α== (3)已知120,X =置信水平:2195%, 1.96Z αα-==,E=4.20置信区间为()2120 4.20115.80,124.20X Z α±=±=5.2(答案精确到小数点后两位)(1)置信区间为28900 1.96(8646.97,9153.03)X Z α±=±=(2)置信区间为28900 1.96(8815.48,8984.52)X Z α±=±=(3)置信区间为28900 1.65(8760.55,9039.45)X Z α±=±=(4)置信区间为28900 2.58(8681.95,9118.05)X Z α±=±= 5.3 (1) 表5.3—1置信水平90%上网时间置信区间报告上网时间5.4(答案精确到小数点后两位)(1)已知N=500,n=50,132n =A. 传统方法:320.6450p ==比例置信区间为0.64(0.51,0.77)p ±=±= B. 现代方法:3220.63504p +==+比例置信区间为0.63(0.50,0.76)p ±=±=(2)已知0.8p =0.1≤得到:16n ≥5.5(1)(2)5.6已知2212121214,7,53.2,43.4,96.8,102.0n n X X s s ======,(1)置信水平195%α-=,12μμ- 置信区间为()(()122 1.86,17.74X X t v α-±= (2)置信水平199%α-=,12μμ- 置信区间为()(()1220.19,19.41X X t v α-±=5.8已知1212250,p 40%,p 30%n n ==== (答案精确到小数点后四位)(1)置信水平190%α-= ,12ππ- 的置信区间为 ()()120.10.0300,0.1700p p -±=±=(2)置信水平195%α-= ,12ππ- 置信区间()()120.10.0168,0.1832p p -±±=5.9 有Excel 得,()2212121220.241609,0.076457,0.058375,0.005846, 2.464484,0.405764s s s s F F αα-======所以,方差比的置信区间为()()22112222122, 4.051926,24.61011s s s s F F αα-⎛⎫ ⎪= ⎪ ⎪ ⎪⎝⎭5.10已知置信水平2195%,Z 1.96,120,20E αασ-====≤ 所以,222138.3Z n E σ=≥ ,取n=139。
第七章 练习题参考答案7.1 (1)已知σ=5,n=40,x =25,α=0.05,z205.0=1.96样本均值的抽样标准差σx=nσ=79.0405=(2)估计误差(也称为边际误差)E=z 2αnσ=1.96*0.79=1.557.2(1)已知σ=15,n=49,x =120,α=0.05,z205.0=1.96(2)样本均值的抽样标准差σx=nσ==4915 2.14估计误差E=z 2αnσ=1.96*=4915 4.2(3)由于总体标准差已知,所以总体均值μ的95%的置信区间为: nx z σα±=120±1.96*2.14=120±4.2,即(115.8,124.2)7.3(1)已知σ=85414,n=100,x =104560,α=0.05,z205.0=1.96由于总体标准差已知,所以总体均值μ的95%的置信区间为: nx z σα±=104560±1.96*=10085414104560±16741.144即(87818.856,121301.144)7.4(1)已知n=100,x =81,s=12,α=0.1,z 21.0=1.645由于n=100为大样本,所以总体均值μ的90%的置信区间为:ns x z 2α±=81±1.645*=1001281±1.974,即(79.026,82.974)(2)已知α=0.05,z205.0=1.96由于n=100为大样本,所以总体均值μ的95%的置信区间为:ns x z 2α±=81±1.96*=1001281±2.352,即(78.648,83.352)(3)已知α=0.01,z201.0=2.58由于n=100为大样本,所以总体均值μ的99%的置信区间为:ns x z 2α±=81±2.58*=1001281±3.096,即(77.94,84.096)7.5(1)已知σ=3.5,n=60,x =25,α=0.05,z205.0=1.96由于总体标准差已知,所以总体均值μ的95%的置信区间为: nx z σα±=25±1.96*=60.5325±0.89,即(24.11,25.89)(2)已知n=75,x =119.6,s=23.89,α=0.02,z 202.0=2.33由于n=75为大样本,所以总体均值μ的98%的置信区间为:ns x z 2α±=119.6±2.33*=759.823119.6±6.43,即(113.17,126.03)(3)已知x =3.419,s=0.974,n=32,α=0.1,z21.0=1.645由于n=32为大样本,所以总体均值μ的90%的置信区间为:ns x z 2α±=3.419±1.645*=3274.90 3.419±0.283,即(3.136,3.702)7.6(1)已知:总体服从正态分布,σ=500,n=15,x =8900,α=0.05,z205.0=1.96由于总体服从正态分布,所以总体均值μ的95%的置信区间为:nx z σα2±=8900±1.96*=155008900±253.03,即(8646.97,9153.03)(2)已知:总体不服从正态分布,σ=500,n=35,x =8900,α=0.05,z205.0=1.96虽然总体不服从正态分布,但由于n=35为大样本,所以总体均值μ的95%的置信区间为:nx z σα2±=8900±1.96*=355008900±165.65,即(8734.35,9065.65)(3)已知:总体不服从正态分布,σ未知, n=35,x =8900,s=500,α=0.1,z 21.0=1.645虽然总体不服从正态分布,但由于n=35为大样本,所以总体均值μ的90%的置信区间为:ns x z 2α±=8900±1.645*=355008900±139.03,即(8760.97,9039.03)(4)已知:总体不服从正态分布,σ未知, n=35,x =8900,s=500,α=0.01,z 01.0=2.58虽然总体不服从正态分布,但由于n=35为大样本,所以总体均值μ的99%的置信区间为:ns x z 2α±=8900±2.58*=355008900±218.05,即(8681.95,9118.05)7.7 已知:n=36,当α=0.1,0.05,0.01时,相应的z21.0=1.645,z205.0=1.96,z201.0=2.58根据样本数据计算得:x =3.32,s=1.61由于n=36为大样本,所以平均上网时间的90%置信区间为:ns x z 2α±=3.32±1.645*=361.61 3.32±0.44,即(2.88,3.76)平均上网时间的95%置信区间为:ns x z 2α±=3.32±1.96*=361.61 3.32±0.53,即(2.79,3.85)平均上网时间的99%置信区间为:ns x z 2α±=3.32±2.58*=361.61 3.32±0.69,即(2.63,4.01)7.8 已知:总体服从正态分布,但σ未知,n=8为小样本,α=0.05,)(18t05.0-=2.365根据样本数据计算得:x =10,s=3.46 总体均值μ的95%的置信区间为:ns x t α±=10±2.365*=83.4610±2.89,即(7.11,12.89)7.9 已知:总体服从正态分布,但σ未知,n=16为小样本,α=0.05,)(116t205.0-=2.131根据样本数据计算得:x =9.375,s=4.113从家里到单位平均距离的95%的置信区间为:ns x t α±=9.375±2.131*=144.1139.375±2.191,即(7.18,11.57)7.10 (1)已知:n=36,x =149.5,α=0.05,z205.0=1.96由于n=36为大样本,所以零件平均长度的95%的置信区间为:ns x z 2α±=149.5±1.96*=361.93149.5±0.63,即(148.87,150.13)(2)在上面的估计中,使用了统计中的中心极限定理。
3.1 为评价家电行业售后服务的质量,随机抽取了由100个家庭构成的一个样本。服务质量的等级分别表示为:A.好;B.较好;C一般;D.较差;E.差。调查结果如下: B E C C A D C B A E D A C B C D E C E E A D B C C A E D C B B A C D E A B D D C C B C E D B C C B C D A C B C D E C E B B E C C A D C B A E B A C E E A B D D C A D B C C A E D C B C B C E D B C C B C 要求: (1)指出上面的数据属于什么类型。 顺序数据 (2)用Excel制作一张频数分布表。 用数据分析——直方图制作:
(3)绘制一张条形图,反映评价等级的分布。 用数据分析——直方图制作:
直方图
02040EDCBA接收频率频率
(4)绘制评价等级的帕累托图。 逆序排序后,制作累计频数分布表: 接收 频数 频率(%) 累计频率(%) C 32 32 32 B 21 21 53 D 17 17 70 E 16 16 86 A 14 14 100
接收 频率 E 16 D 17 C 32 B 21 A 14 05101520253035CDBAE020406080100120频数累计频率(%)
3.2 某行业管理局所属40个企业2002年的产品销售收入数据如下: 152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 97 88 123 115 119 138 112 146 113 126 要求: (1)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率。 1、确定组数: lg40lg()1.602061116.32lg(2)lg20.30103n
K,取k=6
2、确定组距: 组距=( 最大值 - 最小值)÷ 组数=(152-87)÷6=10.83,取10 3、分组频数表
销售收入 频数 频率% 累计频数 累计频率% 80.00 - 89.00 2 5.0 2 5.0 90.00 - 99.00 3 7.5 5 12.5 100.00 - 109.00 9 22.5 14 35.0 110.00 - 119.00 12 30.0 26 65.0 120.00 - 129.00 7 17.5 33 82.5 130.00 - 139.00 4 10.0 37 92.5 140.00 - 149.00 2 5.0 39 97.5 150.00+ 1 2.5 40 100.0 总和 40 100.0
(2)按规定,销售收入在125万元以上为先进企业,115~125万元为良好企业,105~115 万元为一般企业,105万元以下为落后企业,按先进企业、良好企业、一般企业、落后企业进行分组。 频数 频率% 累计频数 累计频率% 先进企业 10 25.0 10 25.0 良好企业 12 30.0 22 55.0 一般企业 9 22.5 31 77.5 落后企业 9 22.5 40 100.0 总和 40 100.0 3.3 某百货公司连续40天的商品销售额如下: 单位:万元 41 25 29 47 38 34 30 38 43 40 46 36 45 37 37 36 45 43 33 44 35 28 46 34 30 37 44 26 38 44 42 36 37 37 49 39 42 32 36 35 要求:根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。 1、确定组数: lg40lg()1.602061116.32lg(2)lg20.30103n
K,取k=6
2、确定组距: 组距=( 最大值 - 最小值)÷ 组数=(49-25)÷6=4,取5 3、分组频数表 销售收入(万元) 频数 频率% 累计频数 累计频率% <= 25 1 2.5 1 2.5 26 - 30 5 12.5 6 15.0 31 - 35 6 15.0 12 30.0 36 - 40 14 35.0 26 65.0 41 - 45 10 25.0 36 90.0 46+ 4 10.0 40 100.0 总和 40 100.0
频数
0246810121416<= 2526 - 3031 - 3536 - 4041 - 4546+销售收入频数频数 3.4 利用下面的数据构建茎叶图和箱线图。 57 29 29 36 31 23 47 23 28 28 35 51 39 18 46 18 26 50 29 33 21 46 41 52 28 21 43 19 42 20
data605040302010 data Stem-and-Leaf Plot Frequency Stem & Leaf 3.00 1 . 889 5.00 2 . 01133 7.00 2 . 6888999 2.00 3 . 13 3.00 3 . 569 3.00 4 . 123 3.00 4 . 667 3.00 5 . 012 1.00 5 . 7 Stem width: 10 Each leaf: 1 case(s)
3.6一种袋装食品用生产线自动装填,每袋重量大约为50g,但由于某些原因,每袋重量不会恰好是50g。下面是随机抽取的100袋食品,测得的重量数据如下: 单位:g 57 46 49 54 55 58 49 61 51 49 51 60 52 54 51 55 60 56 47 47 53 51 48 53 50 52 40 45 57 53 52 51 46 48 47 53 47 53 44 47 50 52 53 47 45 48 54 52 48 46 49 52 59 53 50 43 53 46 57 49 49 44 57 52 42 49 43 47 46 48 51 59 45 45 46 52 55 47 49 50 54 47 48 44 57 47 53 58 52 48 55 53 57 49 56 56 57 53 41 48 要求: (1)构建这些数据的频数分布表。 (2)绘制频数分布的直方图。 (3)说明数据分布的特征。 解:(1)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率。 1、确定组数: lg100lg()21116.64lg(2)lg20.30103n
K,取k=6或7
2、确定组距: 组距=( 最大值 - 最小值)÷ 组数=(61-40)÷6=3.5,取3或者4、5 组距=( 最大值 - 最小值)÷ 组数=(61-40)÷7=3, 3、分组频数表 组距3,上限为小于 频数 百分比 累计频数 累积百分比 有效 40.00 - 42.00 3 3.0 3 3.0 43.00 - 45.00 9 9.0 12 12.0 46.00 - 48.00 24 24.0 36 36.0 49.00 - 51.00 19 19.0 55 55.0 52.00 - 54.00 24 24.0 79 79.0 55.00 - 57.00 14 14.0 93 93.0 58.00+ 7 7.0 100 100.0 合计 100 100.0 直方图: 组距3,小于1086420Frequency3020100
组距3,小于
Mean =5.22Std. Dev. =1.508N =100
组距4,上限为小于等于 频数 百分比 累计频数 累积百分比 有效 <= 40.00 1 1.0 1 1.0 41.00 - 44.00 7 7.0 8 8.0 45.00 - 48.00 28 28.0 36 36.0 49.00 - 52.00 28 28.0 64 64.0 53.00 - 56.00 22 22.0 86 86.0 57.00 - 60.00 13 13.0 99 99.0 61.00+ 1 1.0 100 100.0 合计 100 100.0 直方图: 组距4,小于等于86420Frequency403020100
组距4,小于等于Mean =4.06Std. Dev. =1.221N =100
组距5,上限为小于等于 频数 百分比 累计频数 累积百分比 有效 <= 45.00 12 12.0 12.0 12.0 46.00 - 50.00 37 37.0 49.0 49.0 51.00 - 55.00 34 34.0 83.0 83.0 56.00 - 60.00 16 16.0 99.0 99.0 61.00+ 1 1.0 100.0 100.0 合计 100 100.0 直方图: