【数学】2015-2016年天津市红桥区高三(上)期中数学试卷与答案(理科)

2015-2016学年天津市红桥区高一（下）期中数学试卷一、选择题（共8小题，每小题4分，满分32分）1．（4分）在△ABC中，a=3，b=，A=120°，则B等于（）A．120°B．60°C．45°D．30°2．（4分）已知等差数列{a n}满足a3+a4=12，3a2=a5，则a5=（）A．3B．6C．9D．113．（4分）某企业共有职工150人，其中高级职称15人，中级职称45人，初级职称90人．现采用分层抽取容量为30的样本，则抽取的初级职称的人数为（）A．30B．18C．9D．34．（4分）等差数列{a n}的前n项和为S n，a5=11，S12=186，则a8=（）A．18B．20C．21D．225．（4分）若将一个质点随机投入如图所示的长方形ABCD中，其中AB=4，BC=2，则质点落在以AB为直径的半圆外的空白处的概率是（）A．1﹣B．C．1﹣D．6．（4分）已知等比数列{a n}的前n项和为S n，且S2+a2，S1+2a2，S3+a3，成等差数列，则数列{a n}的公比为（）A．﹣2B．﹣C．2D．7．（4分）在△ABC中，A=60°，AC=2，BC=，则AB等于（）A．1B．2C．3D．8．（4分）某中学举行了一次“环保知识竞赛”活动，为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出如图所示的频率分布直方图，但由于不慎丢失了部分数据．已知得分在[50，60）的有8人，在[90，100）的有2人，由此推测频率分布直方图中的x=（）A．0.04B．0.03C．0.02D．0.01二、填空题（共5小题，每小题4分，满分20分）9．（4分）在数列{a n}中，a1=1，a n=1﹣（n≥2），则a3=．10．（4分）若等比数列{a n}满足a1+a4=10，a2+a5=20，则q=．11．（4分）在五个数字1，2，3，4，5中，若随机取出2个数字，则2个数字之中至少有一个偶数的概率是．12．（4分）如图，设A，B两点在河的两岸，一测量者在A的同侧，在A所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，则A，B两点的距离为m．13．（4分）已知数列{a n}的前n项和为S n，且满足S n﹣2a n﹣n=0（n∈N+），则数列{a n﹣1}的通项公式为．三、解答题（共4小题，满分48分）14．（10分）在锐角△ABC中，内角A，B，C所对的边分别为a，b，c，且满足2bsinA=a．（1）求角B的大小；（2）若a+c=5，且a＞c，b=，求边a，c．15．（12分）甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次．得到甲、乙两位学生成绩的茎叶图．（1）现要从中选派一人参加数学竞赛，从平均状况和方差的角度考虑，你认为哪位学生的成绩更稳定？请说明理由；（2）求在乙同学的6次预赛成绩中，从不小于70分的成绩中随机抽取2个成绩，列出所有结果，并求抽出的2个成绩均大于80分的概率．16．（12分）等差数列{a n}满足：a1=1，a2+a6=14；正项等比数列{b n}满足：b1=2，b3=8．（1）求数列{a n}，{b n}的通项公式a n，b n；（2）求数列{（a n+1）•b n}的前n项和T n．17．（14分）在△ABC中，角A，B，C所对的边分别为a，b，c，sinA，sinC，sinB 成等比数列，且b=2a．（1）求cosC的值；（2）若△ABC的面积为2sinAsinB，求sinA及c的值．2015-2016学年天津市红桥区高一（下）期中数学试卷参考答案与试题解析一、选择题（共8小题，每小题4分，满分32分）1．（4分）在△ABC中，a=3，b=，A=120°，则B等于（）A．120°B．60°C．45°D．30°【解答】解：∵在△ABC中，a=3，b=，A=120°，∴由，可得：sinB===，∵b＜a，B为锐角，∴B=30°．故选：D．2．（4分）已知等差数列{a n}满足a3+a4=12，3a2=a5，则a5=（）A．3B．6C．9D．11【解答】解：∵等差数列{a n}满足a3+a4=12，3a2=a5，∴a2+a5=a3+a4=12，3a2=a5，联立消去a2可得a5=9故选：C．3．（4分）某企业共有职工150人，其中高级职称15人，中级职称45人，初级职称90人．现采用分层抽取容量为30的样本，则抽取的初级职称的人数为（）A．30B．18C．9D．3【解答】解：每个个体被抽到的概率等于=，由于初级职称90人人，故初级职称90人应抽取的人数为90×=18，故选：B．4．（4分）等差数列{a n}的前n项和为S n，a5=11，S12=186，则a8=（）A．18B．20C．21D．22【解答】解：由数列的性质得a1+a12=a5+a8又因为×（a1+a12）=186所以a1+a12=a5+a8=31因为a5=11所以a8=20故选：B．5．（4分）若将一个质点随机投入如图所示的长方形ABCD中，其中AB=4，BC=2，则质点落在以AB为直径的半圆外的空白处的概率是（）A．1﹣B．C．1﹣D．【解答】解：解：∵AB=2BC=4，∴AB=4，BC=2，∴长方体的ABCD的面积S=4×2=8，圆的半径r=2，半圆的面积=•π•22=2π，∴则由几何槪型的概率公式可得质点落在以AB为直径的半圆内的概率是=，∴半圆外的空白处的概率是1﹣，故选：A．6．（4分）已知等比数列{a n}的前n项和为S n，且S2+a2，S1+2a2，S3+a3，成等差数列，则数列{a n}的公比为（）A．﹣2B．﹣C．2D．【解答】解：设等比数列{a n}的公比为q，∵S2+a2，S1+2a2，S3+a3，成等差数列，∴2（S1+2a2）=S3+a3+S2+a2，化为：2a1（1+2q）=2a1+3a2+2a3=a1（2+3q+2q2），化为：2q2﹣q=0，q≠0．则数列{a n}的公比为．故选：B．7．（4分）在△ABC中，A=60°，AC=2，BC=，则AB等于（）A．1B．2C．3D．【解答】解：∵在△ABC中，A=60°，AC=2，BC=，∴由余弦定理得：BC2=AC2+AB2﹣2AC•ABcosA=4+AB2﹣2×2×AB×=7，则解得：AB=﹣1或3（舍去）．故选：C．8．（4分）某中学举行了一次“环保知识竞赛”活动，为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出如图所示的频率分布直方图，但由于不慎丢失了部分数据．已知得分在[50，60）的有8人，在[90，100）的有2人，由此推测频率分布直方图中的x=（）A．0.04B．0.03C．0.02D．0.01【解答】解：∵得分在[50，60）的有8人，在[90，100）的有2人，∴由频率分布直方图，得：y==0.004，∴由频率分布直方图的性质得：（0.004+0.010+0.016+x+0.040）×10=1，解得x=0.03．故选：B．二、填空题（共5小题，每小题4分，满分20分）9．（4分）在数列{a n}中，a1=1，a n=1﹣（n≥2），则a3=．【解答】解：∵a n=1﹣=（n≥2），∴==1+（n≥2），∵=1，∴数列{}是首项、公差均为1的等差数列，∴=n，a n=，故答案为：．10．（4分）若等比数列{a n}满足a1+a4=10，a2+a5=20，则q=2．【解答】解：∵等比数列{a n}满足a1+a4=10，a2+a5=20，∴a2+a5=q（a1+a4）=10q=20，解得q=2．故答案为：2．11．（4分）在五个数字1，2，3，4，5中，若随机取出2个数字，则2个数字之中至少有一个偶数的概率是．【解答】解：在五个数字1，2，3，4，5中，随机取出2个数字，基本事件总数n==10，2个数字之中至少有一个偶数的对立事件是2个数字都是奇数，∴2个数字之中至少有一个偶数的概率是：p=1﹣=．故答案为：．12．（4分）如图，设A，B两点在河的两岸，一测量者在A的同侧，在A所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，则A，B两点的距离为50m．【解答】解：在△ABC中，∵∠ACB=45°，∠CAB=105°∴∠B=30°由正弦定理可得：∴=50m故答案为：5013．（4分）已知数列{a n}的前n项和为S n，且满足S n﹣2a n﹣n=0（n∈N+），则数列{a n﹣1}的通项公式为﹣2n．【解答】解：∵S n﹣2a n﹣n=0（n∈N+），∴S n﹣1﹣2a n﹣1﹣n+1=0（n≥2），两式相减得：a n=2a n﹣1﹣1，变形可得：a n﹣1=2（a n﹣1﹣1），又∵a1=2a1+1，即a1﹣1=﹣1﹣2=﹣2，∴数列{a n﹣1}是首项为﹣2、公比为2的等比数列，∴数列{a n﹣1}=﹣2•2n﹣1=﹣2n，故答案为：﹣2n．三、解答题（共4小题，满分48分）14．（10分）在锐角△ABC中，内角A，B，C所对的边分别为a，b，c，且满足2bsinA=a．（1）求角B的大小；（2）若a+c=5，且a＞c，b=，求边a，c．【解答】解：（1）在锐角△ABC中，∵2bsinA=a，∴2sinBsinA=sinA，sinA≠0，∴sinB=，B∈（0，），∴B=．（2）由余弦定理可得：b2=a2+c2﹣2accosB，∴7=（a+c）2﹣2ac﹣2accos，化为：ac=6，与a+c=5，a＞c，联立解得：a=3，c=2．15．（12分）甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次．得到甲、乙两位学生成绩的茎叶图．（1）现要从中选派一人参加数学竞赛，从平均状况和方差的角度考虑，你认为哪位学生的成绩更稳定？请说明理由；（2）求在乙同学的6次预赛成绩中，从不小于70分的成绩中随机抽取2个成绩，列出所有结果，并求抽出的2个成绩均大于80分的概率．【解答】解：（1）=（69+78+79+79+88+87）=80，=[（69﹣80）2+（78﹣80）2+（79﹣80）2+（79﹣80）2+（88﹣80）2+（87﹣80）2]=40．=（65+77+79+82+88+89）=80，=[（65﹣80）2+（77﹣80）2+（79﹣80）2+（82﹣80）2+（88﹣80）2+（89﹣80）2]=64．∵=，＜，∴甲学生的成绩更稳定．（2）在乙同学的6次预赛成绩中，从不小于70分的成绩中随机抽取2个成绩，列出所有结果为：{（77，79），（77，82），（77，88），（77，89），（79，82），（79，88），（79，89），（82，88），（82，89），（88，89）}，共10个，2个成绩均大于80分的基本事件有：（82，88），（82，89），（88，89），共3个，∴抽出的2个成绩均大于80分的概率p=．16．（12分）等差数列{a n}满足：a1=1，a2+a6=14；正项等比数列{b n}满足：b1=2，b3=8．（1）求数列{a n}，{b n}的通项公式a n，b n；（2）求数列{（a n+1）•b n}的前n项和T n．【解答】解：（1）设等差数列{a n}的公差为d，∵a1=1，a2+a6=14；∴2×1+6d=14，解得d=2．∴a n=1+2（n﹣1）=2n﹣1．设正项等比数列{b n}的公比为q＞0，∵b1=2，b3=8．∴2q2=8，解得q=2．∴b n=2×2n﹣1=2n．（2）（a n+1）•b n=2n×2n=n×2n+1．数列{（a n+1）•b n}的前n项和T n=22+2×23+3×24+…+n×2n+1，2T n=23+2×24+…+（n﹣1）×2n+1+n×2n+2，∴﹣T n=22+23+…+2n+1﹣n×2n+2=﹣n×2n+2=（1﹣n）×2n+2﹣4，∴T n=（n﹣1）×2n+2+4．17．（14分）在△ABC中，角A，B，C所对的边分别为a，b，c，sinA，sinC，sinB 成等比数列，且b=2a．（1）求cosC的值；（2）若△ABC的面积为2sinAsinB，求sinA及c的值．【解答】解：在△ABC中，∵sinA，sinC，sinB成等比数列，∴sin2C=sinA•sinB，∴c2=ab，∵b=2a，∴c=a，∴cosC===；（2）由（1）可得，sin2C=∵△ABC的面积为2sinAsinB，∴△ABC的面积为2sin2C=，∴=，∴=，∴a=，∴b=，c=，∴sinA=，∴sinA=．第11页（共11页）。

2015-2016学年天津市红桥区高二（上）期末数学试卷（理科）一、选择题（本大题12小题，每小题3分，共36分，每小题都给出代号为A,B,C,D的四个答案，其中只有一个是正确的）1．“∀x∈R，x2+x+1＞0“的否定是（）A．∃x0∈R，x02+x0+1＞0 B．∃x0∈R，x02+x0+1≤0C．∀x∈R，x2+x+1＞0 D．∀x∈R，x2+x+1≤02．设p、q是两个命题．如果命题p是命题q的充分不必要条件．那么￢p是￢q的（）A．充要条件 B．必要不充分条件C．充分不必要条件D．既不充分也不必要条件3．2x2﹣5x﹣3＜0的一个必要不充分条件是（）A．﹣＜x＜3 B．﹣＜x＜0 C．﹣3＜x＜ D．﹣1＜x＜64．过点P（﹣2，m）和Q（m，4）的直线斜率等于1，那么m的值等于（）A．1或3 B．4 C．1 D．1或45．椭圆的一焦点与短轴两顶点组成一个等边三角形，则椭圆的离心率为（）A． B． C． D．6．已知椭圆+=1（a＞5）的两个焦点为F1、F2，且|F1F2|=8．弦AB过点F1，则△ABF2的周长为（）A．10 B．20 C．2 D．47．焦点为（0，6），且与双曲线有相同的渐近线的双曲线方程是（）A． B．C． D．8．双曲线虚轴的一个端点为M，两个焦点为F1、F2，∠F1MF2=120°，则双曲线的离心率为（）A． B． C． D．9．抛物线y=2x2的焦点坐标是（）A．（0，）B．（，0）C．（1，0）D．（0，）10．已知抛物线的顶点在原点，焦点在y轴上，其上的点P（m，﹣3）到焦点的距离为5，則抛物线方程为（）A．x2=8y B．x2=4y C．x2=﹣4y D．x2=﹣8y11．已知双曲线方程为，过P（1，0）的直线L与双曲线只有一个公共点，则L的条数共有（）A．4条B．3条C．2条D．1条12．已知a，b为两个不相等的非零实数，则方程ax﹣y+b=0与bx2+ay2=ab所表示的曲线可能是（）A． B． C． D．二、填空题（每小题3分，共24分）13．在直角坐标系中，直线x+y﹣3=0的倾斜角是．14．已知直线l过点A（﹣2，0）且与直线x+2y﹣l=0平行．则直线l的方程是．15．已知圆的﹣条直径的两端点是（2，0），（2，﹣2）．则此圆方程是．16．离心率e=，一个焦点是F（0，﹣3）的椭圆标准方程为．17．己知双曲线的焦点在x轴上．两个顶点的距离为2，焦点到渐近线的距离为，则双曲线的渐近线方程为．18．若直线l过抛物线y=ax2（a＞0）的焦点，并且与y轴垂直，若l被抛物线截得的线段长为4，则a=．19．已知M为抛物线y2=4x上一动点，F为这条抛物线的焦点，有一个定点A（3，2），则|MA|+|MF|的最小值=．20．有红盒、黄盒、蓝盒各一个，只有﹣个盒子里有金币．红盒上写有命题p：金币在这个盒子里；黄盒上写有命题q：金币不在这个金子里；蓝盒上写有命题r：金币不在红盒里．p、q、r中有且只有一个是真命题，则金币在盒子里．三、解答题（本题共4小题，共40分）21．已知两条直线l1：x﹣ay=0（a≠0），l2：x+y﹣3=0．（1）若l1⊥l2，求a的值；（2）在（1）的条件下，如果直线l3经过l1与l2的交点，且经过点A（2，4），求直线l3的方程．22．圆的方程为x2+y2﹣6x﹣8y=0，过坐标原点作长为8的弦，求弦所在的直线方程．23．已知双曲线与椭圆共焦点，它们的离心率之和为，求双曲线方程．24．已知椭圆的离心率，过点A（0，﹣b）和B（a，0）的直线与原点的距离为．（1）求椭圆的方程；（2）已知定点E（﹣1，0），若直线y=kx+2（k≠0）与椭圆交于C、D两点，问：是否存在k的值，使以CD为直径的圆过E点？请说明理由．2015-2016学年天津市红桥区高二（上）期末数学试卷（理科）参考答案与试题解析一、选择题（本大题12小题，每小题3分，共36分，每小题都给出代号为A,B,C,D的四个答案，其中只有一个是正确的）1．“∀x∈R，x2+x+1＞0“的否定是（）A．∃x0∈R，x02+x0+1＞0 B．∃x0∈R，x02+x0+1≤0C．∀x∈R，x2+x+1＞0 D．∀x∈R，x2+x+1≤0【考点】命题的否定．【分析】根据全称命题的否定是特称命题即可得到结论．【解答】解：∵全称命题的否定是特称命题，∴“∀x∈R，x2+x+1＞0“的否定是：∃x0∈R，x02+x0+1≤0，故选：B．2．设p、q是两个命题．如果命题p是命题q的充分不必要条件．那么￢p是￢q的（）A．充要条件 B．必要不充分条件C．充分不必要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据充分条件和必要条件的定义进行判断即可．【解答】解：若命题p是命题q的充分不必要条件，则根据逆否命题的等价性得命题￢q是命题￢p的充分不必要条件，即￢p是￢q的必要不充分条件，故选：B3．2x2﹣5x﹣3＜0的一个必要不充分条件是（）A．﹣＜x＜3 B．﹣＜x＜0 C．﹣3＜x＜ D．﹣1＜x＜6【考点】必要条件、充分条件与充要条件的判断；一元二次不等式的解法．【分析】通过解二次不等式求出2x2﹣5x﹣3＜0的充要条件，通过对四个选项的范围与充要条件的范围间的包含关系的判断，得到2x2﹣5x﹣3＜0的一个必要不充分条件．【解答】解：2x2﹣5x﹣3＜0的充要条件为对于A是2x2﹣5x﹣3＜0的充要条件对于B，是2x2﹣5x﹣3＜0的充分不必要条件对于C，2x2﹣5x﹣3＜0的不充分不必要条件对于D，是2x2﹣5x﹣3＜0的一个必要不充分条件故选D4．过点P（﹣2，m）和Q（m，4）的直线斜率等于1，那么m的值等于（）A．1或3 B．4 C．1 D．1或4【考点】直线的斜率．【分析】利用直线的斜率公式求解．【解答】解：∵过点P（﹣2，m）和Q（m，4）的直线斜率等于1，∴k==1，解得m=1．故选：C．5．椭圆的一焦点与短轴两顶点组成一个等边三角形，则椭圆的离心率为（）A． B． C． D．【考点】椭圆的简单性质．【分析】由题意画出椭圆在平面坐标系中的图象，由图象可知三角形ABC为等比三角形，所以得到2b等于a并用b表示a，又根据椭圆的基本性质可知a2=b2+c2，把a等于2b代入即可用b表示出c，然后根据离心率e=，分别把a与c的式子代入，约分后即可得到值．【解答】解：由题意画出椭圆的图象，得到△ABC为等比三角形，则a=2b，则根据椭圆的性质得到：a2=b2+c2=4b2，解得c=b，所以e===．故选A．6．已知椭圆+=1（a＞5）的两个焦点为F1、F2，且|F1F2|=8．弦AB过点F1，则△ABF2的周长为（）A．10 B．20 C．2 D．4【考点】椭圆的简单性质．【分析】求得椭圆的a，b，c，由椭圆的定义可得△ABF2的周长为|AB|+|AF2|+|BF2|=4a，计算即可得到所求值．【解答】解：由题意可得椭圆+=1的b=5，c=4，a==，由椭圆的定义可得|AF1|+|AF2|=|BF1|+|BF2|=2a，即有△ABF2的周长为|AB|+|AF2|+|BF2|=|AF1|+|AF2|+|BF1|+|BF2|=4a=4．故选：D．．7．焦点为（0，6），且与双曲线有相同的渐近线的双曲线方程是（）A． B．C． D．【考点】双曲线的简单性质．【分析】设所求的双曲线方程是，由焦点（0，6）在y 轴上，知k＜0，故双曲线方程是，据c2=36 求出k值，即得所求的双曲线方程．【解答】解：由题意知，可设所求的双曲线方程是，∵焦点（0，6）在y 轴上，∴k＜0，所求的双曲线方程是，由﹣k+（﹣2k）=c2=36，∴k=﹣12，故所求的双曲线方程是，故选B．8．双曲线虚轴的一个端点为M，两个焦点为F1、F2，∠F1MF2=120°，则双曲线的离心率为（）A． B． C． D．【考点】双曲线的简单性质．【分析】根据双曲线对称性可知∠OMF2=60°，在直角三角形MOF2中可得tan∠OMF2==，进而可得b和c的关系式，进而根据a=求得a和b的关系式．最后代入离心率公式即可求得答案．【解答】解：根据双曲线对称性可知∠OMF2=60°，∴tan∠OMF2===，即c=b，∴a==b，∴e==．故选B．9．抛物线y=2x2的焦点坐标是（）A．（0，）B．（，0）C．（1，0）D．（0，）【考点】抛物线的简单性质．【分析】先将方程化成标准形式，即x2=y，求出p=，即可得到焦点坐标．【解答】解：抛物线y=2x2的方程即x2=y，∴p=，故焦点坐标为（0，），故选：A．10．已知抛物线的顶点在原点，焦点在y轴上，其上的点P（m，﹣3）到焦点的距离为5，則抛物线方程为（）A．x2=8y B．x2=4y C．x2=﹣4y D．x2=﹣8y【考点】抛物线的简单性质．【分析】先假设抛物线的方程，利用抛物线上一点A（m，﹣3）到焦点F的距离为5，建立两个方程，即可求得正数m的值，及此抛物线的方程．【解答】解：依题意，设抛物线方程为为x2=﹣2py （p＞0）点P在抛物线上，到准线的距离为5，又点P到x轴的距离为3，所以准线到x轴的距离为2，∴=2，∴p=4，∴抛物线方程为x2=﹣8y．故选：D．11．已知双曲线方程为，过P（1，0）的直线L与双曲线只有一个公共点，则L的条数共有（）A．4条B．3条C．2条D．1条【考点】直线与圆锥曲线的关系．【分析】由双曲线方程可知其渐近线为y=y=±2x，分别考虑所求直线的情况有①直线的斜率不存在②与渐近线平行【解答】由题意可得：双曲线x2﹣=1的渐近线方程为：y=±2x，点P（1，0）是双曲线的右顶点，故直线x=1 与双曲线只有一个公共点；过点P （1，0）平行于渐近线y=±2x时，直线L与双曲线只有一个公共点，有2条所以，过P（1，0）的直线L与双曲线只有一个公共点，这样的直线共有3条故选B12．已知a，b为两个不相等的非零实数，则方程ax﹣y+b=0与bx2+ay2=ab所表示的曲线可能是（）A． B． C． D．【考点】曲线与方程．【分析】先把曲线方程整理成=1的形式，直线方程整理成y=ax+b，通过观察选项中的直线判断出a和b与0的关系，进而推断曲线方程形式推断其图象．【解答】解：把曲线方程整理成=1的形式，整理直线方程得y=ax+bA，C选项中，直线的斜率a＞0，截距b＜0，则曲线方程为双曲线，焦点在x轴，故C正确，A错误．B项中直线斜率a＜0，则曲线一定不是椭圆，故B项错误．对于D选项观察直线图象可知a＞0，b＞0，则曲线的方程的图象一定是椭圆，故D不符合．故选：C．二、填空题（每小题3分，共24分）13．在直角坐标系中，直线x+y﹣3=0的倾斜角是150°．【考点】直线的一般式方程；直线的倾斜角．【分析】由已知方程得到直线的斜率，根据斜率对于得到倾斜角．【解答】解：由已知直线的方程得到直线的斜率为，设倾斜角为α，则tanα=，α∈[0，180°），所以α=150°；故答案为：150°．14．已知直线l过点A（﹣2，0）且与直线x+2y﹣l=0平行．则直线l的方程是x+2y+2=0．【考点】直线的一般式方程与直线的平行关系．【分析】设与直线x+2y﹣l=0平行的直线方程为+2y+c=0，再把点A（﹣2，0）代入，求出c，从而得到结果．【解答】解：设与直线x+2y﹣l=0平行的直线方程为x+2y+c=0，把点A（﹣2，0）代入，得﹣2+0+c=0，解得c=2，∴过点A（﹣2，0）且与直线x+2y﹣l=0平行的直线方程为x+2y+2=0．故答案为：x+2y+2=0．15．已知圆的﹣条直径的两端点是（2，0），（2，﹣2）．则此圆方程是（x﹣2）2+（y+1）2=1．【考点】圆的一般方程．【分析】根据条件求出圆心和半径即可得到结论．【解答】解：∵圆的﹣条直径的两端点是（2，0），（2，﹣2）．∴圆心坐标为（，），即（2，﹣1），则半径r=1，则圆的方程为（x﹣2）2+（y+1）2=1，故答案为：（x﹣2）2+（y+1）2=116．离心率e=，一个焦点是F（0，﹣3）的椭圆标准方程为．【考点】椭圆的标准方程．【分析】先设出椭圆方程，根据条件列出关于a，b，c的方程，求出a，b，c即可得到结论．【解答】解：由题设椭圆的焦点在y轴上，设方程为：，由题得：解得所以椭圆标准方程为故答案为：．17．己知双曲线的焦点在x轴上．两个顶点的距离为2，焦点到渐近线的距离为，则双曲线的渐近线方程为y=±x．【考点】双曲线的简单性质．【分析】设双曲线的方程为﹣=1（a，b＞0），由题意可得a=1，运用点到直线的距离公式，可得b，进而得到渐近线方程．【解答】解：设双曲线的方程为﹣=1（a，b＞0），由题意可得a=1，设焦点F为（c，0），可得F到渐近线y=x的距离为=b=，可得渐近线方程为y=±x．故答案为：y=±x．18．若直线l过抛物线y=ax2（a＞0）的焦点，并且与y轴垂直，若l被抛物线截得的线段长为4，则a=．【考点】抛物线的应用．【分析】先把抛物线方程整理成标准方程，可得焦点坐标．进而可得l被抛物线截得的线段长，进而求得a．【解答】解：抛物线方程整理得x2=y，焦点（0，）l被抛物线截得的线段长即为通径长，故=4，a=；故答案为．19．已知M为抛物线y2=4x上一动点，F为这条抛物线的焦点，有一个定点A（3，2），则|MA|+|MF|的最小值=4．【考点】抛物线的简单性质．【分析】设点M在准线上的射影为D，则根据抛物线的定义可知|MF|=|MD|进而把问题转化为求|MA|+|MD|取得最小，进而可推断出当D，M，A三点共线时|MA|+|MD|最小，答案可得．【解答】解：设点M在准线上的射影为D，则根据抛物线的定义可知|MF|=|MD|，∴要求|MA|+|MF|取得最小值，即求|MA|+|MD|取得最小，当D，M，A三点共线时|MA|+|MD|最小，为3﹣（﹣1）=4．故答案为：4．20．有红盒、黄盒、蓝盒各一个，只有﹣个盒子里有金币．红盒上写有命题p：金币在这个盒子里；黄盒上写有命题q：金币不在这个金子里；蓝盒上写有命题r：金币不在红盒里．p、q、r中有且只有一个是真命题，则金币在黄盒子里．【考点】进行简单的合情推理．【分析】假设p真，推出不满足条件，可得p是假的，即金币不在红盒里；假设q是真的，退出不满足条件，故q是假的，即金币藏在黄盒里．【解答】解：金币藏在黄盒里．原因是：①若是红盒子的命题p是真的，那么命题q是真的，r是假的，不满足条件，故p是假的，即金币不在红盒里．②若q是真的，则r也是真的，不满足条件，故q是假的，即金币藏在黄盒里．故答案为：黄．三、解答题（本题共4小题，共40分）21．已知两条直线l1：x﹣ay=0（a≠0），l2：x+y﹣3=0．（1）若l1⊥l2，求a的值；（2）在（1）的条件下，如果直线l3经过l1与l2的交点，且经过点A（2，4），求直线l3的方程．【考点】待定系数法求直线方程；直线的一般式方程与直线的垂直关系．【分析】（1）利用直线垂直，得到系数的关系，求a；（2）利用（1）的结论，解方程组求出直线的交点，然后利用待定系数法求直线方程．【解答】解：（1）由l1⊥l2，∴A1B2﹣A2B1=0，…2'∴1﹣a=0即a=1…3'（2）…4'交点坐标为（1.5，1.5）…6'设直线l3的方程为：y=kx+b由直线l3过点（2，4）和点（1.5，1.5），得直线l3的方程为5x﹣y﹣6=0…8'22．圆的方程为x2+y2﹣6x﹣8y=0，过坐标原点作长为8的弦，求弦所在的直线方程．【考点】直线与圆的位置关系．【分析】求出圆心，求出半径，设直线方程，注意斜率存在时设为k，用圆心到直线的距离公式，求出k的值可得直线方程．斜率不存在时直线为x=0，只需验证弦长是否是8即可，是则此直线也符合要求．【解答】解：x2+y2﹣6x﹣8y=0即（x﹣3）2+（y﹣4）2=25，斜率存在时设所求直线为y=kx．∵圆半径为5，圆心M（3，4）到该直线距离为3，∴，∴9k2﹣24k+16=9（k2+1），∴．∴所求直线为y=；当斜率不存在是直线为x=0，验证其弦长为8，所以x=0也是所求直线．故所求直线为：y=或x=0．23．已知双曲线与椭圆共焦点，它们的离心率之和为，求双曲线方程．【考点】双曲线的标准方程；椭圆的简单性质；双曲线的简单性质．【分析】先根据椭圆方程求得椭圆的焦点和离心率，进而根据题意求得双曲线的焦点和离心率，进而求得双曲线方程得长轴和短轴，则双曲线方程可得．【解答】解：依题意可知椭圆方程中a=5，b=3，∴c==4∴椭圆焦点为F（O，±4），离心率为e=所以双曲线的焦点为F（O，±4），离心率为2，从而双曲线中求得c=4，a=2，b=．所以所求双曲线方程为24．已知椭圆的离心率，过点A（0，﹣b）和B（a，0）的直线与原点的距离为．（1）求椭圆的方程；（2）已知定点E（﹣1，0），若直线y=kx+2（k≠0）与椭圆交于C、D两点，问：是否存在k的值，使以CD为直径的圆过E点？请说明理由．【考点】圆与圆锥曲线的综合；椭圆的标准方程．【分析】（1）直线AB方程为bx﹣ay﹣ab=0，依题意可得：，由此能求出椭圆的方程．（2）假设存在这样的值．，得（1+3k2）x2+12kx+9=0，再由根的判别式和根与系数的关系进行求解．【解答】解：（1）直线AB方程为bx﹣ay﹣ab=0，依题意可得：，解得：a2=3，b=1，∴椭圆的方程为．（2）假设存在这样的值．，得（1+3k2）x2+12kx+9=0，∴△=（12k）2﹣36（1+3k2）＞0…①，设C（x1，y1），D（x2，y2），则而y1•y2=（kx1+2）（kx2+2）=k2x1x2+2k（x1+x2）+4，要使以CD为直径的圆过点E（﹣1，0），当且仅当CE⊥DE时，则y1y2+（x1+1）（x2+1）=0，∴（k2+1）x1x2+（2k+1）（x1+x2）+5=0…③将②代入③整理得k=，经验证k=使得①成立综上可知，存在k=使得以CD为直径的圆过点E．2016年5月11日。

2023-2024学年天津市红桥区高三（上）期中数学试卷一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. 1．设集合{|0}1xA x x =<−，{|03}B x x =<<，那么“m A ∈”是“m B ∈”的( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件2．设集合2{|40}A x x =−，{|20}B x x a =+，且{|21}A B x x =−，则(a = )A ．4−B ．2−C ．2D ．43．已知(sin ,cos )a αα=，(2,1)b =−，若a b ⊥，则tan α的值为( ) A ．2−B ．2C ．12D ．12−4．将函数sin()3y x π=−的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移3π个单位，得到的图象对应的解析式是( ) A ．1sin 2y x =B ．1sin()22y x π=−C ．1sin()26y x π=−D ．sin(2)6y x π=−5．设13log 2a =，121log 3b =，0.31()2c =，则( )A ．a b c <<B ．b a c <<C ．b c a <<D ．a c b <<6．已知正方体的所有顶点都在同一个球面上，若这个正方体的表面积为18，则这个球体的体积为( ) A ．92πB ．6πC ．9πD ．18π7．已知等差数列{}n a 满足1210a a +=，432a a −=，等比数列{}n b 满足23b a =，37b a =，则5(b = ) A ．32B ．64C ．128D ．2568．设函数()f x 在R 上可导，其导函数为()f x '，且函数()()g x xf x ='的图象如图所示，则下列结论中一定成立的是( )A ．()f x 有两个极值点B ．()f x 有两个极小值C ．(0)f 为函数的极小值D ．(1)f −为()f x 的极小值9．设函数22,0(),0ax x x f x ax x x ⎧+=⎨−+<⎩当1[2x ∈−，1]2时，恒有()()f x a f x +<，则实数a 的取值范围是( )A ．B ．(−C ．，0)D ．，1]2−二、填空题：本大题共6个小题，每小题5分，共30分.10．已知函数32()1f x ax x =−+在(0,1)上有增区间，则a 的取值范围是 ．11．已知数列{}n a 是公差不为零的等差数列，11a =、若1a 、2a 、5a 成等比数列，则n a =（5分） 12．如图，在ABC ∆中，90C ∠=︒，且3AC BC ==，点M 满足2BM MA =，则CM CB ⋅= ．13．已知函数()sin(2)4f x x π=−，则()f x 的最小正周期为 ；()f x 在区间3[,]88ππ上的取值范围是 ．14．已知向量(2,1)a =−，(1,)b m =−，(1,2)c =−，若()//a b c +，则m = ；若a 与b 的夹角为钝角，则m 的取值范围为 ． 15．若正实数x ，y 满足141x y+=，且不等式234yx m m +>−恒成立，则实数m 的取值范围是 ．三、解答题：本大题共5小题，共75分.解答应写出文字说明、证明过程或演算步骤.16．（14分）在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，且sin cos b A B ． （1）求角B 的大小；（2）若3b =，sin 2sin C A =，求a ，c 的值．17．（15分）如图所示，在三棱柱111ABC A B C −中，侧棱1AA ⊥底面ABC ，AB BC ⊥，D 为AC 的中点．14AA AB ==，6BC =． （Ⅰ）证明：1//AB 平面1BC D ． （Ⅱ）求二面角1C BD C −−的余弦值．18．（15分）已知n S 为数列{}n a 的前n 项和，*3(1)()n n S na n n n N =−−∈，且212a =． （Ⅰ）求1a 的值；（Ⅱ）求数列{}n a 的通项公式； （Ⅲ）求证：1113ni i S =<∑． 19．（15分）已知函数2()(1)f x x a x a =−++， （1）当2a =时，求关于x 的不等式()0f x >的解集； （2）求关于x 的不等式()0f x <的解集；（3）若()20f x x +在区间(1,)+∞上恒成立，求实数a 的取值范围． 20．（16分）已知函数2()1f x x alnx =−−．（1）若()f x 的单调递增区间为[2，)+∞，求a 的值． （2）求()f x 在[1，)+∞上的最小值．2023-2024学年天津市红桥区高三（上）期中数学试卷参考答案与试题解析一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. 1．设集合{|0}1xA x x =<−，{|03}B x x =<<，那么“m A ∈”是“m B ∈”的( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件解：由01xx <−得01x <<，即{|01}A x x =<<， 分析可得A B ，即可知“m A ∈”是“m B ∈”的充分而不必要条件，故选：A ．2．设集合2{|40}A x x =−，{|20}B x x a =+，且{|21}A B x x =−，则(a = )A ．4−B ．2−C ．2D ．4解：集合2{|40}{|22}A x x x x =−=−，1{|20}{|}2B x x a x x a =+=−，由{|21}AB x x =−，可得112a −=，则2a =−．故选：B ．3．已知(sin ,cos )a αα=，(2,1)b =−，若a b ⊥，则tan α的值为( ) A ．2− B ．2C ．12D ．12−解：(sin ,cos )a αα=，(2,1)b =−，a b ⊥，∴2sin cos 0a b αα=−+=，cos 2sin αα∴=， sin 1tan cos 2ααα∴==． 故选：C ．4．将函数sin()3y x π=−的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移3π个单位，得到的图象对应的解析式是( ) A ．1sin 2y x =B ．1sin()22y x π=−C ．1sin()26y x π=−D ．sin(2)6y x π=−解：将图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），可得函数1sin()23y x π=−，再将所得的图象向左平移3π个单位，得函数1sin[()]233y x ππ=+−，即1sin()26y x π=−，故选：C ．5．设13log 2a =，121log 3b =，0.31()2c =，则( )A ．a b c <<B ．b a c <<C ．b c a <<D ．a c b <<解：1133log 210a log =<=， 112211log 132b log =>=， 0.30110()()122c <=<=，a cb ∴<<． 故选：D ．6．已知正方体的所有顶点都在同一个球面上，若这个正方体的表面积为18，则这个球体的体积为( ) A ．92π B ．6π C ．9π D ．18π解：设正方体的棱长为a ，其外接球的半径为R ， 因为正方体的表面积为18， 所以2618a =，所以23,a a = 所以22(2)39R a ==，得32R =， 所以正方体外接球的体积为334439()3322R πππ==，故选：A ．7．已知等差数列{}n a 满足1210a a +=，432a a −=，等比数列{}n b 满足23b a =，37b a =，则5(b = ) A ．32B ．64C ．128D ．256解：等差数列{}n a 满足1210a a +=，432a a −=，∴12102a d d +=⎧⎨=⎩，则14a =，2d =， 则34228a =+⨯=，742616a =+⨯=，则238b a ==，3716b a ==，则公比321628b q b ===， 则25316464b b q ==⨯=， 故选：B ．8．设函数()f x 在R 上可导，其导函数为()f x '，且函数()()g x xf x ='的图象如图所示，则下列结论中一定成立的是( )A ．()f x 有两个极值点B ．()f x 有两个极小值C ．(0)f 为函数的极小值D ．(1)f −为()f x 的极小值解：由函数()()g x xf x '=的图象， 可得当(,2)x ∈−∞−时，()0xf x '>， 所以()0f x '<，()f x 单调递减； 当(2,0)x ∈−时，()0xf x '<， 所以()0f x '>，()f x 单调递增； 当(0,1)x ∈时，()0xf x '<， 所以()0f x '<，()f x 单调递减； 当(1,)x ∈+∞时，()0xf x '>， 所以()0f x '>，()f x 单调递增，综上，当2x =−时，函数()f x 取得极小值； 当0x =时，函数()f x 取得极大值； 当1x =时，函数()f x 取得极小值， 故选项ABC 错误，选项B 正确． 故选：B ．9．设函数22,0(),0ax x x f x ax x x ⎧+=⎨−+<⎩当1[2x ∈−，1]2时，恒有()()f x a f x +<，则实数a 的取值范围是( ) A．B．(− C．，0)D．，1]2−解：0a =时，显然不符题意；当1[2x ∈−，1]2时，恒有()()f x a f x +<，即为()f x 的图象恒在()f x a +的图象之上， 则0a <，即()f x 的图象右移． 故A ，B 错；画出函数22,0()(0),0ax x x f x a ax x x ⎧+=<⎨−+<⎩的图象， 当12x =−时，111()242f a −=−−；而22(),()(),a x a x a x af x a a x a x a x a ⎧+++−+=⎨−+++<−⎩， 则12x =−时，由21111()2242a a a a −−++−=−−，解得a =， 随着()f x a +的图象左移至()f x 的过程中，均有()f x 的图象恒在()f x a +的图象上，则a 的范围是，0)，故选：C ．二、填空题：本大题共6个小题，每小题5分，共30分.10．已知函数32()1f x ax x =−+在(0,1)上有增区间，则a 的取值范围是 2(,)3+∞ ．解：函数32()1f x ax x =−+． 可得2()32f x ax x '=−．函数32()1f x ax x =−+在(0,1)上有增区间，可知导函数在(0,1)上有极值点，导函数在(0,1)上有解，或0a =时，2320ax x −恒成立（显然不成立）． 可得2(0,1)3a ∈，解得：23a >， 故答案为：2(,)3+∞．11．已知数列{}n a 是公差不为零的等差数列，11a =、若1a 、2a 、5a 成等比数列，则n a = 21n − 解：设公差为d ，则21a d =+，514a d =+， 则21(14)(1)d d ⨯+=+，2d ∴=， 21n a n ∴=−， 故答案为：21n −．12．如图，在ABC ∆中，90C ∠=︒，且3AC BC ==，点M 满足2BM MA =，则CM CB ⋅= 3 ．解法一：因为点M 满足2BM MA =，90C ∠=︒，且3AC BC ==， 所以1112()3333CM CA AM CA AB CA CB CA CB CA =+=+=+−=+，所以2212121()3333333CM CB CB CA CB CB CA CB ⋅=+⋅=+⋅=⨯=．解法二：如图，以C 为坐标原点，CA ，CB 所在直线分别为x ，y 轴建立平面直角坐标系，如图所示，则(3,0)A ，(0,3)B ，设(,)M x y ，则由2BM MA =，得2(3)32x x y y =−⎧⎨−=−⎩，解得21x y =⎧⎨=⎩，即M 点的坐标为(2,1)，所以(2,1),(0,3)CM CB ==， 所以20133CM CB ⋅=⨯+⨯=． 故答案为：3．13．已知函数()sin(2)4f x x π=−，则()f x 的最小正周期为 π ；()f x 在区间3[,]88ππ上的取值范围是 ．解：由函数()f x 的解析式，可得最小正周期22T ππ==； 3[,]88x ππ∈，可得2[04x π−∈，]2π，所以()[()8f x f π∈，3()][08f π=，1]．所以()f x 在区间3[,]88ππ上的取值范围是[0，1]．故答案为：π；[0，1]．14．已知向量(2,1)a =−，(1,)b m =−，(1,2)c =−，若()//a b c +，则m = 1− ；若a 与b 的夹角为钝角，则m 的取值范围为 ．解：根据题意，向量(2,1)a =−，(1,)b m =−，(1,2)c =−，则(1,1)a b m +=−， 若()//a b c +，则有2(1)m =−−，解可得1m =−；若a 与b 的夹角为钝角，则2021a b m m ⎧⋅=−−<⎪⎨≠⎪⎩，解可得2m >−且12m ≠，即m 的取值范围为{|2m m >−且1}2m ≠；故答案为：1−，{|2m m >−且1}2m ≠．15．若正实数x ，y 满足141x y+=，且不等式234yx m m +>−恒成立，则实数m 的取值范围是 (1,4)− ．解：因为正实数x ，y 满足141x y+=， 所以144()()22244444y y y x y x x x y x y x +=++=+++=， 当且仅当44y x x y =且141x y+=，即2x =，8y =时取等号，则4yx +的最小值4， 因为234yx m m +>−恒成立， 所以234m m −<，解得14m −<<． 故m 的范围为(1,4)−． 故答案为：(1,4)−．三、解答题：本大题共5小题，共75分.解答应写出文字说明、证明过程或演算步骤.16．（14分）在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，且sin cos b A B ． （1）求角B 的大小；（2）若3b =，sin 2sin C A =，求a ，c 的值．解：（1）sin cos b A B ，由正弦定理可得sin sin cos B A A B ，即得tan B ， 由于：0B π<<， ∴3B π=．（2）sin 2sin C A =， 由正弦定理得2c a =，由余弦定理2222cos b a c ac B =+−， 229422cos3a a a a π=+−⋅，解得a =∴2c a ==．故a =c =17．（15分）如图所示，在三棱柱111ABC A B C −中，侧棱1AA ⊥底面ABC ，AB BC ⊥，D 为AC 的中点．14AA AB ==，6BC =． （Ⅰ）证明：1//AB 平面1BC D ． （Ⅱ）求二面角1C BD C −−的余弦值．（Ⅰ）证明：如图，连接1B C ，设1B C 与1BC 相交于点O ，连接OD ，因为四边形11BCC B 是平行四边形，所以点O 为1B C 的中点，因为D 为AC 的中点，所以OD 为△1AB C 的中位线， 所以1//OD AB ，因为OD ⊂平面1BC D ，1AB ⊂/平面1BC D ，所以1//AB 平面1BC D ；（Ⅱ）解：因为三棱柱111ABC A B C −中，侧棱1AA ⊥底面ABC ，AB BC ⊥， 所以11B C ，1B B ，11B A 两两互相垂直，以1B 为原点，11B C ，1B B ，11B A 所在直线分别为x ，y ，z 轴建立空间直角坐标系，如图所示，则1(6C ，0，0)，(0B ，4，0)，(6C ，4，0)，(3D ，4，2)，所以(3,0,2)BD =，1(6,4,0)BC =−，设平面1BC D 的法向量为(,,)n x y z =，则1320640n BD x z n BC x y ⎧⋅=+=⎪⎨⋅=−=⎪⎩，解得3232z x y x ⎧=−⎪⎪⎨⎪=⎪⎩， 取2x =，得3y =，3z =−，所以(2,3,3)n =−， 由题知平面BCD 得一个法向量为(0,1,0)m =，所以cos ,||||14m n m n m n ⋅<>==⨯由图可知，二面角1C BD C −−为锐二面角，所以二面角1C BD C −−． 18．（15分）已知n S 为数列{}n a 的前n 项和，*3(1)()n n S na n n n N =−−∈，且212a =． （Ⅰ）求1a 的值；（Ⅱ）求数列{}n a 的通项公式；（Ⅲ）求证：1113n i i S =<∑． （Ⅰ）解：由3(1)n n S na n n =−−，得122232(21)a a a +=−⨯⨯−， 即126a a =−，212a =，11266a ∴=−=；（Ⅱ）解：由3(1)n n S na n n =−−，得11(1)3(1)(2)(2)n n S n a n n n −−=−−−−，两式作差得：1(1)66n n n a na n a n −=−−−+，即16(2)n n a a n −−=． ∴数列{}n a 是以6为首项，以6为公差的等差数列， 66(1)6n a n n ∴=+−=；（Ⅲ）证明：6(1)63(1)2n n n S n n n −=+=+， 则11111()3(1)31n S n n n n ==−++， ∴1121111111111111(1)(1)32231313n i i n S S S S n n n ==++⋯+=−+−+⋯+−=−<++∑． 19．（15分）已知函数2()(1)f x x a x a =−++，（1）当2a =时，求关于x 的不等式()0f x >的解集；（2）求关于x 的不等式()0f x <的解集；（3）若()20f x x +在区间(1,)+∞上恒成立，求实数a 的取值范围． 解：（1）当2a =时，则2()32f x x x =−+，由()0f x >，得2320x x −+>， 令2320x x −+=，解得1x =，或2x =∴原不等式的解集为(−∞，1)(2⋃，)+∞（2）由()0f x <得()(1)0x a x −−<，令()(1)0x a x −−=，得1x a =，21x =，5⋯ 分， 当1a >时，原不等式的解集为(1,)a ；6⋯ 分， 当1a =时，原不等式的解集为∅；⋯（7分）， 当1a <时，原不等式的解集为(,1)a ．⋯（8分）．（2）由()20f x x +即20x ax x a −++在(1,)+∞上恒成立， 得2..91x x a x +⋯− 分， 令1(0)t x t =−>，则22(1)1232231x x t t t x t t++++==+++−，13⋯ 分∴223a +．故实数a 的取值范围是(3]14−∞⋯ 分20．（16分）已知函数2()1f x x alnx =−−．（1）若()f x 的单调递增区间为[2，)+∞，求a 的值．（2）求()f x 在[1，)+∞上的最小值．解：（1）已知2()1f x x alnx =−−，函数定义域为(0,)+∞可得22()2a x a f x x x x−'=−=， 若函数()f x 的单调增区间为[2，)+∞，此时0a >；当)x ∈+∞时，()0f x '，所以函数的单调递增区间为)+∞．2=， 解得8a =；（2）易知22()x a f x x−'=，[1x ∈，)+∞ 当0a 时，()0f x '，函数()f x 在[1，)+∞上单调递增， 所以()f x f （1）0=；②当0a >，当x ∈，()0f x '<，()f x 单调递减；当)x ∈+∞时，()0f x '>，()f x 单调递增， 12a ，即02a <时， 函数()f x 在[1，)+∞单调递增，此时()f x f （1）0=，1>，即2a >时，函数()f x 在上单调递减，在)+∞上单调递增； 此时()()12222a a a a f x f ln =−−． 综上所述：当2a 时，最小值为0；当2a >时，最小值为1222a a a ln −−．。

2015-2016学年天津市红桥区高三（上）期中数学试卷（文科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={1，2，4，5，6}，B={1，3，5}，则集合A∩B=( )A．{1，3，5} B．{1，5} C．{2，4，6} D．{1，2，3，4，5.6}2．i是虚数单位，复数=( )A．B．C．D．3．命题“对∀∈R，x2﹣3x+5≤0”的否定是( )A．∃x0∈R，x02﹣3x0+5≤0 B．∃x0∈R，x02﹣3x0+5＞0C．∀x∈R，x2﹣3x+5≤0D．∀x0∈R，x02﹣3x0+5＞04．某程序框图如图所示，则输出的结果S等于( )A．26 B．57 C．60 D．615．设a=log0.32，b=log32，c=20.3，则这三个数的大小关系是( )A．b＞c＞a B．a＞c＞b C．a＞b＞c D．c＞b＞a6．已知=（1，2），=（0，1），=（k，﹣2），若（+2）⊥，则k=( )A．2 B．﹣2 C．8 D．﹣87．将函数y=sin（x+）图象上各点的横坐标缩短到原来的倍（纵坐标不变），再向右平移个单位，那么所得图象的一条对称轴方程为( )A．x=﹣B．x=﹣C．x=D．x=8．如图，在三角形ABC中，已知AB=2，AC=3，∠BAC=θ，点D为BC的三等分点．则的取值范围为( )A．B．C．D．二、填空题：本大题共6个小题，每小题5分，共30分．9．设全集U={1，2，3，4，5，6}，集合A={1，3，5}，B={2，3}，则A∩（∁U B）=__________．10．计算的值为__________．11．计算：log525+lg=__________．12．在△ABC中，AC=，BC=2，B=60°，则△ABC的面积等于__________．13．设函数f（x）=，则f（f（﹣4））的值是__________．14．如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC．过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F．若AB=AC，AE=3，BD=4则线段AF的长为__________．三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．15．（13分）已知集合A={x|（x﹣2）[x﹣（3a+1）]＜0}，B={x|2a＜x＜a2+1}．（Ⅰ）当a=﹣2时，求A∪B；（Ⅱ）求使B⊆A的实数a的取值范围．16．（13分）在等差数列{a n}中，已知a1+a4+a7=9，a3+a6+a9=21，（Ⅰ）求数列{a n}的通项a n；（Ⅱ）求数列{a n}的前9项和S9；（Ⅲ）若，求数列{c n}的前n项和T n．17．（13分）已知cosθ=，（Ⅰ）求sin2θ的值；（Ⅱ）求的值；（Ⅲ）求的值．18．（13分）已知函数f（x）=sin2ωx+cos2ωx．（ω＞0）的最小正周期为4π，（Ⅰ）求ω的值及函数f（x）的单调递减区间；（Ⅱ）将函数y=f（x）的图象上各点的横坐标向右平行移动个单位长度，纵坐标不变，得到函数y=g（x）的图象，求函数g（x）在上的最大值和最小值．19．（14分）已知函数f（x）=ax2+bx+c（a≠0），满足f（0）=2，f（x+1）﹣f（x）=2x﹣1 （Ⅰ）求函数f（x）的解析式；（Ⅱ）当x∈[﹣1，2]时，求函数的最大值和最小值．（Ⅲ）若函数g（x）=f（x）﹣mx的两个零点分别在区间（﹣1，2）和（2，4）内，求m的取值范围．20．（14分）已知：已知函数f（x）=﹣+2ax，（Ⅰ）若曲线y=f（x）在点P（2，f（2））处的切线的斜率为﹣6，求实数a；（Ⅱ）若a=1，求f（x）的极值；（Ⅲ）当0＜a＜2时，f（x）在[1，4]上的最小值为﹣，求f（x）在该区间上的最大值．2015-2016学年天津市红桥区高三（上）期中数学试卷（文科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={1，2，4，5，6}，B={1，3，5}，则集合A∩B=( )A．{1，3，5} B．{1，5} C．{2，4，6} D．{1，2，3，4，5.6}【考点】交集及其运算．【专题】计算题；集合．【分析】由A与B，求出两集合的交集即可．【解答】解：∵A={1，2，4，5，6}，B={1，3，5}，∴A∩B={1，5}，故选：B．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．i是虚数单位，复数=( )A．B．C．D．【考点】复数代数形式的乘除运算．【专题】数系的扩充和复数．【分析】利用复数的运算法则、共轭复数的定义即可得出．【解答】解：复数==，故选：C．【点评】本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．3．命题“对∀∈R，x2﹣3x+5≤0”的否定是( )A．∃x0∈R，x02﹣3x0+5≤0 B．∃x0∈R，x02﹣3x0+5＞0C．∀x∈R，x2﹣3x+5≤0D．∀x0∈R，x02﹣3x0+5＞0【考点】命题的否定．【专题】计算题；规律型；简易逻辑．【分析】直接利用全称命题的否定是特称命题写出结果即可．【解答】解：因为全称命题的否定是特称命题，所以，命题“对∀∈R，x2﹣3x+5≤0”的否定是：∃x0∈R，x02﹣3x0+5＞0．故选：B．【点评】本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．4．某程序框图如图所示，则输出的结果S等于( )A．26 B．57 C．60 D．61【考点】程序框图．【专题】计算题；图表型；分类讨论；试验法；算法和程序框图．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算并输出S值．模拟程序的运行过程，用表格对程序运行过程中各变量的值进行分析，不难得到最终的输出结果．【解答】解：程序在运行过程中各变量的值如下表示：k S 是否继续循环循环前1 1/第一圈2 4 是第二圈3 11 是第三圈4 26 是第四圈5 57 否故最终的输出结果为：57故选：B．【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，属于基础题．5．设a=log0.32，b=log32，c=20.3，则这三个数的大小关系是( )A．b＞c＞a B．a＞c＞b C．a＞b＞c D．c＞b＞a【考点】对数值大小的比较．【专题】转化思想；数学模型法；函数的性质及应用．【分析】利用指数函数与对数函数的单调性即可得出．【解答】解：∵a=log0.32＜0，0＜b=log32＜1，c=20.3＞1，∴c＞b＞a．故选：D．【点评】本题考查了指数函数与对数函数的单调性，考查了推理能力与计算能力，属于中档题．6．已知=（1，2），=（0，1），=（k，﹣2），若（+2）⊥，则k=( )A．2 B．﹣2 C．8 D．﹣8【考点】数量积判断两个平面向量的垂直关系．【专题】平面向量及应用．【分析】由向量的坐标运算易得的坐标，进而由可得它们的数量积为0，可得关于k的方程，解之可得答案．【解答】解：∵=（1，2），=（0，1），∴=（1，4），又因为，所以=k﹣8=0，解得k=8，故选C【点评】本题考查平面向量数量积和向量的垂直关系，属基础题．7．将函数y=sin（x+）图象上各点的横坐标缩短到原来的倍（纵坐标不变），再向右平移个单位，那么所得图象的一条对称轴方程为( )A．x=﹣B．x=﹣C．x=D．x=【考点】函数y=Asin（ωx+φ）的图象变换．【专题】三角函数的图像与性质．【分析】根据函数y=Asin（ωx+φ）的图象变换规律，余弦函数的图象的对称性，可得结论．【解答】解：将函数y=sin（x+）图象上各点的横坐标缩短到原来的倍（纵坐标不变），可得函数y=sin（2x+）的图象，再向右平移个单位，那么所得图象对应的函数解析式为y=sin[2（x﹣）+]=sin（2x﹣）=﹣cos2x，故最后所得函数的图象的一条对称轴方程为2x=kπ，即 x=，k∈z，结合所给的选项可得只有B满足条件，故选：B．【点评】本题主要考查函数y=Asin（ωx+φ）的图象变换规律，余弦函数的图象的对称性，属于中档题．8．如图，在三角形ABC中，已知AB=2，AC=3，∠BAC=θ，点D为BC的三等分点．则的取值范围为( )A．B．C．D．【考点】平面向量数量积的运算．【专题】计算题；转化思想；向量法；平面向量及应用．【分析】直接利用向量的运算法则和数量积运算把化为2cos，然后由﹣1＜cosθ＜1求得答案．【解答】解：∵====，∴=（）•（）=﹣==2cos．∵﹣1＜cosθ＜1，∴﹣＜2cosθ+＜．∴∈（﹣）．故选：D．【点评】本题考查平面向量的数量积运算，熟练掌握向量的运算法则和数量积运算是解题的关键，是中档题．二、填空题：本大题共6个小题，每小题5分，共30分．9．设全集U={1，2，3，4，5，6}，集合A={1，3，5}，B={2，3}，则A∩（∁U B）={1，5}．【考点】交、并、补集的混合运算．【专题】集合思想；综合法；集合．【分析】进行集合的补集、交集运算即可．【解答】解：∁U B={1，4，5，6}；∴A∩（∁U B）={1，5}．故答案为：{1，5}．【点评】考查列举法表示集合，全集的概念，以及补集、交集的运算．10．计算的值为﹣．【考点】运用诱导公式化简求值．【专题】三角函数的求值．【分析】所求式子中的角变形后，利用诱导公式化简，再利用特殊角的三角函数值计算即可得到结果．【解答】解：cos=cos（π+）=﹣cos=﹣．故答案为：﹣【点评】此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．11．计算：log525+lg=．【考点】对数的运算性质．【专题】计算题；函数思想；函数的性质及应用．【分析】直接利用导数的运算法则化简求解即可．【解答】解：log525+lg=2﹣2++1=故答案为：．【点评】本题考查导数的运算法则的应用，考查计算能力．12．在△ABC中，AC=，BC=2，B=60°，则△A BC的面积等于．【考点】余弦定理；三角形的面积公式．【专题】计算题；解三角形．【分析】通过余弦定理求出AB的长，然后利用三角形的面积公式求解即可．【解答】解：设AB=c，在△ABC中，由余弦定理知AC2=AB2+BC2﹣2AB•BCcosB，即7=c2+4﹣2×2×c×cos60°，c2﹣2c﹣3=0，又c＞0，∴c=3．S△ABC=AB•BCsinB=BC•h可知S△ABC==．故答案为：【点评】本题考查三角形的面积求法，余弦定理的应用，考查计算能力．13．设函数f（x）=，则f（f（﹣4））的值是4．【考点】函数的值．【专题】计算题；函数思想；函数的性质及应用．【分析】直接利用分段函数求解函数值即可．【解答】解：函数f（x）=，则f（f（﹣4））=f（16）=log216=4．故答案为：4．【点评】本题考查分段函数的应用，函数值的求法，考查计算能力．14．如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC．过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F．若AB=AC，AE=3，BD=4则线段AF的长为．【考点】与圆有关的比例线段．【专题】综合题；选作题；转化思想；综合法．【分析】由切割线定理得到AE2=EB•ED=EB（EB+BD），求出EB=5，由已知条件推导出四边形AEBC 是平行四边形，从而得到AC=AB=BE=5，BC=AE=3，由△AFC∽△DFB，能求出CF的长．【解答】解：∵AB=AC，AE=3，BD=4，梯形ABCD中，AC∥BD，BD=4，由切割线定理可知：AE2=EB•ED=EB（EB+BD），即45=BE（BE+4），解得EB=5，∵AC∥BD，∴AC∥BE，∵过点A作圆的切线与DB的延长线交于点E，∴∠BAE=∠C，∵AB=AC，∴∠ABC=∠C，∴∠ABC=∠BAE，∴AE∥BC，∴四边形AEBC是平行四边形，∴EB=AC，∴AC=AB=BE=5，∴BC=AE=3，∵△AFC∽△DFB，∴=，即=，解得CF=．故答案为：．【点评】本题考查与圆有关的线段长的求法，是中档题，解题时要认真审题，注意切割线定理的合理运用．三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．15．（13分）已知集合A={x|（x﹣2）[x﹣（3a+1）]＜0}，B={x|2a＜x＜a2+1}．（Ⅰ）当a=﹣2时，求A∪B；（Ⅱ）求使B⊆A的实数a的取值范围．【考点】集合的包含关系判断及应用；并集及其运算．【专题】分类讨论；分类法；集合．【分析】由已知中集合A={x|（x﹣2）（x﹣3a﹣1）＜0}，集合B={x|（x﹣2a）（x﹣a2﹣1）＜0}，我们先对a进行分类讨论后，求出集合A，B，再由B⊆A，我们易构造出一个关于a的不等式组，解不等式组，即可得到实数a的取值范围【解答】（Ⅰ）解：当a=﹣2时，A={x|﹣5＜x＜2}，B={x|﹣4＜x＜5}，∴A∪B={x|﹣5＜x＜5}．（Ⅱ）∵B={x|2a＜x＜a2+1}当时，2＞3a+1，A={x|3a+1＜x＜2}，﹣﹣﹣﹣﹣﹣﹣﹣要使B⊆A必须此时a=﹣1，当时，A=ϕ，使 B⊆A的a不存在；﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当时，2＜3a+1，A={x|2＜x＜3a+1}要使B⊆A必须，故1≤a≤3．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣综上可知，使的实数a的取值范围为[1，3]∪{﹣1}．﹣﹣﹣﹣﹣（13分）【点评】本题考查集合的基本运算，集合关系中的参数取值问题，考查计算能力，分类讨论思想的应用16．（13分）在等差数列{a n}中，已知a1+a4+a7=9，a3+a6+a9=21，（Ⅰ）求数列{a n}的通项a n；（Ⅱ）求数列{a n}的前9项和S9；（Ⅲ）若，求数列{c n}的前n项和T n．【考点】数列的求和；等差数列的通项公式．【专题】计算题；方程思想；数学模型法；等差数列与等比数列．【分析】（I）利用等差数列的通项公式即可得出；（II）利用等差数列的前n项和公式即可得出；（III）利用等比数列的前n项和公式即可得出．【解答】解：（Ⅰ）设等差数列{a n}的公差为d，∵a1+a4+a7=9， a3+a6+a9=21，得，解得a1=﹣3，d=2，∴a n=2n﹣5．（Ⅱ）S9=9a1+36d=9×（﹣3）+36×2=45．（Ⅲ）由（Ⅰ），∴{c n}是首项c1=1，公比q=4的等比数列，∴．【点评】本题考查了等差数列与等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．17．（13分）已知cosθ=，（Ⅰ）求sin2θ的值；（Ⅱ）求的值；（Ⅲ）求的值．【考点】两角和与差的正切函数；两角和与差的余弦函数．【专题】计算题；转化思想；分析法；三角函数的求值．【分析】（Ⅰ）利用同角三角函数关系式可求sinθ的值，根据二倍角的正弦函数公式即可求值．（Ⅱ）利用（Ⅰ）的结论及两角和的余弦函数公式即可求值得解．（Ⅲ）利用同角三角函数关系式可求tanθ的值，根据两角和的正切函数公式即可求值．【解答】（本小题满分13分）解：（Ⅰ）∵，∴．﹣﹣﹣﹣﹣﹣（公式，结论1分）﹣﹣﹣﹣∴．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（公式，结论1分）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（Ⅱ）∴=cosθcos﹣sin==．﹣﹣﹣﹣（公式，函数值，结论1分）﹣﹣（Ⅲ）∵，﹣﹣﹣﹣﹣﹣﹣（公式1分）∴．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（公式，结论1分）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（13分）【点评】本题主要考查了同角三角函数关系式，二倍角的正弦函数公式、余弦函数公式、正切函数公式的应用，考查了计算能力，属于基础题．18．（13分）已知函数f（x）=sin2ωx+cos2ωx．（ω＞0）的最小正周期为4π，（Ⅰ）求ω的值及函数f（x）的单调递减区间；（Ⅱ）将函数y=f（x）的图象上各点的横坐标向右平行移动个单位长度，纵坐标不变，得到函数y=g（x）的图象，求函数g（x）在上的最大值和最小值．【考点】函数y=Asin（ωx+φ）的图象变换；三角函数中的恒等变换应用．【专题】计算题；数形结合；数形结合法；三角函数的图像与性质．【分析】（Ⅰ）利用两角和的正弦函数公式化简可得解析式：f（x）=sin（2ωx+），由周期公式可求ω，解得函数解析式，由，k∈Z*，即可解得f（x）的单调递减区间．（Ⅱ）由函数y=Asin（ωx+φ）的图象变换规律可得解析式，由正弦函数的图象和性质，即可求得函数g（x）在上的最大值和最小值．【解答】（本小题满分13分）解：（Ⅰ）因为，（公式2分）又因为，所以；（公式，结论1分）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣解得：．当，k∈Z*，函数f（x）单调递减，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣所以，函数f（x）的单调递减区间为k∈Z*．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（Ⅱ）将函数y=f（x）的图象上各点的横坐标向右平行移动个单位长度，纵坐标不变，得到函数y=g（x）的图象，，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣g（x）在上单调递增，在上单调递减，，，所以g（x）在上最大值为，最小值为．（单调性，结论各1分）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（13分）【点评】本题主要考查了两角和的正弦函数公式，周期公式，函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象和性质的应用，属于中档题．19．（14分）已知函数f（x）=ax2+bx+c（a≠0），满足f（0）=2，f（x+1）﹣f（x）=2x﹣1 （Ⅰ）求函数f（x）的解析式；（Ⅱ）当x∈[﹣1，2]时，求函数的最大值和最小值．（Ⅲ）若函数g（x）=f（x）﹣mx的两个零点分别在区间（﹣1，2）和（2，4）内，求m的取值范围．【考点】函数的最值及其几何意义；函数零点的判定定理．【专题】计算题；函数思想；转化思想；解题方法；函数的性质及应用．【分析】（Ⅰ）利用f（0）=2，f（x+1）﹣f（x）=2x﹣1，直接求出a、b、c，然后求出函数的解析式．（Ⅱ）利用二次函数的对称轴与区间的关系，直接求解函数的最值．（Ⅲ）利用g（x）的两个零点分别在区间（﹣1，2）和（2，4）内，列出不等式组，即可求出M的范围．【解答】（本小题满分14分）解：（Ⅰ）由f（0）=2，得c=2，又f（x+1）﹣f（x）=2x﹣1得2ax+a+b=2x﹣1，故解得：a=1，b=﹣2，所以f（x）=x2﹣2x+2．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（a，b，c各，解析式1分）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（Ⅱ）f（x）=x2﹣2x+2=（x﹣1）2+1，对称轴为x=1∈[﹣1，2]，故f min（x）=f（1）=1，又f（﹣1）=5，f（2）=2，所以f max（x）=f（﹣1）=5．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（Ⅲ）g（x）=x2﹣（2+m）x+2，若g（x）的两个零点分别在区间（﹣1，2）和（2，4）内，则满足﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣解得：．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）【点评】本题考查二次函数的解析式的求法，二次函数的性质与最值的求法，零点判定定理的应用，考查计算能力．20．（14分）已知：已知函数f（x）=﹣+2ax，（Ⅰ）若曲线y=f（x）在点P（2，f（2））处的切线的斜率为﹣6，求实数a；（Ⅱ）若a=1，求f（x）的极值；（Ⅲ）当0＜a＜2时，f（x）在[1，4]上的最小值为﹣，求f（x）在该区间上的最大值．【考点】利用导数研究曲线上某点切线方程；导数在最大值、最小值问题中的应用．【专题】计算题；规律型；函数思想；方程思想；转化思想；综合法；导数的综合应用．【分析】（Ⅰ）求出曲线y=f（x）在点P（2，f（2））处的导数值等于切线的斜率为﹣6，即可求实数a；（Ⅱ）通过a=1，利用导函数为0，判断导数符号，即可求f（x）的极值；（Ⅲ）当0＜a＜2时，利用导函数的单调性，通过f（x）在[1，4]上的最小值为﹣，即可求出a，然后求f（x）在该区间上的最大值．【解答】（本小题满分14分）解：（Ⅰ）因为f′（x）=﹣x2+x+2a，曲线y=f（x）在点P（2，f（2））处的切线的斜率k=f′（2）=2a﹣2，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣依题意：2a﹣2=﹣6，a=﹣2．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（Ⅱ）当a=1时，，f′（x）=﹣x2+x+2=﹣（x+1）（x﹣2）﹣﹣﹣﹣x （﹣∞，﹣1）﹣1 （﹣1，2） 2 （2，+∞）﹣0 + 0 ﹣f′（x）f（x）单调减单调增单调减所以，f（x）的极大值为，f（x）的极小值为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（Ⅲ）令f′（x）=0，得，，f（x）在（﹣∞，x1），（x2，+∞）上单调递减，在（x1，x2）上单调递增，当0＜a＜2时，有x1＜1＜x2＜4，所以f（x）在[1，4]上的最大值为f（x2），f（4）＜f（1），所以f（x）在[1，4]上的最小值为，解得：a=1，x2=2．故f（x）在[1，4]上的最大值为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）【点评】本题考查导数的综合应用，切线方程以及极值的求法，函数的单调性与函数的最值的关系，考查转化思想以及计算能力．。

2016-2017学年天津市红桥区高二（上）期中数学试卷（理科）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. 1．（4分）命题“∀x∈R，x2+1≥1”的否定是（）A．∀x∈R，x2+1＜1 B．∃x∈R，x2+1≤1 C．∃x∈R，x2+1＜1 D．∃x ∈R，x2+1≥12．（4分）已知点A（2，3，5），B（3，1，4），则A，B两点间的距离为（）A．B．C．D．3．（4分）若直线a，平面α满足a⊄α，则下列结论正确的是（）A．直线a一定与平面α平行B．直线a一定与平面α相交C．直线a一定与平面α平行或相交D．直线a一定与平面α内所有直线异面4．（4分）已知向量是空间的一个基底，其中与向量，一定构成空间另一个基底的向量是（）A．B．C．D．都不可以5．（4分）“a，b不相交”是“a，b异面”的（）A．充分非必要条件 B．必要非充分条件C．充要条件D．非充分非必要条件6．（4分）若直线a平行于平面α，则下列结论正确的是（）A．直线a一定与平面α内所有直线平行B．直线a一定与平面α内所有直线异面C．直线a一定与平面α内唯一一条直线平行D．直线a一定与平面α内一组平行直线平行7．（4分）设O是空间一点，a，b，c是空间三条直线，α，β是空间两个平面，则下列命题中，逆命题不成立的是（）A．当a∩b=O且a⊂α，b⊂α时，若c⊥a，c⊥b，则c⊥αB．当a∩b=O且a⊂α，b⊂α时，若a∥β，b∥β，则α∥βC．当b⊂α时，若b⊥β，则α⊥βD．当b⊂α时，且c⊄α时，若c∥α，则b∥c8．（4分）以下四个命题中，正确命题是（）A．不共面的四点中，其中任意三点不共线B．若点A，B，C，D共面，点A，B，C，E共面，则A，B，C，D，E共面C．若直线a，b共面，直线a，c共面，则直线b，c共面D．依次首尾相接的四条线段必共面二、填空题（每题4分，满分20分，将答案填在答题纸上）9．（4分）写出命题：“若一个四边形两组对边相等，则这个四边形为平行四边形”的逆否命题是．10．（4分）正方体ABCD﹣A1B1C1D1中，若=x（++），则实数x=．11．（4分）已知直线l，m和平面β，若l⊥m，l⊥β，则m与β的位置关系是．12．（4分）棱长为1的正方体ABCD﹣A1B1C1D1中，P，Q分别是D1B，B1C的中点，则PQ的长为．13．（4分）已知ABCD为平行四边形，且A（4，1，3），B（2，﹣5，1），C（3，7，﹣5），则点D的坐标为．三、解答题（本大题共4小题，共48分.解答应写出文字说明、证明过程或演算步骤.）14．（12分）如图，棱长为a的正方体ABCD﹣A1B1C1D1中，点M，N，E分别是棱A1B1，A1D1，C1D1的中点．（1）过AM作一平面，使其与平面END平行（只写作法，不需要证明）；（2）在如图的空间直角坐标系中，求直线AM与平面BMND所成角的正弦值．15．（12分）如图，长方体ABCD﹣A 1B1C1D1中，AA1=，AB=1，AD=2，E为BC 的中点，点M为棱AA1的中点．（1）证明：DE⊥平面A1AE；（2）证明：BM∥平面A1ED．16．（12分）如图，正三棱柱ABC﹣A1B1C1的所有棱长都为2，D为CC1中点．试用空间向量知识解下列问题：（1）求证：平面ABB1A1⊥平面A1BD；（2）求二面角A﹣A1D﹣B的大小．17．（12分）三棱锥P﹣ABC中，已知PA=PB=PC=AC=4，BC=AB=2，O为AC 中点．（1）求证：PO⊥平面ABC；（2）求异面直线AB与PC所成角的余弦值．2016-2017学年天津市红桥区高二（上）期中数学试卷（理科）参考答案与试题解析一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. 1．（4分）命题“∀x∈R，x2+1≥1”的否定是（）A．∀x∈R，x2+1＜1 B．∃x∈R，x2+1≤1 C．∃x∈R，x2+1＜1 D．∃x ∈R，x2+1≥1【解答】解：∵原命题“∀x∈R，有x2+1≥1”∴命题“∀x∈R，有x2+1≥1”的否定是：∃x∈R，使x2+1＜1．故选：C．2．（4分）已知点A（2，3，5），B（3，1，4），则A，B两点间的距离为（）A．B．C．D．【解答】解：点A（2，3，5），B（3，1，4），则A，B两点间的距离为：=．故选：B．3．（4分）若直线a，平面α满足a⊄α，则下列结论正确的是（）A．直线a一定与平面α平行B．直线a一定与平面α相交C．直线a一定与平面α平行或相交D．直线a一定与平面α内所有直线异面【解答】解：∵直线a，平面α满足a⊄α，故直线a一定与平面α平行或相交，故选：C．4．（4分）已知向量是空间的一个基底，其中与向量，一定构成空间另一个基底的向量是（）A．B．C．D．都不可以【解答】解：由题意和空间向量的共面定理，结合+（）=2，得与、是共面向量，同理与、是共面向量所以与、不能构成空间的一个基底；又与、不共面，所以与、能构成空间的一个基底．故选：C．5．（4分）“a，b不相交”是“a，b异面”的（）A．充分非必要条件 B．必要非充分条件C．充要条件D．非充分非必要条件【解答】解：若“a，b不相交”，则a，b平行或a，b异面，不是充分条件，若a，b异面，则a，b不相交，是必要条件，故选：B．6．（4分）若直线a平行于平面α，则下列结论正确的是（）A．直线a一定与平面α内所有直线平行B．直线a一定与平面α内所有直线异面C．直线a一定与平面α内唯一一条直线平行D．直线a一定与平面α内一组平行直线平行【解答】解：由直线a平行于平面α，知：在A中，直线a与平面α内的直线平行或异面，故A错误；在B中，直线a与平面α内的直线平行或异面，故B错误；在C中，直线a与平面α内的无数条直线平行，故C错误；在D中，由线面平行的性质定理得：直线a一定与平面α内一组平行直线平行，故D正确．故选：D．7．（4分）设O是空间一点，a，b，c是空间三条直线，α，β是空间两个平面，则下列命题中，逆命题不成立的是（）A．当a∩b=O且a⊂α，b⊂α时，若c⊥a，c⊥b，则c⊥αB．当a∩b=O且a⊂α，b⊂α时，若a∥β，b∥β，则α∥βC．当b⊂α时，若b⊥β，则α⊥βD．当b⊂α时，且c⊄α时，若c∥α，则b∥c【解答】解：对于A，当a∩b=O且a⊂α，b⊂α时，若c⊥a，c⊥b，则c⊥α的逆命题为：当a∩b=O且a⊂α，b⊂α时，若c⊥α，则c⊥a，c⊥b，由直线与平面垂直的性质定理可知逆命题正确；对于B，当a∩b=O且a⊂α，b⊂α时，若a∥β，b∥β，则α∥β的逆命题为：当a∩b=O且a⊂α，b⊂α时，若α∥β，则a∥β，b∥β，有直线与平面平行的性质定理可知逆命题正确；对于C，当b⊂α时，若b⊥β，则α⊥β的逆命题为：当b⊂α时，若α⊥β，则b ⊥β，显然不正确，可能b与β不垂直，所以逆命题不正确；对于D，当b⊂α时，且c⊄α时，若c∥α，则b∥c的逆命题为：当b⊂α时，且c⊄α时，若b∥c，则c∥α；满足直线与平面平行的判定定理，正确；故选：C．8．（4分）以下四个命题中，正确命题是（）A．不共面的四点中，其中任意三点不共线B．若点A，B，C，D共面，点A，B，C，E共面，则A，B，C，D，E共面C．若直线a，b共面，直线a，c共面，则直线b，c共面D．依次首尾相接的四条线段必共面【解答】解：不共面的四点中，其中任意三点不共线，故A为真命题；若点A，B，C，D共面，点A，B，C，E共面，则A，B，C，D，E可能不共面，故B为假命题；若直线a，b共面，直线a，c共面，则直线b，c可能不共面，故C为假命题；依次首尾相接的四条线段可能不共面，故D为假命题；故选：A．二、填空题（每题4分，满分20分，将答案填在答题纸上）9．（4分）写出命题：“若一个四边形两组对边相等，则这个四边形为平行四边形”的逆否命题是若一个四边形不是平行四边形，则这个四边形的两组对边不都相等．【解答】解：命题：“若一个四边形两组对边相等，则这个四边形为平行四边形”的逆否命题是“若一个四边形不是平行四边形，则这个四边形的两组对边不都相等”．故答案为：若一个四边形不是平行四边形，则这个四边形的两组对边不都相等．10．（4分）正方体ABCD﹣A1B1C1D1中，若=x（++），则实数x=1．【解答】解：根据向量的加法可得，=++，∵=x（++），∴x=1，故答案为1．11．（4分）已知直线l，m和平面β，若l⊥m，l⊥β，则m与β的位置关系是m ⊂β或m∥β．【解答】解：在正方体ABCD﹣A1B1C1D1中，取AA1为l，平面ABCD为β，则l⊥β，当m为AB时，l⊥m，l⊥β，m⊂β，当m为A1B1时，l⊥m，l⊥β，m∥．∴m与β的位置关系是m⊂β或m∥β．故答案为：m⊂β或m∥β．12．（4分）棱长为1的正方体ABCD﹣A1B1C1D1中，P，Q分别是D1B，B1C的中点，则PQ的长为．【解答】解：连接B1D，则经过P，且为B1D的中点，∵Q是B1C的中点，∴PQ∥CD，PQ=CD，∴PQ=．故答案为．13．（4分）已知ABCD为平行四边形，且A（4，1，3），B（2，﹣5，1），C（3，7，﹣5），则点D的坐标为（5，13，﹣3）．【解答】解：由平行四边形的两条对角线互相平分，得A，C两点的坐标和等于B、D两点的坐标和设D点坐标为（x，y，z）则解得：故答案为：（5，13，﹣3）三、解答题（本大题共4小题，共48分.解答应写出文字说明、证明过程或演算步骤.）14．（12分）如图，棱长为a的正方体ABCD﹣A1B1C1D1中，点M，N，E分别是棱A1B1，A1D1，C1D1的中点．（1）过AM作一平面，使其与平面END平行（只写作法，不需要证明）；（2）在如图的空间直角坐标系中，求直线AM与平面BMND所成角的正弦值．【解答】解：（1）连结AC、MC，平面AMC是所求平面﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（3分）（2）如图空间直角坐标系O﹣xyz则A（0，0，0），M（a，0，a），B（a，0，0），D（0，a，0），N（0，a，a）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）（不全对，但对2个以上给1分）=（﹣a，0，a），=（﹣a，a，0），=（a，0，a）﹣﹣﹣﹣﹣﹣﹣（7分）（不全对，但对2个给1分）设平面BMND得法向量n=（x，y，z）则⇒n=（2，2，1）﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（9分）cos＜，n＞==﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（11分）设直线AM与平面BMND所成角为θ则，sinθ=|cos＜，n＞|=直线AM与平面BMND所成角的正弦值为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）15．（12分）如图，长方体ABCD﹣A1B1C1D1中，AA1=，AB=1，AD=2，E为BC 的中点，点M为棱AA1的中点．（1）证明：DE⊥平面A1AE；（2）证明：BM∥平面A1ED．【解答】证明：（1）在△AED中，AE=DE=，AD=2，∴AE⊥DE．∵A1A⊥平面ABCD，∴A1A⊥DE，∴DE⊥平面A1AE．（2）设AD的中点为N，连接MN、BN．在△A1AD中，AM=MA1，AN=ND，∴MN∥A1D，∵BE∥ND且BE=ND，∴四边形BEDN是平行四边形，∴BN∥ED，∴平面BMN∥平面A1ED，∴BM∥平面A1ED．16．（12分）如图，正三棱柱ABC﹣A1B1C1的所有棱长都为2，D为CC1中点．试用空间向量知识解下列问题：（1）求证：平面ABB1A1⊥平面A1BD；（2）求二面角A﹣A1D﹣B的大小．【解答】（1）证明：取BC中点O，连AO，∵△ABC为正三角形，∴AO⊥BC，∵在正三棱柱ABC﹣A1B1C1中，平面ABC⊥平面BCC1B1，∴AD⊥平面BCC1B1，取B1C1中点为O1，以O为原点，，，的方向为x，y，z轴的正方向，建立空间直角坐标系，则．∴，∵，．∴，，∴AB1⊥面A1BD．…（5分）AA1⊂面A1BD所以平面ABB1A1⊥面A1BD﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）AD的法向量为，（2）解：设平面A．，∴，∴⇒，令z=1，得为平面A 1AD的一个法向量，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）由（1）知AB1⊥面A1BD，∴为平面A1AD的法向量，，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（11分）∴二面角A﹣A1D﹣B的正弦值为=．…（12分）17．（12分）三棱锥P﹣ABC中，已知PA=PB=PC=AC=4，BC=AB=2，O为AC 中点．（1）求证：PO⊥平面ABC；（2）求异面直线AB与PC所成角的余弦值．【解答】解：（1）证明：由题意，∵PA=PB=PC=AC=4，AC的中点O，连接OP，OB，易得：OP⊥AC；∵，，∴AC2=AB2+BC2，故得△ABC为Rt△，∴OB=OC=2，PB2=OB2+OP2，∴OP⊥OB．又∵AC∩BO=O且AC、OB⊂面ABC，∴OP⊥平面ABC；（2）分别取PB，BC中点EF，连接OE，OF，EF，则AB∥OF，PC∥EF，故，∠EFO为异面直线AB与PC所成角（或补角）由（Ⅰ）知在直角三角形POB中，，又，；在等腰三角形EOF中，．所以，异面直线AB与PC所成角的余弦值为．。

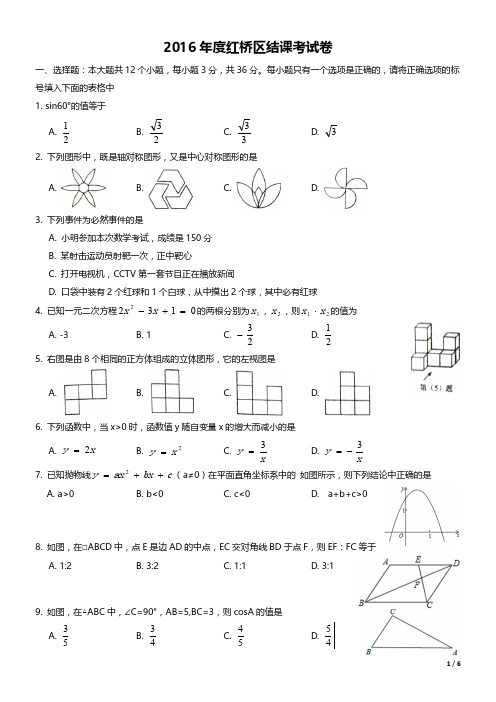
2016年度红桥区结课考试卷一、选择题：本大题共12个小题，每小题3分，共36分。

每小题只有一个选项是正确的，请将正确选项的标号填入下面的表格中 1. sin60°的值等于 A.21 B.23 C.33 D.32. 下列图形中，既是轴对称图形，又是中心对称图形的是A. B. C. D.3. 下列事件为必然事件的是A. 小明参加本次数学考试，成绩是150分B. 某射击运动员射靶一次，正中靶心C. 打开电视机，CCTV 第一套节目正在播放新闻D. 口袋中装有2个红球和1个白球，从中摸出2个球，其中必有红球 4. 已知一元二次方程01322x x 的两根分别为1x ，2x ，则21x x 的值为A. -3B. 1C. 23D.21 5. 右图是由8个相同的正方体组成的立体图形，它的左视图是A. B. C. D.6. 下列函数中，当x>0时，函数值y 随自变量x 的增大而减小的是 A.x y 2B.2x y C. xy 3D. xy 37. 已知抛物线c bx ax y 2（a≠0）在平面直角坐标系中的 如图所示，则下列结论中正确的是A. a>0B. b<0C. c<0D. a+b+c>08. 如图，在□ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F，则EF：FC 等于 A. 1:2B. 3:2C. 1:1D. 3:19. 如图，在△ABC 中，∠C=90°，AB=5,BC=3，则cosA 的值是 A.53 B.43 C.54 D.4510. 若正方形的边长为2，则其外接圆半径与内切圆半径的大小分别为A.2，1B. 2，1C. 2，2D. 22，211. 如图，AB 为⊙O 的直径，PD 切⊙O 于点C，交AB 的延长线于点D，且CO=CD，则∠ACD 的大小为A. 67.5°B. 100°C. 112.5°D. 120°12. 如图，已知点A（3,0），□OABC 的顶点B，C 在第一象限，D 为边AB 的中点，反比例函数xky（k≠0,x>0）的图象经过C，D 两点，若∠COA=60°，则k 的值等于 A. 6 B. 34C. 3D. 32二、填空题：本大题共6小题，每小题3分，共18分，请将答案填写在下面题中的横线上 13. 一元二次方程0442x x的根为14. 分别写有数字0，-1，-2，1，2，3的六张卡片，除数字不同外其他均相同，从中任抽一张，那么抽到写有负数卡片的概率是15. 如图，将矩形ABCD 绕点A 顺时针旋转到矩形AB’C’D’的位置，记旋转角为α（0°<α<90°）。