2015-2016学年苏科版初一下册数学期末试卷及答案

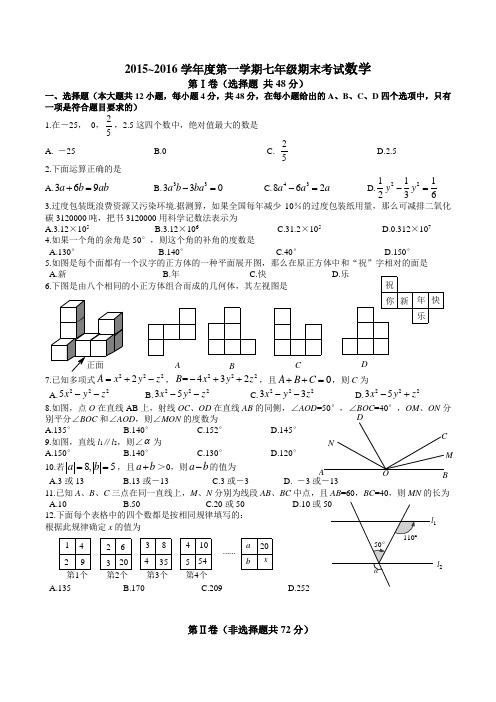
2015~2016学年度第一学期七年级期末考试数学第Ⅰ卷（选择题 共48分）一、选择题（本大题共12小题，每小题4分，共48分，在每小题给出的A 、B 、C 、D 四个选项中，只有一项是符合题目要求的）1.在－25， 0，25，2.5这四个数中，绝对值最大的数是 A. －25 B.0 C. 25D.2.5 2.下面运算正确的是 A.369a b ab += B.33330a b ba -= C.43862a a a -= D.22111236y y -= 3.过度包装既浪费资源又污染环境.据测算，如果全国每年减少10％的过度包装纸用量，那么可减排二氧化碳3120000吨，把书3120000用科学记数法表示为A.3.12×105B.3.12×106C.31.2×105D.0.312×1074.如果一个角的余角是50°，则这个角的补角的度数是A.130°B.140°C.40°D.150°5.如图是每个面都有一个汉字的正方体的一种平面展开图，那么在原正方体中和“祝”字相对的面是A.新B.年C.快D.乐6.下图是由八个相同的小正方体组合而成的几何体，其左视图是7.已知多项式2222A x y z =+-，222=432B x y z -++，且0A B C ++=，则C 为A.2225x y z --B.22235x y z --C.22233x y z --D.22235x y z -+8.如图，点O 在直线AB 上，射线OC 、OD 在直线AB 的同侧，∠AOD =50°，∠BOC =40°，OM 、ON 分别平分∠BOC 和∠AOD ，则∠MON 的度数为A.135°B.140°C.152°D.145° 9.如图，直线l 1∥l 2，则∠α为 A.150° B.140° C.130° D.120° 10.若8,5a b ==，且a b +＞0，则a b -的值为 A.3或13 B.13或－13 C.3或－3 D. －3或－1311.已知A 、B 、C 三点在同一直线上，M 、N 分别为线段AB 、BC 中点，且AB =60，BC =40，则MN 的长为A.10B.50C.20或50D.10或12.下面每个表格中的四个数都是按相同规律填写的： 根据此规律确定x 的值为A.135B.170C.209D.252第Ⅱ卷（非选择题共72分）乐快年新你祝D C B A NMD C B A l 2············第4个第3个第2个第1个35834∙∙∙···x 20b a 541054206329421二、填空题（本大题共4小题，每小题4分，共16分，请将最后答案填在题中横线上）13.312m a b 与212n a b -是同类项，则m n -=________； 14.规定符号＊运算为a ＊b =21ab a b -++，那么－3＊4=_____________；15.若代数式2245x x --的值为6，则2122x x --的值为_________； 16.为庆祝“六·一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛，如图所示：按照上面的规律，摆第（n ）图，需用火柴棒的根数为_____________________.三、解答题（本大题共6个小题，共56分，解答时应写出必要的文字说明或演算步骤.）17.（本小题满分10分）计算与化简：（1）2241325(2)4-+----⨯-（）（） （2）224(6)3(2)x xy x xy +---18.（本小题满分8分）先化简，再求值：2211312()()2323a a b a b ----，其中22,3a b =-=.19.（本小题满分9分）一辆货车从货场A出发，向东走了2千米到达批发部B，继续向东走了1.5千米到达商场C，又向西走了4.5千米到达超市D，最后回到货场.（1）用一个单位长度表示1千米，以东为正方向，货场为原点，画出数轴并在数轴上标明货场A，批发部B，商场C，超市D的位置；（2）超市D距货场A多远？（3）货车一共行驶了多少千米？20.（本小题满分8分）某中学初一（四）班3位教师决定带领本班a名学生在五一期间取北京旅游，A旅行社的收费标准为：教师全价，学生半价；而B旅行社的收费标准为：不分教师、学生，一律八折优惠.（1）分别用代数式表示参加这两家旅行社所需的费用；（2）如果这3位教师要带领该班30名学生参加旅游，你认为选择哪一家旅行社较为合算，为什么？21.（本小题满分10分）如图，已知AB∥CE，∠A=∠E，试说明∠CGD=∠FHB.22.（本小题满分11分）HGFEDCBA将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°，∠E=∠B=45°）.（1）1若∠DCE=45°，则∠ACB的度数为_________：2 若∠ACB=140°，则∠DCE的度数为______；（2）由（1）猜想∠ACB与∠DCE的数量关系，并说明理由；（3）当∠ACE＜180°且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE所有可能的值（不必说明理由）；若不存在，请说明理由.。

2015-2016学年第二学期期末联考试卷七年级数学一、选择题：本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．如果座位表上“5列2行”记作（5，2），那么（4，3）表示（）A．3列5行B．5列3行C．4列3行D．3列4行2．如果a＞b，那么下列不等式中一定成立的是（）A．a2＞b2B．1﹣a＞1﹣b C．1+a＞1﹣b D．1+a＞b﹣13．在下列实数中：0，，﹣3.1415，，，0.343343334…无理数有（）A．1个B．2个C．3个D．4个4．下面调查中，适合采用普查的是（）A．调查全国中学生心理健康现状B．调查你所在的班级同学的身高情况C．调查我市食品合格情况D．调查南京市电视台《今日生活》收视率5．若是方程kx﹣2y=2的一个解，则k等于（）A．B．C．6 D．﹣6．如图，能判定EC∥AB的条件是（）A．∠B=∠ACE B．∠A=∠ECD C．∠B=∠ACB D．∠A=∠ACE7．如图，在平面直角坐标系中，A（﹣3，2）、B（﹣1，0）、C（﹣1，3），将△ABC向右平移4个单位，再向下平移3个单位，得到△A1B1C1，点A、B、C的对应点分别A1、B1、C1，则点A1的坐标为（）A．（3，﹣3）B．（1，﹣1）C．（3，0）D．（2，﹣1）8．在平面直角坐标系中，点（﹣2，﹣2m+3）在第三象限，则m的取值范围是（）A．B．C．D．9．若关于x的不等式组无解，则a的取值范围是（）A．a≤3 B．a≥3 C．a＜3 D．a＞310．已知方程组和有相同的解，则a，b的值为（）A．B．C．D．11．小明要制作一个长方形的相片框架，这个框架的长为25cm，面积不小于500cm2，则宽的长度xcm应满足的不等式组为（）A．B．C．D．12．为了鼓励市民节约用电，某市对居民用电实行“阶梯收费”（总电费=第一阶梯电费+第二阶梯电费）．规定：用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费．如图是张磊家2015年9月和10月所交电费的收据，则该市规定的第一阶梯电价和第二阶梯电价分别为每度（）A．0.5元、0.6元B．0. 4元、0.5元C．0.3元、0.4元D．0.6元、0.7元第6题图第7题图第12题图二、填空题：本大题共6小题，每小题3分，共18分.把答案填在题中横线上.13．的整数部分是．14．某学校为了了解八年级学生的体能情况，随机选取30名学生测试一分钟仰卧起坐次数，并绘制了如图的直方图，学生仰卧起坐次数在25～30之间的频率为．15．已知2x﹣3y﹣1=0，请用含x的代数式表示y：．16．如图，将三角板的直角顶点放在直尺的一边上，若∠1=55°，则∠2的度数为°．17．若不等式组的解集是﹣1＜x ＜1，则b a 212 的立方根为 ． 18．如图，正方形ABCD 的顶点B 、C 都在直角坐标系的x 轴上，若点D 的坐标是（3，4），则点A 的坐标是 ．第14题图 第16题图 第18题图三、解答题：本大题共6小题，共46分.解答应写出必要的文字说明、证明过程或演算步骤.19．（5分）解方程组：20．（6分）解不等式组请结合题意填空，完成本题的解答． （1）解不等式①，得 ；（2）解不等式②，得 ；（3）把不等式①和②的解集在数轴上表示出来：（4）原不等式组的解集为 ．21．（7分）请根据如图所示的对话内容回答下列问题．（1）求该魔方的棱长；（2）求该长方体纸盒的长．22．（8分）已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4．证明：AD∥BE．证明：∵AB∥CD（已知）∴∠4=①（②）∵∠3=∠4（已知）∴∠3=③（④）∵∠1=∠2（已知）∴∠1+∠CAF=∠2+∠CAF（等量代换）即∠BAF=∠DAC∴∠3= ⑤（等量代换）∴AD∥BE（⑥）23．（9分）某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类．在“读书月”活动中，为了了解图书的借阅情况，图书管理员对本月各类图书的借阅进行了统计，表）和图是图书管理员通过采集数据后，绘制的两幅不完整的频率分布表与频数分布直方图．请你根据图表中提供的信息，解答以下问题：（1）表中m=，n=；（2）在图中，将表示“自然科学”的部分补充完整；（3）若该学校打算采购一万册图书，请你估算“哲学”类图书应采购多少册较合适？（4）根据图表提供的信息，请你提出一条合理化的建议．24．（11分）在南宁市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和1台电子白板共需要2万元，购买2台电脑和1台电子白板共需要2.5万元．（1）求每台电脑、每台电子白板各多少万元？（2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过32万元，但不低于30万元，请你通过计算求出有几种购买方案，哪种方案费用最低．2015-2016学年第二学期期末联考七年级数学评分细则一、选择题（本题共12小题，每小题3分，共36分）1-5 CDBBC 6-10 DBBAD 11-12 AA二、填空题（本题共6小题，每小题3分，共18分）13. 4 14. 0.4 15. y=16. 35 17. 2 18. （﹣1，4）三、解答题（本大题共6小题，共46分）注：解答题解法多样，非本细则所述的其他正确解法请阅卷老师酌情给分19. 解：，①+②×2得：7x=7，即x=1，------- 3分把x=1代入①得：y=1，------- 4分则方程组的解为------- 5分20. 解：（1）x＜2，------- 1分（2）x≥﹣1，------- 3分（3）------- 5分（4）-1≤x＜2．------- 6分21. 解：（1）设魔方的棱长为x cm，可得：x3=216，------- 2分解得：x=6．------- 3分（2）设该长方体纸盒的长为y cm，6y2=600，------- 5分y2=100，即y=10．------- 6分答：魔方的棱长6 cm，长方体纸盒的长为10 cm．------- 7分22. 解：①∠BAE ，------- 1分②（两直线平行，同位角相等），------- 3分③∠BAE ------- 4分④（等量代换），------- 5分⑤∠DAC ，------- 6分⑥（内错角相等，两直线平行）．------- 8分23. 解：（1）m= 500 ，------- 2分n= 0.05 ；------- 3分（2）自然科学：2000×0.20=400 册如图，------- 5分（3）10000×0.05=500（册），即估算“哲学”类图书应采购500册较合适；------- 7分（4）鼓励学生多借阅哲学类的书．------- 9分24. 解：（1）设每台电脑x万元，每台电子白板y万元，根据题意得：，------- 3分解得，即每台电脑0.5万元，每台电子白板1.5万元；------- 5分（2）设需购进电脑a台，则购进电子白板（30﹣a）台，根据题意得：，------- 7分解得：13≤a≤15，∵a只能取整数，∴a=13，14，15，------- 9分∴有三种购买方案，方案1：需购进电脑13台，则购进电子白板17台，13×0.5+1.5×17=32（万元），方案2：需购进电脑14台，则购进电子白板16台，14×0.5+1.5×16=31（万元），方案3：需购进电脑15台，则购进电子白板15台，15×0.5+1.5×15=30（万元），∵30＜31＜32，∴购买电脑15台，电子白板15台最省钱．------- 11分。

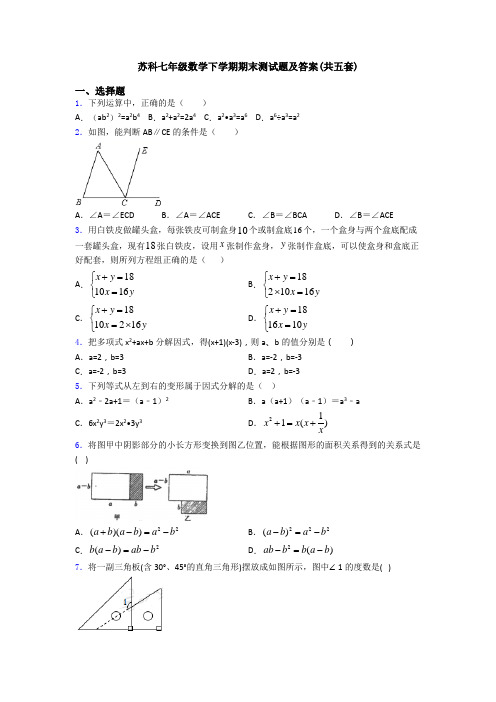
苏科初一数学期末下册考试试卷及答案word 版一、选择题1．计算（﹣2a 2）•3a 的结果是（ ） A ．﹣6a 2B ．﹣6a 3C ．12a 3D ．6a 32．用白铁皮做罐头盒，每张铁皮可制盒身10个或制盒底16个，一个盒身与两个盒底配成一套罐头盒，现有18张白铁皮，设用x 张制作盒身，y 张制作盒底，可以使盒身和盒底正好配套，则所列方程组正确的是（ ） A ．181016x y x y +=⎧⎨=⎩B ．1821016x y x y +=⎧⎨⨯=⎩C ．1810216x y x y+=⎧⎨=⨯⎩D ．181610x y x y+=⎧⎨=⎩3．如图，P 1是一块半径为1的半圆形纸板，在P 1的右上端剪去一个直径为1的半圆后得到图形P 2，然后依次剪去一个更小的半圆(其直径为前一个被剪去的半圆的半径)得到图形P 3、P 4…P n …,记纸板P n 的面积为S n ，则S n -S n +1的值为( )A ．12nπ⎛⎫ ⎪⎝⎭B ．14nπ⎛⎫ ⎪⎝⎭C ．2112n π+⎛⎫ ⎪⎝⎭D ．2112n π-⎛⎫ ⎪⎝⎭4．把多项式228x -分解因式，结果正确的是（ ）A ．22(8)x -B ．22(2)x -C ．D ．42()x x x-5．如果多项式x 2＋mx ＋16是一个二项式的完全平方式，那么m 的值为（ ） A ．4 B ．8 C ．－8D ．±8 6．下列代数运算正确的是（ ）A ．x•x 6=x 6B ．（x 2）3=x 6C ．（x+2）2=x 2+4D ．（2x ）3=2x 3 7．如果 x 2﹣kx ﹣ab ＝（x ﹣a ）（x +b ），则k 应为（ ）A ．a ﹣bB ．a +bC ．b ﹣aD ．﹣a ﹣b8．观察下列等式: 133=，239=，3327=，4381=，53243=，63729=，732187=，试利用上述规律判断算式234202033333+++++…结果的末位数字是( )A ．0B ．1C ．3D ．79．已知关于,x y 的二元一次方程组725ax y x y +=⎧⎨-=⎩和432x y x by +=⎧⎨+=-⎩有相同的解，则-a b 的值是（ ） A ．13B ．9C ．9-D ．13-10．下面图案中可以看作由图案自身的一部分经过平移后而得到的是（ ）A ．B ．C ．D ．11．计算28+（-2）8所得的结果是（ ） A ．0 B ．216 C ．48 D ．29 12．一个多边形的每个内角都等于140°，则这个多边形的边数是（ ）A ．7B ．8C ．9D ．10二、填空题13．已知:()521x x ++=，则x ＝______________．14．已知：12345633,39,327,381,3243,3729,======……，设A=2(3+1)(32+1)(34+1)(316+1)(332+1)+1，则A 的个位数字是__________．15．计算：312-⎛⎫ ⎪⎝⎭＝ . 16．若多项式x 2-kx +25是一个完全平方式，则k 的值是______．17．关于,x y 的方程组3x y m x my n -=⎧⎨-=⎩的解是11x y =⎧⎨=⎩，则n 的值是______．18．已知代数式2x-3y 的值为5，则-4x+6y=______．19．内角和等于外角和2倍的多边形是__________边形．20．若二次三项式x 2+kx+81是一个完全平方式，则k 的值是 ________． 21．已知30m -=，7m n +=，则2m mn +=___________．22．已知关于x 的不等式3()50a b x a b -+->的解集是1x <，则关于x 的不等式4ax b >的解集为_______．三、解答题23．先化简后求值：224(2)(2)(2)x x y x y y x --+---，其中1x =-，2y =-． 24．计算：（1）()2202011 3.142π-⎛⎫-+-+ ⎪⎝⎭（2）()2462322x y x xy --（3）()()22342a b a a b --- （4）()()2323m n m n -++-25．定义：对于任何数a ，符号[]a 表示不大于a 的最大整数. （1）103⎡⎤-=⎢⎥⎣⎦（2）如果2333x -⎡⎤=-⎢⎥⎣⎦，求满足条件的所有整数x 。

2020-2021学年七年级（下）期末数学试卷一、精心选一选(每小题2分，共16分)1．如图所示，AP平分∠BAC，点M，N分别在边AB，AC上，如果添加一个条件，即可推出AM＝AN，那么下面条件不正确的是（）A．PM＝PN B．∠APM＝∠APN C．MN⊥AP D．∠AMP＝∠ANP 2．下列所给的四组条件中，能作出唯一三角形的是（）A．AB＝2cm，BC＝6cm，AC＝3cm B．BC＝3cm，AC＝5cm，∠B＝90°C．∠A＝∠B＝∠C＝60°D．AB＝4cm，AC＝6cm，∠C＝30°3．如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，添加的一组条件不正确的是（）A．BC＝DC，∠A＝∠D B．BC＝EC，AC＝DCC．∠B＝∠E，∠BCE＝∠ACD D．BC＝EC，∠B＝∠E4．打碎的一块三角形玻璃如图所示，现在要去玻璃店配一块完全一样的玻璃，最省事的方法是（）A．带①②去B．带②③去C．带③④去D．带②④去5．如图，AB＝AC，点D、E分别是AB、AC上一点，AD＝AE，BE、CD相交于点M．若∠BAC＝70°，∠C＝30°，则∠BMD的大小为（）A．50°B．65°C．70°D．80°6．边长都为整数的△ABC和△DEF全等，AB与DE是对应边，AB＝2，BC＝4，若△DEF 的周长为奇数，则DF的值为（）A．3B．4C．3或5D．3或4或57．如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE于D，AD＝2cm，BE＝0.5cm，则DE的长为（）A．0.5cm B．1cm C．1.5cm D．2cm8．下列命题中，说法不正确的有（）个．①形状相同的两个三角形全等；②两边和一角对应相等的两个三角形全等；③周长相等的两个等腰三角形全等；④有两角及其中一角的角平分线对应相等的两个三角形全等．A．4个B．3个C．2个D．1个二、细心填一填(每小题2分，共20分)9．一个三角形的三边为3、5、x，另一个三角形的三边为y、3、6，若这两个三角形全等，则x﹣y＝．10．如图，两个三角形全等，根据图中所给条件，可得∠α＝°．11．如图所示，已知AF＝DC，BC∥EF，若要用“SAS”去证△ABC≌△DEF，则需添加的条件是．12．如图，CE⊥AB于点E，BD⊥AC于点D，BD、CE交于点O，且AO平分∠BAC，则图中的全等三角形共有对．13．如图，△ABC≌△DEF，点B、F、C、E在同一条直线上，AC、DF交于点M，∠ACB ＝43°，则∠AMF的度数是°．14．如图，AB＝AC，∠BAC＝90°，BD⊥AE于点D，CE⊥AE于点E，若BD＝2，CE＝3，则四边形CBDE的面积是．15．如图，在由6个相同的小正方形拼成的网格中，∠2﹣∠1＝°．16．如图，在△ACD与△BCE中，AD与BE相交于点P，若AC＝BC，AD＝BE，CD＝CE，∠DCE＝55°，则∠APB的度数为．17．如图，在△ABC中，AB＝6，BC＝5，AC＝4，AD平分∠BAC交BC于点D，在AB上截取AE＝AC，则△BDE的周长为．18如图，已知四边形ABCD中，AB＝10厘米，BC＝8厘米，CD＝12厘米，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为时，能够使△BPE与△CQP全等．三、耐心解一解(本大题共64分)19已知：如图，DE⊥AC，BF⊥AC，AD＝BC，AF＝CE，求证：AD∥BC．20如图，Rt△ABC中，∠ACB＝90°．（1）作∠BAC的角平分线交BC于点D，过点作DE⊥AB于点E（要求：用尺规作图，不写作法，保留作图痕迹）；（2）在（1）的条件下，若AB＝10cm，△ADB的面积为15cm2，求CD的长．21如图，锐角△ABC的两条高BD、CE相交于点O，且CE＝BD，若∠ABC＝65°，求∠CBD的度数．22已知：如图AD、A′D′分别为钝角△ABC和钝角△A′B′C′的边BC、B′C′上的高，且AB＝A′B′，AD＝A′D′请你补充一个条件（只需写出一个你认为适当的条件）使得△ABC≌△A′B′C′，并加以证明．23如图，在△ABC中，AB＝AC＝4，∠B＝∠C＝50°，点D在线段BC上运动（D不与B，C重合），连接AD，作∠ADE＝50°，DE交线段AC于E．（1）当∠BDA＝120°时，∠EDC＝；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；（2）当DC等于多少时，△ABD≌△DCE，请说明理由．24如图，在锐角△ABC中，AD⊥BC于点D，点E在AD上，DE＝DC，BD＝AD，点F为BC的中点，连接EF并延长至点M，使FM＝EF，连接CM．（1）求证：BE＝AC；（2）试判断线段AC与线段MC的关系，并证明你的结论．25如图，在△ABC中，∠C＝90°，AD是∠CAB的角平分线，DE⊥AB于E，点F在边AC 上，连接DF．（1）求证：AC＝AE；（2）若DF＝DB，试说明∠B与∠AFD的数量关系；（3）在（2）的条件下，若AB＝m，AF＝n，求BE的长（用含m，n的代数式表示）．参考答案与试题解析一．选择题（共8小题）1．如图所示，AP平分∠BAC，点M，N分别在边AB，AC上，如果添加一个条件，即可推出AM＝AN，那么下面条件不正确的是（）A．PM＝PN B．∠APM＝∠APN C．MN⊥AP D．∠AMP＝∠ANP 【分析】根据已知条件结合三角形全等的判定方法，验证各选项提交的条件是否能证△APM≌△APN即可．【解答】解：∵AP平分∠BAC，∴∠BAP＝∠CAP，A、由∠BAP＝∠CAP，PM＝PN，AP＝AP，不能判定△APM≌△APN，∴不推出AM＝AN，故选项A符合题意；B、由∠BAP＝∠CAP，AP＝AP，∠APM＝∠APN，能判定△APM≌△APN（ASA），∴AM＝AN，故选项B不符合题意；C、由∠BAP＝∠CAP，AP＝AP，MN⊥AP，能判定△APM≌△APN（ASA），∴AM＝AN，故选项C不符合题意；D、由∠BAP＝∠CAP，AP＝AP，∠AMP＝∠ANP，能判定△APM≌△APN（AAS），∴AM＝AN，故选项D不符合题意；故选：A．2．下列所给的四组条件中，能作出唯一三角形的是（）A．AB＝2cm，BC＝6cm，AC＝3cm B．BC＝3cm，AC＝5cm，∠B＝90°C．∠A＝∠B＝∠C＝60°D．AB＝4cm，AC＝6cm，∠C＝30°【分析】根据三角形三边的关系对A进行判断；根据全等三角形的判定方法对B、C、D 进行判断．【解答】解：A、因为AB+AC＜BC，三条线段不能组成三角形，所以A选项不符合题意；B、BC＝3cm，AC＝5cm，∠B＝90°，根据“SAS”可判断此三角形为唯一三角形，所以B选项符合题意；C、利用∠A＝∠B＝∠C＝60°不能确定三角形的大小，所以C选项不符合题意；D、利用AB＝4cm，AC＝6cm，∠C＝30°可画出两三角形，所以D选项不符合题意．故选：B．3．如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，添加的一组条件不正确的是（）A．BC＝DC，∠A＝∠D B．BC＝EC，AC＝DCC．∠B＝∠E，∠BCE＝∠ACD D．BC＝EC，∠B＝∠E【分析】根据全等三角形的判定定理逐个判断即可．【解答】解：A．AB＝DE，BC＝DC，∠A＝∠D，不符合全等三角形的判定定理，不能推出△ABC≌△DEC，故本选项符合题意；B．AC＝DC，AB＝DE，BC＝EC，符合全等三角形的判定定理SSS，能推出△ABC≌△DEC，故本选项不符合题意；C．∵∠BCE＝∠ACD，∴∠BCE+∠ACE＝∠ACD+∠ACE，即∠ACB＝∠DCE，∵∠B＝∠E，AB＝DE，∴△ABC≌△DEC（AAS），故本选项不符合题意；D．AB＝DE，∠B＝∠E，BC＝EC，符合全等三角形的判定定理SAS，能推出△ABC≌△DEC，故本选项不符合题意；故选：A．4．打碎的一块三角形玻璃如图所示，现在要去玻璃店配一块完全一样的玻璃，最省事的方法是（）A．带①②去B．带②③去C．带③④去D．带②④去【分析】可以采用排除法进行分析从而确定最后的答案．【解答】解：A、带①②去，符合ASA判定，选项符合题意；B、带②③去，仅保留了原三角形的一个角和部分边，不符合任何判定方法，选项不符合题意；C、带③④去，仅保留了原三角形的一个角和部分边，不符合任何判定方法，选项不符合题意；D、带②④去，仅保留了原三角形的两个角和部分边，不符合任何判定方法，选项不符合题意；故选：A．5．如图，AB＝AC，点D、E分别是AB、AC上一点，AD＝AE，BE、CD相交于点M．若∠BAC＝70°，∠C＝30°，则∠BMD的大小为（）A．50°B．65°C．70°D．80°【分析】根据SAS证明△ADC与△AEB全等，利用全等三角形的性质和三角形内角和解答即可．【解答】解：在△ADC与△AEB中，，∴△ADC≌△AEB（SAS），∴∠B＝∠C，∠AEB＝∠ADC，∵∠BAC＝70°，∠C＝30°，∴∠AEB＝∠ADC＝180°﹣∠BAC﹣∠C＝180°﹣70°﹣30°＝80°，∴∠BMC＝∠DME＝360°﹣∠AEB﹣∠ADC﹣∠BAC＝360°﹣80°﹣80°﹣70°＝130°，∴∠BMD＝180°﹣130°＝50°，故选：A．6．边长都为整数的△ABC和△DEF全等，AB与DE是对应边，AB＝2，BC＝4，若△DEF 的周长为奇数，则DF的值为（）A．3B．4C．3或5D．3或4或5【分析】根据三角形的三边关系求得AC的范围，然后根据全等三角形的对应边相等即可求解．【解答】解：AC的范围是2＜AC＜6，则AC的奇数值是3或5．△ABC和△DEF全等，AB与DE是对应边，则DE＝AB＝2，当DF＝AC时，DF＝3或5．当DF＝BC时，DF＝4．故选：D．7．如图，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE于D，AD＝2cm，BE＝0.5cm，则DE的长为（）A．0.5cm B．1cm C．1.5cm D．2cm【分析】先利用等角的余角相等得∠CAD＝∠BCE，则可根据“AAS”证明△ACD≌△CBE，所以AD＝CE＝2，CD＝BE＝0.5，然后计算CE﹣CD即可．【解答】解：∵BE⊥CE，AD⊥CE，∴∠ADC＝∠CEB，∵∠ACB＝90°，即∠ACD+∠BCE＝90°，∠ACD+∠CAD＝90°，∴∠CAD＝∠BCE，在△ACD和△CBE中，，∴△ACD≌△CBE（AAS），∴AD＝CE＝2，CD＝BE＝0.5，∴DE＝CE﹣CD＝2﹣0.5＝1.5（cm）．故选：C．8．下列命题中，说法不正确的有（）个．①形状相同的两个三角形全等；②两边和一角对应相等的两个三角形全等；③周长相等的两个等腰三角形全等；④有两角及其中一角的角平分线对应相等的两个三角形全等．A．4个B．3个C．2个D．1个【分析】利用全等三角形的判定定理分别判断后即可确定正确的选项．【解答】解：①形状、大小完全相同的两个三角形全等，原命题是假命题；②两边和其夹角对应相等的两个三角形全等，原命题是假命题；③周长相等的两个等腰三角形不一定全等，原命题是假命题；④有两角及其中一角的角平分线对应相等的两个三角形全等，是真命题；故选：B．二．填空题（共9小题）9．一个三角形的三边为3、5、x，另一个三角形的三边为y、3、6，若这两个三角形全等，则x﹣y＝1．【分析】根据全等三角形的对应边相等分别求出x、y，计算即可．【解答】解：∵两个三角形全等，∴x＝6，y＝5，∴x﹣y＝6﹣5＝1，故答案为：1．10．如图，两个三角形全等，根据图中所给条件，可得∠α＝60°．【分析】根据全等三角形的对应边相等、对应角相等，可知道∠α＝60°，做题时要找准对应角．【解答】解：左边的三角形中，b所对的角为180°﹣65°﹣55°＝60°，两个三角形全等中，相等的边是对应边，两三角形中，长度为b的边是对应边，它们对的角是对应角，∴∠α＝60°故答案为：60．11．如图所示，已知AF＝DC，BC∥EF，若要用“SAS”去证△ABC≌△DEF，则需添加的条件是BC＝EF．【分析】求出AC＝DF，根据平行线的性质得出∠BCA＝∠EFD，根据全等三角形的判定得出即可．【解答】解：需要添加条件为BC＝EF，理由是：∵AF＝DC，∴AF+FC＝DC+FC，即AC＝DF，∵BC∥EF，∴∠BCA＝∠EFD，∵在△ABC和△DEF中∴△ABC≌△DEF（SAS），故答案为：BC＝EF．12．如图，CE⊥AB于点E，BD⊥AC于点D，BD、CE交于点O，且AO平分∠BAC，则图中的全等三角形共有4对．【分析】根据题目条件，全等三角形有：△ABO≌△ACO，△AEC≌△ADB，△AEO≌△ADO，△BEO≌△CDO共4对．做题时要从已知开始结合判定方法逐个验证，做到由易到难，不重不漏．【解答】解：①在△AEO与△ADO中∵CE⊥AB于点E，BD⊥AC于点D，AO平分∠BAC，∴∠AEO＝∠ADO＝90°，∠EAO＝∠DAO∵AO＝AO∴△AEO≌△ADO（AAS）∴AE＝AD，OE＝OD；②在△OBE与△OCD中∵∠OEB＝∠0DC＝90°，∠EOB＝∠DOC，OE＝OD∴△OBE≌△OCD（AAS）∴OB＝OC，BE＝DC，∠B＝∠C；③在△ABO与△ACO中∵AE＝AD∴AB＝AC∵AB＝AC，AO＝AO，BO＝CO∴△ABO≌△ACO（SSS）④在△AEC与△ADB中∵∠AEC＝∠ADB＝90°，AC＝AB，AE＝AD∴△AEC≌△ADB（HL）所以共有四对全等三角形．13．如图，△ABC≌△DEF，点B、F、C、E在同一条直线上，AC、DF交于点M，∠ACB ＝43°，则∠AMF的度数是86°．【分析】根据全等三角形的性质得到∠DFE＝∠ACB＝43°，根据三角形的外角性质计算，得到答案．【解答】解：∵△ABC≌△DEF，∴∠DFE＝∠ACB＝43°，∵∠AMF是△MFC的一个外角，∴∠AMF＝∠DFE+∠ACB＝86°，故答案为：86．14．如图，AB＝AC，∠BAC＝90°，BD⊥AE于点D，CE⊥AE于点E，若BD＝2，CE＝3，则四边形CBDE的面积是．【分析】证明△ABD≌△CAE得到AD＝CE＝3，BD＝AE＝2，然后根据梯形的面积公式计算．【解答】解：∵BD⊥AE，CE⊥AE，∴∠D＝∠E＝90°，∵∠BAC＝90°，∴∠DAB+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠ABD＝∠CAE，在△ABD和△CAE中，，∴△ABD≌△CAE（AAS），∴AD＝CE＝3，BD＝AE＝2，∴四边形CBDE的面积＝×（2+3）×（2+3）＝．故答案为．15．如图，在由6个相同的小正方形拼成的网格中，∠2﹣∠1＝90°．【分析】连接AC，利用全等三角形的性质解答即可．【解答】解：如图所示：由图可知△ACD与△ECD全等，∴∠BAC＝∠2，∴∠2﹣∠1＝90°，故答案为：90．16．如图，在△ACD与△BCE中，AD与BE相交于点P，若AC＝BC，AD＝BE，CD＝CE，∠DCE＝55°，则∠APB的度数为55°．【分析】先证明△ACD≌△BCD得到∠D＝∠E，再利用三角形内角和得到∠DPE＝∠DCE＝55°，然后根据对顶角相等得到∠APB的度数．【解答】解：在△ACD和△BCE中，，∴△ACD≌△BCE（SSS），∴∠D＝∠E，∵∠DPE+∠1+∠E＝∠DCE+∠2+∠D，而∠1＝∠2，∴∠DPE＝∠DCE＝55°，∴∠APB＝∠DPE＝55°．故答案为55°．17．如图，在△ABC中，AB＝6，BC＝5，AC＝4，AD平分∠BAC交BC于点D，在AB上截取AE＝AC，则△BDE的周长为7．【分析】利用已知条件证明△ADE≌△ADC（SAS），得到ED＝CD，从而BC＝BD+CD ＝DE+BD＝5，即可求得△BDE的周长．【解答】解：∵AD是∠BAC的平分线，∴∠EAD＝∠CAD在△ADE和△ADC中，，∴△ADE≌△ADC（SAS），∴ED＝CD，∴BC＝BD+CD＝DE+BD＝5，∴△BDE的周长＝BE+BD+ED＝（6﹣4）+5＝7．故答案为：718如图，已知四边形ABCD中，AB＝10厘米，BC＝8厘米，CD＝12厘米，∠B＝∠C，点E为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为时，能够使△BPE与△CQP全等．【考点】全等三角形的判定．【专题】图形的全等．【答案】见试题解答内容【分析】分两种情况讨论，依据全等三角形的对应边相等，即可得到点Q的运动速度．【解答】解：设点P运动的时间为t秒，则BP＝3t，CP＝8﹣3t，∵∠B＝∠C，∴①当BE＝CP＝5，BP＝CQ时，△BPE与△CQP全等，此时，5＝8﹣3t，解得t＝1，∴BP＝CQ＝3，此时，点Q的运动速度为3÷1＝3厘米/秒；②当BE＝CQ＝5，BP＝CP时，△BPE与△CQP全等，此时，3t＝8﹣3t，解得t＝，∴点Q的运动速度为5÷＝厘米/秒；故答案为：3厘米/秒或厘米/秒．19已知：如图，DE⊥AC，BF⊥AC，AD＝BC，AF＝CE，求证：AD∥BC．【考点】全等三角形的判定与性质．【专题】图形的全等；推理能力．【答案】证明见解析过程．【分析】利用HL证明Rt△ADE≌Rt△CBF，得到∠DAE＝∠BCF，然后根据平行线的判定定理证明即可．【解答】证明：∵AF＝CE，∴AF﹣EF＝CE﹣EF，即AE＝CF，∵DE⊥AC，BF⊥AC，∴∠AED＝∠BFC＝90°，在Rt△ADE和Rt△CBF中，，∴Rt△ADE≌Rt△CBF（HL），∴∠DAE＝∠BCF，∴AD∥BC．20如图，Rt△ABC中，∠ACB＝90°．（1）作∠BAC的角平分线交BC于点D，过点作DE⊥AB于点E（要求：用尺规作图，不写作法，保留作图痕迹）；（2）在（1）的条件下，若AB＝10cm，△ADB的面积为15cm2，求CD的长．【考点】角平分线的性质；作图—复杂作图．【专题】作图题；几何直观．【答案】（1）作图见解析部分．（3）3cm．【分析】（1）根据要求作出图形即可．（2）利用三角形的面积公式求出DE，再利用角平分线的性质定理求解即可．【解答】解：（1）如图，射线AD，DE即为所求．（2）∵S△ABD＝•AB•DE＝15cm2，AB＝10cm，∴DE＝3（cm），∵AD平分∠BAC，DE⊥AB，DC⊥AC，∴CD＝DE＝3（cm）．21如图，锐角△ABC的两条高BD、CE相交于点O，且CE＝BD，若∠ABC＝65°，求∠CBD的度数．【考点】全等三角形的判定与性质．【专题】图形的全等；推理能力．【答案】25°．【分析】利用HL证明Rt△BCE≌Rt△CBD，根据全等三角形的性质得出∠ABC＝∠ACB ＝65°，再根据直角三角形的两锐角互余即可得解．【解答】解：∵CE⊥AB，BD⊥AC，∴△BCE和△CBD是直角三角形，在Rt△BCE和Rt△CBD中，，∴Rt△BCE≌Rt△CBD（HL），∴∠ABC＝∠ACB，∵∠ABC＝65°，∴∠ACB＝65°，∴∠CBD＝90°﹣∠ACB＝25°．22已知：如图AD、A′D′分别为钝角△ABC和钝角△A′B′C′的边BC、B′C′上的高，且AB＝A′B′，AD＝A′D′请你补充一个条件（只需写出一个你认为适当的条件）使得△ABC≌△A′B′C′，并加以证明．【考点】全等三角形的判定．【答案】见试题解答内容【分析】根据全等三角形的判定方法添加缺少的条件即可，方案有多种．【解答】解：可添条件：BC＝B'C'．证明：∵AB＝A′B′，AD＝A′D′，∠ADB＝∠A′D′B′＝90°，∴在Rt△ADB和Rt△A′D′B′中，，∴Rt△ADB≌Rt△A′D′B′（HL），∴∠B＝∠B′，∵BC＝B′C′，AB＝A′B′，∴在△ABC和△A′B′C′中，，∴△ABC≌△A′B′C′（SAS）．还可添加：DC＝D′C′，或∠ACB＝∠A'C′B'，或AC＝A′C′，或∠BAC＝∠B′A′C′．故答案为：BC＝B'C'（答案不唯一）．23如图，在△ABC中，AB＝AC＝4，∠B＝∠C＝50°，点D在线段BC上运动（D不与B，C重合），连接AD，作∠ADE＝50°，DE交线段AC于E．（1）当∠BDA＝120°时，∠EDC＝；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；（2）当DC等于多少时，△ABD≌△DCE，请说明理由．【考点】全等三角形的判定；等腰三角形的性质．【专题】图形的全等；推理能力．【答案】（1）10°，小；（2）DC＝4．理由见解答．【分析】（1）利用平角的定义计算∠EDC的度数，几何图形可判断点D从B向C运动时，∠BDA逐渐变小；（2）先证明∠CDE＝∠BAD，而∠B＝∠C，则CD＝BA＝4时，可根据“ASA”判定△ABD≌△DCE．【解答】解：（1）∠EDC＝180°﹣∠BDA﹣∠ADE＝180°﹣120°﹣50°＝10°；点D从B向C运动时，∠BDA逐渐变小；故答案为10°，小；（2）当DC等于4时，△ABD≌△DCE．理由如下：∵∠ADC＝∠B+∠BAD，即∠ADE+∠CDE＝∠B+∠BAD，而∠B＝∠ADE＝50°，∴∠CDE＝∠BAD，在△ABD和△DCE中，，∴△ABD≌△DCE（ASA）．24如图，在锐角△ABC中，AD⊥BC于点D，点E在AD上，DE＝DC，BD＝AD，点F为BC的中点，连接EF并延长至点M，使FM＝EF，连接CM．（1）求证：BE＝AC；（2）试判断线段AC与线段MC的关系，并证明你的结论．【考点】全等三角形的判定与性质．【专题】图形的全等；推理能力．【答案】（1）证明见解析过程；（2）AC⊥MC且AC＝MC，理由见解析过程．【分析】（1）根据SAS证明△BDE≌△ADC，再根据全等三角形的性质即可得解；（2）根据SAS证明△BFE≌△CFM，得到∠CBE＝∠BCM，BE＝MC，由（1）得∠CBE ＝∠CAD，BE＝AC，即得AC＝MC，再利用直角三角形的两锐角互余得出AC⊥MC．【解答】（1）证明；∵AD⊥BC，∴∠BDE＝∠ADC＝90°，在△BDE与△ADC中，，∴△BDE≌△ADC（SAS），∴BE＝AC；（2）解：AC⊥MC且AC＝MC，理由如下：∵F为BC中点，∴BF＝CF，在△BFE与△CFM中，，∴△BFE≌△CFM（SAS），∴∠CBE＝∠BCM，BE＝MC，由（1）得：∠CBE＝∠CAD，BE＝AC，∴∠CAD＝∠BCM，AC＝MC，∵∠CAD+∠ACD＝90°，∴∠BCM+∠ACD＝90°，即∠ACM＝90°，∴AC⊥MC，∴AC⊥MC且AC＝MC．25如图，在△ABC中，∠C＝90°，AD是∠CAB的角平分线，DE⊥AB于E，点F在边AC 上，连接DF．（1）求证：AC＝AE；（2）若DF＝DB，试说明∠B与∠AFD的数量关系；（3）在（2）的条件下，若AB＝m，AF＝n，求BE的长（用含m，n的代数式表示）．【考点】列代数式；全等三角形的判定与性质；角平分线的性质．【专题】线段、角、相交线与平行线；图形的全等；推理能力．【答案】（1）证明见解析过程；（2）∠B+∠AFD＝180°，理由见解析过程；（3）（m ﹣n）．【分析】（1）由于DE⊥AB，那么∠AED＝90°，则有∠ACB＝∠AED，联合∠CAD＝∠BAD，AD＝AD，利用AAS即可证明△ACD≌△AED，再根据全等三角形的性质即可得解；（2）由△ACD≌△AED，证得DC＝DE，然后根据HL判定Rt△CDF≌Rt△EDB，得到∠CFD＝∠B，再根据邻补角的定义等量代换即可得解；（3）由AC＝AE，CF＝BE，根据AB＝AE+BE，AC＝AF+CF即可得解．【解答】（1）证明：∵∠C＝90°，DE⊥AB，∴∠C＝∠AED＝90°，在△ACD和△AED中，，∴△ACD≌△AED（AAS），∴AC＝AE；（2）解：∠B+∠AFD＝180°，理由如下：由（1）得：△ACD≌△AED，∴DC＝DE，在Rt△CDF和Rt△EDB中，，∴Rt△CDF≌Rt△EDB（HL），∴∠CFD＝∠B，∵∠CFD+∠AFD＝180°，∴∠B+∠AFD＝180°；（3）解：由（2）知，Rt△CDF≌Rt△EDB，∴CF＝BE，由（1）知AC＝AE，∵AB＝AE+BE，∴AB＝AC+BE，∵AC＝AF+CF，∴AB＝AF+2BE，∵AB＝m，AF＝n，∴BE＝（m﹣n）．。

苏科七年级数学下学期期末测试题及答案(共五套)一、选择题1．下列运算中，正确的是（ ）A ．（ab 2）2=a 2b 4B ．a 2+a 2=2a 4C ．a 2•a 3=a 6D ．a 6÷a 3=a 2 2．如图，能判断AB ∥CE 的条件是（ ）A ．∠A ＝∠ECDB ．∠A ＝∠ACEC ．∠B ＝∠BCAD ．∠B ＝∠ACE3．用白铁皮做罐头盒，每张铁皮可制盒身10个或制盒底16个，一个盒身与两个盒底配成一套罐头盒，现有18张白铁皮，设用x 张制作盒身，y 张制作盒底，可以使盒身和盒底正好配套，则所列方程组正确的是（ ） A ．181016x y x y +=⎧⎨=⎩B ．1821016x y x y +=⎧⎨⨯=⎩C ．1810216x y x y +=⎧⎨=⨯⎩D ．181610x y x y +=⎧⎨=⎩4．把多项式x 2+ax+b 分解因式，得(x+1)(x-3)，则a 、b 的值分别是（ ） A ．a=2，b=3 B ．a=-2，b=-3 C ．a=-2，b=3D ．a=2，b=-35．下列等式从左到右的变形属于因式分解的是（ ）A ．a 2﹣2a+1＝（a ﹣1）2B ．a （a+1）（a ﹣1）＝a 3﹣aC ．6x 2y 3＝2x 2•3y 3D ．211()x x x x+=+6．将图甲中阴影部分的小长方形变换到图乙位置，能根据图形的面积关系得到的关系式是( )A ．22()()a b a b a b +-=-B ．222()a b a b -=-C ．2()b a b ab b -=-D ．2()ab b b a b -=-7．将一副三角板(含30°、45°的直角三角形)摆放成如图所示，图中∠1的度数是( )A ．90°B ．120°C ．135°D ．150° 8．计算28+（-2）8所得的结果是（ ）A ．0B ．216C ．48D ．299．如图，在下列给出的条件下，不能判定AB ∥DF 的是（ ）A ．∠A+∠2=180°B ．∠A=∠3C ．∠1=∠4D ．∠1=∠A 10．下列给出的线段长度不能与4cm ，3cm 能构成三角形的是（ ） A ．4cmB ．3cmC ．2cmD ．1cm11．下列等式由左边到右边的变形中，因式分解正确的是（ ） A ．22816(4)m m m -+=- B ．323346(46)x y x y x y y +=+ C ．()22121x x x x ++=++D ．22()()a b a b a b +-=-12．下列说法：2a -没有算术平方根；若一个数的平方根等于它本身，则这个数是0或1；有理数和数轴上的点一一对应；负数没有立方根，其中正确的是（ ） A ．0个B ．1个C ．2个D ．3个二、填空题13．已知2x +3y -5=0，则9x •27y 的值为______． 14．计算：m 2•m 5=_____．15．一个多边形的内角和与外角和之差为720︒，则这个多边形的边数为______. 16．已知22a b -=，则24a b ÷的值是____．17．20192018512125⎛⎫-⨯ ⎪⎝⎭⎭⎛⎫ ⎪⎝ =______．18．甲、乙两种车辆运土，已知5辆甲车和四辆乙车一次可运土140立方米，3辆甲车和2辆乙车一次可运土76立方米，若每辆甲车每次运土x 立方米，每辆乙车每次运土y 立方米，则可列方程组_________．19．如图，四边形ABCD 中，E 、F 、G 、H 依次是各边中点，O 是形内一点，若四边形AEOH 、四边形BFOE 、四边形CGOF 的面积分别为6、7、8，四边形DHOG 面积为（ ）A ．6B ．7C ．8D ．920．()22x y --＝_____．21．计算212⎛⎫= ⎪⎝⎭______． 22．若2(1)(23)2x x x mx n +-=++，则m n +=________．23．若（x 2+x-1）（px+2）的乘积中，不含x 2项，则p 的值是 ________．24．如图，//PQ MN ，A 、B 分别为直线MN 、PQ 上两点，且45BAN ∠=︒，若射线AM 绕点顺时针旋转至AN 后立即回转，射线BQ 绕点B 逆时针旋转至BP 后立即回转，两射线分别绕点A 、点B 不停地旋转，若射线AM 转动的速度是a ︒/秒，射线BQ 转动的速度是b ︒/秒，且a 、b 满足()2510a b -+-=．若射线AM 绕点A 顺时针先转动18秒，射线BQ 才开始绕点B 逆时针旋转，在射线BQ 到达BA 之前，问射线AM 再转动_______秒时，射线AM 与射线BQ 互相平行．三、解答题25．已知△ABC中，∠A =60°，∠ACB =40°，D 为BC 边延长线上一点，BM 平分∠ABC ，E 为射线BM 上一点． （1）如图1，连接CE ， ①若CE ∥AB ，求∠BEC 的度数； ②若CE 平分∠ACD ，求∠BEC 的度数．（2）若直线CE 垂直于△ABC 的一边，请直接写出∠BEC 的度数．26．因式分解： （1）16x 2－9y 2 （2）(x 2+y 2)2－4x 2y 2 27．解方程组（1）21325x yx y+=⎧⎨-=⎩（2）111231233xyx y⎧-=⎪⎪⎨⎪--=⎪⎩28．好学的小红在学完三角形的角平分线后，遇到下列4个问题，请你帮她解决．如图，在ABC∆中，点I是ABC∠、ACB∠的平分线的交点，点D是MBC∠、NCB∠平分线的交点，,BI DC的延长线交于点E．（1）若50BAC∠=︒，则BIC∠=°；（2）若BAC x∠=︒（090x<<），则当ACB∠等于多少度（用含x的代数式表示）时，//CE AB，并说明理由；（3）若3D E∠=∠，求BAC∠的度数．29．（数学经验）三角形的中线的性质：三角形的中线等分三角形的面积．（经验发展）面积比和线段比的联系：（1）如图1，M为△ABC的AB上一点，且BM=2AM．若△ABC的面积为a，若△CBM的面积为S，则S=_______(用含a的代数式表示)．（结论应用）（2）如图2，已知△CDE的面积为1，14CDAC=，13CECB=，求△ABC的面积．（迁移应用）（3）如图3．在△ABC中，M是AB的三等分点(13AM AB=)，N是BC的中点，若△ABC的面积是1，请直接写出四边形BMDN的面积为________．30．计算：（1）2a（a﹣2a2）；（2）a7＋a﹣（a2）3；（3）（3a＋2b）（2b﹣3a）；（4）（m﹣n）2﹣2m（m﹣n）．31．从边长为a 的正方形中剪掉一个边长为b 的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．（1）上述操作能验证的等式是 ．（请选择正确的选项） A ．a 2﹣b 2＝（a ＋b ）（a ﹣b ） B ．a 2﹣2ab ＋b 2＝（a ﹣b ）2 C ．a 2＋ab ＝a （a ＋b ）（2）若x 2﹣y 2＝16，x ＋y ＝8，求x ﹣y 的值； （3）计算：（1﹣212）（1﹣213）（1﹣214）…（1﹣212019）（1﹣212020）．32．一个多边形的每一个内角都相等，并且每个外角都等于和它相邻的内角的一半． （1）求这个多边形是几边形；（2）求这个多边形的每一个内角的度数．33．如图，有一块长为(3)a b +米，宽为(2)a b +米的长方形空地，计划修筑东西、南北走向的两条道路，其余进行绿化（阴影部分），已知道路宽为a 米，东西走向的道路与空地北边界相距1米，则绿化的面积是多少平方米？并求出当a ＝3，b ＝2时的绿化面积．34．阅读材料：把形如2ax bx c ++的二次三项式（或其一部分）配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写，即222)2(a ab b a b ±+=±.例如：2224213x x x x -+=-++2(1)3x =-+是224x x -+的一种形式的配方；所以，()213x -+，2(2)x -2x +，22213224x x ⎛⎫-+ ⎪⎝⎭是224x x -+的三种不同形式的配方（即“余项”分别是常数项、一次项、二次项）. 请根据阅读材料解决下列问题：（1）比照上面的例子，写出249x x -+三种不同形式的配方；（2）已知22610340x y x y +-++=，求32x y -的值；（3）已知2223240a b c ab b c ++---+=，求a b c ++的值.35．把几个图形拼成一个新的图形，再通过两种不同的方式计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．例如，由图1，可得等式：（a+2b ）（a+b ）＝a 2+3ab+2b 2． （1）由图2，可得等式 ；（2）利用（1）所得等式，解决问题：已知a+b+c ＝11，ab+bc+ac ＝38，求a 2+b 2+c 2的值． （3）如图3，将两个边长为a 、b 的正方形拼在一起，B ，C ，G 三点在同一直线上，连接BD 和BF ，若这两个正方形的边长a 、b 如图标注，且满足a+b ＝10，ab ＝20．请求出阴影部分的面积．（4）图4中给出了边长分别为a 、b 的小正方形纸片和两边长分别为a 、b 的长方形纸片，现有足量的这三种纸片．①请在下面的方框中用所给的纸片拼出一个面积为2a 2+5ab+2b 2的长方形，并仿照图1、图2画出拼法并标注a 、b ；②研究①拼图发现，可以分解因式2a 2+5ab+2b 2＝ ． 36．同一平面内的两条直线有相交和平行两种位置关系．（1）如图a ，若//AB CD ，点P 在AB 、CD 外部，我们过点P 作AB 、CD 的平行线PE ，则有////AB CD PE ，则BPD ∠，B ，D ∠之间的数量关系为_________．将点P 移到AB 、CD 内部，如图b ，以上结论是否成立？若成立，说明理由；若不成立，则BPD ∠、B 、D ∠之间有何数量关系？请证明你的结论．（2）迎“20G ”科技节上，小兰制作了一个“飞旋镖”，在图b 中，将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ，如图c ，他很想知道BPD ∠、ABP ∠、D ∠、BQD ∠之间的数量关系，请你直接写出它们之间的数量关系：__________．（3）设BF 交AC 于点P ，AE 交DF 于点Q ，已知126APB ∠=︒，100AQF ∠=︒，直接写出B E F ∠+∠+∠的度数为_______度，A ∠比F ∠大______度．【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【解析】 【分析】直接利用积的乘方运算法则以及合并同类项法则和同底数幂的乘除运算法则分别分析得出答案. 【详解】解：A 、（ab 2）2=a 2b 4，故此选项正确； B 、a 2+a 2=2a 2，故此选项错误； C 、a 2•a 3=a 5，故此选项错误； D 、a 6÷a 3=a 3，故此选项错误； 故选：A. 【点睛】此题主要考查了积的乘方运算以及合并同类项和同底数幂的乘除运算，正确掌握运算法则是解题关键．2．B解析：B 【解析】 【分析】根据平行线的判定方法：内错角相等两直线平行，即可判断AB ∥CE ． 【详解】解：∵∠A ＝∠ACE ，∴AB ∥CE （内错角相等，两直线平行）． 故选：B ． 【点睛】此题考查了平行线的判定，平行线的判定方法有：同位角相等两直线平行；内错角相等两直线平行；同旁内角互补两直线平行，熟练掌握平行线的判定是解本题的关键．3．B解析：B【分析】根据题意可知，本题中的相等关系是：（1）盒身的个数2⨯=盒底的个数；（2）制作盒身的白铁皮张数+制作盒底的白铁皮张数18=，再列出方程组即可．【详解】解：设用x张制作盒身，y张制作盒底，根据题意得：18 21016x yx y+=⎧⎨⨯=⎩．故选：B．【点睛】此题考查从实际问题中抽出二元一次方程组，根据题目给出的条件，找出合适的等量关系注意运用本题中隐含的一个相等关系：“一个盒身与两个盒底配成一套盒”．4．B解析：B【解析】分析：根据整式的乘法，先还原多项式，然后对应求出a、b即可.详解：（x+1）（x-3）=x2-3x+x-3=x2-2x-3所以a=2，b=-3，故选B．点睛：此题主要考查了整式的乘法和因式分解的关系，利用它们之间的互逆运算的关系是解题关键.5．A解析：A【分析】根据因式分解是把一个多项式转化成几个整式积的形式，可得答案．【详解】A、是因式分解，故A正确；B、是整式的乘法运算，故B错误；C、是单项式的变形，故C错误；D、没把一个多项式转化成几个整式积的形式，故D错误；故选：A．【点睛】本题考查了因式分解的意义，因式分解是把一个多项式转化成几个整式积的形式．6．A【分析】根据长方形的面积=长⨯宽，分别表示出甲乙两个图形的面积，即可得到答案． 【详解】解：()()=S a b a b +-甲，()()2222==S a a b b a b a ab ab b a b -+-=-+--乙．所以()()a b a b +-22=a b - 故选A ． 【点睛】本题考查平方差公式，难度不大，通过计算两个图形的面积即可顺利解题．7．B解析：B 【详解】解：根据题意得：∠1=180°－60°=120°. 故选：B 【点睛】本题考查直角三角板中的角度的计算，难度不大.8．D解析：D 【分析】利用同底数幂的乘法与合并同类项的知识求解即可求得答案． 【详解】 解：28+（-2）8 =28+28 =2×28 =29． 故选：D ． 【点睛】此题考查了同底数幂的乘法的知识．此题比较简单，注意掌握指数与符号的变化是解此题的关键．9．D解析：D 【分析】根据平行线的判定定理对各选项进行逐一判断即可． 【详解】A 、∵∠A ＋∠2＝180°，∴AB ∥DF ，故本选项错误； B 、∵∠A ＝∠3，∴AB ∥DF ，故本选项错误；C 、∵∠1＝∠4，∴AB ∥DF ，故本选项错误；D 、∵∠1＝∠A ，∴AC ∥DE ，故本选项正确．【点睛】点评：本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．10．D解析：D 【分析】根据三角形的三边关系：任意两边之和大于第三边，两边之差小于第三边，即可得答案． 【详解】解：设第三边为xcm ，根据三角形的三边关系：4343x -<<+， 解得：17x <<．故选项ABC 能构成三角形，D 选项1cm 不能构成三角形， 故选：D ． 【点睛】本题主要考查了三角形的三边关系定理：任意两边之和大于第三边，两边之差小于第三边．11．A解析：A 【分析】根据因式分解的意义，可得答案． 【详解】解：A 、属于因式分解，故本选项正确； B 、因式分解不彻底，故B 选项不符合题意；C 、没把一个多项式转化成几个整式积的形式，故C 不符合题意；D 、是整式的乘法，故D 不符合题意； 【点睛】本题考查了因式分解的意义，把一个多项式转化成几个整式积的形式是因式分解．12．A解析：A 【分析】根据负数没有算术平方根判断第一句，由1的平方根是1,± 判断第二句，数轴上的点也可以表示无理数判断第三句，任意实数都有立方根判断第四句． 【详解】解：当20a -=有算术平方根，所以第一句错误， 1的平方根是1,±所以第二句错误，数轴上的点与实数一一对应，所以第三句错误， 任意实数都有立方根，所以第四句错误， 故选A ． 【点睛】本题考查算术平方根、平方根、立方根以及实数与数轴的关系.理解相关定理是解题关键.二、填空题13．243【解析】【分析】先将9x•27y变形为32x+3y，然后再结合同底数幂的乘法的概念和运算法则进行求解即可．【详解】∵2x+3y−5=0，∴2x+3y=5，∴9x27y=32x解析：243【解析】【分析】先将9x•27y变形为32x+3y，然后再结合同底数幂的乘法的概念和运算法则进行求解即可．【详解】∵2x+3y−5=0，∴2x+3y=5，∴9x⋅27y=32x⋅33y=32x+3y=35=243.故答案为：243.【点睛】本题考查了同底数幂的乘法，解题的关键是熟练的掌握同底数幂乘法的概念和运算法则. 14．m7【分析】根据同底数幂的乘法法则，同底数幂相乘，底数不变，指数相加，据此计算即可．【详解】解：m2•m5=m2+5=m7．故答案为：m7．【点睛】本题考查了同底数幂的乘法，熟练掌握同解析：m7【分析】根据同底数幂的乘法法则，同底数幂相乘，底数不变，指数相加，据此计算即可．【详解】解：m 2•m 5=m 2+5=m 7．故答案为：m 7．【点睛】本题考查了同底数幂的乘法，熟练掌握同底数幂的乘法法则是解答本题的关键． 15．8【解析】【分析】根据多边形的内角和公式（n-2）•180°与外角和定理列式求解即可．【详解】设这个多边形的边数是n ，则（n-2）•180°-360°=720°，解得n=8．故答案为解析：8【解析】【分析】根据多边形的内角和公式（n-2）•180°与外角和定理列式求解即可．【详解】设这个多边形的边数是n ，则（n-2）•180°-360°=720°，解得n=8．故答案为8．【点睛】本题考查了多边形的内角和与外角和定理，任意多边形的外角和都是360°，与边数无关．16．【分析】先将化为同底数幂的式子，然后根据幂的除法法则进行合并，再将代入计算即可．【详解】解：==，∵，∴原式=22=4．【点睛】本题考查了幂的除法法则，掌握知识点是解题关键．解析：【分析】先将24a b ÷化为同底数幂的式子，然后根据幂的除法法则进行合并，再将22a b -=代入计算即可．【详解】解：24a b ÷=222a b ÷=()22a b -，∵22a b -=，∴原式=22=4．【点睛】本题考查了幂的除法法则，掌握知识点是解题关键．17．【分析】根据同底数的幂的乘法运算的逆运算，先将分成 ，再根据积的乘方的逆运算，把指数相同的数相乘即可．【详解】解：故答案为： ．【点睛】本题考查幂的乘方和积的乘方，将不同底数 解析：5-12【分析】 根据同底数的幂的乘法运算的逆运算，先将2019512⎛⎫- ⎪⎝⎭分成2018551212⎛⎫⎛⎫-⨯- ⎪ ⎪⎝⎭⎝⎭ ，再根据积的乘方的逆运算，把指数相同的数相乘即可．【详解】 解：20192018512125⎛⎫-⨯ ⎪⎝⎭⎭⎛⎫ ⎪⎝ 20182018551212125⎛⎫⎛⎫⎛⎫=-⨯-⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 20182018512512512⎛⎫⎛⎫⎛⎫=-⨯⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 2018512512512⎛⎫⎛⎫=-⨯⨯- ⎪ ⎪⎝⎭⎝⎭ ()20185112⎛⎫=-⨯- ⎪⎝⎭512 =-故答案为：512 -．【点睛】本题考查幂的乘方和积的乘方，将不同底数且不同指数的幂转化为底数相同或者指数相同的幂是解题关键．18．【分析】设甲种车辆一次运土x立方米，乙车辆一次运土y立方米，根据题意所述的两个等量关系得出方程组.【详解】设甲种车辆一次运土x立方米，乙车辆一次运土y立方米，由题意得，，故答案为：.【解析：54140 3276 x yx y+=⎧⎨+=⎩【分析】设甲种车辆一次运土x立方米，乙车辆一次运土y立方米，根据题意所述的两个等量关系得出方程组.【详解】设甲种车辆一次运土x立方米，乙车辆一次运土y立方米，由题意得，54140 3276x yx y+=⎧⎨+=⎩，故答案为：54140 3276 x yx y+=⎧⎨+=⎩.【点睛】此题考查了二元一次方程组的应用，属于基础题，仔细审题，根据题意的等量关系得出方程是解答本题的关键．19．B【解析】连接OC，OB，OA，OD，∵E、F、G、H依次是各边中点，∴△AOE和△BOE等底等高，所以S△OAE=S△OBE，同理可证，S△OBF=S△OCF，S△ODG=S△OCG，【解析】连接OC，OB，OA，OD，∵E、F、G、H依次是各边中点，∴△AOE和△BOE等底等高，所以S△OAE=S△OBE，同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，∵S四边形AEOH=6，S四边形BFOE=7，S四边形CGOF=8，∴6+8=7+S四边形DHOG，解得S四边形DHOG=7．故答案为7．点睛：本题考查了三角形的面积.解决本题的关键将各个四边形划分,充分利用给出的中点这个条件,证得三角形的面积相等,进而证得结论.20．x2+4xy+4y2【分析】根据完全平方公式进行计算即可．完全平方公式：（a±b）2＝a2±2ab+b2．【详解】解：（﹣x﹣2y）2＝x2+4xy+4y2．故答案为：x2+4xy+4y2解析：x2+4xy+4y2【分析】根据完全平方公式进行计算即可．完全平方公式：（a±b）2＝a2±2ab+b2．【详解】解：（﹣x﹣2y）2＝x2+4xy+4y2．故答案为：x2+4xy+4y2．【点睛】本题考查了完全平方公式，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．该题要求熟练掌握完全平方公式，并灵活运用．21．【分析】根据分式的乘方运算法则，即分式乘方要把分子、分母分别乘方，即可求解．【详解】解：．故答案为．本题目考查分式的乘方运算法则，难度不大，熟练掌握其运算法则是解题的关键． 解析：14【分析】根据分式的乘方运算法则，即分式乘方要把分子、分母分别乘方，即可求解．【详解】 解：222111==224⎛⎫ ⎪⎝⎭． 故答案为14． 【点睛】本题目考查分式的乘方运算法则，难度不大，熟练掌握其运算法则是解题的关键． 22．【分析】根据多项式与多项式相乘的法则进行运算，得一次项系数与常数项分别为、，进而求得 ．【详解】解：∵，∴ 、 ，∴．故答案为．【点睛】本题目考查整式的乘法，难度不大，熟练掌握多项解析：4-【分析】根据多项式与多项式相乘的法则进行运算，得一次项系数与常数项分别为m 、n ，进而求得m n + ．【详解】解：∵22(1)(23)23=2x x x x x mx n +-=--++，∴1m =- 、3n =- ，∴()=13=13=4m n +-+----．故答案为4-．【点睛】本题目考查整式的乘法，难度不大，熟练掌握多项式与多项式相乘的运算方法即可顺利解题．23．【分析】先按照多项式乘以多项式，再把同类项合并，利用不含项即这一项的系数为，即可得到答案．【详解】解：而上式不含项，，故答案为：【点睛】本题考查的是多项式的乘法运算，同时解析：2.-【分析】先按照多项式乘以多项式，再把同类项合并，利用不含2x 项即这一项的系数为0，即可得到答案．【详解】解：()()232212222x x px px x px x px +-+=+++--()()32222px p x p x =+++--而上式不含2x 项，20p ∴+=，2,p ∴=-故答案为： 2.-【点睛】本题考查的是多项式的乘法运算，同时考查多项式的概念中的项的次数，及不含某项的条件，掌握以上知识是解题的关键．24．15或22.5【分析】先由题意得出a ，b 的值，再推出射线AM 绕点A 顺时针先转动18秒后，AM 转动至AM 的位置，∠MAM=18°×5=90°，然后分情况讨论即可．【详解】∵，∴a=5，b=1解析：15或22.5【分析】先由题意得出a ，b 的值，再推出射线AM 绕点A 顺时针先转动18秒后，AM 转动至AM '的位置，∠MAM '=18°×5=90°，然后分情况讨论即可．【详解】 ∵()2510a b -+-=，∴a=5，b=1，设射线AM 再转动t 秒时，射线AM 、射线BQ 互相平行，如图，射线AM 绕点A 顺时针先转动18秒后，AM 转动至AM '的位置，∠MAM '=18°×5=90°，分两种情况：①当9＜t ＜18时，如图，∠QBQ '=t °，∠M 'AM"=5t °，∵∠BAN=45°=∠ABQ ，∴∠ABQ '=45°-t °，∠BAM"=5t-45°，当∠ABQ '=∠BAM"时，BQ '//AM"，此时，45°-t °=5t-45°，解得t=15；②当18＜t ＜27时，如图∠QBQ '=t °，∠NAM"=5t °-90°，∵∠BAN=45°=∠ABQ ，∴∠ABQ '=45°-t °，∠BAM"=45°-（5t °-90°）=135°-5t °，当∠ABQ '=∠BAM"时，BQ '//AM"，此时，45°-t °=135°-5t ，解得t=22.5；综上所述，射线AM 再转动15秒或22.5秒时，射线AM 射线BQ 互相平行．故答案为：15或22.5【点睛】本题考查了非负数的性质，平行线的判定，完全平方公式，掌握知识点是解题关键．三、解答题25．（1）①40°；②30°；(2)50°，130°，10°【解析】试题分析：（1）①根据三角形的内角和得到∠ABC=80°，由角平分线的定义得到∠ABE=12∠ABC=40°，根据平行线的性质即可得到结论；②根据邻补角的定义得到∠ACD=180°-∠ACB=140°，根据角平分线的定义得到∠CBE=12∠ABC=40°，∠ECD=12∠ACD=70°，根据三角形的外角的性质即可得到结论；（2）①如图1，当CE⊥BC时，②如图2，当CE⊥AB于F时，③如图3，当CE⊥AC时，根据垂直的定义和三角形的内角和即可得到结论．试题解析：（1）①∵∠A=60°，∠ACB=40°，∴∠ABC=80°，∵BM平分∠ABC，∴∠ABE=12∠ABC=40°，∵CE∥AB，∴∠BEC=∠ABE=40°；②∵∠A=60°，∠ACB=40°，∴∠ABC=80°，∠ACD=180°-∠ACB=140°，∵BM平分∠ABC，CE平分∠ACD，∴∠CBE=12∠ABC=40°，∠ECD=12∠ACD=70°，∴∠BEC=∠ECD-∠CBE=30°；（2）①如图1，当CE⊥BC时，∵∠CBE=40°，∴∠BEC=50°；②如图2，当CE⊥AB于F时，∵∠ABE=40°，∴∠BEC=90°+40°=130°，③如图3，当CE⊥AC时，∵∠CBE=40°，∠ACB=40°，∴∠BEC=180°-40°-40°-90°=10°．【点睛】本题考查了平行线的性质，角平分线的定义，垂直的定义，三角形的内角和，三角形的外角的性质，正确的画出图形是解题的关键．26．（1）(43)(4-3)x y x y +；（2）22()(-y)x y x +．【分析】（1）直接利用平方差公式22()()a b a b a b +-=-分解即可；（2）先利用平方差公式，再利用完全平方公式222()2a b a ab b ±=±+即可．【详解】（1）原式2243))((x y =-(43)(43)x y x y =+-；（2）原式2222)()(2x y xy =-+2222(2)(2)x y x y xy y x ++=+-22()()x y x y =+-．【点睛】本题考查了利用平方差公式和完全平方公式进行因式分解，熟记公式是解题关键．27．（1）3214x y ⎧=⎪⎪⎨⎪=-⎪⎩；（2）14111211x y ⎧=⎪⎪⎨⎪=-⎪⎩． 【分析】（1）直接利用加减消元法解方程组，即可得到答案；（2）直接利用加减消元法解方程组，即可得到答案；【详解】解：（1）21325x y x y +=⎧⎨-=⎩①②， 由①+②，得46x =， ∴32x =， 把32x =代入①，得14y =-， ∴方程组的解为：3214x y ⎧=⎪⎪⎨⎪=-⎪⎩； （2）111231233x y x y ⎧-=⎪⎪⎨⎪--=⎪⎩①②， 由①3⨯-②，得：11763x =，∴1411x =， 把1411x =代入①，解得：1211y =-， ∴方程组的解为：14111211x y ⎧=⎪⎪⎨⎪=-⎪⎩； 【点睛】本题考查了解二元一次方程组，解题的关键是熟练掌握加减消元法解二元一次方程组．28．（1）115；（2）180-2x ，理由见解析；（3）45°.【分析】（1）已知点I 是两角∠ABC 、∠ACB 平分线的交点，故()()()11118018018018090222BIC IBC ICB ABC ACB A BAC ∠=︒-∠+∠=︒-∠+∠=︒-︒-∠=+∠ ，由此可求∠BIC ；（2）当CE ∥AB 时， ∠ACE=∠A=x °，根据∠ACE=∠A=x °，根据CE 是∠ACG 的角平分线，推出∠ACG=2x °，∠ABC=∠BAC=x °，即可求出ACB ∠的度数．（3）由题意知：△BDE 是直角三角形∠D+∠E=90°，可求出若∠D=3∠E 时，∠BEC=22.5°，再推理出12BEC BAC ∠=∠，即可求出BAC ∠的度数． 【详解】（1）∵点I 是两角∠ABC 、∠ACB 平分线的交点，∴()180BIC IBC ICB ∠=︒-∠+∠ ()11802ABC ACB =-∠+∠︒ ()11801802A =-︒︒-∠ 1901152BAC =+∠=︒； 故答案为：115.（2）当∠ACB 等于（180-2x ）°时，CE ∥AB ．理由如下：∵CE ∥AB ，∴∠ACE=∠A=x °，∵∠ACE=∠A=x °，CE 是∠ACG 的角平分线，∴∠ACG=2∠ACE=2x °，∴∠ABC=∠ACG-∠BAC=2x °-x °=x °，∴∠ACB=180°-∠BAC-∠ABC=（180-2x ）°；（3）由题意知：△BDE 是直角三角形∠D+∠E=90°若∠D=3∠E 时∠BEC=22.5°，∵90BEC BDC ∠=︒-∠190902BAC ⎛⎫=︒-︒-∠ ⎪⎝⎭ 12BAC =∠， ∴45BAC ∠=︒.【点睛】本题考查了三角形的内角、外角平分线的夹角大小与原三角形内角的关系，要充分运用三角形内角和定理，角平分线性质转换．29．（1）23a （2）12（3）512 【分析】（1）根据三角形的面积公式及比例特点即可求解；（2）连接AE ，先求出△ACE 的面积，再得到△ABC 的面积即可；（3）连接BD ，设△ADM 的面积为a ，则△BDM 的面积为2a,设△CDN 的面积为b ，则△BDN 的面积为b ，根据图形的特点列出方程组求出a,b,故可求解．【详解】（1）设△ABC 中BC 边长的高为h ，∵BM =2AM ．∴BM=23AB ∴S=12BM×h=12×23AB×h=23S △ABC =23a 故答案为：23a ； （2）如图2，连接AE ， ∵14CD AC = ∴CD=14AC ∴S △DCE =14S △ACE =1 ∴S △ACE =4， ∵13CE CB = ∴CE=13CB∴S△ACE=13S△ABC=4∴S△ABC=12；（3）如图3，连接BD，设△ADM的面积为a，∵13 AM AB=∴BM=2AM,BM=23 AB，∴S△BDM=2S△ABM=2a, S△BCM=23S△ABC=23设△CDN的面积为b，∵N是BC的中点，∴S△CDN=S△BDN=b，S△ABN=12S△ABC=12∴122223a a bb b a⎧++=⎪⎪⎨⎪++=⎪⎩，解得11214ab⎧=⎪⎪⎨⎪=⎪⎩∴四边形BMDN的面积为2a+b=5 12故答案为5 12．【点睛】此题主要考查三角形面积公式的应用，解题的关键是根据题意找到面积的之间的关系．30．（1）2a2﹣4a3；（2）a7＋a﹣a6；（3）4b2﹣9a2；（4）n2﹣m2【分析】（1）由题意根据单项式乘以多项式法则求出即可；（2）根据题意先算乘方，再合并同类项即可；（3）由题意直接根据平方差公式求出即可；（4）由题意先根据完全平方公式和单项式乘以多项式进行计算，再合并同类项即可．【详解】解：（1）2a（a﹣2a2）＝2a2﹣4a3；（2）a7＋a﹣（a2）3＝a7＋a﹣a6；（3）（3a ＋2b ）（2b ﹣3a ）＝4b 2﹣9a 2；（4）（m ﹣n ）2﹣2m （m ﹣n ）＝m 2﹣2mn ＋n 2﹣2m 2＋2mn＝n 2﹣m 2．【点睛】本题考查整式的混合运算，乘法公式等知识点，能正确根据整式的运算法则进行化简是解此题的关键．31．（1）A ；（2）2；（3）20214040 【分析】（1）由题意直接根据拼接前后的面积相等进行分析计算即可得出答案；（2）根据题意可知x 2﹣y 2＝16，即（x ＋y ）（x ﹣y ）＝16，又x ＋y ＝8，可求出x ﹣y 的值；（3）根据题意利用平方差公式将算式转化为分数的乘积的形式，根据数据规律得出答案．【详解】解：（1）图1的剩余面积为a 2﹣b 2，图2拼接得到的图形面积为（a ＋b ）（a ﹣b ） 因此有，a 2﹣b 2＝（a ＋b ）（a ﹣b ），故答案为：A.（2）∵x 2﹣y 2＝（x ＋y ）（x ﹣y ）＝16，又∵x ＋y ＝8，∴x ﹣y ＝16÷8＝2；（3）（1﹣212）（1﹣213）（1﹣214）…（1﹣212019）（1﹣212020） ＝（1﹣12）（1＋12）（1﹣13）（1＋13）（1﹣14）（1＋14）……（1﹣12019）（1＋12019）（1﹣12020）（1＋12020） ＝12×32×23×43×34×54×……×20182019×20202019×20192020×20212020 ＝12×20212020 ＝20214040． 【点睛】本题考查平方差公式的几何意义及应用，掌握公式的结构特征是正确应用的前提，利用公式进行适当的变形是解题的关键．32．（1）这个多边形是六边形；（2）这个多边形的每一个内角的度数是120°．【分析】（1）先设内角为x ,根据题意可得:外角为12x ,根据相邻内角和外角的关系可得:,x +12x =180°,从而解得:x =120°,即外角等于60°,根据外角和等于360°可得这个多边形的边数为:36060=6, （2）先设内角为x ,根据题意可得:外角为12x ,根据相邻内角和外角的关系可得:,x +12x =180°,从而解得内角:x =120°,内角和=（6﹣2）×180°=720°．【详解】 （1）设内角为x ,则外角为12x , 由题意得,x +12x =180°, 解得:x =120°, 12x =60°, 这个多边形的边数为:36060=6, 答:这个多边形是六边形, （2）设内角为x ,则外角为12x , 由题意得: x +12x =180°, 解得:x =120°,答:这个多边形的每一个内角的度数是120度．内角和=（6﹣2）×180°=720°．【点睛】本题主要考查多边形内角和外角,多边形内角和以及多边形的外角和,解决本题的关键是要熟练掌握多边形内角和外角的关系以及多边形内角和.33．()2223a ab b ++平方米；40平方米． 【分析】（1）根据平移的原理，四块绿化面积可拼成一个长方形，其边长为原边长减去再减去道路宽为a 米，由此即可求绿化的面积的代数式；然后利用多项式乘多项式法则计算，去括号合并得到最简结果，将a 与b 的值代入计算即可求出值．【详解】解：根据题意得：22(3)(2)(2)()23a b a a b a a b a b a ab b +-+-=++=++（平方米）．则绿化的面积是()2223a ab b ++平方米； 当3a =，2b =时，原式2223233240=⨯+⨯⨯+=（平方米）．故当a ＝3，b ＝2时，绿化面积为40平方米．答：绿化的面积是()2223a ab b ++平方米；当a ＝3，b ＝2时，绿化面积为40平方米． 【点睛】此题考查整式的混合运算与代数式求值，掌握长方形的面积计算方法是解决问题的关键．34．（1）2249(2)5x x x -+=-+；2249(3)10x x x x -+=+-；2249(3)2x x x x -+=-+；（2）19；（3）4【分析】（1）根据材料中的三种不同形式的配方，“余项“分别是常数项、一次项、二次项，可解答；（2）将x 2+y 2-6x+10y+34配方，根据平方的非负性可得x 和y 的值，可解答；（3）通过配方后，求得a ，b ，c 的值，再代入代数式求值．【详解】解：（1）249x x -+的三种配方分别为：2249(2)5x x x -+=-+；2249(3)10x x x x -+=+-；2249(3)2x x x x -+=-+（或2222549339x x x x ⎛⎫-+=-+ ⎪⎝⎭； （2）∵x 2+y 2-6x+10y+34=x 2-6x+9+y 2+10y+25=（x-3）2+（y+5）2=0，∴x-3=0，y+5=0，∴x=3，y=-5，∴3x-2y=3×3-2×（-5）=19（3）2223240a b c ab b c ++---+=()2222134421044a ab b b bc c -++-++-+= 22213(2)(1)024a b b c ⎛⎫-+-+-= ⎪⎝⎭ ∴102a b -=，3(2)04b -=，10c -= ∴1a =，2b =，1c =，则4a b c ++=【点睛】本题考查的是配方法的应用，首先利用完全平方公式使等式变为两个非负数和一个正数的和的形式，然后利用非负数的性质解决问题．35．（1）2222()222a b c a b c ab bc ac ++=+++++；（2）45；（3）20；（4）①见解析，②(2)(2)a b a b ++．【分析】（1）根据面积的不同求解方法，可得到不同的表示方法．一种可以是3个正方形的面积和6个矩形的面积；另一种是直接利用正方形的面积公式计算，由此即可得出答案； （2）利用（1）中的等式直接代入即可求得答案；（3）根据阴影部分的面积等于两个正方形的面积之和减去两个直角三角形的面积即可得； （4）①依照前面的拼图方法，画出图形即可；②参照题（1）的方法，根据面积的不同求解方法即可得出答案．【详解】（1）由题意得：2222()222a b c a b c ab bc ac ++=+++++故答案为：2222()222a b c a b c ab bc ac ++=+++++；（2）11,38a b c ab bc ac ++=++= ∴2222()(222)a b c a b c ab bc ac ++++=-++2)2(()a b c ab ac bc -+=+++211238=-⨯45=；（3）四边形ABCD 、四边形ECGF 为正方形，且边长分别为a 、b90A G ∴∠=∠=︒，AB AD BC a ===，FG CG b ==，BG BC CG a b =+=+ ∵10,20a b ab +==∴ABCD ECGF ABD BFG S S S S S =+--阴影221122AB CG AB AD FG BG =+-⋅-⋅ 2211()22a b a a b a b =+-⋅-⋅+ 22111222a b ab =+- 213()22a b ab =+- 213102022=⨯-⨯ 20=；（4）①根据题意，作出图形如下：②根据面积的不同求解方法得：22(2522)(2)a ab b a b a b ++=++故答案为：(2)(2)a b a b ++．【点睛】本题考查了因式分解的几何应用、完全平方公式的几何应用，掌握因式分解的相关知识是解题关键．36．（1）∠BPD=∠B-∠D ；将点P 移到AB 、CD 内部，∠BPD=∠B-∠D 不成立，∠BPD=∠B+∠D ，证明见解析；（2）∠BPD=∠ABP+∠D+∠BQD ；（3）80，46．【分析】（1）由平行线的性质得出∠B=∠BPE ，∠D=∠DPE ，即可得出∠BPD=∠B-∠D ；将点P 移到AB 、CD 内部，延长BP 交DC 于M ，由平行线的性质得出∠B=∠BMD ，即可得出∠BPD=∠B+∠D ；（2）由平行线的性质得出∠A ′BQ=∠BQD ，同（1）得：∠BPD=∠A ′BP+∠D ，即可得出结论；（3）过点E 作EN ∥BF ，则∠B=∠BEN ，同（1）得：∠FQE=∠F+∠QEN ，得出∠EQF=∠B+∠E+∠F ，求出∠EQF=180°-100°=80°，即∠B+∠E+∠F=80°，由∠AMP=∠APB-∠A=126°-∠A ，∠FMQ=180°-∠AQF-∠F=180°-100°-∠F=80°-∠F ，∠AMP=∠FMQ ，得出126°-∠A=80°-∠F ，即可得出结论．【详解】解（1）∵AB ∥CD ∥PE ，∴∠B=∠BPE ，∠D=∠DPE ，∵∠BPE=∠BPD+∠DPE ，∴∠BPD=∠B-∠D ，故答案为：∠BPD=∠B-∠D ；将点P 移到AB 、CD 内部，∠BPD=∠B-∠D 不成立，∠BPD=∠B+∠D ，理由如下：延长BP 交DC 于M ，如图b 所示：∵AB ∥CD ，∴∠B=∠BMD ，∵∠BPD=∠BMD+∠D ，∴∠BPD=∠B+∠D ；（2）∵A ′B ∥CD ，∴∠A ′BQ=∠BQD ，同（1）得：∠BPD=∠A ′BP+∠D ，∴∠BPD=∠ABP+∠D+∠BQD ，故答案为：∠BPD=∠ABP+∠D+∠BQD ；。

苏州市2015--2016学年第二学期初一数学期终复习要点本次考试范围：苏科版义务教育教科书七年级下学期课本全部内容：主要包括第7、8、9、10、11、12章内容。

考试时间：120分钟。

考试题型：选择、填空、解答三类。

分值：130分。

第七章平面图形认识（二）知识点：探索平行线的条件；平行线的性质；图形的平移；认识三角形；多边形内角和与外角和。

1．如图，已知AB∥CD，E是AB上一点，DE平分∠BEC交CD于D，∠C=80°，则∠D的度数是（）A．400B．450C．500D．5502．下列各组线段能组成一个三角形的是（）A．4 cm，6 cm，11 cm B．4 cm，5 cm，l cmC．3 cm，4 cm，5 cm D．2cm，3 cm，6 cm3．如果一个三角形的两边分别为2和4，则第三边长可能是（）A．8 B．6 C． 4 D． 24．若一个多边形的内角和与它的外角和相等，则这个多边形是（）A．三角形B．四边形C．五边形D．六边形5．下列四个图形中，线段BE是△ABC的高的是（）ＡＢＣＤ6．如图，给出下列条件：①∠1=∠2；②∠3=∠4；③∠B=∠DCE；④AD∥BC且∠B=∠D．其中，能推出AB∥DC的是（）A．①④B．②③C．①③D．①③④7．一个多边形的内角和是1080°，这个多边形的边数是（）A．6 B．7C．8 D．98．如图所示，AB∥CD，∠E=37°，∠C=20°，则∠EAB的度数为（）A．57°B．60°C．63°D．123°9．如图，△DEF经过怎样的平移得到△ABC（）A．把△DEF向左平移4个单位，再向下平移2个单位B．把△DEF向右平移4个单位，再向下平移2个单位C．把△DEF向右平移4个单位，再向上平移2个单位D．把△DEF向左平移4个单位，再向上平移2个单位10．如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：①AD∥BC；②∠ACB=2∠ADB；③∠ADC=90°﹣∠ABD；④∠BDC=∠BAC．其中正确的结论有（）A．1个B．2个C．3个D．4个11．如图，四边形EFGH是由四边形ABCD通过平移得到，且点A、E、B，在同一条直线上．若AF=14，BE=6．则AB的长度是________．12．如图，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是___________．（第12题）（第13题）13．如图，在△ABC中，∠B=∠C，BF=CD，BD=CE，∠A=50°，则∠FDE=_______°．14．在△ABC中，∠A=100°，当∠B=°时，△ABC是等腰三角形．15．若三角形三条边长分别是1，a，5(其中a为整数)，则a的取值为▲．16．如图，将三角尺的直角顶点放在直尺的一边上，∠1=25°，∠3=20°则∠2的度数为▲°．17．如图，点B，C，E，F在一直线上，AB∥DC，DE∥GF，∠B=∠F=72°，则∠D= ▲°．（第16题）（第17题）18．内角和等于外角和2倍的多边形是边形．19．如图，在Rt△ABC中，∠A=90°，∠C=30°，D为斜边上的一点且BD=AB，过点D作BC的垂线，交AC于点E．若△CDE的面积为a，则四边形ABDE的面积为．（第19题）（第20题）20．如图，等边三角形ABC的边长为10厘米．点D是边AC的中点．动点P从点C出发，沿BC的延长线以2厘米/秒的速度作匀速运动，设点P的运动时间为t（秒）．若△BDP是等腰三角形，则为t=．21. 叙述三角形内角和定理并将证明过程填写完整．定理：_________．已知：△ABC．求证：∠A +∠B+∠C=180°．证明：作边BC的延长线CD，过C点作CE∥AB．∴∠1=∠A(__________)，∠2=∠B( _____________)，∵∠ACB+∠1+∠2=180°( ____________)，∴∠A+∠B+∠ACB=180°(_____________)．22. 如图，在△ABC中，已知AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．(1)求∠DAE的度数；(2)小明认为如果只知道∠B－∠C=40°，也能算出∠DAE的度数．你认为可以吗?若能，请能写出解题过程；若不能，请说明理由．23. 请将下列证明过程补充完整：已知：如图，AD是△ABC的角平分线，点E在BC上，点G在CA的延长线上，EG交AB于点F，且∠BEF+∠ADC=180°．求证：∠AFG=∠G．证明：∵∠BEF+∠ADC=180°（已知），又∵（平角的定义），∴∠GED=∠ADC（等式的性质），∴AD∥GE（），∴∠AFG=∠BAD（），且∠G=∠CAD（），∵AD是△ABC的角平分线（已知），∴（角平分线的定义），∴∠AFG=∠G．24. △ABC中，∠B＞∠C，∠BAC的平分线交BC于点D，设∠B=x，∠C=y．（1）如图1，若AE⊥BC于点E，试用x、y表示∠EAD，并说明理由．（2）如图2，若点F是AD延长线上的一点，∠BAF、∠BDF的平分线交于点G，则∠G=．（用x、y表示）25. 如图，一个三角形的纸片ABC，其中∠A=∠C．(1) 把△ABC纸片按(如图1) 所示折叠，使点A落在BC边上的点F处，．DE是折痕．说明B C∥DF；(2) 把△ABC纸片沿DE折叠，当点A落在四边形BCED内时(如图2)，探索∠C与∠1+∠2之间的大小关系，并说明理由；(3)当点A落在四边形BCED外时(如图3)，∠C与∠1、∠2的关系是▲．(直接写出结论)26. 如图，在长方形ABCD中，AB=CD=5厘米，AD=BC=4厘米. 动点P从A出发，以1厘米/秒的速度沿A →B运动，到B点停止运动；同时点Q从C点出发，以2厘米/秒的速度沿C→B→A运动，到A点停止运动．设P点运动的时间为t秒(t > 0)，(1) 当点Q在BC边上运动时，t为何值，AP=BQ；(2) 当t为何值时，S△ADP=S△BQD．第八章幂运算、第九章整式乘法与因式分解知识点：同底数幂相乘；幂的乘方与积的乘方；同底数幂的除法；零指数与负指数；科学记数法。

初一数学期末试卷带答案考试范围：xxx ；考试时间：xxx 分钟；出题人：xxx 姓名：___________班级：___________考号：___________1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上一、选择题1.如图，将△ABC 沿直线DE 折叠后，使得点B 与点A 重合．已知AC=5cm ，△ADC 的周长为17cm ，则BC 的长为（ ）A ．7cmB ．10cmC ．12cmD ．22cm2.如图，该图形绕点O 按下列角度旋转后，不能与其自身重合的是（ ）A ．72°B ．108°C ．144°D ．216° 3.下列合并同类项正确的有A ．2a+4a=8a 2B ．3x+2y="5xy"C ．7x 2－3x 2=4D ．9a 2b －9ba 2＝0 4..已知⊙O 的半径为5，AB 是弦，P 是直线AB 上的一点，PB=3，AB=8，则tan ∠OPA 的值为（ ）A ．3B ．C ．或D ．3或 5.下列运用等式的性质，变形不正确的是（ ） A ．若x=y ，则x+5="y+5" B ．若a=b ，则ac=bc C ．若=，则a="b"D ．若x=y ，则=6. 如图，BF 是∠ABD 的平分线，CE 是∠ACD 的平分线， BF 与CE 交于G ，若∠BDC=140O ,∠BGC=110O ,则∠A 的度数为（ ）A．50O B．55O C．800 D．7007.己知，则n的值是 ( )A．0 B．1 C．－1 D．n的值不存在8.若=5，则-的值为（）A．4 B． C．0 D．不能确定9.下列四个图形中是如图展形图的立体图的是（）A．B．C．D．10.若不等式组无解，则实数a的取值范围是（）A．a≥﹣1 B．a＜﹣1 C．a≤1 D．a≤﹣1二、判断题11.判断：如图，线段AB与线段CD不可能互相垂直，因为它们不可能相交.（）12.判断：当2x+y=3时，代数式（2x+y）2-(2x+y)+1的值是7。

2015-2016学年七年级上学期阶段性测试数学试卷（苏科版）（满分100，考试时间120分钟） 2015.10.12一、细心填一填：（每空2分，共30分） 1、112-的倒数是___ ____；绝对值是3的数是 。

2、用“>”或“<”填空：(1) 0 10- ； (2) -3 -5； （3）--⎪⎭⎫⎝⎛--32 。

3、如果向南走20米记为是－20米，那么向北走70米记为____________。

4、在数轴上与表示—2 的点距离 3个单位长度的点表示的数是_____________。

5、若，则a+b= 。

6、绝对值不大于2.5的整数有 ，它们的和是 。

7、某班5名学生在一次数学测验中的成绩以90分为标准，超过的分数记为正数，不足的分数记为负数，记录如下：﹣4，+9，0，﹣1，+6，则他们的平均成绩是 分。

8、如图是一个程序运算，若输入的x 为﹣5，则输出y 的结果为 。

9、规定123*-+=b a b a ，则()6*4-的值为_________。

10、某公交车原坐有22人，经过2个站点时上下车情况如下(上车为正，下车为负)： (＋4，－8)，(－5，6)，则车上还有________人。

11、如下图，每一幅图中均含有若干个正方形，第①幅图中含有1个正方形；第②幅图中含有5个 正方形；……按这样的规律下去，则第（6）幅图中含有 个正方形。

二、精心选一选：（每题2分，共20分）12、3-的相反数是 （ ） A ．3- B ．3 C ．13-D ．3± 13、江阴2013年元旦的最高气温为8℃，最低气温为-2℃，那么这天的最高气温比最低气温高 A ．-10℃B ．-6℃C ．6℃D ．10℃ （ ）14、将6－()+3―()―7＋()－2写成省略加号的和的形式为 （）••••••①②③A .－6－3＋7－2B . 6－3－7－2C . 6－3＋7－2D . 6＋3－7－215、下列结论正确的是 （ ） A ．有理数包括正数和负数 B ．无限不循环小数叫做无理数 C ．0是最小的整数 D ．数轴上原点两侧的数互为相反数 16、在下列数﹣，+1，6.7，﹣14，0，，﹣5，25%中，属于整数的有 （ ）A ． 2个B ． 3个C ． 4个D ． 5个17、下列各对数：+（﹣3）与﹣3，+（+3）与 +3，﹣（﹣3）与+（﹣3），﹣（+3）与+（﹣3）， +（+3）与﹣（﹣3），+3与﹣3中，互为相反数的有 （ ） A ． 3对 B ． 4对 C ． 5对 D ． 6对18、已知a ，b 两数在数轴上对应的点如图所示，下列结论正确的是 （ ）A ． a+b ＞0B ． a ＞bC ． ab ＜0D ． b ﹣a ＞0 19、已知3=x ，y =8，且xy <0，则y x +的值等于（ ）A ．5±B ．11±C ．5-或11D ．5-或11－20、观察以下数组：（2），（4、6），（8、10、12），（14、16、18、20），..问2014在第几组（ ）A ． 44B ． 45C ． 46D ． 无法确定21、如图所示，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字0所对应的点与数轴上的数－2所对应的点重合，再让圆沿着数轴按顺时针方向滚动，那么数轴上的数－2012将与圆周上的哪个数字重合 （ ） A ．0 B ．1 C ．2 D ．322、（本题满分3分）把下列各数：－2.5 ，－1，－|－2|，－（－3），0 在数轴上表示出来， 并用．．“<”．．．把它们连接起来．．．．．．．:23、（本题满分5分）把下列各数填入相应的集合中2013-，883，＋13.5，617-，3.14，12%-，227， 2.013∙-，0，＋5，2.1010010001…, π-， 2.626226222-①正数集合 { …} ②负数集合{ …} ③无理数集合 { …} ④整数集合{…} ⑤分数集合 {…}24、（本题满分24分）计算或化简： （1）（－3）＋（－2）； （2）（－8）－（＋6）；（3）110.5(3) 2.75(7)42---+-+； （4）71721⨯⎪⎭⎫ ⎝⎛-÷；（5）()()()6425848+-⨯--÷-； （6）24436183⨯⎪⎭⎫ ⎝⎛--；（7） （8）（-4）×（-271）+（-8）×（-271）+12×（-271）25．(本题满分5分) 我们知道，在数轴上，|a |表示数a 的点到原点的距离，这是绝对值的几何意义.进一步地，数轴上两个点A 、B ，分别用数a ，b 表示，那么A 、B 两点之间的距离为： AB=|a －b |.利用此结论，回答以下问题：（1）数轴上表示2和5的两点的距离是 ，数轴上表示－2和－5的两点之间的距离是 ， 数轴上表示1和－3的两点之间的距离是 ；（2）数轴上表示x 和－1的两点A ，B 之间的距离是 ，如果AB=2，那么x 是 ；111312()1532114⨯-⨯÷26、（本题满分5分）2010年8月7日夜22点左右，甘肃舟曲发生特大山洪泥石流灾害，甘肃消防总队迅即出动兵力支援灾区．在抗险救灾中，消防官兵的冲锋舟沿东西方向的河流抢救灾民，早晨从A 地出发，晚上到达B 地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：+14，9-， 8+，7-，+13，6-，10+，5-．(1)通过计算说明：B 地在A 地的什么方向，与A 地相距多远？ (2)救灾过程中，最远处离出发点A 有多远？(3)若冲锋舟每千米耗油0. 5升，油箱容量为29升(出发时满油箱)，求途中至少需补充多少升油？27．（本题满分8分）小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题：⑴从中取出2张卡片，使这2张卡片上数字的乘积最大，如何抽取？最大值是多少? 答：我抽取的2张卡片是 、 ，乘积的最大值为 。

学校 班级 姓名 考试号………………………………………………………………………………………………………………………………………………………………201X —201X 学年第二学期七年级数学期末测试卷（满分100分 时间100分钟）一、选择题（每小题3分，共30分）1．下列计算正确的是……………………………………………………………（ ） A ．a ＋2a 2＝3a 2 B ．a 8÷a 2＝a 4 C ．a 3·a 2＝a 6 D ．(a 3)2＝a 62．下列生活现象中，属于平移的是………………………………………………（ ） A ．足球在草地上滚动 B ．拉开抽屉 C ．投影片的文字经投影转换到屏幕上 D ．钟摆的摆动3．下列等式由左边到右边的变形中，属于因式分解的是………………………（ ） A ．x 2＋5x －1＝x (x ＋5)－1 B ．x 2－4＋3x ＝(x ＋2)(x －2)＋3x C ．x 2－9＝(x ＋3)(x －3)D ．(x ＋2)(x －2)＝x 2－44．已知等腰三角形的两条边长分别是7和3，则第三条边的长可能为…………（ ）A ．8B ．7C ．4D ．35．下列命题中，是真命题的是……………………………………………………（ ） A ．同位角相等 B ．相等的角是对顶角 C ．有且只有一条直线与已知直线垂直 D ．互为补角的两个角的和为180°6．如图，点B 是△ADC 的边AD 的延长线上一点，DE ∥AC ，若∠C ＝50°，∠A ＝60°，则∠CDB 的度数等于………………（ ） A ．70°B ．100°C ．110°D ．120°7．下列不等式的变形，正确的是…………………………………………………（ ） A ．若ac ＞bc ，则a ＞b B ．若a ＞b , 则ac 2＞bc 2,C ．若ac 2＞bc 2,，则a ＞bD ．若a ＞0，b ＞0，且1a ＞1b ，则a ＞b8．三角形的下列线段中能将一个三角形的面积分成相等两部分的是…………（ ） A ．中线 B ．角平分线 C ．高 D ．连接三角形两边中点的线段9． 若x ，y 均为正整数，且2x ＋1²4y ＝128，则x ＋y 的值为………………………（ ） A ．3C ．4或5D ．3或4或510 dc ＝ad －bc ，例如42 53＝2³5－3³4＝10－12＝－2．若 x 、y 为两不等的整数，且满足1＜y 1 4x＜3，则x ＋y 的值为………………………（ ） A ．3 B ．2 C ．±3 D ．±2 二、填空题（每小题2分，共16分） 11．计算：a 5÷a 2＝ ．第6题12．世界上最小的开花结果植物是澳大利亚的出水浮萍，它的果实像一个微小的无花果，质量只有0.000000076克，这个数用科学记数法表示为 ．13．已知二元一次方程组⎩⎨⎧5x －2y ＝52x ＋y ＝3，则x －y ＝ ．14．命题“内错角相等”的逆命题是 ． 151617．已知关于x 的不等式组⎩⎨⎧x ＜10x ＞a无解，则a 的取值范围是 ．18．如图1用4个大小相等的正八边形进行拼接，使两个正八边形有一条公共边重合，围成一圈后中间成一个正方形；如图2用n 个大小相等的正六边形进行拼接，围成一圈后中间成一个正多边形，则n的值为 ． 三、解答题（共54分） 19．（6分）计算：（1） (π－3.14)0－(13)－2＋(－2)2 （2）(x 2＋1)2＋2(1－2x 2)－x ²x 320．（6分）因式分解：（1）x 2＋xy ； （2）a 2－1； （3）x 3＋4x 2＋4x .21．（8分）（1）解方程组：⎩⎨⎧2x －y ＝0，3x －2y ＝5． （2）解不等式组：⎩⎪⎨⎪⎧5x －1＞2x －412x ≤x ＋24．22．（8分）某校春季运动会比赛中，七年级(1)班、(3)班的竞技实力相当．关于比赛结果，甲同学说：(1)班与(3)班得分比为6:5；乙同学说：(1)班得分是(3)班得分的2倍少40分．求两个班得分各是多少？第18题23．（8分）如图下列三个条件：①AB ∥CD ，②∠B ＝∠C ．③∠E ＝∠F ．从中任选两个．．作为条件，另一个．．．作为结论，编一道数学题，并说明理由. 已知：_______________________________(只需填写序号) 结论：_______________________________(只需填写序号) 理由：24．（8分）我们知道：平行四边形的面积＝(底边)³(这条底边上的高)．如图，四边形ABCD 都是平行四边形，AD ∥BC ，AB ∥CD ，设它的面积为S ．（1）如图①，点M 为AD 上任意一点，若△BCM 的面积为S 1，则S 1：S ＝ ； （2）如图②，点P 为平行四边形ABCD 内任意一点时，记△PAB 的面积为S ˊ，△PCD 的面积为S 〞，平行四边形ABCD 的面积为S ，猜想得S ˊ、S 〞的和与S 的数量关系式为 ；（3）如图③，已知点P 为平行四边形ABCD 内任意一点，△PAB 的面积为3，△PBC的面积为7，求△PBD 的面积．A C D M 图① BA B C D P 图② A BC D P 图③ A B C D EF25．（10分）无锡某校准备组织学生及学生家长到上海进行社会实践，为了便于管理，所有人员必须乘坐在同一列火车上；根据报名人数，若都买一等座单程火车票需17010元，若都买二等座单程火车票且花钱最少，则需11220元；已知学生家长与教师的人数之比为2:1，无锡到上海的火车票价格(部分)如下表所示：七年级数学期终测试参考答案一、选择题1．D 2．B 3．C 4．B 5．D 6．C 7．C 8．A 9．D 10．C二、填空题11．a312．7.6×10—813．1 14．相等的角是内错角15．4 16．m＜4 17．a≥10 18．6三、解答题19.(1) 原式＝1－9＋4…………2分(2) 原式＝x4＋2x2＋1+2－4x2－x4……2分＝－4………………3分＝－2x2+3……………………3分20.(1)原式＝x (x ＋y )；(2)原式＝(a ＋1) (a －1)； (3) 原式＝x (x 2＋4x ＋4)＝x (x ＋2)2（全对全错） 21.(1) 由①得： y ＝2x ③…………1分，解得： x ＝－5…………2分，y ＝－10…………3分∴⎩⎨⎧x = －5，y = —10． (4)分(2) 由①得：x ＞－1…………1分， 由②得：x ≤2…………3分，∴－1＜x ≤2…………4分 22．解：分别设(1)、(3)班得分为x 分、y 分……………………………………………………1分由题意得：⎩⎨⎧5x = 6y ，x = 2y －40 (5)分解得⎩⎨⎧x = 60，y = 50．………………………………………………………………………………7分答：(1)、(3)班得分为60分、40分．…………………………………………………………8分23．已知：____①②_______（任意选2个都可以）结论：_____③_______（第3个作为结论）………………………………………………2分理由：∵AB ∥CD∴∠B ＝∠CDF …………………………………………………………………………4分∵∠B ＝∠C∴∠C ＝∠CDF …………………………………………………………………………6分∴CE ∥BF∴∠E ＝∠F ……………………………………………………………………………8分24．(1) 1:2……………………………………………………………………………………………2分S …………………………………………………………………………4分分25．(1)设参加社会实践的老师有x 人，学生有y 人，则学生家长有2x 人，若都买二等座单程火车票且花钱最少，则全体学生都需买二等座学生票，依题意得：⎩⎨⎧81(3x ＋y ) ＝1701068×3x ＋51y ＝11220 ．……………………………………………………………………2分解得⎩⎨⎧x = 10，y = 180．……………………………………………………………………………3分则2x =20， (4)分答：参加社会实践的老师、家长与学生分别有10人、20人、180人．(2)解：由（1）知所有参与人员总共有210人，其中学生有180人，①当180≤x ＜210时，最经济的购票方案为：学生都买学生票共180张，（x －180）名成年人买二等座火车票，（210－x ）名成年人买一等座火车票．∴火车票的总费用（单程）y 与x 之间的关系式为： y =51³180＋68（x －180）＋81（210－x ），即y =－13x +13950（180≤x ＜210）， (6)分②当0＜x ＜180时，最经济的购票方案为：一部分学生买学生票共x 张，其余的学生与家长老师一起购买一等座火车票共（210－x ）张，∴火车票的总费用（单程）y 与x 之间的函数关系式为： y =51x +81（210－x ），即y =－30x +17010（0＜x ＜180），…………………8分答：购买火车票的总费用（单程）y 与x 之间的关系式是y =－13x +13950（180≤x＜210）或y =－30x +17010（0＜x ＜180）．（3）由（2）小题知，当180≤x ＜210时，y=－13x +13950，∴当x =209时，y 的值最小，最小值为11233元，当x=180时，y的值最大，最大值为11610元．当0＜x＜180时，y=－30x+17010，∴当x=179时，y的值最小，最小值为11640元，当x=1时，y的值最大，最大值为16980元．所以可以判断按（2）小题中的购票方案，购买一个单程火车票至少要花11233元，最多要花16980元.……………………………………………………………………10分。

2016-2017学年第二学期七年级期末数学模拟试卷二本次考试范围：苏科版七下全部内容，八年级数学上册《全等三角形》；考试题型：选择、填空、解答三大类；考试时间：120分钟；考试分值：130分。

一、选择题（每小题3分，共30分）1．下列运算中，正确的是 （ ） A ．a 2＋a 2＝2a 4 B ．a 2•a 3＝a 6 C ．(－3x )2÷3x ＝3x D ．(－ab 2)2＝－a 2b 42．现有4根小木棒的长度分别为2cm ，3cm ，4cm 和5cm ．用其中3根搭三角形，可以搭出不同三角形的个数是 （ ） A ．1个 B ．2个 C ．3个 D ．4个 3．如下图，下列判断正确的是 （ ）A ．若∠1=∠2，则AD ∥BCB ．若∠1=∠2．则AB ∥CDC ．若∠A =∠3，则 AD ∥BC D ．若∠A +∠ADC =180°，则AD ∥BC4．如果a ＞ b ，那么下列不等式的变形中，正确的是 （ ） A ．a －1＜b －1 B ．2a ＜2b C ．a －b ＜0 D ．－a +2＜－b +2 5．若5x 3m－2n－2y n －m ＋11＝0是二元一次方程，则 ( )A ．m ＝3，n ＝4B ．m ＝2，n ＝1C ．m ＝－1，n ＝2D ．m ＝1，n ＝26．已知方程组⎩⎨⎧3x +5y = k +8，3x +y =－2k ．的解满足x + y = 2 ，则k 的值为 （ ）A ．－4B ．4C ．－2D ．27．若不等式组⎩⎨⎧3x +a ＜0，2x + 7＞4x －1．的解集为x ＜4，则a 的取值范围为 （ ）A ．a ＜－12B ．a ≤－12C ．a ＞－12D ．a ≥－12 8.四个同学对问题“若方程组 111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩，则方程组 111222325325a x b y c a x b y c +=⎧⎨+=⎩的解是 （ ） Ａ⎩⎨⎧==84y x ； B ⎩⎨⎧==129y x ； C ⎩⎨⎧==2015y x ； D ⎩⎨⎧==105y x9. 如图，已知AB=AD ，那么添加下列一个条件后，仍无法判定△ABC ≌△ADC 的是（ ）A ．CB=CDB ．∠BAC=∠DAC C ．∠BCA=∠DCAD ．∠B=∠D=90° 10. 如图，在△ABC 中，∠CAB =65°．将△ABC 在平面内绕点A 旋转到△AB C ''的位置，使得CC '∥AB ，则旋转角的度数为（ ） A ．35° ； B ．40° ； C ．50° ； D ．65° 二、填空题（每空3分，共24分） 11．计算：3x 3·(－2x 2y ) = ． 12．分解因式：4m 2－n 2 = ．第3题图第9题图ABCB ′C ′第10题图13．已知一粒米的质量是0.000021千克，0.000021用科学记数法表示为 __ ．14．若⎩⎨⎧x = 2，y = 1．是方程组⎩⎨⎧2ax +y = 5，x + 2y = b ．的解，则ab ＝ ．15．二元一次方程3x ＋2y ＝15共有_______组正整数解．．．．16．关于x 的不等式(a +1)x>(a +1)的解集为x <1，则a 的范围为 ．17．如图，已知Rt △ABC 中∠A ＝90°，AB ＝3，AC ＝4．将其沿边AB 向右平移2个单位得到△FGE ，则四边形ACEG 的面积为 ．18.某数学兴趣小组开展了一次活动，过程如下：设∠BAC ＝θ（0°＜θ＜90°）.现把小棒依次摆放在两射线A B 、AC 之间，并使小棒两端分别落在两射线上，从点A 1开始，用等长的小棒依次向右摆放，其中A 1A 2为第1根小棒，且A 1A 2＝AA 1. （1）如图1，若已经向右摆放了3根小棒，且恰好有∠A 4A 3A ＝90°，则θ＝ . （2）如图2，若只能．．摆放5根小棒，则θ的范围是 . 三、解答题（共11题，计76分）19．（本题满分6分）计算：(1)(－m )2·(m 2)2÷m 3； (2)（x －3）2－（x ＋2）（x －2）．20．（本题满分6分）分解因式：(1)x 3－4xy 2； (2) 2m 2－12m +18．21．（本题满分6分）(1)解不等式621123x x ++-<； (2)解不等式组()523215122x x x x⎧-<-⎪⎨-<-⎪⎩22．（本题满分6分）已知长方形的长为a ，宽为b ，周长为16，两边的平方和为14．①求此长方形的面积； ②求ab 3+2a 2b 2+a 3b 的值．23．（本题满分6分）在等式y ＝ax ＋b 中，当x ＝1时，y ＝－3；当x ＝－3时，y ＝13． (1)求a 、b 的值；θA 4A 3A 2AA 1BCθA 6A 5A 4A 3A 2AA 1BC图1图2A B CEF G第16题图第18题图(2)当－1<x <2，求y 的取值范围．24. （本题满分6分）如图2，∠A =50°，∠BDC =70°，DE ∥BC ，交AB 于点E ， BD 是△ABC 的角平分线．求∠DEB 的度数．25. （本题满分6分）已知，如图，AC 和BD 相交于点O ，OA=OC ，OB=OD ，求证：AB ∥CD ．26．（本题8分） 某公司准备把240吨白砂糖运往A 、B 两地，用大、小两种货车共20辆，恰好能一次性装完这批白砂糖，相关数据见下表：载重量 运往A 地的费用 运往B 地的费用 大车 15吨/辆 630元/辆 750元/辆 小车10吨/辆420元/辆550元/辆(1)求大、小两种货车各用多少辆？(2)如果安排10辆货车前往A 地，其中大车有m 辆，其余货车前往B 地，且运往A 地的白砂糖不少于115吨．①求m 的取值范围；②请设计出总运费最少的货车调配方案，并求最少总运费．27．（8分）(1)如图①，在凹四边形ABCD 中，∠BDC =135°，∠B =∠C =30°，则∠A = °；(2)如图②，在凹四边形ABCD 中，∠ABD 与∠ACD 的角平分线交于点E ，∠A =60°，∠BDC =140°，则∠E = °；(3)如图③，∠ABD ，∠BAC 的平分线交于点E ，∠C =40°，∠BDC =150°，求∠AEB 的度数；(4)如图④，∠BAC ，∠DBC 的角平分线交于点E ，则∠B ，∠C 与∠E 之间有怎样的数量关系 。