2012年山东高考数学试卷评析

2012年高考数学试卷评析暨2013年高考备考建议（理数）李玉强2012年6月24日2012年高考数学试卷评析暨2013年高考备考建议辉县市高级中学李玉强一、2012年高考数学试卷评析：1.试卷总体评价2012年是我省课改高考第二年，本年我省高考数学试卷的命制稳中有变，试卷重视基础，突出能力，体现课改，着眼稳定，体现教学本质，凸显数学思想，强化思维量，控制运算量，突出综合性。

试题图文并茂，文字阐述清晰，图形设计简明，无论是在试卷的结构安排方面，还是试题背景的设计方面，都进行了大胆的改革和有益的探索。

总体而言，2012年高考数学试卷是一份很有质量且有一定特色的试卷。

2.试卷主要特点：（1）结构合理而鲜活。

既考查了主干，又考查了新增。

函数、三角函数、数列、立体几何、解析几何、概率统计仍是试卷的主要考查内容；算法、三视图、正态分布等题的设计，充分体现了“考新知识”的命题模式；还有几道题目是老知识新考法，可谓“老树新花”。

如：集合题目与组合知识综合，而不是简单地考查集合运算；复数题目与命题综合，考查更全面，很有新意；概率统计题目以贴近生活的出售玫瑰花为背景，且答案不唯一、不死板，更为开放、新颖，更为注重考查学生的能力；解析几何与2011年一样仍为抛物线，改变了传统的考查椭圆的模式（近四年来都以考抛物线为主，这一点应特别注意）。

（2）全面考查，重点突出。

对知识点较单一的内容，考查较全面。

如：复数、排列组合、概率统计、线性规划、程序框图、三视图等，都有专门考查，对核心概念，主干知识的考查仍为重点，如：函数、导数、不等式、数列、三角、解析几何和立体几何等。

部分题目综合程度加深，如：数列、反函数、不等式的求解（恒成立）、极坐标与参数方程等内容的考查向纵深发展。

（3）对数学方法、数学能力、数学思想的考查充分而到位。

数学方法：坐标法、换元法、转化法、定义法、割补法、赋值法等。

数学能力：空间想象能力(7、16、19)推理论证能力（12、16、19、22）抽象概括能力（1、6、10、11、15）运算求解能力（2、3、4、5、8、13、14、17、20、23、24）数据处理能力（15、18、20）数学思想：函数与方程思想、数形结合、分类与整合、特殊与一般、化归与转化。

2012年高考数学试题解析 分项版之专题13 统计 教师版 文 一、选择题: 1.（2012年高考新课标全国卷文科3）在一组样本数据（x1，y1），（x2，y2），…，（xn，yn）（n≥2，x1,x2,…,xn不全相等）的散点图中，若所有样本点（xi，yi）(i=1,2,…,n)都在直线y=x+1上，则这组样本数据的样本相关系数为 （A）－1 （B）0 （C） （D）1 2. (2012年高考山东卷文科4)在某次测量中得到的A样本数据如下：82，84，84，86，86，86，88，88，88，88.若B样本数据恰好是A样本数据都加2后所得数据，则A，B两样本的下列数字特征对应相同的是 (A)众数 (B)平均数 (C)中位数 (D)标准差 3．(2012年高考北京卷文科8)某棵果树前n年的总产量Sn与n之间的关系如图所示，从目前记录的结果看，前m年的年平均产量最高，m的值为 （A）5（B）7（C）9（D）11 【答案】C 【解析】由图可知6,7,8,9这几年增长最快，超过平均值，所以应该加入，因此选C.4. (2012年高考湖南卷文科5)设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x-85.71，则下列结论中不正确的是 A.y与x具有正的线性相关关系 B.回归直线过样本点的中心（，） C.若该大学某女生身高增加1cm，则其体重约增加0.85kg D.若该大学某女生身高为170cm，则可断定其体重必为58.79kg 5. (2012年高考湖北卷文科2) 容量为20的样本数据，分组后的频数如下表 则样本数据落在区间[10,40]的频率为( )A 0.35B 0.45C 0.55D 0.65 6.(2012年高考四川卷文科3)交通管理部门为了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查。

稳中有变凸显特色——2012年高考数学山东卷评析
王桂娟;闫玉新
【期刊名称】《新高考：高二数学》
【年(卷),期】2012(000)007
【摘要】2012年山东高考数学试题，在难度和结构方面与2011年相比基本保持稳定，但稳中有变，更具山东特色．
【总页数】1页(P51-51)
【作者】王桂娟;闫玉新
【作者单位】山东省青州市第一中学
【正文语种】中文
【中图分类】G634.605
【相关文献】
1.考查全面稳中有变能力立意内涵丰富——2012年上海高考数学试卷评析及复习建议 [J], 卫福山
2.稳中有变缓中有新平中有奇——2004睥全国高考数学试题（浙江卷）评析[J], 楼可飞
3.力求创新,稳中有变——2015年高考数学广东卷评析 [J], 孟胜奇
4.稳中有升锐意创新——2012年高考数学湖南卷评析 [J], 张汝波
5.稳中求变变中求新——2012年高考数学北京卷评析 [J], 陈敬川
因版权原因，仅展示原文概要，查看原文内容请购买。

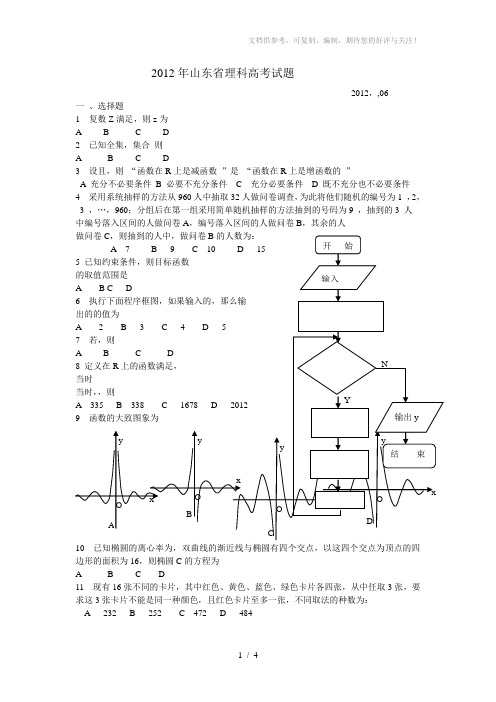
2012年山东省理科高考试题2012，,06一、选择题1 复数Z满足，则z为A B C D2 已知全集，集合则A B C D3 设且，则“函数在R上是减函数”是“函数在R上是增函数的”A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件4 采用系统抽样的方法从960人中抽取32人做问卷调查，为此将他们随机的编号为1 ，2，3 ，…，960；分组后在第一组采用简单随机抽样的方法抽到的号码为9 ，抽到的3 人中编号落入区间的人做问卷A，编号落入区间的人做问卷B，其余的人10 已知椭圆的离心率为，双曲线的渐近线与椭圆有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程为A B C D11 现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各四张，从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多一张，不同取法的种数为：A 232B 252C 472D 48412 设函数 ，，若函数的图象与函数的图象有且仅有两个公共点 、，则下列判断正确的是A 当时，B 当时，C 当时，D 当时，二 、填空题 每小题4分，共16分13 若不等式的解集为，则实数_________14 如图，正方体的棱长为1，E 、F 分别为线段 、上的点，则三棱锥的体积为________ 15设，曲线与直线所 围成的封闭图形的面积为，则__________16 如图，在平面直角坐标系xoy 中，一个单位圆的圆 心的初始位置在，此时圆上一点P 的位置在，圆在x 轴上沿正方向滚动，当圆滚动到圆心位于圆心 位于时，的坐标为___________三 、解答题 ： 本大题共6小题，共74分17 本小题满分12分）已知，，函数的最大值 为6， （1）求A（2） 将函数的图象向左平移个单位，再将所得图象上点的横坐标缩短为原来的倍，纵坐标不变，得到函数的图象，求函数在的值域18 （本小题满分12分）在如图所示的几何体中，四边形ABCD 为等腰梯形，∥，，平面ABCD ，（1）求证：平面AED（2）求二面角的余弦值19 （本小题满分12分） 现有甲、乙两个靶，某射手向甲靶射击一次，命中的概率为，命中得1分，不中得0分；向乙靶射击两次，每次命中的概率为，每命中一次得2分，不中得0分，该射手每次射击结果相互独立，假设该射手完成以上三次射击：求（1）该射手恰好命中一次的概率。

2009-2012四年山东省高考数学试题分析一、近四年高考试题分析从2007年山东省率先进入新课标高考至今，已有六年时间，在这六年中，我们山东数学试题从试卷的结构和试卷的难度上逐渐趋于平稳，稳中有新，形成了自己的风格。

以下是近三年高考数学试题知识点分布及分值分布统计表。

表一：表二：表三：表四：从近四年数学试题知识点分布及分值分布统计表不难看出，试题坚持对基础知识、数学思想方法进行考查，重点考查了高中数学的主体内容，兼顾考查新课标的新增内容，在此基础上，突出了对考生数学思维能力和数学应用意识的考查，体现了新课程改革的理念。

具体来说几个方面：1．整体稳定，覆盖面广山东高考数学卷全面考查了山东省考试说明中各部分的内容，可以说教材中各章的内容都有所涉及，如复数、旋转体、简易逻辑、概率等教学课时较少的内容，在试卷中也都有所考查。

有些内容这几年轮换考查，如统计图、线性回归、直线与圆、线性规划，理科的计数原理、二项式定理、正态分布、条件概率等。

2．重视基础，难度适中试题以考查高中基础知识为主线，在基础中考查能力。

理科前8道选择题都是考查基本概念和公式的题型，相当于课本习题的变式题型。

填空题前三题的难度相对较低，均属常规题型。

解答题的前三道题分别考查解三角形，分布列、数学期望，空间线面位置关系等基础知识，利用空间直角坐标系求二面角，属中低档难度题。

3．突出重点知识重点考查特别注重考查高中数学的基础知识，但并不刻意追求知识的覆盖率，着重考查了支撑学科知识体系的知识主干，以重点知识为主线组织全卷的内容，如函数与导数，2009年文理科分别占30分，2010年文科37分、理科29分，2011年文科26分、理科22分。

还有三角函数、如定积分、函数的零点、三视图、算法框图、直方图与茎叶图、条件概率、几何概型、全称命题与特称命题等。

5．突出通性通法、理性思维和思想方法的考查数学思想方法是对数学知识的最高层次的概括与提炼，是适用于中学数学全部内容的通法，是高考考查的核心。

2012山东高考卷单选解析一、语文部分1. 下列词语中加点字的注音全都正确的一项是：A. 踌躇（chóu chú）憎恶（zēng wù）拙劣（zhuō liè）氛围（fēn wéi）B. 澎湃（péng pài）惬意（qiè yì）稍纵即逝（shāo zòng jí shì）深恶痛疾（shēn wù tòng jí）C. 桎梏（zhì gù）踯躅（zhí zhú）呕心沥血（ǒu xīn lì xuè）溘然长逝（kè rán cháng shì）D. 神祇（shén qí）氛围（fēn wéi）恪守（kè shǒu）瞠目结舌（chēng mù jié shé）2. 下列句子中，加点成语使用正确的一项是：A. 这部电视剧播出后，在社会上引起了强烈反响，老百姓对这一问题拍案叫绝。

B. 为了应对金融危机，我国政府采取了一系列举措，把这场危机化解于无形。

C. 在这次比赛中，他凭借稳定的发挥，终于力挫群雄，赢得了冠军。

D. 老王虽然年过六旬，但依然精神矍铄，干起活来不减当年。

3. 下列句子中，没有语病的一项是：A. 为了确保道路交通安全，防止类似事故不再发生，我们必须加强交通安全意识。

B. 这部电影讲述了一个发生在抗日战争时期，感人至深的故事。

C. 老师告诉我们，在学习过程中，要善于发现问题，并积极解决问题。

D. 通过这次活动，使同学们认识到了保护环境的重要性。

二、数学部分4. 已知函数f(x) = x² 2x + 1，那么f(x)的最小值是：A. 0B. 1C. 1D. 25. 设集合A = {x | x² 3x + 2 = 0}，集合B = {x | x² 4x +3 = 0}，则A∩B的元素个数为：A. 0B. 1C. 2D. 36. 已知等差数列{an}的公差为2，且a1 + a3 + a5 = 12，那么a2的值为：A. 2B. 4C. 6D. 8三、英语部分7. — I'm sorry I broke your glass.— ________. It doesn't matter at all.A. No, it wasn'tB. Yes, it wasC. No, it wasn't yoursD. Yes, it was yours8. The meeting ________ for an hour, but the problem________ solved.A. has been on; hasn't beenB. had been on; wasn'tC. has been on; wasD. had been on; has9. — Can I help you?— ________, but I think I could find it myself.A. Yes, you canB. No, you can'tC. Yes, pleaseD. No, thanks四、物理部分10. 一物体做匀速直线运动，下列说法正确的是：A. 速度不变，加速度为零B. 速度不变，加速度不为零C. 速度变化，加速度为零D. 速度变化，加速度不为零11. 一电阻接入电路时，消耗的电功率为P。

2012年普通高等学校招生全国统一考试数学理工农医类(山东卷)本试卷分第Ⅰ卷和第Ⅱ卷两部分．满分150分．考试用时120分钟．参考公式：锥体的体积公式：V＝13Sh，其中S是锥体的底面积，h是锥体的高．如果事件A，B互斥，那么P(A＋B)＝P(A)＋P(B)．第Ⅰ卷(共60分)一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若复数z满足z(2－i)＝11＋7i(i为虚数单位)，则z为()A．3＋5i B．3－5i C．－3＋5i D．－3－5i2．已知全集U＝{0,1,2,3,4}，集合A＝{1,2,3}，B＝{2,4}，则(U A)∪B为()A．{1,2,4} B．{2,3,4}C．{0,2,4} D．{0,2,3,4}3．设a＞0，且a≠1，则“函数f(x)＝a x在R上是减函数”是“函数g(x)＝(2－a)x3在R上是增函数”的() A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件4．采用系统抽样方法从960人中抽取32人做问卷调查．为此将他们随机编号为1,2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9．抽到的32人中，编号落入区间［1,450］的人做问卷A，编号落入区间［451,750］的人做问卷B，其余的人做问卷C．则抽到的人中，做问卷B的人数为() A．7 B．9 C．10 D．155．设变量x，y满足约束条件222441x yx yx y+≥⎧⎪+≤⎨⎪-≥-⎩，，，则目标函数z＝3x－y的取值范围是()A．［32-，6］B．［32-，－1］C．［－1,6］D．［－6，32］6．执行下面的程序框图，如果输入a＝4，那么输出的n的值为()A．2 B．3 C．4 D．57．若θ∈［π4，π2］，sin2θsinθ＝()A．35B．45CD．348．定义在R上的函数f(x)满足f(x＋6)＝f(x)．当－3≤x＜－1时，f(x)＝－(x＋2)2；当－1≤x＜3时，f(x)＝x．则f(1)＋f(2)＋f(3)＋…＋f(2 012)＝()A．335 B．338 C．1 678 D．2 0129．函数cos622x xxy-=-的图象大致为()10．已知椭圆C：22221x ya b+=(a＞b＞0)的离心率为2．双曲线x2－y2＝1的渐近线与椭圆C有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程为()A．22182x y+=B．221126x y+=C．221164x y+=D．221205x y+=11．现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张．从中任取3张，要求这3张卡片不能是同一种颜色，且红色卡片至多1张．不同取法的种数为()A．232 B．252 C．472 D．48412．设函数1()f xx=，g(x)＝ax2＋bx(a，b∈R，a≠0)．若y＝f(x)的图象与y＝g(x)的图象有且仅有两个不同的公共点A(x1，y1)，B(x2，y2)，则下列判断正确的是()A ．当a ＜0时，x 1＋x 2＜0，y 1＋y 2＞0B ．当a ＜0时，x 1＋x 2＞0，y 1＋y 2＜0C ．当a ＞0时，x 1＋x 2＜0，y 1＋y 2＜0D ．当a ＞0时，x 1＋x 2＞0，y 1＋y 2＞0第Ⅱ卷(共90分)二、填空题：本大题共4小题，每小题4分，共16分．13．若不等式|kx －4|≤2的解集为{x |1≤x ≤3}，则实数k ＝__________．14．如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，E ，F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1－EDF 的体积为__________．15．设a ＞0．若曲线y =x ＝a ，y ＝0所围成封闭图形的面积为a 2，则a ＝__________．16．如图，在平面直角坐标系xOy 中，一单位圆的圆心的初始位置在(0,1)，此时圆上一点P 的位置在(0,0)，圆在x 轴上沿正向滚动．当圆滚动到圆心位于(2,1)时，OP的坐标为__________．三、解答题：本大题共6小题，共74分．17．已知向量m ＝(sin x,1)，n ＝cos x ，2Acos2x )(A ＞0)，函数f (x )＝m ·n 的最大值为6．(1)求A ；(2)将函数y ＝f (x )的图象向左平移π12个单位，再将所得图象上各点的横坐标缩短为原来的12倍，纵坐标不变，得到函数y ＝g (x )的图象，求g (x )在［0，5π24］上的值域．18．在如图所示的几何体中，四边形ABCD 是等腰梯形，AB ∥CD ，∠DAB ＝60°，FC ⊥平面ABCD ，AE ⊥BD ，CB ＝CD ＝CF ．(1)求证：BD ⊥平面AED ；(2)求二面角F －BD －C 的余弦值．19．现有甲、乙两个靶．某射手向甲靶射击一次，命中的概率为34，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为23，每命中一次得2分，没有命中得0分，该射手每次射击的结果相互独立．假设该射手完成以上三次射击．(1)求该射手恰好命中一次的概率；(2)求该射手的总得分X 的分布列及数学期望EX ．20．在等差数列{a n }中，a 3＋a 4＋a 5＝84，a 9＝73． (1)求数列{a n }的通项公式；(2)对任意m ∈N *，将数列{a n }中落入区间(9m,92m )内的项的个数记为b m ，求数列{b m }的前m 项和S m ．21．在平面直角坐标系xOy 中，F 是抛物线C ：x 2＝2py (p ＞0)的焦点，M 是抛物线C 上位于第一象限内的任意一点，过M ，F ，O 三点的圆的圆心为Q ，点Q 到抛物线C 的准线的距离为34． (1)求抛物线C 的方程；(2)是否存在点M ，使得直线MQ 与抛物线C 相切于点M ？若存在，求出点M 的坐标；若不存在，说明理由；(3)若点Ml ：y ＝kx ＋14与抛物线C 有两个不同的交点A ，B ，l 与圆Q 有两个不同的交点D ，E ，求当12≤k ≤2时，|AB |2＋|DE |2的最小值．22．已知函数ln ()exx kf x +=(k 为常数，e ＝2.718 28…是自然对数的底数)，曲线y ＝f (x )在点(1，f (1))处的切线与x 轴平行．(1)求k 的值；(2)求f (x )的单调区间；(3)设g (x )＝(x 2＋x )f ′(x )，其中f ′(x )为f (x )的导函数，证明：对任意x ＞0，g (x )＜1＋e －2．1．A 由已知得2117i (117i)(2i)227i 14i 11i 1525i35i 2i (2i)(2i)55z +++++++=====+--+．2．C 由题知U A ＝{0,4}，所以(U A )∪B ＝{0,2,4}，故选C 项．3． A 由函数f (x )＝a x 在R 上是减函数可得0＜a ＜1，由函数g (x )＝(2－a )x 3在R 上是增函数可得a ＜2，因为0＜a ＜1a ＜2，a ＜20＜a ＜1，所以题干中前者为后者的充分不必要条件，故选A 项．4． C 由题意可得，抽样间隔为30，区间［451,750］恰好为10个完整的组，所以做问卷B 的有10人，故选C 项．5． A 作出可行区域如图所示．目标函数z ＝3x －y 可变为y ＝3x －z ，作l 0：3x －y ＝0，在可行域内平移l 0，可知在A 点处z 取得最小值为32-，在B 点处z 取得最大值6，故选A 项．6． B 由程序框图知，当n ＝0时，P ＝1，Q ＝3；当n ＝1时，P ＝5，Q ＝7；当n ＝2时，P ＝21，Q ＝15，此时n 增加1变为3，满足P ＞Q ，循环结束，输出n ＝3，故选B 项．7． D 由θ∈［π4，π2］，得2θ∈［π2，π］．又37sin2θ=，故1c o s 28θ=-．故1c o s 2s i n 24θθ-==．8． B 由f (x ＋6)＝f (x )得f (x )的周期为6，所以f (1)＋f (2)＋…＋f (2 012)＝335［f (1)＋f (2)＋…＋f (6)］＋f (1)＋f (2)，而f (1)＝1，f (2)＝2，f (3)＝f (－3)＝－1，f (4)＝f (－2)＝0，f (5)＝f (－1)＝－1，f (6)＝f (0)＝0，f (1)＋f (2)＋f (3)＋…＋f (6)＝1，所以f (1)＋f (2)＋…＋f (2 012)＝338，故选B 项．9．D 令cos6()22x x xf x -=-，则f (x )的定义域为(－∞，0)∪(0，＋∞)，而()cos 6()()22x xx f x f x ---==--，所以f (x )为奇函数，故排除A 项．又因为当x ∈(0，16)时，cos6x ＞0,2x －2－x ＞0，即f (x )＞0，故排除B 项，而f (x )＝0有无数个根，所以排除C 项，D 项正确．10． D 双曲线x 2－y 2＝1的渐近线为y ＝±x ，与椭圆C 有四个交点，以这四个交点为顶点的四边形面积为16，可得四边形为正方形，其边长为4，双曲线的渐近线与椭圆C 的一个交点为(2,2)，所以有22441a b+=，又因为32c e a ==，a 2＝b 2＋c 2，联立解方程组得a 2＝20，b 2＝5，故选D 项． 11． C 完成这件事可分为两类，第一类3张卡片颜色各不相同共有31114444C C C C 256=种；第二类3张卡片有两张同色且不是红色卡片共有21213344C C C C 216=种，由分类加法计数原理得共有472种，故选C 项．12． B 由题意知函数1()f x x=，g (x )＝ax 2＋bx (a ，b ∈R ，a ≠0)的图象有且仅有两个公共点A (x 1，y 1)，B (x 2，y 2)，等价于方程1x＝ax 2＋bx (a ，b ∈R ，a ≠0)有两个不同的根x 1，x 2，即方程ax 3＋bx 2－1＝0有两个不同的实根x 1，x 2，因而可设ax 3＋bx 2－1＝a (x －x 1)2(x －x 2)，即ax 3＋bx 2－1＝a (x 3－2x 1x 2＋x 12x －x 2x 2＋2x 1x 2x －x 2x 12)，∴b ＝a (－2x 1－x 2)，x 12＋2x 1x 2＝0，－ax 2x 12＝－1，x 1＋2x 2＝0，ax 2＞0， 当a ＞0时，x 2＞0，∴x 1＋x 2＝－x 2＜0，x 1＜0，∴y 1＋y 2＝121212110x x x x x x ++=>． 当a ＜0时，x 2＜0，∴x 1＋x 2＝－x 2＞0，x 1＞0， ∴y 1＋y 2＝121212110x x x x x x ++=<． 13．答案：2解析：不等式|kx －4|≤2可化为－2≤kx －4≤2，即2≤kx ≤6，而不等式的解集为{x |1≤x ≤3}，所以k ＝2． 14．答案：16解析：三棱锥D 1－EDF 的体积即为三棱锥F －DD 1E 的体积．因为E ，F 分别为AA 1，B 1C 上的点，所以在正方体ABCD －A 1B 1C 1D 1中△EDD 1的面积为定值12，F 到平面AA 1D 1D 的距离为定值1，所以11111326F D D EV -=⨯⨯=． 15．答案：49解析：由题意可得曲线y x =x ＝a ，y ＝0所围成封闭图形的面积33222022πd 033a S x x a a ====⎰，解得49a =． 16．(2－sin2,1－cos2)解析：因为圆心由(0,1)平移到了(2,1)，所以在此过程中P 点所经过的弧长为2，其所对圆心角为2．如图所示，过P 点作x 轴的垂线，垂足为A ，圆心为C ，与x 轴相切于点B ，过C 作P A 的垂线，垂足为D ，则π22PC D ∠=－，|PD |=sin(2－π2)=－cos2，|CD |=cos(2－π2)=sin2，所以P 点坐标为(2－sin2,1－cos2)，即OP 的坐标为(2－sin2,1－cos2)．17．解：(1)f (x )＝m ·n 3sin x cos x ＋2Acos2x ＝A (32sin2x ＋12cos2x )＝A sin(2x ＋π6)．因为A ＞0，由题意知A ＝6．(2)由(1)知f (x )＝6sin(2x ＋π6)． 将函数y ＝f (x )的图象向左平移π12个单位后得到y ＝6sin ［2(x ＋π12)＋π6］＝6sin(2x ＋π3)的图象；再将图象上各点横坐标缩短为原来的12倍，纵坐标不变，得到y ＝6sin(4x ＋π3)的图象．因此g (x )＝6sin(4x ＋π3)．因为x ∈［0，5π24］，所以4x ＋π3∈［π3，7π6］．故g (x )在［0，5π24］上的值域为［－3,6］．18．解：(1)证明：因为四边形ABCD 是等腰梯形，AB ∥CD ，∠DAB ＝60°， 所以∠ADC ＝∠BCD ＝120°． 又CB ＝CD ，所以∠CDB ＝30°． 因此∠ADB ＝90°，AD ⊥BD ．又AE ⊥BD ，且AE ∩AD ＝A ，AE ，AD ⊂平面AED ， 所以BD ⊥平面AED ． (2)方法一：由(1)知AD ⊥BD ，所以AC ⊥BC ．又FC ⊥平面ABCD ，因此CA ，CB ，CF 两两垂直，以C 为坐标原点，分别以CA ，CB ，CF 所在的直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，不妨设CB =1，则C (0,0,0)，B (0,1,0)，D(2，12-,0)，F (0,0,1)，因此BD=(2，2-，BF =(0，－1,1)．设平面BDF 的一个法向量为m =(x ，y ，z )，则m ·BD =0，m ·BF =0，所以x =，取z =1，则m．由于CF=(0,0,1)是平面BDC 的一个法向量，则cos ,CF CF CF⋅===m m m ， 所以二面角F －BD －C方法二：取BD 的中点G ，连接CG ，FG ， 由于CB =CD ，因此CG ⊥BD ．又FC ⊥平面ABCD ，BD 平面ABCD ， 所以FC ⊥BD ．由于FC ∩CG =C ，FC ，CG 平面FCG ， 所以BD ⊥平面FCG ．故BD ⊥FG ． 所以∠FGC 为二面角F －BD －C 的平面角． 在等腰三角形BCD 中，由于∠BCD =120°， 因此12CG CB =． 又CB =CF ，所以GF =，故cos FGC ∠=， 因此二面角F －BD －C19．解：(1)记：“该射手恰好命中一次”为事件A ，“该射手射击甲靶命中”为事件B ，“该射手第一次射击乙靶命中”为事件C ，“该射手第二次射击乙靶命中”为事件D ，由题意知P (B )＝34，P (C )＝P (D )＝23， 由于A BCD BCD BCD =++，根据事件的独立性和互斥性得()()P A P BCD BCD BCD =++＝()()()P BCD P BCD P BCD ++＝()()()+()()()()()()P B P C P D P B P C P D P B P C P D +＝322322322(1)(1)(1)(1)(1)(1)433433433⨯-⨯-+-⨯⨯-+-⨯-⨯ ＝736． (2)根据题意，X 的所有可能取值为0,1,2,3,4,5， 根据事件的独立性和互斥性得(0)()P X P BCD ==＝［1－P (B )］［1－P (C )］［1－P (D )］＝3221 (1)(1)(1)43336 -⨯-⨯-=，(1)()()()() P X P BCD P B P C P D ===＝322(1)(1) 433⨯-⨯-＝1 12，(2)=()()() P X P BCD BCD P BCD P BCD =+=+＝322322 (1)(1)(1)(1)433433 -⨯⨯-+-⨯-⨯＝19，(3)()()() P X P BCD BCD P BCD P BCD ==+=+＝3223221(1)(1) 4334333⨯⨯-+⨯-⨯=，(4)() P X P BCD==＝3221 (1)4339 -⨯⨯=，P(X＝5)＝P(BCD)＝3221 4333⨯⨯=．故X的分布列为所以EX＝0×136＋1×112＋2×9＋3×3＋4×9＋5×3＝12．20．解：(1)因为{a n}是一个等差数列，所以a3＋a4＋a5＝3a4＝84，a4＝28．设数列{a n}的公差为d，则5d＝a9－a4＝73－28＝45，故d＝9．由a4＝a1＋3d得28＝a1＋3×9，即a1＝1．所以a n＝a1＋(n－1)d＝1＋9(n－1)＝9n－8(n∈N*)．(2)对m∈N*，若9m＜a n＜92m，则9m＋8＜9n＜92m＋8．因此9m－1＋1≤n≤92m－1．故得b m＝92m－1－9m－1．于是S m＝b1＋b2＋b3＋…＋b m＝(9＋93＋…＋92m－1)－(1＋9＋…＋9m－1)＝9(181)19 18119m m ⨯-----＝219109180m m+-⨯+．21．解：(1)依题意知F(0，2p)，圆心Q在线段OF的垂直平分线4py=上，因为抛物线C的准线方程为2py=-，所以3344p=，即p＝1，因此抛物线C的方程为x2＝2y．(2)假设存在点M(x0，22x)(x0＞0)满足条件，抛物线C在点M处的切线斜率为y′|x＝x0＝(22x)′|x＝x0＝x0．所以直线MQ的方程为y－22x＝x0(x－x0)，令14y=，得0124Qxxx=+，所以Q(0124xx+，14)．又|QM|＝|OQ|，故2222000001111()()()42424216x x xx x-+-=++，因此2219()416x-=，又x0＞0，所以x=M 1)．故存在点M1)，使得直线MQ与抛物线C相切于点M．(3)当x=(2)得Q(8，14)．Q的半径为r==，所以Q的方程为22127(()432x y+-=．由21214y xy kx⎧=⎪⎪⎨⎪=+⎪⎩，，整理得2x2－4kx－1＝0．设A，B两点的坐标分别为(x1，y1)，(x2，y2)，由于1∆＝16k2＋8＞0，x1＋x2＝2k，1212xx=-，所以|AB|2＝(1＋k2)［(x1＋x2)2－4x1x2］＝(1＋k2)(4k2＋2)．由22127((),84321,4x yy kx⎧-+-=⎪⎪⎨⎪=+⎪⎩整理得(1＋k2)x2－1416x-＝0．设D，E两点的坐标分别为(x3，y3)，(x4，y4)．由于2227048k ∆=+>，3424(1)x x k +=+， 342116(1)x x k =-+， 所以|DE |2＝(1＋k 2)［(x 3＋x 4)2－4x 3x 4］＝22518(1)4k ++． 因此|AB |2＋|DE |2＝(1＋k 2)(4k 2＋2)＋22518(1)4k ++． 令1＋k 2＝t ，由于12≤k ≤2，则54≤t ≤5．所以|AB |2＋|DE |2＝t (4t －2)＋25184t +＝4t 2－2t ＋25184t +， 设g (t )＝4t 2－2t ＋25184t +，t ∈［54，5］， 因为g ′(t )＝8t －2－2258t ，所以当t ∈［54，5］时，g ′(t )≥g ′(54)＝6，即函数g (t )在t ∈［54，5］是增函数，所以当54t =时g (t )取到最小值132，因此当12k =时，|AB |2＋|DE |2取到最小值132．22．解：(1)由ln ()e xx kf x +=，得1ln '()exkx x xf x x --=，x ∈(0，＋∞)， 由于曲线y ＝f (x )在(1，f (1))处的切线与x 轴平行， 所以f ′(1)＝0，因此k ＝1． (2)由(1)得f ′(x )＝1e xx (1－x －x ln x )，x ∈(0，＋∞)， 令h (x )＝1－x －x ln x ，x ∈(0，＋∞)，当x ∈(0,1)时，h (x )＞0；当x ∈(1，＋∞)时，h (x )＜0． 又e x ＞0，所以x ∈(0,1)时，f ′(x )＞0；x ∈(1，＋∞)时，f ′(x )＜0．因此f (x )的单调递增区间为(0,1)，单调递减区间为(1，＋∞)． (3)(理)因为g (x )＝(x 2＋x )f ′(x )， 所以g (x )＝1e xx +(1－x －x ln x )，x ∈(0，＋∞)． 因此对任意x ＞0，g (x )＜1＋e －2等价于1－x －x ln x ＜e 1x x +·(1＋e －2)．由(2)知h (x )＝1－x －x ln x ，x ∈(0，＋∞)，所以h ′(x )＝－ln x －2＝－(ln x －lne －2)，x ∈(0，＋∞)，因此当x ∈(0，e －2)时，h ′(x )＞0，h (x )单调递增；当x ∈(e －2，＋∞)时，h ′(x )＜0，h (x )单调递减．所以h (x )的最大值为h (e －2)＝1＋e －2，故1－x －x ln x ≤1＋e －2． 设φ(x )＝e x －(x ＋1)．因为φ′(x )＝e x －1＝e x －e 0，所以x ∈(0，＋∞)时，φ′(x )＞0，φ(x )单调递增， φ(x )＞φ(0)＝0，故x ∈(0，＋∞)时，φ(x )＝e x －(x ＋1)＞0，即e 11xx >+． 所以1－x －x ln x ≤1＋e －2＜e 1x x +(1＋e －2)．因此对任意x ＞0，g (x )＜1＋e －2． (文)证明：因为g (x )＝xf ′(x )，所以g (x )＝1ex (1－x －x ln x )，x ∈(0，＋∞)． 由(2)知h (x )＝1－x －x ln x ，求导得h ′(x )＝－ln x －2＝－(ln x －lne －2)，所以当x ∈(0，e －2)时，h ′(x )＞0，函数h (x )单调递增；当x ∈(e －2，＋∞)时，h ′(x )＜0，函数h (x )单调递减．所以当x ∈(0，＋∞)时，h (x )≤h (e －2)＝1＋e －2．又当x ∈(0，＋∞)时，0＜1e x ＜1， 所以当x ∈(0，＋∞)时，1ex h (x )＜1＋e －2，即g (x )＜1＋e －2． 综上所述结论成立．。

2012年高考数学理试卷分析2012年新课标高考理科数学试卷分析一.题型、题量全卷包括第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题.第Ⅱ卷为非选择题.考试时间为120分钟，总分为150分.试题分选择题、填空题和解答题.其中，选择题有12个小题，每题5分，共计60分；填空题有4个小题，每题5分，共计20分；解答题有8个题，其中第17题～21题各12分，第22～24题（各10分）选考一题内容分别为选修4—1（几何选讲）、选修4—4（坐标系与参数方程）、4—5（不等式选讲），共计70分.全部试题都要求在答题卡上作答.题型、题量同教育部考试中心近几年命制的新高考数学理科卷相同.总体来看，今年的高考数学题型不变，各题型内容所占比例也基本不变，各题型顺序大同小异，但在传统题目上却非常新颖，别具一格。

在难易的顺序上可谓是在挑战极限。

具体来讲：集合内容占0.03%、排列组合占0.03%、复数占0.03%、向量占0.03%、线性规划占0.03%、算法占0.03%、数列占0.06%、概率占0.114%、立体几何占0.15%、解析几何占0.15%、函数占0.15%、三角函数占0.114%，试题覆盖面广，涉猎高中数学的所有内容。

当学生满怀信心，摩拳擦掌地投入到战斗中去时，才恍然发觉，今非昔比。

和去年相比较，试题的难度着实上了一个很高的台阶。

布1）注重全面考查2012年课标卷中各种知识点题型起点较高、较综合、不易入手，多数试题源数列递推数列、一般数列求和于教材，但考查较深入，强调对基本知识、基本技能和基本方法的考查，又注重考查知识间的紧密联系，第（1）、（5）、（7）、（9）、（13）、（14）题分别对集合、排列组合、等比数列、三视图、三角函数、平面向量、线性规划等基本概念和基本运算进行了考查。

试卷注重考查通性通法，有效检测考生对数学知识所蕴涵的数和方法的掌握情况，第（3）题考查命题，而内容是复数的计算；第（4）、（8）题考查圆锥曲线的性质，注重联系平面几何与平面坐标系的转化；第（6）、（15）题分别考查了新课改中增加的程序框图、正态加强调对新知识定义的理解，更加的贴近实际操作；第（10）、（12）题考查了函数的性质和反函数，研究函数图象在解题中的巧妙作用；第（16）题考查了数列的性质和求和。