川大自动控制原理第八章分解
- 格式:ppt
- 大小:1.51 MB
- 文档页数:63

第八章 非线性控制系统分析练习题及答案8-2 设一阶非线性系统的微分方程为3x x x+-= 试确定系统有几个平衡状态,分析平衡状态的稳定性,并画出系统的相轨迹。
解 令 x=0 得 -+=-=-+=x x x x x x x 321110()()()系统平衡状态x e =-+011,,其中:0=e x :稳定的平衡状态;1,1+-=e x :不稳定平衡状态。
计算列表,画出相轨迹如图解8-1所示。
可见:当x ()01<时,系统最终收敛到稳定的平衡状态;当x ()01>时,系统发散;1)0(-<x 时,x t ()→-∞; 1)0(>x 时,x t ()→∞。
注:系统为一阶,故其相轨迹只有一条,不可能在整个 ~xx 平面上任意分布。
8-3 试确定下列方程的奇点及其类型,并用等倾斜线法绘制相平面图。
(1) x xx ++=0 (5) ⎩⎨⎧+=+=2122112x x xx x x解 (1) 系统方程为x -2 -1 -13 0 131 2x-6 0 0.385 0 -0.385 0 6 x 11 2 01 0211图解8-1 系统相轨迹⎩⎨⎧<=-+I I >=++I )0(0:)0(0:x x x x x x x x令0x x ==,得平衡点:0e x =。
系统特征方程及特征根:21,221,21:10,()2:10, 1.618,0.618()s s s s s s I II ⎧++==-±⎪⎨⎪+-==-+⎩稳定的焦点鞍点(, ) , , x f x x x x dxdxxx x dx dx x x x x x==--=--==--=-+=ααβ111⎪⎪⎩⎪⎪⎨⎧<-=>--=)0(11:II )0(11:I x x βαβα计算列表用等倾斜线法绘制系统相平面图如图解8-2(a )所示。
图解8-2(a )系统相平面图(5) xx x 112=+ ① 2122x x x+= ② 由式①: x xx 211=- ③ 式③代入②: ( )( )x xx x x 111112-=+- 即 x x x 11120--= ④ 令 x x110== 得平衡点: x e =0 由式④得特征方程及特征根为 ⎩⎨⎧-==--414.0414.20122,12λs s (鞍点) 画相轨迹,由④式x xdxdx x x x 1111112===+α xx 112=-α 计算列表用等倾斜线法绘制系统相平面图如图解8-2(b )所示。



8-1求下列函数的z 变换。
(1) /()t T x t a = (2) 2()at x t t e -= (3) ()sin x t t t ω= (4) 2()1t x t e -=+ 解 (1) 查z 变换表得()zX z z a=- (2) 查z 变换表得223(1)() 2(1)T z z x t t z +=→-,由复数位移定理得223()() ()()aT aTataT T z z e e x t t eX z z e ----+=→=- (3) 查z 变换表得2sin ()sin ()2cos 1z Tx t t X z z z T ωωω=→=-+,由z 域微分定理得22222(sin sin 2sin cos 2sin )()sin ()()(2cos 1)d Tz z T T z T T z T y t t t Y z Tz X z dz z z T ωωωωωωω-++=→=-=-+ (4) 查z 变换表得222(21)()1(1)()T T T z z z z e X z z z e z z e -----=+=---- 8-2求下列函数的z 变换。
(1) 3()(1)(2)s X s s s +=++ (2) 21()s X s s+=(3) 1()(1)(2)X s s s s =++ (4) 21()(1)s e X s s s --=+ (1T s =)解 (1) 321()(1)(2)12s X s s s s s +==-++++,查z 变换表得22()T Tz zX z z e z e --=--- (2) 22111()s X s s s s+==+,查z 变换表得22(1)()(1)z z z X z z +-=-(3) 11/211/2()(1)(2)12X s s s s s s s ==-+++++,查z 变换表得 222()()2(1)()(1)()()2(1)()()T T T T T T z z e z e z z z e z z z e X z z z e z e -----------+--=---(4)121221()(1)(1)(1)(1)1(1)1(1)(1)T T T T TX z z Z s s Tz z zz z z z e T e z T e z e z e -------⎡⎤=-⎢⎥+⎣⎦⎡⎤=--+⎢⎥---⎣⎦-++-+=-++ 8-3 求下列函数的z 反变换。

第八章 非线性控制系统分析8-1 非线性控制系统概述1. 研究非线性控制理论的意义以上各章详细地讨论了线性定常控制系统的分析和设计问题。
但实际上,理想的线性系统并不存在,因为组成控制系统的各元件的动态和静态特性都存在着不同程度的非线性。
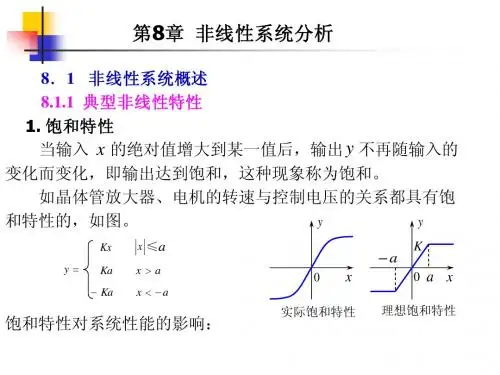
以随动系统为例,放大元件由于受电源电压或输出功率的限制,在输入电压超过放大器的线性工作范围时,输出呈饱和现象,如图8-l(a)所示;执行元件电动机,由于轴上存在着摩擦力矩和负载力矩,只有在电枢电压达到一定数值后,电机才会转动,存在着死区,而当电枢电压超过一定数值时,电机的转速将不再增加,出现饱和现象,其特性如图8-1(b)所示;又如传动机构,受加工和装配精度的限制,换向时存在着间隙特性,如图8-1(c)所示。
在图8-2所示的柱形液位系统中,设H 为液位高度,Q i为液体流入量,Q o 为液体流出量,C 为贮槽的截面积。
根据水力学原理0Q k H = (8-1)其中比例系数k 是取决于液体的粘度和阀阻。
液位系统的动态方程为0i i dH CQ Q Q k H dt =-=-显然,液位H 和液体输入量Q i 的数学关系式为非线性微分方程。
由此可见,实际系统中普遍存在非线性因素。
当系统中含有一个或多个具有非线性特性的元件时,该系统称为非线性系统。
一般地,非线性系统的数学模型可以表示为:(,,...,,)(,,...,,)n m n m d y dy d r dr f t y g t r dt dt dt dt =(8-3)其中f(·)和g(·)为非线性函数。
当非线性程度不严重时,例如不灵敏区较小、输入信号幅值较小、传动机构间隙不大时,可以忽略非线性特性的影响,从而可将非线性环节视为线性环节;当系统方程解析且工作在某一数值附近的较小范围内时,可运用小偏差法将非线性模型线性化。
例如,设图8—2液位系统的液位H 在H 0附近变化,相应的液体输入量Q i 在Q i0,附近变化时,可取ΔH =H −H 0,ΔQ i =Q i −Q i0,对√H 作泰勒级数展开。



第八章 非线性控制系统分析练习题及答案8-2 设一阶非线性系统的微分方程为3x x x+-= 试确定系统有几个平衡状态,分析平衡状态的稳定性,并画出系统的相轨迹。
解 令 x=0 得 -+=-=-+=x x x x x x x 321110()()()系统平衡状态x e =-+011,,其中:0=e x :稳定的平衡状态;1,1+-=e x :不稳定平衡状态。
计算列表,画出相轨迹如图解8-1所示。
可见:当x ()01<时,系统最终收敛到稳定的平衡状态;当x ()01>时,系统发散;1)0(-<x 时,x t ()→-∞; 1)0(>x 时,x t ()→∞。
注:系统为一阶,故其相轨迹只有一条,不可能在整个 ~xx 平面上任意分布。
8-3 试确定下列方程的奇点及其类型,并用等倾斜线法绘制相平面图。
(1) x xx ++=0 (5) ⎩⎨⎧+=+=2122112x x xx x x解 (1) 系统方程为x -2 -1 -13 0 131 2x-6 0 0.385 0 -0.385 0 6 x 11 2 01 0211图解8-1 系统相轨迹⎩⎨⎧<=-+I I >=++I )0(0:)0(0:x x x x x x x x令0x x ==,得平衡点:0e x =。
系统特征方程及特征根:21,221,21:10,()2:10, 1.618,0.618()s s s s s s I II ⎧++==-±⎪⎨⎪+-==-+⎩稳定的焦点鞍点(, ) , , x f x x x x dxdxxx x dx dx x x x x x==--=--==--=-+=ααβ111⎪⎪⎩⎪⎪⎨⎧<-=>--=)0(11:II )0(11:I x x βαβα计算列表用等倾斜线法绘制系统相平面图如图解8-2(a )所示。
图解8-2(a )系统相平面图(5) xx x 112=+ ① 2122x x x+= ② 由式①: x xx 211=- ③ 式③代入②: ( )( )x xx x x 111112-=+- 即 x x x 11120--= ④ 令 x x110== 得平衡点: x e =0 由式④得特征方程及特征根为 ⎩⎨⎧-==--414.0414.20122,12λs s (鞍点) 画相轨迹,由④式x xdxdx x x x 1111112===+α xx 112=-α 计算列表用等倾斜线法绘制系统相平面图如图解8-2(b )所示。


第八章线性离散控制系统8.1 概述8.2 信号采样与保持8.3 离散系统的数学模型8.4 离散控制系统的稳定性8.5 离散控制系统的动态性能分析8.6离散控制系统的稳态误差分析8.7 离散控制系统的最少拍校正8.8利用MATLAB辅助离散控制系统的分析与校正8.9 小结8.1概述本章知识体系离散控制系统的稳定性离散控制系统基本概念信号的采样与保持离散控制系统的数学模型离散控制系统的动态性能分析离散控制系统的稳态误差分析最少拍校正利用MATLAB辅助离散控制系统的分析与校正描述系统分析系统仿真分析、校正系统8.1概述时间上不连续的信号在现实系统中大量存在。
例如许多化工生产过程无法在线连续测量产品的质量指标而是通过定期采样化验就能保证产品质量的稳定。
系统内有一处或多处的信号仅存在于孤立的时间序列点上这类控制系统称为离散时间控制系统简称离散控制系统。
与此相对各处信号均为连续时间函数的控制系统称为连续时间控制系统简称连续控制系统。
8.1概述时间上离散的信号其幅值可能是连续的亦可能是离散的。
将时间上、幅值上都连续的模拟信号转换成时间上离散、但幅值上仍然连续的离散模拟序列信号的过程而这一过程就称为采样又称为波形的离散化过程相应的控制系统则称为采样控制系统。
若由数字计算机实现控制受计算机字长限制还需要进一步将幅值连续的理想化序列信号量化为数字序列信号进一步得到时间和幅值上都是离散的数字序列信号相应的控制系统则称为数字控制系统。
8.1 概述8.1.1 离散控制系统的基本概念 1.采样控制系统大惯性、大滞后控制系统出现的问题采样系统较早出现与某些大惯性、大滞后对象的控制系统中如炉温控制系统。
这类对象的相位滞后非常明显为保证系统的相位裕度开环传递系数一般取很小值难以有很高的稳定精度.提高稳态精度的一个方法在偏差信号和执行电机之间安装一个开关使其每隔较长时间才闭合一次且闭合时间很短。
当开关闭合时系统根据偏差闭环控制电机当开环断开时电机停止等待炉温变化。
8 本章任务§8 非线性控制系统81§8.1引言非线性控制研究的主题:非线性控制系统(至少含有一个非线性元件的系统)的分析与设计为什么要研究非线性控制(续)引言为什么要研究非线性控制(续)引言非线性特性(natural)非线性特性可分为本质(inherent)或自然(natural) 非线性非线性性的主要特征非线性特性常见非线性常见非线性¾跳跃现象Jump phenomenon (Jump phenomenon )例:当输入信号的频率由高变低减小时低减小时,输出响应的幅值突然由C点处的取值落到D点处的取值点取值¾非线性增益(Nonlinear gain )z 阀门流量vs. 压降或阀门开度z 力vs. 弹簧的偏转常见非线性(续)常见非线性¾饱和(Saturation ):输入超出某个值以后,输出幅值止于某一恒定限制值,例如z 放大器饱和z 阀门流量不能大过最大泵压所能产生的流量¾死区(Deadzone ):不敏感区,例如z 继电器等常见非线性常见非线性(续)¾齿隙间游移(Backlash ):多发生于机械联结装置,例如z 齿轮传动等等H steresis )¾滞环(Hysteresis ):多发生于z 电磁电路z 材料常见非线性常见非线性(续)¾库仑摩擦(Coulomb friction )或称静(干)摩擦z 摩擦力只取决于速度的方摩擦取于向¾非线性特征曲线(Nonlinearcharacteristic curve ):例如z 电机的转矩-转速特性曲线阀门的流量-压力曲线z 阀门的流量压力曲线常见非线性imperfections):一类非常重要的非线性常见非线性(续)p )类非常重要的非线性z Ideal relayz Relay with deadzonez Relay with hysteresisz Relay with hysteresis & deadzonevs LTI 系统:x= X:;A:(1)线性vs. 非线性统Ax X: 状态向量; A: 系统矩阵()vs 线性vs. 非线性系统uyvs 线性vs. 非线性特点及性能线性系统非线性系统非线性系统行为举例例1:水下车辆运动用单位阶跃信号作为控制输5秒后改为负单位阶跃信号用单位阶跃信号作为控制输入u ,5秒后改为负单位阶跃信号z 系统对正阶跃输入的响应比其后的负阶跃输入的响应快得非线性系统行为举例例1:(续)控制输入车辆速度 : : u v u v v v =+ 重复此实验,但阶跃幅度设为10;,作为响应的10稳态速度v 对于正阶跃输入的响应值不是10,多平衡点考察一阶系统:.0 2x x x x x=+−= 考察阶系统)(,0线性.非线性极限环常见非线性系统行为特征极限环(续)常见非线性系统行为特征分岔(Bifurcations)当α由正变负时,一个平衡点分为3个:Pitchfork0= 分岔(续)混沌(Chaos )常见非线性系统行为特征3非线性系统行为特征举例例:混沌表现特征==line) (thin ;01.3)0( ,01.2)0xx 5带来的强非线性特性,两个轨迹的在一段时间。