一元线性回归模型的参数估计实验报告

实验一一元线性回归实验目的：掌握一元线性回归的估计与应用，熟悉EViews的基本操作。

实验要求：应用教材P61第12题做一元线性回归分析并做预测。

实验原理：普通最小二乘法。

预备知识：参数估计的普通最小二乘法、t检验、拟合优度检验、回归预测和区间预测。

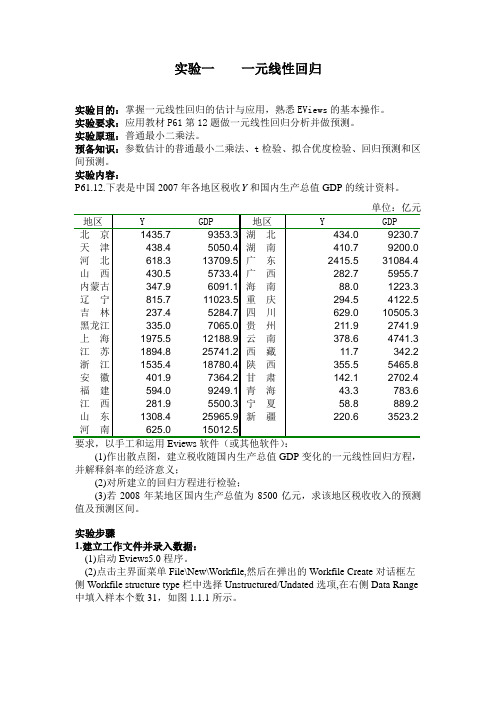
实验内容：P61.12.下表是中国2007年各地区税收Y和国内生产总值GDP的统计资料。

(1)作出散点图，建立税收随国内生产总值GDP变化的一元线性回归方程，并解释斜率的经济意义；(2)对所建立的回归方程进行检验；(3)若2008年某地区国内生产总值为8500亿元，求该地区税收收入的预测值及预测区间。

实验步骤1.建立工作文件并录入数据：(1)启动Eviews5.0程序。

(2)点击主界面菜单File\New\Workfile,然后在弹出的Workfile Create对话框左侧Workfile structure type栏中选择Unstructured/Undated选项,在右侧Data Range 中填入样本个数31，如图1.1.1所示。

图1.1.1 图1.1.2(3)录入数据，在主界面命令栏键入data Y GDP，回车。

在Group表格相应的位置录入Y与GDP的数据，则出现图1.1.2画面。

2.数据的描述性统计和图形统计：以上建立的序列GDP和Y之后，可对其做描述统计和统计以把握该数据的一些统计属性。

⑴描述属性：双击打开对象group1的表格形式，点View/Descriptive Stats\Common Sample，得描述统计结果，如图2.1.1所示，其中：Mean为均值，Std.Dev为标准差。

图2.1.1⑵图形统计：双击序列GDP，点击表格左边View/Graph，可得图2.2.1。

同样可查看序列Y的线形图。

而需要把两个序列放在一个图形中来查看两者的相互关系，用线图或散点图则可以。

在命令栏键入：scat GDP Y，然后回车，就可以得到用散点图来查看GDP和Y 的关系。

数理统计上机报告上机实验题目：用R软件进行一元线性回归上机实验目的：1、进一步理解假设实验的基本思想，学会使用实验检验和进行统计推断。

2、学会利用R软件进行假设实验的方法。

一元线性回归基本理论、方法：基本理论：假设预测目标因变量为Y，影响它变化的一个自变量为X，因变量随自变量的增（减）方向的变化。

一元线性回归分析就是要依据一定数量的观察样本（Xi, Yi），i=1，2…，n，找出回归直线方程Y=a+b*X方法：对应于每一个Xi，根据回归直线方程可以计算出一个因变量估计值Yi。

回归方程估计值Yi 与实际观察值Yj之间的误差记作e-i=Yi-Yi。

显然，n个误差的总和越小，说明回归拟合的直线越能反映两变量间的平均变化线性关系。

据此，回归分析要使拟合所得直线的平均平方离差达到最小，据此，回归分析要使拟合所得直线的平均平方离差达到最小，简称最小二乘法将求出的a和b 代入式（1）就得到回归直线Yi=a+bXi 。

那么，只要给定Xi值，就可以用作因变量Yi的预测值。

（一）实验实例和数据资料：有甲、乙两个实验员，对同一实验的同一指标进行测定，两人测定的结果如试问：甲、乙两人的测定有无显著差异？取显著水平α=0.05.上机实验步骤：1（1）设置假设：H0：u1-u-2=0：H1：u1-u-2<0（2）确定自由度为n1+n2-2=14；显著性水平a=0.05 （3）计算样本均值样本标准差和合并方差统计量的观测值alpha<-0.05;n1<-8;n2<-8;x<-c(4.3,3.2,3.8,3.5,3.5,4.8,3.3,3.9);y<-c(3.7,4.1,3.8,3.8,4.6,3.9,2.8,4.4);var1<-var(x);xbar<-mean(x);var2<-var(y);ybar<-mean(y);Sw2<-((n1-1)*var1+(n2-1)*var2)/(n1+n2-2)t<-(xbar-ybar)/(sqrt(Sw2)*sqrt(1/n1+1/n2));tvalue<-qt(alpha,n1+n2-2)；（4）计算临界值：tvalue<-qt(alpha,n1+n2-2)（5）比较临界值和统计量的观测值，并作出统计推断实例计算结果及分析：alpha<-0.05;> n1<-8;> n2<-8;> x<-c(4.3,3.2,3.8,3.5,3.5,4.8,3.3,3.9);> y<-c(3.7,4.1,3.8,3.8,4.6,3.9,2.8,4.4);> var1<-var(x);> xbar<-mean(x);> var2<-var(y);> ybar<-mean(y);> Sw2<-((n1-1)*var1+(n2-1)*var2)/(n1+n2-2)> t<-(xbar-ybar)/(sqrt(Sw2)*sqrt(1/n1+1/n2));> var1[1] 0.2926786> xbar[1] 3.7875> var2[1] 0.29267862> ybar[1] 3.8875Sw2[1] 0.2926786> t[1] -0.3696873tvalue[1] -1.76131分析：t=-0.3696873>tvalue=-1.76131，所以接受假设H1即甲乙两人的测定无显著性差异。

一元线性回归模型的参数估计----普通最小二乘法1、什么是一元线性回归模型?一元回归模型,是最简单的计量经济学模型.在模型中,只有一个解释变量,被解释变量与解释变量之间存在线性关系.2、一元回归模型的一般形式:y i=β0+β1x i+μi, i=1,2,…n (1)其中,y是被解释变量,x是解释变量,β0、β1是待定参数,μ是随机误差项,yi,xi是随机抽取的n组样本观测值.该方程满足如下条件:E(μi)=0Var(μi)=б2Cov(μi,μj)=0Cov(x i,u i)=0i=1,2,...,n j=1,2,…,n i≠j3、模型参数估计的任务(1)一是求得反映变量之间数量关系的参数(即一元线性回归模型y i=β0+β1x i+μi, i=1,2,…n 中的β0,β1)的估计量;(2)二是求得随机误差项的分布参数.4、模型参数估计的普通最小二乘法普通最小二乘法,是应用最多的参数估计方法.(1)什么是最小二乘原理在已经获得样本观测值y i,x i(i=1,2,…,n)的情况下,假如参数估计量已经求得记为^1^,ββ,我们可以得到直线方程:iixy^1^^ββ+=i=1,2,…,n (2)其中,^iy是被解释变量的估计值,它由参数估计量和解释变量的观测值计算得来.被解释变量的观测值与估计值,在总体上越接近越好.判断的标准是:二者之差平方和21^)(∑-=n i i y y Q 最小.这就是最小二乘原理.[思考]为什么用平方和,而不直接将二者的差简单相加?(2) 从最小二乘原理,根据样本观测值,具体求参数估计值.由于21^)(∑-=n i i y y Q , (又 i i x y ^1^0^ββ+= )=21^1^0)]([∑+-n i i x y ββ我们可以知道,Q 是^1^0,ββ二次函数并且是非负数.所以Q 的极小值总是存在的.(为什么?)根据极值存在的必要条件知,⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂001^0^ββQ Q (为什么不是充分条件?)由此,不难推得:⎪⎩⎪⎨⎧=-+=-+∑∑0)(0)(^1^0^1^0i i i i i x y x y x ββββ (4)进而得到:⎪⎩⎪⎨⎧+=+=∑∑∑∑∑2^1^0^1^0i i i i i i x x x y x n y ββββ (5)于是解得⎪⎪⎩⎪⎪⎨⎧--=--=∑∑∑∑∑∑∑∑∑∑∑22^1222^0)()(i i i i i i i i i i i i i x x n x y x y n x x n x y x y x ββ (6)另外,可以将公式(6)简化变形得⎪⎪⎩⎪⎪⎨⎧-==∑∑•••__^1__^02^1xy x y x i ii βββ (7)其中,____;y y y x x x i i i -=-=••n y y n x x ii ∑∑==____;(3)求随机误差项方差的估计值.记^i i i y y e -=为第i 个样本观测值的残差.即被解释变量的观测值与估计值之差.则随机误差项方差的估计值为:222-=∑n i e μσ (8)证明从略.至此, 普通最小二乘法一元线性回归模型的参数估计问题得到解决.。

1一元线性回归模型的参数估计 1、普通最小二乘估计（OLS ） 对于所研究的经济问题，通常真实的回归直线是观测不到的。收集样本的目的就是要对这条真实的回归直线做出估计。

假如给出了样本观测值（X i ，Y i ）, i=1, 2, …, n （是样本容量）。 ?+β? X i +u ?i （也可以记为e i ） 则样本回归模型（估计的模型）Y i=β01

?和β?分别是 β0 和β1的估计值或估计量，u ?i （或e i ）是的u i 估计值，称为残差β01

（residual ）项，也称为拟合误差。 ?=β?+β? X i ，称为样本回归方程或样本回归线。用来估计样本回归模型的直线写为 Y 01i ?称Y i 的拟合值（fitted value） 其中Y i

如何估计？ （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。 （2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。 （3）最小二乘法的原则是以“残差平方和（residual sum of square, RSS）最小”确定直线位置。

用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。（这种方法对异常值非常敏感）设残差平方和ESS 用Q 表示，

?) 2=?i=∑(Y i -Y Q=∑u i 2i=1 i=1 T T ∑(Y -β? i i=1 n ?X ) 2， -β1i ?和β?的估计值。以β?和β?为变量，把Q 看作是β?则通过Q 最小确定这条直线，即确定β01010?的函数，?和β?的偏导数并令其为零，和β这是一个求极值的问题。求Q 对β得正规方程组， 101

?Q=2 ?β ∑(Y -β? i i=1n n ?X ) (-1)=0 (1) -β1i ?X ) (- X i )=0 (2) -β1i ?Q =2 ?β 1 ∑(Y -β? i i=1 ?=-β? ?β01? ?(X i -)(Y i -) β1=2 (X -) i ? x i y i ?i=Y i -Y ， x i=X i -X 。利用离差的定义有β1=离差y 2 x i _ _ 上例中假设我们不知道总体数据，但是我们通过抽样得到两个样本

实验一案例：下表的数据为2003年全国31个省市自治区的城镇居民年人均可支配收入X与年人均消费支出。

地区Y X 地区Y X北京11123.84 13882.62 湖北5963.25 7321.98天津7867.53 10312.91 湖南6082.62 7674.20河北5439.77 7239.06 广东9636.27 12380.43山西5105.38 7005.03 广西5763.50 7785.04内蒙古5419.14 7012.90 海南5502.43 7259.25辽宁6077.92 7240.58 重庆7118.06 8093.67吉林5492.10 7005.17 四川5759.21 7041.87黑龙江5015.19 6678.90 贵州4948.98 6569.23上海11040.34 14867.49 云南6023.56 7643.57江苏6708.58 9262.46 西藏8045.34 8765.45浙江9712.89 13179.53 陕西5666.54 6806.35安徽5064.34 6778.03 甘肃5298.91 6657.24福建7356.26 9999.54 青海5400.24 6745.32江西4914.55 6901.42 宁夏5330.34 6530.48山东6069.35 8399.91 新疆5540.61 7173.54河南4941.60 6926.12资料来源：《中国统计年鉴2004》，表中数据均以当年价格计算。

一、建立工作文件(研究消费与收入的关系)启动Eviews6.exe后，点击File\New\Workfile ，在弹出的对话框中选择数据的时间频率（frequency）为Unstructure/Undated (截面数据) ，Data range（以只有31个观测值的一元线性模型为例）为31，点击OK即可。

二、输入数据在主菜单点击Quick\Empty Group ，录入X、Y的数据，在窗口中点击数据，就可以修改数据列的名称，点“OK”关闭即可。

案例分析报告（2014——2015学年第一学期）课程名称：预测与决策专业班级：电子商务1202 学号： 2204120202 学生：维维2014 年 11月案例分析（一元线性回归模型）我国城镇居民家庭人均消费支出预测一、研究目的与要求居民消费在社会经济的持续发展中有着重要的作用，居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长，而且这也是人民生活水平的具体体现。

从理论角度讲，消费需求的具体容主要体现在消费结构上，要增加居民消费，就要从研究居民消费结构入手，只有了解居民消费结构变化的趋势和规律，掌握消费需求的热点和发展方向，才能为消费者提供良好的政策环境，引导消费者合理扩大消费，才能促进产业结构调整与消费结构优化升级相协调，才能推动国民经济平稳、健康发展。

例如，2008年全国城镇居民家庭平均每人每年消费支出为11242.85元，最低的省仅为人均8192.56元，最高的市达人均19397.89元，是的2.37倍。

为了研究全国居民消费水平及其变动的原因，需要作具体的分析。

影响各地区居民消费支出有明显差异的因素可能很多，例如，零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。

为了分析什么是影响各地区居民消费支出有明显差异的最主要因素，并分析影响因素与消费水平的数量关系，可以建立相应的计量经济模型去研究。

二、模型设定我研究的对象是各地区居民消费的差异。

居民消费可分为城镇居民消费和农村居民消费，由于各地区的城镇与农村人口比例及经济结构有较大差异，最具有直接对比可比性的是城市居民消费。

而且，由于各地区人口和经济总量不同，只能用“城镇居民每人每年的平均消费支出”来比较，而这正是可从统计年鉴中获得数据的变量。

所以模型的被解释变量Y选定为“城镇居民每人每年的平均消费支出”。

因为研究的目的是各地区城镇居民消费的差异，并不是城镇居民消费在不同时间的变动，所以应选择同一时期各地区城镇居民的消费支出来建立模型。

实验名称：一元线性回归模型的估计与检验（实验序号：B14201102）实验目的：建立数据文件，画散点图，进行估计并检验实验内容考察中国城镇居民2006年人均可支配收入与消费支出的关系（截面数据模型）建立中国居民总量消费函数考察中国居民收入与消费的关系（时间序列数据模型）实验要求：1、掌握对经济现象中的有关变量进行相关分析2、掌握使用OLS方法估计方程，熟悉操作过程中各选项和参数的设置3、着重理解方程OLS估计的输出结果，对实际的输出结果给出有意义的分析实验步骤建立模型模型检验实验记录1、中国城镇居民人均支出模型：截面数据模型表2.6.1 2006年中国内地各地区城镇居民家庭人均全年可支配收入1.建立模型假设拟建立如下一元回归模型：01Y X ββμ=++一般可以写出如下回归分析结果：281.50.714i i Y X =+（1.05） （31.39）20.9714R = 985.66F = .. 1.46DW =其中括号内的数为响应参数的t 检验值，2R 是可决系数，F 与D.W.是有关的两个检验统计量。

Dependent Variable: Y Method: Least Squares Date: 04/06/13 Time: 13:58 Sample: 1 31Included observations: 31Variable Coefficient Std. Error t-Statistic Prob. C 281.4993 268.9497 1.046662 0.3039 X0.7145540.022760 31.395250.0000R-squared 0.971419 Mean dependent var 8401.467 Adjusted R-squared 0.970433 S.D. dependent var 2388.455 S.E. of regression 410.6928 Akaike info criterion 14.93591 Sum squared resid 4891388. Schwarz criterion 15.02842 Log likelihood -229.5066 Hannan-Quinn criter. 14.96607 F-statistic 985.6616 Durbin-Watson stat 1.461502Prob(F-statistic)0.0000002.模型检验从回归估计的结果看，模型拟合较好。