北京市平谷区2013中考数学一模试题

海 淀 区 九 年 级 第 二 学 期 期 中 练 习数 学2013.5一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．2的相反数是A. 2B.2-C.21D.21-2．十八大开幕当天,网站关于此信息的总浏览量达5.5亿次.将5.5亿用科学记数法表示为A. 8105.5⨯B. 81055⨯ C. 755010⨯ D. 10100.55⨯ 3．如图是某几何体的三视图，则这个几何体是A. 圆柱B. 正方体C. 球D. 圆锥4．一个多边形的外角和是内角和的一半，则这个多边形的边数为A. 5B.6C. 7D. 85．小林在元宵节煮了20个元宵，其中10个黑芝麻馅，6个山楂馅，4个红豆馅（除馅料不同外，其它都相同）.煮好后小明随意吃一个，吃到红豆馅元宵的概率是A ．12 B ．13 C ． 15 D ．256.一副三角板如图放置，若∠1＝90︒，则∠2的度数为A ．45°B ．60°C ．75°D ．90°7.在篮球比赛中，某队员连续10场比赛中每场的得分情况如下表所示：则这10场比赛中他得分的中位数和众数分别是A.10, 4B.10，7C.7，13D. 13，48.如图，△ABC 是等边三角形，6AB =厘米，点P 从点B 出发,沿BC 以每秒1厘米的速度运动到点C 停止；同时点M 从点B 出发,沿折线BA -AC 以每秒3厘米的速度运动到点C 停止.如果其中一个点停止运动，则另一个点也停止运动.设点P 的运动时间为t 秒，P 、M 两点之间的距离为y 厘米，则表示y 与t 的函数关系的图象大致是A. B. C. D.二、填空题（本题共16分，每小题4分）9． 分解因式：22369a b ab b -+= ．10．若关于x 的一元二次方程230x x m -+=有实数根，则m 的取值范围是 ．11．如图,将正方形纸片对折，折痕为EF .展开后继续折叠，使点A 落在EF 上，折痕为GB ，则ABG ∠的正切值是 . 12. 如图1所示，圆上均匀分布着11个点12311,,,,A A A A .从A 1起每隔k 个点顺次连接，当再次与点A 1连接时，我们把所形成的图形称为“k +1阶正十一角星”，其中18k ≤≤（k 为正整数）.例如，图2是“2阶正十一角星”，那么1211A A A ∠+∠++∠=°；当1211A A A ∠+∠++∠=900°时，k = .图1 图2三、解答题（本题共30分，每小题5分）EDCBA130112cos301)()8-︒+-- ．14．解不等式组：20,11.2x x x +>⎧⎪⎨-+≥⎪⎩15．先化简，再求值：4212112--÷⎪⎭⎫ ⎝⎛-+x x x ，其中3=x ．16.已知：如图，点A ，D ，C 在同一直线上，AB ∥EC ，AC CE =，.B EDC ∠=∠求证：.BC DE =17. 如图，在平面直角坐标系xOy 中，反比例函数xy 2-=的图象与一次函数k kx y -=的图象的一个交点为(1,)A n -． （1）求这个一次函数的解析式；（2）若P 是x 轴上一点，且满足45APO ∠=︒，直接写出点P 的坐标．18. 列方程（组）解应用题：雅安地震灾情牵动全国人民的心．某厂计划加工1500顶帐篷支援灾区，加工了300顶帐篷后，由于救灾需要，将工作效率提高到原计划的2倍，结果提前4天完成了任务．求原计划每天加工多少顶帐篷.四、解答题（本题共20分，每小题5分） 19.如图，在四边形ABCD 中，对角线AC ,BD 相交于点E ,DAB ∠=CDB ∠=90︒,ABD ∠=45︒,∠DCA =30︒,AB =.求AE 的长和△ADE 的面积．=．以AB为直径的⊙O交BC于点D，过点D作20.已知：如图，在△ABC中，AB ACDE⊥AC于点E.(1)求证：DE与⊙O相切；AB=，(2)延长DE交BA的延长线于点F.若6sin B求线段AF的长.21. 下图为北京某天空气质量指数实时查询的一个结果.为了解今年北京市春节假期空气质量情况，小静查到下表所示的某天15个监测子站的空气质量指数；小博从环境监测网随机抽取了某天部分监测点的空气质量情况，并绘制了以下两个统计图.解答下列问题：（1）小静查到的统计表中重度污染出现的频率为；（2）计算小博抽取的监测点的个数，并补全条形统计图；（3）据统计数据显示，春节期间燃放烟花爆竹成为空气污染的一个重要原因. 市民在今年春节期间自觉减少了购买和燃放烟花爆竹的数量，全市销售烟花爆竹37万余箱，比去年减少35%.求今年比去年同期少销售多少万箱烟花爆竹.（结果保留整数）22.问题：如图1，a、b、c、d是同一平面内的一组等距平行线（相邻平行线间的距离为1）.画出一个正方形ABCD，使它的顶点A、B、C、D分别在直线a、b、d、c上，并计算它的边长.图1 图2小明的思考过程：他利用图1中的等距平行线构造了33⨯的正方形网格，得到了辅助正方形EFGH ，如图2所示, 再分别找到它的四条边的三等分点A 、B 、C 、D ，就可以画出一个满足题目要求的正方形.请回答：图2中正方形ABCD 的边长为 . 请参考小明的方法，解决下列问题：（1）请在图3的菱形网格（最小的菱形有一个内角为60︒，边长为1）中，画出一个等边△ABC ，使它的顶点A 、B 、C 落在格点上，且分别在直线a 、b 、c 上；（3）如图4，1l 、2l 、3l 是同一平面内的三条平行线，1l 、2l 之间的距离是215，2l 、3l 之间的距离是2110，等边△ABC 的三个顶点分别在1l 、2l 、3l 上，直接写出△ABC 的边长.图3 图4五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23.在平面直角坐标系xOy 中，抛物线22y mx mx n =-+与x 轴交于A 、B 两点，点A 的坐标为(2,0)-． （1）求B 点坐标； （2）直线y =12x +4m +n 经过点B . ①求直线和抛物线的解析式；②点P 在抛物线上，过点P 作y 轴的垂线l ，垂足为(0,)D d ．将抛物线在直线l 上方的部分沿直线l 翻折，图象的其余部分保持不变，得到一个新图象G ．请结合图象回答：当图象G 与直线y =12x +4m +n 只有两个公共点时，d 的取值范围是 ．24．在△ABC 中，∠ACB ＝90︒．经过点B 的直线l （l 不与直线AB 重合）与直线BC 的夹角等于ABC ∠，分别过点C 、点A 作直线l 的垂线，垂足分别为点D 、点E ．（1）若45ABC ∠=︒，CD =1（如图），则AE 的长为 ；（2）写出线段AE 、CD 之间的数量关系，并加以证明； （3）若直线CE 、AB 交于点F ， 56CF EF =，CD =4，求BD 的长．25. 在平面直角坐标系xOy 中，抛物线222y x mx m m =-++的顶点为C . (1) 求点C 的坐标（用含m 的代数式表示）；(2) 直线2y x =+与抛物线交于A 、B 两点，点A 在抛物线的对称轴左侧.①若P 为直线OC 上一动点，求△APB 的面积；②抛物线的对称轴与直线AB 交于点M ，作点B 关于直线MC 的对称点'B . 以M 为圆心，MC 为半径的圆上存在一点Q ，使得'QB 的值最小，则这个最小值为 .BC平谷区2012～2013学年度第二学期初三统一练习 数 学 试 卷 2013．4一、选择题（本题共32分，每小题4分）在下列各题的四个备选答案中，只有一个是正确的． 1．3-的倒数是A ．3B ．3-C ．13 D ．13- 2．最新统计，中国注册志愿者总数已超30 000 000人，30 000 000用科学记数法表示为 A ．7310⨯ B ．6310⨯ C ．63010⨯ D ．5310⨯ 3．如图，在□ABCD 中，CE AB ⊥，E 为垂足．如果125A =∠，则BCE =∠ A ．25B ．30C ．35D ．554．某电视台举行歌手大奖赛，每场比赛都有编号为1～10号共10道综合素质测试题供选手随机抽取作答．在某场比赛中，前两位选手分别抽走了2号，7号题，第3位选手抽中8号题的概率是 A ．17B ．18C ．19D ．1105．如图，点D E F ，，分别是ABC △三边的中点，若ABC △的 周长为20cm ，则DEF △ 的周长为 A ．15cmB ．20cm 3C ．5cmD ．10cm6．北京市2013年4月份某一周天气预报的日最高气温（单位：℃） 分别为13，14，17，22，22，15，15，这组数据的众数是 A ．22℃ B ．15℃C ．C ︒22℃和15D ．18.5℃7．将函数267y x x =++进行配方，正确的结果应为 A ．2(3)2y x =+-B ．2(3)2y x =++C ．2(3)2y x =-+D ．2(3)2y x =--AEBCD8．如图，等腰直角三角形ABC 位于第一象限，AB=AC=2，直角顶点A 在直线y =x 上，其中A 点的横坐标为1，且两条直角边AB 、AC 分别平行于x 轴、y 轴，若双曲线ky x=(k ≠0) 与ABC ∆有交点，则k 的取值范围是 A ．12k << B ．13k ≤≤ C ．14k ≤≤ D ．14k <≤ 二、填空题（本题共16分，每小题4分） 9．如果分式31x -的值为正数，那么x 的取值范围是_____________． 10．分解因式：324a ab -=__________ ．11．如图，⊙O 的半径OA =6，弦AB =8，P 为AB 上一动点，则点P 到圆心O 的最短距离为 ．12．如图1、图2、图3，在ABC △中，分别以AB AC 、为边，向ABC △外作正三角形，正四边形，正五边形，BE CD 、相交于点O ．如图4，AB AD 、是以AB 为边向ABC △外所作正n 边形的一组邻边；AC AE 、是以AC 为边向ABC △外所作正n (n 为正整数)边形的一组邻边．BE CD 、的延长相交于点O ．图1中BOC ∠= ； 图4中BOC ∠= （用含n 的式子表示）．三、解答题（本题共30分，每小题5分）13．计算： 011()20132s i n 122--+︒-． 14．已知2250x x --=，求21(21)(2)(2)4()2x x x x x -++---的值．15．已知：如图，AB ∥CD ，AB =EC ，BC =CD . 求证：AC =ED .16．如果2-是一元二次方程280x mx +-=的一个根，求它的另一根． 17．如图，一次函数4+=mx y 的图象与x 轴相交于点A ， 与反比例函数)0(>=x xky 的图象相交于点(16)B ，． （1）求一次函数和反比例函数的解析式；（2）设点P 是x 轴上一点，若18=∆APB S ,直接写出点P 的坐标．OP BAA18．某产品每件成本10元，试销阶段每件产品的销售价x （元）与产品的日销售量y （件）之间的关系如下表：若日销售量y 是销售价x 的一次函数．（1）求出日销售量y （件）与销售价x （元）的函数关系式；（2）求销售价定为30元时，每日的销售利润． 四、解答题（本题共20分，第小题5分） 19．已知：如图，四边形ABCD 中，90A ∠=︒，120D ∠=︒，E 是AD 上一点，∠BED=135°，BE =DC =2DE =求(1)点C 到直线AD 的距离； （2）线段BC 的长．20. 如图，AB 是O ⊙的直径，点C 在O ⊙上，CAB ∠的平分线交O ⊙于点D ，过点D 作AC 的垂线交AC 的延长线于点E ，连接BC 交AD 于点F .（1）求证：ED 是O ⊙的切线；（2）若108AB AD ==，，求CF 的长.21．2010年4月，国务院出台“房贷新政”，确定实行更为严格的差别化住房信贷政策，对楼市产生了较大的影响．下面是某市今年2月~5月商品住宅的月成交量统计图（不完整），请根据图中提供的信息，完成下列问题：（1）该市今年2月~5月共成交商品住宅 套； (2）请你补全条形统计图；（3）该市这4个月商品住宅的月成交量的极差是 套，中位数是 套．22. 对于平面直角坐标系中的任意两点11122(,)()P x y P x y 2、，，我们把1122x x y y -+-叫做12P P 、两点间的直角距离，记作12()d P P ，． （1）已知点12(3,4)(1)P P -、，1，那么12P P 、两点间的直角距离12()d P P ，=_____________；（2）已知O 为坐标原点，动点()P x y ，满足()1d O P =，，请写出x 与y 之间满足的关系式，并在所给的直角坐标系中画出所有满足条件的图形；（3）设0()P x y ，是一定点，()Q x y ，是直线y ax b =+上的动点，我们把0()d P Q ，的最小值叫做点0P 到直线y ax b =+的直角距离.试求点(21)M ，到直线2y x =+的直角距离.五、解答题（本题共22分，第23题7分，第24题7分，第25题23. 已知关于m 的一元二次方程221x mx +-=0. （1）判定方程根的情况；（2）设m 为整数，方程的两个根都大于1-且小于32，当方程的两个根均为有理数时，求m 的值．24．（1）如图(1)，△ABC 是等边三角形，D 、E 分别是 AB 、BC 上的点，且BD CE =，连接AE 、CD 相交于点P . 请你补全图形，并直接写出∠APD 的度数；= （2）如图（2）,Rt △ABC 中，∠B =90°，M 、N 分别是 AB 、BC 上的点，且,AM BC =BM CN =，连接AN 、CM 相交于点P . 请你猜想∠APM =°，并写出你的推理过程25．如图1，在直角坐标系中，已知直线112y x =+与y 轴交于点A ， 与x 轴交于点B ，以线段BC 为边向上作正方形ABCD . （1）点C 的坐标为（ ），点D 的坐标为（ ）； （2）若抛物线22(0)y ax bx a =++≠经过C 、D 两点， 求该抛物线的解析式；（3）若正方形以每秒5个单位长度的速度沿射线 BA 向上平移，直至正方形的顶点C 落在y 轴上时， 正方形停止运动. 在运动过程中，设正方形落在y 轴右侧部分的面积为s ，求s 关于平移时间t （秒）的函数关系式， 并写出相应自变量t 的取值范围.通州区初三年级模拟考试数学试卷2013年5月一、选择题（本题共32分，每小题4分）在每道小题给出的四个备选答案中，只有一个是符合题目要求的，请将所选答案前的字母按规定要求填涂在答题纸第1-8题的相应位置上． 1．3-的倒数是A ．3B ．3-C ．13-D ．132．在下列几何体中，主视图、左视图和俯视图形状都相同的是A B C D3．2012年，北京实现地区生产总值约17800亿元，比2011年增长百分之七点多.将17800用科学记数法表示应为 A ．17.8×103B ．1.78×105C ．0.178×105D ．1.78×44．如图，A 、B 、C 是⊙O 上的三个点，∠ABC =32°， 则∠AOC 的度数是 A ．32°B ．64°C ．16°D ．58°5．端午节吃粽子是中华民族的传统习俗.妈妈买了2只红豆粽和3只咸肉粽，粽子除内部馅料不同外其它均相同．小颖任意吃一个，吃到红豆粽的概率是 A ．25 B ．12C ．15D ．236. 一个扇形的圆心角为90°，半径为2，则这个扇形的面积是 A ．6πB ．4πC ．2πD ．π7．某班开展以“提倡勤俭节约，反对铺张浪费”为主题教育活动. 为了解学生每天使用零花钱的情况，小明随机调查了10名同学，结果如下表：关于这10名同学每天使用的零花钱，下列说法正确的是 A ．平均数是2.5 B ．中位数是3C ．众数是2D ．方差是48． 如图，在直角坐标系xoy 中，已知()01A ，，)B，以线段AB 为边向上作菱形ABCD ，且点D 在y 轴上.若菱形ABCD 以每秒2个单位长度的速度沿射线AB 滑行，直至顶点D 落在x 轴上时停止．设菱形落在x 轴下方部分的面积为S ，则表示S 与滑行时间t 的函数关系的图象为第8题图（1） 第8题图（2）二、填空题（本题共16分，每小题4分） 9．若分式2x x-的值为零，则x = ． 10．分解因式：322x x x -+= ．11．如图，AB ∥CD ，点E 在AB 上，且DC DE =，70AEC ∠=︒，则D ∠的度数是______.12．定义一种对正整数n 的“F 运算”：①当n 为奇数时，结果为31n +；②当n 为偶数时，结果为kn 2（其中k 是使得kn 2为奇数的正整数），并且运算重复进行.例如，取6n =，则：12363105F F F −−−→−−−→−−−→① ②②第次第次第次……，若1n =，则第2次“F 运算”的结第11题图CDA E B果是 ；若13n =，则第2013次“F 运算”的结果是 . 三、解答题（本题共30分，每小题5分） 13．计算：(123tan302--+o14．解不等式组20512(1)x x x -<⎧⎨+>-⎩，．15. 已知：如图，AB ＝AC ，点D 、E 分别在AB 、AC 上，且使AE ＝AD .求证：∠B ＝∠C .16．化简求值：2221y x yx y x⎛⎫-+ ⎪-⎝⎭g ，其中30x y -=，且0y ≠.17．已知(42)A -，，(24)B -，是一次函数y kx b =+的图象和反比例函数my x=图象的两个交点．（1）求反比例函数和一次函数的表达式；（2）将一次函数y kx b =+的图象沿y 轴向上平移n 个单位长度，交y 轴于点C ，若12ABC S =V ，求n 的值.18. 列方程或列方程组解应用题：ECA D B根据城市发展规划设计，某市工程队为该城市修建一条长4800米的公路.铺设600米后，为了缩短工期，该工程队增加了人力和设备，实际每天修建公路的长度是原计划的2倍，结果共用9天完成任务.问原计划每天修建公路多少米? 四、解答题（本题共20分，每小题5分）19．某中学组织全校1000名学生参加了有关“低碳环保”知识竞赛．为了解本次知识竞赛的成绩分布情况，从中随机抽取了部分学生的成绩（得分取正整数，满分为100分），并绘制了如图的频数分布表和频数分布直方图（不完整）．请根据以上提供的信息，解答下列问题：（1）直接写出频数分布表中a ，b 的值，补全频数分布直方图；（2）学校将对成绩在90分以上（不含90分）的学生进行奖励，请估计全校1000名学生中约有多少名获奖？20．如图，在矩形ABCD 中，AB =3，BC DCE 是等边三角形，DE 交AB 于点F ，求△BEF 的周长．21．已知：如图，AB 是⊙O 的直径，AC 是弦．过点A 作∠BAC 的角平分线，交⊙O 于点D ，过点D 作AC 的垂线，交AC 的延长线于点E ．/分A DFEB C（1）求证：直线ED 是⊙O 的切线；（2）连接EO ，交AD 于点F ，若5AC =3AB ，求EOFO的值．22. 如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形ABCD 的边长为2，E 是AD 的中点，沿CE 将菱形ABCD 剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上． （1）在下面的菱形斜网格中画出示意图；（2）若所拼成的直角三角形、等腰梯形、矩形的面积分别记为S 1、S 2、S 3，周长分别记为l 1、l 2、3l ，判断所拼成的三种图形的面积、周长的大小关系（用“=”、“＞”、“＜”、“≤”或“≥”连接）：面积关系是 ； 周长关系是 ．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）第22题图（矩形）（等腰梯形）（直角三角形）第22题图23. 已知二次函数()2214y x k x k =-++的图象与x 轴分别交于点()1,0A x 、()2,0B x ，且32-<1x <12-． （1）求k 的取值范围；（2）设二次函数()2214y x k x k =-++的图象与y 轴交于点M ，若OM OB =，求二次函数的表达式；（3）在(2)的条件下，若点N 是x 轴上的一点，以N 、A 、M 为顶点作平行四边形，该平行四边形的第四个顶点F 在二次函数()2214y x k x k =-++的图象上，请直接写出满足上述条件的平行四边形的面积.24．已知：2AD =，4BD =，以AB 为一边作等边三角形ABC .使C 、D 两点落在直线AB的两侧.（1）如图，当∠ADB=60°时，求AB 及CD 的长；（2）当∠ADB 变化，且其它条件不变时，求CD 的 最大值，及相应∠ADB 的大小.25．我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点（半圆与二次函数图象的连接点除外），那么这条直线叫做“蛋圆”的切线.如图，二次函数223y x x =--的图象与x 轴交于点A 、B ，与y 轴交于点D ，AB 为半圆直径，半圆圆心为点M ,半圆与y 轴的正半轴交于点C . （1）求经过点C 的“蛋圆”的切线的表达式；A DBC（2）求经过点D 的“蛋圆”的切线的表达式；（3）已知点E 是“蛋圆”上一点（不与点A 、点B 重合），点E 关于x 轴的对称点是F ，若点F 也在“蛋圆”上，求点E 的坐标.通州区初三数学模拟考试参考答案及评分标准2013．5 一、选择题：1．C 2．C 3．D 4．B 5．A 6．D 7．B 8．A 二、填空题：9. 2x =； 10. ()21x x -； 11. 40 ； 12. 1，4；三、解答题： 13. 解：原式=1312-+， ……………… 4分；=112+，=32+……………… 5分. 14. ()205121x x x -<⎧⎨+>-⎩， ．①②解：解不等式①，得 2x <， (1)分；解不等式②，5122x x +>-， ……………… 2分； 5221x x ->--， ……………… 3分； 33x >-，1x >-， ……………… 4分；第25题图∴这个不等式组的解集是12x -<< . (5)分.15. 证明：在△ABE 和△AC D 中∵ .AB AC A A AE AD =⎧⎪∠=∠⎨⎪=⎩，， ……………… 3分；∴△ABE ≌△ACD （SAS ）. ……………… 4分；∴B C ∠=∠. ……………… 5分.16． 解：原式=x yx y x y y x y x -∙⎪⎪⎭⎫ ⎝⎛-+--2222222，x yx y x x -∙-=222， ……………… 1分； xyx y x y x x -∙-+=))((2， ……………… 2分； =xx y+. ……………… 3分； 由30x y -=，得3x y =， ……………… 4分； ∴原式=33y y y +=34y y =34. ……………… 5分.17. 解：(1) 把(42)A -，，(24)B -，分别代入y kx b =+和my x=中， ∴42244.2-=k b k b m ⎧⎪-+=⎪+=-⎨⎪⎪⎩，， ……………… 1分；解得：128.k b m =-⎧⎪=-⎨⎪=-⎩，， ……………… 2分；∴反比例函数的表达式为8y x=-，一次函数的表达式为2y x =-- ； （2）设一次函数2y x =--的图象与y 轴的交点为D ,则()0D ，-2，第15题图EDC (3)分；∵12=∆ABC S ， ∴12221421=∙∙+-∙∙CD CD ， ……………… 4分；∴4CD =，∴4n =. (5)分.18. 解法一:解：设原计划每天修建公路x 米, 则实际每天修建公路2x 米， …… 1分；根据题意得：600480060092x x-+=， ……………… 3分； ∴27009x=， ∴300x =.经检验：x =300是原方程的解，且符合实际问题的意义. ……………… 4分； 答： 原计划每天修建公路300米. ……………… 5分. 解法二：解：设铺设600米用x 天, 则增加人力和设备后，用()9x -天完成任务.……………… 1分； 根据题意得：600480060029x x-⨯=-， ……………… 3分； 解得：2x =.经检验：2x =是原方程的解，且符合实际问题的意义. ……………… 4分； ∴6003002=， 答：原计划每天修建公路300米. ……………… 5分. 四、解答题19. （1）0.05a =，24b =. ……………… 2分； 补全频数分布直方图正确； ……………… 4分； （2）0.371000370⨯=. ……………… 5分. 估计全校1000名学生中约有370名获奖.20．解法一：∵矩形ABCD ，△DCE 是等边三角形，∴30ADF ECB ∠=∠=o ，3ED EC ==， 在Rt △ADF 中，90A ∠=o，AD =∴tan AFADF AD∠=，tan 30==o ∴1AF =， ∴312FB AB AF =-=-=，2FD =， ……………… 1分； ∴321EF ED DF =-=-=， ……………… 2分； 过点E 作EG CB ⊥，交CB 的延长线于点G . ……………… 3分；在Rt △ECG 中，90EGC ∠=o ，3EC =，30ECG ∠=o，∴1322EG EC ==，cos GC ECG EC∠=，cos 303GC ==o∴GC =∴GB GC BC =-=由勾股定理得，222EB EG GB =+，∴EB = ……………… 4分； ∴△BEF 的周长=3EF FB EB ++=……………… 5分. 解法二：∵矩形ABCD ，△DCE 是等边三角形，∴60EDC ECD ∠=∠=o，3ED EC ==，过点E 作EH CD ⊥交CD 于点H ，交AB 于点G . ……………… 1分； ∴点H 是DC 的中点，点G 是AB 的中点，30FEG ∠=o，GH AD ==G 第20题图A BDEF在Rt △EHD 中，90EHD ∠=o ，3ED =， ∴sin EHEDH ED∠=，sin 603EH ==o∴EH =∴EG EH GH =-==. 在Rt △EGF 中，90EGF ∠=o ，60EFG ∠=o ， ∴sin EG EFG EF∠=，sin 260EF ==o ∴1EF =， ……………… 2分； ∴1122FG EF ==， ∵点G 是AB 的中点，3AB =，∴1322GB AB ==， ∴13222FB FG GB =+=+=， ……………… 3分；由勾股定理得，222EB EG GB =+，∴EB = ……………… 4分； ∴△BEF 的周长=3EF FB EB ++=……………… 5分. 解法三：∵矩形ABCD ，△DCE 是等边三角形，∴30ADF ECB ∠=∠=o，3ED EC ==，在Rt △ADF 中，90A ∠=o，AD = ∴tan AFADF AD∠=，tan 30==o ∴1AF =，H F E D CBA 第20题图G∴312FB AB AF =-=-=，2FD =， ……………… 1分； ∴321EF ED DF =-=-=， ……………… 2分； 过点B 作BG CE ⊥，交CE 于点G . ……………… 3分； 在Rt △BCG 中，90BGC ∠=o，BC =，30ECB ∠=o ，∴122BG BC ==，cos GC BCG BC ∠=，cos 302==o ， ∴32GC =， ∴33322GE EC GC =-=-=，由勾股定理得，222EB EG GB =+，或BG 是线段EC 的垂直平分线，∴EB =BE =BC ， ………… 4分； ∴△BEF 的周长=3EF FB EB ++=……………… 5分.21． (1)证明：连接OD.∵OD OA =，∴OAD ODA ∠=∠，∵AD 平分BAC ∠，∴BAD CAD ∠=∠，∴ODA CAD ∠=∠， ……………… 1分； ∴AE ∥OD ， ∵DE AE ⊥， ∴ED DO ⊥，∵点D 在⊙O 上，∴ED 是⊙O 的切线； ……………… 2分；（2）解法一：连接CB ,过点O 作OG AC ⊥于点G .…………… 3分； ∵ AB 是⊙O 的直径， ∴90ACB ∠=o， ∵OG AC ⊥，第21题图G 第20题图ABCDEF∴OG ∥CB ， ∴AG ACAO AB=， ∵5AC =3AB ，∴35AG AO =， ……………… 4分； 设35AG x AO x ==，， ∵DE AE ⊥，ED DO ⊥， ∴四边形EGOD 是矩形， ∴EG OD =，AE ∥OD ，∴5DO x =，5GE x =，8AE x =, ∴△AEF ∽△DFO ，∴EF AEFO OD =， ∴85EF FO = ， ∴135EO FO =. ……………… 5分．解法二：连接CB ,过点A 作AH DO ⊥交DO 的延长线于点H . ………… 3分； ∵DE AE ⊥，ED DO ⊥， ∴四边形AHDE 是矩形， ∴EA DH =，AE ∥HD ，AH ∥ED ，∴CAB AOH ∠=∠， ∵ AB 是⊙O 的直径， ∴90ACB ∠=o， ∴ACB AHO ∠=∠， ∴△AHO ∽△BCA ， ∴OH ACAO AB=， ∵5AC =3AB ，∴35OH AO =， ……………… 4分； 设35OH x AO x ==，，第21题图∴5DO x =，8AE DH x ==, ∵AE ∥HD ，∴△AEF ∽△DFO ，∴EF AEFO OD =， ∴85EF FO = ， ∴135EO FO =. ……………… 5分． 解法三：连接CB ,分别延长AB 、ED 交于点G . ………… 3分； ∵DE AE ⊥，ED DO ⊥， ∴AE ∥OD ，90ODG ∠=o ，∴CAB DOG ∠=∠， ∵ AB 是⊙O 的直径， ∴90ACB ∠=o ， ∴ACB ODG ∠=∠， ∴△GDO ∽△BCA ， ∴OD ACOG AB=， ∵5AC =3AB ，∴35OD OG =， ……………… 4分； 设35OD x OG x ==，，∴5AO x =，8AG AO OG x =+=, ∵AE ∥OD ，∴△AEG ∽△ODG ，△AEF ∽△DFO ，∴ AG AEOG OD= ， EF AE FO OD =， ∴85EF FO = ， ∴135EO FO =. ……………… 5分. 22.(1)第21题图画图正确； 每图各1分，共3分；(2)面积关系是 S 1=S 2=S 3 ； ……………… 4分； 周长关系是 l 1>l 2>3l ． ……………… 5分. 五、解答题： 23.解：(1)令0y =，则()22140x k x k -++=解方程得：2x k =或2x =， ……………… 1分； 由题意得：()20A k ，，()20B ，， ∴ 31222-k <<-， ∴3144k -<<-. ……………… 2分；(2)令0x =，则4y k =， ∴()04M k ，， ∵OM OB =，∴ 42k -=， ……………… 3分； ∴ 12k =-， ∴22y x x =--. (4)分；或∵OM OB =，()20B ，， ∴()0M ，-2，把点M 的坐标分别代入()2214y x k x k =-++中，∴42k =-， ……………… 3分； ∴ 12k =-，∴22y x x =--. (4)分；(3)2，5，5. （每个答案各1分） ……………… 7分． 24． 解：（1）过点A 作AG BC ⊥于点G . ∵∠ADB=60°，2AD =， ∴1DG =，AG ∴ 3GB =，∴tan 3AG ABG BG ∠==， ∴30ABG ∠=o，AB = ……………… 1分； ∵ △ABC 是等边三角形，∴ 90DBC ∠=o，BC = ……………… 2分；由勾股定理得：CD ===…… 3分；（2）作60EAD ∠=o，且使AE AD =，连接ED 、EB . ………… 4分；∴△AED 是等边三角形，∴AE AD =，60EAD ∠=o，∵ △ABC 是等边三角形，∴AB AC =，60BAC ∠=o，∴EAD DAB BAC DAB ∠+∠=∠+∠， 即EAB DAC ∠=∠，∴△EAB ≌△DAC . ……………… 5分； ∴EB =DC .当点E 、D 、B 在同一直线上时，EB 最大，∴246EB =+=， ……………… 6分； ∴ CD 的最大值为6，此时120ADB ∠=o. (7)分.另解：作60DBF ∠=o，且使BF BD =，连接DF 、AF .参照上面解法给分. 25．G第24题图D CBA 第24题图ECBA FABCD第24题图解：（1）由题意得：()10A -，，()30B ，，()03-D ，，()10M ，. ∴2AM BM CM ===，∴OC =∴(0C∵GC 是⊙M 的切线， ∴90GCM ∠=o∴cos OM MCOMC MC MG∠==， ……………… 1分； ∴122MG=， ∴4MG =，∴()30G -，，∴直线GC的表达式为y x =……………… 2分； （2）设过点D 的直线表达式为3y kx =-，∴2323,y kx y x x =-⎧⎨=--⎩，∴()220x k x -+=，或1202x x k ==+，0)]2([2=+-=∆k ，或12x x =， (3)分；∴2k =-，∴ 过点D 的“蛋圆”的切线的表达式为23y x =--. (4)分；（3）假设点E 在x 轴上方的“蛋圆”上，设()E m n ，，则点F 的坐标为()m n -，. EF 与x 轴交于点H ，连接EM . ∴222HM EH EM +=，∴()2214m n -+=，……① ………… 5分；∵点F 在二次函数223y x x =--的图象上，∴223m m n --=-，……②解由①②组成的方程组得：11m n ⎧=+⎪⎨=⎪⎩11m n ⎧=⎪⎨=⎪⎩0n =舍去)……………… 6分；由对称性可得：11m n ⎧=+⎪⎨=-⎪⎩11m n ⎧=⎪⎨=-⎪⎩……………… 7分；∴()11E +，()21E ，()311E -，()411E -. (8)分.。

2024北京平谷初三一模数 学一、选择题（共16分，每题2分）第1—8题均有四个选项，符合题意的选项只有一个．1. 从水利部长江水利委员会获悉，截止2024年3月24日，南水北调中线一期工程自2014年12月全面通水以来，已累计调水700亿立方米．其中70 000 000 000用科学记数法表示为( ) A ．8710⨯B ．9710⨯C ．10710⨯D ．11710⨯2. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A. B. C. D.3. 如图，点C 为直线AB 上一点，CD ⊥CE ，若∠1=65°，则∠2的度数是 A.15° B.25° C.35° D.4. 已知1x −＜＜0，下列四个结论中，错误的是 A. x ＜1 B. 0x −＞ C. 1x −＞ D.x+1＞05. 如果正多边形的每个内角都是120°，则它的边数为（ ） A. 5B. 6C. 7D.86. 先后两次抛掷同一枚质地均匀的硬币，则两次都是正面向上的概率是（ ）A. 14B. 13C. 12D. 237.已知两组数据（1）3005,3005,3003,3000,2994；（2）5,5,3,0，-6，设第一组数据的平均值为_1x ，方差为21s ，设第二组数据的平均值为_2x ，方差为22s ，下列结论正确的是：A.__221212,s x x s == B.__221212,s x x s >> C.__221212,s x x s => D.__221212,s x x s >=8. 如图，正方形ABCD 中，点E 、H 、G 、F 分别为AB 、BC 、CD 、AD 边上的点，点K 、M 、N 为对角线BD 上的点，四边形EKNF 和四边形MHCG 均为正方形，它们的面积分别表示为S 1，和S 2，给出下面三个结论：①12S S =；②2DF AF =；③12ABCD 9=S +2S 4S 正方形； A. ② B ①.③C. ②③D. ①②③上述结论中，所有正确结论的序号是（ ） 二、填空题（共16分，每题2分）659.x 的取值范围是______． 10. 分解因式：22x a a ax ++=__________________. 11.化简：3113x x x+−−的结果为 ． 12.写出一个大于1小于4的无理数： ． 13. 如图，反比例函数(0)ky k x=≠经过点A 、点B ，则m=______． 14.若关于x 的一元二次方程220x x k +=+有两个不相等的实数根，则k 的取值范围为_____.15. 如图，△ABC 内接于⊙O ，BC 为⊙O 的直径，D 为⊙O 上一点，连接AD 、DC 若∠D=20°，则ACB ∠的度数为______．16．某工艺坊加工一件艺术品，完成该任务共需A ，B ，C ，D ，E ，F 六道工序，其中A ，B 是前期准备阶段，C ，D ，E 是中期制作阶段，F 为最后的扫尾阶段，三个阶段不能改变顺序，也不能同时进行，但各阶段内的几个工序可以同时进行，完成各道工序所需时间如下表所示：在不考虑其它因素的前提下，加工该件艺术品最少需要_____________分钟；现因情况有变，需将加工时间缩短到30分钟．每道工序加工时间每缩短一分钟需要增加投入费用如上表，则所增加的投入最少是_____________元.三、解答题（共68分，第17—19题，每题5分，第20题，6分，第21题，5分，第22—23题，每题6分，第24—25题，每题5分，第26题6分；第27—28题，每题7分）解答应写出文字说明、演算步骤或证明过程.17. 计算：112cos3012−⎛⎫︒+− ⎪⎝⎭18．解不等式组：32162x x x x −⎧⎪⎨−+⎪⎩＞＜．19. 已知250,x x +−=求代数式(1)(x 1)x(2)x x +−++的值.20. 我国古代数学著作《九章算术》里记载了这样一个有趣的问题：“今有善行者行100步，不善行者60步.今不善行者先行100步，善行者追之，问几何步追之？”其意思是：走路快的人走100步时，走路慢的人只走了60步，现在走路慢的人先走100步，走路快的人去追他，问走路快的人走多少步能够追上他？请你解决该问题.21．在平面直角坐标系xOy 中，一次函数y ＝k x ＋b (k≠0)的图象由函数y x =的图象平移得到，且经过点(0，3)．（1）求这个一次函数的解析式；（2）当x ＞0时，对于x 的每一个值，一次函数12y x n =+的值小于函数y ＝k x ＋b (k≠0)的值且大于0，直接写出n 的取值范围．22.如图，Rt △ABC 中，∠ACB=90°，点D 、E 分别是BC 、AB 边的中点，连接DE 并延长，使EF=2DE ，连接AF 、CE.（1）求证：四边形ACEF 是平行四边形； （2）若∠B=30°，求证：四边形ACEF 是菱形.23．如图，△ABC 内接于O ，∠ACB=45°，连接OA ，过B 作O 的切线交AC 的延长线于点D ，． （1）求证：D OAD ∠=∠；（2）若BC =tanD 34=，求O 半径的长．24.光合作用是指在光的照射下，植物将二氧化碳和水转化为有机物，并产生氧气的过程，呼吸作用指的是植物将有机物和氧气分解成二氧化碳和水以维持植物生命所必要的过程，光合作用产氧速率与呼吸作用耗氧速率差距越大越利于有机物的积累，植物生长越快，水果的品质越好.下表是某农科院为了更好的指导果农种植草莓，在0℃至50℃气温，水资源及光照充分的条件下，对温度对光合作用和呼吸作用的影响进行研究的相关数据：（1）通过观察表格数据可以看出，若设温度为x ，光合作用产氧速率、呼吸作用耗氧速率是这个自变量的函数.建立平面直角坐标系，描出表中各组数值所对应的点，下图中已经描出部分点，请补全其余点，并画出函数图象:（2）结合函数图象，解决问题:（结果取整）①最适合草莓生长的温度约为______℃；②当温度约在什么范围内时，呼吸作用耗氧速率大于光合作用产氧速率，呼吸作用成为植物的主要活动，植物生长缓慢.25．4月24日是中国的航天日.为了激发全民尤其是青少年崇尚科学、勇于创新的热情,某学校在七、八年级进行了一次航天知识竞赛，现从七、八年级参加该活动的学生的成绩中各随机抽取20个数据，分别对这20个数据进行整理、描述和分析，下面给出了部分信息．a ．七年级参加活动的20名学生成绩的数据的频数分布直方图如下（数据分成5组：5060x ≤<，6070x ≤<，7080x ≤<，8090x ≤<，90100x ≤≤）；26.在平面直角坐标系xoy 中，抛物线2y x bx =−． （1）当抛物线过点（2,0）时，求抛物线的解析式；（2）若抛物线上存在两点11(x ,y )A 和22(x ,y )B ,若对于11x 2,≤≤2x 2b =+都有120y y <，求b 的取值范围．27.如图，在△ABC 中，∠BAC=90°，AB =A C ,点D 为BC 边中点，DE ⊥AB 于E ，作∠EDC 的平分线交AC 于点F ，过点E 作DF 的垂线交DF 于点G ，交BC 于点H.(1)依题意补全图形； (2)求证：DH=BE ；(3)判断线段FD 、HC 与BE 之间的数量关系，并证明.28. 平面直角坐标系xOy 中,已知⊙M 和平面上一点P ，若PA 切⊙M 于点A ，PB 切⊙M 于点B ，且90°≤∠APB ＜180°则称点P 为⊙M 的伴随双切点. （1）如果⊙O 的半径为2① 下列各点1(1)P −，02,(2)P −，23,(3,3)P 4,(1,2)P −− 是⊙O 的伴随双切点的是 ；② 直线y x b =+上存在点P 为⊙O 的伴随双切点，则b 的取值范 围 ；（2）已知：点E （1，2）、F （0，-2），过点F 作y 轴的垂线l ，点C （m ，0）是x 轴上一点，若直线l 上存在以CE 为直径的圆伴随双切点，直接写出m 的取值范围.参考答案一、选择题（本题共16分，每小题2分）二、填空题（本题共16分，每小题2分） 三、解答题（共68分，第17—19题，每题5分，第20题，6分，第21题，5分，第22—23题，每题6分，第24—25题，每题5分，第26题6分；第27—28题，每题7分）解答应写出文字说明、演算步骤或证明过程.17.解：112cos3012−⎛⎫︒++− ⎪⎝⎭=2212⨯++−−........................................................4 =1.. (5)18.解不等式组：32162x x x x −⎧⎪⎨−+⎪⎩＞＜解①得1x >−........................................................2 解②得4x <.. (4)14x ∴−<< (5)19.先化简，再求值：(1)(x 1)x(2)x x +−++2212x x x =−++........................................................2 2221x x =+−.. (3)22x 50,+x=5x x +−=∴........................................................4 10-19∴==原式.. (5)20. 解：设走路快的人走了x 步追上走路慢的人 (2)31005x x =+························································4 解得:x=250························································5 答：走路快的人250步追上走路慢的人 (6)（方法不唯一，其他方法依步骤给分）21.（1）∵一次函数y ＝k x ＋b (k≠0)的图象由函数y x =的图象平移得到∴k=1························································1 ∵经过点(0，3)∴b=3 (2)3y x ∴=+（2） 03n ∴≤≤时结论成立.························································5 22．解：（1）∵点D 、E 分别是BC 、AB 边的中点∴DE ∥AC ，且12DE AC =························································1 ∵EF=2DE∴EF=AC (2)∴四边形ACEF 是平行四边形 (3)（2）Rt △ABC 中，∵∠ACB=90°，E 为AB 中点， ∴12CE AB AE ==························································4 ∵∠B=30° ∴∠BAC=60°∴△AEC 是等边三角形························································5 ∴AC=EC∴四边形ACEF 是菱形 (6)23.（1）证明：连接OB ∵BD 是O 的切线∴∠OBD=90° (1)∵∠ACB=45°∴∠AOB=90°························································2 ∴OA ∥BD∴ADB OAD ∠=∠· (3)（2）过点B 作BH ⊥AD 于点H ∴∠AHB=∠DHB=90°∵∠ACB=45°，BC =∴BH=HC=4 (4)∵∠HBM+∠BMH=90° ∠OAM+∠AMO=90° ∠BMH=∠AMO ∴∠MBH=∠OAM=∠D4tanD 3=∴tan ∠MBH 34=∴MH=3，BM=5························································5 设O 的半径为x ∴OM=x-5∵△AOM ∽△BHM 354x x −∴=解得x=20 (6)24.解（1)补全函数图象 (2)(2)①最适合草莓生长的温度约为___36___℃；(33-37均可)························································3 ②064250x x ≤≤≤≤℃℃或℃℃(答案不唯一）························································5 25.(1)补全a 中频数分布直方图； (1)(2)88.5; 94.························································3 (3)435. (5)26.（1）抛物线的对称轴为x=b (1)∵抛物线过点（0,0）和（2,0）∴b=1 (2)∴抛物线的解析式为22y x x =− （2）∵抛物线的对称轴为x=b ，∴（b+2,0）点一定位于对称轴的右侧························································3 情况1：当原点位于对称轴的左侧时此时，有2222b b b +>⎧⎨<⎩解得12b <<························································4 情况2：当原点位于对称轴的右侧时此时，有220b b <+<解得22b b <⎧⎨<−⎩ 解得2b <− (5)综上， 1∴<b<2或b<-2 (6)27.(1)补全图形 (1)(2) 证明： ∵DF 平分∠EDC∴∠1=∠2∵DF ⊥EH∴∠EGD=∠HGD=90°∵∠1=∠2，DG=DG∴△EDG ≌△HDG (2)∴DE=DH∵∠BAC=90°，AB=AC∴∠B=45°∵ DE ⊥AB∴∠BED=90°∴ ∠B=∠EDB=45°∴DE=BE∴DH=BE (3)（3）222BE HC DF += (4)方法1：作DM ⊥AC 于M (5)∵CD=BD ，∠DMC=∠BED=90°，∠B=∠C=45°∴△BED ≌△CMD ∴DE=DM ，∵∠BAC=90°， DE ⊥AB∴DE ∥AC∴∠1＝∠3∵DF 平分∠EDC∴∠1=∠2∴∠2=∠3∴CD=CF (6)∵CM=DM=BE=DH∴CF-CM=CD-DH∴FM=HC在Rt △FDM 中∵222FM DM DF +=∴.222BE HC DF += (7)方法2：在CF 上截取CK=CH ，连接DK 并延长使DM=DK ，连接BM ，EM..........................................5 ∵CD=BD ，DK=DM ，∠KDC=∠BDM∴△KDC ≌△BMD ∴KC=BM ，∠C=∠4∴KC ∥BM∴∠ABM=∠BAC=90°∵∠BAC=90°， DE ⊥AB∴DE ∥AC∴∠1＝∠3∵DF 平分∠EDC∴∠1=∠2∴∠2=∠3∴CD=CF (6)∵ CK=CH∴FK=DH∴DE=FK∵ED ∥AC∴∠EDM=∠5∴△EMD ≌△FDK.∴DF=ME∴222BE HC DF +=.........................................7 方法3：连接AD ，在AB 上截取BM=AF ，连接DM. Rt △ABC 中，∠BAC=90°，D 为BC 中点 ∴AD=BD ，∠4=∠B=45°∵AF=BM∴△ADF ≌△BMD.........................................5 ∴DF=DM∵AB=AC ，BM=AF∴AB-BM=AC-AF∴AM=CF∵∠BAC=90°， DE ⊥AB∴DE ∥AC∴∠1＝∠3∵DF 平分∠EDC∴∠1=∠2∴∠2=∠3∴CD=CF (6)∴AM=CD∵DE ⊥AB ，∠BAD=45°∴AE=DE∴AE=DH∴ME=HC在Rt △EDM 中∵222EM DE DM +=∴222BE HC DF += (7)28．解：（1）①P 2，P 4； (2)②44b −≤≤ (4)（2）11m ≥+≤或m (7)。

2023年北京平谷区初三一模数学试卷一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个. 1.下面几何体中，是圆柱体的为ABCD2. 为了确保我国粮食种植的稳定性，国家提出了“严防死守18亿亩耕地的红线目标”，经过了多年的努力和坚守，我国耕地面积止住了下跌趋势，而且还实现了增长。

到2020年，全国耕地保有量回升至18.65亿亩以上，1865000000用科学计数法表示为A.71.86510⨯B. 818.6510⨯C. 91.86510⨯D. 121.86510⨯3.把一根细线固定在半圆形量角器的圆心处，细线的另一端系一个小重物，制成一个简单的测角仪，如图所示，细线与BC 边重合，则∠A 的度数为 A.30° B. 40°C. 50°D. 75°4.实数a 在数轴上的对应点的位置如图所示.若实数b 满足b a <-，则b 的值可以是A.1B. 0C.1-D.2-5.不透明的袋子中有三个小球，上面分别写着数字“1”“2”“3”，除数字外三个小球无其他差别.从中随机摸出一个小球，记录其数字，不放回，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为3的概率是 A.14 B.13 C.12 D.236.若关于x 的一元二次方程220x x m ++=有两个不相等的实数根，则实数m 的取值范围为 A.1m ≥B. 1m ≤C. 1m >D.1m <7.瓷器上的纹饰是中国古代传统文化的重要载体之一，如图所示的图片即为瓷器上的纹饰，该图形即为中心对称图形也为轴对称图形，该图形的对称轴的条数为 A.1B.2C.4D.58．摄氏温度（℃）与华氏温度（°F ）是表示温度的两种方法，它们的关系如下：若设摄氏温度（℃）为x ，华氏温度（°F ）为y ，y 与x 之间满足如下我们学习过的一种函数关系，则y 与x 满足的函数关系为 A. 正比例函数 B. 一次函数C. 反比例函数D. 二次函数第二部分 非选择题二、填空题（共16分，每题2分） 9.若61x -在实数范围内有意义，则实数x 的取值范围是___________. 10.分解因式：22mx mx m -+=___________. 11.方程31211x x =+-的解为___________. 12.写出一个比3大比4小的无理数___________.13.在平面直角坐标系xOy 中，反比例函数(0)ky k x=≠的图象过点(2,1)(m,2)A B --和，则m =_____14.为了提高大家的环境保护意识，某小区在假期开展了废旧电池回收的志愿者活动，该社区的10名中学生参与了该项活动，回收的旧电池数量如下表：15.如图，在ABC ∆中，∠C=90°，∠A=30°，BD 平分,ABC ∠1BCD S ∆=若，AB D S ∆=则__________.16.某货运公司临时接到一个任务，从工厂同时运送A 、B 两种货物各20箱到展馆，货运公司调派甲货车运送A 种货物，乙货车运送B 种货物，A 种货物每箱80千克，B 种货物每箱70千克，因为两种货物包装箱完全一样，装运工人一时疏忽两车虽然所装货物数量正确，但部分货物却装混了.运送途中安检时，两车过地秤，发现甲车比乙车的货物重160千克，则甲、乙两车各有_____箱货物装错,到达展馆，为了尽快把货物区分开，乙车司机借来了一台最多可以称300千克的秤，精选最优称重方案，根据被错装货物出现的所有可能情况，最多需要称_______次就能把乙车上装错的货物区分出来.三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程. 17.计算：0(2023)2sin 60271π-+-18.解不等式组：241,23.3x x x x +≥-⎧⎪+⎨<⎪⎩19.已知2210,x x +-=求代数式(2)(x 2)x(1)x x +-++的值.20.已知：如图，ABC ∆为锐角三角形.求作：以BC 为一边作Rt △MBC ，使∠MBC=90°，∠M=∠A. 作法：①作AC 边的垂直平分线DE ；②作BC 边的垂直平分线FG ，与直线DE 交于点O ； ③以O 为圆心，OA 为半径作O ；④连接CO 并延长，交O 于点M ，连接BM ；△MBC 即为所求作的三角形（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）； （2）完成下面的证明.证明：∵DE 是AC 的垂直平分线，FG 是BC 的垂直平分线,DE 与FG 交于点O ∴OA=OB=OC∴点A 、B 、C 都在O 上 ∵CM 为O 的直径 ∴MBC ∠= °.∵BC BC ⋂⋂= ∴M A ∠=∠（）（填推理依据）.∴△MBC 即为所求作的三角形.21.如图，在ABCD 中，点E 是BC 中点，点F 是AD 中点，连接AE 、CF 、EF ，EF 平分∠AEC. （1）求证：四边形AECF 是菱形；（2）连接AC 与EF 交于点O ，连接OD ，若AF=5，35sin FAC ∠=，求OD 的长.22.在平面直角坐标系xOy 中，函数(0)y kx b k =+≠的图象经过点(1,0),(0,1)-. （1）求该函数的解析式；（2）当2x >-时，对于x 的每一个值，函数2y x n =+的值大于函数(0)y kx b k =+≠的值，求n 的取值范围.23.明明学完了统计部分的相关知识后,对数据的统计产生了浓厚的兴趣,他从网上查阅了2023年3月1号至10号A 、B 两个城市的日最高气温数据,并对数据进行整理、描述和分析，下面给出了部分信息. a.A 、B 两个城市3月1号至10号的日最高气温数据的折线图：b.A 、B 两个城市3月1号至10号的日最高气温数据的平均数、中位数、众数、极差：（1）求表中m 、n 、z 的值；（2）记A 城市3月1号至10号的日最高气温的方差为21s ，B 城市3月1号至10号的日最高气温的方差为22s ，则21s _________22s （填“>”“<”或“=”）；（3）如果你是明明，请根据以上统计数据，对A 、B 两个城市3月1号至10号的日最高气温情况做简单的分析.（至少从两个方面进行说明）24.如图，AB 是⊙O 的直径，C 、D 是⊙O 上的两点，且DB DC =，过点D 作⊙O 的切线交AC 的延长线于点E .（1）求证：∠E=90°； （2）连接CD .若2cos 3ECD ∠=，9AB =，求CE 的长.25.如图所示，某农场的小麦收割机正在收割小麦，脱离后的谷粒沿着喷射管道飞出，飞行路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系，谷粒从喷射出到着陆的过程中，谷粒的竖直高度y （单位：m ）与距离喷射口的水平距离x （单位：m ）近似满足函数关系2()(0).y a x h k a =-+<（1）谷粒距离喷射口的水平距离x （单位：m ）与竖直高度y （单位：m ）的几组数据如下：的中心点，若货车车厢的中心点距地面1.9米，则货车车厢的中心点应距离喷射口几米？（2）谷粒喷出的同时石子等较重的杂质会跟随谷粒一起在重力作用下沿抛物线①被分离出来，谷皮和颗粒等较轻的杂质也会跟着谷粒一起沿抛物线②被分离出来，若已知两条抛物线的解析式分别为A ：20.09( 3.2) 4.42.y x =--+，B ：20.12( 2.8) 4.44.y x =--+则A 、B 对应的抛物线分别为A ： ；B （写①或②即可）26. 在平面直角坐标系xOy 中，点12(1,y ),(3,y )在抛物线222y x mx m =-+上.（1）求抛物线的对称轴用含（m 的式子表示）； （2）若12y y <，求m 的取值范围；（3若点00(,y )x 在抛物线上，若存在010,x -≤≤102,y y y <<使成立求m 的取值范围.27.在ABC ∆中，BD ⊥AC 于点D ，E 为AB 边中点，连接CE ，BD 与CE 相交于点F ，过E 作EM ⊥EF ，交线段BD 于点M ，连接CM.（1）依题意补全图形； （2）求证：∠EMF=∠ACF ；（3）判断BM 、CM 、AC 的数量关系，并证明.M，我们将点M的横纵坐标交换位置得到点N(n,m) 28.在平面直角坐标系xOy中，已知点(m,n)给出如下定义：对于平面上的点C，若满足NC=1，则称点C为点M的“对炫点”.（1）已知点A(2,0),①下列各点：Q1（0,1），Q2（1,1），Q3（-1,2）中是点A的“对炫点”的是;②点P是直线y=x+2上一点，若点A是点P的“对炫点”，求出点P的坐标；（3）设点A（a，b）是第一象限内一点，点P是直线y=x+b上一点，至少存在一个点P，使得点A 的“对炫点”也是点P的“对炫点”，求a、b的取值范围.平谷区2023年一模试卷评分标准 初 三 数 学 2023年4月一、选择题（本题共16分，每小题2分）三、解答题(本题共68分，第17-20、22、25题，每题5分，第21、23、24、26题，每题6分，第27-28题，每题7分)解答应写出文字说明、演算步骤或证明过程. 17.解：0(2023)2sin 60271π-+-=1+21- ..................................................................... 4 (5)18.解不等式组：241,23.3x x x x +≥-⎧⎪+⎨<⎪⎩解①得1x ≥- ······················································································· 2 解②得3x < ························································································ 4 13x ∴-≤< ······················································································ 5 19.先化简，再求值：(2)(x 2)x(1)x x +-++224x x x =-++ ···························································· (2)2=+- (3)x x2422+-=∴+= (4)x x x210,2x1∴==原式 (5)1-4-320. （1）尺规作图 (2)（2）90 (3)同弧（或等弧)所对的圆周角相等 (5)21．（1）证明：∵四边形ABCD是平行四边形∴AD∥BC，AD=BC (1)∵F是AD中点，E是BC中点∴AF∥EC，AF=EC∴四边形AECF是平行四边形 (2)∵EF平分∠AEC∴∠AEF=∠FEC∵AF∥EC∴∠AFE=∠FEC=∠AEF∴AE=AF∴四边形AECF是菱形 (3)（2）解：∵四边形AECF是菱形∴AO=OC，EO=FO，∠AOF=90° (4)∵EF=6∴FO=3∵AF=5∴AO=4 (5)∵AO=CO ，F 为AD 中点∴CD=2OF=6,CD ∥EF∴∠ACD=90°∵OC=4，CD=6∴OD== (6)22.∵一次函数(0)y kx b k =+≠的图象经过点（-1，0）和（0，1）∴01k b b -+=⎧⎨=⎩········································································· 1 ∴11k b =⎧⎨=⎩ ················································································ 2 1y x ∴=+（2） 当直线y=x+1中x=-2时，y=-1 ··················································· 3 当2y x n =+过点（-2,-1）时，n=3 ············································· 4 3n ∴≥时结论成立. ·........................................................................ 5 23.解：（1）m=12.5，n=14，z=15； . (3)（2）>； (4)(3)A 城市3月1日至10日日平均气温的平均值更高，极差较大，温度波动较大，不稳定， B 城市3月1日至10日日平均气温的平均值较小，极差小，温度变化较稳定。

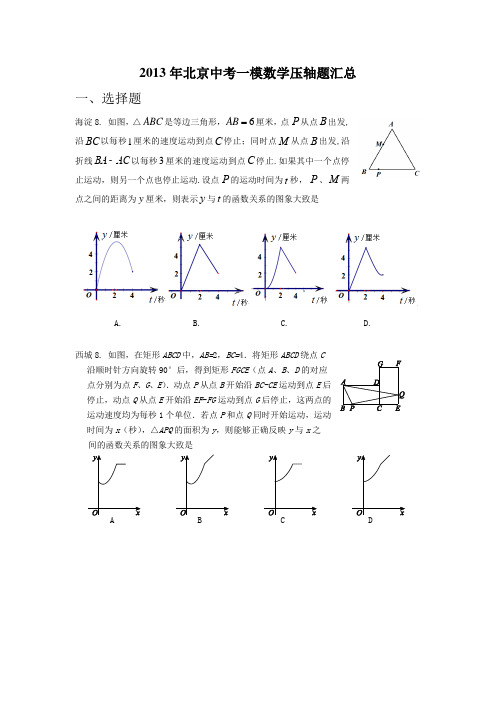
2013年北京中考一模数学压轴题汇总一、选择题海淀8. 如图，△ABC 是等边三角形，6AB 厘米，点从点B 出发,沿BC 以每秒1厘米的速度运动到点C 停止；同时点M 从点B 出发,沿折线BA -AC 以每秒3厘米的速度运动到点C 停止.如果其中一个点停止运动，则另一个点也停止运动.设点的运动时间为t 秒，、M 两点之间的距离为y 厘米，则表示y 与t 的函数关系的图象大致是A. B. C. D.西城8. 如图，在矩形ABCD 中，AB=2，BC=4．将矩形ABCD 绕点C 沿顺时针方向旋转90°后，得到矩形FGCE （点A 、B 、D 的对应点分别为点F 、G 、E ）．动点P 从点B 开始沿BC-CE 运动到点E 后停止，动点Q 从点E 开始沿EF -FG 运动到点G 后停止，这两点的运动速度均为每秒1个单位．若点P 和点Q 同时开始运动，运动时间为x （秒），△APQ 的面积为y ，则能够正确反映y 与x 之 间的函数关系的图象大致是P P P东城8. 如图，在边长为4的正方形ABCD中，动点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD 方向运动，当P运动到B点时，P，Q两点同时停止运动．设P点运动的时间为t，△APQ 的面积为S，则S与t的函数关系的图象是朝阳8．如图，将一张三角形纸片ABC折叠，使点A落在BC边上，折痕EF∥BC，得到△EFG；再继续将纸片沿△BEG的对称轴EM折叠，依照上述做法，再将△CFG折叠，最终得到矩形EMNF，折叠后的△EMG和△FNG的面积分别为1和2，则△ABC的面积为A. 6B. 9C. 12D. 18二、填空题海淀12. 如图1所示，圆上均匀分布着11个点12311,,,,A A A A .从A 1起每隔k 个点顺次连接，当再次与点A 1连接时，我们把所形成的图形称为“k +1阶正十一角星”，其中18k ≤≤（k 为正整数）.例如，图2是“2阶正十一角星”，那么1211A A A ∠+∠++∠= °；当1211A A A ∠+∠++∠= 900°时，k = .图1 图2西城12．在平面直角坐标系xOy 中，有一只电子青蛙在点A (1,0)处．第一次，它从点A 先向右跳跃1个单位，再向上跳跃1个单位到达点A 1； 第二次，它从点A 1先向左跳跃2个单位，再向下跳跃2个单位到达点A 2； 第三次，它从点A 2先向右跳跃3个单位，再向上跳跃3个单位到达点A 3； 第四次，它从点A 3先向左跳跃4个单位，再向下跳跃4个单位到达点A 4； ……依此规律进行，点A 6的坐标为 ；若点A n 的坐标为（2013，2012）， 则n = ．东城12. 在平面直角坐标系中，正方形ABCD 的位置如右图所示，点A 的坐标为（1，0），点D 的坐标为（0，2）．延长CB 交x 轴于点A 1，作正方形A 1B 1C 1C ；延长C 1B 1交x 轴于 点A 2，作正方形A 2B 2C 2C 1，…按这样的规律进行下去，第2013个正方形的面积为 ．朝阳12. 在平面直角坐标系xOy中，动点P从原点O出发，每次向上平行下一次平移．例如第1次平移后可能到达的点是（0，1）、（2，0），第2次平移后可能到达的点是（0，2）、（2，1）、（4，0），第3次平移后可能到达的点是（0，3）、（2，2）、（4，1）、（6，0），依此类推……．我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1，l1=3；第2次平移后可能到达的所有点的横、纵坐标之和为l2，l2=9；第3次平移后可能到达的所有点的横、纵坐标之和为l3，l3=18；按照这样的规律，l4= ；l n= (用含n的式子表示，n是正整数)．三、解答题 海淀22.问题：如图1，a 、b 、c 、d 是同一平面内的一组等距平行线（相邻平行线间的距离为1）.画出一个正方形ABCD ，使它的顶点A 、B 、C 、D 分别在直线a 、b 、d 、c 上，并计算它的边长.图1 图2小明的思考过程：他利用图1中的等距平行线构造了33⨯的正方形网格，得到了辅助正方形EFGH ，如图2所示, 再分别找到它的四条边的三等分点A 、B 、C 、D ，就可以画出一个满足题目要求的正方形.请回答：图2中正方形ABCD 的边长为 . 请参考小明的方法，解决下列问题：（1）请在图3的菱形网格（最小的菱形有一个内角为60︒，边长为1）中，画出一个等边△ABC ，使它的顶点A 、B 、C 落在格点上，且分别在直线a 、b 、c 上；（3）如图4，1l 、2l 、3l 是同一平面内的三条平行线，1l 、2l 之间的距离是215，2l 、3l 之间的距离是2110，等边△ABC 的三个顶点分别在1l 、2l 、3l 上，直接写出△ABC 的边长.图3 图4西城22．先阅读材料，再解答问题：小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图，点A、B、C、D均为⊙O上的点，则有∠C=∠D．小明还发现，若点E在⊙O外，且与点D在直线AB同侧，则有∠D>∠E．请你参考小明得出的结论，解答下列问题：(1) 如图1，在平面直角坐标系xOy中，点A的坐标为(0,7)，点B的坐标为(0,3)，点C的坐标为(3,0)．①在图1中作出△ABC的外接圆（保留必要的作图痕迹，不写作法）；②若在x轴的正半轴上有一点D，且∠ACB =∠ADB，则点D的坐标为；(2) 如图2，在平面直角坐标系xOy中，点A的坐标为(0,m)，点B的坐标为(0,n)，其中m>n>0．点P为x轴正半轴上的一个动点，当∠APB达到最大时，直接写出此时点P的坐标．东城22. 如图，在菱形纸片ABCD中，AB=4cm，∠ABC=120°，按下列步骤进行裁剪和拼图：第一步：如图1，在线段AD上任意取一点E，沿EB，EC剪下一个三角形纸片EBC(余下部分不再使用)；第二步：如图2，沿三角形EBC的中位线GH将纸片剪成两部分，并在线段GH上任意取一点M，线段BC上任意取一点N，沿MN将梯形纸片GBCH剪成两部分；第三步：如图3，将MN左侧纸片绕G点按顺时针方向旋转180°，使线段GB与GE重合，将MN右侧纸片绕H点按逆时针方向旋转180°，使线段HC与HE重合，再与三角形纸片EGH拼成一个与三角形纸片EBC面积相等的四边形纸片．(注：裁剪和拼图过程均无缝且不重叠)（1）请你在图3中画出拼接成的四边形；（2）直接写出拼成的四边形纸片周长的最小值为________cm，最大值为________cm．朝阳22．阅读下面材料：小雨遇到这样一个问题：如图1，直线l1∥l2∥l3，l1与l2之间的距离是1，l2与l3之间的距离是2，试画出一个等腰直角三角形ABC，使三个顶点分别在直线l1、l2、l3上，并求出所画等腰直角三角形ABC的面积．小雨是这样思考的：要想解决这个问题，首先应想办法利用平行线之间的距离，根据所求图形的性质尝试用旋转的方法构造全等三角形解决问题．具体作法如图2所示：在直线l1任取一点A，作AD⊥l2于点D，作∠DAH=90°，在AH上截取AE=AD，过点E作EB⊥AE交l3于点B，连接AB，作∠BAC=90°，交直线l2于点C，连接BC，即可得到等腰直角三角形ABC．请你回答：图2中等腰直角三角形ABC的面积等于．参考小雨同学的方法，解决下列问题：如图3，直线l1∥l2∥l3,l1与l2之间的距离是2，l2与l3 之间的距离是1,试画出一个等边三角形ABC，使三个顶点分别在直线l1、l2、l3上，并直接写出所画等边三角形ABC的面积（保留画图痕迹）．l1l2l3图3l1l2l3图1123图2海淀24．在△ABC 中，∠ACB ＝90︒．经过点B 的直线l （l 不与直线AB 重合）与直线BC 的夹角等于ABC ∠，分别过点C 、点A 作直线l 的垂线，垂足分别为点D 、点E ．（1）若45ABC ∠=︒，CD =1（如图），则AE 的长为 ； （2）写出线段AE 、CD 之间的数量关系，并加以证明； （3）若直线CE 、AB 交于点F ， 56CF EF =，CD =4，求BD 的长．西城24．在Rt △ABC 中，∠ACB =90°，∠ABC =α，点P 在△ABC 的内部．(1) 如图1，AB =2AC ，PB =3，点M 、N 分别在AB 、BC 边上，则cos α=_______， △PMN 周长的最小值为_______；(2) 如图2，若条件AB =2AC 不变，而P A =2，PB =10，PC =1，求△ABC 的面积； (3) 若P A =m ，PB =n ，PC =k ，且cos sin k m n αα==，直接写出∠APB 的度数．东城24. 问题1：如图1，在等腰梯形ABCD 中，AD ∥BC ，AB =BC =CD ，点M ，N 分别在AD ，CD 上，若∠MBN =12∠ABC ，试探究线段MN ，AM ，CN 有怎样的数量关系？请直接写出你的猜想，不用证明；问题2：如图2，在四边形ABCD 中，AB =BC ，∠ABC +∠ADC =180°，点M ，N 分别在DA ，CD 的延长线上，若∠MBN =12∠ABC 仍然成立，请你进一步探究线段MN ，AM ，CN 又有怎样的数量关系？写出你的猜想，并给予证明.朝阳24．在Rt △ABC 中，∠A =90°，D 、E 分别为AB 、AC 上的点．（1）如图1，CE =AB ，BD =AE ，过点C 作CF ∥EB ，且CF =EB ，连接DF 交EB 于点G ，连接BF ，请你直接写出EBDC 的值；（2）如图2，CE =kAB ，BD =kAE ，12EB DC ，求k 的值．图2B 图1FB海淀25. 在平面直角坐标系xOy 中，抛物线222y x mx m m =-++的顶点为C .(1) 求点C 的坐标（用含m 的代数式表示）；(2) 直线2y x =+与抛物线交于A 、B 两点，点A 在抛物线的对称轴左侧.①若P 为直线OC 上一动点，求△APB 的面积；②抛物线的对称轴与直线AB 交于点M ，作点B 关于直线MC 的对称点'B . 以M 为圆心，MC 为半径的圆上存在一点Q ，使得'QB 的值最小，则这个最小值为 .西城25．如图1，在平面直角坐标系xOy 中，直线l ：34y x m =+与x 轴、y 轴分别交于点A 和点B (0,-1)，抛物线212y x bx c =++经过点B ，且与直线l 的另一个交点为C (4,n )．(1) 求n 的值和抛物线的解析式；(2) 点D 在抛物线上，且点D 的横坐标为t （0< t <4）．DE ∥y 轴交直线l 于点E ，点F 在直线l 上，且四边形DFEG 为矩形（如图2）．若矩形DFEG 的周长为p ，求p 与t 的函数关系式以及p 的最大值；(3) M 是平面内一点，将△AOB 绕点M 沿逆时针方向旋转90°后，得到△A 1O 1B 1，点A 、O 、B 的对应点分别是点A 1、O 1、B 1．若△A 1O 1B 1的两个顶点恰好落在抛物线上，请直接写出点A 1的横坐标．．．．图1 图2东城25.在平面直角坐标系xOy 中，抛物线2229y x mx m =-+-与轴交于A ，B 两点（点A 在点B 的左侧，且OA ＜OB ），与y 轴的交点坐标为（0，－5）.点M 是线段AB 上的任意一点，过点M （a ，0）作直线MC ⊥x 轴，交抛物线于点C ，记点C 关于抛物线对称轴的对称点为D （C ，D 不重合），点P 是线段MC 上一点，连结CD ，BD ，PD .（1）求此抛物线的解析式；（2）当1a =时，问点P 在什么位置时，能使得PD ⊥BD ；（3）若点P 满足14MP MC =，作PE ⊥PD 交x 轴于点E ，问是否存在这样的点E ，使得PE =PD ，若存在，求出点E 的坐标；若不存在，请说明理由.朝阳25．如图，二次函数y =ax 2+2ax +4的图象与x 轴交于点A 、B ，与y 轴交于点C ，∠CBO 的正切值是2．(1)求此二次函数的解析式．(2)动直线l 从与直线AC 重合的位置出发，绕点A 顺时针旋转，与直线AB 重合时终止运动，直线l 与BC 交于点D ，P 是线段AD 的中点．①直接写出点P 所经过的路线长．②点D 与B 、C 不重合时，过点D 作DE ⊥AC 于点E 、作DF ⊥AB 于点F ，连接PE 、PF ，在旋转过程中，∠EPF 的大小是否发生变化？若不变，求∠EPF 的度数；若变化，请说明理由．③在②的条件下，连接EF ，求EF 的最小值．x。

2021年北京市平谷区中考数学一模试卷一．选择题（本题共16分，每小题2分）1．（2分）下列几何体中，主视图为三角形的是( )A ．B ．C ．D ．2．（2分）技术融合打破时空限制，2020服贸会全面上“云”，据悉本届服贸会共有境内外5372家企业搭建了线上电子展台，共举办32场纯线上会议和173场线上直播会议，线上发布项目1870个，发起在线洽谈550000次，将550000用科学记数法表示为( )A ．45510⨯B ．55.510⨯C ．65.510⨯D ．60.5510⨯3．（2分）如图，Rt ABC ∆中，90ACB ∠=︒，CD AB ⊥于点D ，则下列结论不一定成立的是( )A ．1290∠+∠=︒B ．23∠=∠C ．14∠=∠D ．130∠=︒4．（2分）2021年3月20日三星堆遗址的最新考古发现又一次让世界为之瞩目，下列三星堆文物图案中，既是中心对称图形又是轴对称图形的是( )A ．B ．C ．D ．5．（2分）正多边形每个内角都是120︒，则它的边数为( )A ．5B ．6C ．7D ．86．（2分）实数a ，b ，c 在数轴上的对应点的位置如图所示．若实数a ，b 满足0a b +=，则下列结论正确的是( )A ．0c =B ．0b <C ．0c >D ．0c <7．（2分）不透明袋子中有1个红球和2个绿球，这些球除颜色外无其他差别．从袋子中随机取出1个球，恰好是红球的概率为( )A ．13B ．12C ．23D ．18．（2分）学习完函数的有关知识之后，强强对函数产生了浓厚的兴趣，他利用绘图软件画出函数12y x =+的图象并对该函数的性质进行了探究．下面推断正确的是( ) ①该函数的定义域为2x ≠-；②该函数与x 轴没有交点；③该函数与y 轴交于点1(0,)2； ④若1(x ，1)y ，2(x ，2)y 是该函数上两点，当12x x <时，一定有12y y >．A ．①②③④B ．①③C ．①②③D ．②③④二、填空题（本题共16分，每小题2分）9．（22x -x 的取值范围是 ．10．（2分）分解因式：22ax ay -= ．11．（2210小的整数 ．12．（2分）计算111a -=+ ． 13．（2分）如图，在ABC ∆和ADC ∆中，AB BC ⊥，AD DC ⊥，只需添加一个条件即可证明ABC ADC ∆≅∆，这个条件可以是 （写出一个即可）．14．（2分）《孙子算经》中记载：“今有三人共车，二车空；二人共车，九人步．问人和车各几何？”其大意是：今有若干人乘车，每3人乘一车，最终剩余2辆空车，若每2人同乘一车，最终剩下9人因无车可乘而步行，问有多少人，多少辆车？设有x 辆车，y 个人，根据题意，可列方程组为 ．15．（2分）如图所示的网格是正方形网格，A ，B ，C ，D 是网格线交点，则ABO ∆的面积与CDO ∆的面积的大小关系为：ABO S ∆ CDO S ∆（填“>”，“ =”或“<” )．16．（2分）某种预防病虫害的农药即将于三月上旬喷洒，需要连续三天完成，又知当最低温度不低于0摄氏度，且昼夜温差不大于10摄氏度时药物效果最佳，为此农广站工作人员查看了三月上旬天气预报，请你结合气温图给出一条合理建议，药剂喷洒可以安排在 日开始进行．三、解答题（本题共68分，第17-22题，每小题5分，第23-26题，每小题5分，第27-28题，每小题5分）解答应写出文字说明、演算步骤或证明过程.17．（5分）计算：11()12|32|3tan302-+++︒． 18．（5分）解不等式组：31232x x x x +>⎧⎪⎨+⎪⎩．19．（5分）先化简，再求值：2210x x +-=，求代数式(1)(1)2(3)x x x -++-的值．20．（5分）已知关于x 的一元二次方程2(1)0x k x k +++=．（1）求证：方程总有两个实数根；（2）选择一个你喜欢的k 值代入，并求此时方程的解．21．（5分）已知：如图，(045)MAN αα∠=︒<<︒．求作：ABC ∆，使得2ABC BAC ∠=∠，作法：①在射线AN 上取点O ，以点O 为圆心，OA 长为半径画圆，交射线AM 于点C ； ②连接CO ；③以点C 为圆心，CO 长为半径画弧，交射线AN 于点B ；连接CB ，ABC ∆就是所求作．（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；（2）完成下面的证明证明：点C 、A 在O 上．2(COB CAB ∴∠=∠ )（填推理依据）．CB CO =，CBA ∴∠= ．2CBA CAB ∴∠=∠．22．（5分）已知：直线1:l y kx b =+过点(1,0)A -，且与双曲线22:l y x =相交于点(,2)B m ． （1）求m 值及直线1l 的解析式；（2）画出1l ，2l 的图象，结合图象直接写出不等式2kx b x+>的解集．23．（6分）如图，Rt ABC ∆中，90ABC ∠=︒，D 是AC 的中点，连接BD ，过点C 作//CE BD ，过B 作//BE AC ，两直线相交于点E ．（1）求证：四边形DBEC 是菱形；（2）若30A ∠=︒，2BC =，求四边形DBEC 的面积．24．（6分）如图，点E 是O 中弦AB 的中点，过点E 作O 的直径CD ，P 是O 上一点，过点P 作O 的切线，与AB 的延长线交于F ，与CD 的延长线交于点G ，连接CP 与AB 交于点M ．（1）求证：FM FP =；（2）若点P 是FG 的中点，3cos 5F ∠=，O 半径长为3，求EM 长．25．（6分）“十三五”时期是北京市迄今为止大气污染治理力度最大，成效最明显的五年，2020年空气质量优良天数继续增加，大气主要污染物中细颗粒物 2.5()PM 年均浓度首次实现38微克/立方米，空气质量改善取得标志性、历史性突破．下面对20132020-年北京市的空气质量有关数据进行收集、整理、描述和分析，给出了部分信息：.20132020a -年北京市空气质量指数为优良级别天数变化：b ．收集了2021年3月北京市16个城区的 2.5PM 的浓度均值（单位：微克/立方米）:79 79 80 81 83 79 83 83 81 83 84 84 84 84 86 84．并整理如表： 2.5PM 的浓度 7980 81 83 84 86 区的个数m 1 2 n 5 1 .2021C 年3月北京市每日的 2.5PM 的浓度（单位：微克/立方米）统计情况如下：（1）2020年北京市空气质量优良天数比2013年增加了 天； （2）m 的值为 ；n 的值为 ；（3）2021年3月北京市16个城区的 2.5PM 浓度值的中位数是 ；（4）依据2021年3月北京市每日的 2.5PM 的浓度情况统计图，若三月上旬(115-日）北京市的 2.5PM 的浓度平均值为1x ，方差为21S ，三月下旬(1631-日）北京市的 2.5PM 的浓度平均值为2x ，方差为22S ，则1x 2x ，21S 22S （填“>”，“ =”或“<” )．26．（6分）已知关于x 的二次函数223y x mx =--．（1）当抛物线过点(2,3)-时，求抛物线的表达式，并求它与y 轴的交点坐标；（2）求这个二次函数的对称轴（用含m 的式子表示）；（3）若抛物线上存在两点(,)A a a 和(,)B b b -，当0a <，0b >时，总有0a b +>，求m 的取值范围．27．（7分）在ABC ∆中，90ACB ∠=︒，AC BC =，D 是直线AB 上一点（点D 不与点A 、B 重合），连接DC 并延长到E ，使得CE CD =，过点E 作EF ⊥直线BC ，交直线BC 于点F ．（1）如图1，当点D 为线段AB 的上任意一点时，用等式表示线段EF 、CF 、AC 的数量关系，并证明；（2）如图2，当点D 为线段BA 的延长线上一点时，依题意补全图2，猜想线段EF 、CF 、AC 的数量关系是否发生改变，并证明．28．（7分）已知点P 、Q 分别为图形M 和图形N 上的任意点，若存在点P 、Q 使得1PQ =，我们就称图形M 、N 为友好图形，P 、Q 为关于图形M 、N 的一对友好点．（1）已知点(1,0)A ，1(0,)2B ，(1,1)C -中， 与点O 为一对友好点； （2）已知O 半径1r =，若直线y x b =+与O 有且只有一对友好点，求b 的值；（3）已知点(,2)D m ，D 半径1r =，若直线y x m =+与D 是友好图形，求m 的取值范围．2021年北京市平谷区中考数学一模试卷参考答案与试题解析一．选择题（本题共16分，每小题2分）1．（2分）下列几何体中，主视图为三角形的是( )A ．B ．C ．D ．【解答】解：A 、主视图是三角形，故此选项符合题意；B 、主视图是矩形，故此选项不合题意；C 、主视图是圆，故此选项不合题意；D 、主视图是矩形，故此选项不合题意；故选：A ．2．（2分）技术融合打破时空限制，2020服贸会全面上“云”，据悉本届服贸会共有境内外5372家企业搭建了线上电子展台，共举办32场纯线上会议和173场线上直播会议，线上发布项目1870个，发起在线洽谈550000次，将550000用科学记数法表示为( )A ．45510⨯B ．55.510⨯C ．65.510⨯D ．60.5510⨯【解答】解：将550000用科学记数法表示是55.510⨯．故选：B ．3．（2分）如图，Rt ABC ∆中，90ACB ∠=︒，CD AB ⊥于点D ，则下列结论不一定成立的是( )A ．1290∠+∠=︒B ．23∠=∠C ．14∠=∠D ．130∠=︒【解答】解：A ．90ACB ∠=︒，1290∴∠+∠=︒，故本选项不符合题意；B ．CD AB ⊥，90ADC ∴∠=︒，1390∴∠+∠=︒，∠+∠=︒，1290∴∠=∠，故本选项不符合题意；23C．CD AB⊥，∴∠=︒，BDC90∴∠+∠=︒，2490∠+∠=︒，1290∴∠=∠，故本选项不符合题意；14D．根据已知条件不能推出130∠=︒，故本选项符合题意；故选：D．4．（2分）2021年3月20日三星堆遗址的最新考古发现又一次让世界为之瞩目，下列三星堆文物图案中，既是中心对称图形又是轴对称图形的是()A．B．C．D．【解答】解：A、是轴对称图形，不是中心对称图形，故本选项不合题意；B、不是轴对称图形，是中心对称图形，故本选项不合题意；C、不是轴对称图形，也不是中心对称图形，故本选项不合题意；D、既是轴对称图形，又是中心对称图形，故本选项符合题意．故选：D．5．（2分）正多边形每个内角都是120︒，则它的边数为()A．5B．6C．7D．8【解答】解：设正多边形是n边形，由内角和公式得n n-︒=︒⨯，解得，6(2)180120n=，故选：B．6．（2分）实数a，b，c在数轴上的对应点的位置如图所示．若实数a，b满足0+=，a b则下列结论正确的是( )A ．0c =B ．0b <C ．0c >D ．0c <【解答】解：0a b +=． a ∴，b 互为相反数．所以原点是a ，b 对应点的中点． ∴点C 在原点左侧．0b ∴>，0c <．故选：D ．7．（2分）不透明袋子中有1个红球和2个绿球，这些球除颜色外无其他差别．从袋子中随机取出1个球，恰好是红球的概率为( )A ．13B ．12C ．23D ．1【解答】解：袋子中共有3个小球，其中红球有1个，∴摸出一个球是红球的概率是13，故选：A ．8．（2分）学习完函数的有关知识之后，强强对函数产生了浓厚的兴趣，他利用绘图软件画出函数12y x =+的图象并对该函数的性质进行了探究．下面推断正确的是( ) ①该函数的定义域为2x ≠-； ②该函数与x 轴没有交点；③该函数与y 轴交于点1(0,)2；④若1(x ，1)y ，2(x ，2)y 是该函数上两点，当12x x <时，一定有12y y >．A ．①②③④B ．①③C ．①②③D ．②③④【解答】解：由分母不为0可得，2x ≠-，即该函数的定义域为2x ≠-，故①正确； 由函数12y x =+的图象可得，图象与x 轴无交点，故②正确； 当0x =时，12y =，故该函数与y 轴交于点1(0,)2，故③正确； 由函数的图象可知，当122x x <-<时，有12y y <，故④不正确； 因此正确的结论有：①②③， 故选：C ．二、填空题（本题共16分，每小题2分）9．（22x -x 的取值范围是 2x ． 【解答】解：2x -20x ∴-， 2x ∴．故答案为2x ．10．（2分）分解因式：22ax ay -= ()()a x y x y +- ． 【解答】解：22ax ay -，22()a x y =-，()()a x y x y =+-．故答案为：()()a x y x y +-．11．（2210小的整数 2或3 ．【解答】解：21>，103>，∴22310<<<，即比2大且比10小的整数有两个是2和3． 故答案为：2或3． 12．（2分）计算111a -=+1a a + ． 【解答】解：原式1111a a a +=-++ 1a a =+ 故答案为：1a a + 13．（2分）如图，在ABC ∆和ADC ∆中，AB BC ⊥，AD DC ⊥，只需添加一个条件即可证明ABC ADC ∆≅∆，这个条件可以是 CB CD =（或AB AD =或ACB ACD ∠=∠或)BAC DAC ∠=∠ （写出一个即可）．【解答】解：AB BC ⊥，AD DC ⊥，90B D ∴∠=∠=︒， AC AC =，∴当添加CB CD =或AB AD =时，则可根据“HL ”判断ABC ADC ∆≅∆；当添加ACB ACD ∠=∠或BAC DAC ∠=∠时，则可根据“AAS ”判断ABC ADC ∆≅∆． 故答案为CB CD =（或AB AD =或ACB ACD ∠=∠或)BAC DAC ∠=∠．14．（2分）《孙子算经》中记载：“今有三人共车，二车空；二人共车，九人步．问人和车各几何？”其大意是：今有若干人乘车，每3人乘一车，最终剩余2辆空车，若每2人同乘一车，最终剩下9人因无车可乘而步行，问有多少人，多少辆车？设有x 辆车，y 个人，根据题意，可列方程组为 3(2)29x yx y -=⎧⎨+=⎩ ．【解答】解：依题意，得：3(2)29x yx y -=⎧⎨+=⎩．故答案为：3(2)29x yx y -=⎧⎨+=⎩．15．（2分）如图所示的网格是正方形网格，A ，B ，C ，D 是网格线交点，则ABO ∆的面积与CDO ∆的面积的大小关系为：ABO S ∆ = CDO S ∆（填“>”，“ =”或“<” )．【解答】解：设每个小正方形的边长为a ，由图可得，2533622ABC BEC ABE a a a aS S S a ∆∆∆⋅⋅=-=-=， 24362DCA a aS a ∆⋅==， ABC DCA S S ∆∆∴=，ABC ABO ACO S S S ∆∆∆=+，DCA CDO ACO S S S ∆∆∆=+， ABO CDO S S ∆∆∴=，故答案为：=．16．（2分）某种预防病虫害的农药即将于三月上旬喷洒，需要连续三天完成，又知当最低温度不低于0摄氏度，且昼夜温差不大于10摄氏度时药物效果最佳，为此农广站工作人员查看了三月上旬天气预报，请你结合气温图给出一条合理建议，药剂喷洒可以安排在 3或12 日开始进行．【解答】解：根据图象知：1日、2日、6日、7日最低温度低于0摄氏度， 9日、11日、15日昼夜温差大于10摄氏度，连续三天符合以上两条的有3日、4日、5日和12日、13日、14日， 故药剂喷洒可以安排在3日或12日开始进行， 故答案为：3或12．三、解答题（本题共68分，第17-22题，每小题5分，第23-26题，每小题5分，第27-28题，每小题5分）解答应写出文字说明、演算步骤或证明过程.17．（5分）计算：11()12|32|3tan302-+++︒．【解答】解：原式132323312=+ 223233=+4=．18．（5分）解不等式组：31232x x x x +>⎧⎪⎨+⎪⎩．【解答】解：解不等式312x x +>，得：1x >-， 解不等式32x x +，得：3x ， 则不等式组的解集为13x -<．19．（5分）先化简，再求值：2210x x +-=，求代数式(1)(1)2(3)x x x -++-的值． 【解答】解：原式2126x x =-+-227x x =+-， 2210x x +-=， 221x x ∴+=，则原式176=-=-．20．（5分）已知关于x 的一元二次方程2(1)0x k x k +++=． （1）求证：方程总有两个实数根；（2）选择一个你喜欢的k 值代入，并求此时方程的解． 【解答】解：（1）△22(1)4(1)0k k k =+-=-， ∴方程总有两个实数根（2）解：当0k =时，方程为20x x +=， 解方程得10x =，21x =-．21．（5分）已知：如图，(045)MAN αα∠=︒<<︒． 求作：ABC ∆，使得2ABC BAC ∠=∠，作法：①在射线AN 上取点O ，以点O 为圆心，OA 长为半径画圆，交射线AM 于点C ； ②连接CO ；③以点C 为圆心，CO 长为半径画弧，交射线AN 于点B ；连接CB ，ABC ∆就是所求作． （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）； （2）完成下面的证明 证明：点C 、A 在O 上．2(COB CAB ∴∠=∠ 一条弧所对圆周角是它所对的圆心角的一半 )（填推理依据）．CB CO =， CBA ∴∠= ． 2CBA CAB ∴∠=∠．【解答】解：（1）如图，ABC ∆为所作；（2）证明：点C 、A 在O 上．2COB CAB ∴∠=∠（一条弧所对圆周角是它所对的圆心角的一半）， CB CO =， CBA COB ∴∠=∠． 2CBA CAB ∴∠=∠．故答案为：一条弧所对圆周角是它所对的圆心角的一半，COB ∠． 22．（5分）已知：直线1:l y kx b =+过点(1,0)A -，且与双曲线22:l y x=相交于点(,2)B m ． （1）求m 值及直线1l 的解析式；（2）画出1l ，2l 的图象，结合图象直接写出不等式2kx b x+>的解集．【解答】解：（1）将点B的坐标代入反比例函数表达式的：22m=，解得1m=，故点B的坐标为(1,2)，(0)y kx b k=+≠过点(1,0)A-和(1,2)B，∴2k bk b-+=⎧⎨+=⎩，解得11bk=⎧⎨=⎩，1y x∴=+；（2）函数大致图象如下：从图象看，2kx bx+>的解集为1x>或20x-<<．23．（6分）如图，Rt ABC∆中，90ABC∠=︒，D是AC的中点，连接BD，过点C作//CE BD，过B作//BE AC，两直线相交于点E．（1）求证：四边形DBEC是菱形；（2）若30A∠=︒，2BC=，求四边形DBEC的面积．【解答】证明：（1）//CE BD ，//BE AC ， ∴四边形BECD 是平行四边形，90ABC ∠=︒，D 是AC 中点， BD DC ∴=，∴四边形DBEC 是菱形；（2）30A ∠=︒，90ABC ∠=︒，2BC =， 24AC BC ∴==，323AB BC ==，1112233222CDB ABC S S ∆∆∴==⨯⨯⨯=，四边形BECD 是菱形 223CDB DBEC S S ∆∴==菱形．24．（6分）如图，点E 是O 中弦AB 的中点，过点E 作O 的直径CD ，P 是O 上一点，过点P 作O 的切线，与AB 的延长线交于F ，与CD 的延长线交于点G ，连接CP 与AB 交于点M ．（1）求证：FM FP =；（2）若点P 是FG 的中点，3cos 5F ∠=，O 半径长为3，求EM 长．【解答】（1）证明：连接OP ，CD 为O 的直径，E 为弦AB 的中点， 90CEF ∴∠=︒，90C CME ∴∠+∠=︒， GF 是O 的切线， 90OPF ∴∠=︒， 90FPM OPC ∴∠+∠=︒， OC OP =， C OPC ∴∠=∠， FPM CME ∴∠=∠， CME FMP ∠=∠，FMP FPM ∴∠=∠， FM FP ∴=；（2）解：90OEF ∠=︒， 90G F ∴∠+∠=︒， 90GOP G ∠+∠=︒， GOP F ∴∠=∠，3cos cos 5GOP F ∴∠=∠=，即35OP OG =， 3OP =， 5OG ∴=，4PG ∴==， 点P 是FG 的中点， 4PF PG ∴==， 8GF ∴=，3cos 5F ∠=， ∴35EF FG =， 245EF ∴=， 45EM EF FM ∴===．25．（6分）“十三五”时期是北京市迄今为止大气污染治理力度最大，成效最明显的五年，2020年空气质量优良天数继续增加，大气主要污染物中细颗粒物 2.5()PM 年均浓度首次实现38微克/立方米，空气质量改善取得标志性、历史性突破．下面对20132020-年北京市的空气质量有关数据进行收集、整理、描述和分析，给出了部分信息： .20132020a -年北京市空气质量指数为优良级别天数变化：b ．收集了2021年3月北京市16个城区的 2.5PM 的浓度均值（单位：微克/立方米）:79 79 80 81 83 79 83 83 81 83 84 84 84 84 86 84．并整理如表： 2.5PM 的浓度79 80 81 83 84 86 区的个数m12n51.2021C 年3月北京市每日的 2.5PM 的浓度（单位：微克/立方米）统计情况如下：（1）2020年北京市空气质量优良天数比2013年增加了 100 天； （2）m 的值为 ；n 的值为 ；（3）2021年3月北京市16个城区的 2.5PM 浓度值的中位数是 ；（4）依据2021年3月北京市每日的 2.5PM 的浓度情况统计图，若三月上旬(115-日）北京市的 2.5PM 的浓度平均值为1x ，方差为21S ，三月下旬(1631-日）北京市的 2.5PM 的浓度平均值为2x ，方差为22S ，则1x 2x ，21S 22S （填“>”，“ =”或“<” )． 【解答】解：（1）已知2013年的优良天数为176，2020年的优良天数为276， 故2020年北京市空气质量优良天数比2013年增加了100天， 故答案为：100； （2）从b 中数据可知： 2.579PM =时有3个， 3m ∴=，2.583PM =时有4个， 4n ∴=，故答案为：3、4；（3）将该16个区域的 2.5PM 从小到大排列后为：79，79，79，80，81，81，83，83，83，83，84，84，84，84，84，86 中位数8383832+==，故答案为：83； （4）从c 中图表可知：三月上旬多在50~150之间，而三月下旬多在0~100之间， 故可直观推出12x x >，f 方差表示的是数据的离散趋势，离散越大，方差也越大，从c 图可看出三月上旬的变化幅度大，故2212s s >，故答案为：>．26．（6分）已知关于x 的二次函数223y x mx =--．（1）当抛物线过点(2,3)-时，求抛物线的表达式，并求它与y 轴的交点坐标； （2）求这个二次函数的对称轴（用含m 的式子表示）；（3）若抛物线上存在两点(,)A a a 和(,)B b b -，当0a <，0b >时，总有0a b +>，求m 的取值范围．【解答】解：（1）抛物线过点(2,3)-， 3443m ∴-=--， 1m ∴=，∴抛物线为：223y x x =--，令0x =，则3y =-， ∴抛物线与y 轴交点(0,3)-；（2）二次函数223y x mx =--，∴对称轴221mx m -=-=⨯； （3）0a b +>， b a ∴>-， 0a <，0b >，||||a b ∴<，点(,)A a a 和(,)B b b -是抛物线223y x mx =--上的两点， ∴抛物线的对称轴在y 轴的右侧，0m ∴>．27．（7分）在ABC ∆中，90ACB ∠=︒，AC BC =，D 是直线AB 上一点（点D 不与点A 、B 重合），连接DC 并延长到E ，使得CE CD =，过点E 作EF ⊥直线BC ，交直线BC 于点F ．（1）如图1，当点D 为线段AB 的上任意一点时，用等式表示线段EF 、CF 、AC 的数量关系，并证明；（2）如图2，当点D 为线段BA 的延长线上一点时，依题意补全图2，猜想线段EF 、CF 、AC 的数量关系是否发生改变，并证明．【解答】解：（1）结论：AC EF FC =+， 理由如下：过D 作DH CB ⊥于H ，EF CF ⊥，90EFC DHC ∴∠=∠=︒，在FEC ∆和HDC ∆中， 90EFC DHC FCE DCHEC CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ()FEC HDC AAS ∴∆≅∆，CH FC ∴=，DH EF =， 90DHB ∠=︒，45B ∠=︒，DH HB EF ∴==，AC BC CH BH FC EF ∴==+=+；（2）依题意补全图形，结论：EF FC AC =+， 理由如下：过D 作DH CB ⊥交CB 的延长线于H ， EF CF ⊥，90EFC DHC ∴∠=∠=︒，在FEC ∆和HDC ∆中， 90FCE DCH EFC DHC EC DC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ()FEC HDC AAS ∴∆≅∆，CH FC ∴=，DH EF =， 90DHB ∠=︒，45B ∠=︒，DH HB EF ∴==，EF CH BC FC AC ∴=+=+．28．（7分）已知点P 、Q 分别为图形M 和图形N 上的任意点，若存在点P 、Q 使得1PQ =，我们就称图形M 、N 为友好图形，P 、Q 为关于图形M 、N 的一对友好点．（1）已知点(1,0)A ，1(0,)2B ，(1,1)C -中， A 与点O 为一对友好点；（2）已知O 半径1r =，若直线y x b =+与O 有且只有一对友好点，求b 的值； （3）已知点(2)D m ，D 半径1r =，若直线y x m =+与D 是友好图形，求m 的取值范围．【解答】解：（1）(1,0)A ，1(0,)2B ，(1,1)C -，1OA ∴=，12OB =，2OC =， ∴点A 与O 是一对友好点．故答案为：A ．（2）如图1中，以O 为圆心，2为半径作O ．当直线y x b =+与大圆D 相切时，满足条件，此时直线经过(2A -，2)或(2B 2)， 22b ∴=或22-（3）当0m <时，以D 为圆心，2为半径作D ，当直线y x m =+与大圆D 相切时，设切点为Q ，交y 轴于(0,)m ，连接DQ 交y 轴于K ．则2KE m =+，2DK KQ +=，222m m ∴--=，2m ∴=-， 当0m >时此时有：22m m +- 32m ∴， 观察图像可知，满足条件的m 的值为：232m．。

2024北京市平谷区中考一模数学试题1．从水利部长江水利委员会获悉，截止2024年3月24日，南水北调中线一期工程自2014年12月全面通水以来，已累计调水700亿立方米．其中70000000000用科学记数法表示为（）A ．8710⨯B ．9710⨯C ．10710⨯D ．11710⨯2．下列图形中，既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．3．如图，点C 为直线AB 上一点，CD CE ⊥，若165∠=︒，则2∠的度数是（）A ．15︒B ．25︒C ．35︒D ．65︒4．已知10x -<<，下列四个结论中，错误的是（）A ．1x <B ．0x ->C ．1x ->D ．10x +>5．正多边形每个内角都是120°，则它的边数为（）A ．5B ．6C ．7D ．86．先后两次抛掷同一枚质地均匀的硬币，则两次都是正面向上的概率是（）A ．14B ．13C ．12D ．237．已知两组数据（1）3005，3005，3003，3000，2994；（2）5，5，3，0，6-．设第一组数据的平均值为1x ，方差为21s ，设第二组数据的平均值为2x ，方差为22s ，下列结论正确的是（）A ．12x x >，2212s s <B ．12x x >，2212s s >C ．12x x =，2212s s =D ．12x x >，2212s s =8．如图，正方形ABCD 中，点E 、H 、G 、F 分别为AB 、BC 、CD 、AD 边上的点，点K 、M 、N 为对角线BD 上的点，四边形EKNF 和四边形MHCG 均为正方形，它们的面积分别表示为1S 和2S ，给出下面三个结论：①12S S =；②2DF AF =；③12924ABCD S S S =+正方形．上述结论中，所有正确结论的序号是（）A ．②B ．①③C ．②③D ．①②③91x -x 的取值范围是．10．分解因式：22ab ab a ++=．11．化简：3311x x x+--的结果为．12．请写出一个大于1小于4的无理数.13．如图，反比例函数()0ky k x=≠经过点A 、点B ，则m =．14．关于x 的一元二次方程x 2+2x +k ＝0有两个不相等的实数根，则k 的取值范围是．15．如图，ABC 内接于O ，BC 为O 的直径，D 为O 上一点，连接AD CD 、．若20D ∠=︒，则ACB ∠的度数为．16．某工艺坊加工一件艺术品，完成该任务共需A ，B ，C ，D ，E ，F 六道工序，其中A ，B 是前期准备阶段，C ，D ，E 是中期制作阶段，F 为最后的扫尾阶段，三个阶段不能改变顺序，也不能同时进行，但各阶段内的几个工序可以同时进行，完成各道工序所需时间如下表所示：阶段准备阶段中期制作阶段扫尾阶段工序ABC D EF 所需时间/分钟1115201763加工时间每缩短一分钟需要增加投入费用/元100701008050不能缩短在不考虑其它因素的前提下，加工该件艺术品最少需要分钟；现因情况有变，需将加工时间缩短到30分钟．每道工序加工时间每缩短一分钟需要增加投入费用如上表，则所增加的投入最少是元．17．计算：112cos3031122-⎛⎫︒++-- ⎪⎝⎭．18．解不等式组：32162x x x x >-⎧⎪⎨<-+⎪⎩．19．已知250x x +-=，求代数式()()()112x x x x +-++的值．20．我国古代数学著作《九章算术》里记载了这样一个有趣的问题：“今有善行者行100步，不善行者60步．今不善行者先行100步，善行者追之，问几何步追之？”其意思是：走路快的人走100步时，走路慢的人只走了60步，现在走路慢的人先走100步，走路快的人去追他，问走路快的人走多少步能够追上他？请你解决该问题．21．在平面直角坐标系xOy 中，一次函数()0y kx b k =+≠的图象由函数y x =的图象平移得到，且经过点()0,3．(1)求这个一次函数的解析式；(2)当0x >时，对于x 的每一个值，一次函数12y x n =+的值小于函数()0y kx b k =+≠的值且大于0，直接写出n 的取值范围．22．如图，Rt ABC △中，90ACB ∠=︒，点D 、E 分别是BC AB 、边的中点，连接DE 并延长，使2EF DE =，连接AF CE 、．(1)求证：四边形ACEF 是平行四边形；(2)若30B ∠=︒，求证：四边形ACEF 是菱形．23．如图，ABC 内接于O ，45ACB ∠=︒，连接OA ，过B 作O 的切线交AC 的延长线于点D ．(1)求证：D OAD ∠=∠；(2)若BC =3tan4D =，求O 半径的长．24．光合作用是指在光的照射下，植物将二氧化碳和水转化为有机物，并产生氧气的过程，呼吸作用指的是植物将有机物和氧气分解成二氧化碳和水以维持植物生命所必要的过程，光合作用产氧速率与呼吸作用耗氧速率差距越大越利于有机物的积累，植物生长越快，水果的品质越好．下表是某农科院为了更好的指导果农种植草莓，在0℃至50℃气温，水资源及光照充分的条件下，对温度对光合作用和呼吸作用的影响进行研究的相关数据：温度（℃）5101520253035404550光合作用产氧速0.020.180.300.400.580.821.420.900.400.02率（2mol/m s μ）呼吸作用耗氧速率（2mol/m s μ）0.030.100.150.200.280.370.420.600.820.60(1)通过观察表格数据可以看出，若设温度为x ，光合作用产氧速率、呼吸作用耗氧速率是这个自变量的函数；建立平面直角坐标系，描出表中各组数值所对应的点，下图中已经描出部分点，请补全其余点，并画出函数图象；(2)结合函数图象，解决问题：（结果取整）①最适合草莓生长的温度约为______℃；②当温度约在什么范围内时，呼吸作用耗氧速率大于光合作用产氧速率，呼吸作用成为植物的主要活动，植物生长缓慢．25．4月24日是中国的航天日．为了激发全民尤其是青少年崇尚科学、勇于创新的热情，某学校在七、八年级进行了一次航天知识竞赛．现从七、八年级参加该活动的学生的成绩中各随机抽取20个数据，分别对这20个数据进行整理、描述和分析，下面给出了部分信息：a ．七年级参加活动的20名学生成绩的数据的频数分布直方图如下（数据分成5组：5060x ≤<，6070x ≤<，7080x ≤<，8090x ≤<，90100x ≤≤）；b ．七年级参加活动的20名学生成绩的数据在8090x ≤<这一组的是：84858586868889c ．八年级参加活动的20名学生成绩的数据如下：分数738182858891929496100人数1323131411根据以上信息，解答下列问题：(1)补全a 中频数分布直方图；(2)七年级参加活动的20名学生成绩的数据的中位数是______；八年级参加活动的20名学生成绩的数据的众数是______；(3)已知七八两个年级各有300名学生参加这次活动，若85分（含85分）以上算作优秀，估计这两个年级共有多少人达到了优秀．26．在平面直角坐标系xOy 中，抛物线22=-y x bx ．(1)当抛物线过点(2,0)时，求抛物线的解析式；(2)若抛物线上存在两点()11,A x y 和()22,B x y ，若对于112x ≤≤，22x b =+，都有120y y ⋅<，求b 的取值范围．27．如图，在ABC 中，90BAC ∠=︒，AB AC =，点D 为BC 边中点，DE AB ⊥于E ，作EDC ∠的平分线交AC 于点F ，过点E 作DF 的垂线交DF 于点G ，交BC 于点H ．(1)依题意补全图形；(2)求证：DH BE =；(3)判断线段FD 、HC 与BE 之间的数量关系，并证明．28．平面直角坐标系xOy 中，已知O 和平面上一点P ，若PA 切O 于点A ，PB 切O 于点B ，且90180APB ︒≤∠<︒，则称点P 为O 的伴随双切点．(1)如果O 的半径为2①下列各点()11,0P -，()22,2P -，()33,3P ，()41,2P --是O 的伴随双切点的是______；②直线y x b =+上存在点P 为O 的伴随双切点，则b 的取值范围______；(2)已知点()()1,20,2E F -、，过点F 作y 轴的垂线l ，点()0C m ，是x 轴上一点，若直线l 上存在以CE 为直径的圆的伴随双切点，直接写出m 的取值范围.参考答案：1．C【分析】本题考查科学记数法表示绝对值大于1的数，将70000000000写成10n a ⨯的形式即可，其中110a ≤<，n 的值与小数点移动位数相同．【详解】解：7000000000010710=⨯，故选C ．2．D【分析】本题主要考查了轴对称图形和中心对称图形的识别，根据中心对称图形的定义和轴对称图形的定义进行逐一判断即可：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；把一个图形绕着某一个点旋转180︒，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．【详解】解：A ．是轴对称图形不是中心对称图形，故该选项不符合题意；B ．是轴对称图形不是中心对称图形，故该选项不符合题意；C ．是中心对称图形不是轴对称图形，故该选项不符合题意；D ．既是轴对称图形又是中心对称图形，故该选项符合题意；故选：D ．3．B【分析】本题考查角的运算，垂线，平角的定义，解题的关键是熟练运用垂直的定义，平角的定义．根据垂直的定义可得90DCE ∠=︒，然后利用平角的定义即可求解．【详解】解： CD CE ⊥，∴90DCE ∠=︒，165∠=︒，∴21801180906525DCE ∠=︒-∠-∠=︒-︒-︒=︒，故选：B ．4．C【分析】本题主要考查了不等式的性质，绝对值，熟知不等式的性质是解题的关键：不等式两边同时加上或减去一个数或者式子，不等号不改变方向，不等式两边乘以乘以或除以一个正数，不等号不改变方向，不等式两边同时乘以或除以一个负数，不等号改变方向．根据不等式的性质逐一判断即可．【详解】解：由题意得：10x -<<，A 、1x <的解集为：11x -<<，故该选项正确，不符合题意；B 、0x ->，则0x <，故该选项正确，不符合题意；C 、1x ->，则1x <-，故该选项错误，符合题意；D 、10x +>，则1x >-，故该选项正确，不符合题意；故选：C ．5．B【分析】设所求正多边形边数为n ，根据内角与外角互为邻补角，可以求出外角的度数．根据任何多边形的外角和都是360度，由60°•n =360°，求解即可．【详解】解：设所求正多边形边数为n ，∵正n 边形的每个内角都等于120°，∴正n 边形的每个外角都等于180°-120°=60°．又因为多边形的外角和为360°，即60°•n =360°，∴n =6．故选：B【点睛】本题考查了多边形内角和外角的知识，解答本题的关键在于熟练掌握任何多边形的外角和都是360°并根据外角和求出正多边形的边数．6．A【分析】本题考查列表法与树状图法，列表可得出所有等可能的结果数以及两次都是正面向上的结果数，再利用概率公式可得出答案，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．【详解】解：列表如下：正反正正正正反反反正反反共有4种等可能的结果，其中两次都是正面向上的结果有1种，∴两次都是正面向上的概率为14．故选：A ．7．D【分析】本题考查了平均数的定义，方差的定义，解题的关键是掌握平均数的定义，方差的定义，先求出两组数据的平均数，再求出方差即可求解．【详解】解：（1）的平均数为：300523003300029943001.45⨯+++=，方差是：()()()()2222130053001.4230033001.430003001.429943001.417.045⎡⎤-⨯+-+-+-=⎣⎦，（2）的平均数是：523061.45⨯++-=，方差是：()()()()222215 1.423 1.40 1.46 1.417.045⎡⎤-⨯+-+-+--=⎣⎦，∴12x x >，2212s s =，故选：D ．8．C【分析】本题考查了正方形的性质，等腰直角三角形的性质，解题的关键是掌握正方形的性质．根据正方形的性质和等腰直角三角形的性质可得12BH CH MH BC ===，BK EK KN ==，DN KN =，进而得到133EK BD ==，根据正方形的面积公式即可判断①；根据DF =，E F F =，FN EF =，即可判断②；由212299ABCD S BC S ==正方形，221144ABCD S BC S ==正方形，可判断③．【详解】解：① 四边形ABCD 是正方形，∴45ABD CBD ∠=∠=︒，四边形EKNF 和四边形MHCG 均为正方形，∴90BHM CHM ∠=∠=︒，90BKE NKE ∠=∠=︒，∴BEK △和BMH V 都是等腰直角三角形，∴12BH CH MH BC ===，BK EK KN ==，同理可得DN KN =，∴133EK BD ==，∴2221239S EK BC ⎛⎫=== ⎪ ⎪⎝⎭，22221124S MH BC BC ⎛⎫=== ⎪⎝⎭，∴12S S ≠，故①错误；② AEF △和DFN △都是等腰直角三角形，∴DF =，EF =，四边形EKNF 为正方形，∴FN EF =，∴2DF AF =，故②正确；③由①知：212299ABCD S BC S ==正方形，221144ABCD S BC S ==正方形，∴122919244249ABCD ABCD ABCD S S S S S ++=⨯⨯=正方形正方形正方形，故③正确；故选：C ．9．x ＜1．【分析】根据二次根式的性质可以得到x -1是负数，由此即可求解．∴x -1＜0，∴x ＜1．实数x 的取值范围是x ＜1．故答案为：x ＜1．【点睛】此题主要考查了二次根式有意义的条件，根据被开方数是非负数即可解决问题．10．()21a b +【分析】先提取公因式，再用完全平方公式进行因式分解即可．【详解】解：()()2222211ab ab a a b b a b ++=++=+，故答案为：()21a b +．【点睛】本题主要考查了综合提取公因式和公式法进行因式分解，解题的关键是正确找出公因式，并掌握完全平方公式()2222a b a ab b ±=±+．11．3【分析】本题考查了分式的加减法．根据同分母的分式的加减法运算法则进行计算．【详解】解：3311x x x +--原式3311x x x =---331x x -=-()311x x -=-3=故答案为：3．12【分析】根据实数的大小关系，结合数轴和无理数的定义可分析出答案.只要是被开方数大于1而小于16，且不是完全平方数的都可．【详解】根据题意可知：大于1小于4的无理数有如π13．2【分析】本题主要考查反比例函数的图像与性质，解题的关键是熟知待定系数法确定函数关系式．把A 点坐标代入解析式求出k ，进而求出反比例函数的解析式，然后将3,2B m ⎛⎫ ⎪⎝⎭代入反比例函数的解析式即可．【详解】解：由图可知()3,1A --，3,2B m ⎛⎫ ⎪⎝⎭，将()3,1A --代入()0k y k x=≠，得：()()313k =-⨯-=，∴3y x=，将3,2B m ⎛⎫ ⎪⎝⎭代入得：332m =，解得：2m =，故答案为：2．14．k ＜1．【分析】由方程有两个不等实数根可得出关于k 的一元一次不等式，解不等式即可得出结论．【详解】∵关于x 的一元二次方程x 2+2x+k=0有两个不相等的实数根，∴△=2241k 0-⨯⨯>，解得：k 1<，故答案为k 1<.【点睛】本题考查了根的判别式以及解一元一次不等式，解题的关键是得出关于k 的一元一次不等式．熟知“在一元二次方程()2ax bx c 0a 0++=≠中，若方程有两个不相等的实数根，则△=2b 4ac 0->”是解答本题的关键.15．70︒/70度【分析】本题考查了直径所对的圆周角为直角，同弧所对的圆周角相等，三角形内角和定理等知识．熟练掌握直径所对的圆周角为直角，同弧所对的圆周角相等是解题的关键．由BC 为O 的直径，可得90BAC ∠=︒，由 AC AC =，可得20ABC D ∠=∠=︒，根据180ACB BAC ABC ∠=︒-∠-∠，计算求解即可．【详解】解：∵BC 为O 的直径，∴90BAC ∠=︒，∵ AC AC =，∴20ABC D ∠=∠=︒，∴18070ACB BAC ABC ∠=︒-∠-∠=︒，故答案为：70︒．16．38750【分析】本题考查了有理数的混合运算，理解题意是解题得到关键．求出各个阶段的工序最长时间和即可求出加工该件艺术品最少需要的时间；在准备阶段若缩短4分钟，在制作阶段若缩短3分钟，最后1分钟则看两个阶段谁投入的费用少，即可求解．【详解】解： 一共有三个阶段，各阶段内的几个工序可以同时进行，则加工该件艺术品最少需要：1520338++=（分钟）；需将加工时间缩短到30分钟，则共需要缩短8分钟，在准备阶段若缩短4分钟，则需要投入470280⨯=（元），在制作阶段若缩短3分钟，则需要投入3100300⨯=（元），还要1分钟，在准备阶段缩短1分钟需要投入10070170+=（元），在制作阶段缩短1分钟需要投入10080180+=（元），170180<，综上，最少投入为：280300170750++=（元），故答案为：38，750．17．1【分析】本题考查了含三角函数的混合运算，解题的关键是掌握相关的运算法则．先算三角函数、负整数指数幂、绝对值和二次根式，再算加减即可．【详解】解：112cos3012-⎛⎫︒++- ⎪⎝⎭=2212+--=118．14x -<<【分析】本题考查的是解一元一次不等式组，分别求出各不等式的解集，再求出其公共解集即可．熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．【详解】解：32162x x x x >-⎧⎪⎨<-+⎪⎩①②，解由①得，1x >-，由②得，4x <，∴14x -<<．19．9【分析】本题考查了整式的化简求值，先根据平方差公式和单项式乘多项式展开，再合并同类项，然后将250x x +-=变形为25x x +=，最后代入计算即可．【详解】解：()()()112x x x x +-++2212x x x=-++2221x x =+-()221x x =+-250x x +-= 25x x ∴+=∴原式2519=⨯-=．20．250步【分析】本题主要考查了一元一次方程的实际应用，设走路快的人走了x 步追上走路慢的人，根据走路快的人走100步时，走路慢的人只走了60步，可知相同时间内走路慢的人所走路程为60100x 步，据此列出方程求解即可．【详解】解：设走路快的人走了x 步追上走路慢的人．由题意得，60100100x x =+解得：250x =，答：走路快的人250步追上走路慢的人21．(1)3y x =+(2)03n ≤≤【分析】本题考查一次函数图象的平移，求一次函数解析式，一次函数与不等式等知识．利用数形结合的思想是解题关键．（1）由题意结合函数图象平移的特点可得出1k =，再将()0,3代入，求出b 的值即可；（2）画出大致图形，结合图形即得出当03n ≤≤时，当0x >时，对于x 的每一个值，一次函数12y x n =+的值小于函数3y x =+的值且大于0．【详解】（1）解：∵一次函数()0y kx b k =+≠的图象由函数y x =的图象平移得到，∴1k =，∴y x b =+．∵该一次函数经过点()0,3，∴30b =+，即3b =，∴这个一次函数的解析式为3y x =+；（2）解：如图，由图可知当03n ≤≤时，当0x >时，对于x 的每一个值，一次函数12y x n =+的值小于函数3y x =+的值且大于0，∴n 的取值范围是03n ≤≤．22．(1)见解析(2)见解析【分析】（1）由点D 、E 分别是BC AB 、边的中点，可得∥DE AC ，且12DE AC =，则EF AC =，进而可证四边形ACEF 是平行四边形；（2）由E 为AB 中点，可得12CE AB AE ==，由30B ∠=︒，可得60BAC ∠=︒，证明AEC △是等边三角形，则AC EC =，进而可证四边形ACEF 是菱形．【详解】（1）证明：∵点D 、E 分别是BC AB 、边的中点，∴∥DE AC ，且12DE AC =，∵2EF DE =，∴EF AC =，∴四边形ACEF 是平行四边形；（2）证明：Rt ABC △中，90ACB ∠=︒，E 为AB 中点，∴12CE AB AE ==，∵30B ∠=︒，∴60BAC ∠=︒，∴AEC △是等边三角形，∴AC EC =，∴四边形ACEF 是菱形．【点睛】本题考查了中位线，平行四边形的判定，直角三角形斜边的中线等于斜边的一半，等边三角形的判定与性质，菱形的判定等知识．熟练掌握中位线，平行四边形的判定，直角三角形斜边的中线等于斜边的一半，等边三角形的判定与性质，菱形的判定是解题的关键．23．(1)见解析(2)20【分析】（1）连接OB ，根据圆周角定理可得90AOB ∠=︒，然后利用平行线的性质即可解答；（2）过点B 作BH AD ⊥于点H ，直角三角形的性质以及勾股定理，得4BH HC ==，再证明MBH OAM D ∠=∠=∠即可．【详解】（1）证明：连接OB ，∵BD 是O 的切线，90OBD ∴∠=︒，45ACB =︒∠ ，90AOB OBD ∴∠=∠=︒，OA BD ∴∥，∴D OAD ∠=∠；（2）解：过点B 作BH AD ⊥于点H ，90AHB DHB ∴∠=∠=︒，∵45ACB ∠=︒，BC =ACB HBC ∴∠∠=，BH HC ∴=，222BH HC BC +=，4BH HC ∴==，90HBM BMH ∠+∠=︒ ，90OAM AMO ∠∠=︒＋，BMH AMO ∠=∠，MBH OAM D ∴∠=∠=∠，3tan 4D = ，3tan 4MBH ∴∠=，35MH BM ∴==，，设O 的半径为x ，5OM x ∴=-，53tan tan 4OM x OAM D OA x -∴∠====，解得20x =，O ∴ 半径的长20．【点睛】本题考查切线的性质，圆周角定理，三角函数，掌握切线的判定方法和性质，圆周角定理正确解答的关键．24．(1)见解析(2)①35；②57x ≤<或4250x <≤【分析】本题考查了函数的应用，描点并作出函数图象是解题的关键．（1）描点并用光滑的曲线连接起来即可；（2）①根据图象，光合作用产氧速率与呼吸作用耗氧速率差距最大时对应的温度最适合草莓生长；②根据图象作答即可．【详解】（1）解：描点及图象如图所示：（2）①由图象可知，当35x =时，光合作用产氧速率与呼吸作用耗氧速率差距最大，故答案为：35；②由图象可知，当57x ≤<或4250x <≤时，呼吸作用耗氧速率大于光合作用产氧速率．25．(1)见解析(2)88.5；94(3)435【分析】本题考查的是频数分布直方图，用样本估计总体，中位数和众数，从题目图表中获取有用信息是解题的关键．（1）根据频数分布直方图的数据可得成绩为7080x ≤<的学生人数，即可补全频数分布直方图；（2）根据中位数和众数的定义求解即可；（3）求出七、八年级学生参加活动的成绩为优秀的百分比可得答案．【详解】（1）解：成绩为7080x ≤<的学生人数为2011792----=（人），补全的频数分布直方图如图所示：（2）将七年级参加活动的20名学生成绩按从小到大的顺序排列，中位数是888988.52+=（分）八年级参加活动的20名学生成绩的数据的众数是94；故答案为：88.5；94；（3）69143003004352020+⨯+⨯=（人）答：估计这两个年级共有435人达到了优秀．26．(1)22y x x=-(2)12b <<或2b <-【分析】本题考查二次函数的性质，理解图像性质，利用数形结合思想解题是关键．（1）利用待定系数法求解即可；（2）分情况讨论：当原点位于对称轴的左侧时，当原点位于对称轴的右侧时，根据112x ≤≤，22x b =+，都有120y y ⋅<，确定b 的取值范围．【详解】（1）解：∵抛物线过点(2,0)∴440b -=，解得：1b =∴抛物线的解析式为22y x x =-（2）解：∵抛物线的对称轴为x b =，当0y =时220x bx -=解得120,2x x b==故与x 轴的交点为()()0.02,0b ，情况1：当原点位于对称轴的左侧时，要满足对于112x ≤≤，22x b =+，都有120y y ⋅<，此时，有2222b b b+>⎧⎨<⎩解得12b <<情况2：当原点位于对称轴的右侧时要满足对于112x ≤≤，22x b =+，都有120y y ⋅<，此时，有220b b <+<，解得22b b <⎧⎨<-⎩，解得2b <-综上，12b <<或2b <-27．(1)见解析(2)见解析(3)222BE HC DF +=，见解析【分析】（1）根据题意补全图形即可；（2）通过ASA 证明EDG HDG ≌，得到DE DH =，根据题意易得45B ∠=︒，由DE AB ⊥，可得BDE △为等腰直角三角形，于是BE DE DH ==；（3）过点F 作FN CD ⊥于点N ，得DE 为ABC 的中位线，则BD CD =，根据三角形内角和定理求得67.5CDF CFD ∠=∠=︒，于是CD CF BD ==，进而CN FN BE DE DH ====，以此得出CD DH CD CN -=-，即CH DN =，在Rt DFN 中，利用勾股定理即可得到结论．【详解】（1）解：补全图形如图所示．（2）证明：DF 平分EDC ∠，EDG HDG ∴∠=∠，EH DF ⊥ ，90EGD HGD ∴∠=∠=︒，在EDG △和HDG △中，EGD HGD ∠=∠，DG DG =，EDG HDG ∠=∠，(ASA)EDG HDG ∴ ≌，D E D H ∴=，在ABC 中，90BAC ∠=︒，AB AC =，ABC ∴ 为等腰直角三角形，45B ∴∠=︒，又DE AB ∵⊥，即90DEB ∠=︒，BDE ∴ 为等腰直角三角形，BE DE DH ∴==．（3）解：222HC BE FD +=，证明如下：如图，过点F 作FN CD ⊥于点N ，则CFN 为等腰直角三角形，90DEB CAB ∠=∠=︒ ，DE AC ∴∥，又E 为AB 的中点，DE ∴为ABC 的中位线，BD CD ∴=，45BDE ∠=︒ ，135CDE ∴∠=︒，DF 平分EDC ∠，67.5EDF CDF ∴∠=∠=︒，45C ∠=︒ ，18067.5CFD CDF C ∴∠=︒-∠-∠=︒，即CDF CFD ∠=∠，CD CF BD ∴==，CN FN BE DE DH ∴====，CD DH CD CN ∴-=-，即CH DN =，在Rt DFN 中，由勾股定理得222DN FN DF +=，222HC BE FD ∴+=．【点睛】本题主要考查等腰三角形的判定与性质、全等三角形的判定于性质、三角形中位线定理、角平分线的定义、勾股定理，解题关键是利用等腰直角三角形的性质将目标线段转化到直角三角形中，再根据勾股定理解决问题．28．(1)①2P ，4P ；②44b -≤≤(2)1m ≥或1m ≤【分析】（1）求出点P 为O 的伴随双切线的条件，①根据求出的条件进行判断即可；②根据得出的条件，判断原点到直线y x b =+的距离的关系，从而得出解；（2）根据（1）得出点P 存在的条件，判断以CE 为直径的圆的圆心和半径的数量关系，从而得解．【详解】（1）解：①根据定义，由PA ，PB 是O 的切线，∴90OAP OBP ∠=∠=︒，∵OA OB =，OP OP =，∴AOP BOP ≌△△，∴APO BPO ∠=∠．∵90180APB ︒≤∠<︒，∴4590APO ︒≤∠<︒，∴sin 12APO ≤∠<．∵sin OA OP APO =∠，=2AO ，∴2OP <≤．∵点1(1,0)-P ，2(22)P -，，3(3,3)P ，4(1,2)P --，∴12341OP OP OP OP ====，∵2OP <≤，∴点24P P ，是O 的伴随双切点．故答案为：24P P ，；②∵直线y x b =+上存在点P 为O 的伴随双切点．∴圆心O 到直线y x b =+的距离不大于设直线y x b =+与x 轴，y 的交点为C ，D ，过点O 作OE CD ⊥于点E ，如图．令0x =，则y b =，令0y =，则x b =-，∴点(,0)C b -，(0,)D b ，∴OC OD b ==，∴COD △为等腰直角三角形，∴2222OE b =，2222b ≤∴44b -≤≤．故答案为：44b -≤≤；（2）设CE 的中点为F ，∴1(,1)2m F +．∵l y ⊥轴，F 过直线l ，∴直线l 的表达式为=2y -，∴圆心F 到直线l 的距离为1(2)3--=，由（1）可知32EF ≤，∴322EF ≥∴32CE ≥，22(1)232m -+≥∴141m ≥+或114m ≤【点睛】本题是一道圆的综合问题，考查了切线的性质，锐角三角函数，勾股定理等，准确的理解新定义是解题的关键。

PBCDA OOP DFE 2013北京模拟：平面几何证明 1、（2013海淀期末，理5）如图，PC 与圆O 相切于点C ，直线PO 交圆O 于A ，B 两点，弦CD 垂直AB 于E ，则下面结论中，错误的是（ ）A 、BEC DEA △∽△B 、ACE ACP ∠=∠C 、2DE OE EP =⋅ D 、2PC PA AB =⋅第1题图 第2题图 第3题图 第4题图2、（2013朝阳期末，理10）如图，AB ，CD 是半径为a 的圆O 的两条弦，它们相交于AB 中点P ，若23aPD =，30OAP ∠=°，则AB = ；CP = 。

（用a 表示） 3、（2013西城期末，理10）如图，Rt △ABC ，90ABC ∠=°，3AC =，4BC =，以AC 为直径的圆交AB 于点D ，则BD = ；CD = 。

4、（2013石景山期末，理10）如图，从圆O 外一点P 引圆O 的割线PAB 和PCD ，PCD 过圆心O ，已知1PA =，2AB =，3PO =，则圆O 的半径等于 。

5、（2013丰台一模，理11）如图，直线PD 切圆O 与点D ，直线PO 交圆O 于点E ，F ，若23PF =+，1PD =，则圆O 的半径为 ，EFD ∠= 。

第5题图 第6题图 第7题图6、（2013石景山，理5）如图，直线AM 与圆相切于点M ，ABC 与ADE 是圆的两条割线，且BD AD ⊥，连结MD 、EC ，则下面结论中，错误的是（ ）A 、90ECA ∠=°B 、CEM DMA DBA ∠=∠+∠C 、2AM AD AE =⋅ D 、AD DE AB BC ⋅=⋅ 7、（2013海淀一模，理11）如图，AP 与圆O 切于点A ，交弦BD 延长线于点P ，过点B 作圆O 的切线交AP 于点C ，若90ACB ∠=°，3BC =，4CP =，则弦BD 的长为 。

中考数学专题复习《数与式》测试卷（附带答案) 学校:___________班级:___________姓名:___________考号:___________一．科学记数法—表示较大的数（共13小题）1．（2024•平谷区一模）从水利部长江水利委员会获悉，截止2024年3月24日，南水北调中线一期工程自2014年12月全面通水以来，已累计调水700亿立方米．其中70000000000用科学记数法表示为（）A．7×108B．7×109C．7×1010D．7×10112．（2024•房山区一模）据中国国家铁路集团有限公司消息：在2024年为期40天的春运期间，全国铁路累计发送旅客4.84亿人次，日均发送12089000人次．将12089000用科学记数法表示应为（）A．12.089×106B．1.2089×106C．1.2089×107D．0.12089×1083．（2024•石景山区一模）2023年10月26日，搭载神舟十七号载人飞船的长征二号F摇十七运载火箭在酒泉卫星发射中心成功发射．长征二号F（代号：CZ﹣2F，简称：长二F，绰号：神箭）主要用于发射神舟飞船和大型目标飞行器到近地轨道，其近地轨道运载能力是8500千克．将8500用科学记数法表示应为（）A．85×102B．8.5×102C．8.5×103D．0.85×1044．（2024•通州区一模）2024年政府工作报告中提出“大力推进现代化产业体系建设，加快发展新质生产力”．北京正在建设国际科技创新中心，人工智能产业是北京的主导产业之一．目前，人工智能相关企业数量约2200家，全国40%人工智能企业聚集于此．2023年，北京在人工智能领域融资总额约223亿元，约占全国四分之一．数据22300000000用科学记数法表示应为（）A．0.223×1011B．2.23×1010C．22.3×109D．223×1085．（2024•北京一模）2023年，我国共授权发明专利92.1万件，同比增长15.4%．将921000用科学记数法表示应为（）A．92.1×104B．9.21×104C．9.21×105D．0.921×1066．（2024•西城区一模）2024年5.5G技术正式开始商用，它的数据下载的最高速率从5G初期的1Gbps 提升到10Gbps，给我们的智慧生活“提速”．其中10Gbps表示每秒传输10000000000位（bit）的数据．将10000000000用科学记数法表示应为（）A．0.1×1011B．1×1010C．1×1011D．10×1097．（2024•朝阳区一模）2024年1月21日北京市第十六届人民代表大会第二次会议开幕，在政府工作报告中提到，2023年北京向天津、河北输出技术合同成交额74870000000元，将74870000000用科学记数法表示应为（）A．74.87×109B．7.487×1010C．7.487×109D．0.7487×10118．（2024•大兴区一模）2024年是京津冀协同发展十周年，高标准建设雄安新区成效显著．从新区设立至2023年底，累计开发面积184平方公里，4017栋楼宇拔地而起，总建筑面积4370万平方米．将43700000用科学记数法表示应为（）A．43.7×106B．4.37×107C．4.37×108D．0.437×1099．（2024•海淀区一模）据报道，2024年春节假期北京接待游客约1750万人次，旅游收入同比增长近四成．将17500000用科学记数法表示应为（）A．175×105B．1.75×106C．1.75×107D．0.175×10810．（2024•东城区一模）2024年2月29日，在国家统计局发布的《中华人民共和国2023年国民经济和社会发展统计公报》中，2023年全年完成造林面积400万公顷，其中人工造林面积133万公顷．将数字1330000用科学记数法表示应为（）A．1.33×107B．13.3×105C．1.33×106D．0.13×10711．（2024•丰台区一模）2023年5月28日，我国自主研发的C919国产大飞机商业首航取得圆满成功．一架C919飞机最大储油量超过19000千克．将数据19000用科学记数法表示为（）A．0.19×105B．1.9×104C．1.9×103D．19×10312．（2024•顺义区一模）全国绿化委员会办公室发布的《2023年中国国土绿化状况公报》显示，2023年全国完成国土绿化任务超800万公顷，其中造林3998000公顷．将3998000用科学记数法表示应为（）A．3.998×107B．3.998×106C．3998×103D．3.998×10313．（2024•门头沟区一模）近几年全国各省市都在发展旅游业，让游客充分感受地域文化，据统计，某市2023年的游客接待量为210000000人次，将210000000用科学记数法表示为（）A．2.1×107B．2.1×108C．2.1×109D．2.1×1010二．实数与数轴（共4小题）14．（2024•大兴区一模）实数a，b，c在数轴上的对应点的位置如图所示，下列结论中正确的是（）A．b﹣c＞0B．ac＞0C．b+c＜0D．ab＜115．（2024•海淀区一模）实数a在数轴上的对应点的位置如图所示，下列结论中正确的是（）A．a≥﹣2B．a＜﹣3C．﹣a＞2D．﹣a≥316．（2024•东城区一模）若实数a，b在数轴上的对应点的位置如图所示，在下列结论中，正确的是（）A．|a|＜|b|B．a+1＜b+1C．a2＜b2D．a＞﹣b17．（2024•顺义区一模）实数a，b在数轴上对应点的位置如图所示，下列结论正确的是（）A．a＞﹣1B．b＞1C．﹣a＜b D．﹣b＞a三．估算无理数的大小（共1小题）18．（2024•平谷区一模）写出一个大于1且小于4的无理数．（答案不唯一）四．实数的运算（共12小题）19．（2024•平谷区一模）计算：2cos30°+（）﹣1+|﹣1|﹣．20．（2024•房山区一模）计算：．21．（2024•石景山区一模）计算：．22．（2024•通州区一模）计算：．23．（2024•北京一模）计算：4sin45°+|﹣2|﹣+（）﹣1．24．（2024•西城区一模）计算：|﹣|﹣（）﹣1+2sin60°﹣．25．（2024•朝阳区一模）计算：+|1﹣|+（2﹣π）0﹣2sin45°．26．（2024•大兴区一模）计算：．27．（2024•海淀区一模）计算：2sin60°+|﹣1|+（）﹣1﹣．28．（2024•东城区一模）计算：．29．（2024•丰台区一模）计算：|﹣3|+2cos30°﹣．30．（2024•顺义区一模）计算：．五．整式的混合运算—化简求值（共5小题）31．（2024•通州区一模）已知2x2﹣x﹣1＝0，求代数式4x（x﹣1）+（2x+1）（2x﹣1）的值．31．（2024•北京一模）已知2x2﹣x﹣1＝0，求代数式（3x+2）（3x﹣2）﹣3x（x+1）的值．32．（2024•西城区一模）已知x2﹣x﹣4＝0，求代数式（x﹣2）2+（x﹣1）（x+3）的值．33．（2024•大兴区一模）已知a2+3a﹣1＝0，求代数式（a+1）2+a（a+4）﹣2的值．34．（2024•顺义区一模）已知x2+2x＝1，求代数式4（x+1）+（x﹣1）2的值．六．提公因式法与公式法的综合运用（共11小题）36．（2024•平谷区一模）分解因式：ax2+2ax+a＝．37．（2024•房山区一模）分解因式：x2y﹣4y＝．38．（2024•石景山区一模）分解因式：xy2﹣4x＝．39．（2024•北京一模）分解因式：8a2﹣8b2＝．40．（2024•西城区一模）分解因式：x2y﹣12xy+36y＝．41．（2024•朝阳区一模）分解因式：3x2+6xy+3y2＝．42．（2024•大兴区一模）分解因式：ax2﹣4a＝．43．（2024•海淀区一模）分解因式：a3﹣4a＝．44．（2024•东城区一模）因式分解：2xy2﹣18x＝．45．（2024•丰台区一模）分解因式：ax2﹣4ay2＝．46．（2024•顺义区一模）分解因式：4m2﹣4＝．七．分式有意义的条件（共3小题）47．（2024•房山区一模）若代数式有意义，则实数x的取值范围是．48．（2024•丰台区一模）若代数式有意义，则实数x的取值范围是．49．（2024•顺义区一模）代数式有意义，则实数x的取值范围是．八．分式的值（共2小题）50．（2024•海淀区一模）已知b2﹣4a＝0，求代数式的值．51．（2024•东城区一模）已知2x﹣y﹣9＝0，求代数式的值．九．分式的加减法（共1小题）52．（2024•平谷区一模）化简：的结果为．一十．分式的化简求值（共2小题）52．（2024•石景山区一模）已知x2﹣3x﹣6＝0，求代数式的值．53．（2024•丰台区一模）已知x﹣3y﹣2＝0，求代数式的值．一十一．二次根式有意义的条件（共6小题）55．（2024•平谷区一模）若代数式有意义，则实数x的取值范围是．56．（2024•石景山区一模）若在实数范围内有意义，则实数x的取值范围是．57．（2024•通州区一模）若在实数范围内有意义，则实数x的取值范围为．58．（2024•朝阳区一模）若式子在实数范围内有意义，则x的取值范围是．59．（2024•海淀区一模）代数式在实数范围内有意义，则x的取值范围是．60．（2024•东城区一模）若二次根式有意义，则实数x的取值范围是．参考答案与试题解析一．科学记数法—表示较大的数（共13小题）1．（2024•平谷区一模）从水利部长江水利委员会获悉，截止2024年3月24日，南水北调中线一期工程自2014年12月全面通水以来，已累计调水700亿立方米．其中70000000000用科学记数法表示为（）A．7×108B．7×109C．7×1010D．7×1011【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正数；当原数的绝对值＜1时，n是负数．【解答】解：70000000000＝7×1010．故选：C．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．2．（2024•房山区一模）据中国国家铁路集团有限公司消息：在2024年为期40天的春运期间，全国铁路累计发送旅客4.84亿人次，日均发送12089000人次．将12089000用科学记数法表示应为（）A．12.089×106B．1.2089×106C．1.2089×107D．0.12089×108【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数；当原数的绝对值＜1时，n是负整数．【解答】解：12089000＝1.2089×107故选：C．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．3．（2024•石景山区一模）2023年10月26日，搭载神舟十七号载人飞船的长征二号F摇十七运载火箭在酒泉卫星发射中心成功发射．长征二号F（代号：CZ﹣2F，简称：长二F，绰号：神箭）主要用于发射神舟飞船和大型目标飞行器到近地轨道，其近地轨道运载能力是8500千克．将8500用科学记数法表示应为（）A．85×102B．8.5×102C．8.5×103D．0.85×104【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数；当原数的绝对值＜1时，n是负整数．【解答】解：8500＝8.5×103故选：C．【点评】本题考查了科学记数法表示绝对值较大的数的方法，掌握科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数是关键．4．（2024•通州区一模）2024年政府工作报告中提出“大力推进现代化产业体系建设，加快发展新质生产力”．北京正在建设国际科技创新中心，人工智能产业是北京的主导产业之一．目前，人工智能相关企业数量约2200家，全国40%人工智能企业聚集于此．2023年，北京在人工智能领域融资总额约223亿元，约占全国四分之一．数据22300000000用科学记数法表示应为（）A．0.223×1011B．2.23×1010C．22.3×109D．223×108【分析】将一个数表示成a×10n的形式，其中1≤|a|＜10，n为整数，这种记数方法叫做科学记数法，据此即可求得答案．【解答】解：22300000000＝2.23×1010故选：B．【点评】本题考查科学记数法表示较大的数，熟练掌握其定义是解题的关键．5．（2024•北京一模）2023年，我国共授权发明专利92.1万件，同比增长15.4%．将921000用科学记数法表示应为（）A．92.1×104B．9.21×104C．9.21×105D．0.921×106【分析】将一个数表示成a×10n的形式，其中1≤|a|＜10，n为整数，这种记数方法叫做科学记数法，据此即可求得答案．【解答】解：921000＝9.21×105故选：C．【点评】本题考查科学记数法表示较大的数，熟练掌握其定义是解题的关键．6．（2024•西城区一模）2024年5.5G技术正式开始商用，它的数据下载的最高速率从5G初期的1Gbps 提升到10Gbps，给我们的智慧生活“提速”．其中10Gbps表示每秒传输10000000000位（bit）的数据．将10000000000用科学记数法表示应为（）A．0.1×1011B．1×1010C．1×1011D．10×109【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数，当原数绝对值＜1时，n是负整数．【解答】解：10000000000＝1×1010．故选：B．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．7．（2024•朝阳区一模）2024年1月21日北京市第十六届人民代表大会第二次会议开幕，在政府工作报告中提到，2023年北京向天津、河北输出技术合同成交额74870000000元，将74870000000用科学记数法表示应为（）A．74.87×109B．7.487×1010C．7.487×109D．0.7487×1011【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数；当原数的绝对值＜1时，n是负整数．【解答】解：74870000000＝7.487×1010故选：B．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．8．（2024•大兴区一模）2024年是京津冀协同发展十周年，高标准建设雄安新区成效显著．从新区设立至2023年底，累计开发面积184平方公里，4017栋楼宇拔地而起，总建筑面积4370万平方米．将43700000用科学记数法表示应为（）A．43.7×106B．4.37×107C．4.37×108D．0.437×109【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，据此判断即可．【解答】解：43700000＝4.37×107．故选：B．【点评】此题主要考查了用科学记数法表示较大的数，一般形式为a×10n，其中1≤|a|＜10，确定a与n的值是解题的关键．9．（2024•海淀区一模）据报道，2024年春节假期北京接待游客约1750万人次，旅游收入同比增长近四成．将17500000用科学记数法表示应为（）A．175×105B．1.75×106C．1.75×107D．0.175×108【分析】根据科学记数法的规则进行作答即可．【解答】解：17500000＝1.75×107．故选：C．【点评】本题主要考查科学记数法，解题的关键是熟练掌握科学记数法的规则．10．（2024•东城区一模）2024年2月29日，在国家统计局发布的《中华人民共和国2023年国民经济和社会发展统计公报》中，2023年全年完成造林面积400万公顷，其中人工造林面积133万公顷．将数字1330000用科学记数法表示应为（）A．1.33×107B．13.3×105C．1.33×106D．0.13×107【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数，当原数绝对值＜1时，n是负整数．【解答】解：1330000＝1.33×106．故选：C．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．11．（2024•丰台区一模）2023年5月28日，我国自主研发的C919国产大飞机商业首航取得圆满成功．一架C919飞机最大储油量超过19000千克．将数据19000用科学记数法表示为（）A．0.19×105B．1.9×104C．1.9×103D．19×103【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数，当原数绝对值＜1时，n是负整数．【解答】解：19000＝1.9×104．故选：B．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．12．（2024•顺义区一模）全国绿化委员会办公室发布的《2023年中国国土绿化状况公报》显示，2023年全国完成国土绿化任务超800万公顷，其中造林3998000公顷．将3998000用科学记数法表示应为（）A．3.998×107B．3.998×106C．3998×103D．3.998×103【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数，当原数绝对值＜1时，n是负整数．【解答】解：3998000＝3.998×106．故选：B．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．13．（2024•门头沟区一模）近几年全国各省市都在发展旅游业，让游客充分感受地域文化，据统计，某市2023年的游客接待量为210000000人次，将210000000用科学记数法表示为（）A．2.1×107B．2.1×108C．2.1×109D．2.1×1010【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正整数；当原数的绝对值＜1时，n是负整数．【解答】解：210000000＝2.1×108故选：B．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．二．实数与数轴（共4小题）14．（2024•大兴区一模）实数a，b，c在数轴上的对应点的位置如图所示，下列结论中正确的是（）A．b﹣c＞0B．ac＞0C．b+c＜0D．ab＜1【分析】根据数轴可知：﹣3＜a＜﹣2＜b＜﹣1＜0＜c＜1，由此逐一判断各选项即可．【解答】解：由数轴可知：﹣3＜a＜﹣2＜b＜﹣1＜0＜c＜1A、∵﹣2＜b＜﹣1，0＜c＜1，∴b﹣c＜0，故选项A不符合题意；B、∵﹣3＜a＜﹣2，0＜c＜1，∴ac＜0，故选项B不符合题意；C、∵﹣2＜b＜﹣1，0＜c＜1，∴b+c＜0，故选项C符合题意；D、∵﹣3＜a＜﹣2＜b＜﹣1，∴ab＞1，故选项D不符合题意；故选：C．【点评】本题考查的是实数与数轴，熟悉数轴上各点的分布特点是解题的关键．15．（2024•海淀区一模）实数a在数轴上的对应点的位置如图所示，下列结论中正确的是（）A．a≥﹣2B．a＜﹣3C．﹣a＞2D．﹣a≥3【分析】由数轴可知，﹣3＜a＜﹣2，由此逐一判断各选项即可．【解答】解：由数轴可知，﹣3＜a＜﹣2A、﹣3＜a＜﹣2，故选项A不符合题意；B、﹣3＜a＜﹣2，故选项B不符合题意；C、∵﹣3＜a＜﹣2，∴2＜﹣a＜3，故选项C符合题意；D、∵﹣3＜a＜﹣2，∴2＜﹣a＜3，故选项D不符合题意；故选：C．【点评】本题考查的是实数与数轴，从题目中提取已知条件是解题的关键．16．（2024•东城区一模）若实数a，b在数轴上的对应点的位置如图所示，在下列结论中，正确的是（）A．|a|＜|b|B．a+1＜b+1C．a2＜b2D．a＞﹣b【分析】根据图示，可得﹣2＜a＜﹣1，0＜b＜1，据此逐项判断即可．【解答】解：根据图示，可得﹣2＜a＜﹣1，0＜b＜1∵﹣2＜a＜﹣1，0＜b＜1∴1＜|a|＜2，0＜|b|＜1∴|a|＞|b|∴选项A不符合题意；∵﹣2＜a＜﹣1，0＜b＜1∴a＜b∴a+1＜b+1∴选项B符合题意；∵﹣2＜a＜﹣1，0＜b＜1∴1＜a2＜4，0＜b2＜1∴a2＞b2∴选项C不符合题意；∵0＜b＜1∴﹣1＜﹣b＜0∵﹣2＜a＜﹣1∴a＜﹣b∴选项D不符合题意．故选：B．【点评】此题主要考查了实数大小比较的方法，以及数轴的特征：一般来说，当数轴正方向朝右时，右边的数总比左边的数大．17．（2024•顺义区一模）实数a，b在数轴上对应点的位置如图所示，下列结论正确的是（）A．a＞﹣1B．b＞1C．﹣a＜b D．﹣b＞a【分析】根据图示，可得﹣2＜a＜﹣1，0＜b＜1，据此逐项判断即可．【解答】解：根据图示，可得﹣2＜a＜﹣1，0＜b＜1∵a＜﹣1∴选项A不符合题意；∵b＜1∴选项B不符合题意；∵﹣2＜a＜﹣1∴1＜﹣a＜2∵0＜b＜1∴﹣a＞b∴选项C不符合题意；∵0＜b＜1∴﹣1＜﹣b＜0∵﹣2＜a＜﹣1∴﹣b＞a∴选项D符合题意．故选：D．【点评】此题主要考查了实数大小比较的方法，以及数轴的特征：一般来说，当数轴正方向朝右时，右边的数总比左边的数大．三．估算无理数的大小（共1小题）18．（2024•平谷区一模）写出一个大于1且小于4的无理数π．（答案不唯一）【分析】由于开方开不尽的数是无理数，然后确定的所求数的范围即可求解．【解答】解：∵1＝，4＝∴只要是被开方数大于1而小于16，且不是完全平方数的都可．同时π也符合条件．【点评】此题主要考查了无理数的大小的比较，其中无理数包括开方开不尽的数，和π有关的数，有规律的无限不循环小数．四．实数的运算（共12小题）19．（2024•平谷区一模）计算：2cos30°+（）﹣1+|﹣1|﹣．【分析】根据特殊角的三角函数值、负整数指数幂、绝对值、二次根式的化简分别计算即可．【解答】解：2cos30°+（）﹣1+|﹣1|﹣＝＝＝1．【点评】本题考查了实数的运算，熟练掌握特殊角的三角函数值、负整数指数幂、绝对值、二次根式的化简是解题的关键．20．（2024•房山区一模）计算：．【分析】利用特殊锐角三角函数值，负整数指数幂，绝对值的性质，二次根式的性质计算即可．【解答】解：原式＝6×+2+3﹣3＝3+2+3﹣3＝5．【点评】本题考查实数的运算，熟练掌握相关运算法则是解题的关键．21．（2024•石景山区一模）计算：．【分析】利用绝对值的性质，二次根式的性质，特殊锐角三角函数值及负整数指数幂计算即可．【解答】解：原式＝2﹣+2﹣2×+5＝2﹣+2﹣+5＝7．【点评】本题考查实数的运算，熟练掌握相关运算法则是解题的关键．22．（2024•通州区一模）计算：．【分析】直接利用特殊角的三角函数值以及零指数幂的性质和负整数指数幂的性质分别化简得出答案．【解答】解：原式＝4×＝2+4+1＝5．【点评】此题主要考查了实数运算，正确化简各数是解题关键．23．（2024•北京一模）计算：4sin45°+|﹣2|﹣+（）﹣1．【分析】sin45°＝，再根据实数和指数幂的运算法则计算即可．【解答】解：原式＝4×+2﹣3+2＝2﹣3+4＝4．【点评】本题考查的是实数的运算，指数幂和特殊角的三角函数值，熟练掌握上述知识点是解题的关键．24．（2024•西城区一模）计算：|﹣|﹣（）﹣1+2sin60°﹣．【分析】利用特殊角的三角函数值及绝对值的代数意义化简，计算即可得到结果．【解答】解：原式＝＝＝﹣．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．25．（2024•朝阳区一模）计算：+|1﹣|+（2﹣π）0﹣2sin45°．【分析】分别根据绝对值、零指数幂及特殊角的三角函数值计算出各数，再根据实数混合运算的法则进行计算即可．【解答】解：原式＝2＝3＝2．【点评】本题考查的是实数的运算，熟知绝对值、零指数幂的运算法则，熟记特殊角的三角函数值是解答此题的关键．26．（2024•大兴区一模）计算：．【分析】cos45°＝，再根据实数和指数幂的运算法则计算即可．【解答】解：原式＝＝．【点评】本题考查的是实数的运算，指数幂和特殊角的三角函数值，熟练掌握上述知识点是解题的关键．27．（2024•海淀区一模）计算：2sin60°+|﹣1|+（）﹣1﹣．【分析】根据实数的运算法则、负整数指数幂和特殊角的三角函数值的定义进行计算．【解答】解：原式＝2×+1+2﹣2＝+1+2﹣2＝3﹣．【点评】本题考查了实数的运算法则、负整数指数幂和特殊角的三角函数值，掌握实数的运算法则、负整数指数幂和特殊角的三角函数值的定义是关键．28．（2024•东城区一模）计算：．【分析】利用二次根式的性质，特殊锐角三角函数值，零指数幂，绝对值的性质计算即可．【解答】解：原式＝4﹣2×+1﹣2＝4﹣+1﹣2＝3﹣1．【点评】本题考查实数的运算，熟练掌握相关运算法则是解题的关键．29．（2024•丰台区一模）计算：|﹣3|+2cos30°﹣．【分析】直接利用特殊角的三角函数值、负整数指数幂的性质、二次根式的性质、绝对值的性质分别化简，进而计算得出答案．【解答】解：原式＝3+2×﹣3﹣2＝3+﹣3﹣2＝﹣．【点评】此题主要考查了实数的运算，正确化简各数是解题关键．30．（2024•顺义区一模）计算：．【分析】利用负整数指数幂，特殊锐角三角函数值，二次根式的性质，零指数幂计算即可．【解答】解：原式＝﹣4×+2+1＝﹣2+2+1＝．【点评】本题考查实数的运算，熟练掌握相关运算法则是解题的关键．五．整式的混合运算—化简求值（共5小题）31．（2024•通州区一模）已知2x2﹣x﹣1＝0，求代数式4x（x﹣1）+（2x+1）（2x﹣1）的值．【分析】利用平方差公式，单项式乘多项式的法则进行计算，然后把2x2﹣x＝1代入化简后的式子进行计算，即可解答．【解答】解：4x（x﹣1）+（2x+1）（2x﹣1）＝4x2﹣4x+4x2﹣1＝8x2﹣4x﹣1∵2x2﹣x﹣1＝0∴2x2﹣x＝1∴当2x2﹣x＝1时，原式＝4（2x2﹣x）﹣1＝4×1﹣1＝4﹣1＝3．【点评】本题考查了整式的混合运算﹣化简求值，平方差公式，准确熟练地进行计算是解题的关键．32．（2024•北京一模）已知2x2﹣x﹣1＝0，求代数式（3x+2）（3x﹣2）﹣3x（x+1）的值．【分析】利用平方差公式，单项式乘多项式的法则进行计算，然后把2x2﹣x＝1代入化简后的式子进行计算，即可解答．【解答】解：（3x+2）（3x﹣2）﹣3x（x+1）＝9x2﹣4﹣3x2﹣3x＝6x2﹣3x﹣4∵2x2﹣x﹣1＝0∴2x2﹣x＝1当2x2﹣x＝1时，原式＝3（2x2﹣x）﹣4＝3×1﹣4＝3﹣4＝﹣1．【点评】本题考查了整式的混合运算﹣化简求值，平方差公式，准确熟练地进行计算是解题的关键．33．（2024•西城区一模）已知x2﹣x﹣4＝0，求代数式（x﹣2）2+（x﹣1）（x+3）的值．【分析】利用完全平方公式，多项式乘多项式的法则进行计算，然后把x2﹣x＝4代入化简后的式子进行计算，即可解答．【解答】解：（x﹣2）2+（x﹣1）（x+3）＝x2﹣4x+4+x2+3x﹣x﹣3＝2x2﹣2x+1∵x2﹣x﹣4＝0∴x2﹣x＝4∴当x2﹣x＝4时，原式＝2（x2﹣x）+1＝2×4+1＝8+1＝9．【点评】本题考查了整式的混合运算﹣化简求值，完全平方公式，准确熟练地进行计算是解题的关键．34．（2024•大兴区一模）已知a2+3a﹣1＝0，求代数式（a+1）2+a（a+4）﹣2的值．【分析】利用完全平方公式，单项式乘多项式法则进行计算，然后把a2+3a＝1代入化简后的式子进行计算即可解答．【解答】解：（a+1）2+a（a+4）﹣2＝a2+2a+1+a2+4a﹣2＝a2+a2+2a+4a+1﹣2＝2a2+6a﹣1∵a2+3a﹣1＝0∴a2+3a＝1当a2+3a＝1时，原式＝2（a2+3a）﹣1＝2×1﹣1＝2﹣1＝1．【点评】本题考查了整式的混合运算﹣化简求值，完全平方公式，准确熟练地进行计算是解题的关键．35．（2024•顺义区一模）已知x2+2x＝1，求代数式4（x+1）+（x﹣1）2的值．【分析】利用完全平方公式，单项式乘多项式的法则进行计算，然后把x2+2x＝1代入化简后的式子进行计算，即可解答．【解答】解：4（x+1）+（x﹣1）2＝4x+4+x2﹣2x+1＝x2+2x+5当x2+2x＝1时，原式＝1+5＝6．【点评】本题考查了整式的混合运算﹣化简求值，代数式求值，完全平方公式，准确熟练地进行计算是解题的关键．六．提公因式法与公式法的综合运用（共11小题）【分析】先提取公因式，再根据完全平方公式进行二次分解．完全平方公式：a2±2ab+b2＝（a±b）2．【解答】解：ax2+2ax+a＝a（x2+2x+1）﹣﹣（提取公因式）＝a（x+1）2．﹣﹣（完全平方公式）【点评】本题考查了提公因式法与公式法分解因式，提取公因式后利用完全平方公式进行二次分解，注意要分解彻底．37．（2024•房山区一模）分解因式：x2y﹣4y＝y（x+2）（x﹣2）．【分析】先提公因式，再利用平方差公式继续分解即可解答．【解答】解：x2y﹣4y＝y（x2﹣4）＝y（x+2）（x﹣2）故答案为：y（x+2）（x﹣2）．【点评】本题考查了提公因式法与公式法的综合运用，一定要注意如果多项式的各项含有公因式，必须先提公因式．38．（2024•石景山区一模）分解因式：xy2﹣4x＝x（y+2）（y﹣2）．【分析】原式提取x，再利用平方差公式分解即可．【解答】解：原式＝x（y2﹣4）＝x（y+2）（y﹣2）故答案为：x（y+2）（y﹣2）【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．39．（2024•北京一模）分解因式：8a2﹣8b2＝8（a+b）（a﹣b）．【分析】提公因式后利用平方差公式因式分解即可．【解答】解：原式＝8（a2﹣b2）＝8（a+b）（a﹣b）故答案为：8（a+b）（a﹣b）．【点评】本题考查因式分解，熟练掌握因式分解的方法是解题的关键．40．（2024•西城区一模）分解因式：x2y﹣12xy+36y＝y（x﹣6）2．【分析】提取公因式后用完全平方公式分解即可．【解答】解：x2y﹣12xy+36y＝y（x2﹣12x+36）＝y（x﹣6）2故答案为：y（x﹣6）2．【点评】本题考查了因式分解，熟练掌握提取公因式和公式法分解因式是关键．【分析】先利用提取公因式法提取数字3，再利用完全平方公式继续进行分解．【解答】解：3x2+6xy+3y2＝3（x2+2xy+y2）＝3（x+y）2【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．42．（2024•大兴区一模）分解因式：ax2﹣4a＝a（x+2）（x﹣2）．【分析】先提取公因式a，再对余下的多项式利用平方差公式继续分解．【解答】解：ax2﹣4a＝a（x2﹣4）＝a（x+2）（x﹣2）．【点评】本题考查用提公因式法和公式法进行因式分解的能力，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．43．（2024•海淀区一模）分解因式：a3﹣4a＝a（a+2）（a﹣2）．【分析】原式提取a，再利用平方差公式分解即可．【解答】解：原式＝a（a2﹣4）＝a（a+2）（a﹣2）．故答案为：a（a+2）（a﹣2）【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．44．（2024•东城区一模）因式分解：2xy2﹣18x＝2x（y+3）（y﹣3）．【分析】提取公因式后再用平方差公式分解即可．【解答】解：2xy2﹣18x＝2x（y2﹣9）＝2x（y+3）（y﹣3）．故答案为：2x（y+3）（y﹣3）．【点评】本题考查了因式分解，熟练掌握公式法和提取公因式法是关键．45．（2024•丰台区一模）分解因式：ax2﹣4ay2＝a（x+2y）（x﹣2y）．【分析】观察原式ax2﹣4ay2，找到公因式a，提出公因式后发现x2﹣4y2符合平方差公式，利用平方差公式继续分解可得．【解答】解：ax2﹣4ay2＝a（x2﹣4y2）。