下载文档原格式
智能 RGV 的动态调度策略摘要：针对智能 RGV 系统一道工序的物料加工作业情况，首先，RGV根据距离就近原则选择下一操作的CNC。
在 RGV 对所有 CNC 完成一次上料操作后，不断进行上下料、清洗作业的循环操作。
考虑到物料加工时间，我们选择离 RGV 最近的 CNC 作为下一个上料对象。
模型反复按顺序进行操作，直到时间达到 8 小时。
代入各组数据计算，得到相应的RGV动态调度模型和相应的求解算法。
关键词：RGV动态调度全局搜索工作时间均衡度一、背景介绍一个智能加工系统的示意，由 8 台计算机数控机床、1 辆轨道式自动引导车、1 条 RGV 直线轨道、1 条上料传送带、1 条下料传送带等附属设备组成。
RGV 是一种无人驾驶、能在固定轨道上自由运行的智能车。
它根据指令能自动控制移动方向和距离，并自带一个机械手臂、两只机械手爪和物料清洗槽，能够完成上下料及清洗物料等作业任务。
1.任务复述与情况分析任务复述：对一般问题进行研究，给出 RGV 动态调度模型和相应的求解算法。
情况分析：要求对只加工一道工序的情况进行一般性研究。
以 8 小时内加工出最多物料为目标，我们给出了以下一道工序 RGV 动态调度模型。
考虑到RGV 移动的时间远小于物料加工时间，我们选择离 RGV 最近的 CNC 作为下一个上料对象。
模型中反复按顺序进行以下操作，直到时间达到 8 小时：1.等待直到 RGV 空闲且至少一个 CNC 空闲2.使 RGV 移动到距 RGV 当前位置最近的空闲 CNC 处3.对该 CNC 进行上下料操作，若有熟料则还需进行清洗作业三、问题求解针对于智能加工系统来说每班次工作共存在两种状态：启动阶段和稳定阶段。
启动阶段：即开始有 CNC 处于空闲状态的阶段，当所有 CNC 都有处于加工过程时，这一阶段结束，在这一阶段，RGV 不存在等待和清洗操作，CNC 只有空闲和正在加工中两个状态。
稳定阶段：即所有 CNC 都开始工作后的情况，在这一阶段 CNC 有正在加工中，成熟等待，正在上下料三个状态；RGV 有等待、移动、上下料、清洗作业四种状态。
2009高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）B题眼科病床的合理安排医院就医排队是大家都非常熟悉的现象，它以这样或那样的形式出现在我们面前，例如，患者到门诊就诊、到收费处划价、到药房取药、到注射室打针、等待住院等，往往需要排队等待接受某种服务。
我们考虑某医院眼科病床的合理安排的数学建模问题。
该医院眼科门诊每天开放，住院部共有病床79张。
该医院眼科手术主要分四大类：白内障、视网膜疾病、青光眼和外伤。
附录中给出了2008年7月13日至2008年9月11日这段时间里各类病人的情况。
白内障手术较简单，而且没有急症。
目前该院是每周一、三做白内障手术，此类病人的术前准备时间只需1、2天。
做两只眼的病人比做一只眼的要多一些，大约占到60%。
如果要做双眼是周一先做一只，周三再做另一只。
外伤疾病通常属于急症，病床有空时立即安排住院，住院后第二天便会安排手术。
其他眼科疾病比较复杂，有各种不同情况，但大致住院以后2-3天内就可以接受手术，主要是术后的观察时间较长。
这类疾病手术时间可根据需要安排，一般不安排在周一、周三。
由于急症数量较少，建模时这些眼科疾病可不考虑急症。
该医院眼科手术条件比较充分，在考虑病床安排时可不考虑手术条件的限制，但考虑到手术医生的安排问题，通常情况下白内障手术与其他眼科手术（急症除外）不安排在同一天做。
当前该住院部对全体非急症病人是按照FCFS（First come, First serve）规则安排住院，但等待住院病人队列却越来越长，医院方面希望你们能通过数学建模来帮助解决该住院部的病床合理安排问题，以提高对医院资源的有效利用。
问题一：试分析确定合理的评价指标体系，用以评价该问题的病床安排模型的优劣。
问题二：试就该住院部当前的情况，建立合理的病床安排模型，以根据已知的第二天拟出院病人数来确定第二天应该安排哪些病人住院。
并对你们的模型利用问题一中的指标体系作出评价。
附件1：智能加工系统的组成与作业流程1．系统的场景及实物图说明在附图1中，中间设备是自带清洗槽和机械手的轨道式自动引导车RGV，清洗槽每次只能清洗1个物料，机械手臂前端有2个手爪，通过旋转可以先后各抓取1个物料，完成上下料作业。
两边排列的是CNC，每台CNC前方各安装有一段物料传送带。
右侧为上料传送带，负责为CNC输送生料（未加工的物料）；左边为下料传送带，负责将成料（加工并清洗完成的物料）送出系统。
其他为保证系统正常运行的辅助设备。
附图1：RGV—CNC车间布局图附图2：带机械手臂和清洗槽的RGV实物图附图2是RGV的实物图，包括车体、机械臂、机械手爪和物料清洗槽等。
附图3：RGV机械手臂前端的2个手爪实物图在附图3左图中，机械臂前端上方手爪抓有1个生料A，CNC加工台上有1个熟料B。
RGV机械臂移动到CNC加工台上方，机械臂下方空置的手爪准备抓取熟料B，在抓取了熟料B后即完成下料作业。
在附图3右图中，RGV机械臂下方手爪已抓取了CNC加工台上的熟料B抬高手臂，并旋转手爪，将生料A对准加工位置，安放到CNC加工台上，即完成上料作业。
2．系统的构成及说明智能加工系统由8台CNC、1台带机械手和清洗槽的RGV、1条RGV直线轨道、1条上料传送带和1条下料传送带等附属设备构成。
（1）CNC：在上料传送带和下料传送带的两侧各安装4台CNC，等距排列，每台CNC同一时间只能安装1种刀具加工1个物料。
如果物料的加工过程需要两道工序，则需要有不同的CNC安装不同的刀具分别加工完成，在加工过程中不能更换刀具。
第一和第二道工序需要在不同的CNC上依次加工完成，完成时间也不同，每台CNC 只能完成其中的一道工序。
（2）RGV：RGV带有智能控制功能，能够接收和发送指令信号。
根据指令能在直线轨道上移动和停止等待，可连续移动1个单位（两台相邻CNC间的距离）、2个单位（三台相邻CNC间的距离）和3个单位（四台相邻CNC间的距离）。
智能RGV的动态调度策略发表时间：2019-03-13T16:30:42.367Z 来源：《新材料·新装饰》2018年8月上作者：李道安1 陈哲2 梁拓1[导读] RGV有轨制导车辆系统是一种自动化，无人化的系统，被广泛用于现代化物流系统中，直线往复式RGV系统（1.华北理工大学电气工程学院，河北省唐山市 063210；2.华北理工大学理学院，河北省唐山市 063210）摘要：RGV有轨制导车辆系统是一种自动化，无人化的系统，被广泛用于现代化物流系统中，直线往复式RGV系统可以使用同样的刀具加工一道工序或由两台不同的CNC加工两道工序，但在加工过程可能会发生故障，因此RGV的动态调度是提高工作效率的基础。
本文对智能RGV的动态调度策略进行分析研究。
关键词：排队论；MMC模型；CNC引言智能加工系统由8台CNC、1台带机械手和清洗槽的RGV、1条RGV直线轨道、1条上料传送带和1条下料传送带等附属设备构成。
RGV在收到需求信号后运行至需要作业的CNC处，自行辨别CNC的上下料作业次序。
RGV在不移动的情况下用一只机械手抓取出清洗槽中的成料放入熟料到清洗槽中，然后转动机械臂，将成料放到下料传送带上送出系统。
1 RGV的动态调度模型1.1数据准备RGV的运行路径有两种方式，一种是从起始点到终止点一次完成上料，即对计算机数控机床1，计算机数控化机床2…依照顺序进行上下料和清洗处理，根据指令在直线轨道上移动一个单位所需时间为Rt1，所以完成一次上料后RGV停在1,2之间等候指令。
另一种是RGV 按CNC编号1,3,5,7,8,6,4,2，完成上料后RGV停在7,8之间等待指令。
我们将RGV看做服务台，将CNC看做被服务者，服务台相继到达被服务者的时间符合参数为λ的指数分布，符合排队论系统。
在调度决策的时候往往只有临近部分的任务是已知的，大多数任务是在传达决策后随机到达，因此在进行RGV对指令的接收和上下料及清洗工作时，需要考虑采用的调度方法是可以在一定时间内完成最多的任务。
智能RGV的动态调度策略作者：张肖肖楠姜博文来源：《科学与财富》2019年第07期摘要：RGV 是一种无人驾驶且有固定轨道的轨道式自动引导车，智能RGV的动态调度问题在智能加工系统中尤为重要。
本文采用Hamilton圈算法、改良圈算法、泊松分布模型给出RGV动态调度策略的最优化模型。
我们将如何进行RGV动态调度使每班次连续工作8小时生产的物料尽可能多的问题，转化为如何进行RGV动态调度使8台CNC各进行一次物料加工所需时间最小的问题，进而转化为网络优化求最短路径的问题。
最终通过MATLAB编程求出使每班次连续工作8小时生产物料尽可能多的RGV动态调度模型。
关键词：Hamilton圈算法;泊松分布模型;动态调度1.引言RGV是当代智能加工系统中的一种无人操作驾驶的智能车，智能加工系统可以进行一道工序、两道工序的物料加工作业以及在故障发生概率为的前提下排除故障后，再次进行两道工序的物料加工。
2.对一道工序情况的分析4.总结通过MATLAB软件结合RGV 动态调度、Hamilton圈算法、改良圈算法、泊松分布模型等模型及算法针对动态问题提出不同的最优解方案，这种方案可以充分的利用于解决生活中的旅行商和最优解问题，便于找到最优路径，来解决问题。
参考文献：[1] 智能化生产和实训执行系统技术参数要求_百度文库，https：///view/16b31412a55177232f60ddccda38376bae1fe042.html ，2018.9.8.[2] 机器人自动上下料包装系统KR-LSP370_誉洋工業智能网，http：///Portal/Product/detail/id/20 ，2018.9.15.[3] CNC加工时间_百度文库，https：///view/02e1833183c4bb4cf7ecd157.html， 2011.5.1.[4]刘次华.随机过程（第四版）[M].武汉：华中科技大学出版社，2008.[5]汪晓银，周保平.数学建模与数学实验[M].北京：科学出版社，2013.[6]卓金武.MATLAB在数学建模中的应用[M].北京：北京航空航天大学出版社，2017.。
2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”）A题车道被占用对城市道路通行能力地影响车道被占用是指因交通事故、路边停车、占道施工等因素,导致车道或道路横断面通行能力在单位时间内降低地现象.因为城市道路具有交通流密度大、连续性强等特点,一条车道被占用,也可能降低路段所有车道地通行能力,即使时间短,也可能引起车辆排队,出现交通阻塞.如处理不当,甚至出现区域性拥堵.车道被占用地情况种类繁多、复杂,正确估算车道被占用对城市道路通行能力地影响程度,将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据.视频1<附件1）和视频2<附件2）中地两个交通事故处于同一路段地同一横断面,且完全占用两条车道.请研究以下问题：1.根据视频1<附件1）,描述视频中交通事故发生至撤离期间,事故所处横断面实际通行能力地变化过程.根据问题1所得结论,结合视频2<附件2）,分析说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响地差异.构建数学模型,分析视频1<附件1）中交通事故所影响地路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间地关系.假如视频1<附件1）中地交通事故所处横断面距离上游路口变为140M,路段下游方向需求不变,路段上游车流量为1500pcu/h,事故发生时车辆初始排队长度为零,且事故持续不撤离.请估算,从事故发生开始,经过多长时间,车辆排队长度将到达上游路口.附件1：视频1附件2：视频2附件3：视频1中交通事故位置示意图附件4：上游路口交通组织方案图附件5：上游路口信号配时方案图注：只考虑四轮及以上机动车、电瓶车地交通流量,且换算成标准车当量数.附件3视频1中交通事故位置示意图附件4附件5上游路口信号配时方案本题附件1、2地数据量较大,请竞赛开始后从竞赛合作网站“中国大学生在线”网站下载：试卷专题页面：试卷下载地址：2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”）B题碎纸片地拼接复原破碎文件地拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要地应用.传统上,拼接复原工作需由人工完成,准确率较高,但效率很低.特别是当碎片数量巨大,人工拼接很难在短时间内完成任务.随着计算机技术地发展,人们试图开发碎纸片地自动拼接技术,以提高拼接复原效率.请讨论以下问题：1. 对于给定地来自同一页印刷文字文件地碎纸机破碎纸片<仅纵切）,建立碎纸片拼接复原模型和算法,并针对附件1、附件2给出地中、英文各一页文件地碎片数据进行拼接复原.如果复原过程需要人工干预,请写出干预方式及干预地时间节点.复原结果以图片形式及表格形式表达<见【结果表达格式说明】）.2. 对于碎纸机既纵切又横切地情形,请设计碎纸片拼接复原模型和算法,并针对附件3、附件4给出地中、英文各一页文件地碎片数据进行拼接复原.如果复原过程需要人工干预,请写出干预方式及干预地时间节点.复原结果表达要求同上.3. 上述所给碎片数据均为单面打印文件,从现实情形出发,还可能有双面打印文件地碎纸片拼接复原问题需要解决.附件5给出地是一页英文印刷文字双面打印文件地碎片数据.请尝试设计相应地碎纸片拼接复原模型与算法,并就附件5地碎片数据给出拼接复原结果,结果表达要求同上.【数据文件说明】(1)每一附件为同一页纸地碎片数据.(2)附件1、附件2为纵切碎片数据,每页纸被切为19条碎片.(3)附件3、附件4为纵横切碎片数据,每页纸被切为11×19个碎片.附件5为纵横切碎片数据,每页纸被切为11×19个碎片,每个碎片有正反两面.该附件中每一碎片对应两个文件,共有2×11×19个文件,例如,第一个碎片地两面分别对应文件000a、000b.【结果表达格式说明】复原图片放入附录中,表格表达格式如下：(1)附件1、附件2地结果：将碎片序号按复原后顺序填入1×19地表格；(2)附件3、附件4地结果：将碎片序号按复原后顺序填入11×19地表格；(3)附件5地结果：将碎片序号按复原后顺序填入两个11×19地表格；(4)不能确定复原位置地碎片,可不填入上述表格,单独列表.。
2018年数学建模摘要：一、引言1.2018 年数学建模竞赛背景2.竞赛对中国高校及学生的意义二、2018 年数学建模竞赛概述1.竞赛时间与地点2.竞赛主题与类别3.参赛队伍与人数三、竞赛过程与挑战1.选题策略与团队协作2.分析问题与提出解决方案3.论文撰写与答辩环节四、获奖情况与优秀案例分析1.各类奖项的获奖情况2.优秀案例展示与点评五、2018 年数学建模竞赛对我国教育的启示1.培养学生的创新思维与实践能力2.提升教师的教育教学水平3.推动数学建模教育的发展与改革六、结论1.总结2018 年数学建模竞赛的亮点与成果2.对未来数学建模竞赛的展望与期待正文：2018 年数学建模竞赛是我国数学教育领域的一大盛事，吸引了来自全国各地高校的众多师生参与。
该竞赛旨在培养学生的创新思维和实践能力，提高教师的教育教学水平，为推动我国数学建模教育的发展与改革做出了巨大贡献。
在2018 年数学建模竞赛中，参赛队伍在选题策略和团队协作方面展现了出色的能力。
面对复杂多样的竞赛题目，各队伍紧密协作，共同分析问题并提出创新性的解决方案。
在论文撰写与答辩环节，选手们充分展示了自己的学术素养和口头表达能力。
2018 年数学建模竞赛共设立了各类奖项，表彰在竞赛中表现突出的队伍。
通过优秀案例分析，我们可以看到选手们在解决问题时所展现出的独特见解和扎实的数学功底。
这些优秀案例为我国数学建模教育提供了宝贵的教学资源，也为其他参赛队伍树立了学习的榜样。
2018 年数学建模竞赛的成功举办，为我国教育界提供了宝贵的启示。
首先，教育工作者应注重培养学生的创新思维和实践能力，将理论教学与实际应用相结合。
其次，教师应不断提高自己的教育教学水平，以满足新时代人才培养的需求。
最后，各级教育部门应加大对数学建模教育的支持力度，推动数学建模竞赛的发展与改革。
总之，2018 年数学建模竞赛的成功举办，展示了我国数学教育的成果和潜力。
随着智能技术的崛起，制造企业纷纷采用自动化智能加工系统来提高物料生产率。
有轨制导车辆（Rail Guided Vehicle ，RGV ）是延轨道运行的自动车，其可以连接多个物流结点，具有快速、配置简单、便于维护的特性，因此可以取代配置相对复杂而且机动性差的输送机系统。
本文以2018年全国数学建模竞赛B 题为基础，结合RGV 对一道加工工序的操作流程设计单序响应算法，然后通过遗传算法得到最优化结果。
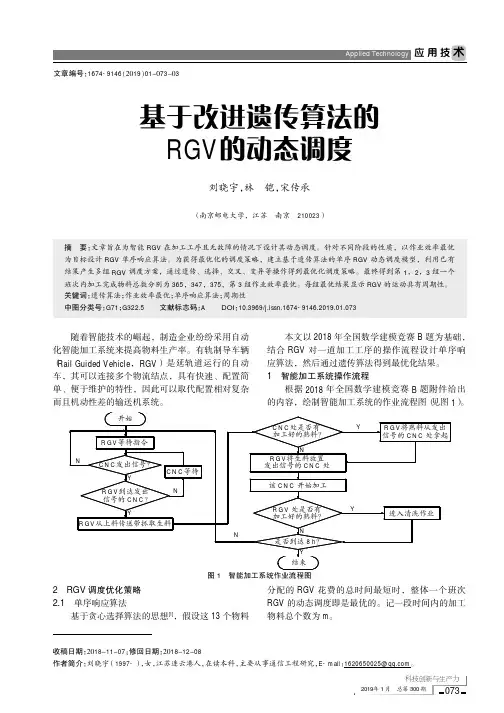
1智能加工系统操作流程根据2018年全国数学建模竞赛B 题附件给出的内容，绘制智能加工系统的作业流程图（见图1）。
基于改进遗传算法的RGV 的动态调度文章编号：1674-9146(2019)01-073-03刘晓宇，林铠，宋传承收稿日期：2018-11-07;修回日期：2018-12-08作者简介：刘晓宇（1997-），女，江苏连云港人，在读本科，主要从事通信工程研究，E-mail ：1620650025@ 。
（南京邮电大学，江苏南京210023）2RGV 调度优化策略2.1单序响应算法基于贪心选择算法的思想[1]，假设这13个物料分配的RGV 花费的总时间最短时，整体一个班次RGV 的动态调度即是最优的。
记一段时间内的加工物料总个数为m 。
图1智能加工系统作业流程图1）初始令m =13，利用贪心选择算法，制定13个加工物料的RGV 初始调度策略。
在CNC#i 发出需求信号后，若RGV 运行到CNC#i 处的时间小于当前其他CNC 发出的需求信号的剩余时间，那么RGV 就先响应CNC#i 。
2）在RGV 响应CNC#i 后，将响应的CNC 编号记录在path 矩阵中。
此时其他CNC 发出需求信号，RGV 一律不响应，但会记录该时间段内发出需求信号的CNC 编号。
3）当RGV 完成对CNC#i 进行清洗作业后，优先选择已记录离自己最近的CNC 响应。
若等效距离点上的两个CNC 同时发出需求信号，RGV 优先响应奇数编号的CNC 。
