遗传算法实验六演示文稿

遗传算法实验报告专业：自动化：张俊峰学号：13351067 摘要：遗传算法，是基于达尔文进化理论发展起来的一种应用广泛、高效的随机搜索与优化方法。

本实验利用遗传算法来实现求函数最大值的优化问题，其中的步骤包括初始化群体、个体评价、选择运算、交叉运算、变异运算、终止条件判断。

该算法具有覆盖面大、减少进入局部最优解的风险、自主性等特点。

此外，遗传算法不是采用确定性原则而是采用概率的变迁规则来指导搜索方向，具有动态自适应的优点。

关键词：串集最优化评估迭代变异一：实验目的熟悉和掌握遗传算法的运行机制和求解的基本方法。

遗传算法是一种基于空间搜索的算法，它通过自然选择、遗传、变异等操作以及达尔文的适者生存的理论，模拟自然进化过程来寻找所求问题的答案。

其求解过程是个最优化的过程。

一般遗传算法的主要步骤如下：（1）随机产生一个确定长度的特征字符串组成的初始种群。

〔2〕对该字符春种群迭代地执行下面的步骤a和步骤b，直到满足停止准则为止：a计算种群中每个个体字符串的适应值；b应用复制、交叉和变异等遗传算子产生下一代种群。

〔3〕把在后代中表现的最好的个体字符串指定为遗传算法的执行结果，即为问题的一个解。

二：实验要求已知函数y=f〔x1,x2,x3,x4〕=1/(x12+x22+x32+x42+1),其中-5≤x1,x2,x3,x4≤5,用遗传算法求y的最大值。

三：实验环境操作系统：Microsoft Windows 7软件：Microsoft Visual studio 2010四：实验原理与步骤1、遗传算法的思想生物的进化是以集团为主体的。

与此相对应，遗传算法的运算对象是由M个个体所组成的集合，称为群体。

与生物一代一代的自然进化过程相类似，遗传算法的运算过程也是一个反复迭代过程，第t代群体极为P〔t〕，进过一代遗传和进化后，得到第t+1代群体，他们也是由多个个体组成的集合，记做P〔t+1〕。

这个群体不断地经过遗传和进化操作，并且每次都按照有优胜劣汰的规则将适应度较高的个体更多地遗传到下一代，这样最终在群体中将会得到一个优良的个体X，它所对应的表现性X将到达或接近于问题的最优解。

实验六：遗传算法求解TSP问题实验2篇第一篇：遗传算法的原理与实现1. 引言旅行商问题（TSP问题）是一个典型的组合优化问题，它要求在给定一组城市和每对城市之间的距离后，找到一条路径，使得旅行商能够在所有城市中恰好访问一次并回到起点，并且总旅行距离最短。

遗传算法作为一种生物启发式算法，在解决TSP问题中具有一定的优势。

本实验将运用遗传算法求解TSP问题，以此来探讨和研究遗传算法在优化问题上的应用。

2. 遗传算法的基本原理遗传算法是模拟自然界生物进化过程的一种优化算法。

其基本原理可以概括为：选择、交叉和变异。

（1）选择：根据问题的目标函数，以适应度函数来评估个体的优劣程度，并按照适应度值进行选择，优秀的个体被保留下来用于下一代。

（2）交叉：从选出的个体中随机选择两个个体，进行基因的交换，以产生新的个体。

交叉算子的选择及实现方式会对算法效果产生很大的影响。

（3）变异：对新生成的个体进行基因的变异操作，以保证算法的搜索能够足够广泛、全面。

通过选择、交叉和变异操作，不断迭代生成新一代的个体，遗传算法能够逐步优化解，并最终找到问题的全局最优解。

3. 实验设计与实施（1）问题定义：给定一组城市和每对城市之间的距离数据，要求找到一条路径，访问所有城市一次并回到起点，使得旅行距离最短。

（2）数据集准备：选择适当规模的城市数据集，包括城市坐标和每对城市之间的距离，用于验证遗传算法的性能。

（3）遗传算法的实现：根据遗传算法的基本原理，设计相应的选择、交叉和变异操作，确定适应度函数的定义，以及选择和优化参数的设置。

（4）实验流程：a. 初始化种群：随机生成初始种群，每个个体表示一种解（路径）。

b. 计算适应度：根据适应度函数，计算每个个体的适应度值。

c. 选择操作：根据适应度值选择一定数量的个体，作为下一代的父代。

d. 交叉操作：对父代进行交叉操作，生成新的个体。

e. 变异操作：对新生成的个体进行变异操作，以增加搜索的多样性。

实验六：遗传算法求解TSP问题实验3篇以下是关于遗传算法求解TSP问题的实验报告，分为三个部分，总计超过3000字。

一、实验背景与原理1.1 实验背景旅行商问题（Traveling Salesman Problem，TSP）是组合优化中的经典问题。

给定一组城市和每两个城市之间的距离，求解访问每个城市一次并返回出发城市的最短路径。

TSP 问题具有很高的研究价值，广泛应用于物流、交通运输、路径规划等领域。

1.2 遗传算法原理遗传算法（Genetic Algorithm，GA）是一种模拟自然选择和遗传机制的搜索算法。

它通过选择、交叉和变异操作生成新一代解，逐步优化问题的解。

遗传算法具有全局搜索能力强、适用于多种优化问题等优点。

二、实验设计与实现2.1 实验设计本实验使用遗传算法求解TSP问题，主要包括以下步骤：（1）初始化种群：随机生成一定数量的个体（路径），每个个体代表一条访问城市的路径。

（2）计算适应度：根据路径长度计算每个个体的适应度，适应度越高，路径越短。

（3）选择操作：根据适应度选择优秀的个体进入下一代。

（4）交叉操作：随机选择两个个体进行交叉，生成新的个体。

（5）变异操作：对交叉后的个体进行变异，增加解的多样性。

（6）更新种群：将新生成的个体替换掉上一代适应度较低的个体。

（7）迭代：重复步骤（2）至（6），直至满足终止条件。

2.2 实验实现本实验使用Python语言实现遗传算法求解TSP问题。

以下为实现过程中的关键代码：（1）初始化种群```pythondef initialize_population(city_num, population_size): population = []for _ in range(population_size):individual = list(range(city_num))random.shuffle(individual)population.append(individual)return population```（2）计算适应度```pythondef calculate_fitness(population, distance_matrix): fitness = []for individual in population:path_length =sum([distance_matrix[individual[i]][individual[i+1]] for i in range(len(individual) 1)])fitness.append(1 / path_length)return fitness```（3）选择操作```pythondef selection(population, fitness, population_size): selected_population = []fitness_sum = sum(fitness)fitness_probability = [f / fitness_sum for f in fitness]for _ in range(population_size):individual = random.choices(population, fitness_probability)[0]selected_population.append(individual)return selected_population```（4）交叉操作```pythondef crossover(parent1, parent2):index1 = random.randint(0, len(parent1) 2)index2 = random.randint(index1 + 1, len(parent1) 1)child1 = parent1[:index1] +parent2[index1:index2] + parent1[index2:]child2 = parent2[:index1] +parent1[index1:index2] + parent2[index2:]return child1, child2```（5）变异操作```pythondef mutation(individual, mutation_rate):for i in range(len(individual)):if random.random() < mutation_rate:j = random.randint(0, len(individual) 1) individual[i], individual[j] = individual[j], individual[i]return individual```（6）更新种群```pythondef update_population(parent_population, child_population, fitness):fitness_sum = sum(fitness)fitness_probability = [f / fitness_sum for f in fitness]new_population =random.choices(parent_population + child_population, fitness_probability, k=len(parent_population)) return new_population```（7）迭代```pythondef genetic_algorithm(city_num, population_size, crossover_rate, mutation_rate, max_iterations): distance_matrix =create_distance_matrix(city_num)population = initialize_population(city_num, population_size)for _ in range(max_iterations):fitness = calculate_fitness(population, distance_matrix)selected_population = selection(population, fitness, population_size)parent_population = []child_population = []for i in range(0, population_size, 2):parent1, parent2 = selected_population[i], selected_population[i+1]child1, child2 = crossover(parent1, parent2)child1 = mutation(child1, mutation_rate)child2 = mutation(child2, mutation_rate)parent_population.extend([parent1, parent2]) child_population.extend([child1, child2])population =update_population(parent_population, child_population, fitness)best_individual =population[fitness.index(max(fitness))]best_path_length =sum([distance_matrix[best_individual[i]][best_individual[i +1]] for i in range(len(best_individual) 1)])return best_individual, best_path_length```三、实验结果与分析3.1 实验结果本实验选取了10个城市进行测试，遗传算法参数设置如下：种群大小：50交叉率：0.8变异率：0.1最大迭代次数：100实验得到的最佳路径长度为：1953.53.2 实验分析（1）参数设置对算法性能的影响种群大小：种群大小会影响算法的搜索能力和收敛速度。

人工智能实验报告学号：姓名：实验名称：遗传算法实验日期：2016.1.5【实验名称】遗传算法【实验目的】掌握遗传算法的基本原理，熟悉遗传算法的运行机制，学会用遗传算法来求解问题。

【实验原理】遗传算法（ Genetic Algorithm ）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体组成。

每个个体实际上是染色体带有特征的实体。

在一开始需要实现从表现型到基因型的映射即编码工作。

由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

遗传算法程度流程图为：【实验名称】遗传算法【实验目的】掌握遗传算法的基本原理，熟悉遗传算法的运行机制，学会用遗传算法来求解问题。

【实验原理】遗传算法（ Genetic Algorithm ）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体组成。

每个个体实际上是染色体带有特征的实体。

在一开始需要实现从表现型到基因型的映射即编码工作。

由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。

遗传算法求函数最大值实验报告遗传算法是一种模拟自然界进化过程的优化算法，它通过模拟生物进化过程中的遗传、交叉和变异等机制，逐步优化解空间中的个体，以找到问题的最优解。

在本次实验中，我们利用遗传算法来求解一个函数的最大值。

下面我们将详细介绍实验的过程和结果。

首先，我们选择了一个简单的函数作为实验对象，即f(x) = x^2，在x的范围为[-10, 10]。

我们的目标是找到使函数值最大的x。

首先，我们需要定义遗传算法中的基本元素，包括编码方式、适应度函数、选择策略、交叉和变异操作等。

在本实验中，我们选择二进制编码方式，将x的范围[-10, 10]离散化为10位的二进制编码。

适应度函数即为f(x) = x^2，它表示个体的适应度。

选择策略采用轮盘赌选择算法，交叉操作采用单点交叉，变异操作采用随机位变异。

接下来，我们需要初始化种群，并迭代进行交叉和变异操作，直到满足终止条件。

在每一代中，我们根据适应度函数对种群中的个体进行评估，并根据选择策略选择父代个体进行交叉和变异操作。

通过交叉和变异操作，产生新的子代个体，并替代原有种群中的个体。

在本次实验中，我们设置了100个个体的种群，并进行了100代的迭代。

实验结果显示，经过多次迭代，算法逐渐优化到了最优解。

最终找到了使函数值最大的x，即x=10，对应的函数值为100。

总结起来，本次实验利用遗传算法求解函数的最大值，展示了遗传算法在优化问题中的应用。

通过适当选择编码方式、适应度函数和操作策略，我们可以有效地找到问题的最优解。

在后续的研究中，我们可以进一步探索遗传算法在更复杂问题上的应用，并通过改进算法的参数和操作策略来提高算法的性能。

实验六：遗传算法求解TSP问题实验一、实验目的熟悉和掌握遗传算法的原理、流程和编码策略，并利用遗传求解函数优化问题，理解求解TSP问题的流程并测试主要参数对结果的影响。

用遗传算法对TSP问题进行了求解，熟悉遗传算法地算法流程，证明遗传算法在求解TSP问题时具有可行性。

二、实验内容参考实验系统给出的遗传算法核心代码，用遗传算法求解TSP的优化问题，分析遗传算法求解不同规模TSP问题的算法性能。

对于同一个TSP问题，分析种群规模、交叉概率和变异概率对算法结果的影响。

增加1种变异策略和1种个体选择概率分配策略，比较求解同一TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。

1. 最短路径问题所谓旅行商问题(Travelling Salesman Problem , TSP)，即最短路径问题，就是在给定的起始点S到终止点T的通路集合中，寻求距离最小的通路，这样的通路成为S点到T点的最短路径。

在寻找最短路径问题上，有时不仅要知道两个指定顶点间的最短路径，还需要知道某个顶点到其他任意顶点间的最短路径。

遗传算法方法的本质是处理复杂问题的一种鲁棒性强的启发性随机搜索算法，用遗传算法解决这类问题，没有太多的约束条件和有关解的限制，因而可以很快地求出任意两点间的最短路径以及一批次短路径。

假设平面上有n个点代表n个城市的位置, 寻找一条最短的闭合路径, 使得可以遍历每一个城市恰好一次。

这就是旅行商问题。

旅行商的路线可以看作是对n个城市所设计的一个环形, 或者是对一列n个城市的排列。

由于对n个城市所有可能的遍历数目可达(n- 1)!个, 因此解决这个问题需要0(n!)的计算时间。

假设每个城市和其他任一城市之间都以欧氏距离直接相连。

也就是说, 城市间距可以满足三角不等式, 也就意味着任何两座城市之间的直接距离都小于两城市之间的间接距离。

2. 遗传算法遗传算法是由美国J.Holland教授于1975年在他的专著《自然界和人工系统的适应性》中首先提出的，它是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。

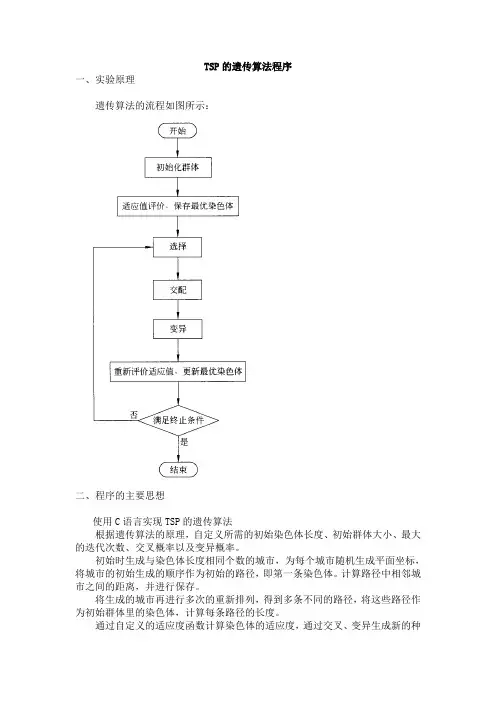
TSP的遗传算法程序一、实验原理遗传算法的流程如图所示：二、程序的主要思想使用C语言实现TSP的遗传算法根据遗传算法的原理，自定义所需的初始染色体长度、初始群体大小、最大的迭代次数、交叉概率以及变异概率。

初始时生成与染色体长度相同个数的城市，为每个城市随机生成平面坐标，将城市的初始生成的顺序作为初始的路径，即第一条染色体。

计算路径中相邻城市之间的距离，并进行保存。

将生成的城市再进行多次的重新排列，得到多条不同的路径，将这些路径作为初始群体里的染色体，计算每条路径的长度。

通过自定义的适应度函数计算染色体的适应度，通过交叉、变异生成新的种群。

对新种群继续迭代操作，直到达到初始定义的迭代次数，获得最终的路径及路径图。

三、程序的主要步骤①染色体初始化的子函数1)void initialize()2){int k,j,minx,miny,maxx,maxy;3)initdata();4)minx=0;5)miny=0;6)maxx=0;maxy=0;7)for(k=0;k<lchrom;k++)8){x[k]=rand();9)if(x[k]>maxx)maxx=x[k];10)if(x[k]<minx)minx=x[k];11)y[k]=rand();12)if(y[k]>maxy)maxy=y[k];13)if(y[k]<miny)miny=y[k];14)}15)if((maxx-minx)>(maxy-miny))16){maxxy=maxx-minx;}17)else {maxxy=maxy-miny;}18)maxdd=0.0;19)for(k=0;k<lchrom;k++)20)for(j=0;j<lchrom;j++)21){dd[k*lchrom+j]=hypot(x[k]-x[j],y[k]-y[j]);22)if(maxdd<dd[k*lchrom+j])maxdd=dd[k*lchrom+j];23)}24)refpd=dd[lchrom-1];25)for(k=0;k<lchrom;k++)26)refpd=refpd+dd[k*lchrom+k+2];27)for(j=0;j<lchrom;j++)28)dd[j*lchrom+j]=4.0*maxdd;29)ff=(0.765*maxxy*pow(lchrom,0.5));30)minpp=0;31)min=dd[lchrom-1];32)for(j=0;j<lchrom-1;j++)33){if(dd[lchrom*j+lchrom-1]<min)34){min=dd[lchrom*j+lchrom-1];35)minpp=j;36)}37)}38)initpop();39)statistics(oldpop);40)initreport();41)}7） for(k=0;k<lchrom;k++)8） {x[k]=rand();9） if(x[k]>maxx)maxx=x[k];10）if(x[k]<minx)minx=x[k];11）y[k]=rand();12）if(y[k]>maxy)maxy=y[k]13）if(y[k]<miny)miny=y[k];14）}此段程序是初始化多个城市的坐标值（x,y），其中（x[k],y[k]）代表第k+1个城市的坐标值，也相当于初始染色体的第k+1个基因值。