2011中考冲刺数学专题1-填空选择题

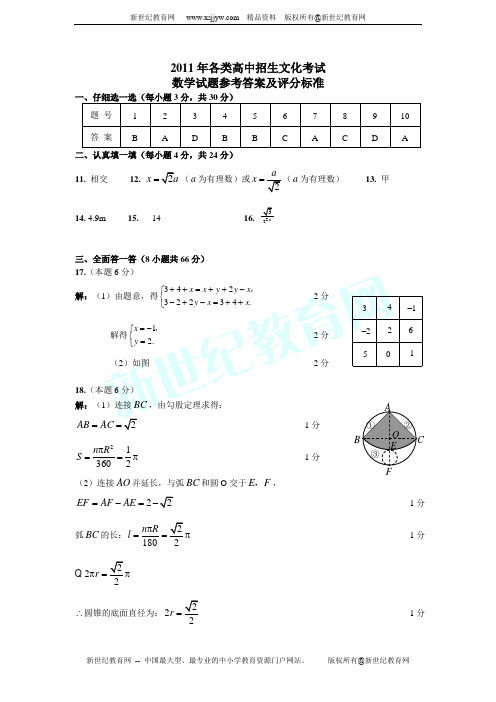
2011年各类高中招生文化考试 数学试题参考答案及评分标准一、仔细选一选（每小题3分，共30分）题 号 1 2 3 4 5 6 7 8 9 10 答 案BADBBCACDA二、认真填一填（每小题4分，共24分） 11. 相交 12. 2x a =（a 为有理数）或2ax =（a 为有理数） 13. 甲 14. 4.9m 15. 14 16. 223n三、全面答一答（8小题共66分） 17.（本题6分）解：（1）由题意，得34232234.x x y y x y x x ++=++-⎧⎨-+-=++⎩，················· 2分解得12.x y =-⎧⎨=⎩，····················································· 2分（2）如图 ················································ 2分18.（本题6分）解：（1）连接BC ，由勾股定理求得：2AB AC == ························································· 1分213602n R S π==π ························································ 1分 （2）连接AO 并延长，与弧BC 和圆O 交于E F ，，22EF AF AE =-=- ················································································ 1分弧BC 的长：21802n R l π==π ·········································································· 1分 222r π=π ∴圆锥的底面直径为：222r =········································································ 1分 –2 3 4 –1 6 152 ABCO ①②③E F2222-<，∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥． ············ 1分19.（本题6分）解：（1）如图，木柜的表面展开图是两个矩形11ABC D '和11ACC A ．蚂蚁能够最快到达目的地的可能路径有如图的11AC '和1AC ．…………………………2分（2）蚂蚁沿着木柜表面经线段11A B 到1C ，爬过的路径的长是2214(45)97l =++=．……………………………………1分蚂蚁沿着木柜表面经线段1BB 到1C ， 爬过的路径的长是222(44)589l =++=． ····················································· 1分12l l >，最短路径的长是289l =． ··································································· 2分 20.（本题8分）解：（1）作图如右，ABC ∆即为所求的直角三角形；……………4分 （2）由勾股定理得，AC =52cm ， ……………2分 ∵直角三角形斜边的中线等于斜边的一半∴斜边上的中线长为5． ……………2分21.（本题8分）解：（1）8，0.16…………………………………2分 补全频率分布直方图并正确． ···················· 2分 （2）中位数落在4.55~4.85组内．……………2分（3）15100030050⨯=（人）答：该校初三学生视力正常的人数约为300人． ··················································· 2分22.（本题10分）解：（1）∵△ABC 是等边三角形，DG ∥BC ， ∴△AGD 是等边三角形AG ＝GD ＝AD ，∠AGD ＝60° --------------------------------2分 ∵DE ＝DC ，∴GE ＝GD ＋DE ＝AD ＋DC ＝AC ＝AB ∵∠AGD ＝∠BAD ，AG ＝AD ，∴△AGE ≌△DAB --------------------------------3分 （2）由（1）知AE ＝BD ，∠ABD ＝∠AEG -----（1分）频率 组距视力0 3.95 4.25 4.55 4.85 5.15 5.45C A EA 1B 1C 1D 11C 'B∵EF ∥DB ，DG ∥BC ，∴四边形BFED 是平行四边形 -------------2分 ∴EF ＝BD ， ∴EF ＝AE ． --------------------------1分 ∵∠DBC ＝∠DEF ，∴∠ABD ＋∠DBC ＝∠AEG ＋∠DEF ,即∠AEF ＝∠ABC ＝60° ---1分 ∴△ABC 是等边三角形，∠AFE ＝60° --------------------------1分23.（本题10分）解：（1）设甲单独x 天喝完1包茶叶，则每天喝的茶叶为x1， ………… ………1分乙单独(x+48)天喝完1包茶叶，则每天喝的茶叶为481+x . …………………1分110)4811(=⨯++x x …………………2分 解得x=12或x =－40(舍去)，x+48=60 …………………2分 ∴甲单独12天喝完1包茶叶，乙单独60天喝完1包茶叶 …………………1分 （2）甲单独喝咖啡：1÷（201121-）=30天 …………………1分 ∴30天后甲喝完咖啡而乙只喝完茶叶的一半，故剩下的茶叶变成两人合喝，由题意可知，他们两人还能喝5天.∴两人35天才全部喝完． …………………2分 24.（本题12分）解：解：（1）∵抛物线23y ax x =-+（0a ≠）的对称轴为直线2x =-．∴122a --=-，∴14a =-， ∴2134y x x =--+． ···················································································· 2分∴(24)D -，． ································································································ 1分（2）探究一：当04t <<时，W 有最大值． ∵抛物线2134y x x =--+交x 轴于A B 、两点，交y 轴于点C ， ∴(60)A -，，(20)B ，，(03)C ，， ∴63OA OC ==，． (1)分当04t <<时，作DM y ⊥轴于M ， 则24DM OM ==，． ∵(0)P t ，，∴4OP t MP OM OP t ==-=-，． ∵PAD AOP DMP OADM S S S S =--△△△梯形y xOC B AD MP111()222DM OA OM OA OP DM MP =+-- 111(26)462(4)222t t =+⨯-⨯⨯-⨯⨯-122t =- ·························································································· 2分∴2(122)2(3)18W t t t =-=--+ ····································································· 1分 ∴当3t =时，W 有最大值，18W =最大值． ························································· 1分 探究二：存在．分三种情况：①当190PDA ∠=°时，作DE x ⊥轴于E ，则2490OE DE DEA ==∠=，，°， ∴624AE OA OE DE =-=-==．∴45DAE ADE ∠=∠=°，242AD DE ==， ∴11904545PDE PDA ADE ∠=∠-∠=-=°°°． ∵DM y ⊥轴，OA y ⊥轴，∴DM OA ∥，∴90MDE DEA ∠=∠=°， ∴11904545MDP MDE PDE ∠=∠-∠=-=°°°． ∴12PM DM ==，1222PD DM ==． 此时1324OC OA PD AD ==，又因为190AOC PDA ∠=∠=°， ∴1Rt Rt ADP AOC △∽△，∴11422OP OM PM =-=-=，∴1(02)P ，． ∴当190PDA ∠=°时，存在点1P ，使1Rt Rt ADP AOC △∽△，此时1P 点的坐标为（0，2）． ·········································· 2分（结论1分，过程1分） ②当290P AD ∠=°时，则245P AO ∠=°， ∴262cos 45OA P A ==°，∴26226P A OA ==．∵423AD OC =，∴2P A AD OC OA ≠． ∴2P AD △与AOC △不相似，此时点2P 不存在．··············· 2分（结论1分，过程1分） y xOC B AD MP 1 E P 2③当390AP D ∠=°时，以AD 为直径作1O ⊙，则1O ⊙的半径222ADr ==， 圆心1O 到y 轴的距离4d =．∵d r >，∴1O ⊙与y 轴相离． 不存在点3P ，使390APD ∠=°． ∴综上所述，只存在一点(02)P ，使Rt ADP △与Rt AOC △相似． ··················································· 14分（结论1分，过程1分）（其它方法可参照此答案给分）。

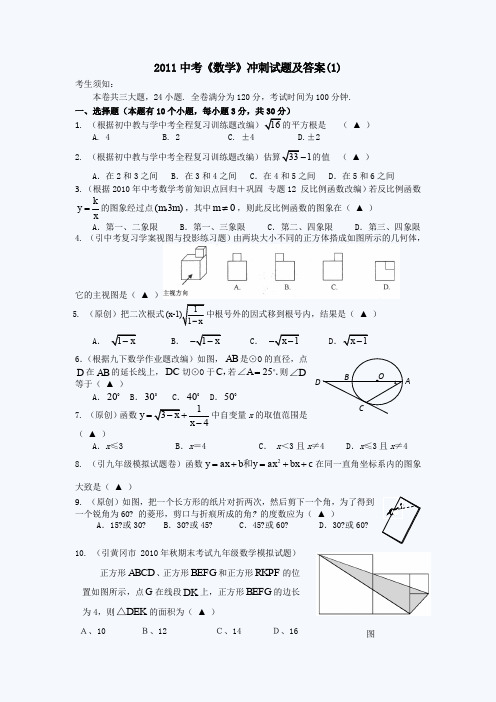
?2011中考《数学》冲刺试题及答案(1)考生须知：本卷共三大题，24小题. 全卷满分为120分，考试时间为100分钟. 一、选择题（本题有10个小题，每小题3分，共30分）1. （根据初中教与学中考全程复习训练题改编）16的平方根是 （ ▲ ）A. 4B. 2C. ±4D.±2 2. （根据初中教与学中考全程复习训练题改编）估算331-的值 （ ▲ ）A ．在2和3之间B ．在3和4之间C ．在4和5之间D ．在5和6之间 3. （根据2010年中考数学考前知识点回归＋巩固 专题12 反比例函数改编）若反比例函数ky x=的图象经过点(3)m m ，，其中0m ≠，则此反比例函数的图象在（ ▲ ） A ．第一、二象限 B ．第一、三象限 C ．第二、四象限 D ．第三、四象限 4. （引中考复习学案视图与投影练习题）由两块大小不同的正方体搭成如图所示的几何体，它的主视图是（ ▲ ）5. （原创）把二次根式1(x-1)1x-中根号外的因式移到根号内，结果是（ ▲ ） A ． 1x -B ． 1x --C ． 1x --D ．1x -6．（根据九下数学作业题改编）如图，AB 是⊙O 的直径，点D 在AB 的延长线上，DC 切⊙O 于C ，若25A =∠．则D ∠等于（ ▲ ）A ．20 B ．30 C ．40 D ．50 7. （原创）函数134y x x =-+-中自变量x 的取值范围是（ ▲ ）A ．x ≤3B ．x ＝4C ． x ＜3且x ≠4D ．x ≤3且x ≠4 8. （引九年级模拟试题卷）函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是（ ▲ ）9. （原创）如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个锐角为60? 的菱形，剪口与折痕所成的角? 的度数应为（ ▲ ）A ．15?或30?B ．30?或45?C ．45?或60?D ．30?或60? 10. （引黄冈市 2010年秋期末考试九年级数学模拟试题）正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示，点G 在线段DK 上，正方形BEFG 的边长为4，则DEK △的面积为（▲ ）Ａ、10 Ｂ、12 Ｃ、14 Ｄ、16图CBDAOA DEPBC二、填空题（共6小题，每题4分．共24分）11. （根据黄冈市2010年秋期末考试九年级数学模拟试题改编）一条弦把圆分成2:3两部分，那么这条弦所对的圆周角的度数为____▲______. 12. （根据2011年中考调研试卷改编）一串有趣的图案按一定的规律排列(如图)：按此规律在右边的圆中画出的第2011个图案：。

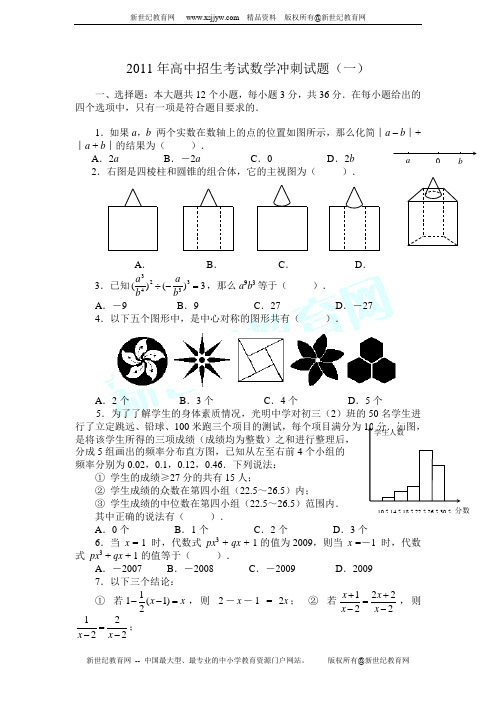
2011年高中招生考试数学冲刺试题（一）一、选择题：本大题共12个小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．如果a ，b 两个实数在数轴上的点的位置如图所示，那么化简︱a – b ︱+︱a + b ︱的结果为（ ）．A ．2aB ．－2aC ．0D ．2b 2．右图是四棱柱和圆锥的组合体，它的主视图为（ ）．A ．B ．C ．D ．3．已知3)()(33243=-÷ba b a ，那么a 9b 3等于（ ）． A ．－9 B ．9 C ．27 D ．－274．以下五个图形中，是中心对称的图形共有（ ）．A ．2个B ．3个C ．4个D ．5个5．为了了解学生的身体素质情况，光明中学对初三（2）班的50名学生进行了立定跳远、铅球、100米跑三个项目的测试，每个项目满分为10分．如图， 是将该学生所得的三项成绩（成绩均为整数）之和进行整理后，分成5组画出的频率分布直方图，已知从左至右前4个小组的频率分别为0.02，0.1，0.12，0.46．下列说法：① 学生的成绩≥27分的共有15人；② 学生成绩的众数在第四小组（22.5～26.5）内；③ 学生成绩的中位数在第四小组（22.5～26.5）范围内． 其中正确的说法有（ ）．A ．0个B ．1个C ．2个D ．3个6．当 x = 1 时，代数式 px 3 + qx + 1的值为2009，则当 x =－1 时，代数式 px 3 + qx + 1的值等于（ ）．A ．－2007B ．－2008C ．－2009D ．20097．以下三个结论：① 若x x =--)1(211，则 2－x －1 = 2x ； ② 若22221-+=-+x x x x ，则2221-=-x x ； 0 ba 10.5 14.5 18.5 22.5 26.5 30.5 分数 学生人数③ 若xx x -=--1111，则 x －1 = 1．其中正确的结论共有（ ）． A ．0个 B ．1个 C ．2个 D ．3个8．△ABC 中，若∠A :∠B :∠C = 1:2:3， CD ⊥AB 于D ，AB = a ，则DB 等于（ ）．A ．4aB ．3aC ．2aD ．43a 9．函数y = k （1－x ）和xk y = （k ≠0） 在同一平面直角坐标系中的图像可能是（ ）．A ．B ．C ．D ． 10．如图，△ABC 中，AB = AC ，∠BAC = 90°，直角∠EPF 的顶点P 是BC 的中点，两边PE ，PF 分别交AB 、AC 于E 、F ． 给出以下三个结论： ① AE = CF ； ② △PEF 是等腰直角三角形； ③ S 四边形AEPF =21S △ABC ． 当∠EPF 在△ABC 内绕顶点P 旋转时（点E 不与A 、B 重合），上述结论始终正确的是（ ）．A ．①②B ．①③C ．②③D ．①②③11．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图像可能是（ ）．A ．B ．C ．D ．解 根据汽车加速行驶221at s =，匀速行驶s = vt ，减速行驶221at s -=结合函数图像可知选A ．12．有若干个数，第一个数记为a 1，第二个数记为a 2，第三个数记为a 3，……，第n 个数记为a n ，若211-=a ，从第二个数起，每个数都等于“1与前面的那个数的差的倒数”，则a 2009等于（ ）．A ．21- B ．32 C ．3 D ．32-二、填空题：本大题共6个小题，每小题4分，共24分．将答案直接填写在题中横线上． x y O x y O x y O x y O P EF A B Ct s O t s O t s Ot s O13．已知2a －3 = 0，则代数式 a （a 2－a ）+ a 2（5－a ）－9 的值等于 ．14．不等式组⎪⎩⎪⎨⎧≤--+<+-1312412x x x x ，的整数解为 ． 15．若将一颗质地均匀的骰子（一种各面上分别标有1，2，3，4，5，6个点的正方体玩具），先后抛掷两次，则出现向上的点数之和为4的概率是等于 ．16．已知二次函数图象过点A （2，1）、B （4，1）且最大值为2，则二次函数的解析式为 ．17．如图，Rt △ABC 中，∠C = 90︒，AC =2，BC = 1，若 以C 为圆心，CB 为半径的圆交AB 于点P ，则AP = ．18．如图，直线834+-=x y 与x 轴、y 轴分别交于点A 和B ， M 是OB 上的一点，若将△ABM 沿AM 折叠，点B 恰好落在x 轴上的点B ′ 处，则直线AM 的解析式为 ． 三、解答题：本大题共7个小题，共90分．解答应写出文字 说明、证明过程或演算步骤．19．（本题共2个小题，每小题8分，共16分）（1）计算：01)3()21(45cos 8--+︒-π． （2）解方程组：⎩⎨⎧=-=.12,7xy x y20．（本题满分12分）如图，在Rt △ABC 中，∠ACB = 90︒，AC = BC = 10，CD 是射线，若∠BCE = 60︒，点D 在AB 上，AF 、BE 分别垂直于CD （或延长线）于E 、F ，（1）求EF 的长；（2）若∠BCE = α，试用α 的三 角函数来表示EF 的长，并指出当α 为何值时，EF 最小．21．（本题满分12分）如图，△ABC 和△ECD 都是等腰直角三角形，∠ACB A B P C B ′ O A M B x y D A C F B E=∠DCE = 90 ，D 为AB 边上一点，求证：（1）△ACE ≌△BCD ； （2）AD 2 + AE 2 = DE 2．22．（本题满分12分）网瘾低龄化问题已引起社会各界的高度关注．有关部门在全国范围内对12～35岁的网瘾人群进行了抽样调查．下图是用来表示在调查的样本中不同年龄段的网瘾人数的，其中30～35岁的网瘾人数占样本总人数的20%．（1）被抽样调查的样本总人数为 人；（2）请把统计图中缺失的数据、图形补充完整；（3）据报道，目前我国12～35岁网瘾人数约为200万人，那么其中12～17岁的网瘾人数约有多少人？23．（本题满分12分）在一块长16 m 、宽12 m 的矩形荒地上，要建造一个花园，并使花园所占的面积为荒地面积的一半．小明的设计方案如图甲所示，其中花园四周小路的宽度都相等．小明通过列方程，并解方程，得到小路的宽为2 m 或12 m ．小亮的设计方案如图乙所示，其中花园每个角上的扇形（四分之一圆弧）都相同．解答下列问题： D C B A E 网瘾人数(人) 0 600 576480 年龄(岁) 744 750 700 650 600 550 500450 12～17 18～23 24～29 30～35 网瘾人数(人) 0 600 576 480 年龄(岁) 750 700650 600 550500 450 12～17 18～23 24～29 30～35（1）小明的结果对吗？为什么？（2）请你帮小亮求出图乙中的x ？（3）你还有其他设计方案吗？甲 乙24．（本题满分12分）如图，已知AP 是⊙O 的切线，P 为 切点，AC 与⊙O 相交于B 、C 两点，圆心O 在∠PAC 的内部，点M 是BC 的中点． （1）证明：A ，P ，O ，M 四点共圆； （2）求∠OAM +∠APM 的大小．25．（本题满分14分）已知直线l 1：x y 21 和l 2：y =－x + m ，二次函数C ：y = x 2 + px + q 图像的顶点为M ．（1）若M 恰在直线l 1与l 2的交点处，试证明：无论m 取何实数值，二次函数C 的图像与直线l 2总有两个不同的交点；（2）在（1）的条件下，若直线l 2过点D （0，－3），求二次函数C 的表达式；（3）在（2）的条件下，若二次函数C 的图像与y 轴交于点C ，与x 轴的左交点为A ，试在抛物线的对称轴上求点P ，使得△PAC 为等腰三角形．M C B P O A 12 m16 m 12 m 16 m 12 m 16 mx m。

2011年高中招生考试数学冲刺试题（三）一、选择题：本大题共12个小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．用四舍五入法把0.06097精确到千分位后，所得近似值的有效数字是（ ）．DA ．0，6，0B ．0，6，1，0C ．6，0，9D ．6，12．下列等式正确的是（ ）．DA ．（－1）5 = 1B ．（－2）3×（－2）2 = 26C ．（－5）8 ÷（－5）2 =－56D ．（－4）0 = 13．已知 x + y = x －1 + y －1≠0，则xy 的值为（ ）．CA ．－1B ．0C ．1D ．24．如图，涪江河电站（青义）工程，需开挖土石方约53万m 3，要求34个月完成．施工队加班加点，提前两个月完工．施工队实际挖洞所用的时间t （月）与剩余土石方量M （万m 3）的函数关系图象大致是（ ）．AA ．B ．C ．D ．5．已知等腰三角形的两边长分别为6 cm ，3 cm ，则该等腰三角形的周长是（ ）．DA ．9 cmB ．12 cm 或15 cmC ．12 cmD ．15 cm6．某次射击训练中，一小组的成绩如下表：环数7 8 9 人数2 3 已知该小组的平均成绩为8.1环，那么成绩为8环的人数是（ ）．AA ．5人B ．6人C ．4人D ．7人7．若方程组⎩⎨⎧=-+=+3)1(,134y a ax y x 的解x 与y 相等，则a 的值等于（ ）． C A ．4 B ．10 C ．11 D ．128．如图，以点O 为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P 为切点，且AB = 4，OP = 2．连结OA交小圆于点E ，则扇形OEP 的面积为（ ）．CA ．4πB ．3πC ．2πD ．8π 9．△ABC 中，A （－1，2），B （－3，1），C （0，－1）．若将△ABC 绕点C 顺时针旋转180︒后得到△A ′B ′C ′，则A 点的对应点A ′ 的坐标是（ ）．DA ．（2，－3）B ．（1，－3）C ．（2，－4）D ．（1，－4）10．已知函数xy 21=，y 2 = x + 1，若y 1＞y 2，则x 的取值范围是（ ）． D A ．x ＜－1 或 0＜x ＜2 B ．－1＜x ＜0 或 x ＞2C ．－2＜x ＜0 或 x ＞1D ．x ＜－2 或 0＜x ＜111．设b ＞0，二次函数y = ax 2 + bx + a 2－1的图象为下列之一：t /月 O M /万m 3 32 53 t /月 O M /万m 3 34 53 t /月 O M /万m 332 53 t /月 O M /万m 3 34 53 E A BP O O x y 1 -1 O x y 1 -1 O x y O x y则a 的值为（ ）．A ．1B ．－1C ．251--D ．251+- 解 ∵ b ＞0，∴ 不是前两个图形．从后两个图形看a b 2-＞0，∴ a ＜0，故应是第3个图形．由于过原点，∴ a 2－1 = 0，结合a ＜0，得a =－1，选B ．12．如图，l 1、l 2、l 3 是同一平面内的三条平行直线，l 1与l 2间的距离是1，l 2与l 3间的距离是2，正三角形ABC 的三顶点分别在l 1、l 2、l 3上，则△ABC 的边长a 是（ ）．A ．32B ．364C ．4173D ．3212 解 作高AE 、BG 、CF （如图）．设 AD = x ，则 CD = 2x ，于是 2x DG =，x x BG 233323=⋅=． 由 Rt △BCG ∽ Rt △CDF ，得 DF DG CF BG =，即DF x x 22233=，得 332=DF ． ∴ 331=DE ，因此 272827112=+=AD ， ∴ 32122728333===AD x ．二、填空题：本大题共6个小题，每小题4分，共24分．将答案直接填写在题中横线上．13．21-的倒数是 ．－2 14．计算：（9a 2b －6ab 2）÷（3ab ）= ．3a －2b15．代数式11-x 有意义时，字母x 的取值范围是 ．x ＞1 16．如图，在等腰梯形ABCD 中，AD ∥BC ，AB = CD ，对角线AC 、BD 相交于点O ，如下有四个结论：① 梯形ABCD 是轴对称图形； ② ∠DAC =∠DCA ；③ △AOB ≌△DOC ； ④ △AOD ∽△BOC ． 请把正确的结论的序号填在横线上： ．①③④ 17．如图，在直角三角形ABC 中，∠ACB = 90︒，CA = 4．点P 是半圆弧AC 的中点，连接BP ，线段BP 把图形APCB分成两部分，则这两部分面积之差的绝对值是 ． 解 如图，设AC 与BP 相交于点D ，点D 关于圆心O 的对称 点记为点E ，线段BP 把图形APCB 分成两部分，这两部分面积之差的绝对值是△BEP 的面积，即△BOP 面积的两倍．而 S △BOP =21PO ×CO =21×2×2 = 2．因此，这两部分面积之差的绝对值是4． 18．口袋中有20个球，其中白球9个，红球5个，黑球6个．现从中任取10个球，使得白球不少于2个但不多于8个，红球不少于2个，黑球不多于3个，那么上述取法的种数是 ．16B D A OC OD C BE P A BC A l 1 l 2 l 3解 用枚举法：红球个数 白球个数 黑球个数 种数5 2，3，4，5 3，2，1，0 44 3，4，5，6 3，2，1，0 43 4，5，6，7 3，2，1，0 42 5，6，7，8 3，2，1，0 4所以，共16种．三、解答题：本大题共7个小题，共90分．解答应写出文字说明、证明过程或演算步骤．19．（本题共2个小题，每小题8分，共16分）（1）计算：︒+︒+︒30tan 160sin 160cos ． （2）先化简，再求值：)2(2ab ab a a b a --÷-，其中a = 1 +3，b = 1． 19．（1）原式=323121++=23321=++； （2）原式=a b ab a a b a 222+-÷-=b a b a b a -=--1)(2． 把a = 1 +3，b = 1代入，可得原式=33． 20．（本题满分12分）房屋交易会期间，某公司对参加本次房交会的消费者进行了随机问卷调查．共发放1 000份调查问卷，并全部收回，根据调查问卷，将消费者年收入的情况整理后，制成表格如下：年收人（万元）1.2 1.8 3.0 5.0 10.0 被调查的消费者数（人）200 500 200 70 30 将消费者打算购买住房面积的情况调查后，做出部分频数分布直方图：注：每组包含最小值不包含最大值，且住房的面积取整数．请你根据以上信息，回答下列问题：（1）根据表格可得，被调查的消费者平均年收人为 万元；被调查的消费者年收入的中位数是 万元；在平均数、中位数这两个数中 更能反映被调查的消费者年收入的一般水平；（2）根据频数分布直方图可得，打算购买100－120平方米房子的人数为 人；打算购买住房面积小于100平方米的消费者人数与被调查人数的百分数是 面积／平方米；（3）在图中补全这个频数分布直方图．40 60 80 100 120 140 160 住房面积 人数 360 200 120 40 40 60 80 100 120 140 160 住房面积 人数 360 240 200 120 4020．（1）2.39，1.8，中位数 （2）240，52% （3）如图（见前）21．（本题满分12分）如图，请在下列四个等式中，选出两个作为条件，推出△AED 是等腰三角形，并予以证明．（写出一种即可）等式：① AB = DC ， ② BE = CE ，③ ∠B =∠C ， ④∠BAE =∠CDE ． 21．已知：①③（或①④，或②③，或②④）证明：在△ABE 和△DCE 中， ∵ ∠B =∠C ，∠BEA =∠CED ，AB = DC ，∴ △ABE ≌△DCE ，∴ AE = DE ．△AED 是等腰三角形．22．（本题满分12分）平面直角坐标系中，点A 在第一象限，点B 的坐标为（3，0），OA = 2，∠AOB = 60︒．（1）求点A 的坐标； （2）若直线AB 交y 轴于点C ，求△AOC 的面积．22．（1）过点A 作x 轴的垂线，垂足为D ．在Rt △OAD 中，OA = 2，∠AOB = 60︒，∴ ∠OAD = 30︒，OD =21OA = 1，于是 AD =3．A （1，3）． （2）设直线AB 的解析式为y = kx + b ，把A （1，3），B （3，0）分别代入，得⎩⎨⎧+=+=,30,3b k b k 解得23-=k ，233=b ． ∴ AB 的解析式为y =23-x +233．令 x = 0 得 y =233，则C （0，233）． 所以，S △AOC =21OC ×1 =433．23．（本题满分12分）青年旅行社为吸引市民组团去香水湾风景区旅游，推出了如下收费标准：某单位组织员工去香水湾风景区旅游，共支付给青年旅行社旅游费用27000元，请问该单位这次共有多少员工去香水湾风景区旅游？23．设该单位这次共有x 名员工去香水湾风景区旅游，因为1000×25 = 25000＜27000，所以员工人数一定超过25人．可得方程 [ 1000－20（x －25）] x = 27000， 整理，得 x 2－75x + 1350 = 0， 解得 x 1 = 45，x 2 = 30．当x 1 = 45时，1000－20（x －25）= 600＜700，故舍去x 1．当x 2 = 30时，1000－20（x －25）= 900＞700，符合题意．答：该单位这次共有30名员工去香水湾风景区旅游．O B y xA 如果人数不超过25人，人均旅游费用为1000元 如果人数超过25人，每增加1人，人均旅游费用降低20元，但人均旅游费用不得低于700元 BA D E C24．（本题满分12分）如图，AB ，AC ，AD 是圆中的三条弦， 点E 在AD 上，且AB = AC = AE ．请你说明以下各式成立的理由．（1）∠CAD = 2∠DBE ；（2）AD 2－AB 2 = BD · DC ．24．（1）如图，连接BC ，∵ AB = AC = AE ，∴ ∠5 =∠2，∠2 +∠3 =∠6．又 ∠4 +∠5 =∠6 =∠2 +∠3， ∴ ∠4 =∠3．而 ∠1 =∠4 +∠3，∴ ∠1 = 2∠4，即 ∠CAD = 2∠DBE ． （2）设BC 与AD 的交点为G ． ∵ ∠2 = ∠5，∠BAG =∠DAB ， ∴ △BAG ∽△DAB ， ∴ AB 2 = AG · AD ． ∴ AD 2－AB 2 = AD 2－AG · AD = AD （AD －AG ）= AD · DG ．又 ∵ ∠5 =∠ADC ，∠DBG =∠1， ∴ △BDG ∽△ADC ，∴ DB : AD = DG :DC ，AG · AD = BD · DC ．∴ AD 2－AB 2 = BD · DC ．25．（本题满分14分）设抛物线y = ax 2 + bx －2与x 轴交于两个不同的点 A （－1，0）、B （m ，0），与y 轴交于点C ．且∠ACB = 90°． （1）求m 的值和抛物线的解析式； （2）已知点D （1，n ）在抛物线上，过点A 的直线y = x + 1交抛物线于另一点E ．若点P 在x 轴上，以点P 、B 、D 为顶点的三角形与△AEB 相似，求点P 的坐标．25．（1）在y = ax 2 + bx －2中，令x = 0，得 y =－2， ∴ C （0，－2）． ∵ ∠ACB = 90°，CO ⊥AB ，∴ △AOC ∽△COB ，∴ OA ·OB = OC 2，∴ OB = 4，即 m = 4． 将A （－1，0），B （4，0）代入y = ax 2 + bx －2，解得21=a ，23-=b ． ∴ 抛物线的解析式为223212--=x x y ． （2）D （1，n ）代入223212--=x x y ，得 n =－3． 由 y = x + 1和223212--=x x y 解得 ⎩⎨⎧=-=01y x 或 ⎩⎨⎧==76y x ∴ E （6，7）．过E 作EH ⊥x 轴于H ，则H （6，0），∴ AH = EH = 7，∴ ∠EAH = 45°． 过D 作DF ⊥x 轴于F ，则F （1，0），∴ BF = DF = 3，∴ ∠DBF = 45°， ∴ ∠EAH =∠DBF = 45°．从而 ∠DBH = 135°，90°＜∠EBA ＜135°，则点P 只能在点B 的左侧：① 若△DBP 1∽△EAB ，则AEBD AB BP =1， ∴ 715272351=⨯=⋅=AE BD AB BP ，∴ 71371541=-=OP ，得 ），（07131P ． D A C E B D A C E B 1 2 4 5 6 3 H E D B C A O y x F② 若△DBP 2∽△BAE ，则AB BD AE BP =2，∴ 542523272=⨯=⋅=AB BD AE BP ， ∴ 52245422=-=OP ， 得 ），（05222-P ． 综合①、②，点P 的坐标为），（07131P 或），（05222-P ．P 1 H E D B C A Oy xF P 2。

2011年九年级数学模拟试题(卷)（满分150分）题 号 一 二 三 四 总 分得 分一、选择题：（本题有12道小题，每小题3分，共36分.每小题只有一个选项是正确的，不选、多选、错选均不得分）1、下列图形中不是中心对称图形的是 （ ）A B C D2、要使分式55||--x x 的值为零，x 的值应为 （ ） A. 5 B. -5 C. +5 D . 0 3、圆柱底面直径为2cm,高为4cm,则圆柱的侧面积为（ ） A. 8π B. 16π C. 17π D . 25π 4、在⊿ABC 中，∠C=900，∠B=2∠A,则cosA 等于 （ ） A. 23B. 21C.3 D . 335、小明本学期6次数学考试成绩依次是92分、87分、87分、72分、67分、75分，老师要求把6次测试平均水平告知家长，小明应选择哪个值能使家长感觉他的成绩不错 （ ） A. 平均数 B. 众数 C. 中位数 D . 极差6、在半径为1的⊙0中，弦AB=1，则弧AB 的长为 （ ）A. B. C. D . 评卷人 得 分6π4π3π2πA OB东北7. 若x=1是方程x 2+kx+2=0的一个根，则方程的另一个根与k 的值是（ ） A. 2,3 B. -2,3 C.-2，-3 D . 2，-3 8. 已知⊙O 1与⊙O 2内切，它们的半径分别为2和3，则这两圆的圆心距d 满足 （ ） A 、d=5 B 、d=1 C 、1<d<5 D 、d>59.如图，AB 是⊙O 的直径，AC 是⊙O 的切线，A 为切点，连接BC ，若∠ABC =45°，则下列结论正确的是（ ）A ． AC ＞AB B ． AC =AB C ． AC ＜ABD ． AC =12B C10.在同一直角坐标系中，一次函数y =ax +c 和二次函数y =ax 2+c 的图象大致为( )11.如图，小雅家（图中点O 处）门前有一条东西走向的公路，经测得有一水塔（图中点A 处）在她家北偏东60度500m 处，那么水塔所在的位置到公路的距离AB 是（ ）．AB O C45°xy O Axy O Bxy O CxyO D第11题图A ．250mB ．2503mC ．50033m D ．250 2m 12.“圆柱与球的组合体”如图所示，则它的三视图是（ ）．二、填空题本10小题，每小题各4分，共40分。

2011中考数学分类总复习检测题（一）一、选择题 二、填空题1112、3 13、()()22a b a b +- 14、1 15、 2 16、17 三、解答题17、解：原式＝4283+⨯-＝43+＝1． 18、13+ 19、解：2212111(1)(1)(1)(1)a a a a a a a -+=+-++-+- 11(1)(1)1a a a a +==+--当3a =时，原式1111312a ===--． 20、1 21、选一：212()242x A B C x x x ⎛⎫-÷=-÷⎪--+⎝⎭=222x x x x x +⨯+-()()=12x -． 当3x =时，原式=1132=-． 选二：212242x A B C x x x -÷=-÷--+ 122222x x x x x+=-⨯-+-()() =122(2)x x x --- 题号 1 2 3 4 5 6 7 8 9 10 答案 ABBBCBCDBA=21(2)x x x x-=-．当3x =时，原式=13． 22、31-23、原方程可化为25265x x -=-．（下面请大家用配方法写出解此方程的详细过程） 解：（1）15x =，215x =； （2）21a a+（或1a a +）；（3）二次项系数化为1，得22615x x -=-． 配方，得2222613131555x x ⎛⎫⎛⎫-+-=-+- ⎪ ⎪⎝⎭⎝⎭，213144525x ⎛⎫-=⎪⎝⎭． 开方，得131255x -=±． 解得15x =，215x =．经检验，15x =，215x =都是原方程的解24、4 25、（1）111n n -+ （2）证明：n 1－11+n ＝)1(1++n n n －)1(+n n n ＝1(1)n n n n +-+＝)1(1+n n . （3）原式＝1－12＋12－31＋31－41＋…＋20091－20101＝12009120102010-=.2011中考数学分类总复习检测题（二）一、选择题二、填空题11、6 12、100 13、2=x 14、10 15、 1 16、4 三、解答题 17、 3.x =18、⎩⎨⎧==515y x19、15138-=x 20、523x y ⎧⎪=⎨⎪=-⎩21、解：设甲种帐篷x 顶，乙种帐篷y 顶 依题意，得⎩⎨⎧=+=+2600001000800300y x y x解以上方程组，得x =200，y =100 答：甲、乙两种帐篷分别是200顶和100顶.22、成本价100元23、解：设一类门票的单价为x 元/张，二类门票的单价为y 元/张.则有25180061600x y x y +=⎧⎨+=⎩解得：400200x y =⎧⎨=⎩答：一类门票的单价为400元/张，二类门票的单价为200元/张24、解：（1）地面总面积为：（6x ＋2y ＋18）m 2；（2）由题意，得6221,6218152.x y x y y -=⎧⎨++=⨯⎩解之，得4,3.2x y =⎧⎪⎨=⎪⎩∴地面总面积为：6x ＋2y ＋18＝6×4＋2×32＋18＝45（m 2）． ∵铺1m 2地砖的平均费用为80元，∴铺地砖的总费用为：45×80＝3600（元）．题号 1 2 3 4 5 67 8 9 10 答案A A C C D C BBAD25、解：（1）设8W 节能灯的价格为x 元，24W 节能灯的价格为y 元．则43292217x y x y +=⎧⎨+=⎩， ①． ②解之 3.55x y =⎧⎨=⎩，．答：该县财政补贴50%后，8W 节能灯的价格为3.5元，24W 节能灯的价格为5元． （2）全国一年大约可节约电费：2.3500013.5850⨯≈（亿元） 大约减排二氧化碳：43.55000255.9850⨯≈（万吨）2011中考数学分类总复习检测题（三）一、选择题二、填空题11、X=5 12、X=0或 X=2 13、10℅ 14、64m m >-≠-且 15、-2 16、5 三、解答题17、12x =-18、解：1a =，2b =-，1c =-224(2)41(1)8b ac -=--⨯⨯-=∴x =1282⨯±1=±2方程的解为：11x =21x =注：用配方法解同理给分.19、解：由题意可知 0= ．即 2(4)4(1)0m ---=．解得 5m =．当5m =时，原方程化为2440x x -+=． 解得 122x x ==．所以原方程的根为 122x x ==． 20、解：设正方形观光休息亭的边长为x 米.依题意，有(1002)(502) 3 600.x x --=题号 1 2 3 4 5 6 7 89 10 答案C B B A B CD A BD整理，得2753500.x x -+= 解得12570.x x ==，7050x => ，不合题意，舍去， 5.x ∴=答：矩形花园各角处的正方形观点休息亭的边长为5米. 21、解：由题意得：05)1()1(2=-⨯-+-m 解得：4-=m当4-=m 时，方程为：0542=--x x 解得：11-=x ，52=x 所以方程的另一个根为：52=x22、设原计划每天生产x 吨纯净水，则依据题意，得：,35.118001800=-xx 整理，得：4.5x =900， 解之，得：x =200， 把x 代入原方程，成立， ∴x =200是原方程的解．答：原计划每天生产200吨纯净水．24、（1）略（2）5,5,221-==-=x x m25、解：(1)设乙独做x 天完成此项工程，则甲独做（30x +）天完成此项工程. 由题意得：20（3011++x x ）=1整理得：2106000x x --= 解得：130x =，220x =-经检验：130x =，220x =-都是分式方程的解， 但220x =-不符合题意舍去答：甲、乙两工程队单独完成此项工程各需要60天、30天 （2）设甲独做a 天后，甲、乙再合做（20-3a）天，可以完成此项工程. （3）由题意得：1×(1 2.5)(20)643a a ++-≤解得：36a ≥答：甲工程队至少要独做36天后，再由甲、乙两队合作完成剩下的此项工程，才能使施工费不超过64万元.2011中考数学分类总复习检测题（四）一、选择题二、填空题11、1，2，3 12、2x <≤4 13、10 14、117 15、 -1 16、1<k 三、解答题17、解：3315>--x x 42>x2>x18、2 3.x <≤ 19、略20、59<<-x 21、3或32-a22、由题意得：⎪⎩⎪⎨⎧<---=--->--)3(0)5(4)4()2(0)7(4)6()1(0)3(4222b a b a b a 解之得：a=2 ,b=323、解:设选购B 种服装x 件，则选购A 种服装为（2x +4）件，由题意得⎩⎨⎧≤+≥++4842174032)42(25x x x解之得⎩⎨⎧≥≤2022x x∴20≤x ≤22∵x 为正整数 ∴x 1＝20，x 2＝21，x 3＝22. ∴当x 1＝20时，42+x ＝2×20+4＝44， 当x 2＝21时，42+x ＝2×21+4＝46，当x 3＝22时，42+x ＝2×22+4＝48.∴老板有三种选购方案：购进B 种品牌服装20件，购进A 种品牌服装44件；购进B 种品牌服装21件，购进A 种品牌服装46件； 购进B 种品牌服装22件，购进A 种品牌服装48件24、解：（1）设单独租用35座客车需x 辆，由题意得：3555(1)45x x =--,解得：5x =.∴35355175x =⨯=（人）.答：该校八年级参加社会实践活动的人数为175人．（2）设租35座客车y 辆，则租55座客车（4y -）辆，由题意得：题号 1 2 3 4 5 6 7 89 10 答案D D B A A C B C DC3555(4)175320400(4)1500y y y y +-⎧⎨+-⎩≥≤，解这个不等式组，得111244y ≤≤．∵y 取正整数， ∴y = 2.∴4－y = 4－2 = 2.∴320×2＋400×2 = 1440（元）.所以本次社会实践活动所需车辆的租金为1440元．25、（1）3种（2）3264元2011中考数学分类总复习检测题（五）一、选择题 二、填空题11、1 12、 2 13、2>m 14、 -12 15、 2 16、 (12)--， 三、解答题 17、2,2-==b k 18、12+=x y 19、22-=x y 20、323-=x y21、(1) )1,2(- )1,2( )1,0(- (2) 略 22、(1) 900 (2) 慢车75 快车 150 (3) 略23、证明：解：（1）设反比例函数解析式为ky x = ，点()14A ，在反比例函数的图象上 441kk ∴=∴=∴，，反比例函数的解析式为4y x =（2）设直线AB 的解析式为()00y ax b a b =+>>，题号1 2 3 4 5 6 7 8 9 10 答案 DDABCADBCB联立2440y ax bx xy ax b⎧=⎪⇒+-=⎨⎪=+⎩（★）y ax b =+ 过点()1A ，4 4a b ∴+=4b a ∴=-代入（★）得：()2440ax a x +--=方法1.由114a -⨯可得1x =或4x a =-显然1x =是A 点的横坐标，4x a=-是B 点的横坐标.设直线AB 交y 轴于点C ，则()0C b ，，即()04C a -， 由()112AOB AOC BOC S S S a =+=⨯+△△△·4-()141522a a ⎛⎫=⎪⎝⎭·4-，整理得 215160a a +-=1a ∴=或16a =-（舍去）413b ∴=-=∴直线AB 的解析式为3y x =+方法2.同方法1.得()2440ax a x +--=由求根公式也可得1x =或4x a=- 方法3.同方法1.得()2440ax a x +--=由2111522AOB S OC x x =-=△·()21440a a x x a a a ++-===> 4OC b a ==-可得()1415422a a a +⎛⎫-= ⎪⎝⎭解得1a =或16=-（舍去） 24、略25、（1）由题意知 2166k =⨯=∴反比例函数的解析式为6y x=． 又(3)B a ，在6y x=的图象上，2a ∴=．(23)B ∴，． 直线1y k x b =+过16A(，)，(23)B ，两点，11623k b k b +=⎧∴⎨+=⎩，． 139k b =-⎧∴⎨=⎩，． （2）x 的取值范围为12x <<． （3）当12OBCD S =梯形，PC PE =．设点P 的坐标为()m n ，,23BC OD CE OD BO CD B ⊥= ∥，，，（，），(3)322C m CE BC m OD m ∴==-=+，，，，. 2OBCD BC OD S CE +∴=⨯梯形，即221232m m -++=⨯． 4m ∴=．又362mn n =∴=，．即12PE CE =．PC PE ∴=．2011中考数学分类总复习检测题（六）一、选择题 二、填空题11、（3，0） 12、8 13、132+-=x y 14、)2,6(或)2,6(- 15、X=2 16、-4 三、解答题 17、 略 18、)4,1(19、解：(1)把A (2，0)、B (0，-6)代入c bx x y ++-=221 得:2206b c c -++=⎧⎨=-⎩解得46b c =⎧⎨=-⎩∴这个二次函数的解析式为21462y x x =-+- (2) ∵该抛物线对称轴为直线4412()2x =-=⨯-∴点C 的坐标为(4，0) ∴AC=OC －OA =4－2=2题号 1 2 3 4 5 6 7 8 9 10 答案 DBADDABDBA∴1126622ABC S AC OB =⨯⨯=⨯⨯=△ 20、解：（1）过点C 作CD AB ⊥，垂足为D ，则12CD CA CB ===，，∴DB DA ==点(1A，点10)B ，．（2）延长DC ，交C 于点P ．由题意可知，P 为抛物线的顶点，并可求得点(13)P ，． 设此抛物线的表达式为2(1)3y a x =-+，又∵抛物线过点10)B ，，则2011)3a =-+，得1a =-． 所以此抛物线的解析式为22(1)322y x x x =--+=-++． 21、(1) 232+-=x x y (2) 31><x x 或22、(1)m=-5 c=-2 (2) ），顶点坐标（对称轴1111)1(2222-=---=-+-=x x x x y 23、)6(542121)6(54456)5(654,3-∙∙=∙=∴-==-=∴∆∆⊥<-===∴==∆∆x x FD AE S x FD FD x BC FD AB AF ACB Rt ADF Rt DAC FD F AF x AF x AE AB BC AC ABC Rt AEF 得即相似于作过点，则中解：在 C E A24、解：（1）AB 为直径，90ACB ∴∠=︒．又90PC CD PCD ⊥∴∠=︒ ，而AC BCCAB CPD ABC PCD PC CD∠=∠∴∴=，△∽△，·AC CD PC BC ∴=·；（2）当点P 运动到AB 弧中点时，过点B 作BE PC ⊥于点E ，P 是AB 中点452PCB CE BE BC ∴∠=︒===，又CAB CPB ∠=∠ 43tan tan 3tan 4BE CPB CAB PE CPB ∴∠=∠=∴==∠，3422BE BC ⎛⎫== ⎪ ⎪⎝⎭从而2PC PE EC =+=，由（1）得433CD PC ==（3）当点P 在AB 上运动时，12PCD S PC CD =△·，由（1）可知，43CD PC = 223PCD S PC ∴=△故PC 最大时，PCD S △取最大值时；而PC 为直径时最大. PCD S ∴△的最大值2250533S =⨯=.25、略2011中考数学分类总复习检测题（七）一、选择题二、填空题11、40 , 4.6 12、15.2 , 3040 13、200 14、4 , 0.1 15、1.61 16、37770三、解答题 17、3564018、(1) 26 (2) 27 19、(1) 41 (2) 4920020、(1) 45 (2) 众数90 ， 中位数80 21、(1) 85.5 (2) 87.75 22、解：（1）设调查的人数为x ，则根据题意：题号 1 2 3 4 5 6 7 8 9 10答案A D A CB A DC B CP30300x x =∴=·10%， ∴一共调查了300人（2）由（1）可知，完整的统计图如图所示（3）设该市民支持“强制戒烟”的概率为P ，由（1）可知，40%0.4P ==支持“警示戒烟”这种方式的人有1000035%3500=·(人).23、(1) 165 (2)3300 24、解：（1）补图正确（如图）； （2）1520- （3）11025、(1) 3.0,12,8===c b a (2) 略 (3) 602011中考数学分类总复习检测题（八）一、选择题 二、填空题 11、15岁，52 12、52 13、41 14、3115、10，20 16、0.3 三、解答题17、解：（1）P （取出绿球）=53521=-； （2）设袋中绿球有x 个，则5312=+x x解得x =18经检验x =18是方程的解，所以袋中的绿球有18个. 18、 (1)41(2) 24 题号 12 3 4 5 6 7 8 9 10 答案 DCACBAADAC替代品戒烟 警示戒烟 药物戒烟强制戒烟10% 15%戒烟 戒烟 戒烟 戒烟 60 3035% 40%19、(1) 32(2) 略 20、(1) 略 (2) 6121、(1)平均分 众数 中位数 马琳 8.7 11 9.0 王励勤9.71111(2)8011161602016160503232000=∴=⨯：刘敏同学中奖的概率为22、解：（1）由题意，画树状图如下：A －D ；A －E ；A －F ；B －D ；B －E ；B －F ；C －D ；C －E ；C －F ． 共有9种情况并且这9种情况出现的可能性相同（2）首场比赛中两个队都为部队文工团的情况有3种，即A －D ；B －D ；C －D 所以P=3193=． 23、 略24、(1) 30 20 (2)21(3) 500 25、(1) 15000 (2) 801 4012011中考数学分类总复习检测题（九）一、选择题 二、填空题11、70 12、 70 13、25 14、略 15、90 16、60 三、解答题 17、53 18、 110 19、3cm 20、 25题号1 2 3 4 5 6 7 8 9 10 答案 B C A C D A D C B B21、22、略23、(1)40 (2) 6 24、略 25、略2011中考数学分类总复习检测题（十）一、选择题二、填空题11、65 12、10 13、 80 14、180 15、(1a 16、3或5 三、解答题17、证明：∵AD BC ∥ ∴A C ∠=∠ ∵AE FC = ∴AF CE =在ADF △和CBE △中AD CB A C AF CE =⎧⎪∠=∠⎨⎪=⎩∴ADF CBE △≌△∴BE DF = 6分 18、菱形19、解： 在Rt ABC △中，9030C A ∠=︒∠=︒,，BD 是ABC ∠的平分线,30.ABD CBD AD DB ∴∠=∠=∴=°.又 在Rt ,5CBD CD =△中cm.10BD ∴=cm.题号 1 2 3 4 5 6 7 8 9 10 答案 BCBBCACBCBAEC AFC AECAFC ECD EAB AFC ECD EAB AFC AEC ECF EAF FCD FAB AEC FCD FAB AFC ECD EAB AEC ∠=∠∴∠+∠=∠+∠+∠=∠+∠+∠=∠∴∠+∠+∠+∠=∠∠+∠=∠∠+∠=∠4341)(414141, 解：BC ∴=2AB BC ==cm20、1）∠B = ∠F 或 AB ∥EF 或 AC = ED . （2）证明：当∠B = ∠F 时 在△ABC 和△EFD 中A B E F B F BC FD =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△EFD (SAS) （本题其它证法参照此标准给分） 21、解：（1）（作出点E 给1分，作出点P 给1分，连AP 得角平分线AD 给1分）（2）∵AD 平分∠BAC ．∴∠CAD ＝∠EAD在△CAD 与△EAD 中 AD ＝AD （公共边） ∠CAD ＝∠EAD AC ＝AE （已知） ∴△CAD ≌△EAD∴∠DEA ＝∠DCA ＝90° ∴DE ⊥AB22、解：猜测 AE BD AE BD =，⊥．理由如下：90ACD BCE ∠=∠= °，ACD DCE BCE DCE ∴∠+∠=∠+∠，即.ACE DCB ∠=∠ ACD ∴△和BCE △都是等腰直角三角形. AC CD CE CB ∴==，，ACE DCB ∴△≌△． AE BD ∴=，.CAE CDB ∠=∠ 90AFC DFH DHF ACD ∠=∠∴∠=∠= ，°．AE BD ∴⊥．23、证明：（1）∵∠A=30°，∠ACB=90°，D 是AB 的中点． ∴BC=BD ， ∠B=60° ∴△BCD 是等边三角形． 又∵CN ⊥DB ，∴12DN DB =∵∠EDF=90°，△BCD 是等边三角形． ∴∠ADG =30°，而∠A =30°． ∴GA=GD ．∵GM ⊥AB∴12AM AD =又∵AD=DB ∴AM=DN （2）∵DF ∥AC∴∠1=∠A=30°，∠AGD=∠GDH=90°， ∴∠ADG=60°． ∵∠B=60°，AD=DB ， ∴△ADG ≌△DBH ∴AG=DH ，又∵∠1=∠A ，GM ⊥AB ，HN ⊥AB ， ∴△AMG ≌△DNH ． ∴AM=DN ．24、(1) 等边三角形 (2) )30(33232≤≤+-=t t t S (3) 略 25、解：（1）在四边形ABCD 中，AB BC ⊥，DC BC AB DC ∴⊥，∥， ∴四边形ABCD 为直角梯形（或矩形）． 过点P 作PQ BC ⊥，垂足为Q ，PQ AB ∴∥， 又点P 是AD 的中点，∴点Q 是BC 的中点， 又111()()222PQ AB CD a b BC =+=+=， PQ BQ QC ∴==，PQB ∴△与PQC △是全等的等腰直角三角形， 90BPC BPQ QPC PB PC ∴∠=∠+∠==°，， PBC ∴△是等腰直角三角形．（2）存在点M 使AM MD ⊥．图②BPD CBA Q E M 2M 1以AD 为直径，P 为圆心作圆P ．当a b =时，四边形ABCD 为矩形，PA PD PQ ==，圆P 与BC 相切于点Q ，此时，M 点与Q 点重合，存在点M ，使得AM MD ⊥，此时1()2BM a b =+． 当a b <时，四边形ABCD 为直角梯形，AD BC >，PA PD PQ =>，圆心P 到BC 的距离PQ 小于圆P 的半径，圆P 与BC 相交，BC 上存在两点12M M ，，使AM MD ⊥，过点A 作AE DC ⊥，在Rt AED △中，AE a b DE b a =+=-，，22222222AD AE DE AD a b AD =+=+，，连结12PM PM ，，则12PM PM ==在直角三角形1PQM中，12b aQM -===， 11BM BQ M Q a ∴=-=．同理可得：22BM BQ M Q b =+=．综上所述，在线段BC 上存在点M ，使AM MD ⊥． 当a b =时，有一点M ，2a bBM +=；当a b <时，有两点12M M ，，12BM a BM b ==，． 2011中考数学分类总复习检测题（十一）一、选择题二、填空题11、17 12、20 13、22.5 14、20 15、菱形16、8 三、解答题17、证明：四边形ABCD 为等腰梯形，B DCB ∴∠=∠． GE DC GEB DCB ∴∠=∠ ∥，． GEB B GB GE ∴∠=∠∴=．． 在GEF △和HCG △中， GE DC GEF HCF ∴∠=∠ ∥，． F 是EC 的中点，FE FC ∴=． 而GFE CFH ∠=∠（对顶角相等）， GEF HCF ∴△≌△． GE HC BG CH ∴=∴=，．18、DF BE =,DF BE // 提示：证明CEB AFD ∆≅∆题号 1 2 3 4 5 67 8 9 10 答案B BC CD C B B D A19、解：如图，过点D 作DF AB ∥，分别交AC BC ，于点E F ，．AB AC ⊥ ，90AED BAC ∴∠=∠= ． AD BC ∥，18045DAE B BAC ∴∠=-∠-∠= ．在Rt ABC △中，90BAC ∠=，45B ∠=，BC =sin 4542AC BC ∴===在Rt ADE △中，90AED ∠=，45DAE ∠=，AD ，1DE AE ∴==．3CE AC AE ∴=-=．在Rt DEC △中，90CED ∠=，DC ∴==20、证明：（1）∵DE ⊥AG ，BF ⊥AG ， ∴∠AED =∠AFB =90°．∵ABCD 是正方形，DE ⊥AG ，∴∠BAF +∠DAE =90°，∠ADE +∠DAE =90°， ∴∠BAF =∠ADE ．又在正方形ABCD 中，AB =AD ．在△ABF 与△DAE 中，∠AFB =∠DEA =90°， ∠BAF =∠ADE ，AB =DA ， ∴△ABF ≌△DAE ．（2）∵△ABF ≌△DAE ，∴AE =BF ，DE =AF ． 又 AF=AE+EF ，∴AF=EF+FB ，∴DE=EF+FB ． 21、(1) 略 (2) 222b ac +=22、(1) CF AD = (2) 提示：证明CFD ADE∆∆~23、解：（1）D E ，是AB ，AC 的中点， DE BC ∴∥，2BC DE =． 又2BE DE =，EF BE =，BC BE EF ∴==，EF BC ∥． ∴四边形BCFE 是菱形．（2）连接BF 交CE 于点O ．在菱形BCFE 中，130BCF ∠= ，4CE =，BF CE ∴⊥，1652BCO BCF ∠=∠= ，122OC CE ==． 在Rt BOC △中，tan 65OB OC= ，2tan 65OB ∴= ，4tan 65BF =．ADE F CGBABCDFEA C DF EO∴菱形BCFE 的面积1144tan 658tan 6517.222CE BF ==⨯⨯=≈ ．24、（1）证明： 四边形ABCD 是菱形，BC CD ∴=， AC 平分BCD ∠．而CE CE =，BCE DCE ∴△≌△ EBC EDC ∴∠=∠．又AB DC ∥，APD CDP ∴∠=∠ EBC APD ∴∠=∠（2）当P 点运动到AB 边的中点时，ADP △的面积等于菱形ABCD 面积的14． 连接DB ．60DAB ∠= °，AD AB =， ABD ∴△是等边三角形而P 是AB 边的中点，DP AB ∴⊥12ADP S AP DP = △，ABCD S AB DP = 菱形12AP AB = ，∴111224ADP ABCD S AB DP S =⨯= △菱形即ADP △的面积等于菱形ABCD 面积的14．25、解：（1）设抛物线的解析式为2y ax =，12B ⎛- ⎝⎭在抛物线上，把12B ⎛- ⎝⎭代入23y ax =+得a =∴抛物线解析式为2y x =+． （2）点1(02B A ⎛- ⎝⎭，，CB ∴== CB CB OA '∴==．又2CA ==，1.AB ∴==ABDCEP图AD CPAB AB OC '∴==．∴四边形AOCB '是矩形．1CB OC '== ，B '∴点的坐标为．当1x =时，代入2y =+得y =B '∴在抛物线上．（3）存在．理由是：设BA 的解析式为y kx b =+，1220k b b ⎧-+=⎪∴⎨⎪+=⎩k b ⎧=⎪∴⎨=⎪⎩ BA ∴的解析式为y =P F ，分别在直线BA 和抛物线上，且PF AD ∥，∴设2(P m F m ⎛ ⎝⎭，，2PF AD =+-⎭==， 如果PF AD =，则有2-+=⎝⎭解得10m =（不符合题意舍去），232m =． ∴当32m =时，PF AD =， 存在四边形ADFP 是平行四边形．当32m ==P ∴点的坐标是32⎛ ⎝⎭．2011中考数学分类总复习检测题（十二）一、选择题 二、填空题11、48 12、相切 13、15π 14、 15、7 16、4π 三、解答题 17、40度 18、30度 19、略20、证明：（1）连结OD ．由O 、E 分别是BC 、AC 中点得OE ∥AB ． ∴∠1=∠2，∠B =∠3，又OB=OD ． ∴∠2=∠3． 而OD=OC ，OE=OE ∴△OCE ≌△ODE ． ∴∠OCE=∠ODE ．又∠C=90°，故∠ODE =90°． ∴DE 是⊙O 的切线． （2）在Rt △ODE 中，由32OD =，DE =2 得52OE =又∵O 、E 分别是CB 、CA 的中点∴AB =2·5252OE =⨯=∴所求AB 的长是5cm ．21、AD=2 ,AC=222、(1)提示：连接BC, 证明：90=∠ACB (2) 提示：证明：ACD ACB ∆∆~23、 (1) 略 (2) AD=2224、解：（1）分别过A O ，两点作AE CD OF CD ⊥⊥，，垂足分别为点E ，点F ， AE OF OF ∴∥，就是圆心O 到CD 的距离． 四边形ABCD 是平行四边形，题号 1 2 3 4 5 6 7 8 9 10 答案 BBDCADCABCBAB CD AE OF ∴∴=∥，．在Rt ADE △中，60sin sin 60AE AED D AD AD∠=∠==°，，°，AE AE OF AE m ====，，， 圆心到CD 的距离OF（2）OF =， AB 为O ⊙的直径，且10AB =，∴当5OF =时，CD 与O ⊙相切于F 点，5m ==，， ∴当m =时，CD 与O ⊙相切． 25、(1)B(1,3) C(0,332) (2) 3323+=x y ，(3) 略2011中考数学分类总复习检测题（十三）一、选择题 二、填空题11、(2, 2) 12、72度 13、214、(0, 0) 15、4 16、6 三、解答题 17、211<<-a 18、 （1）画图1(04)B ，题号1 2 3 4 5 6 7 8 9 10 答案 CAACCCBACD图（1）图（2）（2）画图5OB ==∴点B 旋转到点2B 时，经过的路线长为25π5π42⨯⨯=． 19、（1）（2，3）； （2）图形略．（0，6-）；（3）（7-3，）或(53)--，或(33)，．20、3 21、（1）如图（2）5（3）∠CAD ，55(或∠ADC ，552)（4）2122、(1, 3)23、(1) A 1 (1, 1) B 1 (2, 2) C 1 (0, 4) (2) A 2 (6, 4) B 2 (4, 2) C 2 (5, 1)(3) 直线X=3 24、解：（1）BD MF BD MF =，⊥． 延长FM 交BD 于点N ，由题意得：BAD MAF △≌△． ∴BD MF =，ADB AFM ∠=∠． 又∵DMN AMF ∠=∠，∴90ADB DMN AFM AMF ∠+∠=∠+∠=°， ∴90DNM ∠=°，∴BD MF ⊥．（2）β的度数为60°或15°（答对一个得2分） （3）由题意得矩形2PNA A ．设2A A x =，则PN x =， 在222Rt A M F △中，∵228F M FM ==，∴22224A M A F ==，，∴2AF x =． ∵290PAF ∠=°，230PF A ∠=°，∴2tan 304AP AF x == °．DM N BAP 2M 2 F 2FCD MABENABEC D∴4PD AD AP x=-=．∵NP AB∥，∴DNP B∠=∠．∵D D∠=∠，∴DPN DAB△∽△．∴PN DPAB DA=．∴44xx+=，解得6x=-．即26A A=-答：平移的距离是(6-cm．（其它方法可参照此答案给分）25、(1) DE=EF (2) NE=BF2011中考数学分类总复习检测题（十四）一、选择题二、填空题11、4112、16.5 13、325014、12 15、1 : 2 16、三、解答题17、2518、36 ,3419、9.920、52021、解：延长AD交BC的延长线于点E在Rt△ABE中,AB=200,∠A=60°得AE=400在Rt△CDE中,CD=100,∠CED=30°得CE=2CD=200,DE=1003≈227(m)所以，AD=400-1003BC=2003-200≈146 (m)22、(1) PC=32(2) 45度23、1.3124、20320-题号 1 2 3 4 5 6 7 8 9 10答案 B B A D A B C B D CBDCAE25、(1) 略 (2) 38=r 2011中考数学分类总复习检测题（十五）一、选择题 二、填空题 11、100 12、41313、 78 14、4 15、 OA=OB 16、 4 三、解答题 17、略18、提示：连接CD19、(1) ACD ABE ∆≅∆ (2) 略 20、提示：证明EBA AFD ∆≅∆21、(1) 略 (2) 提示：证明：角B=90度22、解：（1）证明：∵AF 平分∠BAC ，∴∠CAD =∠DAB =12∠BAC ．∵D 与A 关于E 对称，∴E 为AD 中点．∵BC ⊥AD ，∴BC 为AD 的中垂线，∴AC =CD ． 在Rt △ACE 和Rt △ABE 中，∠CAD +∠ACE =∠DAB +∠ABE =90°， ∠CAD =∠DAB ． ∴∠ACE =∠ABE ，∴AC =AB ． ∴AB =CD ． （2）∵∠BAC =2∠MPC ， 又∵∠BAC =2∠CAD ，∴∠MPC =∠CAD ．∵AC =CD ，∴∠CAD =∠CDA ， ∴∠MPC =∠CDA ． ∴∠MP F=∠CDM ．∵AC =AB ，AE ⊥BC ，∴CE =BE ． ∴AM 为BC 的中垂线，∴CM =BM ．∵EM ⊥BC ，∴EM 平分∠CMB ，（等腰三角形三线合一） ∴∠C ME =∠BME ． ∵∠BME =∠PMF ， ∴∠PMF =∠C M E ，∴∠MCD =∠F （三角形内角和）．23、(1) 略 (2)X=2时, Y 最大，最大值是124、（1）猜想：BG DE = BC DC =90BCG DCE ∠=∠=° CG CE =∴BCG DCE △≌△（SAS ） （2）在BCG △与DHG △中 由（1）得CBG CDE ∠=∠ CGB DGH ∠=∠90DHB BCG ∴∠=∠=° BH DE ∴⊥．题号 1 2 3 4 5 6 7 8 9 10 答案 CAABBACBBBFM PE D CBA25、证明：（1）∵∠A=30°，∠ACB=90°，D是AB的中点．∴BC=BD，∠B=60°∴△BCD是等边三角形．又∵CN⊥DB，∴12 DN DB=∵∠EDF=90°，△BCD是等边三角形．∴∠ADG=30°，而∠A=30°．∴GA=GD．∵GM⊥AB∴12 AM AD=又∵AD=DB∴AM=DN（2）∵DF∥AC∴∠1=∠A=30°，∠AGD=∠GDH=90°，∴∠ADG=60°．∵∠B=60°，AD=DB，∴△ADG≌△DBH∴AG=DH，又∵∠1=∠A，GM⊥AB，HN⊥AB，∴△AMG≌△DNH．∴AM=DN．图②B。

3 C E A 2011九年级数学中考冲刺测试题（满分：120分 考试时间：120分钟）一、选择题（本大题共10小题，每小题3分，共30分．每题的四个选项中，只有一个选项是符合要求的．）1．若3)2(⨯-=x ，则x 的相反数是A ．61- B ． 61C ．－6D ．62．下列运算正确的是A ．236·a a a =B ． 221-=-C 4=±D ．|6|6-=3．图中圆与圆之间不同的位置关系有A ．2种B ．3种C ．4种D ．5种4. 右图是由四个小正方体叠成的一个立体图形，那么它的主视图是5l5户家庭的日用电量，日用电量，下列说法错误的是A 众数是6平均数是6.8度 C 中位数是6度差是5度6．如图，⊙P 的直径AB ＝10，点C 在半圆上，BC ＝6．PE ⊥AB 交AC 于点E ，则PE 的长是 A ．154 B ．4 C ．5 D ．152 7. 如图，利用四边形的不稳定性改变矩形ABCD 的形状， 得到□A1BCD1，若□A1BCD1的面积是矩形 ABCD 面积的一半，则∠ABA1的度数是A ．15°B ．30°C ．45°D ．60° 8,将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次，记第一次掷出的点数为a ，第二次掷出的点数为b ，则关于x,y 的方程组ax+by=3x+2y=2 只有正数解的概率为A.1/12B.2/9C.5/18D.13/369．如图，等腰直角△ABC 中，AC ＝BC ，∠ACB ＝90°，AF 为△ABC 的角平分线，分别过点C 、B 作AF 的垂线，垂足分别为E 、D ．以下结论：①CE ＝DE ＝22 BD ；②AF ＝2BD ；③CE ＋EF ＝12 AE ；④DF AF ＝2－12．其中结论正确的序号是 A ．①②③A ．BD ACB ．①②④C ．①③④D ．②③④10．已知：如图，点P 是正方形ABCD 的对角线AC 上的一个动点(A 、C 除外)，作AB PE ⊥于点E ，作BC PF ⊥于点F ，设正方形ABCD 的边长为x ，矩形PEBF 的周长为y ，在下列图象中，大致表示y 与x 之间的函数关系的是18115120°， 12．△ABC 中，∠C=90°，AB=8，cosA=43，则AC 的长是 。

2011年中考《数学》冲刺试题及答案一、选择题（本大题共10小题，每小题3分，共30分 1.16的帄方根是（ ▲ ）A 〃4B 〃－4C 〃±4D 〃±82.下列运算正确的是（ ▲ ）A 〃743)(x x= B 〃532)(x x x =⋅-C 〃34)(x x x -=÷- D. 23x x x +=3.下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（ ▲ ）A 〃1个B 〃 2个C 〃 3个D 〃 4个4.如图，桌面上有一个一次性纸杯，它的俯视图应是（ ▲ ）5.某学习小组为了解本城市500万成年人中大约有多少人吸烟，随机调查了50个成年人，结果其中有10个成年人吸烟〃对于这个数据收集与处理的问题，下列说法正确的是（ ▲ ） A 〃该调查的方式是普查 B 〃本地区只有40个成年人不吸烟 C 〃样本容量是50 D 〃本城市一定有100万人吸烟6.已知圆锥的底面半径为1cm ，母线长为3cm ，则圆锥的侧面积是（ ▲ ）A. 6cm 2B. 3πcm 2C 〃6πcm 2D 〃23πcm 27.两圆的半径分别为3和7，圆心距为7，则两圆的位置关系是（ ▲ ） A. 内切 B. 相交 C. 外切 D. 外离 8.在△ABC 中，D 、E 分别是边AB 、AC 的中点，若BC ＝5，则DE 的长是（ ▲ ） A 〃2.5B 〃5C 〃10D 〃159.如右图，一次函数y ＝kx ＋b 的图象经过A 、B 两点， 则不等式kx ＋b < 0的解集是（ ▲ ）A. x ＜0B. ０＜ x ＜１C.x ＜１D. x ＞１10.某剧场为希望工程义演的文艺表演有60元和100元两种票价，某团体需购买140元的票数不少于票价为60元的票数的两倍，则购买这两种票最少共需要（ ▲） A. 12120元 B. 12140元 C. 12160元 D. 12200元 二、填空题（本大题共8小题，每小题3分，共计24分〃）11〃 计算818-的结果是 〃12〃分解因式：32a ab -= 〃13〃函数2+=x y 中，自变量x 的取值范围是 〃14〃农科院对甲、乙两种甜玉米各10块试验田进行试验后，得到甲、乙两个品种每公顷的帄均产量相同，而甲、乙两个品种产量的方差分别为20.01S ≈甲，20.002S ≈乙，则产量较为稳定的品种是_____________（填“甲”或“乙”）〃15. 如图，早上10点小东测得某树的影长为2m ，到了下午5时又测得A B C D下午5时早上10时该树的影长为8m ，若两次日照的光线互相垂直，则树的高度约为_________m.（第15题）16〃已知圆锥的底面半径为1cm ，母线长为1cm 17〃如图，在帄面直角坐标系中，A ⊙与y 点，若点M 的坐标是(42)--，，则弦M N18〃如图，已知△OP 1A 1、△A 1P 2A 2、△A 2P 3A 3三角形，直角顶点P 1、P 2、 P 3、……在函数4y x=图象上，点A 1、A 2、 A 3、……在x 的横坐标为 .三、解答题（本大题共10小题，共96分〃） 19.(本题满分10分) （1）计算：︒-+---30cos 4)21(|1|123（2）化简2)1(111-÷⎪⎭⎫⎝⎛--+x x x x x 20.(本题满分10分)（1）解方程：32321---=-xxx ； （2）解不等式组：⎪⎩⎪⎨⎧-≤-+>-x x x x 237121)1(32521〃（本小题满分8分）有A 、B 两个黑布袋，A 布袋中有两个完全相同的小球，分别标有数字1和2〃B 布袋中有三个完全相同的小球，分别标有数字2-，3-和－4〃小明从A 布袋中随机取出一个小球，记录其标有的数字为x ，再从B 布袋中随机取出一个小球，记录其标有的数字为y ，这样就确定点Q 的一个坐标为(x ，y ).（1）用列表或画树状图的方法写出点Q 的所有可能坐标； （2）求点Q 落在直线y =2x --上的概率〃22〃（本题满分8分）如图，一辆汽车在一个十字路口遇到红灯刹车停下，汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA ＝30°和∠DCB ＝60°，如果斑马线的宽度是AB ＝3米，驾驶员与车头的距离是0.8米，这时汽车车头与斑马线的距离x 是多少?1023.（本题满分10分）已知：如图，AB 是⊙O 的直径，C 、D 为⊙O 上两点，CF ⊥AB 于点F ，CE ⊥AD 的延长线于点E ，且 CE ＝CF 〃 （1）求证：CE 是⊙O 的切线；（2）若AD ＝CD ＝6，求四边形ABCD 的面积〃24〃（本题满分10分）已知∠MAN ，AC 帄分∠MAN .⑴ 在图1中，若∠MAN =120°，∠ABC =∠ADC =90°，我们可得结论：AB +AD =AC ；在图2中，若∠MAN =120°，∠ABC +∠ADC =180°，则上面的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（2）在图3中：（只要填空，不需要证明）.①若∠MAN =60°，∠ABC +∠ADC =180°，则AB +AD = AC ；②若∠MAN =α（0°＜α＜180°），∠ABC +∠ADC =180°，则AB +AD = AC （用含α的三角函数表示）。

2011年中考《数学》冲刺试题及答案一、选择题（本大题共8小题，每小题4分，共32分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．2-的相反数是A . 2B .2-C .12 D . 12- 2．二元一次方程21-=x y 有无数多个解，下列四组值中不是．．该方程的解的是 A ．012x y =⎧⎪⎨=-⎪⎩ B ．11x y =⎧⎨=⎩ C ．10x y =⎧⎨=⎩ D ．11x y =-⎧⎨=-⎩ 3．小华将一张如图1所示矩形纸片沿对角线剪开，他利用所得的两个直角三角形通过图形变换构成了下列四个图形，这四个图形中不是．．轴对称图形的是 AB C D4．下列计算正确的是Ａ．()222x y x y +=+ B ．()2222x y x xy y -=-- C ．()()22222x y x y x y +-=-D ．()2222x y x xy y -+=-+5．“恒盛”超市购进一批大米，大米的标准包装为每袋30kg ，售货员任选6袋进行了称重检验，超过标准重量的记作“+”， 不足标准重量的记作“-”，他记录的结果是0.5+，0.5-，0，0.5-，0.5-，1+，那么这6袋大米重量．．的平均数和极差分别是 A ．0，1.5 B ．29.5，1 C ． 30，1.5 D ．30.5，06．不等式312->+x 的解集在数轴上表示正确的是7．如图2，小聪在作线段AB 的垂直平分线时，他是这样操作的：分别以A 和B为圆心，大于12AB 的长为半径画弧，两弧相交于C 、D ，则直线CD 即为所求．根据他的作图方法可知四边形ADBC 一定是．．． A ．矩形 B ．菱形C ．正方形D ．等腰梯形8．如图3，小路的正中间有一路灯，晚上小红由A 处径直走到B 处，她在灯光照射下的影长l 与行走的路程s 之间的变化关系用图象刻画出来，大致图象是 二、填空题（本大题共5小题，每小题4分，共20分．把答案填在答题卡．．．中对应题号后的横线上） 90 将这个数用科学记数法可记为 ． 10ABC ＝100°，则∠CBE的度数为 11．如图5，AB 是⊙O 的切线，半径OA =2，OBAC 的长是 ．（结果保留π）12．分式方程231-=x x 的解为 ． Ａ -2 0 A B C DBA CD图2图1AB图313．在1-，1，2这三个数中任选2个数分别作为P 点的横坐标和纵坐标，过P 点画双曲线ky x=，该双曲线位于第一、三象限的概率是 ．三、解答题（本大题共2小题，每小题6分，共12分）14()032-+-．15．如图6，在梯形ABCD 中，AB ∥CD ，AD =DC ，求证：AC 是∠DAB 的平分线． 四、解答题（本大题共3小题，每小题8分，共24分）16．观察下列算式：① 1 × 3 - 22= 3 - 4 = -1 ② 2 × 4 - 32= 8 - 9 = -1 ③ 3 × 5 - 42= 15 - 16 = -1 ④……（1）请你按以上规律写出第4个算式； （2）把这个规律用含字母的式子表示出来；（3）你认为（2）中所写出的式子一定成立吗？并说明理由．17．某校宣传栏中公示了担任下学期七年级班主任的12位老师的情况（见下表），小凤准备到该校就读七年级，请根据表中信息帮小凤进行如下统计分析： （1）该校下学期七年级班主任老师年龄的众数是多少？（2）在图7(1)中，将反映老师学历情况的条形统计图补充完整； （3）在图7(2)中，标注扇形统计图中表示老师职称为初级和高级的百分比； （4）小凤到该校就读七年级，班主任老师是女老师的概率是多少？18．如图8,AE 撑起拉线高为12平线AC B 、C 略不计）．(参考数据:sin67.4°≈13 ,cos67.4°≈13 ,tan67.4°≈5) 五、解答题（本大题共2小题，每小题10分，共20分）19．某地为了鼓励居民节约用水，决定实行两级收费制，即每月用水量不超过14吨（含14吨）时，每吨按政府补贴优惠价收费；每月超过14吨时，超过部分每吨按市场调节价收费．小英家1月份用水20吨，交水费29元；2月份用水18吨，交水费24元．（1）求每吨水的政府补贴优惠价和市场调节价分别是多少？（2）设每月用水量为x 吨，应交水费为y 元，写出y 与x 之间的函数关系式； （3）小英家3月份用水24吨，她家应交水费多少元？ 20．如图9，已知抛物线经过定点．．A （1，0），它的顶点P 是y 轴正半轴上的一个动点，P 点关于x 轴的对称40图6D A B C图8图7学历 本科 大专 中专 图7(1) 学历情况条形统计图 图7(2) 职称情况扇形统计图点为P′，过P′ 作x 轴的平行线交抛物线于B 、D 两点（B 点在y 轴右侧），直线BA 交y 轴于C 点．按从特殊到一般的规律探究线段CA 与CB 的比值：（1）当P 点坐标为（0，1）时，写出抛物线的解析式并求线段CA 与CB 的比值； （2）若P 点坐标为（0，m ）时（m 为任意正实数），线段CA 与CB 的比值是否与⑴ 所求的比值相同？请说明理由．六、解答题（本题满分12分）21．图10是小红设计的钻石形商标，△ABC 是边长为2的等边三角形，四边形ACDE 是等腰梯形，AC ∥ED ，∠EAC =60°，AE =1．（1）证明：△ABE ≌△CBD ；（2）图中存在多对相似三角形，请你找出一对进行证明，并求出其相似比（不添加辅助线， 不找全等的相似三角形）；（3）小红发现AM =MN =NC ，请证明此结论； （4）求线段BD 的长．益阳市2011年普通初中毕业学业考试 数学参考答案及评分标准一．选择题（本大题共8小题，每小题4分，共32分）二．填空题（本大题共5小题，每小题4分，共20分）9. 81.210⨯ 10. 30︒ 11.23π 12. 1x =- 13. 13三．解答题（本大题共2小题，每小题6分，共12分）14．解：原式＝２－１＋２＝３. ………………………………………………６分15．解：∵AB CD //， ∴CAB DCA ∠=∠. ……………………………………2分AD DC =，∴DAC DCA ∠=∠ . ……………………………4分 ∴DAC CAB ∠=∠ ， 即AC 是DAB ∠的角平分线. …………………6分 四、解答题（本大题共3小题，每小题8分，共24分）16．解：⑴246524251⨯-=-=-； …………………………………………………2分⑵答案不唯一.如()()2211n n n +-+=-； …………………………5分⑶()()221n n n +-+ ()22221n n n n =+-++ ………………………7分1=-. ……………………………………8分17．解：⑴ 该校下学期七年级班主任老师年龄的众数是40； …………………2分 ⑵ 大专４人，中专２人（图略）； ………………………………………4分E CD AM N图10 B⑶ %%高级：25，初级：33.3 ； …………………………………6分⑷班主任老师是女老师的概率是41123= . ……………………………8分18．解：⑴在Rt ∆DBC 中，sin BDDCB CD∠=， 666.512sin sin 67.413BD CD DCB ∴====∠（m ）. ……………………………3分DF AE F ABDF ⊥作于，则四边形为矩形， …………………………4分8DF AB ∴==，6AF BD ==，6EF AE AF ∴=-=， ……………………5分10Rt EFD ED ∆=在中,（m ）. ……………7分10 6.516.5L ∴=+=（m ） ……………………………………8分五、解答题（本大题共2小题，每小题10分，共20分）19．解:⑴ 设每吨水的政府补贴优惠价为x 元，市场调节价为y 元． ………1分()()1420142914181424x y x y +-=⎧⎪⎨+-=⎪⎩，； …………………………………………3分 答：每吨水的政府补贴优惠价为1元，市场调节价为2.5元． ………4分⑵14x y x ≤≤=当0时，；()1414 2.5 2.521x x x >-⨯=-当时，y=14+， ……………………6分 所求函数关系式为：()()0142.52114.x x y x x ≤≤⎧⎪=⎨->⎪⎩， …………………………8分⑶2414x =>，24 2.521x y x ∴=-把=代入,得: 2.5242139y =⨯-=.答：小英家三月份应交水费39元. …………………………………………10分 20．解：⑴ 设抛物线的解析式为21(0)y ax a =+≠ ， ……………………1分抛物线经过()1,0A ，01,1a a ∴=+=- ，21y x ∴=-+. ……………………………………2分(),0,1P P x P '、关于轴对称且,()01P '∴点的坐标为，－P B '∥x 轴,1B ∴-点的纵坐标为,由21x x -=-=+1 解得)1B∴-,P B '∴…………………………………………3分OA P B '//，CP B '∴∆∽COA ∆， …………………………………4分CA OA CB P B ∴='． …………………………………5分⑵ 设抛物线的解析式为2(0)y ax m a =+≠ ……………………6分 ()01A 抛物线经过，，0,a m a m ∴+=-＝2y mx m ∴=-+． ………………………………………………7分 P B '∥x 轴B m ∴-点的纵坐标为， 2y m mx m m =--+=-当时，()220m x ∴-=，0m >，220x ∴-=，x ∴=)Bm ∴-，P B '∴ ………………………………………8分同⑴得CA OA CB P B ===' ………………………………9分2CA m CB ∴=为任意正实数时，． …………………………10分 六、解答题（本题满分12分）21．⑴证明：ABC ∆是等边三角形 ，AB BC ∴=，60BAC BCA ∠=∠=． ……………………1分60ACDE EAC ∠四边形是等腰梯形，＝， 60AE CD ACD CAE ∴=∠=∠=︒，，+120+BAC CAE BCA ACD ∴∠∠=︒=∠∠，BAE BCD ∠=∠即． ……………………2分在ABE BCD ∆∆和中.AB CB BAE BCD AE CD =⎧⎪∠=∠⎨⎪=⎩，，ABE CBD ∴∆≅∆． …………3分⑵答案不唯一．如ABN CDN ∆∆∽．证明：60BAN DCN ∠=︒=∠，ANB DNC ∠=∠，ANB CND ∴∆∆∽ ． ………………………………………5分其相似比为：221AB DC ==． ……………………………………………6分 ⑶ 由（2）得2AN AB CN CD ==，1123CN AN AC ∴==． ………………8分 同理13AM AC =.AM MN NC ∴==． ………………………………………9分 ⑷作DF BC BC F ⊥交的延长线于，120BCD ∠=︒，60DCF ∴∠=︒． ……………………………………1O 分Rt CDF ∆在中，30CDF ∴∠=︒，1122CF CD ∴==，DF ∴=． ………………………………11分Rt BDF ∆在中，152,22BF BC CF DF =+=+==，BD ∴= …………………………12分。

2011年中考数学模拟考试答案一、选择题：1、D 2、B 3、B 4、B 5、B 6、C 7、C 8、B9、B 10、C二、填空题：11、3 12、x(x+2)(x-2) 13、21(2)44y x =-++ （-2，4） 14、2或-3 15、80°和20°或50°和50° 16、5603π 17、29°18、6643（7294096）三、全面答一答19、（1） (2)2132224134=+-⨯---=-=-----------原式分分 解:分原方程无解是原方程的增根所以时，检验：当分分（去分母得：分42x 02x 2x 32163121)231121321---------==-=--------------=-=-+-----=-+------=+-x x x x x x x x20、∵AD 是中线 ∴BD=DC ----------1分 ∵CE ⊥AD ，BF ⊥AD∴∠CED=∠BFD=90-----------------------2分 在△CED 和△BFD 中，∵∠BDF=∠ADC ∠CED=∠BFDBD=DC--------------------------5分∴△CED ≌△BFD （AAS ） ∴BF=CE----------------6分21、(本小题满分6分)（1）画出△A 2B 2C 2…………2分 （2）90°…………4分（3）21x5x2+41πx 25＝5+425π…………6分22、图略-------3分,,P(王杨胜)=3/12=1/4----4分,P(刘非胜)=9/12=3/4,-----5分, 不公平----6分 23、解：﹙1﹚80； …………………………………………………………2分﹙2﹚26.4， 27， 27； ………………………………………………﹙每空1分﹚5分(第18题)﹙3﹚396804472080231227720=⨯=+++⨯﹙人﹚． ………………………………8分24、连结OB ．∵BC//OP ，∴∠BCO =∠POA ，∠CBO =∠POB ． 又∵OC=OB ，∴∠BCO =∠CBO ，∴∠POB=∠POA ．-----------------------------------------------------------------1分 又∵PO=PO ，OB=OA ， ∴△POB ≌△POA ．∴∠PBO =∠PAO =90°．∴PB 是⊙O 的切线．-----------------------------------------------------------2分COADPB（2）2PO =3BC （写PO=23BC 亦可）． 证明：∵△POB ≌△POA ，∴PB=PA ．∵BD =2PA ，∴BD =2PB ．-----------------------------------------------3分 ∵BC//OP ，∴△DBC ∽△DPO ． ∴23BC BD PO PD ==．∴2PO =3BC ．----------------------------------5分 注：开始没有写出判断结论，正确证明也给满分． （3）∵△DBC ∽△DPO ，∴23DC BD DO PD ==，即DC=23OD ．∴DC =2OC ．----6分 设OA =x ，PA =y ．则OD =3x ，DB =2y ．在Rt △OBD 中，由勾股定理，得(3x )2= x 2+(2y )2．即2 x 2= y 2．∵x >0，y >0，∴y =2x ．OP =223x y x +=．------------------------------------------7分∴sin ∠OPA =13333OA x OP x ===．-------------------------------------------------------------8分25、解：（1）设打包成件的毛巾被有x 件，则320)80(=-+x x ………………………………………2分 200=x12080=-x ………………………………………3分答：打包成件的毛巾被和棉帐篷分别为200件和120件． （注：用算术方法做也给满分．）（2）设租用甲种飞机x 辆，则⎩⎨⎧≥-+≥-+120)8(2010200)8(2040x x x x ………………………………………5分 得42≤≤x ………………………………………………………6分 ∴x ＝2或3或4，中国军队安排甲、乙两种飞机时有3种方案．设计方案分别为：①甲飞机2辆，乙飞机6辆；②甲飞机3辆，乙飞机5辆；③甲飞机4辆，乙飞机4辆． ………………………7分 （3）3种方案的运费分别为：①2×4000+6×3600＝29600；②3×4000+5×3600＝30000；③4×4000+4×3600＝30400． ………………………………9分∴方案①运费最少，最少运费是29600元．…………………10分 （注：用一次函数的性质说明方案①最少也可．）26、⑴∵∠EFB ＝90°，∠ABC ＝30°∴∠EBG ＝30° ∵∠E ＝30° ∴∠E ＝∠EBG ∴EG ＝BG∴△EGB 是等腰三角形------------------3分⑵30°------------------------------------------------------4分 在Rt △ABC 中，∠C ＝90°，∠ABC ＝30°，AB ＝4∴BC ＝32；在Rt △DEF 中，∠EFD ＝90°，∠E ＝30°，DE ＝4 ∴DF ＝2∴CF ＝232-．---------------------6分 ∵四边形ACDE 成为以ED 为底的梯形 ∴ED ∥AC ∵∠ACB ＝90° ∴ED ⊥CB∵DE ＝4∴DF ＝2∴F 到ED 的距离为3------------------------------7分∴梯形的高为2333232-=+--------------------------------------8分27、∵CE ⊥AF ，FB ⊥AF ，∴∠DEC ＝∠DFB ＝90°又∵AD 为BC 边上的中线，∴BD ＝CD ， 且∠EDC ＝∠FDB （对顶角相等） ∴所以△BFD ≌△CDE （AAS ），∴BF =CE ． 28、解：（1）设EF 的解析式为y=k x +b,把E （－3，1）、F （433-,0）的坐标代入 1=－3k+b 解得：k=3 0=433-k+b b=4 所以，直线EF 的解析式为y=3x +4------------------------------------3分 (2)设矩形沿直线EF 向右下方翻折，B 、C 的对应点分别为B ′、C ′ ∵BE=33-3=23；∴B ′E= BE=23--------------------4分在Rt △AE B ′中，根据勾股定理，求得： A B ′＝3，∴B ′的坐标为（0，-2）----5分 设二次函数的解析式为：y=ax 2+b x +c把点B （－33，1）、E （－3，1）、B ′（0，-2）代入-2=c a=13- 3a －3b+c=1 解得： b=433- 27a －33b+c=1 c=－2 ∴二次函数的解析式为y=13-x 2433-x －2------------------------------7分（3）能，可以在直线EF 上找到点P,连接C,交直线EF 于点P ，连接BP.由于B ′P=BP,此时，点P 与C 、B ′在一条直线上，所以，BP+PC = B ′P+PC 的和最小，由于BC 为定长，所以满足△PBC 周长最小。