4GPS绝对定位——20141009(2)

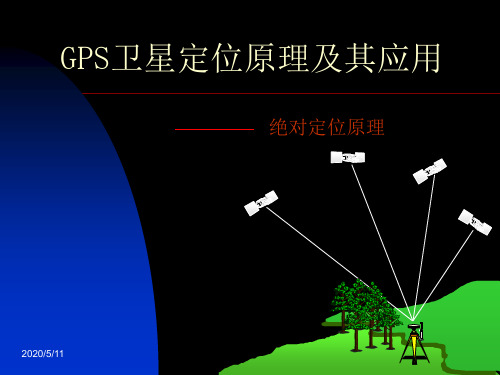
全球定位系统原理_绝对定位原理全球定位系统（Global Positioning System，简称GPS）是一种使用卫星和地面设备来确定地球上任意位置的导航和定位系统。

GPS通过接收来自卫星的信号，可以实现高精度的绝对定位和导航功能。

其原理主要基于以下几个关键要素：1.卫星定位GPS系统由一组24颗卫星组成，这些卫星分布在地球轨道上，每颗卫星都有精确的轨道和运行时间。

卫星定位的原理是通过接收来自至少四颗卫星的信号来确定接收器的位置。

卫星发射的信号包含卫星的精确位置和时间信息。

2.接收器接收卫星信号GPS接收器是用来接收并处理来自卫星的信号的设备。

接收器内部包含一个天线，用于接收卫星发射的信号。

接收器将接收到的信号传递给处理器进行处理。

3.三角定位原理GPS定位原理基于三角定位原理。

接收器通过接收至少四颗卫星的信号，可以测量这些卫星和接收器之间的距离。

由于卫星的位置是已知的，接收器可以通过测量这些距离来确定自己的位置。

接收器利用一个复杂的数学算法和时间测量技术来计算自己的位置。

4.精确时间同步GPS系统的精度与时间的同步性密切相关。

因为GPS信号的传播速度是已知的，接收器可以通过测量信号的传播时间来计算出距离。

然而，精确的时间同步对于距离的计算至关重要。

GPS系统中的卫星都有精确的内部时钟，接收器通过接收卫星发射的时间信号来与卫星进行时间同步。

5.加速度计和陀螺仪GPS系统还可以结合加速度计和陀螺仪等辅助设备，提供更精确和准确的定位和导航功能。

加速度计可以测量加速度和速度的变化，从而帮助用户确定自己的移动方向和速度。

陀螺仪可以测量旋转速度和姿态，进一步提高定位的精度和准确性。

总之，全球定位系统的原理主要基于卫星定位、接收器接收卫星信号、三角定位原理、精确时间同步和辅助设备等多个要素。

通过利用卫星发射的信号和接收器的计算能力，GPS系统可以实现高精度的绝对定位和导航功能。

这种原理已广泛应用于航空、航海、军事、车辆导航和移动设备等领域。

绝对定向的基本原理
1. 卫星定位系统，绝对定向依赖于卫星定位系统，最常用的是
全球定位系统（GPS）。

GPS系统由一组卫星组成，它们围绕地球轨
道运行，并向接收器发送信号。

接收器接收这些信号，并根据信号
的时间差来计算接收器与卫星之间的距离。

通过同时接收多颗卫星
的信号，接收器可以确定自身的位置。

2. 接收器和传感器，绝对定向中的接收器是用于接收卫星信号
的设备。

除了卫星信号，接收器还可以配备其他传感器，如陀螺仪、加速度计和磁力计等。

这些传感器可以提供关于设备的方向、速度
和姿态等信息，从而帮助确定导航路径。

3. 数据处理和算法，接收器接收到的卫星信号以及其他传感器
提供的数据会被送入数据处理系统和算法中进行处理。

这些算法会
利用卫星信号的时间差、传感器提供的数据以及地图数据等信息，
来计算设备的精确位置和导航路径。

这些算法可以采用三角测量、
卡尔曼滤波等技术来提高定位的准确性和稳定性。

4. 地图数据，为了实现绝对定向，需要使用地图数据。

地图数
据可以包含道路、建筑物、地标等信息。

通过将接收器确定的位置
与地图数据进行比对，可以确定设备在地图上的位置，并进一步规划导航路径。

总结起来，绝对定向的基本原理是通过卫星定位系统来获取设备的精确位置，结合其他传感器提供的数据进行计算和处理，最终确定导航路径。

这个过程涉及到卫星信号的接收、数据处理和算法运算，以及与地图数据的比对。

这样的综合使用可以实现准确、可靠的绝对定向导航。

第六章 GPS静态定位在GPS导航系统中．可根据待测点的运动状态分为静态定位和动态定位；又可根据待测点在协议地球坐标系中的绝对位置或相对位置，分为绝对定位(单点定位)或相对定位：本章将介绍GPS静态定位中的基本概念和常用的定位方法，在GPS静态定位中，包含着静态绝对(单点)定位和静态相对定位两种类型。

定位方法有所谓测码伪距法、测相伪距法和射电干涉测量法。

鉴丁GPS精密定位的重要性，因而在载波相位测量中将对有关整周未知数的确定，整周跳变以及求差法(或称差分法)等问题做较详细的介绍。

6．1 基本概念6.1.1 静态定位和动态定位如果待测点相对于其周围的固定点没有位置变化，或者虽然有可察觉到的运动，但这种运动相当缓慢，以致于在一次观测期间(一般为数小时至若干天)无法被察觉到，而只有在两次观测之间(一般为几个月至几年)，这些相对运动才反映出来，从而使得在每次进行GPS观测资料的处理时，待测点在协议地球坐标系中的位量可以认为是固定不变的(静态)。

确定这些待测点的位量称为静态定位。

如果待测点相对于其周围的固定点，在一次观测期间有可察觉到的运动或明显的运动，确定这些动态待测点的位置称为动态定位。

严格说来，静态定位和动态定位的根本区别并不在于待测点是否处于运动状态，而在于建立数学模型中待测点的位置是否可看成常数。

也就是说，在观测期间待测点的位移量和允许的定位误差相比是否显著，能否忽略不计。

由于进行静态定位时，待测点的位置可视为固定不动，因而就有可能通过大量的重复观测来提高定位精度。

静态定位在大地测量、精密工积测量、地球动力学及地震监测等领域内有着广泛的应用。

随着解算整周模糊度的快速算法的出现，静态定位的作业时间可大为缩短，因而在国防精密定位领域(比如飞机起飞前或火箭升空前的初始给定等)也有广泛的应用前景。

6.1.2 单点定位和相对（多点)定位采用单个GPS接收机独立确定待测点在协议地球坐标系中的绝对位置的方法称为单点定位或绝对定位。

第五章 GPS 绝对定位• 定义– 单独利用一台接收机确定待定点在地固坐标系中绝对位置的方法 •定位结果－与所用星历同属一坐标系的绝对坐标，也称单点定位– 采用广播星历时属WGS-84– 采用IGS – International GPS Service 精密星历时为ITRF – InternationalTerrestrial Reference Frames•特点– 优点：一台接收机单独定位，观测简单，可瞬时定位 – 缺点：精度主要受系统性偏差的影响，定位精度低5.1动态绝对定位1.测码伪距动态绝对定位法测码伪距的误差方程为：当仅观测4颗卫星时，无多余观测量，解算是唯一的。

如果同步观测的卫星数nj 大于4颗时，则需利用最小二乘法平差求解。

误差方程组的一般形式为 根据最小二乘法平差求解 )()()(t t t i i i i l Z a v +=δ[][])()()()(1t t t t i T i i Ti i l a a a Z --=δ)(-)(-)(-)(~)(-)](),(),([t V 0j i t T t I t t t t c X t n t m t l j i g j i j i j i i i j i j i j i δρδρρρδδ+=）（在GPS 中，同时出现在地平线以上的可见卫星数不会多于12个。

测码伪距绝对定位模型广泛用于船只、飞机、车辆等运动目标的导航、监督和管理。

2.测相伪距动态绝对定位法 测相伪距误差方程为：于历元t ，观测nj 颗卫星，误差方程可写为：误差方程的一般式为：式中：观测量的总数和观测卫星数nj 相同，而待定未知数为nj+4。

所以无法解算。

一般无法用测相伪距来进行动态绝对定位。

若于历元 t 同步观测nj 颗卫星，初始整周未知数Nij 已知，则可列出nj 个误差方程：此时，若同步观测卫星数大于等于4时，也可获得唯一实时解。

但载体在运动过程中，要始终保持对所测卫星的连续跟踪，目前在技术上尚有一定困难，同时目前动态解算整⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡)(...)()()(1)()()(1.........1)()()(1)()()()(...)()(2122211121t L t L t L t Z Y X t n t m t l t n t m t l t n t m t l t v t v t v j jj j j n i i i i i i i n i n i n i i i i i i i n i i i δρδδδ)(-)(-)(-)()()(-)](),(),([t V 00j i t T t I t t t N t t c X t n t m t l j i g j i j i j i j i i i j i j i j i δρδρρλϕλδδ++=）（⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡)(...)()()(...)()(1000............00100001)(t c 1)()()(1.........1)()()(1)()()()(...)()(210020122211121t L t L t L t N t N t N t Z Y X t n t m t l t n t m t l t n t m t l t v t v t v j j j j j j n i i i n i i i i i i i n i n i n i i i i i i i n i i iλδδδδ)()()()()()(t t t t t t i i i i i i i i l N e ρb X a v +++=δδ[][][][][]Tn i i i i Tn i i i i Ti i i i Ti Tn ii i i j jjN N N t L t L t L t Z Y X t t v t v t v t ...)(...)()()(1...11)()(...)()()(212121===---==N l X b v δδδδ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=1...000.........0...100...01)()()()(.........)()()()()()()(222111t t n t m t l t n t m t l t n t m t l t i n i n i n i i i i i i i i jj je a周未知数的方法，在应用上也有局限性。