山东省莱芜市莱城区腰关中学2014-2015学年七年级数学上学期第三模块测试试题(无答案,五四制)
- 格式:doc
- 大小:239.50 KB
- 文档页数:5

山东省莱芜市莱城区腰关中学2014-2015学年七年级英语上学期第三模块测试试题(无答案,五四制)(满分120分,考试时间120分钟)注意事项:1、本试题分第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷为选择题,65分;第Ⅱ卷为非选择题,55分;共120分。
2、答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上。
第Ⅰ卷(选择题,共65分)一、听力选择(一)听句子,回答问题,每个句子读一遍。
(5分)1.What does he grow ?A. applesB.orangesC.vegetables2.Where did they go ?A.the mountainB.the museum Cthe park3..Who did Amy climb a mountain with ?A. her parentsB.her friendsC.her sisters4. What did Ken do when he was young ?A. milk a cow Bfeed chickens C.ride a horse5. What did you do in the countryside ?A. pick apples Bpick strawberries C.pick flowers(二)听句子,选择最佳应答语。
每个句子读两遍。
(5分)6. A. Yes,there were . B.They were red . C.Very delicious7. A. It was great . B.I was late . C.To the zoo.8. A. Yes,I do . B.No,I didn’t.. C.No, I’m not9. A. Good idea . B.Sorry, I can’t . C.Sounds good10. A. Four two hours . B.It was interesting . C.We picked grapes(三)听对话,选择正确答案。

山东省莱芜市莱城区腰关中学2014-2015学年八年级数学上学期第三模块测试试题(五四制)一、填空题:1、下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.2、若分式的值为零,则x的值为()3、分解因式x2y﹣y3结果正确的是()4、雷霆队的杜兰特当选为2013﹣2014赛季NBA常规赛MVP,下表是他8场比赛的得分,则这8场比赛得分的众数与中位数分别为()5、如下图,在四边形中,对角线、相交于点,下列条件不能..判定四边形为平行四边形的是()A. AB∥CD,AD∥BCB. OA=OC,OB=ODC. AD=BC,AB∥CDD. AB=CD,AD=BC6、如上图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为().7、如图在△ABC中,E,D,F分别是AB,BC,CA的中点,AB=6,AC=4,则四边形AEDF•的周长是()A.10 B.20 C.30 D.408、如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )9.如图,将Rt △ABC 绕直角顶点顺时针旋转90°,得到△A ′B ′C ,连结AA ′, 若∠1=20°,则∠B 的度数是( )A .70°B .65°C .60°D .55°10、小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了,设公共汽车的平均速度为x 千米/时,则下面列出的方程中正确的是( )11、(3x +2)(﹣x 6+3x 5)+(3x +2)(﹣2x 6+x 5)+(x +1)(3x 6﹣4x 5)与下列哪一个式子相同?( )A .(3x 6﹣4x 5)(2x +1)B .(3x 6﹣4x 5)(2x +3)C .﹣(3x 6﹣4x 5)(2x +1)D .﹣(3x 6﹣4x 5)(2x +3)12、若关于x 的分式方程132--+x x m =x2无解,则m 的值为( ) A. -1.5 B. 1 C.-1.5或 2 D.-0.5或-1.5二、填空题:13、.把多项式6xy 2﹣9x 2y ﹣y 3因式分解,最后结果为 ________14、一个多边形的内角和比外角和的3倍多180°,则它的边数是 ________.15、已知a 2+3ab +b 2=0(a ≠0,b ≠0),则代数式 +的值等于 ________16、如图,▱ABCD 的周长为36,对角线AC ,BD 相交于点O .点E 是CD 的中点,BD =12,则△DOE 的周长为 ________17、如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= ________18、若a﹣b=1,则代数式a2﹣b2﹣2b的值为________.19、如图,▱ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为________三、解答题:20.(1)先化简,再求值:(a+)÷(a﹣2+),其中a=2(2)解分式方程:+=1.21.八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):(1)甲队成绩的中位数是 ___ 分,乙队成绩的众数是 _____分; (2)计算乙队的平均成绩和方差;(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.(3)根据(2)的坐标系作出与△ABC 关于原点对称的图形△A 2B 2C 2,并标出B 2、C 2两点的坐标.23、(1)化简:作乘法:))((22y xy x y x +-+=_____________________, ))((22y xy x y x ++-=_____________________,(2)利用上面两个公式把下列各式分解因式: 338b a +=_____________________,; 16-m =_____________________,24、如图,四边形ABCD 是平行四边形,E 、F 是对角线BD 上的点,∠1=∠2. (1)求证:BE =DF ; (2)求证:AF ∥CE .25、佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.(1)求第一次水果的进价是每千克多少元?(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?26、如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB 的中点,连接AD并延长交OC于E.(1)求证:四边形ABCE是平行四边形;(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.19、解:原式=÷=•=,当即a=2时,原式=3.20、解:方程两边都乘以(x+3)(x﹣3),得3+x(x+3)=x2﹣93+x2+3x=x2﹣9解得x=﹣4检验:把x=﹣4代入(x+3)(x﹣3)≠0,∴x=﹣4是原分式方程的解.21、解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是9.5分;10出现了4次,出现的次数最多,则乙队成绩的众数是10分;故答案为:9.5,10;(2)乙队的平均成绩是:(10×4+8×2+7+9×3)=9,则方差是:[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,∴成绩较为整齐的是乙队;22、解:(1)△AB1C1如图所示;(2)如图所示,A(0,1),C(﹣3,1);(3)△A2B2C2如图所示,B2(3,﹣5),C2(3,﹣1).23、(1)x3+y3,x3-y3(2)(a+2b)(a2-2ab+4b2),(m+1)(m-1)(m2+m+1)24、证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠5=∠3,∵∠1=∠2,∴∠AEB=∠4,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴BE=DF;(2)由(1)得△ABE≌△CDF,∴AE=CF,∵∠1=∠2,∴AE∥CF,∴四边形AECF是平行四边形,∴AF∥CE.25、解:(1)设第一次购买的单价为x元,则第二次的单价为1.1x元,根据题意得:﹣=20,解得:x=6,经检验,x=6是原方程的解,(2)第一次购水果1200÷6=200(千克).第二次购水果200+20=220(千克).第一次赚钱为200×(8﹣6)=400(元).第二次赚钱为100×(9﹣6.6)+120×(9×0.5﹣6×1.1)=﹣12(元).所以两次共赚钱400﹣12=388(元),答:第一次水果的进价为每千克6元,该老板两次卖水果总体上是赚钱了,共赚了388元.26、解答:(1)证明:∵Rt△OAB中,D为OB的中点,∴DO=DA,∴∠DAO=∠DOA=30°,∠EOA=90°,∴∠A EO=60°,又∵△OBC为等边三角形,∴∠BCO=∠AEO=60°,∴BC∥AE,∵∠BAO=∠COA=90°,∴CO∥A B,∴四边形ABCE是平行四边形;(2)解:设OG=x,由折叠可得:AG=GC=8﹣x,在Rt△ABO中,∵∠OAB=90°,∠AOB=30°,BO=8,∴AB=1/2BO=4∴OA2=BO2-AB2=82-42=48在Rt△OAG中,OG2+OA2=AG2,x2+48=(8﹣x)2,解得:x=1,∴OG=1.。

2014-2015学年山东省莱芜七年级(上)第二次月考数学试卷(五四学制)一、选择题(每小题3分,共计36分)1.下列图案中,是轴对称图形的是()A.B.C.D.2.实数(相邻两个1之间依次多一个0),其中无理数有()A.1个 B.2个C.3个D.4个3.的算术平方根是()A.±4 B.4 C.±2 D.24.一直角三角形的两边长分别为3和4.则第三边的长为()A.5 B.C.D.5或5.在平面直角坐标系中,点P(﹣2,3)关于x轴的对称点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限6.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.4个B.3个C.2个D.1个7.如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为()A.55° B.50° C.45° D.40°8.点P在第二象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为()A.(﹣4,3)B.(﹣3,﹣4)C.(﹣3,4)D.(3,﹣4)9.将一张正方形纸片按图①、图②所示的方式依次对折后,再沿图③中的虚线剪裁,最后将图④中的纸片打开铺平,所得到的图案是()A.B.C.D.10.如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是()A.7 B.8 C.9 D.1011.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是()A.B.C.D.12.如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为()A.6 B.12 C.32 D.64二、填空题(每小题4分,共计20分)13.若点P(m+3,m+1)在x轴上,则点P的坐标为.14.如图,等腰三角形ABC的顶角为120°,腰长为10,则底边上的高AD= .15.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为cm2.16.如图的方格图(每个小方格的边长为1)是某学校平面示意图,若建立适当的平面直角坐标系,花坛的位置可用坐标(3,0)表示,则校门的位置用坐标表示为.17.若(a﹣1)2+|b﹣2|=0,则以a、b为边长的等腰三角形的周长为.三、解答题(要写出必要的计算过程或推理步骤)18.计算:﹣|1﹣|+(﹣2)0.19.如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.求证:AC=OD.20.有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)21.如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.22.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?23.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.24.如图,在公路l的同旁有两个仓库A、B,现需要建一货物中转站,要求到A、B两仓库的距离和最短,这个中转站M应建在公路旁的哪个位置比较合理?25.如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?26.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为cm.2014-2015学年山东省莱芜实验中学七年级(上)第二次月考数学试卷(五四学制)参考答案与试题解析一、选择题(每小题3分,共计36分)1.下列图案中,是轴对称图形的是()A.B.C.D.考点:轴对称图形.分析:根据轴对称图形的概念求解.解答:解:A、不是轴对称图形,故错误;B、不是轴对称图形,故错误;C、不是轴对称图形,故错误;D、是轴对称图形,故正确.故选D.点评:本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.实数(相邻两个1之间依次多一个0),其中无理数有()A.1个B.2个C.3个D.4个考点:无理数.分析:根据无理数的定义(无理数就是无限不循环小数)判断即可.解答:解:无理数有﹣π,0.1010010001…,共2个,故选B.点评:本题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.3.的算术平方根是()A.±4 B.4 C.±2 D.2考点:算术平方根.分析:首先根据算术平方根的定义求出的值,然后再利用算术平方根的定义即可求出结果.解答:解:∵=4,∴4的算术平方根是2,∴的算术平方根是2;故选D.点评:此题主要考查了算术平方根的定义,解题的关键先计算出的值,再根据算术平方根的定义进行求解.4.一直角三角形的两边长分别为3和4.则第三边的长为()A.5 B.C.D.5或考点:勾股定理.专题:分类讨论.分析:本题中没有指明哪个是直角边哪个是斜边,故应该分情况进行分析.解答:解:(1)当两边均为直角边时,由勾股定理得,第三边为5,(2)当4为斜边时,由勾股定理得,第三边为,故选:D.点评:题主要考查学生对勾股定理的运用,注意分情况进行分析.5.在平面直角坐标系中,点P(﹣2,3)关于x轴的对称点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限考点:关于x轴、y轴对称的点的坐标.分析:首先根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得对称点的坐标,再根据坐标符号判断所在象限即可.解答:解:点P(﹣2,3)关于x轴的对称点为(﹣2,﹣3),(﹣2,﹣3)在第三象限.故选:C.点评:此题主要考查了关于x轴对称点的坐标特点,关键是掌握点的坐标的变化特点.6.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.4个B.3个C.2个D.1个考点:全等三角形的判定.分析:∠1=∠2,∠BAC=∠EAD,AC=AD,根据三角形全等的判定方法,可加一角或已知角的另一边.解答:解:已知∠1=∠2,AC=AD,由∠1=∠2可知∠BAC=∠EAD,加①AB=AE,就可以用SAS判定△ABC≌△AED;加③∠C=∠D,就可以用ASA判定△ABC≌△AED;加④∠B=∠E,就可以用AAS判定△ABC≌△AED;加②BC=ED只是具备SSA,不能判定三角形全等.其中能使△ABC≌△AED的条件有:①③④故选:B.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.做题时要根据已知条件在图形上的位置,结合判定方法,进行添加.7.如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为()A.55° B.50° C.45° D.40°考点:平行线的性质.分析:首先根据平行线的性质可得∠ABC+∠DCB=180°,进而得到∠BCD的度数,再根据角平分线的性质可得答案.解答:解:∵CD∥AB,∴∠ABC+∠DCB=180°(两直线平行,同旁内角互补),∵∠BCD=70°,∴∠ABC=180°﹣70°=110°,∵BD平分∠ABC,∴∠ABD=55°,故选:A.点评:此题主要考查了平行线的性质以及角平分线定义,关键是掌握两直线平行,同旁内角互补.8.点P在第二象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为()A.(﹣4,3)B.(﹣3,﹣4)C.(﹣3,4)D.(3,﹣4)考点:点的坐标.分析:先根据P在第二象限内判断出点P横纵坐标的符号,再根据点到坐标轴距离的意义即可求出点P的坐标.解答:解:∵点P在第二象限内,∴点的横坐标<0,纵坐标>0,又∵P到x轴的距离是4,即纵坐标是4,到y轴的距离是3,横坐标是﹣3,∴点P的坐标为(﹣3,4).故选:C.点评:解答此题的关键是熟记平面直角坐标系中各个象限内点的坐标符号,及点的坐标的几何意义.9.将一张正方形纸片按图①、图②所示的方式依次对折后,再沿图③中的虚线剪裁,最后将图④中的纸片打开铺平,所得到的图案是()A.B.C.D.考点:剪纸问题.分析:根据题中所给剪纸方法,进行动手操作,答案就会很直观地呈现.解答:解:严格按照图中的顺序进行操作,展开得到的图形如选项B中所示.故选B.点评:本题考查的是剪纸问题,此类题目主要考查学生的动手能力及空间想象能力,对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.10.如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是()A.7 B.8 C.9 D.10考点:翻折变换(折叠问题).专题:探究型.分析:先根据翻折变换的性质得出EF=AE=5,在Rt△BEF中利用勾股定理求出BE的长,再根据AB=AE+BE求出AB的长,再由矩形的性质即可得出结论.解答:解:∵△DEF由△DEA翻折而成,∴EF=AE=5,在Rt△BEF中,∵EF=5,BF=3,∴BE===4,∴AB=AE+BE=5+4=9,∵四边形ABCD是矩形,∴CD=AB=9.故选C.点评:本题考查的是图形的翻折变换,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.11.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是()A.B.C.D.考点:勾股定理;点到直线的距离;三角形的面积.专题:计算题.分析:根据题意画出相应的图形,如图所示,在直角三角形ABC中,由AC及BC的长,利用勾股定理求出AB的长,然后过C作CD垂直于AB,由直角三角形的面积可以由两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD除以2来求,两者相等,将AC,AB 及BC的长代入求出CD的长,即为C到AB的距离.解答:解:根据题意画出相应的图形,如图所示:在Rt△ABC中,AC=9,BC=12,根据勾股定理得:AB==15,过C作CD⊥AB,交AB于点D,又S△ABC=AC•BC=AB•CD,∴CD===,则点C到AB的距离是.故选A点评:此题考查了勾股定理,点到直线的距离,以及三角形面积的求法,熟练掌握勾股定理是解本题的关键.12.如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为()A.6 B.12 C.32 D.64考点:等边三角形的性质;含30度角的直角三角形.专题:压轴题;规律型.分析:根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.解答:解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,∵∠MON=30°,∴∠1=180°﹣120°﹣30°=30°,又∵∠3=60°,∴∠5=180°﹣60°﹣30°=90°,∵∠MON=∠1=30°,∴OA1=A1B1=1,∴A2B1=1,∵△A2B2A3、△A3B3A4是等边三角形,∴∠11=∠10=60°,∠13=60°,∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16,以此类推:A6B6=32B1A2=32.故选:C.点评:此题主要考查了等边三角形的性质以及等腰三角形的性质,根据已知得出A3B3=4B1A2,A4B4=8B1A2,A5B5=16B1A2进而发现规律是解题关键.二、填空题(每小题4分,共计20分)13.若点P(m+3,m+1)在x轴上,则点P的坐标为(2,0).考点:点的坐标.专题:计算题.分析:根据x轴上的点纵坐标等于0列出方程求解得到m的值,再进行计算即可得解.解答:解:∵点P(m+3,m+1)在x轴上,∴m+1=0,解得m=﹣1,∴m+3=﹣1+3=2,∴点P的坐标为(2,0).故答案为:(2,0).点评:本题考查了点的坐标,熟记x轴上的点的纵坐标等于0是解题的关键.14.如图,等腰三角形ABC的顶角为120°,腰长为10,则底边上的高AD= 5 .考点:等腰三角形的性质;解直角三角形.分析:先求出底角等于30°,再根据30°的直角三角形的性质求解.解答:解:如图.∵∠BAC=120°,AB=AC,∴∠B=(180°﹣120°)=30°.∴AD==5.(直角三角形中30°所对直角边等于斜边的一半)即底边上的高AD=5.点评:本题考查了等腰三角形的三线合一性质和含30°角的直角三角形的性质.15.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为49 cm2.考点:勾股定理.分析:根据正方形的面积公式,连续运用勾股定理,发现:四个小正方形的面积和等于最大正方形的面积.解答:解:由图形可知四个小正方形的面积和等于最大正方形的面积,故正方形A,B,C,D的面积之和=49cm2.故答案为:49cm2.点评:熟练运用勾股定理进行面积的转换.16.如图的方格图(每个小方格的边长为1)是某学校平面示意图,若建立适当的平面直角坐标系,花坛的位置可用坐标(3,0)表示,则校门的位置用坐标表示为(1,﹣1).考点:坐标确定位置.专题:数形结合.分析:先根据花坛的坐标画出直角坐标系,然后写出校门的坐标.解答:解:如图,校门的位置用坐标表示为(1,﹣1).故答案为(1,﹣1).点评:本题考查了坐标确定位置:平面内的点与有序实数对一一对应;记住直角坐标系中特殊位置点的坐标.17.若(a﹣1)2+|b﹣2|=0,则以a、b为边长的等腰三角形的周长为 5 .考点:等腰三角形的性质;非负数的性质:绝对值;非负数的性质:偶次方;三角形三边关系.专题:分类讨论.分析:先根据非负数的性质列式求出a、b再分情况讨论求解即可.解答:解:根据题意得,a﹣1=0,b﹣2=0,解得a=1,b=2,①若a=1是腰长,则底边为2,三角形的三边分别为1、1、2,∵1+1=2,∴不能组成三角形,②若a=2是腰长,则底边为1,三角形的三边分别为2、2、1,能组成三角形,周长=2+2+1=5.故答案为:5.点评:本题考查了等腰三角形的性质,非负数的性质,以及三角形的三边关系,难点在于要讨论求解.三、解答题(要写出必要的计算过程或推理步骤)18.计算:﹣|1﹣|+(﹣2)0.考点:实数的运算;零指数幂.分析:分别根据0指数幂的运算法则、数的开方法则及绝对值的性质计算出各数,再根据实数混合运算的法则进行计算即可.解答:解:原式=1﹣+1+1=3﹣.点评:本题考查的是实数的运算,熟知0指数幂的运算法则、数的开方法则及绝对值的性质是解答此题的关键.19.如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.求证:AC=OD.考点:全等三角形的判定与性质.专题:证明题.分析:根据同角的余角相等求出∠A=∠BOD,然后利用“角角边”证明△AOC和△OBD全等,根据全等三角形对应边相等证明即可.解答:证明:∵∠AOB=90°,∴∠AOC+∠BOD=90°,∵AC⊥l,BD⊥l,∴∠ACO=∠BDO=90°,∴∠A+∠AOC=90°,∴∠A=∠BOD,在△AOC和△OBD中,,∴△AOC≌△OBD(AAS),∴AC=OD.点评:本题考查了全等三角形的判定与性质,同角的余角相等的性质,利用三角形全等证明边相等是常用的方法之一,要熟练掌握并灵活运用.20.有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)考点:作图—应用与设计作图.分析:根据题意知道,点C应满足两个条件,一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是它们的交点.(1)作两条公路夹角的平分线OD或OE;(2)作线段AB的垂直平分线FG;则射线OD,OE与直线FG的交点C1,C2就是所求的位置.解答:解:作图如下:C1,C2就是所求的位置.点评:此题考查了作图﹣应用与设计作图,本题的关键是:①对角平分线、线段垂直平分线作法的运用,②对题意的正确理解.21.如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.考点:等腰三角形的性质;三角形内角和定理.专题:计算题.分析:首先由AB=AC,利用等边对等角和∠A的度数求出∠ABC和∠C的度数,然后由BD 是∠ABC的平分线,利用角平分线的定义求出∠DBC的度数,再根据三角形的内角和定理即可求出∠BDC的度数.解答:解:∵AB=AC,∠A=40°,∴∠ABC=∠C==70°,∵BD是∠ABC的平分线,∴∠DBC=∠ABC=35°,∴∠BDC=180°﹣∠DBC﹣∠C=75°.点评:本题考查了等腰三角形的性质,角平分线的定义,三角形内角和定理等知识,解答本题的关键是正确识图,利用等腰三角形的性质:等边对等角求出∠ABC与∠C的度数.22.已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?考点:勾股定理的应用.专题:应用题;压轴题.分析:仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD 中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.解答:解:连接BD,在Rt△ABD中,BD2=AB2+AD2=32+42=52,在△CBD中,CD2=132BC2=122,而122+52=132,即BC2+BD2=CD2,∴∠DBC=90°,S四边形ABCD=S△BAD+S△DBC=,==36.所以需费用36×200=7200(元).点评:通过勾股定理由边与边的关系也可证明直角三角形,这样解题较为简单.23.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.考点:角平分线的性质;勾股定理.分析:(1)根据角平分线性质得出CD=DE,代入求出即可;(2)利用勾股定理求出A B的长,然后计算△ADB的面积.解答:解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE,∵CD=3,∴DE=3;(2)在Rt△ABC中,由勾股定理得:AB===10,∴△ADB的面积为S△A DB=AB•DE=×10×3=15.点评:本题考查了角平分线性质和勾股定理的运用,注意:角平分线上的点到角两边的距离相等.24.如图,在公路l的同旁有两个仓库A、B,现需要建一货物中转站,要求到A、B两仓库的距离和最短,这个中转站M应建在公路旁的哪个位置比较合理?考点:轴对称-最短路线问题;作图—应用与设计作图.分析:作A点关于l的对称点A′,连接A′B,交直线l于M,此时AM+MB的和最小,M 所处的位置即为中转站应建的位置.解答:解:作A点关于l的对称点A′.连接A′B交l于点M,连接AM,此时AM+MB的和最小,M即为所求.点评:本题主要考查了轴对称﹣﹣最短路线问题,作出其中一点的对称点,并利用两点之间线段最短是解题的关键.25.如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?考点:平面展开-最短路径问题.分析:先将圆柱的侧面展开,再根据勾股定理求解即可.解答:解:如图所示,∵圆柱形玻璃容器,高16cm,底面周长为24cm,∴SD=12cm,∴AB==20.∴蚂蚁A处到达B处的最短距离为20cm.点评:本题考查的是平面展开﹣最短路径问题,将图形展开,利用勾股定理进行计算是解题的关键.26.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为20 cm.考点:平面展开-最短路径问题.专题:操作型.分析:将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B 的长度即为所求.解答:解:如图:将杯子侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B===20(cm).故答案为:20.点评:本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.。

山东省莱芜市莱城区腰关中学2014-2015学年七年级历史上学期第三模块测试试题(五四制)一、单项选择题:本大题共25小题,每小题2分,共50分。
1.中国近代第一个不平等条约是A.《南京条约》B.《北京条约》C.《天津条约》D.《马关条约》2.右面这幅图片是一场战争后留下的建筑物残迹,它记录着列强在近代中国所犯下的滔天罪行,这场战争是A.鸦片战争B.第二次鸦片战争C.甲午中日战争D.八国联军侵华战争3.根据《马关条约》的规定A.赔款白银4.5亿两。
B.赔款2100万元。
C.清政府严禁人民参加反帝活动 D.增辟通商口岸4.右图中的人物曾留下“有心杀贼,无力回天”的遗憾,他的名字是A.康有为B.梁启超C.谭嗣同D.康广仁5.辛亥革命的指导思想是A.社会主义B.马克思主义C.三民主义D.绝对平均主义6.同盟会的机关刊物是A.《资政新篇》B.《民报》C.《中华民国约法》D.《中华人民共和国宪法》7.在右图所示的刊物上提出过的著名口号是A.师夷长技以制夷B.物竞天择,适者生存C.民主和科学D.联俄、联共、扶助农工8.1920年秋,中国共产党的第一个早期组织诞生于A.上海B.北京C.武汉D.长沙9.1926年,国民政府决定出师北伐。
北伐的主要对象不.包括A.吴佩孚B.孙传芳C.张作霖D.段祺瑞10.1924年6月,国民党创立的陆军军官学校的校址是在A.武汉B.广州C.重庆D.北京11.今天,中国人民解放军的建军节是为了纪念A.北伐战争B.秋收起义C.南昌起义D.井冈山会师12.今年是红军长征胜利70周年纪念,小明暑假准备参加某旅行社组织的“重走长征路”红色旅游活动,以下是旅行社所制定的活动路线,你认为正确的是A. 遵义—瑞金—赤水—大渡河—雪山—金沙江—吴起镇B. 瑞金—遵义—赤水—金沙江—雪山—大渡河—吴起镇C. 遵义—瑞金—赤水—金沙江—大渡河—雪山—吴起镇D. 瑞金—遵义—赤水—金沙江—大渡河—雪山—吴起镇13.标志着十年内战基本结束,促进了国共合作抗日局面出现的事件是A.中国人民的局部抗战开始B.张学良、杨虎城对蒋介石“兵谏”C.西安事变和平解决D.工农红军改编为八路军、新四军14.日本发动全面侵华战争的标志是A.九一八事变B.“一·二八”事变C.七七事变D.八一三事变15.1937年12月,日军占领南京后,制造了震惊中外的“南京大屠杀”事件,杀害我同胞达A.19多万人B.20多万人C.30多万人D.40多万人16.台儿庄战役是抗战以来取得的重大胜利,这次战役的指挥者是A.张自忠B.李宗仁C.彭德怀D.朱德17.1945年陪同毛泽东去重庆谈判的是A.周恩来、叶剑英B.周恩来、陈毅C.周恩来、董必武D.周恩来、王若飞18.人民解放军转入战略进攻开始的标志是A.转战陕北B.挺进大别山C.发动三大战役D.渡江作战19.奠定了解放长江以南各省基础的战役是A.淮海战役B.辽沈战役C.平津战役D.渡江战役20.中国近代民族工业产生于19世纪A.四五十年代B.六七十年代C.七八十年代D.八九十年代21.提出“父教育而母实业”(即以实业养教育,以教育促进实业)口号的是A.荣德生B.荣宗敬C.张謇D.周学熙22.1872年在上海创办的中国近代最著作的报刊是A.《中外纪闻》B.《民报》C.《中外新报》D.《申报》23.第一条由中国人自已设计和施工修建的铁路是A.京张铁路B.唐胥铁路C.京汉铁路D.京九铁路24.北京大学的前身是A.京师同文馆B.广州万木草堂C.京师大学堂D.江南制造总局翻译馆25.魏源写成的我国最早一部系统介绍世界各国情况的著作是A.《海国图志》B.《敬告青年》C.《天演论》D.《四洲志》二、非选择题:本大题共4小题,满分50分。

山东省莱芜实验中学2014~2015学年度七年级上学期期中数学试卷一、选择题(每小题3分,共36分)1.下面是实验中学初二的同学为自己班设计的几个班徽,是轴对称的有()A.1个B.2个C.3个D.4个2.如图,把一个正方形三次对折后沿虚线剪去一个角,则所得图形展开后是()A.B.C.D.3.如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为()A.1 B. 2 C. 3 D. 44.如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若AB=m,CD=n,则△ABD 的面积等于()A.mn B.C.2mn D.5.如图,一圆柱体的底面周长为24cm,高BD为5cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程大约是()A.6cm B.12cm C.13cm D.16cm6.如图,AB∥CD,∠A+∠E=75°,则∠C为()A.60° B.65° C.75° D.80°7.若等腰三角形的两边长分别为4和8,则它的周长为()A.12 B.16 C.20 D.16或208.如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是()A.△ABD≌△ACD B.AF垂直平分EGC.直线BG,CE的交点在AF上D.△DEG是等边三角形9.如图,在△ABC中,∠B=40°,EF∥AB,∠1=50°,CE=3,EF比CF大1,则EF的长为()A.5 B. 6 C. 3 D. 410.E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为()A.25 B.12 C.13 D.1911.若△ABC的三边a,b,c满足a2+b2﹣8a﹣10b+29+|c﹣3|=0,则()A.△ABC是直角三角形且∠C=90° B.△ABC是锐角三角形C.△ABC是直角三角形且∠B=90° D.△ABC是直角三角形且∠A=90°12.如图,△ABC≌△ADE,则下列结论成立的是()①AB=AD,②∠E=∠C,③若∠BAE=120°,∠BAD=40°,则∠BAC=80°,④BC=DE.A.① B.①② C.①②③ D.①②③④二、填空题(每小题4分,共20分)13.若三角形三内角的度数之比为1:2:3,最大边的长是16cm,则最小边的长是.14.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,则P点到直线AB的距离是cm.15.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,则∠AMB=.16.△ABC中,DE分别是BC,AD的中点,且△ABC的面积为4,则阴影部分的面积是.17.△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,AP+BP+CP的最小值为.三、解答题18.先化简,再求值:﹣2+2ab2÷a,其中a=3,b=5.19.如图是一个四边形的边角料,木工师傅通过测量,获得了如下数据:AB=3cm,BC=12cm,CD=13cm,AD=4cm,BD=5cm木工师傅由此认为这个四边形中∠A恰好是直角,你认为木工师傅的判断正确吗?如果你认为他正确,请说明其中的理由;如果你认为他不正确,那你认为需要什么条件,才可以判断∠A是直角?请求出木料的面积.20.如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:(1)∠D=∠B;AE∥CF.21.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?22.某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?23.数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:(1)特殊情况•探索结论当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AEDB(填“>”,“<”或“=”).特例启发,解答题目解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)(3)拓展结论,设计新题在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).2014015学年山东省莱芜实验中学2014~2015学年度七年级上学期期中数学试卷参考答案与试题解析一、选择题(每小题3分,共36分)1.下面是实验中学初二的同学为自己班设计的几个班徽,是轴对称的有()A.1个B.2个C.3个D.4个考点:轴对称图形.分析:根据轴对称图形的概念求解.解答:解:第二个、第三个图形是轴对称图形.故选B.点评:本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.2.如图,把一个正方形三次对折后沿虚线剪去一个角,则所得图形展开后是()A.B.C.D.考点:剪纸问题.分析:把一个正方形的纸片向上对折,向右对折,向右下方对折,从上部剪去一个等腰直角三角形,展开,看得到的图形为选项中的哪个即可.解答:解:从折叠的图形中剪去8个等腰直角三角形,易得将从正方形纸片中剪去4个小正方形,故选C.点评:此题主要考查剪纸问题,此类问题根据图示进行折叠,然后剪纸,可直接得到答案.3.如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为()A.1 B. 2 C.3 D. 4考点:矩形的性质;翻折变换(折叠问题).分析:根据矩形的对边相等可得CD=AB,再根据翻折变换的性质可得C′D=CD,代入数据即可得解.解答:解:在矩形ABCD中,CD=AB,∵矩形ABCD沿对角线BD折叠后点C和点C′重合,∴C′D=CD,∴C′D=AB,∵AB=2,∴C′D=2.故选B.点评:本题考查了矩形的对边相等的性质,翻折变换的性质,是基础题,熟记性质是解题的关键.4.如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若AB=m,CD=n,则△ABD 的面积等于()A.mn B.C.2mn D.考点:角平分线的性质.分析:根据角平分线上的点到角的两边的距离相等可得DE=CD,然后由三角形的面积公式进行解答即可.解答:解:如图,过点D作DE⊥AB于点E.∵∠C=90°,BD是∠ABC的平分线,CD=n,∴DE=CD=n,∵AB=m,∴△ABD的面积是:AB•DE=mn.故选:B.点评:本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并准确识图是解题的关键.5.如图,一圆柱体的底面周长为24cm,高BD为5cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程大约是()A.6cm B.12cm C.13cm D.16cm考点:平面展开-最短路径问题.分析:根据题意,先将圆柱体展开,再根据两点之间线段最短.解答:解:将圆柱体展开,连接DC,圆柱体的底面周长为24cm,则DE=12cm,根据两点之间线段最短,CD==13(cm).而走B﹣D﹣C的距离更短,∵BD=5,BC=,∴BD+BC≈12.故选:B.点评:本题考查了平面展开﹣﹣最短路径问题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答即可.6.如图,AB∥CD,∠A+∠E=75°,则∠C为()A.60° B.65° C.75° D.80°考点:平行线的性质.分析:根据三角形外角性质求出∠EOB,根据平行线性质得出∠C=∠EOB,代入即可得出答案.解答:解:∵∠A+∠E=75°,∴∠EOB=∠A+∠E=75°,∵AB∥CD,∴∠C=∠EOB=75°,故选C.点评:本题考查了平行线性质和三角形外角性质的应用,关键是得出∠C=∠EOB和求出∠EOB的度数.7.若等腰三角形的两边长分别为4和8,则它的周长为()A.12 B.16 C.20 D.16或20考点:等腰三角形的性质;三角形三边关系.分析:由于题中没有指明哪边是底哪边是腰,则应该分两种情况进行分析.解答:解:①当4为腰时,4+4=8,故此种情况不存在;②当8为腰时,8﹣4<8<8+4,符合题意.故此三角形的周长=8+8+4=20.故选C.点评:本题考查的是等腰三角形的性质和三边关系,解答此题时注意分类讨论,不要漏解.8.如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是()A.△ABD≌△ACD B.AF垂直平分EGC.直线BG,CE的交点在AF上D.△DEG是等边三角形考点:轴对称的性质.分析:认真观察图形,根据轴对称图形的性质得选项A、B、C都是正确的,没有理由能够证明△DEG 是等边三角形.解答:解:A、因为此图形是轴对称图形,正确;B、对称轴垂直平分对应点连线,正确;C、由三角形全等可知,BG=CE,且直线BG,CE的交点在AF上,正确;D、题目中没有60°条件,不能判断是等边三角形,错误.故选D.点评:本题考查了轴对称的性质;解决此题要注意,不要受图形误导,要找准各选项正误的具体原因是正确解答本题的关键.9.如图,在△ABC中,∠B=40°,EF∥AB,∠1=50°,CE=3,EF比CF大1,则EF的长为()A.5 B. 6 C. 3 D. 4考点:勾股定理;平行线的性质.分析:由平行线的性质得出∠A=∠1=50°,得出∠C=90°,设CF=x,则EF=x+1,根据勾股定理得出方程,解方程求出x,即可得出EF的长.解答:解:∵EF∥AB,∴∠A=∠1=50°,∴∠A+∠B=50°+40°=90°,∴∠C=90°,设CF=x,则EF=x+1,根据勾股定理得:CE2+CF2=EF2,即32+x2=(x+1)2,解得:x=4,∴EF=4+1=5,故选:A.点评:本题考查了平行线的性质、直角三角形的判定、勾股定理;熟练掌握平行线的性质,并能进行推理论证与计算是解决问题的关键.10.E为正方形ABCD内部一点,且AE=3,BE=4,∠E=90°,则阴影部分的面积为()A.25 B.12 C.13 D.19考点:勾股定理.分析:根据勾股定理求出AB,分别求出△AEB和正方形ABCD的面积,即可求出答案.解答:解:∵在Rt△AEB中,∠AEB=90°,AE=3,BE=4,由勾股定理得:AB=5,∴正方形的面积是5×5=25,∵△AEB的面积是AE×BE=×3×4=6,∴阴影部分的面积是25﹣6=19,故选D.点评:本题考查了正方形的性质,勾股定理的运用,利用勾股定理求出正方形的边长并观察出阴影部分的面积的表示是解题的关键.11.若△ABC的三边a,b,c满足a2+b2﹣8a﹣10b+29+|c﹣3|=0,则()A.△ABC是直角三角形且∠C=90° B.△ABC是锐角三角形C.△ABC是直角三角形且∠B=90° D.△ABC是直角三角形且∠A=90°考点:勾股定理的逆定理;非负数的性质:偶次方;配方法的应用.分析:先将式子变形为(a﹣4)2+(b﹣5)2+|c﹣3|=12,找到满足式子的一组值,根据勾股定理的逆定理即可求解.解答:解:a2+b2﹣8a﹣10b+29+|c﹣3|=0,a2﹣8a+16+b2﹣10b+25+|c﹣3|=12,(a﹣4)2+(b﹣5)2+|c﹣3|=12,当a=6,b=7,c=7时,满足上面的式子,∵62+72>72,∴△ABC是锐角三角形.故选:B.点评:考查了勾股定理的逆定理,配方法的应用,非负数的性质:偶次方,关键是将式子变形为(a ﹣4)2+(b﹣5)2+|c﹣3|=12.12.如图,△ABC≌△ADE,则下列结论成立的是()①AB=AD,②∠E=∠C,③若∠BAE=120°,∠BAD=40°,则∠BAC=80°,④BC=DE.A.① B.①② C.①②③ D.①②③④考点:全等三角形的性质.分析:根据△ABC≌△ADE,可得其对应边对应角相等,即可得AB=AD,∠E=∠C,∠BAC=∠DAE;由∠DAC是公共角易证得∠BAD=∠CAE,已知∠BAE=120°,∠BAD=40°,即可求得∠BAC的度数.解答:解:∵△ABC≌△ADE,∴AB=AD,BC=DE,∠E=∠C,∠BAC=∠DAE;∵∠DAC是公共角∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,已知∠BAE=120°,∠BAD=40°,∴∠CAE=40°,∠BAC=∠BAE﹣∠CAE=120°﹣40°=80°.故选D.点评:本题考查了全等三角形的性质及比较角的大小,解题的关键是找到两全等三角形的对应角、对应边.二、填空题(每小题4分,共20分)13.若三角形三内角的度数之比为1:2:3,最大边的长是16cm,则最小边的长是8cm.考点:含30度角的直角三角形.分析:根据三角形的内角和等于180°求出最大角和最小角,然后根据直角三角形30°角所对的直角边等于斜边的一半解答.解答:解:∵三角形三内角的度数之比为1:2:3,∴三角形的最大的内角度数是:180°×=90°,最小的内角度数是:180°×=30°,∴此三角形是有一个锐角是30°的直角三角形,∵最大边的长是16cm,∴则最小边的长是16×=8cm.点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的内角和定理,熟记性质并求出此三角形是有一个锐角是30°的直角三角形是解题的关键.14.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,则P点到直线AB的距离是3cm.考点:线段垂直平分线的性质.分析:由已知条件,根据垂直平分线的性质得出AB=BC,可得到∠ABD=∠DBC,再利用角平分线上的点到角两边的距离相等得到答案.解答:解:过点P作PM⊥AB与点M,∵BD垂直平分线段AC,∴AB=CB,∴∠ABD=∠DBC,即BD为角平分线,又PM⊥AB,PE⊥CB,∴PM=PE=3.故答案为:3.点评:此题主要考查线段的垂直平分线的性质等几何知识.得到三角形全等是正确解答本题的关键,也可直接应用角平分线的性质求解.15.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,则∠AMB=70°.考点:平行线的性质;三角形的外角性质.分析:根据平行线的性质求出∠BAM,再由三角形的内角和定理可得出∠AMB.解答:解:∵AB∥CD,∴∠A+∠MDN=180°,∴∠A=180°﹣∠MDN=45°,在△ABM中,∠AMB=180°﹣∠A﹣∠B=70°.故答案为:70°.点评:本题考查了平行线的性质,解答本题的关键是掌握:两直线平行同胖内角互补,及三角形的内角和定理.16.△ABC中,DE分别是BC,AD的中点,且△ABC的面积为4,则阴影部分的面积是1.考点:三角形的面积.分析:根据中线将三角形面积分为相等的两部分可知:△ADC是阴影部分的面积的2倍,△ABC 的面积是△ADC的面积的2倍,依此即可求解.解答:解:∵D、E分别是BC,AD的中点,∴S△AEC=,S△ACD=S△ABC,∴S△AEC=S△ABC==1.点评:本题考查了三角形的面积和中线的性质:三角形的中线将三角形分为相等的两部分,知道中线将三角形面积分为相等的两部分是解题的关键.17.△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,AP+BP+CP的最小值为9.8.考点:等腰三角形的性质;垂线段最短;勾股定理.分析:若AP+BP+CP最小,就是说当BP最小时,AP+BP+CP才最小,因为不论点P在AC上的那一点,AP+CP都等于AC.那么就需从B向AC作垂线段,交AC于P.先设AP=x,再利用勾股定理可得关于x的方程,解即可求x,在Rt△ABP中,利用勾股定理可求BP.那么AP+BP+CP的最小值可求.解答:解:从B向AC作垂线段BP,交AC于P,设AP=x,则CP=5﹣x,在Rt△ABP中,BP2=AB2﹣AP2,在Rt△BCP中,BP2=BC2﹣CP2,∴AB2﹣AP2=BC2﹣CP2,∴52﹣x2=62﹣(5﹣x)2解得x=1.4,在Rt△ABP中,BP===4.8,∴AP+BP+CP=AC+BP=5+4.8=9.8.故答案为:9.8.点评:考查了等腰三角形的性质及勾股定理等知识,直线外一点与直线上各点连接的所有线段中,垂线段最短.因此先从B向AC作垂线段BP,交AB于P,再利用勾股定理解题即可.三、解答题18.先化简,再求值:﹣2+2ab2÷a,其中a=3,b=5.考点:整式的混合运算—化简求值.分析:先算乘法和除法,再合并同类项,最后代入求出即可.解答:解:﹣2+2ab2÷a=4a2﹣b2﹣4a2+4ab﹣b2+2b2=4ab,当a=3,b=5时,原式=4×3×5=60.点评:本题考查了整式的混合运算和求值的应用,能正确运用整式的运算法则进行化简是解此题的关键.19.如图是一个四边形的边角料,木工师傅通过测量,获得了如下数据:AB=3cm,BC=12cm,CD=13cm,AD=4cm,BD=5cm木工师傅由此认为这个四边形中∠A恰好是直角,你认为木工师傅的判断正确吗?如果你认为他正确,请说明其中的理由;如果你认为他不正确,那你认为需要什么条件,才可以判断∠A是直角?请求出木料的面积.考点:勾股定理的逆定理;勾股定理.分析:根据AB=3cm,BD=5cm,AD=4cm利用勾股定理逆定理可得AB2+AD2=BD2,因此∠A=90°;再利用勾股定理逆定理可判定∠DBC=90°,然后再计算出面积即可.解答:解:正确,∵32+42=52,∴AB2+AD2=BD2,∴∠A=90°,∵122+52=132,∴BD2+BC2=CD2,∴∠DBC=90°,∴木料的面积为:×4×3+×12×5=6+30=36(cm2).答:木工师傅的判断正确,木料的面积为36cm2.点评:此题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.20.如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:(1)∠D=∠B;AE∥CF.考点:全等三角形的判定与性质.专题:证明题.分析:(1)根据SSS推出△ADE≌△CBF,根据全等三角形的性质推出即可.根据全等三角形的性质推出∠AED=∠CFB,求出∠AEO=∠CFO,根据平行线的判定推出即可.解答:解:(1)∵在△ADE和△CBF中∴△ADE≌△CBF(SSS),∴∠D=∠B.∵△ADE≌△CBF,∴∠AED=∠CFB,∵∠AED+∠AEO=180°,∠CFB+∠CFO=180°,∴∠AEO=∠CFO,∴AE∥CF.点评:本题考查了全等三角形的性质和判定,平行线的判定的应用,注意:全等三角形的对应角相等.21.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?考点:轴对称-最短路线问题.专题:应用题.分析:先作A关于MN的对称点,连接A′B,构建直角三角形,利用勾股定理即可得出答案.解答:解:如图,作出A点关于MN的对称点A′,连接A′B交MN于点P,则A′B就是最短路线,在Rt△A′DB中,由勾股定理求得A′B=DA==17km,答:他要完成这件事情所走的最短路程是17km.点评:本题考查的是勾股定理和轴对称在实际生活中的运用,需要同学们联系实际,题目是一道比较典型的题目,难度适中.22.某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行?为什么?考点:勾股定理的应用;方向角.分析:根据路程=速度×时间分别求得PQ、PR的长,再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形,从而求解.解答:解:根据题意,得PQ=16×1.5=24(海里),PR=12×1.5=18(海里),QR=30(海里).∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.由“远航号”沿东北方向航行可知,∠QPS=45°,则∠SPR=45°,即“海天”号沿西北方向航行.点评:此题主要是能够根据勾股定理的逆定理发现直角三角形.23.数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:(1)特殊情况•探索结论当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE=DB (填“>”,“<”或“=”).特例启发,解答题目解:题目中,AE与DB的大小关系是:AE=DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)(3)拓展结论,设计新题在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).考点:全等三角形的判定与性质;三角形内角和定理;等边三角形的判定与性质.专题:计算题;证明题;压轴题;分类讨论.分析:(1)根据等边三角形的性质和三角形的内角和定理求出∠D=∠ECB=30°,∠ABC=60°,求出∠D=∠DEB=30°,推出DB=BE=AE即可得到答案;作EF∥BC,证出等边三角形AEF,再证△DBE≌△EFC即可得到答案;(3)分为四种情况:画出图形,根据等边三角形性质求出符合条件的CD即可.解答:解:(1)答案为:=.答案为:=.证明:在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,∵EF∥BC,∴∠AEF=∠ABC,∠AFE=∠ACB,∴∠AEF=∠AFE=∠BAC=60°,∴AE=AF=EF,∴AB﹣AE=AC﹣AF,即BE=CF,∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,∵ED=EC,∴∠EDB=∠ECB,∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,∴∠BED=∠FCE,在△DBE和△EFC中,∴△DBE≌△EFC(SAS),∴DB=EF,∴AE=BD.(3)解:分为四种情况:如图1:∵AB=AC=1,AE=2,∴B是AE的中点,∵△ABC是等边三角形,∴AB=AC=BC=1,△ACE是直角三角形(根据直角三角形斜边的中线等于斜边的一半),∴∠ACE=90°,∠AEC=30°,∴∠D=∠ECB=∠BEC=30°,∠DBE=∠ABC=60°,∴∠DEB=180°﹣30°﹣60°=90°,即△DEB是直角三角形.∴BD=2BE=2(30°所对的直角边等于斜边的一半),即CD=1+2=3.如图2,过A作AN⊥BC于N,过E作EM⊥CD于M,∵等边三角形ABC,EC=ED,∴BN=CN=BC=,CM=MD=CD,AN∥EM,∴△BAN∽△BEM,∴=,∵△ABC边长是1,AE=2,∴=,∴MN=1,∴CM=MN﹣CN=1﹣=,∴CD=2CM=1;如图3,∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,∴此时不存在EC=ED;如图4∵∠EDC<∠ABC,∠ECB>∠ACB,又∵∠ABC=∠ACB=60°,∴∠ECD>∠EDC,即此时ED≠EC,∴此时情况不存在,答:CD的长是3或1.点评:本题主要考查对全等三角形的性质和判定,三角形的内角和定理,等边三角形的性质和判定等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.。
2014-2015学年山东省莱芜七年级(上)第一次质检数学试卷(五四学制)一、选择题1.下列交通标志图案是轴对称图形的是()A.B.C.D.2.下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是()A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,43.如图所示,其中三角形的个数是()A.2个B.3个C.4个D.5个4.下列各图中,∠1大于∠2的是()A.B.C.D.5.如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有()A.1对B.2对C.3对D.4对6.如图,∠1=100°,∠C=70°,则∠A的大小是()A.10° B.20° C.30° D.80°7.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?()A.0根B.1根C.2根D.3根8.不一定在三角形内部的线段是()A.三角形的角平分线 B.三角形的中线C.三角形的高D.三角形的中位线9.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为()A.10° B.20° C.25° D.30°10.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是()A.BC=EC,∠B=∠E B.BC=EC,AC=DC C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D11.如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上一点,CF ⊥AD于H,下面判断正确的有()①AD是△ABE的角平分线;②BE是△ABD边AD上的中线;③CH是△ACD边AD上的高;④AH是△ACF的角平分线和高.A.1个B.2个C.3个D.4个12.如图所示,在△ABC中,∠ACB是钝角,让点C在射线BD上向右移动,则()A.△ABC将先变成直角三角形,然后再变成锐角三角形,而不会再是钝角三角形B.△ABC将变成锐角三角形,而不会再是钝角三角形C.△ABC将先变成直角三角形,然后再变成锐角三角形,接着又由锐角三角形变为钝角三角形D.△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形二、填空题13.△ABC中,∠BAC:∠ACB:∠ABC=4:3:2,且△ABC≌△DEF,则∠DEF= 度.14.如图,已知OQ平分∠AOB,QC⊥OA于C,QD⊥OB于D,OC=2,则OD的长为.15.如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= °.16.请按规律在空白处填上适当的图案.17.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为.三、解答题18.先化简,再求值:8x2﹣(x+2)(2﹣x)﹣2(x﹣5)2,其中x=﹣3.19.2014年经过莱芜的中南高速铁路即将竣工,届时与京沪高速公路使得莱芜区位发展优势将更加凸显.为了充分利用资源,市政府决定在莱城区与钢城区之间的A区建设一个物资中转站,要求与铁路与公路的距离相同,且与两区的距离也相同,请在下图中画出中转站的位置.(保留作图痕迹,不写作法)20.如图,在△ABC中,∠C=90°,AB的垂直平分线交BC于点D,交AB于点E,∠DAE与∠DAC的度数比为2:1,求∠B的度数.21.如图,在△ABC中,BE,CF分别是边AC,AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG,则AG与AD有何关系?试给出你的结论的理由.22.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.23.(1)将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和,这种方法称之为配方法.这种方法常常被用到式子的恒等变形中,以挖掘题目中的隐含条件,是解题的有力手段之一.例如,求x2+4x+5的最小值.解:原式=x2+4x+4+1=(x+2)2+1∵(x+2)2≥0∴(x+2)2+1≥1∴当x=﹣2时,原式取得最小值是1请求出x2+6x﹣4的最小值.(2)非负性的含义是指大于或等于零.在现初中阶段,我们主要学习了绝对值的非负性与平方的非负性,几个非负算式的和等于0,只能是这几个式子的值均为0.请根据非负算式的性质解答下题:已知△ABC的三边a,b,c满足a2﹣6a+b2﹣8b+25+|c﹣5|=0,求△ABC的周长.(3)已知△ABC的三边a,b,c满足a2+b2+c2=ab+bc+ac.试判断△ABC的形状.2014-2015学年山东省莱芜实验中学七年级(上)第一次质检数学试卷(五四学制)参考答案与试题解析一、选择题1.下列交通标志图案是轴对称图形的是()A.B.C.D.考点:轴对称图形.专题:常规题型.分析:根据轴对称的定义结合选项所给的特点即可得出答案.解答:解:A、不是轴对称图形,故本选项错误;B、是轴对称图形,故本选项正确;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误;故选:B.点评:本题考查了轴对称图形,掌握中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是()A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4考点:三角形三边关系.分析:根据三角形的三边关系:三角形两边之和大于第三边,计算两个较小的边的和,看看是否大于第三边即可.解答:解:A、1+2<6,不能组成三角形,故此选项错误;B、2+2=4,不能组成三角形,故此选项错误;C、1+2=3,不能组成三角形,故此选项错误;D、2+3>4,能组成三角形,故此选项正确;故选:D.点评:此题主要考查了三角形的三边关系,关键是掌握三角形的三边关系定理.3.如图所示,其中三角形的个数是()A.2个B.3个C.4个D.5个考点:三角形.分析:根据三角形的定义得到图中有△ABE,△DEC,△BEC,△ABC,△DBC共5个.解答:解:△ABE,△DEC,△BEC,△ABC,△DBC共5个.故选D.点评:三条线段,两两相交在一起所构成的一个密闭的平面图形叫做三角形.4.下列各图中,∠1大于∠2的是()A.B.C.D.考点:三角形的外角性质;对顶角、邻补角;平行线的性质;等腰三角形的性质.分析:根据三角形的内角,对顶角相等,同旁内角,三角形的外角性质逐个判断即可.解答:解:A不能判断∠1和∠2的大小,故本选项错误;B、∠1=∠2,故本选项错误;C、不能判断∠1和∠2的大小,故本选项错误;D、∠1>∠2,故本选项正确;故选D.点评:本题考查了三角形的内角,对顶角相等,同旁内角,三角形的外角性质的应用,主要考查学生的理解能力和判断能力.5.如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有()A.1对B.2对C.3对D.4对考点:全等三角形的判定.分析:首先证明△ABC≌△ADC,根据全等三角形的性质可得∠BAC=∠DAC,∠BCA=∠DCA,再证明△ABO≌△ADO,△BOC≌△DOC.解答:解:∵在△ABC和△ADC中,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,∠BCA=∠DCA,∵在△ABO和△ADO中,∴△ABO≌△ADO(SAS),∵在△BOC和△DOC中,∴△BOC≌△DOC(SAS),故选:C.点评:考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.6.如图,∠1=100°,∠C=70°,则∠A的大小是()A.10° B.20° C.30° D.80°考点:三角形的外角性质.分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解.解答:解:∵∠1=100°,∠C=70°,∴∠A=∠1﹣∠C=100°﹣70°=30°.故选C.点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.7.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?()A.0根B.1根C.2根D.3根考点:三角形的稳定性.专题:存在型.分析:根据三角形的稳定性进行解答即可.解答:解:加上AC后,原不稳定的四边形ABCD中具有了稳定的△ACD及△ABC,故这种做法根据的是三角形的稳定性.故选:B.点评:本题考查的是三角形的稳定性在实际生活中的应用,比较简单.8.不一定在三角形内部的线段是()A.三角形的角平分线 B.三角形的中线C.三角形的高D.三角形的中位线考点:三角形的角平分线、中线和高;三角形中位线定理.专题:计算题.分析:根据三角形的高、中线、角平分线的性质解答.解答:解:因为在三角形中,它的中线、角平分线一定在三角形的内部,而钝角三角形的高在三角形的外部.故选C.点评:本题考查了三角形的高、中线和角平分线,要熟悉它们的性质方可解答.9.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为()A.10° B.20° C.25° D.30°考点:平行线的性质.分析:延长AB交CF于E,求出∠ABC,根据三角形外角性质求出∠AEC,根据平行线性质得出∠2=∠AEC,代入求出即可.解答:解:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵∠1=35°,∴∠AEC=∠ABC﹣∠1=25°,∵GH∥EF,∴∠2=∠AEC=25°,故选C.点评:本题考查了三角形的内角和定理,三角形外角性质,平行线性质的应用,主要考查学生的推理能力.10.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是()A.BC=EC,∠B=∠E B.BC=EC,AC=DC C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D考点:全等三角形的判定.分析:根据全等三角形的判定方法分别进行判定即可.解答:解:A、已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC≌△DEC,故此选项不合题意;B、已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;C、已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;D、已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意;故选:C.点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.11.如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上一点,CF ⊥AD于H,下面判断正确的有()①AD是△ABE的角平分线;②BE是△ABD边AD上的中线;③CH是△ACD边AD上的高;④AH是△ACF的角平分线和高.A.1个B.2个C.3个D.4个考点:三角形的角平分线、中线和高.分析:根据三角形的角平分线、三角形的中线、三角形的高的概念进行判断.连接三角形的顶点和对边中点的线段即为三角形的中线;三角形的一个角的角平分线和对边相交,顶点和交点间的线段叫三角形的角平分线;从三角形的一个顶点向对边引垂线,顶点和垂足间的线段叫三角形的高.解答:解:①根据三角形的角平分线的概念,知AG是△ABE的角平分线,故此说法错误;②根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法错误;③根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法正确;④根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.故选B.点评:本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.12.如图所示,在△ABC中,∠ACB是钝角,让点C在射线BD上向右移动,则()A.△ABC将先变成直角三角形,然后再变成锐角三角形,而不会再是钝角三角形B.△ABC将变成锐角三角形,而不会再是钝角三角形C.△ABC将先变成直角三角形,然后再变成锐角三角形,接着又由锐角三角形变为钝角三角形D.△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形考点:三角形.分析:因为BC边变大,∠A也随着变大,∠C在变小.所以此题的变化为:△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形.解答:解:根据∠A的旋转变化规律可知:△ABC先由钝角三角形变为直角三角形,再变为锐角三角形,接着又变为直角三角形,然后再次变为钝角三角形.故选D.点评:解题时要注意三角形的变化:∠B不变,∠A变大,∠C在变小.二、填空题13.△ABC中,∠BAC:∠ACB:∠ABC=4:3:2,且△ABC≌△DEF,则∠DEF= 40 度.考点:全等三角形的性质.分析:先运用三角形内角和求出∠ABC=40°再运用全等三角形的性质即可得.解答:解:设∠BAC为4x,则∠ACB为3x,∠ABC为2x∵∠BAC+∠ACB+∠ABC=180°∴4x+3x+2x=180,解得x=20∴∠ABC=2x=40°∵△ABC≌△DEF∴∠DEF=∠ABC=40°.故填40.点评:本题考查了全等三角形的性质及三角形的内角和的应用;当题中出现比的问题时,应设比中的每一份为未知数.本题用到的知识点为:全等三角形的对应角相等.14.如图,已知OQ平分∠AOB,QC⊥OA于C,QD⊥OB于D,OC=2,则OD的长为 2 .考点:角平分线的性质.分析:根据角平分线上的点到角的两边距离相等可得QC=QD,再利用“HL”证明Rt△OCQ 和Rt△ODQ全等,根据全等三角形对应边相等可得OC=OD.解答:解:∵OQ平分∠AOB,QC⊥OA,QD⊥OB,∴QC=QD,在Rt△OCQ和Rt△ODQ中,,∴Rt△OCQ≌Rt△ODQ(HL),∴OC=OD=2.故答案为:2.点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并求出三角形全等是解题的关键.15.如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= 95 °.考点:平行线的性质;三角形内角和定理;翻折变换(折叠问题).分析:根据两直线平行,同位角相等求出∠BMF、∠BNF,再根据翻折的性质求出∠BMN和∠BNM,然后利用三角形的内角和定理列式计算即可得解.解答:解:∵MF∥AD,FN∥DC,∴∠BMF=∠A=100°,∠BNF=∠C=70°,∵△BMN沿MN翻折得△FMN,∴∠BMN=∠BMF=×100°=50°,∠BNM=∠BNF=×70°=35°,在△BMN中,∠B=180°﹣(∠BMN+∠BNM)=180°﹣(50°+35°)=180°﹣85°=95°.故答案为:95.点评:本题考查了两直线平行,同位角相等的性质,翻折变换的性质,三角形的内角和定理,熟记性质并准确识图是解题的关键.16.请按规律在空白处填上适当的图案∂ 6 .考点:规律型:图形的变化类.分析:根据已知可以得出此图形是连续的数字,得出空白处是∂6,并且是轴对称图形,得出答案即可.解答:解:根据已知可以得出此图形是连续的数字,并且是轴对称图形,∴横线上的空白出的图形是:∂6.故答案为:∂6.点评:此题主要考查了轴对称图形的定义,根据图形规律得出答案是解决问题的关键.17.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为30°.考点:三角形内角和定理.专题:新定义.分析:根据已知一个内角α是另一个内角β的两倍得出β的度数,进而求出最小内角即可.解答:解:由题意得:α=2β,α=100°,则β=50°,180°﹣100°﹣50°=30°,故答案为:30°.点评:此题主要考查了新定义以及三角形的内角和定理,根据已知得出β的度数是解题关键.三、解答题18.先化简,再求值:8x2﹣(x+2)(2﹣x)﹣2(x﹣5)2,其中x=﹣3.考点:整式的混合运算—化简求值.分析:先算乘法,再合并同类项,最后代入求出即可.解答:解:8x2﹣(x+2)(2﹣x)﹣2(x﹣5)2=8x2﹣4+x2﹣2x2+20x﹣50=7x2+20x﹣54,当x=﹣3时,原式=7×(﹣3)2+20×(﹣3)﹣54=﹣51.点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算和化简能力.19.2014年经过莱芜的中南高速铁路即将竣工,届时与京沪高速公路使得莱芜区位发展优势将更加凸显.为了充分利用资源,市政府决定在莱城区与钢城区之间的A区建设一个物资中转站,要求与铁路与公路的距离相同,且与两区的距离也相同,请在下图中画出中转站的位置.(保留作图痕迹,不写作法)考点:作图—应用与设计作图.分析:利用角平分线的性质以及线段垂直平分线的性质得出其交点即可得出答案.解答:解:如图所示:点P即为所求.点评:此题主要考查了应用设计与作图,熟练应用角平分线的性质以及线段垂直平分线的性质是解题关键.20.如图,在△ABC中,∠C=90°,AB的垂直平分线交BC于点D,交AB于点E,∠DAE与∠DAC的度数比为2:1,求∠B的度数.考点:线段垂直平分线的性质.分析:先根据线段垂直平分线及等腰三角形的性质得出∠B=∠DAB,再根据∠DAE与∠DAC 的度数比为2:1可设出∠B的度数,再根据直角三角形的性质列出方程,求出∠B的度数即可.解答:解:∵D是线段AB垂直平分线上的点,∴AD=BD,∴△DAB是等腰三角形,∠B=∠DAB,∵∠DAE与∠DAC的度数比为2:1,∴设∠DAC=x,则∠B=∠DAB=2x,∴x+2x+2x=90°,∴x=18°,即∠B=36°.点评:本题考查的是线段垂直平分线的性质,属较简单题目.21.如图,在△ABC中,BE,CF分别是边AC,AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG,则AG与AD有何关系?试给出你的结论的理由.考点:全等三角形的判定与性质.分析:求出∠ABD=∠AG,证△ABD≌△GCA,推出AG=AD,∠AGC=∠BAD,根据∠AFO=90°求出∠BAD+∠AOF=90°,推出∠AGC+∠AOF=90°,求出∠GAD=90°,即可得出答案.解答:解:AG=AD,AG⊥AD,理由是:∵在△ABC中,BE,CF分别是边AC,AB上的高,∴∠BFP=∠CEP=∠AFO=90°,∴∠ABD+∠FPB=90°,∠ACG+∠EPC=90°,∵∠FPB=∠EPC,∴∠ACG=∠ABD,在△ABD和△GCA中,,∴△ABD≌△GCA(SAS),∴AG=AD,∠AGC=∠BAD,∵∠AFO=90°,∴∠BAD+∠AOF=90°,∴∠AGC+∠AOF=90°,∴∠GAD=180°﹣90°=90°,∴AG⊥AD.点评:本题考查了全等三角形的性质和判定,三角形的内角和定理的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.22.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.考点:全等三角形的应用.专题:探究型.分析:证角相等,常常通过把角放到两个全等三角形中来证,本题OA=OA公共边,可考虑SSS证明三角形全等,从而推出角相等.解答:解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,理由如下:∵AB=AC,AE=AB,AF=AC,∴AE=AF,在△AOE与△AOF中,,∴△AOE≌△AOF(SSS),∴∠BAD=∠CAD.点评:本题考查全等三角形的应用.在实际生活中,常常通过两个全等三角形,得出对应角相等.23.(1)将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和,这种方法称之为配方法.这种方法常常被用到式子的恒等变形中,以挖掘题目中的隐含条件,是解题的有力手段之一.例如,求x2+4x+5的最小值.解:原式=x2+4x+4+1=(x+2)2+1∵(x+2)2≥0∴(x+2)2+1≥1∴当x=﹣2时,原式取得最小值是1请求出x2+6x﹣4的最小值.(2)非负性的含义是指大于或等于零.在现初中阶段,我们主要学习了绝对值的非负性与平方的非负性,几个非负算式的和等于0,只能是这几个式子的值均为0.请根据非负算式的性质解答下题:已知△ABC的三边a,b,c满足a2﹣6a+b2﹣8b+25+|c﹣5|=0,求△ABC的周长.(3)已知△ABC的三边a,b,c满足a2+b2+c2=ab+bc+ac.试判断△ABC的形状.考点:配方法的应用;非负数的性质:绝对值;非负数的性质:偶次方;因式分解的应用.分析:(1)利用配方法得出最小值即可;(2)利用非负数的性质得出a、b、c的值,进一步求得周长即可;(3)整理得(a﹣b)2+(b﹣c)2+(c﹣a)2=0,由非负数的性质求得三边相等,所以这是一个等边三角形解答:解:(1)x2+6x﹣4=x2+6x+9﹣9﹣4=(x+3)2﹣13,∵(x+3)2≥0∴(x+3)2﹣13≥﹣13∴当x=﹣3时,原式取得最小值是﹣13.(2)∵a2﹣6a+b2﹣8b+25+|c﹣5|=0,∴(a﹣3)2+(b﹣4)2+|c﹣5|=0,∴a﹣3=0,b﹣4=0,c﹣5=0,∴a=3,b=4.c=5,∴△ABC的周长=3+4+5=12.(3)△ABC为等边三角形.理由如下:∵a2+b2+c2=ab+bc+ac,∴a2+b2+c2﹣ac﹣ab﹣bc=0,∴2a2+2b2+2c2﹣2ac﹣2ab﹣2bc=0,即a2+b2﹣2ab+b2+c2﹣2bc+a2+c2﹣2ac=0,∴(a﹣b)2+(b﹣c)2+(c﹣a)2=0,∴a﹣b=0,b﹣c=0,c﹣a=0,∴a=b=c,∴△ABC为等边三角形.点评:此题考查了配方法的运用,非负数的性质,完全平方公式,等边三角形的判断.解题的关键是构建完全平方式,根据非负数的性质解题.。
某某省莱芜市莱城区腰关中学2014-2015学年八年级英语上学期第三模块测试试题一、听力测试(共20小题,计20分)(一)录音中有五个句子,每个句子听一遍,然后从每小题A、B、C中选出能对每个句子做出适当反应的答语。
()1. What book has the speaker read many times?A B C()2. Which one is the speaker’s favorite?A B C()3. Where has Tom gone?A B C()4. Which one isn’t mentioned?A B C()5. What does Alice do?A B C(二)根据所听对话的内容和所提的问题,在各题所给的三个选项中选出一个最佳选项,并将答案写在题前的括号内。
每段对话听两遍。
()6. Where has the woman been many times?A. The Great Wall.B. The Palace Museum.C. The Terracotta Army.()7. How long has the man worked in the school?A. For 8 years.B. For 9 years.C. Since 2006.()8. Has the man ever been to Singapore?A. Yes, he has.B. No, he hasn’t.C. We don’t know.()9. How many times has the man been to Beijing?A. Once.B. Twice.C. Three times.()10. How long haven’t they seen each other?A. For a year.B. For half a year.C. For 18 months.(三)录音中有一段对话,听对话两遍后,从每小题A、B、C中选出能回答所给问題的正确答案。
山东省莱芜市莱城区腰关中学2014-2015学年七年级政治上学期第三模块测试试题第︱卷一、单项选择题:(40分。
每小题2分)1.如果说人的情绪是奔腾的“洪水”,那么,理智就像一道坚固的“闸门”。
这句话表明( )A .情绪是不可以控制的B.应顺其自然让情绪自由发展C.要理智就不应该要情绪D.应该用理智来调控情绪2.新浪教育报道,福建省2010年理科状元骆雅婷在介绍自己的成功经验时说:我去的好成绩的主要原因是良好的心态加正确的学习方法。
每次考试前,我都提醒自己保持良好的心态,这是我超水平发挥的一个重要因素。
骆雅婷的经验给我们的启示有( )①我们要保持和培养积极的情绪②积极的情绪对我们的学习有积极的作用③只要放松身心,就有好成绩④积极进行自我暗示,能够遏制不良情绪的产生A.①②③B.②③④C.①③④D.①②④3.下列情绪表现中,属于消极情绪的是()①得到自己喜欢的礼物时,我感到很高兴②我的脚崴了,不能走路时,感到焦虑、急躁③爸爸把我喜欢看的电视节目关了,我很不高兴④我在同学面前被家长当众斥责时,感到恼羞成怒A. ①③④B. ①②④C. ②③④D. ①②③4.短跑运动员在上场比赛时,常常心里默念:“我是最棒的”“我一定能跑赢别人”。
这种调控情绪的方法()A、幽默化解B、目标转移C、换位思考D、自我暗示5.下列行为属于高雅情趣的是( )①小东很注重外表,每天早晨梳头、化妆要用去半个多小时②节假日小军喜欢和爸爸一起上网,查找学习资料,关心社会新闻③小孟爱好集邮,有时碰见别人没取得信件上有自己喜欢的邮票,就偷偷地撕下来,据为己有④小雨热爱滑冰,每个星期六总是抽时间去练习A.①②B. ③④C. ①③D.②④小倩原来是个文静,气质优雅的学生,同学们都很喜欢她,后来,小倩开始盲目的追星,还染黄头发,去歌舞厅,与所谓的朋友一起玩牌赌博,许多同学渐渐的疏远了她,由于好奇,他又染上了毒品,依法受到处罚。
据此,回答6-7题6.小倩发生变化的原因有( )①受猎奇和盲目从众心理的驱使②自控能力差③辨别是非的能力不强④交友不慎A.①②③④B.①③④C.①②③D.②③7.从小倩的演变过程中,我们可以看出( )①猎奇和盲目从众心理不利于个人身心健康发展②预防违法犯罪,必须从杜绝不良行为做起③未成年人抵制不住不良诱惑④只有防微杜渐,才能防患于未然A.①②③B.②③④C.①③④D.①②④8.近来我国各地的博物馆、文化馆、科技馆、体育馆、公园等场所,相继对中小学生免费或优惠开放。
山东省莱芜市莱城区腰关中学(五四制)2015届九年级上学期第三模块测试数学试题一、选择题(每题3分,共36分)1、在正方形网格中,△ABC 的位置如图1所示,则cos ∠B 的值为( )A.21 B. 22 C. 23 D. 332、抛物线经过平移得到,平移方法是( )A .向左平移1个单位,再向下平移3个单位B .向左平移1个单位,再向上平移3个单位C .向右平移1个单位,再向下平移3个单位D .向右平移1个单位,再向上平移3个单位 3、下列命题错误..的是( ) A .经过三个点一定可以作圆B .三角形的外心到三角形各顶点的距离相等C .同圆或等圆中,相等的圆心角所对的弧相等D .经过切点且垂直于切线的直线必经过圆心4、已知,⊙O 1与⊙O 2的半径分别是4和6,O 1O 2=2,则⊙O 1与⊙O 2的位置关系是( ) A .外切 B .相交 C .内切 D .外离5、 将量角器按如图所示的方式放置在三角形纸板上,使点C 在半圆上.点A 、B 的读数分别为88°、30°,则∠ACB 的大小为( ) A .15︒ B .28︒ C .29︒ D .34︒6、如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是( )A.4π B.π42 C. π22D. 2π 7、如图24—A —5,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B ,CD 切⊙O 于点E ,分别交PA 、PB 于点C 、D ,若PA=5,则△PCD 的周长为( ) A .5 B .7 C .8 D .108、已知在△ABC 中,AB=AC=13,BC=10,那么△ABC 的内切圆的半径为( )图24—A —5图1A .310 B .512 C .2 D .3 9、一个圆锥的底面积为π4cm 2,母线长为6cm ,则该圆锥的侧面展开图中圆心角为( ) A .40º B .80º C .120º D .150º10、如图,AB 为半圆的直径,且AB=4,半圆绕点B 顺时针旋转45°,点A 旋转到A′的位置,则图中阴影部分的面积为( ) A . π B . 2π C .21π D . 4π11、在同一平面直角坐标系中,一次函数y ax b =+和二次函数2y ax bx =++c 的图象可能为( )12、如图所示的二次函数2y ax bx c =++的图象中,刘星同学观察得出了下面四条信息: (1)240b ac ->;(2)c>1;(3)2a -b<0;(4)a+b+c<0。
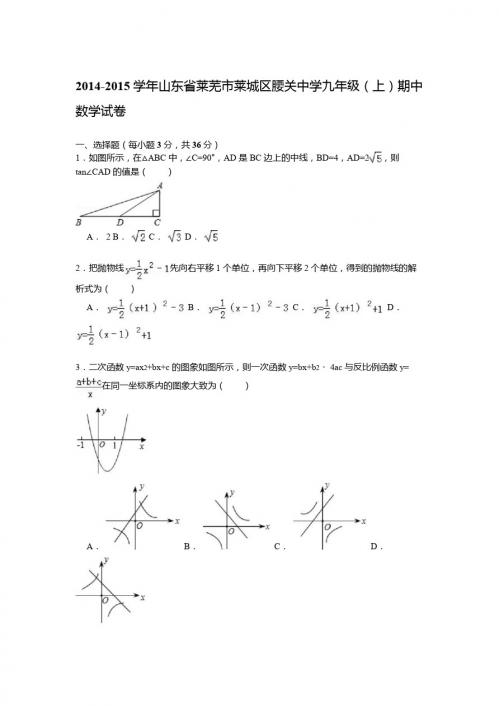
山东省莱芜市莱城区腰关中学2014-2015学年七年级数学上学期第三模块测
试试题(无答案,五四制)
1.在给出的一组数()0
2
-,π,
5,3.14,39,-0.333…,
7
22
中,无理数有( ) A .1个 B .2个 C .3个 D .5个 2.4的算术平方根是( )
A .4
B .2
C .2
D .2±
3.适合下列条件的△ABC 中, 直角三角形的个数为( )
①∠A:∠B:∠C=1:2:3 ②,6=a b=6,∠A=450
; ③∠A=320
,∠B=580
; ④;25,24,7===c b a ⑤.4,2,2===c b a A 、2个 B 、3个 C 、4个 D 、5个
4. 某一次函数的图象经过点(1,2),且y 随x 的增大而减小,则这个函数的表达式可能是( ) A .42+=x y B .13-=x y C . 13+-=x y D .42+-=x y
5. 在直角坐标系中,将点P (-2,3)沿x 轴方向向右平移3个单位得到点Q ,则点Q 的坐标是( ) A.(-2,6)
B.(-2,0)
C.(-5,3)
D.(1,3)
6.下列各式中,正确的是 A
±4 B .2)2(2-=- C
= -3 D
- 4
7. 如图,将三角尺的直角顶点放在直尺的一边上, 130250∠=∠=°,°,则3∠的度数等于( ) A .50° B .30° C .20° D .15°
8、某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过
程中洗衣机内水量y (升)与时间x (分)之间的函数关系对应的图象大致为( )
9、小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( )
1 2
3
第7题
A .21:10
B .10:21
C .10:51
D .12:01
10.油箱中存油20升,油从油箱中均匀流出,流速为0.2升/分钟,则油箱中剩余油量 Q (升)与流出时间t(分钟)的函数关系是( )
A .Q =0.2t
B .Q =20-0.2t
C .t=0.2Q
D .t=20—0.2Q 二、填空题(每小题3分,共30分)
11. a 是9的平方根,而b 的算术平方根是4,则a+b= 12.已知a 的平方根是8±,则它的立方根是 . 13. 如右图,数轴上点A 表示的数是 .
14. 如上右图所示,有一圆柱,其高为12cm ,它的底面半径为3cm ,在圆柱下底面A 处有一只蚂蚁,
它想得到上面B 处的食物,则蚂蚁经过的最短距离为________ cm 。
(π取3)
15.P (-3,-4)到x 轴的距离是 ,到y 轴的距离是 ,到原点的距离是 .
16. 已知点P 在第二象限,且到x 轴的距离是2,到y 轴的距离是3,则P 点关于y 轴的对称点坐标为___________
17. 已知O (0, 0),A (-3, 0),B (-1, -2),则△AOB 的面积为___
18.若一个正数的平方根是2a -1和-a+2,则a= ,这个正数是 。
19. 若一次函数()0≠+=k b kx y 与函数12
1
+=
x y 的图象关于X 轴对称,且交点在X 轴上,则这个函数的表达式为:
20. 如图,在Rt △ABC 中,∠C =90°,BC =6cm ,AC =8cm ,按图中所示方法将△BCD 沿BD 折叠,使点C 落在AB 边的C ′点,那么△ADC ′的面积是
三、解答题(本题60分)
21. (8分)计算:①4
1
804.03--+ (2)2323--;
③)23)(23()132(2-++- (4)()2
2-x =9
第20 题图
22、(4分)比较大小: (1)325-与3-
24. (本题6分) 已知21a +的平方根是±3,522a b +-的算术平方根是4,求34a b -的平方根
25.(本题6分) 在等腰△ABC 中,AB=AC,D 是AC 上一点,且AD=BD=BC,求△ABC 各角的度数.
26、(本题6分)如图,A ,B 是公路l (l 为东西走向)两旁的两个村庄,A 村到公路l 的距离AC =1km ,B 村到公路l 的距离BD =2km ,B 村在A 村的南偏东45方向上. (1)求出A ,B 两村之间的距离;
(2)为方便村民出行,计划在公路边新建一个公共汽车站P ,要求该站到两村的距离相等,请用尺规在图中作出点P 的位置(保留清晰的作图痕迹,并简要写明作法)
.8
5
215)
2(与-A
B
C
D
27.(6分)初二(1)班同学到野外上数学活动课,为测量池塘两端A 、B 的距离,设计了如下方案: (Ⅰ)如图(27-1),先在平地上取一个可直接到达A 、B 的点C ,连接AC 、BC ,并分别延长AC 至D ,BC 至E ,使DC=AC ,EC=BC ,最后测出DE 的距离即为AB 的长; (Ⅱ)如图(27-2),先过B 点作AB 的垂线BF ,再在BF 上取C 、D 两点使BC=CD ,接着过D 作BD 的垂线DE ,交AC 的延长线于E ,则测出DE 的长即为AB 的距离
.
(27-1) (27-2)
阅读后回答下列问题:(1)方案(Ⅰ)是否可行?请说明理由。
(2)方案(Ⅱ)是否可行?请说明理由。
28、(6分)如图所示,点B 、F 、C 、E 在同一直线上,AC 、DF 相交于G ,AB ⊥BE ,垂足为B ,DE ⊥BE ,垂足为E ,且AB =DE,BF =CE 。
求证:(1)△ABC ≌△DEF ; (2)如果GF=4,求GC 的长。
29、(6分)如图,小明在做数学作业时,遇到了这样一个问题,AB=CD ,BC=AD ,小明动手量了一下,发现∠A 确实与∠C 相等,但他不能说明其中的道理,请帮助他说明这个道理。
北
东
A
C
D
l。