数独技巧图示

数独九宫格高级技巧公式法摘要：1.数独介绍及九宫格高级技巧意义2.常见九宫格谜题类型及解题方法3.公式法原理及具体应用4.实例演示5.总结与提高正文：数独作为一种益智游戏，深受广大玩家喜爱。

在数独游戏中，九宫格是一种较为复杂的谜题类型。

为了更好地解决这类谜题，这里向大家介绍九宫格高级技巧——公式法。

公式法是基于数独九宫格谜题的特性，通过一定的逻辑推理，找出某些数字的唯一位置。

常见九宫格谜题类型有以下几种：1.唯一候选数：在某个宫位中，只有一个数字可能出现。

例如，在第一宫中，只有数字1可能出现。

2.唯一候选行：在某个行中，只有一个数字可能出现。

例如，在第一行中，只有数字1、2、3、4、5、6、7、8、9可能出现。

3.唯一候选列：在某个列中，只有一个数字可能出现。

例如，在第一列中，只有数字1、2、3、4、5、6、7、8、9可能出现。

4.唯一候选对角线：在某个对角线中，只有一个数字可能出现。

例如，在左上到右下的对角线中，只有数字1、2、3、4、5、6、7、8、9可能出现。

针对这些类型，我们可以运用公式法进行解题。

公式法原理是根据数独九宫格的特性，通过逻辑推理，找出某些数字的唯一位置。

具体应用如下：1.利用唯一候选数法，我们可以先找出某个宫位中只有一个数字的宫格，将其填入相应的数字。

2.利用唯一候选行、列或对角线法，我们可以先找出某个行、列或对角线中只有一个数字的宫格，将其填入相应的数字。

3.在填入数字的过程中，要注意观察已填数字对其他宫格数字的影响，不断调整候选数字，直至完成九宫格。

下面通过一个实例来演示公式法的应用：假设我们有以下九宫格数独谜题：```1 2 34 5 67 8 99 4 19 5 63 7 88 6 37 9 21 5 4```步骤1：观察发现第一行中，唯一候选数为9的宫格为（1，1），填入9。

步骤2：观察发现第一列中，唯一候选数为4的宫格为（1，3），填入4。

步骤3：观察发现右下角宫格中，唯一候选数为1的宫格为（3，3），填入1。

数独入门：你必须掌握的那些规则和技巧数独的规则在空格内填入数字1-9，使得每行、每列和每个宫内数字都不重复。

注意：数独题目满足条件的答案是唯一的。

数独的元素数独的元素主要包括行、列和宫。

这三者划分出数独有三种不同形态的区域，而数独规则就是要求在这些区域内出现的数字都为1~9。

元素坐标图：行：数独盘面内横向一组九格的区域，用字母表示其位置；列：数独盘面内纵向一组九格的区域，用数字表示其位置；宫：数独盘面内3×3格被粗线划分的区域，用中文数字表示其位置。

格的坐标：利用表示行位置的字母和表示列位置的数字定位数独盘面内每个格子的具体位置，如A3格，F8格等。

数独技巧1.?宫内排除法排除法就是利用数独中行、列和宫内不能填入相同数字的规则，利用已出现的数字对同行、同列和同宫内其他格进行排斥相同数字的方法。

宫内排除法就是将一个宫作为目标，用某个数字对它进行排除，最终得到这个宫内只有一格出现该数字的方法。

技巧示意图：宫内排除法如上图所示，A2、B4和F7三格内的1都对三宫进行排除，这时三宫内只有C9格可以填入1，本图例就是对三宫运用的排除法。

2.?行列排除法行列排除法就是将一行或一列作为目标，用某个数字对它进行排除，最终得到这个行列内只有一格出现该数字的方法。

技巧示意图：行列排除法如上图所示，D2和B8两格内的6都对F行进行排除，这时F行内只有F5格可以填入6，本图例就是对F行运用的排除法。

3.?区块排除法区块排除法就是先利用宫内排除法在某个宫内形成一个区块，利用该区块的排除再结合其他已知数共同确定某宫内只有一格出现该数字的方法。

技巧示意图：区块排除法如上图所示，B4格的7对五宫进行排除，在五宫内形成了一个含数字7的区块。

无论该区块中F5格是7还是F6格是7，都可以对F行其他格的7进行排除。

再结合H7格的7同时对六宫进行排除，得到六宫内只有D8格可以填7。

4.?宫内数对占位法数对占位法指的是在某个区域中使得某两数只能出现在某两格内，这时虽然无法判断这两个数字的位置，但可以利用两数的占位排斥掉其他数字出现在这两格，再结合排除法就可以间接填出下个数字。

数独的方法和技巧1. 使用“唯一候选数法”，即在确定某个数字所在位置后，检查该位置的行、列、九宫格中的空格，将已经确定的数字从候选数字列表中去掉。

2. 利用“排除法”确定某个位置可能的数字，即通过查找行、列、九宫格中已经确定的数字，来排除某些候选数字，从而缩小可能的范围。

3. 学会“交叉排除法”，即通过行或列中的一个区域确定了某个数字的位置后，再通过同一个行或列的其他区域来进一步缩小数字的位置。

4. 利用“唯一数字法”，即在某一行、列或九宫格中，找出只有一个位置能放某个数字的情况，从而确定该位置的数字。

5. 掌握“候选数对数法”，当两个格子中的候选数字只有两种时，这两种数字一定只在这两个格子中出现，从而可以排除其他格子的相应候选数字。

6. 学会“三链数法”，即当三个候选数字在同一行、列或九宫格中，可以形成一个闭环，从而确定这三个位置的数字。

7. 利用“XYZ链法”，当三个数字在同一行、列或九宫格中，且它们中的两个数字在行、列或九宫格中形成一个闭环，从而可以确定第三个数字的位置。

8. 使用“X-Wing法”，即当某一数字在两行或两列中只出现在相同的两个区域中，就可以确定该数字不会出现在这两个区域之外的其他行或列中。

9. 掌握“Swordfish法”，当某一数字在三行或三列中只出现在三个相同的区域中，就可以确定该数字不会出现在这三个区域之外的其他行或列中。

10. 学会“Jellyfish法”，当某一数字在四行或四列中只出现在四个相同的区域中，就可以确定该数字不会出现在这四个区域之外的其他行或列中。

11. 使用“显式候选法”，即通过排除法和唯一候选数法无法解决时，可以通过将所有可能的候选数字都填入格子中，然后逐步根据规则排除不符合要求的数字，直到解决数独。

12. 掌握“隐式候选法”，即通过观察某一行、列或九宫格中已经确定的数字，推断出其他格子中的候选数字。

13. 使用“矩形判断法”，即当某一数字在两行和两列的交叉区域内形成一个矩形时，可以确定矩形内另外两个位置不可能出现相同的数字。

5*51. 像这种题型的结构特点是，各个图形很分散，问号处在最靠边的一列或行；问号在3个图形交汇处，相邻两格一格有图形一格没图形；问号的下一行（列）的图形间隔出现。

∙解题思路：先看问号的下一行（列），三个空白，由（1,3）和（5,5）的三角形可得出第三列和第五列填不了三角形，所以（4,1）肯定是三角形。

所以问号处可以排除四个，问号为圆。

∙这种题型的结构和解题思路大抵如此，经常会旋转一下位置。

一般来说，用来排除的（1,3）和（5,5）的三角形位置也很少会变，也都是在最靠边的两行（列）。

2. 结构特点：第三行（列）有四个图形连续排列，问号紧邻第三行（列）；问号那一行（列）只有一个图形，三个空白。

∙解题思路：碰到有四个图形连续排列的，第一步一定先把第五个填出来，可得出（3，1）为三角形，接下来就豁然开朗啦。

由（3,1）（1,2）（5，5）的三角形可得出，问号所处的第四行的三个空白处都填不了三角形，所以问号就是三角形。

∙这种题型的结构和解题思路大抵如此，经常会旋转一下位置。

一般来说，用来排除的（1,2）和（5,5）的三角形位置也很少会变，也都是在最靠边的两行（列）。

楼主后来发现，一般第三行缺的那个图形就是问号处的图形啦，没遇见过例外，但是保险起见，大家还是都按套路走一遍吧~3. 结构特点：对角线有三个一样的图形间隔出现，问号处在第二或四行（列），问号所处一行（列）图形间隔出现。

∙解题思路：由三个星星的位置可知剩下两个星星肯定在第二列/第四列和第二行/第四行的4个交汇点。

由于（4,2）的圆占了一个交汇点，所以第二列的星星只能出现在（2,2），所以问号就是三角形。

∙这种题型的结构和解题思路大抵如此，经常会旋转一下位置。

一般来说，用来排除的（4,2）的圆形位置只有两种情况，一是（4,2），一是（4,4）。

如果在（4,4），则问号就直接是星星（就本题位置来说）。

4. 结构特点：最靠边的一行（列）有四个图形连续排列；问号所处的一列（行）只有中间一格是空白；第三行（列）中间位置有两个图形。

数独是一种基于逻辑推理的数字填充游戏，其解题诀窍和技巧众多，以下是几个关键的解题策略：1. **唯一解法（唯一候选数法/唯一余数法）**：- 在一个单元格（行、列或宫格）中，如果只剩下唯一一个位置可以放置某个数字，那么这个数字就应该填在那里。

2. **排除法（隐性唯一候选数法）**：- 在一个单元格所在的行、列或宫格中，如果一个数字在其他位置都已经出现，那么这个数字就不能出现在当前单元格中。

3. **区块排除法（区块唯一候选数法）**：- 在一个较大的连续空间里，如果一个数字仅在一个小的区块（比如两个行或列的交叉部分）内有候选位置，那么这个数字就在那个区块内唯一的空格里。

4. **单元内排除法**：- 观察某一行、列或宫格中已知的数字，可以排除掉同一行、列或宫格内剩余单元格的对应数字。

5. **对角线分析**：- 在某些变形数独（如对角线数独）中，需要考虑对角线上数字的唯一性和排除法。

6. **连锁反应（显性或隐性数对、三元组、四元组等）**：- 数对：在同一个宫格、行或列内，如果两个单元格共享相同的两个候选数字，那么这两个数字只能分别填在这两个单元格中。

- 类似的逻辑还可扩展到三元组（三个单元格共享三个候选数字）和四元组等更复杂的情形。

7. **区块分析**：- 在某些特定区域（如宫格内部、宫格外围等）内，通过观察数字的分布情况，可以进一步缩小其他单元格的候选数字范围。

8. **十字交叉法**：- 当某行或某列只剩下一个宫格未填数字，而这个宫格在对应的行或列中也只有唯一一个候选数字时，可以确定这个数字的位置。

通过反复应用这些技巧和不断的逻辑推理，即使是复杂的数独也能逐一破解。

记住，数独解题的关键是观察和逻辑推理，而不是盲目的猜测。

数独4宫格的解题方法和技巧
四宫格数独的方法技巧与规律如下：
1、唯一说法
已知第二宫内的三个数字为1、2、3，根据唯一数法则，剩下的一个数字为4。

以此类推，还有行、列唯一数法则。

2、宫内排除法
四宫格中有三个数字黑色字体，根据唯一数法则可知，下图中黄色格内不可以是数字3，那么用宫内排除法可以得出，第一宫内的另外两个数字。

3、行列排除法
四宫格中有三个数字黑色字体，观察第一列可以看出剩余两个是3或者4，排除法可知，数字4应在红色字体标记的格内。

4、唯余法
唯余法需要同时观察差行、列和宫。

数独由来：
数独（shùdú）是源自18世纪瑞士的一种数学游戏。

是一种运用纸、笔进行演算的逻辑游戏。

玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫（3x3）内的数字均含1-9，不重复。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次，所以又称“九宫格”。

九宫格数独的技巧数独的元素数独的元素主要包括行、列和宫。

这三者划分出数独有三种不同形态的区域，而数独规则就是要求在这些区域内出现的数字都为1~9。

元素坐标图：行：数独盘面内横向一组九格的区域，用字母表示其位置；列：数独盘面内纵向一组九格的区域，用数字表示其位置；宫：数独盘面内3×3格被粗线划分的区域，用中文数字表示其位置。

格的坐标：利用表示行位置的字母和表示列位置的数字定位数独盘面内每个格子的具体位置，如A3格，F8格等。

数独技巧1. 宫内排除法排除法就是利用数独中行、列和宫内不能填入相同数字的规则，利用已出现的数字对同行、同列和同宫内其他格进行排斥相同数字的方法。

宫内排除法就是将一个宫作为目标，用某个数字对它进行排除，最终得到这个宫内只有一格出现该数字的方法。

技巧示意图：宫内排除法如上图所示，A2、B4和F7三格内的1都对三宫进行排除，这时三宫内只有C9格可以填入1，本图例就是对三宫运用的排除法。

2. 行列排除法行列排除法就是将一行或一列作为目标，用某个数字对它进行排除，最终得到这个行列内只有一格出现该数字的方法。

技巧示意图：行列排除法如上图所示，D2和B8两格内的6都对F行进行排除，这时F行内只有F5格可以填入6，本图例就是对F行运用的排除法。

3. 区块排除法区块排除法就是先利用宫内排除法在某个宫内形成一个区块，利用该区块的排除再结合其他已知数共同确定某宫内只有一格出现该数字的方法。

技巧示意图：区块排除法如上图所示，B4格的7对五宫进行排除，在五宫内形成了一个含数字7的区块。

无论该区块中F5格是7还是F6格是7，都可以对F行其他格的7进行排除。

再结合H7格的7同时对六宫进行排除，得到六宫内只有D8格可以填7。

4. 宫内数对占位法数对占位法指的是在某个区域中使得某两数只能出现在某两格内，这时虽然无法判断这两个数字的位置，但可以利用两数的占位排斥掉其他数字出现在这两格，再结合排除法就可以间接填出下个数字。

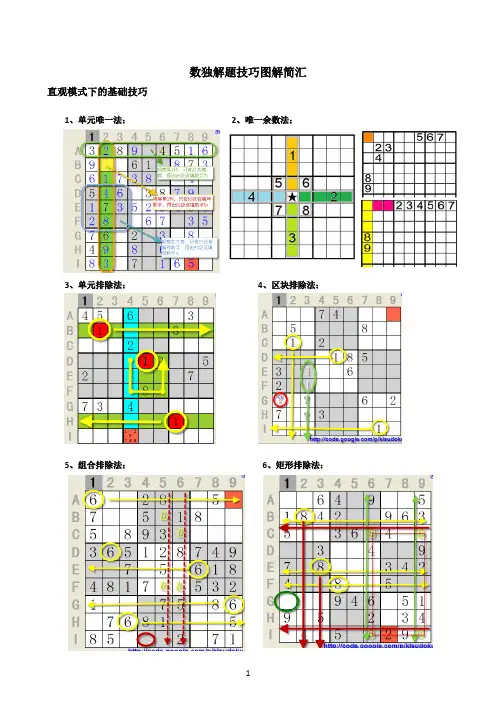
数独解题技巧图解简汇直观模式下的基础技巧1、单元唯一法：2、唯一余数法：3、单元排除法：4、区块排除法：5、组合排除法：6、矩形排除法：7、数对占位排除法：候选数模式下的解题技巧1、显式唯一数法：如某格只包含一个候选数，2、隐式唯一数法：如某格所含候选数字在该单元即可将该数字填入该单元格。

格只出现一次，则该格即可填入该数字。

3、区块删除法：先确定某区块一定包含某个数字，再以此为已知条件对相关区其他单元格进行该数字删除。

4、显式数对法：利用一组显性数对，对所在区其他单元格内的与显性数对数字相同的候选数进行删除。

显性数对为格外删除。

5、隐式数对法：在同一区中只有两个单元格出现某两个候选数字，且该区其他单元格均不包含这两个候选数，则可将该两格内的其他候选数进行删除。

隐性数对为格内删除。

6、显式三数集法：利用一组显性数组对所在区其他单元格内的与显性数组数字相同的候选数进行删除。

该行既含359显式三数集也含17隐式数对，二者均可将4和6两格中359进行删除。

7、隐式三数集法：在同一区中只有三个单元格出现某三个候选数字（每格至少包含其中的两个数字），且该区其他单元格均不包含这三个候选数，则可将该三格内的其他候选数进行删除。

该H行既含589隐式三数集也含1234显式四数集，二者均可将H1、H3中134进行删除。

8、显式四数集法：该行既含89隐式数对也含2356显式四数集，二者均可将D3、D7中356进行删除。

9、隐式四数集法：该行既含2489隐式四数集也含17显式数对，二者均可将A4A6A7A8中17进行删除。

10、矩形对角线法：如果一个数字正好出现且只出现在某两行的相同的两列上，则这个数字就可以从这两列上其他的单元格的候选数中删除。

或，如果一个数字正好出现且只出现在某两列的相同的两行上，则这个数字就可以从这两行上的其他单元格的候选数中删除。

在B G两行中，7都出现两次，且都位于第2列和在第1列和第7列上，数字9出现两次且只出第7列上，故第2列中的A2，第7列中的C7，D7 现在行C和行G上，故行C上的[C4] 和[C5]和E7的候选数7均可删除。

九宫格数独数独概述数独顾名思义——每个数字只能出现一次。

数独是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数字谜题。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次(如下图中已经填写完整的那样，不能重复，独立存在)。

这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式。

数独的历史数独前身为“九宫格”，最早起源于中国。

数千年前，我们的祖先就发明了洛书，其特点较之现在的数独更为复杂，要求纵向、横向、斜向上的三个数字之和等于15，而非简单的九个数字不能重复。

儒家典籍《易经》中的“九宫图”也源于此，故称“洛书九宫图”。

而“九宫”之名也因《易经》在中华文化发展史上的重要地位而保存、沿用至今。

1783年，瑞士数学家莱昂哈德·欧拉发明了一种当时称作“拉丁方块”（Latin Square）的游戏，这个游戏是一个n×n的数字方阵，每一行和每一列都是由不重复的n个数字或者字母组成的。

19世纪70年代，美国的一家数学逻辑游戏杂志《戴尔铅笔字谜和词语游戏》（Dell Puzzle Mαgαzines）开始刊登现在称为“数独”的这种游戏，当时人们称之为“数字拼图”（Number Place），在这个时候，9×9的81格数字游戏才开始成型。

1984年4月，在日本游戏杂志《字谜通讯Nikoil》（《パズル通信ニコリ》）上出现了“数独”游戏，提出了“独立的数字”的概念，意思就是“这个数字只能出现一次”或者“这个数字必须是惟一的”，并将这个游戏命名为“数独”（sudoku）。

一位前任香港高等法院的新西兰籍法官高乐德（Wayne Gould）在1997年3月到日本东京旅游时，无意中发现了。