矩形波导中电磁波的传播模式
- 格式：docx
- 大小：53.98 KB
- 文档页数：6
下载文档原格式
合集下载
电磁波与天线---矩形波导
mπ 当x=0时，A2=0.当x=a时, k x = a 同理可得， nπ 当y=0时，B2=0,当y=b时， y = k b
最后得： 最后得
mπ x nπ y − j β z H z = H 0 cos e cos a b
ˆ ax ∂ ∂x Hx ˆ ay ∂ ∂y Hy
(9) ( n = 0 ,1, 2 , L )
（1） TE10 模的场结构
• 在（10）式中，令 m=1, n=0, 并注意到 ）式中， • 那么， 那么，
mπ 2 nπ 2 π 2 kc = ( ) +( ) =( ) a b a
2
H z = H 0 cos( x)e− j β z a π a H x = j β H 0 sin( x)e − j β z π a a π E y = − jωµ H 0 sin( x)e − j β z π a
−
∂H
y
= jω ε E
x
同理，可得 在直角坐标系中展开可得 在直角坐标系中展开可得： 同理，可得E在直角坐标系中展开可得：
解式中的变量Z因 解式中的变量 因 − jβ z 为e ，所以上面 的两式可以对Z的偏 的两式可以对 的偏 导数化解。 导数化解。我们仅 对其中的4个式子进 对其中的 个式子进 行化解
2 2
∇ H =0
利用公式：∇×(∇×H) =∇∇•H)−∇ H (
2
• 得：
∇ H + ω µε H = ∇ H + k H = 0
2
2
2
2
• 式中： • 同理
k = ω µε
2
∇ E+k E =0
2 2
• 导波系统中，我们用直角坐标系，在 直角坐标系中，我们以E为例分解：
矩形波导的模式
矩形波导的模式
矩形波导是使⽤最⼴泛的⼀种传输线。
给定尺⼨的波导可以传播⽆限多频率的电磁波，本⽂主要写矩形波导的场求解问题及矩形波导的相关特性。
在波导内部，认为为⽆源空间，所以不存在传导电流和电荷，即J ＝ 0
⼀
对式2继续取旋度，得
同理对式1取旋度，可得到两个Helmheltz⽅程如下
求解的过程可总结为
每个Helmholtz⽅向是⼀个⽮量⽅程，在矩形波导中可以分解为三个⽅向x\y\z的三个标题⽅程，从⽽得到波传播⽅向z⽅向的标量⽅程
假设E z\H z可分离变量，分离变量法可得到
且
其中为截⽌波数，
解的第⼀部分是⼊射波，第⼆部分是反射波。
只考虑⼊射波得
横向分量⽤纵向分量表⽰
整理Ex、Hy得
整理Hx、Ey得
写成矩阵形式
⼆以TE波为例
H（x,y）可分离变量，H（x,y)=X(x)Y(y)
得
⼀般解为：
总的解为
矩形波导的基模是TE10模
TE10模功率容量。
《电磁场与微波技术教学课件》2.2 矩形波导
Hx j Kc H 2 0 m m sin a a n x cos b y e j z
n m n j z H y 2 H0 cos x sin y e b a b Kc
n m n j z Ex j 2 H 0 cos x sin y e b a b Kc
* （5）由 S E H ，在z向有实功率，传输能量；在横向是虚功率，
只存储能量。
§2.2 矩形波导
2.截止波长和简并波形 截止波数:
n 2 2 2 m Kc Kx Ky a b
2 2
m n Kc a b
§2.2 矩形波导
通解也可以写成下面的形式 X A cos( K x x x ) (2-70) Y B cos( K y y y ) (2-71)
A、φx、 B、 φy 、Kx、Ky为待定常数 （6个） 当考虑纵向行波传输规律时，电场强度可写成
Ez ( x, y, z) X ( x)Y ( y)Z ( z) E0 cos(Kx x x ) cos(K y y y )e jz (2-72)
内表面上的切向磁场强度 横向磁场决定纵向电流; 纵向磁场决定横向电流
§2.2 矩形波导
H10波各波导壁上的面电流密度为：
在x=0窄壁上
ˆz ˆH 0 cos(t z) J y ˆH z y J S n H x
在x=a窄壁上
ˆz ˆH 0 cos cos(t z) J y ˆH z y J S n H x
m, n 0
§2.2 矩形波导
分析： （1） m、n为自然数，分别表示常量沿x轴和y轴出现的 半周期数； （2） 不同的m、n对应一种波型TEmn，m、n不能同时为零， 但有一个可以取零。 最低次波型为TE10(a>b)或TE01 (a<b)。
n m n j z H y 2 H0 cos x sin y e b a b Kc
n m n j z Ex j 2 H 0 cos x sin y e b a b Kc
* （5）由 S E H ，在z向有实功率，传输能量；在横向是虚功率，
只存储能量。
§2.2 矩形波导
2.截止波长和简并波形 截止波数:
n 2 2 2 m Kc Kx Ky a b
2 2
m n Kc a b
§2.2 矩形波导
通解也可以写成下面的形式 X A cos( K x x x ) (2-70) Y B cos( K y y y ) (2-71)
A、φx、 B、 φy 、Kx、Ky为待定常数 （6个） 当考虑纵向行波传输规律时，电场强度可写成
Ez ( x, y, z) X ( x)Y ( y)Z ( z) E0 cos(Kx x x ) cos(K y y y )e jz (2-72)
内表面上的切向磁场强度 横向磁场决定纵向电流; 纵向磁场决定横向电流
§2.2 矩形波导
H10波各波导壁上的面电流密度为：
在x=0窄壁上
ˆz ˆH 0 cos(t z) J y ˆH z y J S n H x
在x=a窄壁上
ˆz ˆH 0 cos cos(t z) J y ˆH z y J S n H x
m, n 0
§2.2 矩形波导
分析： （1） m、n为自然数，分别表示常量沿x轴和y轴出现的 半周期数； （2） 不同的m、n对应一种波型TEmn，m、n不能同时为零， 但有一个可以取零。 最低次波型为TE10(a>b)或TE01 (a<b)。
卫星上行通路波导传输环节常见问题分析
1 引言波导元件作为传输微波频段电磁波的装置，是连接高功放和辐射天线的关键元件，是卫星上行系统十分重要的环节，其指标性能直接制约和影响整个卫星上行系统的上行能力。
因此，在对系统进行设计时要对系统采用波导元件进行合理选择和连接，使其充分发挥对电磁波的传导作用，使电磁波以最大能量输出是非常重要的。
2 电磁波在波导中的传播目前我国卫星上行站主要使用的波导为矩形波导和圆形波导。
2.1矩形波导中电磁波的传播形式矩形波导主要用于1GHz 到220GHz 波段的各种标准波导的元件。
中空矩形波导可以传播TM 模和TE 模，但是不能传输TEM 波。
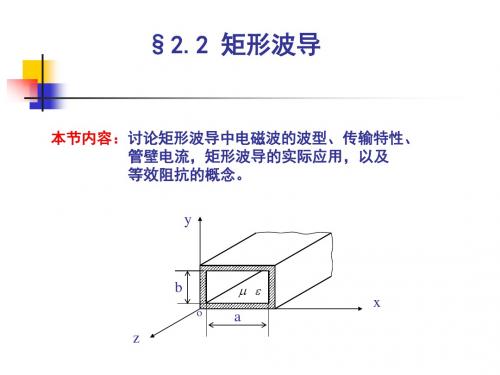
矩形波导的几何结构如图1所示，设波导中的填充材料介电常数为ε，磁导系数为μ，TE 模的截止频率为， m和n 分别代表沿x 轴和y 轴方向分布的半波数。
a 和b 分别为波导内壁宽边和窄边的尺寸。
可见矩形截面波导TE mn 模和TM mn 模的截止频率取决于波导口径尺寸a 和b 及模式标数。
同一口径的矩形截面波导，不同模式的截止频率不同，而不同口径尺寸的矩形截面波导相同标数模式的截止频率也不同。
2.2圆截面波导中电磁波的传播形式圆形横截面的中空金属导管也支持TE 和TM 波导模，图2为内径为a 的圆形波导横截面图。
圆形波导TE 模的截止频率为，TM模的截止频率为，其中P nm 和P nm 为给定值，a 为圆形波导内径。
圆形波导中有3种较重要模式的电磁波，TE11、TE01和TM01模，如图3所示。
TE11模是圆截面波导中的主模，截止波长最长的模式，容易实现单模传输，但是由于加工工艺等问题出现微小的不均匀性时，会出现极化面偏转。
一般情况下工作于 TE11模的圆截面波导仅用作短距离传输。
TM01模的特点是其场结构以波导轴线为轴旋转对称，因此当两段工作于TM01模的圆截面波导相对转动时，并不影响其中电磁波的传输，不会发生传输模式的变化。
所以当需要摘要：本文针对日常运行维护中波导传输环节易出现的问题进行分析，探讨如何正确选择和连接波导。
22 矩形波导
vp vg v2
§2.2 矩形波导
4. 壁电流分布
电磁波在波导中传播，将在波导壁上产生高频感应电流。
根据边界条件，面电流密度: 内壁的法向单位矢量
Js nˆ H
内表面上的切向磁场强度
横向磁场决定纵向电流; 纵向磁场决定横向电流
§2.2 矩形波导
H10波各波导壁上的面电流密度为：
在x=0窄壁上
Kc2
K
2 x
K
2 y
m
a
2
n
b
2
Ey
j
Kc2
H0
m
a
sin m
a
xcos n
b
y e j z
Kc
m
2
n
2
a b
§2.2 矩形波导
通解也可以写成下面的形式
X Acos(Kxx x ) (2-70) Y B cos(K y y y ) (2-71)
A、φx、 B、 φy 、Kx、Ky为待定常数 （6个） 当考虑纵向行波传输规律时，电场强度可写成
§2.2 矩形波导
2.2.3 矩形波导中的波型
1.波型 截止波数的表达式为 分析：
Kc
K
2 x
K
2 y
m
2
n
2
a b
（1）m、n为自然数，分别表示常量沿x轴和y轴出现的半周期 数，也是半驻波数;
（2）不同的m、n对应一种波型TMmn，但不存在TMm0、TM0n、 TM00 （3三）种场波量型沿，z轴最为低行次波波，型沿为xT轴M和11y; 轴为纯驻波;
a b
截止波长:
c
2
Kc
2
m a
矩形波导中的基模
结构
矩形波导由宽边和窄边组成，电 磁波在波导内部以横向电磁场（ TE模）或横向磁场（TM模）的形 式传播。
传输模式及特点
传输模式
矩形波导中可存在多种传输模式，包 括TE模和TM模，每种模式又有不同 的模式序号。
特点
不同传输模式具有不同的截止频率和 场结构，且高次模比基模更容易被激 励。
基模在矩形波导中重要性
器件结构设计与优化
结构设计
矩形波导基模激励器件的结构设计需要考虑波导的尺寸、材料、传输模式等因 素。一般采用同轴或微带线等传输线与矩形波导进行连接，实现微波信号的输 入与输出。
优化方法
为了提高基模激励的效率，可以采用多种优化方法，如阻抗匹配、模式转换等。 阻抗匹配可以通过调整传输线的特性阻抗或添加匹配网络来实现，模式转换则 可以通过设计特定的结构或采用模式转换器来实现。
THANKS FOR WATCHING
感谢您的观看
耦合强度
模式间耦合强度与波导结 构、工作频率、作用探讨
基模特性
基模是矩形波导中的主模，具有最低的截止频率和最高的传输效 率。
基模与其他模式关系
在多模传输时，基模往往起到主导作用，其他高次模则作为补充。
基模对传输性能影响
基模的存在可以提高传输效率，减少信号失真和衰减，但同时也可 能引入模式间干扰。
电场与磁场分布规律
在矩形波导中，基模的电场和 磁场分布具有特定的规律。
对于TE10模（横电波基模）， 电场主要分布在波导的宽边， 而磁场主要分布在波导的窄边。
对于TM11模（横磁波基模）， 电场和磁场都分布在波导的两 个维度上，但具有不同的相位 和幅度。
截止频率与通带特性
矩形波导的基模具有特定的截止 频率，低于该频率时，基模不能
矩形波导由宽边和窄边组成，电 磁波在波导内部以横向电磁场（ TE模）或横向磁场（TM模）的形 式传播。
传输模式及特点
传输模式
矩形波导中可存在多种传输模式，包 括TE模和TM模，每种模式又有不同 的模式序号。
特点
不同传输模式具有不同的截止频率和 场结构，且高次模比基模更容易被激 励。
基模在矩形波导中重要性
器件结构设计与优化
结构设计
矩形波导基模激励器件的结构设计需要考虑波导的尺寸、材料、传输模式等因 素。一般采用同轴或微带线等传输线与矩形波导进行连接，实现微波信号的输 入与输出。
优化方法
为了提高基模激励的效率，可以采用多种优化方法，如阻抗匹配、模式转换等。 阻抗匹配可以通过调整传输线的特性阻抗或添加匹配网络来实现，模式转换则 可以通过设计特定的结构或采用模式转换器来实现。
THANKS FOR WATCHING
感谢您的观看
耦合强度
模式间耦合强度与波导结 构、工作频率、作用探讨
基模特性
基模是矩形波导中的主模，具有最低的截止频率和最高的传输效 率。
基模与其他模式关系
在多模传输时，基模往往起到主导作用，其他高次模则作为补充。
基模对传输性能影响
基模的存在可以提高传输效率，减少信号失真和衰减，但同时也可 能引入模式间干扰。
电场与磁场分布规律
在矩形波导中，基模的电场和 磁场分布具有特定的规律。
对于TE10模（横电波基模）， 电场主要分布在波导的宽边， 而磁场主要分布在波导的窄边。
对于TM11模（横磁波基模）， 电场和磁场都分布在波导的两 个维度上，但具有不同的相位 和幅度。
截止频率与通带特性
矩形波导的基模具有特定的截止 频率，低于该频率时，基模不能
矩形波导表面波
矩形波导表面波（Rectangular Waveguide Surface Wave）指的是在矩形波导中传播
的一种特殊类型的电磁波，这种波通常被称为表面波或表面等离子体波。
特点和性质：
1.波导结构：
▪矩形波导是一种具有矩形截面的金属管道结构，用于在微波频段传输电磁波。
通常，矩形波导的截面可以是正方形或矩形。
2.表面波：
▪表面波是沿着导体表面传播的电磁波，其能量主要集中在导体表面附近。
在矩形波导中，这种表面波也可以称为矩形波导表面波。
3.频率范围：
▪表面波通常在相对较低的频率范围内工作，一般处于微波或射频频段。
频率范围的选择取决于波导的尺寸和工作环境。
4.模式：
▪矩形波导表面波通常具有多种模式，其中最常见的是TE（横向电场）和TM（横向磁场）模式。
这些模式代表了电场或磁场的分布方式。
5.应用：
▪表面波在矩形波导中的应用主要集中在微波通信、雷达系统、微波导滤波器等领域。
由于表面波主要集中在导体表面附近，可以通过适当
的设计实现对电磁波的有效控制。
表面波的数学描述：
表面波的数学描述通常涉及矩形波导的电磁场方程，包括Maxwell方程组的适当
形式。
这些方程的解决方案可以得到表面波的传播特性、模式和频率范围等信息。
总体而言，矩形波导表面波是一种在矩形波导结构中传播的电磁波，具有特定的频率范围和模式。
它在微波和射频技术中有着重要的应用。
第三章3矩形波导
Ex = ±ηTE H y jβ = 2 ηTE k2 H0 cos(k1x +ϕ1) sin( k2 y +ϕ2 ) (3 − 61d ) kc Ey = mηTE Hx jβ = − 2 ηTE k1H0 sin( k1x +ϕ1) cos(k2 y +ϕ2 ) (3 − 61e) kc ωµ0 其中 ηTE = Ez = 0 (3 − 61 f ) β
∂2 ∂2 2 ( 2 + 2 )Hz (x, y) + kc Hz (x, y) = 0 ∂x ∂ y (3 − 54)
− jωµ 0 ∂Hz Ex = = ±ηTE H y 2 kc ∂y jωµ 0 ∂Hz Ey = = mηTE Hx 2
(3 − 34a)
(3 − 34b)
进一步对H 分离变量， 进一步对 z分离变量，令 Hz (x, y) = X (x)Y ( y) (3 − 55) 代入（3-54），得 ， 代入
(3 − 66)
Ez (x, y) = E0 cos(k1x +ϕ1)cos(k2 y +ϕ2 )
2 k12 + k2 =kc2
(3 − 67)
Ez( x , y )为各内壁切向方向，边界条件是所有四壁 为各内壁切向方向， 为各内壁切向方向 为零，代入(3-67) 上Ez为零，代入
Ez
Ez
x=0
= 0 ⇒ cosϕ1 = 0或ϕ1 = π 2
Ex (x, y, z) = ±ηTE Hy (x, y) e
m jβ z
jω µ 0 H0 nπ mπ nπ = x) sin( y)em jβ z kc2 b a b
(3 − 65d )'
Ey (x, y, z) = mηTE Hx (x, y)em jβ z
∂2 ∂2 2 ( 2 + 2 )Hz (x, y) + kc Hz (x, y) = 0 ∂x ∂ y (3 − 54)
− jωµ 0 ∂Hz Ex = = ±ηTE H y 2 kc ∂y jωµ 0 ∂Hz Ey = = mηTE Hx 2
(3 − 34a)
(3 − 34b)
进一步对H 分离变量， 进一步对 z分离变量，令 Hz (x, y) = X (x)Y ( y) (3 − 55) 代入（3-54），得 ， 代入
(3 − 66)
Ez (x, y) = E0 cos(k1x +ϕ1)cos(k2 y +ϕ2 )
2 k12 + k2 =kc2
(3 − 67)
Ez( x , y )为各内壁切向方向，边界条件是所有四壁 为各内壁切向方向， 为各内壁切向方向 为零，代入(3-67) 上Ez为零，代入
Ez
Ez
x=0
= 0 ⇒ cosϕ1 = 0或ϕ1 = π 2
Ex (x, y, z) = ±ηTE Hy (x, y) e
m jβ z
jω µ 0 H0 nπ mπ nπ = x) sin( y)em jβ z kc2 b a b
(3 − 65d )'
Ey (x, y, z) = mηTE Hx (x, y)em jβ z
9-3矩形波导中的TE10波
a x b
y
y
Hz
a
Ey
Hx
x
电场线
磁场线
y
g
Hx
z
TE10 波电场强度振幅和磁 场强度振幅的空间分布(电 场和磁场合在一起）
传播方向垂直于电场方向
y Hz
Ey
电场方向垂直于磁场方向
2019/6/15
电磁场理论
8
第九章 导行电磁波
几种高次模的场分布
TE10
TE11
TE20
TE21
第九章 导行电磁波
电磁场理论
第9章 导行电磁波 9-3 矩形波导中的TE10波
2019/6/15
电磁场与电磁波
1
第九章 导行电磁波 复习9-2矩形波导的传播特性(1)
矩形波导截止频率：能够传输的最低频率 y
fc
=
2
kc
2
1
(m)2 (n)2 ab
b ,
x
a
z
频率大于截止频率的电磁波才能在矩形波导中传输。
ez
jkz (
a )H0
sin( a
x)
exH0
cos(
a
x)
2019/6/15
z x
电磁场理论
x
a
内壁电流
11
第九章 导行电磁波
TE10波的主要传播特性参数
截止频率
fc
=
c 2
(1)2 (0)2 c a b 2a
截止波长 c 2
(1)2 (0)2 =2a ab
纵向波矢 kz k 1 ( fc f )2 k 1 ( c )2 波导波波长 g 1 ( fc f )2 1 ( c )2
第2-5章 矩形波导
Ey Ez Hx
m 1 n 1
j n mx ny j (t z ) E mn sin cos e 2 a b kc b mx ny j (t z ) E mn sin sin e a b j n mx ny j (t z ) E mn sin cos e 2 b a b kc j m mx ny j (t z ) E mn cos sin e 2 a a b kc
如为虚数，令j=a, 则有 EZ=E0Ze-az为衰减波，在波导中为：
2 v c kc f c
2
m / a n / b
2
2
2
则可得截止频率为：
fc v 1 1 m n m n c 2 2 a b 2 a b kc
代入纵横关系式，可得传输型TE模场分量(P52)：
Ex Ey
m 0 n 0
j n mx ny j (t z ) H mn cos sin e 2 b a b kc
j m mx ny j (t z ) H mn sin cos e 2 a a b kc m 0 n 0
式中
k
2 c
k
2
2
由于波导中不存在TEM波，故只有TE波和TM波。
1）TE模
E z 0, H z 0
磁场的纵向分量应满足本征值方程：
2 抖H 0 z + 2 抖 x 2
H0z + kc2 H 0 z = 0 y2
对于 H 0 z ( x, y ) 应用分离变量法求解：
H 0 z ( x, y ) X ( x)Y ( y )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
矩形波导中电磁波的传播模式 ［摘要］人类进入21世纪的信息时代，电子与信息科学技术在飞速发
展，要求人们制造各种高科技的仪器。在电磁学领域，能约束或引导电磁波能 量定向传输的传输线或装置是导波系统。•矩形波导适用于频率较高的频段，但 当频率足够高的时候，可以使多个波导模式同时工作， 所以我们有必要对波导 中的电磁波传播模式参数进行研究 关键词：矩形波导 TM波TE波
矩形波导由良导体制作而成，一般为了提高导电性能和抗腐蚀性能，在波 导内壁镀上一层高电导率的金或银， 它是最常见的波导，许多波导元件都 是由矩形波导构成的。为了简化分 析，在讨论中我们将波导的良导电体 壁近似为理想导电壁。由前面的讨论 我们知道，矩形波导中不能传输TEM 波，只能传输TE波和TM波。设矩 形波导宽为a,高为b, (a>b)沿Z轴 放置，如图(1)所示。下面分别求 解矩形波导中传输的TE波和TM波
仃M波 对于TM波，Hz=O, Ez可以表示为； Ez(x, y,z) = E°(x, y)e*z (1)
式中Eo(x,y)满足齐次亥姆霍兹方程，故有 ' 2Eo(x,y) kC⅛°(x,y) = O ⑵ 采用分离变量法解此方程，在直角坐标系中，令 E°(x,y)=X(x)Y(y) ⑶ 将(3)式代入(2)式中，并在等式两边同除以 X(χ)Y(y)得: XW Xiy) k2
C x(χ) Y(y)
上式中第一项仅是X的函数，第二项仅是Y的函数，第三项是与X、Y无关的 常数，要使上式对任何 X、Y都成立，第一和第二项也应分别是常数，记为:
X''(X) kχJX(X^ 0 ⑸ Y''(y) k：Y(y「0 ⑹
2 2 2 kc = kχ + ky ⑺
常微分方程(5)和(6)的通解为
Y(X)=Ci cos(kχX) C2Sin(kχX)
Y(y) =C3C0s(kyy) C4Sin(kyy) 将(8)式和(9)式代入(3)式，再代入(1)式，就得到 Ez的通解为 Ez(x, y, z) - C1 cos(kχX) C2 sin( kχX) IC3 cos( ky y) C4 sin( kyy) ^jkZZ 由矩形波导理想导电壁的边界条件 E = 0，确定上式中的几个常数，在4个理想 导电壁上，EZ是切向分量，因此有：
(1) 在X "的波导壁上，由EZ(X=O,y,z)=0得C1 =0 ； (2) 在Y=0的波导壁上，由Ez(x,y =0,z) =0得C^0； (3) 在X = a的波导壁上，要使Ez (x = a, y, z) = 0有Sin(kxa) = 0，从而必须有 kχa =m二，其中m =1.,2,3^为整数，由此得
(4) 在 X = b 的波导壁上，要使 Ez(x,y =b, z) =0有，Sin(kyb) =0 从而必定有 kyb= n二，其中n =1.,2,3…也为整数，由此得
x''(χ) X(χ) -k 这样就得到两个常微分议程和 Y''(y) _ Y (y) 3个常数所满足的方程:
(8) (9)
kχ
m∙
(10) (11) ""b
将以上利用边界条件求出的常数代入后，波导中 TM波的电场纵向分量为 Ez(x, y,z) = EoSin( )sin( a b
E。=C2C4 ,由电磁波源确定。 在无源区，麦克斯韦方程组中的两个旋度方程为: '、H= j； ： E
E(x,y,z) = Eo(x,y,)ijkzz
H(x,y,z) = H°(x,y)e 一jkzz
将3个矢量方程分解为6个标量方程:
n∙ (12)
HZ
■y jkzHy = j E
x (13―― a)
-jkzHx (13―― b)
Hy ： HX
L= ] ； T- F
Z X y
(13―― C)
EZ
-jkZEX .
-b lHx (13―― d)
(13―― e) EEy CE I-X
X ：y
由(13―― a)和(13―― e)以及(13―― b)和 1 CEZ Il CHZ
Ex-jkz 一 z - j，. Z)
PHZ (13—— f)
(13―― d)可得:
(14―― a) 1 记作TM mπ
(1) 矩形波导中的TM波m,π至少一个从零开始，否则全部的场分量为零, 当m,π =1,2,3,…对应有无限多组解; (2) 对于给定m,π值的每一组解，如果kz为实数，其场为沿Z方向传播的非 均匀平面波，在X、Y方向为驻波分布，m,π分别表示在宽边和窄边上 驻波的波腹个数； (3) 对于不同m,π值的场，有两方面不同：一是横截面的场分布不同：二是 沿传播方向的kz不同。我们将波导中一对
( — jk -ZE -X (14——b)
HX 二(j；旦- kc :y
jkZ亠
EX (14―― C)
1 SEz
Hy=庐
kc X
式代入(20)式中，就可以得到波导中TM波的其他场分量 kz
jk^-H-Z) :y (14——d)
将 (18) Ex(x,y,z^ - j-τ( kc a
k n 二
-j-2(-)E0Sin( kc b
—)E0 cosm X)Sin(匸 y)rjkzz
a b (14―― a)
Ey(x,y, Z)- ∏JT 一 y)cos( x)e a
b
HkZZ
Hχ(x, y,z)= m7 ；■■? ■- n 二 m 二 n
二 .l
j r(-)EoSiπ(-y)cos(-)^jkZZ
kc b a b
Hy(χ, y, Z)二 ∙kτ(m-)E°cos(m- X)Siπ(± y)e%Z kc a a b
(14—— -b) (14—— C)
(14— -d)
其中 k： k2 (15)
(15) 从式 13)式中可以看出:
m,π值对应的一个TM模式, 2TE波 对于TE波,Ez=O用求解TM波的方法可以得到TE波各场分量的表达式
(1) 矩形波导中的TE波中的 m,n不可同时为零，当m,n
=1,2,3^值取不同值的
无限多组解； (2) 对于给定m,n值，如果kz为实数，其场为沿Z方向传播的非均匀平面波，在 X、Y方向为驻波分布，m,n也分别表示在宽边和窄边上驻波的波腹的个数 m或n等
于零意味着场在对应方向无变化，是均匀的； (3) 对于不同m,n值的场，也同样有两个方面不同：一是横截面的场分布不同;
二是沿传播方向的kz不同。我们将波导中一对m,n值对应的TE波称为一个T E 模式，记作TEmn。如当m=1, n =0,对应的TE模应为TEg。
上述的TM mn和TEmn模统称为矩形波导内的正规模，具有很重要的特性。容易 看出矩形波导内的正规模构成了一个完备的正交系。所以，波导内传输的任意 电磁波可以表示为正规模的线性叠加。这就是正规模的正交性和完备性。所谓 正交性是指正规模能够独立存在，能量互不耦合；所谓完备性是指任意电磁波 都可以用正规模线性叠
Hz(χ, y,z)= zmπ
CO X COy < a 丿 < b J (16—a)
Hχ(χ, y,z)= kC2
m 二 (一 a
zmπ
)H0 si n —— I a X cos J
y ^
jkZZ
(16— b)
Hy(χ, y,z)二
j⅛s
n 二
)H O COS
——X
Sin a J Je
-jkzZ
(16— C)
Ex(x, y,z) COS m
π
Sin 'nπ
、
,b y丿
X
Ia丿
Ey(X, y,z)
由上式可以看出：
+HOSin ——X
COS a J
y ^
jkZZ
(16— e)
J
e-jkzz H
O
jkzz e (16—
ω卩
+ HO