2011——2012年南昌市八年级(初二)数学期中试卷答案

八年级数学期中测试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 若一个三角形的两边长分别为8cm和10cm，且这两边的夹角为60°，则这个三角形的周长为多少cm？A. 16cmB. 26cmC. 28cmD. 36cm2. 下列函数中，哪一个函数在其定义域内是增函数？A. y = -2x + 3B. y = x^2C. y = 1/xD. y = 3x 23. 在平面直角坐标系中，点A(2, -3)关于y轴的对称点坐标为？A. (-2, -3)B. (2, 3)C. (-2, 3)D. (3, -2)4. 一个等差数列的前三项分别为2，5，8，则该数列的第10项为多少？A. 29B. 30C. 31D. 325. 若一个圆的半径为5cm，则该圆的面积为多少平方厘米？A. 25πcm²B. 50πcm²C. 75πcm²D. 100πcm²二、判断题（每题1分，共5分）1. 两个锐角互余。

（）2. 一元二次方程ax^2 + bx + c = 0 (a ≠ 0)的解为x = [-b ± √(b^2 4ac)] / 2a。

（）3. 对角线互相垂直平分的四边形一定是菱形。

（）4. 在一次函数y = kx + b中，若k > 0，则函数从左到右上升。

（）5. 两个相似三角形的对应边长之比等于它们的面积之比。

（）三、填空题（每题1分，共5分）1. 若|a| = 3，则a的值为______。

2. 在直角坐标系中，点P(4, -2)关于原点对称的点的坐标为______。

3. 若一个等差数列的首项为2，公差为3，则该数列的第5项为______。

4. 一个圆的周长为31.4cm，则该圆的半径为______cm。

5. 若sinθ = 1/2，且θ是锐角，则θ的度数为______°。

四、简答题（每题2分，共10分）1. 解释什么是等腰三角形，并给出一个等腰三角形的例子。

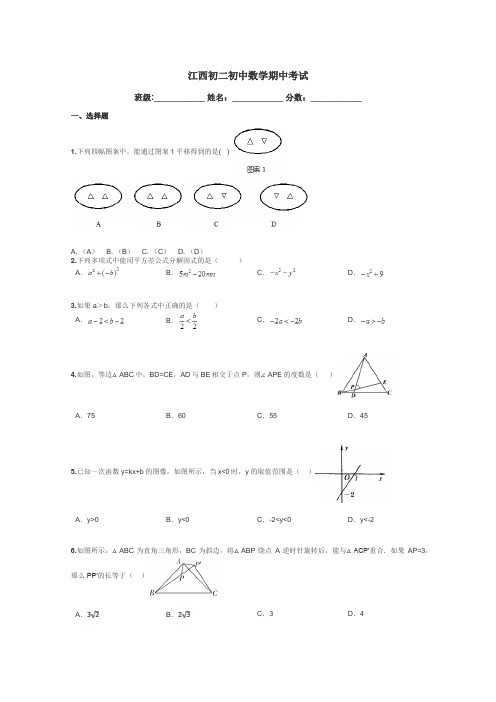
江西初二初中数学期中考试班级:___________ 姓名：___________ 分数：___________一、选择题1.下列四幅图案中，能通过图案1平移得到的是( )A. （A）B. （B）C. （C）D. （D）2.下列多项式中能用平方差公式分解因式的是（）A．B．C．D．3.如果a＞b，那么下列各式中正确的是（）A．B．C．D．4.如图，等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是（）A．75°B．60°C．55°D．45°5.已知一次函数y=kx+b的图像，如图所示，当x<0时，y的取值范围是（）A．y>0B．y<0C．-2<y<0D．y<-26.如图所示，△ABC为直角三角形，BC为斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合．如果AP=3，那么PP′的长等于（）A．B．C．3D．4二、填空题1.已知等腰三角形的两条边长是3和7，那么第三条边长是__________．2.分解因式结果为_____________.3.如图，将△AOB绕点O按逆时针方向旋转45°后得到，若∠AOB＝15°，则的度数是_________.4.如图，已知函数和的图象交点为P，则不等式的解集为________．5.若，则x的取值范围___________.6.如图，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点C出发，按C→B→A的路径，以2cm每秒的速度运动，设运动时间为t秒，当t为___________时，△ACP是等腰三角形．7.分解因式：三、解答题1.解不等式组，并把它们的解集在数轴上表示出来．2.如图，在10×10正方形网格中，每个小正方形的边长均为1个单位．（1）将△ABC向下平移5个单位，得到的△A’B’C’；（2）将△A’B’C’绕点顺时针旋转90°，得到的△A”B”C’；请你画出△A’B’C’和△A”B”C’。

图 3 CA DB E 图1 图5m nCABABCD E F图4图2 45321DAOECB DAC B初二数学期中考试试卷一、选一选，看完四个选项后再做决定呀！（每小题3分，共24分） 1．已知等腰三角形的一个内角为50o，则这个等腰三角形的顶角为【 】. （A ）50o（B ）80o（C ）50o 或80o（D ）40o 或65o2. 已知一个三角形的两边长分别是2厘米和9厘米，且第三边为奇数，则第三边长为【 】. （A ）5厘米 （B ）7厘米 （C ）9厘米 （D ）11厘米3. 工人师傅常用角尺平分一个任意角．做法如下：如图1所示，∠AOB 是一个任意角，在边OA ，OB 上分别取OM =ON ，移动角尺，使角尺两边相同的刻度分别与M ，N 重合．过角尺顶点C 的射线OC 即是∠AOB 的平分线．这种做法的道理是 【 】. （A ）HL （B ）SSS （C ）SAS （D ）ASA4. 在图2所示的3×3正方形网格中，∠1＋∠2＋∠3＋∠4＋∠5等于 【 】. （A ）145° （B ）180° （C ）225° （D ）270°5. 根据下列条件，能判定△ABC ≌△A ′B ′C ′的是 【 】. （A ）AB =A ′B ′，BC =B ′C ′，∠A =∠A ′ （B ）∠A =∠A ′，∠B =∠B ′，AC =B ′C ′（C ）∠A =∠A ′，∠B =∠B ′，∠C =∠C ′（D ）AB =A ′B ′，BC =B ′C ′，△ABC 的周长等于△A ′B ′C ′的周长 6. 如图3所示，△ABC 中，∠C =90°，点D 在AB 上，BC =BD ，DE ⊥AB 交AC 于点E ．△ABC 的周长为12，△ADE 的周长为6．则BC 的长为 【 】. （A ）3 （B ）4 （C ）5 （D ）67. 将一副直角三角尺如图4所示放置，已知AE BC ∥，则AFD ∠的度数是 【 】. （A ）45o（B ）50o （C ）60o（D ）75o图6 图78. 如图5所示，m ∥n ，点B ，C 是直线n 上两点，点A 是直线m 上一点，在直线m 上另找一点D ，使得以点D ，B ，C 为顶点的三角形和△ABC 全等，这样的点D 【 】. （A ）不存在 （B ）有1个 （C ）有3个 （D ）有无数个图10 图8 A 'A DB E 21图9C AD EF D AEC B 二、填一填，要相信自己的能力！（每小题3分，共24分） 1．在ABC ∆中，若A ∠=1123B C ∠=∠，则ABC ∆是 三角形.2. 如图6所示，BD 是ABC ∆的中线，2AD =，5AB BC +=，则ABC ∆的周长是 .3. 如7所示所示，在ABC ∆中，BD ，CE 分别是AC 、AB 边上的高，且BD 与CE 相交于点O ，如果135BOC ∠=︒，那么A ∠的度数为 .4. 如图8所示，将纸片△ABC 沿DE 折叠，点A 落在点A ′处，已知∠1＋∠2=100°，则∠A 的大小等于_____度．5. 如图9所示，有两个长度相同的滑梯(即BC =EF )，左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，则△ABC ≌△DEF ，理由是______．6. 如图10所示，AD ∥BC ，AB ∥DC ，点O 为线段AC 的中点，过点O 作一条直线分别与AB 、CD 交于点M 、N ．点E 、F 在直线MN 上，且OE =OF ．图中全等的三角形共有____对．7. 如图10所示，要测量河两岸相对的两点A 、B 的距离，在AB 的垂线BF 上取两点C 、D ，使BC =CD ，过D 作BF 的垂线DE ，与AC 的延长线交于点E ，则∠ABC =∠CDE =90°，BC =DC ，∠1=______，△ABC ≌_________，若测得DE 的长为25 米，则河宽AB 长为_________．8. 如图11所示，三角形纸片ABC ，AB =10厘米，BC =7厘米，AC =6厘米．沿 过点B 的直线折叠这个三角形，使顶点C 落在AB 边上的点E 处，折痕为BD ，则△AED 的周长为______厘米．三、做一做，（本大题共25分） 1．（8分）如图所示，在ABC ∆中，已知AD BC ⊥，64B ∠=︒，56C ∠=︒. （1）求BAD ∠和DAC ∠的度数；（2）若DE 平分ADB ∠，求AED ∠的度数.图11 C A D BE2.（8分）如图；为人民公园的荷花池，现要测量此荷花池两旁A 、B 两棵树间的距离(不能直接测量)，请你根据所学三角形全等的知识，设计一种测量方案求出AB 的长(要求画出草图，写出测量方案和理由)． 3．（9分）如图所示，△ADF 和△BCE 中，∠A =∠B ，点D ，E ，F ，C 在同—直线上，有如下三个关系式：①AD =BC ；②DE =CF ；③BE ∥AF ．(1)请用其中两个关系式作为条件，另一个作为结论，写出所有你认为正确的结论． (2)选择(1)中你写出的—个正确结论，说明它正确的理由．四、拓广探索！（本大题共27分）1.（13分）如图，在△ABC 中，点E 在AB 上，点D 在BC 上，BD ＝BE ，∠BAD ＝∠BCE ，AD 与CE 相交于点F ，试判断△AFC 的形状，并说明理由.FE BDA C BC D FAE2．（14分）两个大小不同的等腰直角三角形三角板如图①所示放置，图20②是由它抽象出的几何图形，B C E ，，在同一条直线上，连结DC ．（1）请找出图②中的全等三角形，并给予说明（说明：结论中不得含有未标识的字母）； （2）试说明：DC BE ⊥．参考答案一、1～8 C C B CD ADB. 二、1. 直角. 2.9. 3. 45°. 4. 50. 5. HL. 6.4. 7. ∠2,△EDC ，25 m. 8. 9.三、1. （1）90905634DAC C ∠=︒-∠=︒-︒=︒. （2）109AED ∠=︒. 2．方案不惟一，画图及理由略．3．(1)如果①、③，那么②或如果②、③，那么①； (2)选择“如果①、③，那么②”证明，过程略． 四、1. △AFC 是等腰三角形.． 2．（1）图2中ABE ACD △≌△．理由如下：ABC Q △与AED △均为等腰直角三角形AB AC ∴=，AE AD =，90BAC EAD ∠=∠=o ， BAC CAE EAD CAE ∴∠+∠=∠+∠， 即BAE CAD ∠=∠ ， ABE ACD ∴△≌△．（2）说明：由（1）ABE ACD △≌△知45ACD ABE ∠=∠=o， 又45ACB ∠=o①②90∴∠=∠+∠=o，BCD ACB ACD∴⊥DC BE。

2011～2012学年度上学期期中考试八年级数学答案1、B2、A3、A4、D5、B6、B7、C8、B9、B 10、D 11、D 12、C 13、3, 3, 4 14、25 15、 44° 16、(6，2)或（4，6）或（3，3）17．解: ()4433+-＝－4＋2 ……4分＝－2 ……6分18．解:依题意得 (a-6)+(3a-2)=0 ……4分 ∴a=2……6分19．证明：在△ABE 和△ACD 中∵AB AC A A AE AD =⎧⎪∠=∠⎨⎪=⎩……3分 ∴△ABE ≌△ACD （SAS ）……5分 ∴∠B ＝∠C ……6分20．证明∵BF ＝CE ，∴BF ＋FC ＝CE ＋FC ，即BC ＝EF …2分∵AC ∥DF ∴∠B ＝∠E …4分在△ABC和△DEF 中∵AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩…5分∴△ABC ≌△DEF （SAS ）…6分∴AC =DF …7分21．（1）正确画图…2分，B 1（3，2）…4分； （2）正确画图…5分，B 2（5，2）…7分22．证明：连接BD ，则∠ADB=∠CDB=90°， ……1分又∠EDF=90°，∴∠EDB+∠BDF=∠BDF ＋∠CDF=90°，∴∠EDB=∠CDF ……3分又∠EBD=∠DCF=45°，BD=AD=CD. ……5分∴△EBD ≌△FCD ……6分 ∴D E=DF ，……7分又∠EDF=90°， ∴∠DEF =450． ……8分23、（1）①∵△ABC 、△ADF 都是等边三角形∴AB=AC ，AD =AF , ∠BAC =∠DAF =60° ……2分∴∠BAC +∠CAD =∠DAF +∠CAD, 即∠BAD =∠CAF , ……3分∴△ABD ≌△ACF , ∴BF =CF ……4分②由（1）中△ABD ≌△ACF , 得∠ACF =∠ABD =60° ……5分又∠ACB =60°, ∴∠FCD =180°-（∠ACB +∠ACF ）=60°. ……6分（2）正确画图； ……8分 ∠AFC +∠DAC =120°. ……10分24、（1）∠AOC =90°，BO =OA =OC ……2分（2）S △AOA 1= S △BOC 1证明：方法一：过点O 作MN ⊥BC 1于M ，交AA 1于N ……3分由OB =OC 1得BM =C 1M ，∠BOM =∠C 1OM ……4分由∠AOB =∠A 1OC 1=90°得∠AON =∠BOM =∠A 1ON +∠C 1OM =90°∴∠AON =∠A 1ON 又OA =OA 1 ∴ON ⊥AA 1 AN =NA 1 ……5分再证Rt △A 1ON ≌Rt △OC 1M ，得OM =A 1N ，MC 1=ON ……6分方法二：过A 1作A 1H ⊥OA 于H ，过C 1作C 1P ⊥BO 于P∵∠AOA 1+∠BOC 1=180°，又∠BOC 1+∠C 1OP =180°∴∠AOA 1=∠C 1OP ，又OA 1=OC 1，∠A 1HO =∠C 1PO∴△A 1OH ≌△C 1OP ∴A 1H =C 1P又OA =BO ，即21·OA ·A 1H =21BO ·C 1P ∴S △AOA 1= S △BOC 1 （3）延长NP 至E ，使PE =NP ，连接CE ，AN ，AE .则△PCE ≌△PMN ，∴CE =NM =BN, ∠MNP =∠PEC ……7分∴CE ∥MN 设EC 的延长线交BN 的延长线于O ，由∠BNM =90°得∠BOC =90°,又∠BAC =90°，在四边形ABOC 中，∠ACE =∠ABN …8分 又AB =AC ∴△ABN ≌△ACE ……9分 ∴AN =AE ，又点P 为NE 的中点 , ∴P A=PN ． ……10分25、（1）45° ……2分（2）作AM ⊥OB 于M ，AN ⊥OC 于N ，∵A （4，4）, ∴AM =AN =4，OM =ON =4 ……3分 ∴21OC ×AN +21OB ×AM =16, ∴OC +OB =8=ON+OM ……4分 即ON -OC =OB -OM ∴CN =BM ， ……5分∠ANC =∠AMB =90°, ∴△ANC ≌△AMB ……6分∴∠NAC=∠MAB ∴∠CAB =∠CAM+∠MAB =∠NAM =90° ……7分（3）MN =2OH ，在Rt △OMH 中，∠HON +∠NMO +∠NOM =90°,又∠NOM =45°，∠HON =∠NMO, ∴∠HON =∠NMO =22.5°……9分方法一：延长OH 至点P 使PH =PO ，连接MP 交OA 于L ……10分∴OM =MP ，∠OMP =2∠OMN =45°, ∴∠OLM =90°∴OL =ML ……11分∴Rt △OLP ≌Rt △MLN, ∴MN =OP =2HO ……12分方法二：作MN 的中垂线EF 交MN 于E ，交OM 于F ，连接NF ，则FN =FM ，∠FNE =∠FME =22.5°=∠NOH ， ……10分∠NFM =∠FNE +∠FME =22.5°+22.5°=45°=∠NOM ∴ON =NF ，……11分又∠OHN =∠FEN =90°，∴△HON ≌△ENF∴OH =NE =EM ，即NM =2HO ……12分。