三角形的边、三角形的高、中线与角平分线、三角形的稳定性 要点详析

《三角形的高、中线和角平分线，三角形的稳定性》知识全解 课标要求掌握三角形的高、角平分线、中线的概念，会做三角形的三线，知道三角形的三线的表示方法，理解三角形的稳定性。

知识结构（1）三角形的主要线段的定义：①三角形的角平分线：三角形的一个角的平分线和这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线．②三角形的中线：在三角形中，连结一个顶点和它的对边中点的线段叫做三角形的中线． ③三角形的高：从三角形一个顶点向它的对边画垂线，顶点和垂足间的线段叫做三角形的高线，简称三角形的高．（2）三角形的主要线段的表示法：三角形的角平分线的表示法：如上图根据具体情况使用以下任意一种方式表示：①AD 是∆ABC 的角平分线；②AD 平分∠BAC ，交BC 于D ；③如果AD 是∆ABC 的角平分线，那么∠BAD =∠DAC =21∠BAC ． 三角形的中线表示法：如上图根据具体情况使用以下任意一种方式表示：①AE 是∆ABC 的中线；②AE 是∆ABC 中BC 边上的中线；③如果AE 是∆ABC 的中线，那么BE =EC =21BC ． 三角线的高的表示法：如下图，据具体情况，使用以下任意一种方式表示：①AM 是∆ABC 的高；②AM 是∆ABC 中BC 边上的高；③如果AM是∆ABC中BC边上高，那么AM⊥BC，垂足是E；④如果AM是∆ABC中BC边上的高，那么∠AMB=∠AMC=90︒．（3）三角形的稳定性三角形具有稳定性，四边形没有稳定性．内容解析本节课主要有：动手画三角形的高，在了解三角形的高的基础上学习三角形的中线、角平分线，归纳三角形的三条重要线段的概念，掌握其画法．这是以后学习各种特殊三角形的基础，也是研究其他图形的基础知识．从生活中体验三角形的稳定性．重点难点本节课的重点是：三角形的高、中线与角平分线的概念,会用工具准确画出三角形的高、中线与角平分线．难点是钝角三角形的高的画法．教法导引引导学生动手画图，从作图中总结发现概念，从而使学生掌握三角形的高、中线与角平分线的画法．联系生活实际，了解三角形的稳定性在生产、生活中的实际应用．学法建议经过动手画图，积极参与交流，增强学生克服困难和战胜困难的自信心．通过观察和实地操作得到三角形具有稳定性，四边形没有稳定性，联系稳定性与没有稳定性在生产、生活中的广泛应用．。

初中数学知识归纳三角形的中线角平分线高线初中数学知识归纳：三角形的中线、角平分线、高线三角形是初中数学学习中最基础的几何图形之一，它具有丰富的性质和特点。

本文将归纳总结三角形的中线、角平分线和高线的相关性质，帮助读者更好地理解和掌握这些概念。

一、三角形的中线中线是连接三角形的两个顶点和中点的线段。

三角形的中线有以下特点：1. 任意三角形的三条中线交于一点，这一点称为三角形的重心。

重心所在的位置离三角形的三个顶点距离相等，且重心将中线分成2:1的比例。

2. 三角形的重心到顶点的距离是中线对应中点到顶点距离的2倍，也就是说，如果连接重心和顶点，那么重心到顶点的距离是连接中点和顶点的线段的2倍。

3. 在等边三角形中，三条中线重合，即三条中线交于一点，同时这个点也是三角形的重心。

二、三角形的角平分线角平分线是指从一个角的顶点出发，将该角分成两个相等的角的线段。

三角形的角平分线有以下特点：1. 三角形的三条角平分线交于一点，称为三角形的内心。

内心所在的位置距离三角形的三条边的距离相等，且内心到三边的距离之和等于三角形的周长。

2. 在等腰三角形中，三条角平分线重合，即三条角平分线交于一点，同时这个点也是三角形的内心。

3. 角平分线和对边、邻边有如下关系：角平分线等分对边和邻边上的对应角；对边和邻边上的线段与角平分线比例相等。

三、三角形的高线高线是从一个顶点出发，与对边垂直相交的线段。

三角形的高线有以下特点：1. 任意三角形都有三条高线，它们分别从三个顶点出发，并与对边垂直相交。

2. 等腰三角形的高线同时也是角平分线和中线。

3. 在直角三角形中，高线就是斜边上的中线。

总结：三角形的中线、角平分线和高线都有各自的特点和性质。

通过了解和掌握这些性质，我们可以更好地理解和解决与三角形相关的问题。

在实际应用中，这些概念和性质也有着广泛的应用，例如在建筑、制图、几何证明等方面都可以看到它们的身影。

通过本文的归纳和总结，我们希望读者能够对三角形的中线、角平分线和高线有更全面的了解，并在实际问题中能够运用到这些知识，提高数学解题的能力。

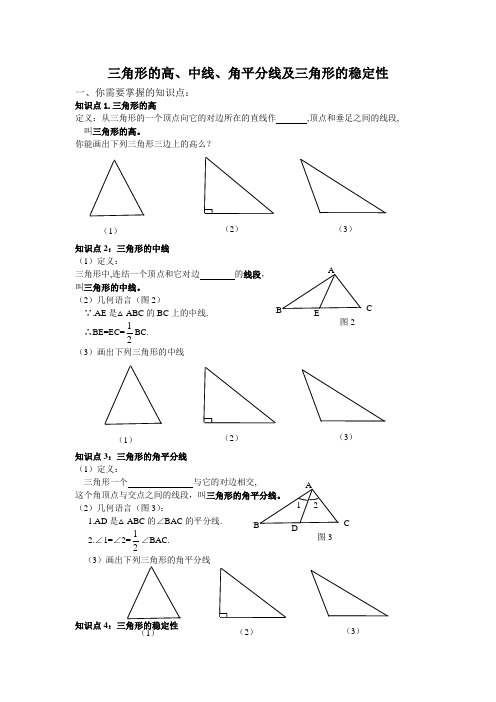
三角形的高、中线、角平分线及三角形的稳定性一、你需要掌握的知识点：知识点1.三角形的高定义：从三角形的一个顶点向它的对边所在的直线作 ,顶点和垂足之间的线段,叫三角形的高。

你能画出下列三角形三边上的高么？知识点2：三角形的中线（1）定义： 三角形中,连结一个顶点和它对边 的线段，叫三角形的中线。

（2）几何语言（图2） ∵.AE 是△ABC 的BC 上的中线. ∴BE=EC=12BC. （3）画出下列三角形的中线知识点3：三角形的角平分线（1）定义：三角形一个 与它的对边相交, 这个角顶点与交点之间的线段，叫三角形的角平分线。

（2）几何语言（图3）：1.AD 是△ABC 的∠BAC 的平分线.2.∠1=∠2=12∠BAC. （3）画出下列三角形的角平分线知识点4：三角形的稳定性 （1） （2） （3） 图2 A B C E （1） （2） （3） （1）（2） （3） 图3 AB C D 1 21、用三根木条用钉子钉成一个三角形木架，然后扭动它，它的形状会改变吗？2、用四根木条用钉子钉成一个四边形木架，然后扭动它，它的形状会改变吗？3、在四边形的木架上再钉一根木条，将它的一对顶点连接起来，然后扭动它，它的形状会改变吗？从上面实验过程你能得出什么结论？与同伴交流。

二、典型例题在△ABC中,AB=AC,AD是中线,△ABC的周长为34cm,△ABD的周长为30cm, 求AD的长.三、牛刀小试1、以下说法错误的是（）A．三角形的三条高一定在三角形内部交于一点B．三角形的三条中线一定在三角形内部交于一点C．三角形的三条角平分线一定在三角形内部交于一点D．三角形的三条高可能相交于外部一点2、三角形的三条高在（）A.三角形的内部B.三角形的外部C.三角形的边上D.三角形的内部，外部或边上3.如右图，）的长为（则的中线，已知是,2,6BDDEECABCAE==∆4.等腰三角形周长为21cm,一中线将周长分成的两部分差为3cm,则这个三角形三边长为________.5.三角形三边的长为15、20、25，则三条高的比为 .6.如图5，在等腰三角形ABC中，AB=AC，一腰上的中线BD将这个等腰三角形的周长分为15和6两部分，求该等腰三角形的腰长及底边长．7.有一块三角形优良品种试验基地，如图所示，•由于引进四个优良品种进行对比试验，需将这块土地分成面积相等的四块，请你制定出两种以上的划分方案供选择（画图说明）．AB CE。

2·三角形的高、中线、角平分线及三角形的稳定性预习归纳1·从三角形的一个顶点向它的对边 作垂线 ．与顶点和 垂 足 间的 线段 叫角形的高． 2·在三角形中，连接一个顶点和它的对边的中点的线段叫做三角形的中线． 3· 三角形三条中线的交点叫做三角形的重心．4·角形的一个角的平分线与这个角的对边相交，连接顶点与对边交点的线段叫做三角形的角平分线．5·三角形的三边确定了，那么三角形的形状就确定了．这个性质叫做三角形的稳定性 而四边形没有稳定性． 例题讲解[例]如图，画△ABC 的边BC 的高正确的是( )DCBACCCC基础题训练1．如图，在△ABC 中，BD 是∠ABC 的角平分线，已知∠ABC =80°，则∠DBC =2．如图， 当 _时， AD 是△ABC 的中线． 当 时，AD 是△ABC 的角平分线．3．如图，用4根木条钉成一个四边形木架，要使这个木架不变形，他至少要再钉上几根木条 A ．0根B ．1根C ．2根D ．3根4．如图所示，AM 是△ABC 的中线，那么若用S 表示△ABM 的面积，用S 表示△ACM 的面积，则S 1和S 2的大小关系是（ ）A ．S 1>S 2B ． S 1<S 2C ． S 1=S 2D ．以上三种情况都有可能BC5．如图，若∠1=∠2，∠3=∠4，下列结论错误的是（ ）A ．AD 是△ABC 的角平分线B ．CE 是△ACD 的角平分线C ．132ACB ∠=∠ D ．CE 是△ABC 的角平分线3124EBCA6．在直角三角形ABC 中， ∠ACB =90°， AC =3cm ，BC =4cm ，CD 是AB 边的中线，则AC 边上的高为 cm ，三角形BCD 的面积= cm ．CBA7．如图，已知△ABC 和△EFD ，在图中分别画出这两个三角形的三条高．中档题训练8．如图，△ABC 中，∠A =80°，高BE 和CH 的交点为O ，则∠BOC 等于（ ） A ．80° B ． 120° C ．100° D ．150°9．(2013·常德改编）如图,AD是△ABC的中线，CE是△ACD的中线，DF是△CDE的中线，如果△DEF 的面积是2，那么△ABC的面积为（）A．12 B．11 C．16 D．1810．如图所示，AC为BC的垂线，CD为AB的垂线，DE为BC的垂线，D、E分别在△ABC的边AB和BC上，则下列说法：①△ABC中，AC是BC边上的高；②△BCD中，DE是BC边上的高；③△DBE中，DE是BE边上的高；④△ACD中，AD是CD边上的高．其中正确的是11．如图AD是△ABC的角平分线，点P为AD上一点，PM//AC交AB于M，PN//AB交AC于N，求证:P A 平分∠MPN．12．如图，AD、CE是△ABC的两条高，已知AD=10，CE＝9，AB＝12．（1）求△ABC的面积；（2）求BC的长．13．在△ABC中，AB＝AC，DB为△ABC的中线，且BD将△ABC周长分为12cm与15cm两部分，求三角形各边长．综合题训练14．张爷爷家有一块三角形的花圃△ABC张爷爷准备将其分成面积相等的四部分，分别种上不同的花卉．请你帮张爷爷设计三种不同的方案．。

解三角形中的“三线”问题在解三角形的过程中，我们常常会遇到“三线”问题，即中线、角平分线和高线。

这些线段在三角形中具有特殊的意义和作用，了解它们的性质和特点是解决三角形问题的关键。

一、中线中线是指连接三角形的一个顶点和它所对的边的中点的线段。

中线的性质主要有：1、三角形中线的三条中线线段相等，且相互平行。

2、三角形中线的交点称为三角形的重心，重心分每条中线线段为两段，且这两段长度相等。

3、三角形三边中线的长度分别等于对应边长的一半。

在解三角形时，可以利用中线的性质进行证明和计算。

例如，可以利用中线的平行性质证明某个线段平行于三角形的某一边；利用中线的长度性质解决一些等量关系的问题。

二、角平分线角平分线是指将三角形的两个相等的角平分的线段。

角平分线的性质主要有：1、三角形的一个角平分线与这个角的对边相交，连接这个角的顶点和交点的线段称为三角形的角平分线。

2、三角形任意两角平分线的夹角为90度，这个夹角的平分线称为三角形的内切线。

3、角平分线上的点到这个角的两边的距离相等。

4、三角形三条角平分线交于一点，这个交点称为三角形的内心，内心到三角形的三边的距离相等。

在解三角形时，可以利用角平分线的性质进行证明和计算。

例如，可以利用角平分线的性质证明某个线段平行于三角形的某一边；利用角平分线的长度性质解决一些等量关系的问题。

三、高线高线是指从三角形的顶点向底边垂下的线段。

高线的性质主要有：1、三角形的高线所在的直线是三角形的对称轴。

2、三角形的高线与对应边的夹角为90度。

3、三角形任意两高线的夹角为钝角。

4、三角形三条高线交于一点，这个交点称为三角形的垂心，垂心到三角形的三边的距离相等。

在解三角形时，可以利用高线的性质进行证明和计算。

例如，可以利用高线的对称性质证明某个图形是轴对称的；利用高线的长度性质解决一些等量关系的问题。

“三线”问题在解三角形中具有重要的意义和作用。

掌握它们的性质和特点是解决三角形问题的关键之一。

初中数学知识归纳三角形的中线高线角平分线三角形是初中数学中的基础知识之一，而了解它的特性和性质对于解题和理解其他几何概念都至关重要。

本文将对三角形的中线、高线和角平分线进行归纳总结，帮助同学们更好地理解和运用这些概念。

一、三角形的中线中线是指连接三角形两个顶点和对边中点的线段。

对于任意三角形ABC，连接顶点A和边BC的中点D所得的线段AD就是三角形ABC的中线。

1.1 中线的性质：（1）中线的长度相等：对于任意三角形ABC，三条中线AD、BE、CF的长度相等，即AD = BE = CF。

（2）中线互相平分：三条中线相交于同一个点G，且点G将每条中线分成两等分，即AG = GD，BG = GE，CG = GF。

（3）中线平行于对边：在三角形ABC中，若DE为BC的中线，则DE∥AC，EF为AC的中线，则EF∥BC，FD为AB的中线，则FD∥BC。

二、三角形的高线高线是指从三角形的顶点向对边的垂线段。

对于任意三角形ABC，连接顶点A和边BC的垂线段AH就是三角形ABC的高线。

2.1 高线的性质：（1）高线相交于同一点：对于任意三角形ABC，三条高线AH、BH、CH交于同一个点O，也称为垂心。

（2）高线与对边垂直：在三角形ABC中，高线AH垂直于边BC，高线BH垂直于边AC，高线CH垂直于边AB。

（3）高线长度关系：对于任意三角形ABC，三条高线AH、BH、CH的长度满足关系：AH＝2R（这里的R表示三角形的外接圆半径），BH=2R，CH=2R。

三、三角形的角平分线角平分线是指将一个角平分为两个相等的角的线段。

对于任意三角形ABC，若角A的平分线AD，则称线段AD为三角形ABC的角A的平分线。

3.1 角平分线的性质：（1）角平分线的性质：“角的平分线上的点与角的两边垂直，而且与角的两边所夹的两个小角相等。

”（2）角平分线交于同一点：对于任意三角形ABC，三条角平分线AD、BE、CF交于同一个点I，也被称为内心。