仿射变换在椭圆问题中的应用举例

浅议仿射变换的应用作者：姚金江朱萌来源：《科技资讯》2017年第13期摘要：变换是一种重要的数学思想。

利用变换去解决问题往往可以达到事半功倍的效果。

仿射变换是几何学中的一个重要变换，是从运动变换向射影变换的重要手段。

根据仿射变换的性质，可以把特殊图形的重要结论直接推广到一般图形，达到复杂问题的简单化求解。

关键词：仿射变换仿射不变性单比中图分类号：TP391.41 文献标识码：A 文章编号：1672-3791（2017）05（a）-0156-02仿射变换是几何学中一个基本的变换，图形在变换中保持许多不变性质和不变量；这些不变性质与不变量为人们解决复杂几何问题提供了理论根据，仿射变换基本的不变性质与不变量有：同素性不变，即把直线变成直线、点变成点；平行性不变，即把平行直线变成平行直线；共线三点的单比不变，两个三点形的面积比不变。

结论1[1] 两个多边形的面积之比是仿射不变量。

结论2[1] 两个封闭图形的面积之比是仿射不变量。

根据以上性质我们得到：三角形变为三角形（正三角形或斜三角型）、圆变为椭圆、等腰梯形变为一般梯形等。

1 应用方法正三角形、等腰梯形、圆都是特殊的几何图形，有明显的几何性质；它们的某些性质可推广到一般图形中去，并可以利用相关结论解决实际几何问题。

例如正三角形3条中线把正三角形分成6个面积相等的小三角形，根据仿射性质知道，一般三角形也有这个结论。

对于任意的一个一般三角形，在适当的仿射变换下，它可以变为正三角形。

因此，我们要证明有关三角形的结论时，若题目中的条件都是图形的仿射性质或仿射不变量，那么我们只需要证明这个结论在正三角形中成立即可。

任意的一个平行四边形，经过合适的仿射变换，它可以转换为长方形或正方形。

因此要解决关于平行四边形的符合仿射性质或数量的结论时，可以考虑正方形，只要这个结论在正方形中成立，那么它在原平行四边形当中也成立，从而使解题过程变得简单。

一般梯形在仿射变换下能转化为等腰梯形。

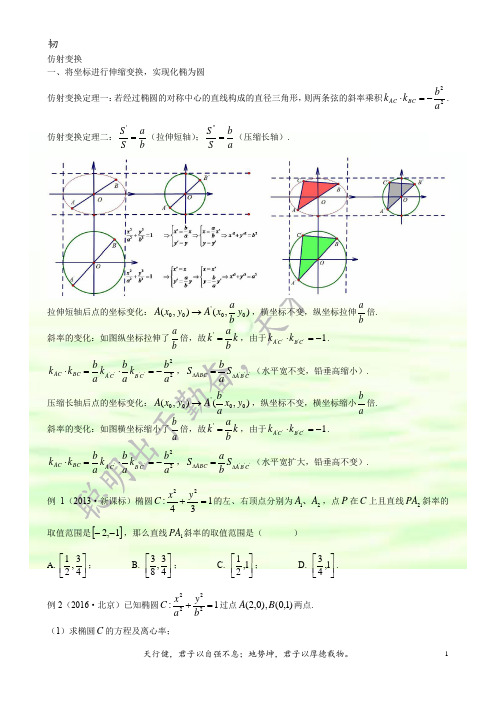
仿射变换一、将坐标进行伸缩变换，实现化椭为圆仿射变换定理一：若经过椭圆的对称中心的直线构成的直径三角形，则两条弦的斜率乘积22ab k k BCAC -=⋅.仿射变换定理二：b a S S ='（拉伸短轴）；ab S S =''（压缩长轴）.拉伸短轴后点的坐标变化：),(),(00'00y b a x A y x A →，横坐标不变，纵坐标拉伸ba倍. 斜率的变化：如图纵坐标拉伸了b a 倍，故k ba k ='，由于1''''-=⋅C B C A k k .22''''a b k a b k a b k k C B C A BCAC -=⋅=⋅，'''C B A ABC S abS ∆∆=（水平宽不变，铅垂高缩小）. 压缩长轴后点的坐标变化：),(),(00'00y x a b A y x A →，纵坐标不变，横坐标缩小ab倍. 斜率的变化：如图横坐标缩小了a b 倍，故k ba k ='，由于1''''-=⋅C B C A k k .22''''a b k a b k a b k k C B C A BCAC -=⋅=⋅，'''C B A ABC S baS ∆∆=（水平宽扩大，铅垂高不变）. 例1（2013·新课标）椭圆134:22=+y x C 的左、右顶点分别为21A A 、，点P 在C 上且直线2PA 斜率的取值范围是[]1,2--，那么直线1PA 斜率的取值范围是（ ）A. ⎥⎦⎤⎢⎣⎡43,21；B. ⎥⎦⎤⎢⎣⎡43,83；C. ⎥⎦⎤⎢⎣⎡1,21；D. ⎥⎦⎤⎢⎣⎡1,43.例2（2016·北京）已知椭圆1:2222=+by a x C 过点)1,0(),0,2(B A 两点.（1）求椭圆C 的方程及离心率；（2）设P 为第三象限内一点且在椭圆C 上，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ，求证：四边形ABNM 的面积为定值.例3（2014·新课标Ⅰ）已知点)2,0(-A ，椭圆)0(1:2222>>=+b a by a x E 离心率为23，F 是椭圆的右焦点，直线AF 的斜率为332，O 为坐标原点. （1）求E 的方程；（2）设过点A 的直线l 与E 相交于Q P 、OPQ ∆的面积最大时，求l 的方程.二、椭圆的角平分线定理仿射变换定理三：若点B A ,是椭圆)0(12222>>=+b a by a x 上的点，AB 与椭圆长轴交点为N ，在长轴上一定存在一个点M ，当且仅当2a x x N M =⋅时，BMN AMN ∠=∠，即长轴为角平分线.若点B A ,是椭圆)0(12222>>=+b a by a x 上的点，AB 与椭圆短轴交点为N ，在短轴上一定存在一个点M ，当且仅当2b y y N M =⋅时，BMN AMN ∠=∠，即短轴为角平分线.例4（2018·全国卷Ⅰ）设椭圆12:22=+y x C 的右焦点为F ，过F 的直线l 与C 交于B A ,两点，点M 的坐标为)0,2(.（1）当l 与x 轴垂直时，求直线AM 的方程； （2）设O 为坐标原点，证明：OMB OMA ∠=∠.三、放射变换后圆心角为直角问题仿射变换定理四：若以椭圆12222=+b y a x 的对称中心引出两条直线交椭圆于B A ,两点，且22ab k k OB OA -=⋅，则经过仿射变换后1''-=⋅OB OA k k ，所以AOB S ∆为定值.仿射变换定理五：若椭圆12222=+b y a x 上三点M B A ,,，满足①22a b k k OB OA -=⋅；②2abS AOB =∆；③))2,0((,cos sin πααα∈⋅+⋅=OB OA OM 例5（2011·山东）已知直线l 与椭圆123:22=+y x C 交于),(),,(2211y x Q y x P 两不同点，且OPQ ∆的面积26=∆OPQ S ，其中O 为坐标原点. （1）证明2221x x +和2221y y +均为定值；（2）设线段PQ 的中点为M ，求PQ OM ⋅的最大值；（3）椭圆C 上是否存在点G E D ,,，使得26===∆∆OEG ODG ODE S S S ？若存在，判断DEG ∆的形状；若不存在，请说明理由.例6（2016·浙江二模）已知椭圆)0(1:2222>>=+b a b y a x C 经过点)54,56(，其离心率为23，设MB A ,,是椭圆C 上的三点，且满足))2,0((,sin cos πααα∈⋅+⋅=OB OA OM ，其中O 为坐标原点.（1）求椭圆C 的标准方程；（2）证明：OAB ∆的面积是一个常数.四、中点弦与中垂线问题（无需点差法也可证明） 仿射变换定理六：中点弦问题，22a b k k ABOP -=⋅；中垂线问题，22a b k k MP OP =，且20220,b y c y a x c x N M ==. 拓展1：椭圆内接ABC ∆中，若原点O 为重心，则仿射后一定得到''C OB ∆为120的等腰三角形；'''C B A ∆为等边三角形.拓展2：椭圆内接的平行四边形OAPB ，B P A ,,在椭圆上，则仿射后一定得到菱形'''B P OA .例7（2015·新课标Ⅱ）已知椭圆)0(9:222>=+m y x C ，直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点B A ,，线段AB 的中点为M .（1）证明：直线OM 的斜率与l 的斜率的乘积为定值； （2）若l 过点),3(m m，延长线段OM 与C 交于点P ，四边形OAPB 能否为平行四边形？若能，求此时l 的斜率；若不能，请说明理由.例82015·浙江）已知椭圆1222=+y x 上两个不同的点B A ,关于直线21+=mx y 对称. （1）求实数m 的取值范围；（2）求AOB ∆面积的最大值（O 为坐标原点）.五、利用仿射变换解决椭圆与圆结合的面积问题若椭圆内含有圆与直线相切，如图直线AB 与圆相切于P ，交椭圆12222=+by a x 于点B A ,，求OAB S ∆的最大值.首先进行仿射变换：⎪⎩⎪⎨⎧=+=+22222221ryxbyax，令⎪⎩⎪⎨⎧=+=+⇒⎪⎩⎪⎨⎧==222'22'22'2'''raybxayxybayxx，拉伸后可知，''OBAAOBSabS∆∆=，故当''2sin21''OBAaSOBA∠=∆最大时，90''=∠OBA，关键在于看''OBA∠的取值范围；根据几何性质，''BA平行于x轴时，α=∠''OBA最小，''BA平行于y轴时，β=∠''OBA最大.例9（2018·武汉模拟）已知椭圆)0(1:2222>=+babyaxC的右焦点为)0,2(，离心率为36.（1）求椭圆C的方程；（2）若直线l与椭圆C相交于BA,两点，且以AB为直径的圆经过原点O，求证：点O到直线AB的距离为定值；（3）在（2）的条件下，求OAB∆面积的最大值.例10（2018·江苏）如图，在平面直角坐标系xOy中，椭圆C过点)21,3(，焦点)0,3(),0,3(21FF-，圆的直径为21FF.（1）求椭圆C及圆O的方程；（2）设直线l与圆O相切于第一象限内的点P.①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标； ②直线l 与椭圆C 交于B A ,两点，若OAB ∆的面积为762，求直线l 的方程.六、定比分点和弦长公式仿射变换定理七：定比分点的比值不变性原理，CB AC C B A C y y y y x x x x B C C A B C C A CBAC --=--====''''''''''''λ.仿射变换定理八：弦长公式的转化，纵向拉伸并不改变横向的性质，设,(),,(2211y x B y x A ，则2122212''212)(111x x k b a x x k B A x x k AB -+=-+=⇒-+=，即222'')(11k ba k BA AB++=.例11（2011·重庆）如图，椭圆O 的中心为原点，离心率22=e，一条准线的方程是22=x . （1）求椭圆的标准方程；（2）设动点P 满足ON OM OP 2+=，其中N M 、是椭圆上的点，直线OM 与ON 的斜率之积为21-，问：是否存在定点，使得PF 与点P 到直线102:x l 的距离之比为定值；若存在，求点F 的坐标，若不存在，说明理由.例12（2016·四川）已知椭圆)0(1:2222>>=+b a by a x E 的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线3:+-=x y l 与椭圆有且只有一个公共点T . （1）求椭圆E 的方程及点T 的坐标；（2）设O 是坐标原点，直线'l 平行于OT ，与椭圆E 交于不同的两点B A 、，且与直线l 交于点P . 求证：存在常数λ，使得PB PA PT ⋅=λ2，并求λ的值.例13（2016·重庆模拟）椭圆)0(1:2222>>=+b a by a x C ，作直线l 交椭圆于Q P ,两点，M 为线段PQ 的中点，O 为坐标原点，设直线l 的斜率为1k ，直线OM 的斜率为2k ，3221-=k k . （1）求椭圆C 的离心率；（2）设直线l 与x 轴交于点)0,5(-D ，且满足DQ DP 2=，当OPQ ∆的面积最大时，求椭圆C 的方程.达标训练1（2018·三明期末）设椭圆)0(1:2222>>=+b a by a x M 的离心率为2，且内切于圆422=+y x .（1）求椭圆M 的方程； （2）若直线m x y +=2交椭圆于两点，椭圆上一点)2,1(P ，求PAB ∆面积的最大值.2（2018·龙海期末）已知点)2,0(A ，椭圆)0(1:2222>>=+b a by a x E 的离心率为23，F 是椭圆E 的右焦点，直线AF 的斜率为332，O 是坐标原点. （1）求E 的方程；（2）设过点A 的直线l 与E 相交于Q P ,两点，当OPQ ∆的面积最大时，求直线l 的方程.3. 如图，已知C B A 、、是长轴为4的椭圆上的三点，点A 是长轴的右顶点，BC 过椭圆中心O ，且0=⋅BC AC AC BC =（1）求椭圆的标准方程；（2）若过C 关于y 轴对称的点D 作椭圆的切线DE ，则AB 与DE 有什么位置关系？证明你的结论.4（2016·佛山二模）已知点M 是圆4:22=+y x C 上一动点，点D 是M 在x 轴上的投影，P 为线段MD 上一点，且与点Q 关于原点O 对称，满足OD OM QP +=. （1）求动点P 的轨迹E 的方程；（2）过点P 做E 的切线l 与圆C 相交于B A ,两点，当QAB ∆面积取最大值时，求l 的方程.5（2018·株洲期末）椭圆141622=+y x 上的两点B A 、关于直线0322=--y x 对称，则弦AB 的中点坐标为（ ）A. )21,1(-；B. )1,21(-；C. )2,21(；D. )21,2(.6（2016·兰州模拟）已知椭圆C 的焦点坐标是)0,1()0,1(2F F 、-，过点2F 垂直于长轴的直线l 交椭圆C 于D B 、两点，且3=BD . （1）求椭圆C 的方程；（2）过定点)2,0(P 且斜率为k 的直线l 与椭圆C 相交于不同两点N M 、，试判断：在x 轴上是否存在点)0,(m A ，使得以AN AM ,为邻边的平行四边形为菱形？若存在，求出实数m 的取值范围，若不存在，请说明理由.7（2018·抚顺模拟）已知离心率为21的椭圆)0(1:2222>>=+b a b y a x C ，右焦点在椭圆上的点的距离的最大值为3.（1）求椭圆C 的方程；（2）设点B A ,是椭圆C 上的两个动点，直线OB OA ,与椭圆的另一个交点分别为11,B A ，且直线OB OA ,的斜率之积等于43-，问四边形11B ABA 的面积S 是否为定值？请说明理由.8（2017·淮北一模）已知椭圆1416:221=+y x C ，直线)0(:1>+=m m kx y l 与圆1)1(:222=+-y x C 相切且与椭圆1C 交于B A ,两点. （1）若线段AB 中点的横坐标为34，求m 的值； （2）过原点O 作1l 的平行线2l 交椭圆于D C ,两点，设CD AB λ=，求λ的最小值.9（2012·山东）如图，椭圆)0(1:2222>>=+a by a x M 的离心率为23，直线a x ±=和b y ±=所围成的矩形ABCD 的面积为8.（1）求椭圆M 的标准方程；（2）设直线)(:R m m x y l ∈+=与椭圆M 有两个不同的交点Q P ,，l 与矩形ABCD 有两个不同的交点T S ,，求STPQ 的最大值及取得最大值时m 的值.10（2019·成都模拟）已知椭圆)0(1:2222>>=+b a by a x C 的离心率为23，且以坐标原点为圆心，椭圆的短半轴长为半径的圆与直线02=+-y x 相切. （1）求椭圆C 的标准方程；（2）若一条不过原点的直线l 与椭圆相交于B A ,两点，设直线OB l OA ,,的斜率分别为21,,k k k ，且21,,k k k 恰好构成等比数列，求22OB OA +的值.11. 如图，已知椭圆C 的中心在原点O ，左焦点为)0,1(1-F ，左顶点为A ，且1F 为AO 的中点. （1）求椭圆C 的方程；（2）若椭圆1C 的方程为)0(12222>>=+n m n y m x ，椭圆2C 的方程为)1,0(2222≠>=+λλλ且ny m x ，则称椭圆2是椭圆1C 的λ倍相似椭圆，已知2C 是椭圆C 的3倍相似椭圆，若椭圆C 的任意一条切线l 交椭圆2C 于两点N M ,，试求弦长MN 的最大值.韧天行健，君子以自强不息；地势坤，君子以厚德载物。

椭圆仿射变换公式椭圆的仿射变换公式可以通过矩阵运算来表示。

假设我们有一个原始的椭圆，其方程为：(x/a)^2 + (y/b)^2 = 1其中，a和b分别为椭圆的长半轴和短半轴。

现在，我们进行仿射变换，可以通过以下矩阵运算来实现：1.平移：通过平移操作，我们可以将椭圆在平面上移动到指定位置。

假设平移的向量为 (h, k)，则椭圆的新方程为：(x/a)^2 + (y/b)^2 = 1其中，x'和y'为平移后的椭圆上的点，与原始坐标之间的关系为：x' = x + h y' = y + k2.缩放：通过缩放操作，我们可以改变椭圆的大小。

假设缩放的比例因子为 (s_x, s_y)，则椭圆的新方程为：((x'/a)^2)/s_x^2 + ((y'/b)^2)/s_y^2 = 1其中，x'和y'为缩放后的椭圆上的点，与平移后的坐标之间的关系为：x' = s_x * x y' = s_y * y3.旋转：通过旋转操作，我们可以改变椭圆的方向。

假设旋转角度为θ，则椭圆的新方程为：((x'/a)^2 + (y'/b)^2)/cos^2(θ) - ((x'/a)^2 - (y'/b)^2)sin^2(θ) = 1其中，x'和y'为旋转后的椭圆上的点，与缩放后的坐标之间的关系为：x' = x * cos(θ) - y * sin(θ) y' = x * sin(θ) + y * cos(θ)通过以上的仿射变换公式，我们可以对椭圆进行平移、缩放和旋转操作，得到新的椭圆。

这些操作可以帮助我们在几何计算和图形处理中对椭圆进行变换和调整。

用仿射变换求解椭圆问题
彭明用
【期刊名称】《数理天地:高中版》
【年(卷),期】2022()9
【摘要】通过仿射变换将椭圆里有关斜率、面积、弦长的问题转换为圆中与其相对应的问题,然后用圆的有关知识求解椭圆问题.
【总页数】2页(P20-21)
【作者】彭明用
【作者单位】贵州师范大学附属中学
【正文语种】中文
【中图分类】G634.6
【相关文献】
1.仿射变换在椭圆问题中的应用举例
2.仿射变换在解决有关椭圆的仿射性质问题中的应用
3.也谈“RMI原理”与仿射变换下有关圆与椭圆的若干问题
4.仿射变换下一类椭圆问题的简单解法
5.仿射变换观点下的中学椭圆问题
因版权原因，仅展示原文概要，查看原文内容请购买。

仿射几何在研究圆锥曲线中的一些应用仁化县仁化中学 谢祖福摘要：本文主要结合实例，运用仿射几何的性质在解决圆锥曲线的问题作了一些尝试，以期达到对圆锥曲线问题的解法的化繁为简，化难为易，并且开阔数学视野，培养唯物辨证观点的目的。

关键词：仿射几何 仿射性质 仿射变换 圆锥曲线高等几何是从古典几何过渡到近世几何的桥梁，它对中学初等几何和解析几何的教学有重大的指导意义，其中仿射几何是高等几何的重要组成部分，是联结高等几何与初等几何的纽带，是应用高等几何解决初等几何的一条重要通道。

在这里，笔者试图利用仿射几何的一些基本性质，在仿射变换下，通过特殊的图形去研究复杂的图形，从而解决一些高中解析几何中圆锥曲线一类的问题。

我们知道，椭圆、双曲线、抛物线经过仿射变换，它们对应的图形分别是圆、特殊的双曲线即等轴双曲线x 2－y 2=±1和特殊的抛物线y 2=2x 。

所以我们只要研究圆、双曲线x 2－y 2=±1和抛物线y 2=2x 的相应性质，利用其平行性、结合性、简比、面积比等仿射性质，其对应的椭圆、双曲线、抛物线的性质就相应知道了，从而能取得事半功倍的效果。

一、利用仿射性质解决一些圆锥曲线的最值问题。

例：求椭圆12222=+by a x 的内接三角形面积的最大值。

解：如图，设此椭圆可以由一圆经过仿射变换T 后得到的。

A'变换TA设圆的半径为r ，椭圆的长、短半轴分别为a 、b ，则椭圆的面积为πab ，且圆内接三角形面积最大的为圆内接正三角形，面积为433r 2。

根据仿射变换的性质 =椭圆圆S S ABCC B A S S ∆∆‘’‘ =常量即ab r ππ2=ABC S r∆2433，则ABC S ∆=433ab 为所求的最大值。

同理，此结论可以推广到求椭圆的内接矩形的最大值。

例：求证椭圆的最大内接矩形的面积为2ab 。

（此题留给读者自己证明） 二、利用仿射几何的基本性质证明一些定值问题。

章主要讨论透视仿射对应，仿射对应，仿射变换及其关系，图形的仿射性质和仿射变换的特例。

关键词：透视仿射对应，仿射变换，仿射对应，仿射坐标，图形的仿射性质，单比，同素性，结合性，平行性;引言在欧氏平面上建立仿射坐标系，研究仿射变换下图形的仿射性质（单比，同素性，结合性，平行性）及仿射变换的特例（正交变换，位似变换，相似变换，压缩变换等）为以后学习射影变换和图形的射影性质打下基础。

1. 预备知识1.1单比定义1：设1P ,2P 是有向直线上的两个定点， P 是这有向直线的另一点，P 分有向线段12p p 为两个有向线段1p p 和2p p ，则其量数的比12P P P P叫做三点12,,P P P的单比；记为()12P P P ，即()12P P P =12P P P P，其中 1P ，2P 叫做基点，P 叫做分点显然 当P 在1P ,2P 之间时,()120p p p 〈当P 在1P ,2P 之外时, ()120p p p 〉 当P 与1P 重合时,()120p p p = 当P 与2P 重合时, ()12P P P 不存在 当P 为线段1P 2P 的中点时, ()12P P P =-1.如果已知一直线上三点的单比()12P P P ,另一直线上两点12,p p '',则在第二直线上可以唯一地确定一点p '而使()12p p p '''=()12P P P 。

现在我们将共线三点的单比用坐标表示。

定理：设共线三点123,,P P P 的仿射坐标顺次为()()()112233,,,,,,x y x y x y 则单比 ()123p p p =31313232x x y y x x y y --=--； 这就是单比的坐标表示。

1.2 透视仿射对应1.2.1. 透射仿射对应的分类 一般透射仿射对应可以分为两个： （1）二直线间的透视仿射对应lA'A B 'B C'C a'a X定义1：在一平面上设有直线a 和a '，l 为此平面上与a ，a '均不平行的另一直线，通过直线a 上各点,,A B C 分别作与l 平行的直线，顺次交a '于,,A B C ''' 这样（图1）使得到直线a 上点到a '上点的一个一一对应,称为透视仿射对应。

仿射变换理论及其在几何中的应用仿射变换理论在儿何中地位非常重要，它比正交变换解决的问题范围更广.本文中我们将看到仿射坐标系，在仿射坐标系中我们了解仿射变换和仿射变换的基本性质，例如包括仿射变换将直线变为直线，将平行的两条直线变为半行的两直线。

本文中还介绍单比，利用它证明了梅内劳斯(Menelaus)定理。

后來本文介绍了仿射不变性质，例如两个三角形面积的比是仿射不变量。

最后本文介绍了利用本文的有关性质解决一些问题。

这样使得读者更好的了解这篇文章。

欧式儿何就是研究正交变换下图形的不变性质与不变量，因此在初等平面儿何中都是讨论图形的那些与距离，角度,面积，等有关的性质，如三角形全等，平行，垂直等•但是图形的各种变形中，保持任意两点之间的距离不变的变换是十分特殊.例如，图形的放大，物体在阳光照射下变成它们的影子等，都不具有这种性质，即都不是正交变换•因此，我们考虑较正交变换广泛一点的点变换，即仿射变换.本文讨论了仿射变换的槪念及其性质，同时给出了其在儿何中的应用.1平面上的仿射坐标系与仿射变换我们引进仿射坐标系：在半面上任取一点。

及两个不共线的向量5 二O 瓦,=OE2(不一定是单位向量，EG,.不一定垂直的)这样我们就建立了仿射坐标系如图1对于平面上任一点尸，则向量。

户可唯一地表示为OP = xei + yei数组&y)称为关于仿射坐标系仁由,/},的仿射坐标.定理1. 0在仿射坐标系下，直线方程一定是关于仿射坐标系的一次方程Ax+By+C = 0,(1. 00)反之也真.证明在直线上任取两点小演，乂)，2(9,%),对于直线上任一点P幺有联II鹤，即&-演K-K'或(工一占)(治一必)一(丁一九)(毛一%)二。

，这是关于X,y的一次方程.反之，在(1.00)±取£ (公弘)及《(毛用)的坐标适合方程，即Ar. + B\,+C = 0, (1. 02)A V3 + By： + C = 0. (1. 03)只要证明任一坐标适合方程的点P' 3, y') 一定与共线即可，由TAx + By + C = Q, (1. 04)因A, B,C不全为零,(1.02), (1.03), (1.04)可理解为关于A, 5, C ,的齐次线性方程组，由于A,民。