奥数小六课堂4-9：组合问题 逻辑推理二

数字谜从形式上可以分为横式数字谜与竖式数字谜，从运算法则上可以分为加减乘除四种形式的数字谜。

横式与竖式亦可以互相转换，本讲中将主要介绍数字谜的一般解题技巧。

主要横式数字谜问题，因此，会需要利用数论的简单奇偶性等知识解决数字谜问题一、基本概念填算符：指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。

算符：指 +、-、×、÷、（）、[]、｛｝。

二、解决巧填算符的基本方法（1）凑数法：根据所给的数，凑出一个与结果比较接近的数，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。

（2）逆推法：常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。

三、奇数和偶数的简单性质（一）定义：整数可以分为奇数和偶数两类（1）我们把1，3，5，7，9和个位数字是1，3，5，7，9的数叫奇数. （2）把0，2，4，6，8和个位数是0，2，4，6，8的数叫偶数.（二）性质： ①奇数≠偶数.②整数的加法有以下性质： 奇数+奇数=偶数； 奇数+偶数=奇数； 偶数+偶数=偶数.③整数的减法有以下性质： 奇数-奇数=偶数； 奇数-偶数=奇数； 偶数-奇数=奇数；知识点拨教学目标5-1-1-2.算式谜（二）偶数-偶数=偶数.④整数的乘法有以下性质：奇数×奇数=奇数； 奇数×偶数=偶数；偶数×偶数=偶数.模块一、填横式数字谜【例 1】 将数字1~9填入下面方框，每个数字恰用一次，使得下列等式成立；()200724=+÷+-★□□□□□□□现在“2”、“4”已经填入，当把其它数字都填入后，算式中唯一的减数（★处）是 ．【考点】填横式数字谜之复杂的横式数字谜 【难度】4星 【题型】填空 【关键词】2007年，迎春杯，高年级，初赛，3试题【解析】 方法一：首先可以估算四位数的取值范围：四位数不大于()2007913428010+-⨯-=，不小于()2007198427638+-⨯-=．显然四位数的千位数字只能是7．再由四位数与2的和能被4整除，可以确定四位数的个位数字一定是偶数，只能是6或8．若为6，由个位是8而能被4整除的数其十位数字是偶数，可知四位数只能为7986，而()7986241997+÷=，故只需利用剩下的数凑出10即可．剩下的数字是1，3，5，不能凑出10．所以四位数的个位数字不是6．四位数的个位数字是8时，由个位是0而能被4整除的数其十位数字是偶数，故四位数的十位数字是1、3、7或9．当四位数的十位数字是1时，四位数只可能是7918，而()7918241980+÷=，故只需利用剩下的数凑出27即可．剩下的数字是3，5，6，不能凑出27；当四位数的十位数字是3时，四位数只可能是7938，而()7938241985+÷=，故只需利用用剩下的数凑出22即可．剩下的数字是1，5，6，不能凑出22；当四位数的十位数字是5时，四位数只可能是7658或7958，若为7958，则由()7958241990+÷=，需利用剩下的数凑出17即可．剩下的数字是1，3，6，不能凑出17；若为7658，有()7658249312007+÷+-=；当四位数的十位数字是9时，四位数只可能是7698，而()7968241925+÷=，故只需利用剩下的数凑出82即可．剩下的数字是3，5，6，不能凑出82；故此题只有惟一答案：()7658249312007+÷+-=．算式中唯一的减数是1．方法二：根据弃九法，7□□□+2+4+□□+★被9整除，而(7□□□+2)÷4+□□-★也被9整除。

小学六年级奥数题:六年级奥数专题训练之组合１.从分别写有2、4、6、8、10的五张卡片中任取两张，作两个一位数乘法，问：有多少种不同的乘法算式？有多少个不同的乘积？２.从分别写有4、5、6、7的四张卡片中任取两张作两个一位数加法。

问：有多少种不同的加法算式？有多少个不同的和？３.从分别写有3、4、5、6、7、8的六张卡片中任取三张，作三个一位数的乘法。

问：有多少种不同的乘法算式？有多少个不同的乘积？４.在一个圆周上有10个点，以这些点为端点或顶点，可以画出多少条或多少个不同的(1)直线；(2)三角形；(3)四边形。

５.在图6-11的四幅分图中分别有多少个不同的线段、角、矩形和长方体？６.直线a、b上分别有5个点和4个点(图6-12)，以这些点为顶点，可以画出多少个不同的(1)三角形；(2)四边形。

７.在一个半圆环上共有12个点(图6-13)，以这些点为顶点可画出多少个三角形？８.三条平行线分别有2、4、3个点(图6-14)，已知在不同直线上的任意三个点都不共线。

问：以这些点为顶点可以画出多少个不同的三角形？９.从15名同学中选5名参加数学竞赛，求分别满足下列条件的选法各有多少种：(1)某两人必须入选；(2)某两人中至少有一人入选；(3)某三人中恰入选一人；(4)某三人不能同时都入选。

１０.学校乒乓球队有10名男生、8名女生，现在要选8人参加区里的比赛，在下列条件下，分别有多少种选法：(1)恰有3名女生入选；(2)至少有两名女生入选；(3)某两名女生、某两名男生必须入选；(4)某两名女生、某两名男生不能同时都入选；(5)某两名女生、某两名男生最多入选两人；(6)某两名女生最多入选一人，某两名男生至少入选一人。

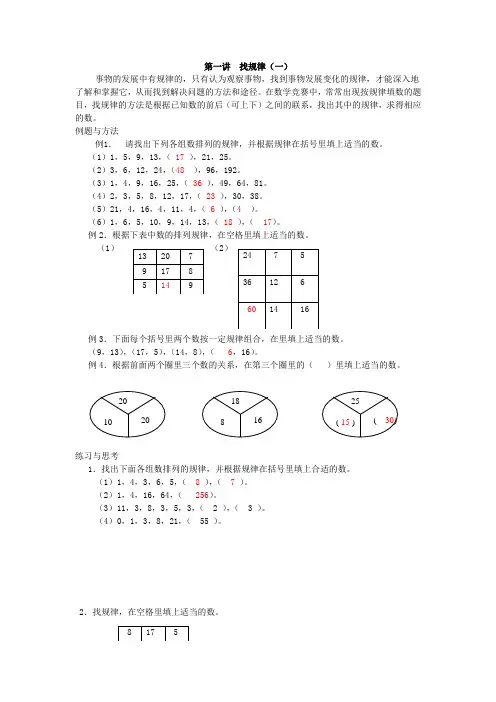
第一讲 找规律（一）事物的发展中有规律的，只有认为观察事物，找到事物发展变化的规律，才能深入地了解和掌握它，从而找到解决问题的方法和途径。

在数学竞赛中，常常出现按规律填数的题目，找规律的方法是根据已知数的前后（可上下）之间的联系，找出其中的规律，求得相应的数。

例题与方法例1． 请找出下列各组数排列的规律，并根据规律在括号里填上适当的数。

（1）1，5，9，13，（ 17 ），21，25。

（2）3，6，12，24，（48 ），96，192。

（3）1，4，9，16，25，（ 36 ），49，64，81。

（4）2，3，5，8，12，17，（ 23 ），30，38。

（5）21，4，16，4，11，4，（ 6 ），（4 ）。

（6）1，6，5，10，9，14，13，（ 18 ），（ 17）。

例2．根据下表中数的排列规律，在空格里填上适当的数。

（1）（2）例3．下面每个括号里两个数按一定规律组合，在里填上适当的数。

（9，13），（17，5），（14，8），（ 6，16）。

例4．根据前面两个圈里三个数的关系，在第三个圈里的（）里填上适当的数。

练习与思考1．找出下面各组数排列的规律，并根据规律在括号里填上合适的数。

（1）1，4，3，6，5，（ 8 ），（ 7 ）。

（2）1，4，16，64，（ 256）。

（3）11，3，8，3，5，3，（ 2 ），（ 3 ）。

（4）0，1，3，8，21，（ 55 ）。

2．找规律，在空格里填上适当的数。

（1）（2）3．下面括号里和两个数是按一定规律组合，根据规律在 里填上适当的数。

（1）（8，7），（6，9），（10，5），（ 2 ，13）。

（2）（1，3），（5，9），（7，13），（9，17 ）。

4．根据前面两个圈里三个数的关系，在第三个圈里的（ ）里填上适当的数。

(1) (2)(2)第二讲 找规律（二）例1．请先计算下面一组算式的前三题，然后找出其中的规律，并根据规律直接写出后六题的得数。

小学奥数经典专题点拨：排列与组合第一篇：小学奥数经典专题点拨：排列与组合排列与组合【有条件排列组合】例1 用0、1、2、3、4、5、6、7、8、9这十个数字能够组成______个没有重复数字的三位数。

（哈尔滨市第七届小学数学竞赛试题）讲析：用这十个数字排列成一个不重复数字的三位数时，百位上不能为0，故共有9种不同的取法。

因为百位上已取走一个数字，所以十位上只剩下9个数字了，故十位上有9种取法。

同理，百位上和个位上各取走一个数字，所以还剩下8个数字，供个位上取。

所以，组成没有重复数字的三位数共有9×9×8=648（个）。

例2 甲、乙、丙、丁四个同学排成一排，从左到右数，如果甲不排在第一个位置上，乙不排在第二个位置上，丙不排在第三个位置上，丁不排在第四个位置上，那么不同的排法共有______种。

（1994年全国小学数学奥林匹克初赛试题）讲析：因每个人都不排在原来的位置上，所以，当乙排在第一位时，其他几人的排法共有3种；同理，当丙、丁排在第一位时，其他几人的排法也各有3种。

因此，一共有9种排法。

例3 有一种用六位数表示日期的方法，如890817表示1989年8月17日，也就是从左到右第一、二位数表示年，第三、四位数表示月，第五、六位数表示日。

如果用这种方法表示1991年的日期，那么全年中六个数字都不相同的日期共有______天。

（1991年全国小学数学奥林匹克决赛试题）讲析：第一、二位数字显然只能取9和1，于是第三位只能取0。

第五位数字只能取0、1、2或3，而0和1已取走，当取3时，第六位上只能取0和1，显然不行。

因此，第五位上只能取2。

于是，第四位上只能取3、4、5、6、7、8；第六位上也只能取3、4、5、6、7、8，且第四、六位上数字不能取同。

所以，一共有6×5=30（种）。

【环形排列】例1 编号为1、2、3、4的四把椅子，摆成一个圆圈。

现有甲、乙、丙、丁四人去坐，规定甲、乙两人必须坐在相邻座位上，一共有多少种坐法？（长沙市奥林匹克代表队集训试题）讲析：如图5.87，四把椅子排成一个圆圈。

四年级奥数试题及答案### 四年级奥数试题及答案#### 一、逻辑推理题题目：小明、小红和小刚三个人在玩捉迷藏。

小明说：“我不是第一个被找到的。

”小红说：“我不是最后一个被找到的。

”小刚说：“我是最后一个被找到的。

”根据这些信息，请问谁第一个被找到？答案：根据小刚的说法，他是最后一个被找到的。

因为小红说她不是最后一个，所以她不能是最后一个被找到的。

因此，小红是第一个被找到的。

那么，小明就是第二个被找到的。

#### 二、数学计算题题目：一个数列的前三项是 2, 3, 5，从第四项开始，每一项都是前三项的和。

求这个数列的前六项。

答案：数列的前三项是 2, 3, 5。

第四项：2 + 3 + 5 = 10第五项：3 + 5 + 10 = 18第六项：5 + 10 + 18 = 33所以数列的前六项是：2, 3, 5, 10, 18, 33。

#### 三、几何图形题题目：一个正方形的边长是 10 厘米，求这个正方形的周长和面积。

答案：正方形的周长是边长的四倍，所以周长是 10 厘米× 4 = 40 厘米。

正方形的面积是边长的平方，所以面积是 10 厘米× 10 厘米 = 100 平方厘米。

#### 四、应用题题目：小华有 50 元钱，他想买 3 支铅笔和 2 本笔记本，每支铅笔 2 元，每本笔记本 5 元。

如果他想全部花完，还需要再买多少支铅笔？答案：首先计算小华已经花费的金额：3 支铅笔× 2 元/支 + 2 本笔记本× 5 元/本 = 6 元 + 10 元 = 16 元。

小华剩余的钱是 50 元 - 16 元 = 34 元。

每支铅笔 2 元，所以他还可以买 34 元÷ 2 元/支 = 17 支铅笔。

#### 五、组合问题题目：有 5 个不同的球和 3 个不同的盒子，要求每个盒子至少有一个球。

问有多少种不同的放球方式？答案：首先，将一个球放入一个盒子，有 3 种选择。

二年奥数题及答案大全奥数，即奥林匹克数学竞赛，是一种旨在培养学生数学思维和解决问题能力的竞赛活动。

以下是一些适合二年级学生的奥数题目及答案：# 题目1：数字填空在下面的加法算式中，填入合适的数字：```□ + □ = 10```答案：1 + 9 = 10# 题目2：逻辑推理小明有三个盒子，分别标记为A、B和C。

A盒子里有苹果，B盒子里有橘子，C盒子里有梨。

如果A盒子不是苹果，那么B盒子里是什么？答案：如果A盒子不是苹果，那么A盒子里是梨，因为C盒子已经有梨了，所以B盒子里是苹果。

# 题目3：图形识别下面哪个图形是正方形？```A. □□□□B. ○○○○C. △△△△D. □□□□□```答案：A# 题目4：简单计算如果一个班级有20名学生，每个学生需要2支铅笔，那么这个班级总共需要多少支铅笔？答案：40支# 题目5：时间问题小明从家到学校需要30分钟，如果他7:00离开家，他将在什么时间到达学校？答案：7:30# 题目6：序列问题下面的数列中缺少的数字是什么？```2, 4, 6, 8, □```答案：10# 题目7：图形分割一个正方形可以被分割成多少个相等的三角形？答案：4个# 题目8：排列组合如果有一个数字“123”，可以组成多少个不同的两位数？答案：6个（12, 21, 13, 31, 23, 32）# 题目9：简单概率如果一个袋子里有3个红球和2个蓝球，随机取出一个球，拿到红球的概率是多少？答案：3/5# 题目10：年龄问题如果爸爸比小明大30岁，小明现在是10岁，那么5年后爸爸比小明大多少岁？答案：30岁这些题目涵盖了基础的数学概念和逻辑推理，适合二年级学生进行练习和提高。

数学初一奥数题及答案题目一：数列问题题目描述：有一个数列：2, 4, 7, 11, ... 这个数列的第10项是多少？解题思路：观察数列可以发现，每一项与前一项的差值依次为2, 3, 4, 5, ... 这是一个等差数列，差值的公差为1。

因此，第n项与第1项的差值是1+2+3+...+(n-1)。

答案：首先计算第10项与第1项的差值，即1+2+3+...+9，这是一个等差数列求和问题，公式为\( S = \frac{n(n+1)}{2} \)，代入n=9得到\( S = \frac{9 \times 10}{2} = 45 \)。

所以第10项是2 + 45 = 47。

题目二：几何问题题目描述：在一个直角三角形ABC中，∠C是直角，AC=6，BC=8，求斜边AB的长度。

解题思路：根据勾股定理，直角三角形的斜边的平方等于两直角边的平方和。

答案：根据勾股定理，\( AB^2 = AC^2 + BC^2 \)，代入AC=6，BC=8，得到\( AB^2 = 6^2 + 8^2 = 36 + 64 = 100 \)，所以AB = √100 = 10。

题目三：逻辑推理问题题目描述：有5个盒子，每个盒子里装有不同数量的球，分别是1, 2, 3, 4, 5个。

现在将这5个盒子重新排列，使得每个盒子里的球数都比前一个盒子多1个。

问：重新排列后的盒子里球的数量分别是多少？解题思路：由于每个盒子里的球数都比前一个盒子多1个，我们可以从最小的数开始排列，即5, 4, 3, 2, 1。

答案：重新排列后的盒子里球的数量分别是5, 4, 3, 2, 1。

题目四：组合问题题目描述：有红、黄、蓝三种颜色的球各10个，现在要从中选出5个球，求有多少种不同的选法？解题思路：这是一个组合问题，可以使用组合公式\( C(n, k) =\frac{n!}{k!(n-k)!} \)来计算，其中n是总数，k是选出的数量。

答案：首先考虑不考虑颜色的情况下，从30个球中选出5个球的组合数为\( C(30, 5) \)。

◆ 熟悉排列与组合问题。

◆ 运用加法原理和乘法原理解决问题。

在日常生活中我们经常会遇到像下面这样的两类问题：问题一：从A 地道B 地，可以乘火车，也可以乘汽车或乘轮船。

一天中，火车有4班，汽车有3班，轮船有2班。

那么从A 地道B 地共有多少种不同的走法？问题二：从甲村到乙村有两条道路，从乙村去丙村有3条道路（如下图）。

从甲村经乙村去丙村，共有多少种不同的走法？解决上述两类问题就是运用加法原理和乘法原理。

➢ 加法原理：为了完成一件事，有几类方法。

第一类方法中有1m 种不同的方法，第二类方法中有2m 种不同的方法…….第n 类方法中有n m 种不同的方法。

那么，完成这件事共有12n N m m m =++⋅⋅⋅+种不同的方法。

➢ 乘法原理：为了完成一件事，需要n 个步骤。

做第一步有1m 种不同的方法，做第二步有2m 种不同的方法……做第n 步有n m 种不同的方法。

那么，完成这件事共有12n N m m m =⨯⨯⋅⋅⋅⨯种不同的方法。

【例题1】每天从武汉到北京去，有4班火车，2班飞机，1班汽车。

请问：每天从武汉到北京去，乘坐这些交通工具共有多少种不同的走法？解:4+2+1=7(种)【拓展1】学校开展读书竞赛活动，小明要从4本故事书、2本文艺书、3本科技书里任意选取一本书，共有多少种不同的选法?第4讲 排列与组合【例题2】如图，从家村去乙村有3条道路，从乙村去丙村有2条道路，从丙村去丁村有4条道路。

小华从甲村经乙村、丙村去丁村，共有多少种不同的走法？【拓展2】（2008年第六届“走进美妙的数学花园”中国青少年解题技能展示大赛试题）在右图的每个方格中各放1枚围棋子（黑子或白子），共有多少种不同的放法？【例题3】数学活动课上，张老师要求同学们用0、1、2、3这四个数字组成三位数，请问：（1）可以组成多少个没有重复数字的三位数？（2）可以组成多少个不相等的三位数？解：（１）3×3×2=18（个）（3）3×4×4=48（个）【拓展3】用1、2、3、4这四个数可以组成多少个没有重复数字的四位数?【例题4】十把钥匙开十把锁。

六年级奥数题及答案-为什么最后一定得到9呢？
今天小编为六年级的同学准备了一道奥数应用题，大家要仔细对待这道锻炼逻辑思维能力的应用题。

下面就开始六年级奥数题及答案：C=9
任意写一个4位数，例如1996。

把这个数乘以3456，乘积记为A：A= 1996×3456=6898176。

然后把A的各位数字相加，得到的数记为B：B=6+8+9+8+1+7+6=45。

最后再把B的各位数字相加，得到的数记为C：C=4+5=9。

如果有好几位朋友在一起，可以请朋友们各写各的4位数，各算各的A、B、C，算完以后，大家凑在一起对答数。

只要计算正确，不管当初写的4位数是什么，最后答数一定是C=9。

为什么最后一定得到9呢?
解答：因为最初求A时，总是乘以3456。

在这里，3456是9的倍数。

所以A是9的倍数。

如果一个数是9的倍数，那么它的各位数字的和也是9的倍数。

所以B也是9的倍数。

同理C，也是9的倍数。

A是两个4位数的乘积，所以A至多是8位数。

A的各位数字相加，不会大于 8个9的和，所以B值不超过72。

B又是9的倍数，所以B 的数字的和等于9，也就是C=9。

三、课堂达标检测1.甲、乙、丙、丁与小军五人参加围棋比赛，每两人都要比赛一盘，到现在为止，甲已经赛了四盘，乙赛了三盘，丙赛了两盘，丁赛了一盘，小军赛了多少盘？答案：22.数学竞赛后，小明、小华和小强各获得一枚奖牌，其中一人得金牌，一人得银牌，一人得铜牌老师猜测：“小明得金牌，小华不得金牌，小强不得铜牌”结果老师只猜对了一个，那么谁得金牌，谁得银牌，谁得铜牌？答案：小华得金牌，小强得银牌，小明得铜牌一、专题精讲A班人数比B班的人数多；C班人数比D班人数多，比E班人数少；D班人数比B班人数多；E班人数比A班人数少。

请把这五个班的人数按从多到少的顺序排列起来。

1、A，E，C，D，B现有红、黄、蓝、白、紫五种颜色的珠子各一颗，用纸包着，在桌子上排成一行，由甲、乙、丙、丁、戊五人，猜各包内珠子的颜色，每人只许猜两包甲猜：第二包是紫的，第三包是黄的；乙猜：第二包是蓝的，第四包是红的；丙猜：第一包是红的，第五包是白的；丁猜：第三包是蓝的，第四包是白的；戊猜：第二包是黄的，第五包足紫的；然后打开纸包，发现每人都只猜对了一包，并且每包都只有一人猜对，问他们各猜对的是哪一种颜色的珠子？2．甲黄，乙蓝、丙红、丁白、戊紫在一桩谋杀案中，有两个嫌疑犯甲和乙，另有四个证人正在受到询问：第一个证人说：“我只知道甲是无罪的。

”第二个证人说：“我只知道乙是无罪的。

”第三个证人说：“前面两个证词中至少有一个是真的。

”第四个证人说；“我可以肯定第三个证人的证词是假的。

”通过调查研究，已证实第四个证人说了实话，请你分析一下，凶手是谁？3、甲和乙都是凶手二、专题过关某宾馆二楼住着六位旅客．姓张、王、李的三位是会议代表，一个是科学家，一个是技术员，一个是记者，另外三位是出差的旅客，分别来自北京、上海、广州，他们的姓也是张、王、李，服务员介绍的情况是：(1)姓李的旅客从北京来；(2)技术员在广州的一家工厂工作；(3)姓王的旅客说话结结巴巴；(4)与技术员同姓的旅客来自上海；(5)技术员与职业是教师的那位旅客从同一地方来；(6)姓张的代表打羽毛球时，总是输给记者请判断他们六人各姓什么。

六年级中的奥数题及答案奥数，即奥林匹克数学竞赛，是一种旨在培养学生数学思维和解决问题能力的竞赛形式。

以下是一些适合六年级学生的奥数题目及对应的答案：# 题目1：数字问题一个数字，它加上100后是一个完全平方数，它加上129后也是一个完全平方数。

这个数字是多少？答案：设这个数字为 \( x \)。

根据题意，我们有：\[ x + 100 = a^2 \]\[ x + 129 = b^2 \]其中 \( a \) 和 \( b \) 是整数。

两式相减，得到：\[ b^2 - a^2 = 29 \]由于 \( b^2 - a^2 \) 可以分解为 \( (b - a)(b + a) \)，所以\( b - a \) 和 \( b + a \) 都是29的因数。

29是质数，所以 \( b - a \) 只能是1，那么 \( b + a \) 就是29。

解得 \( b = 15 \)，\( a = 14 \)。

因此：\[ x = b^2 - 129 = 15^2 - 129 = 225 - 129 = 96 \]# 题目2：几何问题一个直角三角形的两条直角边分别为3厘米和4厘米，求斜边的长度。

答案：根据勾股定理，直角三角形的斜边长度 \( c \) 可以通过以下公式计算：\[ c = \sqrt{a^2 + b^2} \]其中 \( a \) 和 \( b \) 是直角边的长度。

代入数值：\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]所以斜边长度为5厘米。

# 题目3：逻辑问题一个班级里有学生喜欢数学、科学和历史。

如果喜欢数学的学生中有一半也喜欢科学，喜欢科学的所有学生都喜欢历史，那么如果一个学生喜欢历史，他一定也喜欢数学吗？答案：不一定。

根据题目描述，我们可以得出以下关系：- 喜欢数学的学生中有一半也喜欢科学。

- 喜欢科学的所有学生都喜欢历史。

奥数的七大模块包括：计算、数论、几何、行程、应用题、计数和杂题模块一：计算模块1、速算与巧算2、分数小数四则混合运算及繁分数运算3、循环小数化分数与混合运算4、等差及等比数列5、计算公式综合6、分数计算技巧之裂项、换元、通项归纳7、比较与估算8、定义新运算9、解方程模块二：数论模块1、质数与合数2、因数与倍数3、数的整除特征及整除性质4、位值原理5、余数的性质6、同余问题7、中国剩余定理（逐级满足法）8、完全平方数9、奇偶分析10、不定方程11、进制问题12、最值问题模块三：几何模块（一）直线型1、长度与角度2、格点与割补3、三角形等积变换与一半模型4、勾股定理与弦图5、五大模型（二）曲线型1、圆与扇形的周长与面积2、图形旋转扫过的面积问题（三）立体几何1、立体图形的面积与体积2、平面图形旋转成的立体图形问题3、平面展开图4、液体浸物问题模块四：行程模块1、简单相遇与追及问题2、环形跑道问题3、流水行船问题4、火车过桥问题5、电梯问题6、发车间隔问题7、接送问题8、时钟问题9、多人相遇与追及问题10、多次相遇追及问题11、方程与比例法解行程问题模块五：应用题模块1、列方程解应用题2、分数、百分数应用题3、比例应用题4、工程问题5、浓度问题6、经济问题7、牛吃草问题模块六：计数模块1、枚举法之分类枚举、标数法、树形图法2、分类枚举之整体法、对应法、排除法3、加乘原理4、排列组合5、容斥原理6、抽屉原理7、归纳与递推8、几何计数9、数论计数模块七：杂题1、从简单情况入手2、对应与转化思想3、从反面与从特殊情况入手思想4、染色与覆盖5、游戏与对策6、体育比赛问题7、逻辑推理问题8、数字谜9、数独。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

5-1-1-2.算式谜（二）教学目标数字谜从形式上可以分为横式数字谜与竖式数字谜，从运算法则上可以分为加减乘除四种形式的数字谜。

横式与竖式亦可以互相转换，本讲中将主要介绍数字谜的一般解题技巧。

主要横式数字谜问题，因此，会需要利用数论的简单奇偶性等知识解决数字谜问题知识点拨一、基本概念填算符：指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。

算符：指 +、-、×、÷、（）、[]、｛｝。

二、解决巧填算符的基本方法（1）凑数法：根据所给的数，凑出一个与结果比较接近的数，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。

（2）逆推法：常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。

三、奇数和偶数的简单性质（一）定义：整数可以分为奇数和偶数两类（1）我们把1，3，5，7，9和个位数字是1，3，5，7，9的数叫奇数.（2）把0，2，4，6，8和个位数是0，2，4，6，8的数叫偶数.（二）性质：①奇数≠偶数.②整数的加法有以下性质：奇数+奇数=偶数；奇数+偶数=奇数；偶数+偶数=偶数.③整数的减法有以下性质：奇数-奇数=偶数；奇数-偶数=奇数；偶数-奇数=奇数；偶数-偶数=偶数.④整数的乘法有以下性质：奇数×奇数=奇数；奇数×偶数=偶数；偶数×偶数=偶数.例题精讲模块一、填横式数字谜【例 1】 将数字1~9填入下面方框，每个数字恰用一次，使得下列等式成立；()200724=+÷+-★□□□□□□□现在“2”、“4”已经填入，当把其它数字都填入后，算式中唯一的减数（★处）是 ．【考点】填横式数字谜之复杂的横式数字谜 【难度】4星 【题型】填空 【关键词】迎春杯，高年级，初赛，3试题 【解析】 方法一：首先可以估算四位数的取值范围：四位数不大于()2007913428010+-⨯-=，不小于()2007198427638+-⨯-=．显然四位数的千位数字只能是7．再由四位数与2的和能被4整除，可以确定四位数的个位数字一定是偶数，只能是6或8．若为6，由个位是8而能被4整除的数其十位数字是偶数，可知四位数只能为7986，而()7986241997+÷=，故只需利用剩下的数凑出10即可．剩下的数字是1，3，5，不能凑出10．所以四位数的个位数字不是6．四位数的个位数字是8时，由个位是0而能被4整除的数其十位数字是偶数，故四位数的十位数字是1、3、7或9．当四位数的十位数字是1时，四位数只可能是7918，而()7918241980+÷=，故只需利用剩下的数凑出27即可．剩下的数字是3，5，6，不能凑出27；当四位数的十位数字是3时，四位数只可能是7938，而()7938241985+÷=，故只需利用用剩下的数凑出22即可．剩下的数字是1，5，6，不能凑出22；当四位数的十位数字是5时，四位数只可能是7658或7958，若为7958，则由()7958241990+÷=，需利用剩下的数凑出17即可．剩下的数字是1，3，6，不能凑出17；若为7658，有()7658249312007+÷+-=；当四位数的十位数字是9时，四位数只可能是7698，而()7968241925+÷=，故只需利用剩下的数凑出82即可．剩下的数字是3，5，6，不能凑出82；故此题只有惟一答案：()7658249312007+÷+-=．算式中唯一的减数是1．方法二：根据弃九法，7□□□+2+4+□□+★被9整除，而(7□□□+2)÷4+□□-★也被9整除。