大学物理实验 g不确定度计算

物理实验中的不确定度及其在声速测量过程的应用不确定度;声速;物理实验中圈分类号:O241.1文献标识码:A1不确定度的概述不确定度是表示由于测量误差的存在而对被测量值不能确定的程度,它反映了可能存在的误差分布范围.它与给定的置信概率相联系,并且可求出其确定位.不确定度的大小反映了测量结果的可信赖程度,不确定度小的测量结果可信赖程度高,反之则低.2不确定度的分类不确定度按其数值的评定分为两类,分别为A类不确定度和B类不确定度.凡是经过多次测量后,用统计方法求出的不确定度为A类不确定度,而由非统计方法求出的不确定度为B类不确定度.在相同测量条件下,当对某一物理量进行,1次测量时得一测量列I,2,……,其最佳值为算术平均值,即:=-=.1∑(1)的标准估计值的贝赛尔公式为=算术平均值X的标准差估计值为=上式算术平均值的标准差即为A类标准不确定度.当测量次数,l≥5时,可认为其置信概率为P=68.3%(国际标准推荐) 收稿日期:2OO5—09—20(2)(3)一7l一对于类不确定度,在测量范围内无法用统计办法评定,则采用不确定度也需要由各直接测量量的不确定度通过传递公式计算出来.设间接测量量与直接测量量间的关系为Y=Xl,X2,……)则间接测量量Y的标准不确定度为=其中毛为各相互独立的直接测量量,u为各直接测量量的标准不确定度.测量结果的表达式应Y=Y-4-￡,,3应用实例(7)声波在空气中的速度—,其中为声波波长,为声波频率.声波频率f由低频信号发生器直接读出,声波波长由实验测得.测量声波波长的方法是用超声波干涉即驻波法进行测量,这种方法是通过发射传感器与接收传感器探头之间的距离改变一定数值后,记录下这一过程中声波波形变化的周期数,再利用公式=,求出波长‘,’r=.由上式知,是L的间接测量量,是的间接测量量,而￡是直接测量量.具体数据见表1.表1实验数据表==2L=×41820:346804(mms_1):346.80(ms-*)由方差合成原理求的不确定度计算公式,由()=(a△Lt,32+()一72—,可得.=两△￡的A类不确定度△工.:——AL,_ALp.√婴:=垫:垡2:±.重E戛耍巫巫Ys(5一I)=0.019(mm)△￡的类不确定度△===..0058(一),△倪为螺旋测徽仪的仪器精度△￡的总不确定度△工√(o’zx工1)+(△n)4o.o192+0.0058:0.019(ram)输出频率,的不确定度zxf=5X10～X41820—4Hz,这里.仪器输出频率为418201~则::3Hz‘33速度的合成标准不确定度O”u=c,√)+)2=0.4(瞄-Ir￡,=(346.8±0.4),一’则测量结果可表示为:{一E(￡,):or,=0.1%◆考文■【1】刘志t.不确定原理.中国计量出版社.1993[2】刘才明.大学物理实验中测量不确定度的评定与表示大学物理.199”/UNCERTAINTY ANDITSSONICSPEEn TESTINGPROCESSAPPLICA TIONINPHYSICAlEXPERImeNTl(IngWeifangXueY uchun(N,mhe~ElectricPowerInmitme.JiIjn.132012)Act:11liI_…cleilllrodt~essystemoti~y?inthephy.icIl戗p.峨ertIinty.whichi.-pIllied.olbelyppIlysicIl”喇mthe.onic’peeding?Theimp~eeuneemin~yindataplo 嘲?jnsiIlnle矗pefi.meriti8shown.Keywords:uncerl~y;mnlcspeed;physical矗pefi删一73—。

液体粘滞系数的不确定度的计算杨阳（02008208）（东南大学机械工程学院南京 211189）摘要：在液体粘滞系数实验数据的处理中，本文利用微分法求解其不确定度，并比较各个变量对实验结果影响的大小。

关键词：液体粘滞系数数据处理不确定度The Calculation of Uncertainty of Liquid viscosityYangYang(School of Mechanical Engineering, Southeast University, Nanjing ,211189)Abstract: In the data processing of measurement of liquid viscosity, differential analysis was used to the calculation of uncertainty of liquid viscosity. The influence of the variable quantities were compared .key words: Uncertainty of Liquid viscosity Data processing of experiment The Calculation测定液体粘滞系数实验需要测定若干物理量，但测定之前并不知道哪些数据测定时需要特别注意精度。

本文通过对液体粘滞系数不确定度公式的推导，进而数据处理，得到各组物理量对实验结果的影响大小。

对以后的实验操作具有一定的指导意义。

在物理实验中或其它实验数据的处理中，考虑到不确定度的统计性质，间接测量量不确定度用方和根形式。

[1]本文使用估算间接测得量的误差的基本方法——微分法直接求得不确定度。

作者简介：杨阳,1990年，男，本科生,uu1990718@ 1.实验原理[2]根据斯托克斯定律，光滑的小球在无限广延的液体中运动时，当液体的粘滞性较大，小球的半径很小，且在运动中不产生旋涡，那么小球所受到的粘滞阻力f为vdfπη3-=（1）式中d是小球的直径，v是小球的速度，η为液体粘滞系数。

主尺
粗动手轮读数窗口
微动手轮
最后读数为：33.52246mm
（3）沿原先转动方向继续转动微调手轮，记下条 纹中心亮暗每变化25个周期对应的读数d，用逐差 法求激光波长。
注意:计算不确定度时,只计算A类分量(课本 第6页公式3）
注意事项
1、 调节平面镜后的螺丝时，不可太用力，以免螺丝滑扣； 2、 转动微调手轮时，动作要轻，不要碰撞桌面，以免影响
b.置上观察屏，调节M2的水平及垂直拉 簧，使条纹中心在视场中央。
实验现象
2、测氦氖激光的波长
（1）向同方向转动微调手轮，使条纹连续从中央 冒出（或向中央陷入），此时可开始读数；
（2）先记下M1初始读数d0，（导轨侧面主尺读出 整mm数；读数窗读出0.××mm；手轮估读到 0.00×××mm，三者相加）
他人实验； 3、 观察两组激光点时，要准确判断各自的最亮点，调节平
面镜后的螺丝使各自对应的光点重合； 4、 测量过程中，手轮的转动方向要始终一致，以免产生回
程差，影响测量结果。 5、 在数条纹中心亮暗变化周期时，可能会让眼睛产生疲劳，
在读数过程中要让眼睛适当休息，避免数错亮暗变化周 期； 6、 过读在几数第十误一圈差次，。记让录齿M1镜轮的、初精始密位螺置杆前充，分要咬让合微，调以手免轮M1镜预位先置转了解迈克尔逊干涉仪的结构，学习调 节和使用方法。
利用点光源产生的同心圆环干涉条纹 测量单色光的波长。
实验原理
• 实验背景、仪器构造及光路
d
M1
迈
1
M2'
克 尔
逊
干
激光器
S
G1 G2
涉 仪 光
路
2
原
半反射层K
1

的关系：
k
PC
( x)dx
k
p(x)
P1
(x)dx 68.3%
1.96
P2
(x)dx 95%
1.96
3
P3
(x)dx 99.7%
3
-σ 0 σ
x
偶然误差的处理方法
假定系统误差已消除，对同一个物理量进行n次测量，测得
的值为xi (i =1, 2，…，n) n
(1) 用多次测量的算术平均值作为x0的估计值：x ( xi ) / n i 1
1
n(n 1)
n i 1
( xi
x)2
e 3
● 由A、 B合成总不确定度u : u ΔA2 ΔB2
● 给出直接测量的最后结果：
x E
xu u 100%
x
例：用一级螺旋测微计测某一圆柱体的直径d共6次，测量值如下表：
i
1
2
3
4
5
Di /mm 8.345 8.348 8.344 8.343 8.347
(2) 用算术平均值的标准差 x 作为 的估计值
按贝塞耳公式求出：
测量结果可以表述为：
x
Y xx
1
n(n 1)
n i1
(xi
x)2
不确定度
•为了估计测量结果的可靠程度，测量结果应写成
Y N N
•不确定度 ΔN 是概率意义上对测量结果精确程度的评价。
•表示测量结果是一个范围 N N, N N
•它表示待测物理量的真值有一定的概率落在上述范围内
（关键是找出 置信区间与置信概率的关系）
若置信概率为100%，则相应的 N 就称为极限误差，
用 e 表示，写作： Y N e

对物理量X做n 次等精度测量，得到包含n个测 量值x1 ，x2 ， x3 …， xn的一个测量列
最佳值（真值)
1 n x xi n i 1
标准差σ：

x
n i 1
i
x

2
n(n 1)
粗大误差
由于观测者未正确地使用仪器、观察错 误或记录错数据等不正常情况下引起的 误差。应将其剔除。
2.2、B类标准不确定度 基础物理实验中，因缺乏必须的信息和 资料，作为简化处理 主要考虑仪器误差。
1）用概率分布估算 u B u仪 k 仪 k p 仪 p C 3
Δ仪: 仪器的最大允许误差 kp：置信因子 ，与置信概率P有关(P=0.68 kp=1)
C：置信系数，与误差分布特性有关
示波器的调节和使用 多功能摆的设计与研究 分光计的调整与折射率测定 密立根油滴实验 超声声速的测量 电子元件伏安特性的测量
直流电桥及其应用
第一册
科技楼北楼
104、105
霍尔效应与应用设计
第一册
科技楼北楼
211、214
由于设备更新，5、6、7三个实验与书 上有些差别，为了方便同学们写预习报告和 实验，在网上挂有电子版讲义。 IP:218.199.86.171/bbs
例：测量某物体长度
ｎ
1 2 3 4 5 6 7 8 9
ｂｍｍ
42.35 42.45 42.37 42.33
42.30 42.40 42.48 42.35 42.49
1 长度的最佳值： b bi ＝42.369 mm 9 i 1
9


i 1
9
xi
42.369 9 1
2

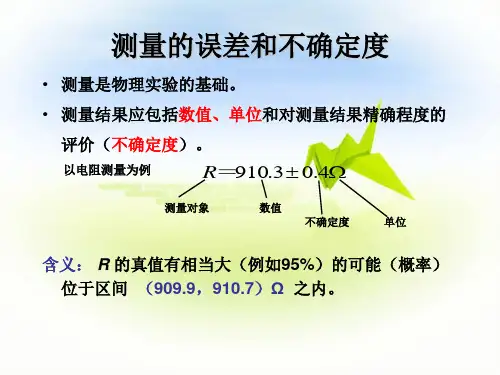
物理实验中的不确定度简化计算陈玉林 ，徐 飞，刘彦力（南京信息工程大学物理实验教学中心，江苏 南京 210044）摘 要：为本文以《JJF1059—1999测量不确定度评定与表示》为基础，阐述了测量不确定度评定的简化计算，并给出了测量不确定度评定的结果表示。

关键词：不确定度；标准偏差；置信概率我国计量科学研究院于l999年经国家质量技术监督局批准，发布了《JJF1059—1999测量不确定度评定与表示》（以下简称《评定与表示》）的中国国家计量技术规范，明确提出了测量结果的最终形式要用不确定度来进行评定与表示，由此不确定度在我国开始进入推广使用阶段[1]。

近几年来，很多院校已在物理实验教学中采用不确定度来评定实验结果，但许多教材关于不确定度的评定方法和测量结果的表示不统一，学生的疑问也较多，但最新的《评定与表示》关于不确定度的计算对物理实验的初学者来说又显得十分复杂。

本文根据各兄弟院校教材和《评定与表示》的精神，结合多年物理实验教学实践，讨论测量不确定度评定的简化计算。

1 测量不确定度的基本概念1.1 测量不确定度的定义测量不确定度（简称不确定度），从词义上理解，意味着对测量结果有效性的可疑程度或不肯定程度。

从传统上理解，它是被测量真值所处范围的估计值。

但是真值作为一个理想化的概念，实际上往往是难以操作的或是未知量，而可以具体操作的则是测量结果的变化。

因此，现代的测量不确定度按《评定与表示》被定义为：“表征合理地赋予被测量之值的分散性、与测量结果相联系的参数”[2]。

在测量结果的完整表述中，应包括测量不确定度。

测量不确定度如误差有系统误差、随机误差等一样，也由多个分量组成，并且这些分量可用统计方法、概率分布、经验判断等来评定，为一个正值。

或者说不确定度是一种表征被测量值所处范围的评定，真值以一定置信概率落在测量平均值附近的一个范围内。

即 u x x ±=（置信概率P ），u 为测量不确定度，区间) ,(u x u x +-称置信区间。

0下载券文档一键搜索 VIP用户可在搜索时使用专有高级功能：一键搜索0下载券文档，下载券不够用不再有压力！
内容特 无限次复制特权 权 文档格式转换
VIP有效期内可以无限次复制文档内容，不用下载即可获取文档内容 VIP有效期内可以将PDF文档转换成word或ppt格式，一键转换，轻松编辑！
阅读页去广告
量结果的最后一位应与不确定度的最后一位对齐 ，后面的数按“四舍六入五凑偶”的法则取舍。 例 3.相对不确定度可以取两位。 4.不确定度截取剩余尾数一律采取进位法处理
北方民族大学物理实验中心 Fundamental physics experiment 9
1. D 5.604cm D 0.2cm D 5.6 0.2cm
二.直接测量结果的不确定度评定
将测量得到的数据整理、计算得出有关 结果,并对结果的好坏作出客观地评价。数据 处理是整个实验中一个关键环节。
北方民族大学物理实验中心 Fundamental physics experiment 7
1、合成不确定度
u(x)
u
2 AΒιβλιοθήκη uB2(k 1)＊各不确定度相互独立
例：求y=3C-4D的不确定度 解： dy=3(dC)-4(dD) U y (3UC )2 (4UD )2 9UC2 16UD2
北方民族大学物理实验中心 Fundamental physics experiment 20
对于以乘、除运算为主的函数
取 对 数 ln N ln f x, y, z,
再微分 dN ln f dx ln f dy ln f dz
N x
y
z
以微小量替换微元
N ln f x ln f y ln f z
N x

大学物理实验中测量不确定度的评定方法大学物理实验是科学证明的关键，因此对实验结果的准确性和可靠性要求至关重要。

实验结果的不确定度是检验实验结果的一种重要指标，它反映了实验的可重复性和有效性。

因此，不确定度的评定是大学物理实验中的重要内容。

不确定度的评定由两个主要步骤组成：测量不确定度的衡量原理和评估不确定度的方法。

在理论上，对实验结果的测量不确定度衡量原理应具有舍入误差、限制实验精度、可重复性误差、有限性测量原理、数据处理原理五个基本原理。

在实操中，评估不确定度的方法应根据不确定度的评估模型，分别采用测量不确定度、可重复性误差、舍入误差、有限性测量和可能的数据处理误差。

首先，对实验结果的不确定度进行测量。

实验中应尽量采取有效措施减少误差，进行可靠的数据测量，并正确记录测量结果，以确定实验的准确性和可靠性。

其次，进行可重复性误差的评估。

在实验中，实验者应重复测量多次，得出稳定的结果后，计算实验结果的可重复性误差。

再次，对舍入误差进行评估。

实验过程中，数据测量值应尽可能准确，但实际数值不一定是很精确的，应根据实际情况舍入，并考虑舍入的真实影响。

第四，执行有限性测量，即考虑实验测量设备和仪器的性能范围，根据测量设备性能，对实验结果进行准确和正确的评估。

最后，根据可能会发生的数据处理误差和统计误差，进行数据处理。

由于数据处理错误可能是实验失误的主要原因，因此，实验者应采取有效措施避免出现数据处理错误，影响实验结果的正确性。

实验结果的不确定度是检验实验结果的重要指标，对大学物理实验的准确性和可靠性具有重要意义。

大学物理实验中测量不确定度的评定方法，其基本流程是以理论指导为基础，采取测量不确定度、可重复性误差、舍入误差、有限性测量和可能的数据处理误差，用有效方法检验实验结果，以保证实验结果的准确性和可靠性。

大学物理实验中测量不确定度的评定方法
在大学物理实验中，测量不确定度是一项重要的任务。

不确定度
的评定方法在测量精度和准确度评估中起着至关重要的作用，以便识
别物理实验数据中的任何可能源导致的误差。

测量不确定度的评定，
可归纳为两个步骤：步骤一，识别影响测量结果的因素；步骤二，应
用不同方法子测量不确定度。

首先，确定可能影响测量结果的因素是评估不确定度的关键。

不
同的物理实验可能存在不同的变量，需要分析和识别的变量可以是无
量纲变量，比如电流、电压、时间间隔以及定量变量，如温度、湿度、压力等。

通过分析实验中所有可能影响结果的变量，可以找出误差的
源头，有助于提高测量精度。

其次，在确定影响测量结果的变量的基础上，可以采用不同的方
法来评估不确定度，并可以尝试多种评估方法，以更准确地衡量不确
定程度。

比如，可以分析设备的精度，采用估算的统计方法，以及采
用假设检验。

这些方法的使用可能会受到实验条件的限制，但是，一
旦选定了合适的方法，就可以得到非常准确的反馈，有助于准确衡量
物理实验中的不确定度。

总之，大学物理实验中测量不确定度的评定方法，主要有：识别
影响结果的变量，以及确定的基础上，选择合适的测量方法衡量不确
定程度。

只有经过科学的分析和准确的测量，才能准确衡量物理实验
数据中的不确定度。

一、实验名称：单摆法测重力加速度二、实验的目的：1、掌握游标卡尺读数原理；2、掌握电子秒表的使用方法；3．掌握单摆法测量重力加速度的方法；三、实验仪器：单摆仪、游标卡尺、螺旋测微计、米尺、秒表四、实验原理：单摆的一级近似的周期公式为:由此通过测量周期T，摆长，可求重力加速度g五、实验内容和步骤1. 用游标卡尺测量摆球的直径将摆球放到游标卡尺上，移动游标直至卡紧摆球，锁紧游标，先读出主尺读数，再读出副尺读数。

取下小球，按照上述步骤重复测量多次。

2. 用米尺测量摆线的长度将米尺的零刻度线对准摆线的一段，并且令米尺与摆线保持平行，读出结果。

取下摆线，按照上述步骤重复测量多次。

3. 用电子秒表测量单摆的周期将摆球上拉到一定高度（不超过5度）后静止放下，等到摆球上升到某个周期的最高点时开始计时，计时若干个周期后（N>=10）结束计时。

让摆球停止摆动，按照上述步骤重复测量多次。

（要减去共计0.2s的人类反应时间）六、实验数据记录与处理1、用游标卡尺测量摆球的直径d测量次数 1 2 3 4 5 6 平均值不确定度直径d（mm）20.62 20.6220.620.620.620.60 20.61 0.02摆球直径d的测量结果表示为: 20.61+-0.022、用米尺测量摆线的长度l（只测一次）： 700.0mm摆线的长度l的测量结果表示为: 700+-1mm3、单摆的摆长为：700+20.61/2=710.305mm单摆摆长的测量结果表示为：L710.30+-1.024、用电子秒表测量单摆摆动10个周期的时间t测量次数 1 2 3 4 5 6 平均值不确定度t（s）17.22 17.2317.2317.3117.1917.23 17.24 0.02单摆的周期： 1.724单摆的不确度：0.002单摆周期的测量结果表示为：T 1.724+-0.002 5、计算和不确定度955.9pi^2mm/s^2重力加速度的不确定度： 2.61重力加速度的测量结果表示为：g955.9pi^2+-2.6mm/s^2七、误差分析与讨论1、米尺测量摆线长度时要注意与摆线尽量靠近且保持平行，还要注意摆线要拉直。

分类号密级U D C 编号本科毕业论文(设计)题目测重力加速度的几种方法比较及误差分析系别专业名称物理学年级学生姓名学号指导教师二00 八年五月摘要：地球表面及附近的物体受到地球重力的作用，如果忽略空气摩擦的影响，则所有落地物体都将以同一加速度下落，这个加速度称为重力加速度。

重力加速度是一个重要的地球物理常数，准确测定它的量值，不仅在理论上，而且在生产上、科研上都有着极其重要的意义。

在实验室内测量重力加速度的方法有很多种。

本文利用实验室的仪器，通过单摆法、电磁打点计时器法、倾斜气垫导轨法以及复摆法进行测量重力加速度的实验。

通过实验原理、实验方法、实验记录数据、误差分析、最终结果等方面进行比较与研究，针对可能造成较大误差的变量，提出可实施的改进办法，提高实验测量值的可靠性。

关键词：重力加速度单摆电磁打点计时器气垫导轨复摆Abstract: On Earth, everything feels the downward force of gravity. If we neglect the friction force of the air, all the masses will be falling freely with the same downward acceleration because gravity is the only force acting. This is the acceleration of free fall. The constant acceleration, g, is very important. Measuring exactly plays a significant role in theory, production and scientific research. There are many methods for measuring g in laboratories. The major content about this thesis is doing experiments through using the simple pendulum, the electromagnetic pointing set, the sloping air track and the compound pendulum. Then compare the principle, method or result of the four experiments and analyze the error. At the end, suggest practicable and improvable measures in accordance with the larger error for raising accuracy.Key words: acceleration of gravity simple pendulum electromagnetic pointing set air track compound pendulum文献综述一、概述测量重力加速度的方法有很多种，包括用单摆测重力加速度、用电磁打点计时器测重力加速度、用自由落体法测重力加速度、用复摆测重力加速度、用凯特摆测重力加速度、倾斜气垫导轨上测重力加速度以及频闪照相法测重力加速度等。

出的
,
取 其最 小分 度值 为该直 尺 的误差 极 限
,
。
以伏 安
法 测 电阻 实验 所 测量 得 到 的 实验 数 据进 行说 明 图 关系图
。
是 根 据表
伏 安法 测 电 阻 的 数据 表格 作
作者 简介
范士 民
大 学物 理 实验
一
,
男
一
,
实验 师
,
享 阳 师 范 学 院 物 理 与 电 子 科 学学 院 研 究 方 向
・
・
” “
,
电流
的不 确定 度
声,
声又
,
根 据 电压 电流 求得 的相 应 的不 确 定度
可 以计 算 出 电阻
的不 确定度
一
一
第六 居 全 目 龙等 李谈 物 搜 实 脸 教 李研 衬 奋伦 大 票
产,
・
下
红
产
一
、
,
。
测 量 结果 的 正 确表 述
士产
. 士 0 4 6 ) x l o ’( 。 )
k
(
。)
. 4 2 逐 差 法不 确定 度 的 评定
结 合相 关系 数 r 的 表 达 式
,
可 以求 出相 应 的
. 声 (k ) = 2 9 4 6 x 10
r = 0 9993365 .
一,
(
。
一
,
)
一 117一
第六 居 令 田 龙等 嵘教 物 理 实 脸 散 学研 付 套伦 文 集 ( 下 )
第六 居 个 日 龙等 檬谈 物 理 实脸教 檬研 讨 套伦 次 集
下
常用 三 种 方 法 处 理 实验 数 据 结 果 的 不 确 定 度 评定

2020/3/12
大学物理实验中心
21
➢计算出平均值和标准偏差
长度A （10-3m）
宽度B （10-3m）
高度C （10-3m）
平均值 14.47 32.65 12.10
标准偏差 0.021 0.024 0.009
2020/3/12
大学物理实验中心
22
➢计算出不确定度
2020/3/12
UA
UB
U
UmA Sm 0.93Sm 0.032g n
UmB 0.04g
Um
U2 mA
U2
mB
0.051g
m m Um
=50.550.05 g
2020/3/12
大学物理实验中心
25
间接测量结果的不确定度的估 计
如果w = f ( x , y , z , )， 而x , y , z , 是彼此独立的直接测量，则总不确定度
2020/3/12
大学物理实验中心
17
直接测量结果的不确定度估计
直接测量结果的不确定度是A、B两类分量用方和根合成
A类不确定度分量 UA （统计方法评定），由标准偏差S乘以概率为0.95时的t因子得 到，
大学物理实验中心
18
直接测量结果的不确定度估计
B类不确定度分量 （根据经验和其它信息评估）
只考虑测量仪器误差或者测试条件不符合要求而引起的附加误差所带来的B类分量。 记为：UB = ins
2. 测量结果的末位数字（欠准数）与不确定度的 数字对齐；不确定度的首数字较小为1，2时， 建议取两位有效数字；在运算的中间过程，结果 一般可多保留 一位数字
大学物理实验中心
37
有效数字的正确使用 3. 数字前面的0只是表示小数点的位置，而非有效数字， 数字后面的0是有效数字, 表示测量的误差位,不能 随意舍去

单摆、复摆法测重⼒加速度⼤学物理实验⼀、复摆法测重⼒加速度⼀.实验⽬得1、了解复摆得物理特性,⽤复摆测定重⼒加速度,2、学会⽤作图法研究问题及处理数据。

⼆.实验原理复摆实验通常⽤于研究周期与摆轴位置得关系,并测定重⼒加速度。

复摆就是⼀刚体绕固定⽔平轴在重⼒作⽤下作微⼩摆动得动⼒运动体系。

如图1,刚体绕固定轴Ｏ在竖直平⾯内作左右摆动，Ｇ就是该物体得质⼼,与轴Ｏ得距离为，为其摆动⾓度。

若规定右转⾓为正,此时刚体所受⼒矩与⾓位移⽅向相反,则有, （1)⼜据转动定律，该复摆⼜有, (2) （为该物体转动惯量) 由（1）与（2）可得，(3）其中。

若很⼩时（在5°以内)近似有, (4)此⽅程说明该复摆在⼩⾓度下作简谐振动，该复摆振动周期为, (5）设为转轴过质⼼且与O轴平⾏时得转动惯量，那么根据平⾏轴定律可知, (6)代⼊上式得， (７）设（６）式中得,代⼊（7）式，得, （1１）ｋ为复摆对G(质⼼)轴得回转半径,h为质⼼到转轴得距离。

对(11)式平⽅则有， (1２）设,则（12)式改写成, (1３)（13）式为直线⽅程,实验中（实验前摆锤A与B已经取下）测出n组（x,y)值，⽤作图法求直线得截距A与斜率B,由于,所以(1４）由（14)式可求得重⼒加速度ｇ与回转半径k。

三.实验所⽤仪器复摆装置、秒表。

四．实验内容1.将复摆悬挂于⽀架⼑⼝上，调节复摆底座得两个旋钮，使复摆与⽴柱对正且平⾏，以使圆孔上沿能与⽀架上得⼑⼝密合。

2.轻轻启动复摆，测摆30个周期得时间、共测六个悬挂点，依次就是：6ｃm ８cm 10cm 1２cm 14cm １6cｍ处。

每个点连测两次,再测时不需重启复摆。

3.启动复摆测量时，摆⾓不能过⼤(＜),摆幅约为⽴柱得宽度。

复摆每次改变⾼度悬挂时，圆孔必须套在⼑⼝得相同位置上.五.实验数据处理1、由 ,分别计算出各个x与y值，填⼊数据表格.2、以x为横坐标，y为纵坐标,⽤坐标纸绘制ｘ—ｙ直线图。

空气中质量 铝片的密度测量 完全侵没水中视重 水的密度
密度ρ = 2.687 g/cm3
密度的不确定度=
1.2E-02 g/cm3
密度结果=
2.69±0.02
测量铝片的数据 天平的仪器误差 铝片的密度计算
19.15 0.025 2.697 确定度=
12.05 0.025
铝的密度测量不
1.000 1.000 铝片的密度测量结果 1.1E-02 2.70.004 0.025
次序 1 2 3 4 5 6
外径D
平均值 标准偏差 平均值标准偏差 A类不确定度 B类不确定度 合成不确定度 测量结果 2. 用游标卡尺和千分尺测量圆柱体的尺寸和密度（单位：mm），用天平测量其质量（单位：g）
29.50 19.62 25.10 29.56 19.70 25.18 29.56 19.68 25.20 29.52 19.68 25.16 29.48 19.72 25.18 29.60 19.64 25.18 29.537 19.673 25.167 4.5E-02 3.7E-02 3.5E-02 1.8E-02 1.5E-02 1.4E-02 4.7E-02 3.9E-02 3.7E-02 2.0E-02 2.0E-02 2.0E-02 5.1E-02 4.4E-02 4.2E-02 29.54±0.05 19.67±0.05 25.17±0.05 21.0±0.1
圆柱体的尺寸数据记录
20.90 21.10 20.94 20.96 21.10 21.04 21.007 8.5E-02 3.5E-02 8.9E-02 2.0E-02 9.2E-02
1 2 3 4 5 6
平均值 标准偏差 平均值标准偏差 A类不确定度 B类不确定度 合成不确定度 测量结果