数学模型第四版课后答案姜启源版

人猫鸡米渡河问题的数学模型(总13页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--人猫鸡米渡河问题的数学模型摘要：人带着猫、鸡、米过河，从左岸到右岸，船除了需要人划之外（船除了要载人外），只能载猫、鸡、米三者之一，而当人不在场时猫要吃鸡、鸡要吃米。

本文将设计一个安全过河方案，使渡河次数尽量地少。

模仿“商人过河”的模型设计出新的数学模型。

关键字：穷举法，Matlab运算求解。

一、问题的提出课本:模仿“商人过河”模型，做下面游戏：人带着猫、鸡、米过河，船除需要人划之外，至多能载猫、鸡、米三者之一，而当人不在场时猫要吃鸡、鸡要吃米。

设计一个过河方案，建立数学模型，并使渡河次数尽量地少。

二、问题的分析因为这是个简单问题，研究对象少，所以可以用穷举法，简单运算即可解题。

此问题是从状态向量A（1,1,1,1）经过奇数次运算向量B变为状态向量A（0,0,0,0）的状态。

转移过程为什么是奇数次？我们注意到过河有两种，奇数次的为从左岸到右岸，而偶数的为右岸回到左岸，因此得到下述转移过程，所以最后应该是过河完成时状态转移数为奇数次。

三、问题的假设：假设船除了载人之外，至多只能载猫、鸡、米三者之一。

：当人不在场时，猫一定会吃鸡、鸡一定会吃米。

四、定义符号说明：我们将人，猫，鸡，米依次用四维向量中的分量表示，当一物在左岸时，相应的分量记为1，在右岸时记为0.如向量（1,0,1,0）表示人和鸡在左岸，猫和米在右岸，并将这些向量称为状态向量。

例如（1,1,1,1）表示它们都在左岸，（0,1,1,0）表示猫，鸡在左岸，人，米在右岸；由于问题中的限制条件，有些状态是允许的，有些状态是不允许的。

凡问题可以允许存在的状态称为可取状态。

A 向量定义为状态变量。

比如()11,0,1,0A 是一个可取状态向量，但()20,0,1,1A 是一个不可取状态向量。

此外，B 向量定义为运载变量。

把每运载一次也用一个四维向量来表示。

综合题目参考答案1. 赛程安排(2002年全国大学生数学建模竞赛D 题)(1)用多种方法都能给出一个达到要求的赛程.(2)用多种方法可以证明支球队“各队每两场比赛最小相隔场次n r 的上界”(如=5时上界为1)是n ⎥⎦⎤⎢⎣⎡-23n ,如: 设赛程中某场比赛是,i j 两队, 队参加的下一场比赛是,两队(≠i i k k j ),要使各队每两场比赛最小相隔场次为r ,则上述两场比赛之间必须有除i ,j ,以外的2k r 支球队参赛,于是,注意到32+≥r n r 为整数即得⎥⎦⎤⎢⎣⎡-≤23n r . (3)用构造性的办法可以证明这个上界是可以达到的,即对任意的编排出达到该上界的赛程.如对于n =8, =9可以得到: n n 1A 2A 3A 4A 5A 6A 7A 8A 每两场比赛相隔场次数 相隔场次总数1A× 1 5 9 13 17 21 25 3,3,3,3,3,3 18 2A 1 × 20 6 23 11 26 16 4,4,4,3,2,2 193A 5 20 × 24 10 27 15 2 2,4,4,4,3,2 19 4A 9 6 24 × 28 24 3 19 2,2,4,4,4,3 19 5A 13 23 10 28 × 4 18 7 2,2,2,4,4,4 18 6A 17 11 27 14 4 × 8 22 3,2,2,2,4,4 177A 21 26 15 3 18 8 × 12 4,3,2,2,2,4 178A25 16 2 19 7 22 12 × 4,4,3,2,2,2 17w w w .k h d a w .c o m 课后答案网1A 2A 3A 4A 5A 6A 7A 8A 9A 每两场比赛相隔场次数 相隔场次总数1A× 36 6 31 11 26 16 21 1 4,4,4,4,4,4,4, 28 2A 36 × 2 27 7 22 12 17 32 4,4,4,4,4,4,3 27 3A 6 2 × 35 15 30 20 25 10 3,3,4,4,4,4,4 26 4A 31 27 35 × 3 18 8 13 234,4,4,4,3,3,3 25 5A 11 7 15 3 × 34 24 29 193,3,3,3,4,4,4 24 6A 26 22 30 18 34 × 4 9 144,4,3,3,3,3 23 7A16 12 20 8 24 4 × 33 28 3,3,3,3,3,3,4 22 8A21 17 25 13 29 9 33 × 53,3,3,3,3,3,3, 21 9A 1 32 10 23 19 14 28 5 × 3,4,3,4,3,4,3 24 可以看到, =8时每两场比赛相隔场次数只有2,3,4, =9时每两场比赛相隔场次数只有3,4,以上结果可以推广,即为偶数时每两场比赛相隔场次数只有n n n 22-n ,12-n ,2n ,n 数时只有为奇23-n ,21-n . 量赛程优劣其他指标如(4)衡的平均相隔场次 记第i 队第j 个ij c ,2,2,1,,,2,1-==n j n i ,间隔场次数为则平均相隔场次为∑∑=n i 1-=n r 21 =-j n n 1)2(ij c r 是赛程整体意义下的指标,它越大越好.可以计算=8,=9的n n r ,并讨论它是否达到上界. 相隔场次的最大偏差 定义||,r c Max f ij j i -=∑---=2)2(|n r n c Max g =1|j ijw w w .k h d a w .c o m 课后答案网f 为整个赛程相隔场次的最大偏差, 为球队之间相隔场次的最大偏差,它们都是越小越好.可以计算=8,=9的,g ,并讨论它是否达到上界.g n n f 参考文献工程数学学报第20卷第5期20032. 影院座位设计建立满意度函数),(βαf ,可以认为α和β无关, ()()βαβαh g f -=),(,g ,取尽量简单的形式,h 如αα=)(g ;0)(=βh (),030≤β0)(h h =β)30(0>β.(1)可将作为必要条件,以030≤βα最大为最佳座位的标准.在上图中以第1排座位为坐标原点建立坐标轴x ,可以得到 ⎪⎭⎫ ⎝⎛+----⎪⎭⎫ ⎝⎛+--=⎪⎭⎫ ⎝⎛+--=d x x h c H d x x c H d x x c H θθαθβtan arctan tan arctan ,tan arctan β是x 的减函数.可得x ≈1.7m,即第3(或4)排处.又通过计算或分析可知030=βα也是x 的减函数,所以第3(或4)排处是最佳座位.(2)设定一个座位间隔(如0.5m), l x 从0(或处)到030≤βd D -按离散,对于计算l )20~0(00θα的平均值,得时其值最大. 020=θ(3)可设地板线是x 的二次曲线,寻求,b 使2bx ax +a α的平均值最大. 实际上,还应考虑前排不应挡住后排的视线. 3.节水洗衣机(1996年全国大学生数学建模竞赛B 题) 该问题不要求对洗衣机的微观机制(物理、化学方面)深入研究,只需要从宏观层次去把握.宏观上洗衣的基本原理是用洗涤剂通过漂洗把吸附在衣物上的污物溶于水中,再脱去污水带走污物;洗衣的过程是通过“加水——漂洗——脱水”程序的反复运行,使残留在衣物的污物越来越少,直到满意的程度;洗涤剂也是不希望留在衣物上的东西,可将“污物”定义为衣物上原有污物与洗涤剂的总和. w w w .k h da w .c o m 课后答案网假设每轮漂洗后污物均匀地溶于水中;每轮脱水后衣物含水量为常数.~初始污水量,第轮加水量,~第k 轮脱水量c 0x ~k u k k x ),,2,1( =k .设每轮脱水前后污物在水中的浓度不变.于是cx c u x u c x n n n =+==--111,,, c x 2c x +21u x 10, 得到)()(210c u c u u c x x n n n ++= . 在最终污物量与初始污物量之比小于给定的清洁度条件下,求各轮加水量,使总用水量最小,即0/x x n k u ),,1(n k =∑=nk k u u Min k 1()ε<++)(..21c u c u u c t s n n 等价于)()(21c u c u u Min n u k +++++ α=++)()(..21c u c u u t s na 为常数可得c u c u u n +==+= 21,即第轮加水量n ~2u u k =(常数),第1轮加水量.c u u +=1令,问题简化为cx u =nx Min u n , ε<⎪⎭⎫ ⎝⎛+n x t s 11.. 其解为,即,而0→x 0→u ∞→n n .这与实际上是不合理的.应该加上对u 的限制:.则得n ,其中 21v u v ≤≤max min n n ≤≤max min n n ≤≤,1+)/1ln(2min ⎥⎦⎤⎢⎣⎡+=c v n αn 这样,为有限的几个数,可一一比较,具体数据计算从略.参考文献:《数学的实践与认识》第27卷第1期,1997w w w .k h d a w .c o m 课后答案网4.教师工资调整方案(1995年美国大学生数学建模竞赛B 题)题目对职称提升年限表述得不甚清楚(如未提及助理教授的提升),教龄也未区分是什么职称下工作的年限,所以应该作出一些相应的简化假设.按所给信息,工资仅取决于职称和教龄.建立新方案的一种办法是将职称折合成教龄,如定义x=教龄t+7×k (对于讲师、助理教授、副教授、教授,k 分别取值0,1,2,3),然后寻求工资函数I(x),使之满足题目的要求,如I(0)=27000,I(7)=32000等,以及x 较大时022<dxI d .另一种办法是职称、教龄分别对待,工资函数J(k,t)从多种函数中选择,如最简单的线性函数J(k,t)=k k k k b a t b a ,,+(k=0,1,2,3)根据一定条件确定.按照第一种办法得到的新工资方案,以职称和教龄综合指标为x 的教师的工资都应为I(x),而人们的目前工资会低于或高于它.根据题目要求,高工资不应降低,低工资则应逐渐提高,尽快达到理想值I(x).需要做的只是根据每人(目前)工资与(理想值的)差额,制定学校提供的提薪资金的分配方案.它应该是简单、合理、容易被人接受的. 按以上原则可以建立不同的模型,应通过检验比较其恶劣.检验可基于题目所给数据,按照提薪计划运行若干年,考察接近理想方案的情况,即用过渡时期的情况检验模型;也可进行随机模拟,按照一定规则随机产生数据(可以包括聘用、提职、解聘、退休的人数和时间等),再按照提薪计划运行,考察接近理想方案的情况.参考文献：叶其孝，《大学生数学建模竞赛辅导教材》（四），湖南教育出版社，20015. 一个飞行管理问题（1995年全国大学生数学建模竞赛A 题）设为第i 架飞机与第j 架飞机的碰撞角（即ij a )8arcsin(ij ij r a =其中为这两架飞机连线的长度），ij r ij β为第i 架飞机相对于第j 架飞机的相对速度（矢量）与这两架飞机连线（从i 指向j 的矢量）的夹角（以连线矢量为基准，逆时针方向为正，顺时针方向为负），i θ为第架飞机飞行方向角调整量. 本问题中的优化目标函数可以有不同的形式：如使所有飞机的最大调整量最小；所有飞机的调整量绝对值之和最小等.以所有飞机的调整量绝对值之和最小，可以得到如下的数学规划模型：w w w .k h d a w .c o m 课后答案网∑=61i i Min θ s.t. ,)(21ij j i ij a >++θθβ j i j i ≠=,6,,1,30≤i θ , 6,,1 =i 为了利用LINGO 求解这个数学规划模型，可以首先采用其他数学软件计算出ij α和ij β.其实，ij α和ij β也是可以直接使用LINGO 来计算的，这相当于解关于ij α和ij β的方程，只是解方程并非LINDO 软件的特长，这里我们作为一个例子，看看如何利用LINGO 计算ij α，可输入如下模型到LINGO 求解ij α：MIDEL ：1]SETS:2] PLANE/1..6/：x0,y0; 3] link(plane,plane):alpha,sin2: 4]ENDSETS5] @FOR(LINK(I,J)|I#NE#J:6] sin2(I,J)=64/((X0(I)-X0(J))*(X0(I)-X0(J))+7] (Y0(I)-Y0(J))*(Y0(I)-Y0(J)));8] ）；9] @FOR(LINK(I,J)|I#NE#J: 10] (@SIN(alpha*3.14159265/180.0))^2=SIN2; 11] ); 12]DATA:13] X0=150,85,150,145,130,0; 14] Y0=140,85,155,50,150,0; 15]endataEND计算结果如下：w w w .k h d a w .c o m 课后答案网ij a j=1 2 3 4 5 6i=1 0.000 0 5.3912 32.231 05.091 8 20.963 4 2.234 5 2 5.391 2 0.000 0 4.8046.613 5 5.807 9 3.815 9 3 32.231 0 4.804 0 0.0004.364 7 22.833 7 2.125 5 45.091 86.613 5 4.36470.000 0 4.4.537 2.989 8 5 20.963 4 5.807 922.8337 4.537 70.000 0 2.309 8 6 2.234 5 3.815 9 2.125 5 2.989 82.309 80.000 0 ij β也可类似地利用LINGO 求得，计算结果如下： ij β j=1 2 3 4 5 6 i=1 0.000 0 109.263 6 -128.250 0 24.1798173.065 1 14.474 9 2 109.263 6 0.000 0-88.871 1 -42.2436-92.304 8 9.000 03 -128.250 0 -88.871 1 0.000 012.4763-58.786 2 0.310 84 24.179 8 -42.243 6 12.476 30.000 0 5.969 2-3.525.65 173.065 1 -92.304 8 -58.78625.969 20.000 0 1.914 4614.474 9 9.000 00.310 8-3.5256 1.914 4 0.000 0w w w .k h d a w .c o m 课后答案网于是，该飞机管理的数学规划模型可如下输入LINGO 求解：MODEL:1]SETS2] plane/1..6/:cita:3] link(plane,plane):alpha,beta;4]ENDSETS5] min=@sum(plane:@abs(cita));6] @for(plane(I):7] @bnd(-30,cita(I),30);8] );9] @fpr(link(I,j)|I#NE#J:10] @ABS(beta(I,J)+0.5*cit(I)+0.5*cita(J))11] >alpha(I,J);12] ）;13]DATA:14] A;[JA=0.000 0 5.391.2….. …2.309 8 0.000 020] ;21] BETA=0.000 010 9.263 6………1.914 4 0.000 027] ;28]enddata END[注] alpha,beta 中数据略去，见上面表格. 求解结果如下： OPTIMUM FOUND AT STEP 197 SOLUTION OBJECTIVE V ALUE= 3.630 V ARIABLE V ALUE REDUCED COST CITA(1) 0.2974033E-06 -1.000 000 CITA(2) -0.1424833E-05 -0.715 033 4 w w w .k h d a w .c o m 课后答案网CITA(3) 2.557 866 1.000 000 CITA(4) -0.3856641E-04 0.0000000E+00CITA(5) 0.2098838E-05 -1.000 000CITA(6) 1.071 594 0.0000000E+00………. (以下略)由此可知最优解为： （其它调整角度为0）. ︒︒≈≈07.1,56.263θθ 评注：如果将目标改为最大调整量最小，则可进一步化简得到线形规划模型，也可用LINDO 或LINGO 求解.参考文献：《数学的实践与认识》第26卷第1期，19966. 降落伞的选择这个优化问题的决策变量是降落伞数量n 和每一个伞的半径r ，可先将n 和r 看作连续变量，建立优化模型，求得最优解后，再按题目要求作适当调整. 目标函数之降落伞的费用，可以根据表1数据拟合伞面费用与伞的半径r 的关系。

2 1 3许多人提前很长时间预订机票，总有旅客因为各种变故不能按时登机，航空公司为了减少按座位定额售票导致空位运行所蒙受的经济损失，通常采用超额售票策略，每个航班超额多售几张票.《公共航空运输航班超售处置规范》要求，航班超售时在使用优先乘机规则前应寻找放弃登机的自愿者，向自愿者提供免费或减价航空运输、赠送里程等作为补偿.2 13 4考虑机票价格、飞行费用、补偿金额等因素，建立一个数学模型来确定超额售票的数量.在获取最大经济收益的同时，尽量维护社会声誉，避免出现过多旅客无法登机的情况.经济收益可用机票收入扣除飞行费用和补偿金额后的利润来衡量.社会声誉可以用因飞机满员而无法登机的旅客限制在一定数量为标准.321由于订票旅客是否按时前来登机是随机变量，经济收益和社会声誉的指标都应该在平均意义或概率意义下衡量.两目标优化问题的解决步骤：先分析经济收益，以收益最大为目标确定超额售票的数量，再考虑如何维护社会声誉.建立经济收益最大的超额售票模型预订机票而不按时登机旅客的数量是随机变量, 航空公司需要估计出其概率分布.飞机容量为n ，超额售票数量为q ，已订票的n +q 位旅客中不按时登机的数量为r (随机变量).每位订票旅客不按时登机的概率为p ，他们是否按时登机的行为相互独立.每张机票价格为s 1，因飞机满员而无法登机的每位旅客得到的补偿金额为s 2.213收益s 1n –s 2(q –r )收益s 1(n +q –r )q ：超额售票数量，r ：订票不按时登机旅客数量，n ：飞机容量，s 1：机票价格，s 2：补偿金额.r ≤q n 位旅客登机, 机票收入s 1nq –r 位旅客得到补偿s 2(q –r )r >q 航空公司收益s (r,q )= s 1n −s 2q −r ,r ≤q s 1n +q −r ,r >q按时登机旅客数量n +q –r ≥n按时登机旅客数量n +q –r <nf (r ) ：已订票的n +q 位旅客中有r 位不按时登机的概率.E q = r=0n+q S r,q f r= r=0q s 1−s 2q −r f r + r=q+1n+qs 1(n +q −r)f rp ：每位订票旅客不按时登机的概率，且他们是否按时登机相互独立.f (r )=C n+qr p r (1−p)n+q−r ,r =0,1,…,n +q 二项分布航班的平均收益：已知s 1,s 2, n , p , 求超额售票数量q 使平均收益E (q )最大.E q = r=0q s 1−s 2q −r f r + r=q+1n+qs 1(n +q −r)f r成立的最小q 使E (q )达到最大.P r ≤q = r=0q C n+q r p r (1−p)n+q−r ≥s 1s 1+s 2不等式s =s 2/s 1 : 补偿金额s 2与机票价格s 1之比,P r ≤q = r=0q C n+q r p r (1−p)n+q−r ≥ 11+s分析q 增加时从E (q )到E (q +1)的变化命令x = binoinv (y, n, p)P r ≤q = r=0q C n+q r p r (1−p)n+q−r ≥ 11+sy=1/(1+s), s=1/3s=1/2s=1s=1/3s=1/2s=1p =0.01443p =0.0311109p =0.05181716平均收益最大的超额售票数量q (n =300)n=300+q p =0.05. x平均收益最大的超额售票数量q(n=300)s=1/3s=1/2s=1 p=0.01443p=0.0311109p=0.05181716考虑社会声誉的超额售票模型从维护社会声誉角度，应对因飞机满员而无法登机的旅客数量加以限制, 由于订票旅客按时登机的随机性, 所谓限制只能以概率表示.P j (q ) ~ 因飞机满员无法登机旅客数量超过j 人的概率P j q = r=0q−(j+1)C n+q r p r (1−p)n+q−r ≤αj 可视为维护社会声誉的“门槛”, 限制P j (q )不超过某个可以接受的数值α.无法登机旅客数量超过j 人订票旅客不来登机的不超过q -(j +1)人•Matlab 二项分布函数命令y = binocdf (x, n, p)计算，其中x=q -(j +1)，y=P j (q ).•给定p , s , 先算出平均收益最大的超额售票数量q ，再设定门槛j ，计算P j (q )，与可以接受的数值α比较，最后确定q 和j .因飞机满员无法登机旅客数量超过j 人的概率P j (q )P j q = r=0q−(j+1)C n+q r p r (1−p)n+q−r ≤α要求s=1/3s=1/2s=1p =0.01, j =10.41310.41310.1932p =0.03, j =30.28280.17670.0968p =0.05, j =50.19310.12820.0791平均收益最大的P j (q ), 取j 约为q 的1/3 s=1/3s=1/2s=1p =0.01443p =0.0311109p =0.05181716平均收益最大的超额售票数量q (n =300)•P j (q )与费用参数s 无关，同一行中P j (q )数值的变化是由q 的不同所致.•q 变大, 概率P j (q )增加.拓展2 1 3对于收益最大超额售票数量q和考虑社会声誉门槛j, 若无法登机旅客超过j人的概率Pj(q)太大,可以适当减小q, 牺牲收益来换取Pj(q)的降低.订票乘客不按时登机的概率p对经济收益和社会声誉的影响较大, 需针对不同航班、不同时间(季节、假日等因素), 利用统计数据实时调整概率p,以提高模型的准确度.实际订票复杂很多：价格也是决策变量，价格随着时间怎么变化? 怎么打折？不同等级的顾客，不同的舱位等等，4日常商务活动，比如旅店、汽车的租赁是不是有类似的营销策略？参考文献[1].姜启源，谢金星，叶俊. 数学模型（第四版）.北京：高等教育出版社，2011.[2].姜启源，谢金星，叶俊. 数学模型（第五版）.北京：高等教育出版社，2018.谢谢大家！本视频课程中的部分图片、视频引自有关图书、网络，特向这些图片、视频的制作者和有关图书的出版者和相关网络表示感谢；因多种原因，事先未与作者和出版社取得联系，特向他们表示歉意。

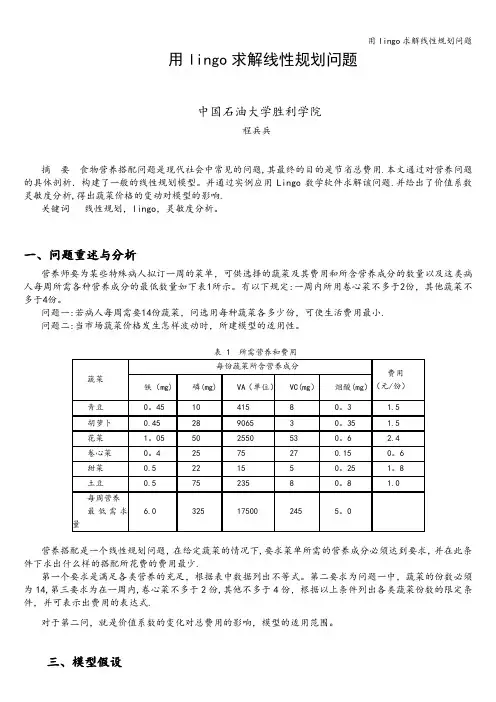
用lingo求解线性规划问题中国石油大学胜利学院程兵兵摘要食物营养搭配问题是现代社会中常见的问题,其最终的目的是节省总费用.本文通过对营养问题的具体剖析．构建了一般的线性规划模型。

并通过实例应用Lingo数学软件求解该问题.并给出了价值系数灵敏度分析,得出蔬菜价格的变动对模型的影响.关键词线性规划，lingo，灵敏度分析。

一、问题重述与分析营养师要为某些特殊病人拟订一周的菜单，可供选择的蔬菜及其费用和所含营养成分的数量以及这类病人每周所需各种营养成分的最低数量如下表1所示。

有以下规定:一周内所用卷心菜不多于2份，其他蔬菜不多于4份。

问题一:若病人每周需要14份蔬菜，问选用每种蔬菜各多少份，可使生活费用最小.问题二:当市场蔬菜价格发生怎样波动时，所建模型的适用性。

表 1 所需营养和费用营养搭配是一个线性规划问题，在给定蔬菜的情况下,要求菜单所需的营养成分必须达到要求，并在此条件下求出什么样的搭配所花费的费用最少.第一个要求是满足各类营养的充足，根据表中数据列出不等式。

第二要求为问题一中，蔬菜的份数必须为14,第三要求为在一周内,卷心菜不多于2份,其他不多于4份，根据以上条件列出各类蔬菜份数的限定条件，并可表示出费用的表达式.对于第二问，就是价值系数的变化对总费用的影响，模型的适用范围。

三、模型假设第一,假设各蔬菜营养成分保持稳定，满足题干要求。

第二,假设各蔬菜价格在一定时间内保持相对稳定。

第三，假设各类蔬菜供应全部到位，满足所需要求量. 第四,假设所求出最优解时不要求一定为整数。

四、符号约定（1)Z 代表目标函数,此题即为费用。

(2）i c 为价值系数，此题即为每份蔬菜的价格。

下标i 代表蔬菜的种类。

(3）i x 为决策变量，表示各种蔬菜的数量。

(4）i b 为最低限定条件,表示蔬菜最低营养需要。

五、模型建立根据以上各种假设和符号约定，建立模型如下。

所求的值就是min,也就是最优化结果.s 。

2006高教社杯全国大学生数学建模竞赛山西赛区吕梁高等专科学校第五队参赛队员：1. 张晶晶2. 刘美琴3. 王超鹏指导教师：***2006 年 9 月 18 日承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： C我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：吕梁高等专科学校参赛队员(打印并签名) ：1. 张晶晶2. 刘美琴3. 王超鹏指导教师或指导教师组负责人(打印并签名)：王亮亮日期： 2006 年 9 月 18 日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：易拉罐形状和尺寸的设计摘要本文研究易拉罐的形状和尺寸的设计问题。

体积给定的圆柱体，其表面积最小的尺寸（半径和高）为多少？从纯数学的观念出发，这个尺寸（半径和高）为1：2。

也就是说，对于易拉罐而言，当高是半径的2倍时，其表面积最小。

即易拉罐设计成等边圆柱时，消耗的材料较少，生产成本较低。

但在实际生活中，我们所看到的易拉罐不是等边圆柱的，有的长些，有的短些，生活中（市场上）的易拉罐为什么会是这样呢？经过我们调查测量，也发现销量很大的饮料的饮料罐（即易拉罐）的形状和尺寸几乎是一样的。

经过测量生活中（市场上）饮料罐胖的部分的直径和高的比为6.4/10.3=0.621，非常接近黄金分割比0.618。

湖南第一师范学院HUNAN FIRST NORMAL UNIVERSITY论文题目: 导弹攻击姓名专业班级及学号分工队员1 李丽11402050122 建立模型，计算队员2 盛名11402050128 建立模型，编程队员3 张旋11402050148 建立模型，画图摘要本文研究导弹攻击敌艇的问题。

首先，本文关于可改变角度的导弹攻击敌艇的问题建立了相关数学模型。

针对第一问，研究速度大小恒定，速度方向随时间改变的导弹，来攻击沿水平方向运动，速度大小不变的敌艇的问题。

由于导弹在任意时刻都指向敌艇，我们通过图形找到了速度和坐标的相似三角形，又根据速度和时间有函数关系，以及对导弹合速度的分解，使用了微分方程模型。

在第二个问题中，由于敌艇的运动方向与导弹每个时刻都成固定90度的角，再利用第一问的方法不再那么简单。

所以采取微元思想把整个攻击过程划分为非常小的时间段来进行研究，然后再用数学归纳法得出一般化的迭代格式，再利用迭代格式得到击中点。

在第三个问题中，本文对第二个问题的特殊角度进行了推广来得出最优逃离角度，即逃离时间周期最长的角度。

第四问根据前三问算出来的数据和画出的图像得出结论。

针对模型的求解，本文第一问使用偏微分方程和参数方程的求解方法计算出，并只用c语言编写程序求解出第二，三问题。

本文模型方法简单易懂，结果采用相关程序用计算机计算，并用matlab画出图像，明了，准确。

在模型的检验模型中，本文分别讨论了以上模型的精度和稳定性。

最后通过修改模型，得出导弹追击敌艇的模型。

关键词：微分方程模型、微元思想、数学归纳法、迭代公式一、问题重述1、问题背景：导弹自第二次世界大战问世以来，受到各国普遍重视，得到很快发展。

导弹的使用，使战争的突然性和破坏性增大，规模和范围扩大，进程加快，从而改变了过去常规战争的时空观念，给现代战争的战略战术带来巨大而深远的影响。

导弹技术是现代科学技术的高度集成，它的发展既依赖于科学与工业技术的进步，同时又推动科学技术的发展，因而导弹技术水平成为衡量一个国家军事实力的重要标志之一。

数学模型第五版姜启源课件1. 引言数学模型是一种以数学方法描述、分析和解决实际问题的工具。

它是现代科学、工程和社会学科中不可或缺的一部分。

姜启源的《数学模型》是国内外广泛采用的教材之一，这份课件是对第五版《数学模型》的经典章节进行概要的总结和讲解。

2. 背景与目的数学模型的研究对象可以是自然界的现象、社会经济问题或工程技术等。

通过建立数学模型，我们可以更好地理解问题的本质，并探索解决问题的方法。

数学模型的建立需要一定的理论基础和技巧，本课件旨在帮助读者快速掌握数学模型的基本概念和建模方法。

3. 数学模型的基本概念数学模型是对实际问题进行抽象和描述的数学形式。

它由问题的假设、变量、关系和约束等要素组成。

本部分介绍了数学模型的基本概念，包括：3.1 假设与逼近数学模型的建立需要对实际问题进行适当的假设和逼近。

假设是对问题中不确定因素的简化和规定，而逼近是对问题中不精确因素的近似和描述。

3.2 变量与参数变量是数学模型中描述问题状态的符号，它可以是数值、向量、矩阵等。

参数是数学模型中的固定值，它们可以是已知的或未知的。

3.3 关系与方程关系是数学模型中描述变量之间相互关系的数学表达式。

方程是关系中等号左右两边相等的表达式。

3.4 约束条件与目标函数约束条件是数学模型中描述问题限制条件的不等式或等式。

目标函数是数学模型中描述问题目标的数学表达式。

4. 常见的数学模型本部分介绍了一些常见的数学模型及其应用场景，包括：4.1 线性模型线性模型是最简单的数学模型之一，它的关系和约束条件可以表示为线性方程或线性不等式。

线性模型广泛应用于经济学、管理学、物理学、工程学等领域。

4.2 非线性模型非线性模型是一类不满足线性关系的数学模型。

它的关系和约束条件可以表示为非线性方程或非线性不等式。

非线性模型常用于生物学、化学、地球物理学等领域的研究。

4.3 动态模型动态模型是描述系统随时间变化的数学模型。

它可以采用微分方程、差分方程或积分方程等形式进行建模。

数学建模第五版姜启源课后题答案第6章代码
第六章代数方程与差分方程模型代码
概述差分方程的类型
6.1贷款购房
6.2管住嘴迈开腿
6.3动物的繁殖与收获
6.4中国人口增长预测
一、差分方程的基本概念
1.差分的定义
定义规定t只取非负整数，设函数y，表示变量y在t点的取值y=f（t），t=0，?，?，，土n，.
称
Ay，=y1-y，=f（t+1）-f（t）为函数y，的一阶差分；称A2y，=△（Ay，）=Ay1-Ay.
=（y42-y21）-（y21-y）
=y42-2y1+y
依此类推，函数的n阶差分定义为：A"y，=△（A-1y）
二阶及二阶以上的差分统称为高阶差分。

例1求△（t2），△2（t2），A3（t2）.
解设y，=t2，则Ay，=A（t2）=（t+1）2-t2=2t+1，
△2（y，）=A2（t2）=△（Ay，）=△（2t+1）
=（2（t+1）+1）-（2t+1）
=2，A2（y，）=△（A2y，）
=△（2）=2-2=0.
2.差分方程
例设某种商品t时期的供给量S，与需求量D都是这一时期价格P，的线性函数：S，=-a+b（a，b>0），D=c-d（c，d>0）.
则t时期的价格P，由t-1时期的价格P.1与供给量及需求量之差S.a-D.按以下关系确定P=P1-2（S1-D-1）（a为常数），即P-[1-2（b+d）JP，=a（a+c）.。

数学建模练习与思考题第⼀部分练习与思考题第1章建⽴数学模型1.1 在稳定的椅⼦问题中，如设椅⼦的四脚连线呈长⽅形，结论如何？（稳定的椅⼦问题见姜启源《数学模型》第6页）1.2 在商⼈们安全过河问题中，若商⼈和随从各四⼈，怎样才能安全过河呢？⼀般地，有n 名商⼈带n 名随从过河，船每次能渡k ⼈过河，试讨论商⼈们能安全过河时，n 与k 应满⾜什么关系。

（商⼈们安全过河问题见姜启源《数学模型》第7页）1.3 ⼈、狗、鸡、⽶均要过河，船需要⼈划，另外⾄多还能载⼀物，⽽当⼈不在时，狗要吃鸡，鸡要吃⽶。

问⼈、狗、鸡、⽶怎样过河？1.4 有3对夫妻过河，船⾄多载两⼈，条件是任⼀⼥⼦不能在其丈夫不在的情况下与其他的男⼦在⼀起。

问怎样过河？1.5 如果银⾏存款年利率为5.5%，问如果要求到2010年本利积累为100000元，那么在1990年应在银⾏存⼊多少元？⽽到2000年的本利积累为多少元？1.6 某城市的Logistic 模型为2610251251N N dt dN ?-=，如果不考虑该市的流动⼈⼝的影响以及⾮正常死亡。

设该市1990年⼈⼝总数为8000000⼈，试求该市在未来的⼈⼝总数。

当∞→t 时发⽣什么情况。

1.7 假设⼈⼝增长服从这样规律：时刻t 的⼈⼝为)(t x ，最⼤允许⼈⼝为m x ，t 到t t ?+时间内⼈⼝数量与)(t x x m -成正⽐。

试建⽴模型并求解，作出解的图形并与指数增长模型和阻滞增长模型的结果进⾏⽐较。

1.8 ⼀昼夜有多少时刻互换长短针后仍表⽰⼀个时间？如何求出这些时间？1.9 你在⼗层楼上欲乘电梯下楼，如果你想知道需要等待的时间，请问你需要有哪些信息？如果你不愿久等，则需要爬上或爬下⼏个楼层？1.10 居民的⽤⽔来⾃⼀个由远处⽔库供⽔的⽔塔，⽔库的⽔来⾃降⾬和流⼊的河流。

⽔库的⽔可以通过河床的渗透和⽔⾯的蒸发流失。

如果要你建⽴⼀个数学模型来预测任何时刻⽔塔的⽔位，你需要哪些信息？第2章初等模型2.1 学校共1000名学⽣，235⼈住在A 宿舍，333⼈住在B 宿舍，432⼈住在C 宿舍。

单循环赛制安排的数学模型陈晔1，祝文康1，何荣坚21．韶关学院2001级数学与应用数学本科1班,广东韶关 512005;2．韶关学院2002级计算机科学技术本科3班,广东韶关 512005[摘要]: 本文首先通过对５支足球队单场地单循环赛程安排的问题，考虑对各队公平的相隔场次的情况下用排除假设法给出至少相隔一场的赛程安排的方法，遵循小数先走的原则时恰好发现了击剑比赛时n＝５的赛程安排规律，并讨论其不合理性．分奇、偶参赛队的情况给出只考虑相隔场次时的最大均等时相隔场次次数的最小上限证明．在编制n=８，n=９支球队赛程的过程中进一步研究多种循环赛制安排的方法，还给出Matlab编制的一般性的赛程安排程序．同时通过引入对实力的排序、比赛的精彩度、各球队机会最大均等、奇数队参赛必然遇到不公平的情况等展开讨论一些赛程安排方法的不足之处．关键词:最大均等; 轮转法; 实力指数; 精彩度１问题的提出你所在的年级有5个班，每班一支球队在同一块场地上进行单循环赛，共要进行10场比赛，如何安排赛程使对各队来说都尽量公平？下面是一个随便安排的赛程：记5支球队为A，B，C，D，E，在下表左半部分的右上三角的10个空格中，随手填上1，2，⋯10，就得到一个赛程，即第1场A对B，第2场B对C，⋯，第10场C对E．为方便起见将这些数字沿对角线对称地填入左下三角．这个赛程的公平性如何呢，不妨只看看各队每两场比赛中间得到的休整时间是否均等．表的右半部分是各队每两场比赛间相隔的场次数，显然这个赛程对A，E有利，对D则不公平．从上面的例子出发讨论以下问题1)对于5支球队的比赛，给出一个各队每两场比赛中间都至少相隔一场的赛程．2)当n支球队比赛时，各队每两场比赛间相隔的场次数的上限是多少．3)在达到2）的上限的条件下，给出n=8、n=9的赛程，并说明它们的编制过程．4)除了每场间相隔场次数这一指标外，你还能给出哪些指标来衡量一个赛程的优劣，并说明3）中给出的赛程达到这些指标的程度．2 基本假设1）单循环赛中，n为偶数队参赛时，所有队都安排参加一次后为一轮比赛，轮数为n-1，奇数队参赛时，n-1队安排参赛一次后为一轮比赛，轮数为n ．2）参赛队A、B、C、D……通过以往比赛成绩的排名或社会评价的排名按实力从大到小顺序记为1、2、3、……n队．3 模型的分析、建立与求解1）第一轮第一场比赛安排A对B，第二场比赛安排C对D，在各参赛队每两场比赛间至少相隔一场的前提下，第二轮第一场安排除C、D外的任意两支球队比赛，第二场安排前一场没有参赛的任意两队参赛，曾经比赛交战过的队不再安排对决，以此类推，共安排5轮共10场比赛，以下只给出安排过程的部分分支：AB —CD依照题意排出的赛程如上表所示，观察表1，对与上轮轮空队比赛的队会不公平，其中E 从第三轮开始就连续遭遇不公平三场，A 遭遇一场，其他队在这种安排下则有优势．出现这种情况的原因是由于这种安排方法导致的．观察图1，发现E 队遭遇不幸的第四轮和第五轮是在不能选择其他分支的情况下安排E 的两场比赛．也就是说这种安排方法必然导致不公平．继续将图中所有分支排列出，会发现不一定能排出十场比赛，能走到最后的16条分支，有两条只能排出八场比赛，有六条排出九场比赛，有八条排出十场比赛．其中，如果在每一次分支中遵循小数先走的原则，如：第一个分支中有AE 和BE 供选择，选择AE ，BC 和BD 则选BC ，能排出十场比赛，恰好是至今仍没研究出的击剑赛程安排规则中参赛队n=5时赛程安排的规律．然而，当n=6，n=7，n=8时用的就不是这个办法了．2）可设赛程中某场比赛是i ，j 两队，i 队参加的下一场比赛是i ，k 两队(k ≠j)．要 使每两场比赛最小相隔场次为r ，则上述两场比赛之间必须有除i ，j ，k 以外的2r 支球队参加赛，于是n ≥2r+3，注意到r 为整数即是⎥⎦⎤⎢⎣⎡-≤23n r ．经过计算，当有5支队伍比赛时，各队每两场比赛中间相隔的场次数的上限为1=r ，也就是说可以找出一种编排赛程的方法，使得各队每两场比赛中间相隔的场次数为1．或可分参赛队的奇、偶分别证明：1．设n 为奇数， n = 2k + 1． 共比赛 N =2n C = k (2k + 1)场． 考察前k + 1场， 有2k +2个队参赛， 于是至少有1个队两次参赛， 这个队在这两场比赛间相隔场次数为r n k k =⎥⎦⎤⎢⎣⎡-=-=--+23111)1(． 2．设n 为偶数， n = 2k ． 共比赛 N = k (2k - 1)场． 同上， 在前k + 1场中，有2k+2个队参赛，其中至少有1个队(记这样的一个队为A)两次参赛， 记A 第j 场比赛在赛程中是第a j 场， 于是1,121+≤≥k a a ．① 若12+<k a ，即k a ≤2， 则r n k k a a =⎥⎦⎤⎢⎣⎡-=-≤--=--23211112; ②若12+=k a ，但11>a ，即21≥a ，同样有r n k k a a =⎥⎦⎤⎢⎣⎡-=-≤--+=--232121112; ③若1,121+==k a a ， 在前k + 1场中除A 外有2k 个队参赛， 于是至少又有1个队(记这样的一个队为B)两次参赛， 记B 第j 场比赛在赛程中是第b j 场， 则必有1,121+<≥k b b ， 或1,121+≤>k b b (即不可能1,121+==k b b )， 故r n k b b =⎥⎦⎤⎢⎣⎡-=-≤--232112． 3）n=8时，以数字1、2、3、……8记为参赛的八支队，用1号固定左上角逆时针轮可得出下表：经计算，这种轮转法安排出的赛程满足2）中每两场比赛间相隔的场次数的上限r=2．随着比赛发展，每一轮中所安排的比赛，观察实力越强的的队间的比赛安排，第一轮里实力最接近的比赛是4队与5队间的比赛，第二轮是3队与4队的比赛，第三轮2队与3队，第四轮4队与6队，第五轮7队与8队，第六轮6队与7队，最后一轮有最精彩的，也是实力最强的1队与2队的比赛．这种安排使比赛进程没有什么规律。

《数学模型》课程教学大纲课程编码：ZB0240121课程类别：专业核心必修适用专业及层次：信息与计算科学（本科）学分：4理论学时：48实践学时：32先修课程：数学分析，高等代数，数学实验，概率论等。

一、课程的性质、目的和任务本课程是信息与计算科学专业（本科）的一门专业核心必修课.也是学生参加数学建模竞赛的基础课程.数学模型是一门重要的数学技术课，目标在于培养学生利用数学知识及相关专业知识建立数学模型分析、解决实际问题的能力，并从中培养和提高学生的创新意识、创新能力及综合应用能力.设置该课程的目的是要向学生介绍数学模型的数学理论和方法，使学生了解并初步掌握应用所学的数学知识建立数学模型的基本方法和基本过程，从而培养学生应用数学的思维、知识、方法解决实际问题的意识和能力.二、课程教学的基本要求通过本课程的学习（课堂讲授、上机实习和作业），应达到目的和要求如下：1、培养学生运用数学工具解决现实生活中实际问题的能力。

2、用数学方法解决问题的能力以及用自己的研究结果解释、指导实际问题的能力，从无到有的创新能力以及写作能力。

3、通过本课程的学习，使学生了解数学建模是利用数学知识构造刻画客观事物原型的数学模型，利用计算机解决实际问题的一种科学方法。

掌握数学建模的基本步骤，即从实际问题出发，遵循“实践一一认识一一实践”的辩证唯物主义认识规律，紧紧围绕建模的目的，运用观察力、想象力和逻辑思维，对实际问题进行抽象、简化、反复探索、逐步完善，直到构造出一个能够用于分析、研究和解决实际问题的数学模型。

会利用数学知识和计算机解决问题，并能够撰写符合要求的数学建模论文。

三、课程教学内容第一章线性规划【授课学时】2【教学内容】第一节线性规划问题第二节投资的收益和风险【教学要求】通过本章学习，掌握求解线性规划问题的方法和一般步骤、投资的收益和风险.【教学重难点】建立数学规划的步骤，常见处理约束条件的方法技巧。

第二章整数规划【授课学时】2【教学内容】第一节概论第二节0-1型整数规划第三节蒙特卡洛法【教学要求】通过本章学习，掌握整形规划和线性规划的区别和联系、整形规划问题的类型和常用的求解方法.【教学重难点】常见处理约束条件的方法技巧，整形规划问题的计算机求解。

参考文献
[1]陈东彦，李冬梅，王树忠：数学建模，科学出版社2007年版
[2]曹喜望：管理科学中的数学模型，北京大学出版社2006年版
[3]方道元，韦明俊：数学建模：方法导引与案例分析，浙江大学出版社2011年版
[4]姜启源，谢金星：数学建模案例选集，高等教育出版社2006年版
[5]姜启源，谢金星，叶俊：数学模型（第4版），高等教育出版社2011年版
[6]李大潜：中国大学生数学建模竞赛，高等教育出版社1998年版
[7]马莉：MATLAB数学实验与建模，清华大学出版社2010年版
[8]束金龙、闻人凯，柴俊：线性规划理论与模型应用，科学出版社2007年版
[9]谭勇基，朱晓明：经济管理数学模型案例教程，高等教育出版社2006年版
[10]杨启帆，方道元：数学建模，浙江大学出版社1999年版
[11]姚恩瑜，何勇，陈仕平：数学规划与组合优化，浙江大学出版社2001版。

（1）由题目可看出以下几点：在决策时采用不同的决策方法会产生不同的结果；对方决策透明了后，就不存在博弈问题了；不同决策会产生不同结果时才会产生博弈问题，即不同决策产生相同结果时就不存在博弈了。

赛马前田忌与齐王都不知道对方马的出场顺序时，而双方都想通过调整马的出场顺序赢得比赛，则这是博弈问题。

反之，如果一方出场顺序已被对方知道，即对方决策已确定且被知道，那么这就是单人决策问题。

（2）该博弈不存在纯战略纳什均衡，具体证明及混合纳什均衡的模型见以下数学模型：一、问题重述“田忌赛马”是一个家喻户晓的故事：战国时期，齐国将军田忌经常与齐王赛马，设重金赌注，孙膑发现田忌与齐王的马脚力都差不多，可分为上、中、下三等。

于是孙膑对田忌说：“您只管下大赌注，我能帮你取胜。

”田忌相信并答应了他，与齐王用千金来赌注。

比赛即将开始，孙膑对田忌说：“现在用您的下等马对付他的上等马，拿您的上等马对付他的中等马，拿您的中等马对付他的下等马。

”三场比赛完后，田忌只有一场不胜而另两场胜，最终赢得齐王的千金赌注。

现在假定齐王与田忌约定比赛开始前双方同时决定马的出场顺序，并且以后不可改变。

二、基本假设1齐王与田忌约定比赛开始前双方同时决定马的出场顺序，并且以后不可改变；2比赛过程不会发生其他的意外情况；3双方马的脚力每等齐王的比田忌的都略强。

三、问题分析该问题可以看成是一个博弈问题，双方有三种马的出场顺序，不同的出场顺序产生不同结果，通过建立数学模型来分析双方以怎样的出场顺序会得到怎样的结果。

由于齐王的各等马均略强于田忌的，因此田忌只有通过合理的安排马的出场顺序才能赢得比赛。

四、模型建立参与博弈的双方用N=（1,2）表示，1为田忌，2为齐王；田忌：a1(1 2 3) a2(1 3 2) a3(2 1 3)a4(2 3 1) a5(3 2 1) a6(3 1 2)表示其六种出场顺序；齐王：b1(1 2 3) b2(1 3 2) b3(2 1 3)b4(2 3 1) b5(3 2 1) b6(3 1 2)表示其六种出场顺序。