信号与系统的MATLAB仿真(燕庆明第四版配套)
- 格式:doc
- 大小:1.11 MB
- 文档页数:27


16第四章MATLAB仿真系统第四章MATLAB仿真系统仿真是衡量系统性能的工具,它通过仿真的仿真结果来推断原系统的性能,从而为新系统的建立或原系统的改造提供可靠的参考。
通过仿真,可以降低新系统失败的可能性。
消除系统中潜在的瓶颈,防止对系统中某些功能部件造成过量的负载,优化系统的整体性能。
实际的通信系统是一个功能结构相当复杂的系统,对这个系统做出的任何改变都可能影响到整个系统的性能和稳定。
因此,在对原有的通信系统做改进或建立一个新系统之前,通常需要对这个系统进行建模和仿真,通过仿真结果衡量方案的可行性,从中选择最合理的系统配置和参数设置,然后应用在实际系统中。
§ 4.1通信仿真的概念通信仿真是衡量通信系统性能的工具。
通信仿真可以分成离散和连续仿真。
在离散事件仿真中只对离散事件作出响应,而在连续仿真中,系统对输入信号产生连续的输出信号。
离散事件仿真是对实际通信系统的一种简化,它的仿真建模比较简单,整个过程需要花费的时间也比连续仿真少。
虽然离散事件仿真舍弃了一些仿真细节,但仍然是通信仿真的主要方式。
与一般的仿真过程类似,在对通信系统实施仿真前,首先需要研究通信系统的特性,通过归纳和抽象建立通信系统的仿真模型。
通信系统是一个循环往复的过程,它从当前系统出发,通过分析建立起一个能够在一定程度上描述原通信系统的仿真模型,然后通过仿真实验得到相关的数据。
通过对仿真数据的分析可以得到相应的结论,然后把这个结论应用到当前通信系统的改造中。
值得注意的是,在整个通信系统的仿真过程中,人为因素自始至终起着相当重要的作用。
除了仿真程序的运行之外,通信仿真的每个步骤都需要进行人工干预,由于人对当前的情况做出正确的判断。
因此,通信仿真并不是一个机械的过程,它实际上是人的思维活动在计算机协助下的一种延伸。
§4.2通信仿真的一般步骤通信仿真一般分成三个步骤,即仿真建模、仿真试验和方针分析。
通信仿真是一个螺旋式发展的过程,因此这三个步骤可能要执行多次后才能获得令人满意的效果。

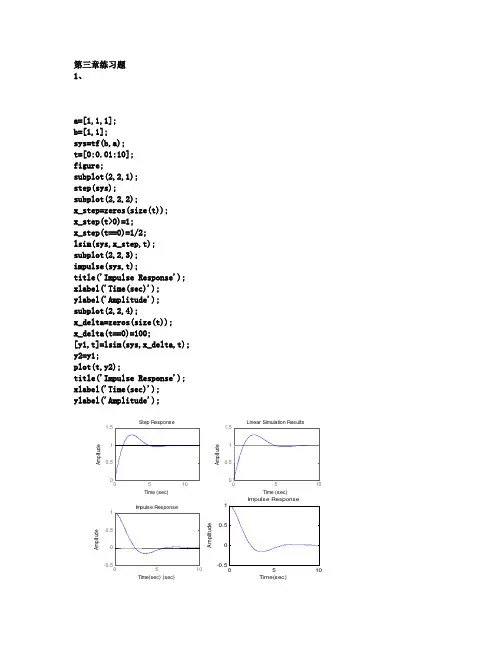
第三章练习题 1、a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d eLinear Simulation ResultsTime (sec)A m p l i t u d e-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d eImpulse ResponseTime(sec)A m p l i t u d e2、函数int1如下:function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf));tF=tf;for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n);end验证如下:t=[-1:0.01:4];e=zeros(size(t));e=(t>-1/2&t<1);[z,zz]=intl(e,t,-1);figure;plot(zz,z);第四章练习题1、T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered2、fsana 函数如下:function F=fsana(t,f,N); omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下:function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数第五章练习题1、(a) Residue计算a1=[1,5,6];b1=[4,5];[r1,p1,k1]=residue(b1,a1); t=[0:0.01:10];e1=zeros(size(t));for n=1:size(r1);e1=e1+r1(n)*exp(p1(n)*t); end;figure;subplot(1,2,1);plot(t,e1);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([4,5],[1,5,6]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h1=lsim(sys1,delta,t); subplot(1,2,2);plot(t,h1);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同(b)Residue计算t=[0,0.01,10];delta=zeros(size(t));delta(t==0)=100;e2=sin(t);figure;subplot(2,1,1);plot(t,e2);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([1,0,2],[1,0,1]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h2=lism(sys1,delta,t); subplot(2,1,2);plot(h,t2);axis([0,10,-1,1]);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同2、S=isstable(sys)函数:Function s=isstable(sys);X=ploe(sys);S=1;For n=1:Size(x)If x(n)>0S=0;break;End;End;稳定系统:Sys=tf(1,[1,2]);S=isstable(sys);S=1不稳定系统:Sys=tf(1,[1,-2]);S=isstable(sys);S=第七章练习题1、a=[1,0.5,-0.2,-0.1]; b=[1,-0.3];n=[0:10]';[hi,t]=impz(b,a,n); subplot(1,2,1);stem(n,hi);u=(n>=0);hn=filter(b,a,u); subplot(1,2,2);stem(n,hn);2、n1=[0:9]';n2=[10:19]';x1=(n1>=0);x2=-(n2>=10);a1=[1,-0.2,-0.1];a2=[1,-0.2,0.5];b=[1,0.01];[y1,wf1]=filter(b,a1,x1,[0,1]); [y2,wf2]=filter(b,a2,x2,wf1); stem(n1,y1);hold on;stem(n2,y2);。
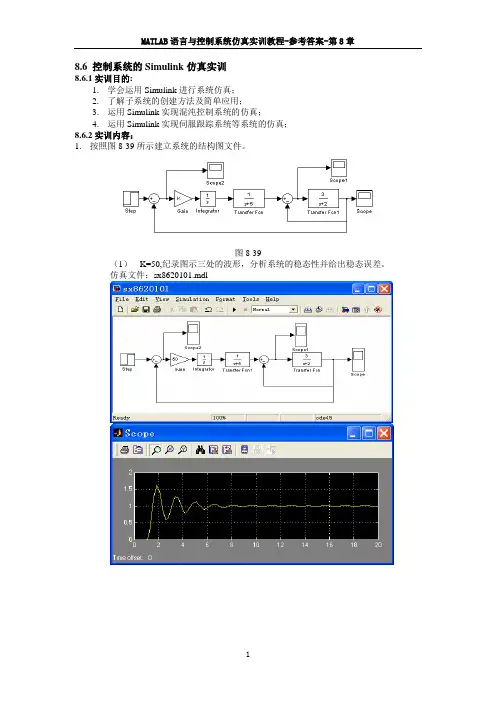
8.6 控制系统的Simulink仿真实训8.6.1实训目的:1.学会运用Simulink进行系统仿真;2.了解子系统的创建方法及简单应用;3.运用Simulink实现混沌控制系统的仿真;4.运用Simulink实现伺服跟踪系统等系统的仿真;8.6.2实训内容:1.按照图8-39所示建立系统的结构图文件。
图8-39(1)K=50,纪录图示三处的波形,分析系统的稳态性并给出稳态误差。
仿真文件:sx8620101.mdl系统稳定,稳态误差为0;(2)K=200,纪录图示三处的波形,根据曲线分析系统的稳定性。
仿真文件:sx8620102.mdl由输出曲线可以看出闭环系统不稳定;(3)编写程序求取K=200时的闭环传递函数,求出系统的闭环极点(特征根),说明系统的稳定性,分析与(2)得出的结论是否一致。
%实训8620103.mn1=3;d1=[1,2];[n2,d2]=cloop(n1,d1);sysa=tf(n2,d2);sysb=tf([200],[1,0])*tf([1],[1,5]);sysc=sysa*sysb/(1+sysa*sysb);[nc,dc]=tfdata(sysc,'v');roots(dc)>> ans =-12.0549 1.0275 + 6.9797i 1.0275 - 6.9797i -5.0000 + 0.0000i -5.0000 - 0.0000i有两个特征根在右半平面,闭环系统不稳定;与(2)得出的稳定性结论一致。
2. 子系统创建实验 (1)建立如下系统。
(2)选定范围,创建子系统并定义变量a 。
图8-40(3)利用创建的子系统,分别记录10,8,6,4,2 a 时所示系统的输出波形。
a=2a=4a=6a=8a=103.已知四维混沌系统的运动方程如下,试用Simulink 进行仿真。
⎪⎪⎩⎪⎪⎨⎧+-=+-=-+=+-=321444213343121243212110)(10)(35x x x x xx x x x x x x x x x xx x x x x x (1)四个积分器的初始值自定,建议在(0.01,3.0)范围内随机给出。

信号与线性系统分析(第四版):探索信号处理的数学基石一、信号与线性系统的基本概念在信息技术飞速发展的今天,信号与线性系统分析已成为电子工程、通信工程等领域不可或缺的基础知识。
本版书籍旨在为您提供一个清晰、系统的学习路径,帮助您深入理解信号处理的理论与实践。
1. 信号的定义与分类(1)确定性信号与随机信号:确定性信号在任意时刻都有明确的函数值,而随机信号则具有不确定性。
(2)周期信号与非周期信号:周期信号在时间轴上呈周期性重复,而非周期信号则不具备这一特性。
(3)能量信号与功率信号:能量信号在有限时间内具有有限的能量,而功率信号则具有有限的功率。
2. 线性系统的特性(1)叠加原理:多个输入信号经过线性系统处理后,其输出信号等于各输入信号单独处理后的输出信号之和。
(2)齐次性原理:输入信号经过线性系统放大或缩小后,输出信号也会相应地放大或缩小。
二、线性时不变系统描述1. 冲激响应与卷积积分冲激响应是描述LTI系统特性的重要工具。
通过冲激响应,我们可以利用卷积积分求出系统对任意输入信号的响应。
2. 系统函数与频率响应系统函数是LTI系统在频域的描述方式,它揭示了系统对不同频率信号的响应特性。
频率响应则是对系统函数在特定频率下的直观展示。
3. 状态空间描述状态空间描述是一种更为全面的LTI系统描述方法,它将系统的内部状态与输入、输出联系起来,为分析和设计复杂系统提供了有力工具。
三、信号的傅里叶分析1. 傅里叶级数傅里叶级数将周期信号分解为一系列正弦波和余弦波,揭示了周期信号在频域的组成。
2. 傅里叶变换傅里叶变换将时间域的非周期信号转换为频域信号,为信号处理提供了强大的分析工具。
四、拉普拉斯变换与z变换的应用1. 拉普拉斯变换拉普拉斯变换将时间域的信号转换到复频域,它是分析线性时不变系统在复频域特性的关键工具。
在本版书籍中,我们将探讨:(1)拉普拉斯变换的基本性质和收敛域。
(2)利用拉普拉斯变换求解微分方程和积分方程。


学号:***********信号与系统实验报告学生姓名石正禄班级电子14-1BF 院部物理与电子学院专业电子科学与技术任课老师王晓明指导老师王晓明二0一五——二0一六学年第二学期实验项目名称:信号的表示与信号的产生实验成绩:实验日期: 2016.05.28 实验室: 6404一、实验目的1.熟悉常见信号的特性及波形。
2.学会掌握MATLAB表示信号的方法。
3.学会使用MATLAB绘制信号的波形和实现信号的基本运算。
二、实验原理(1).连续时间信号所谓连续时间信号,是指其自变量的取值是连续的,并且除了若干不连续的点外,对于一切自变量的取值,信号都有确定的值与之对应。
从严格意义上讲,MATLAB并不能处理连续信号。
在MATLAB中,是用连续信号在等时间间隔点上的样值来近似表示的,当取样时间间隔足够小时,这些离散的样值就能较好地近似出连续信号。
一些常见连续信号在MATLAB中表示。
1.指数信号指数信号Ae at在MATLAB中可以用exp函数表示,其调用形式为y=A∗exp (a∗t)2.正弦信号正弦信号Acos(ωt+φ)和Asin(ωt+φ)分别用MATLAB的内部函数cos和sin表示,其调用形式为y=A∗cos (ω∗t+φ)y=A∗sin (ω∗t+φ)3.抽样函数Sa(t)抽样函数Sa(t)在MATLAB中用sinc函数表示,定义为Sinc(t)=sin(πt)πt其调用形式为y=sinc(t)4.矩形脉冲信号矩形脉冲信号在MATLAB中用rectpuls函数表示,其调用形式为y=rectpuls(t,width)产生一个幅度为1,宽度为width,以零点对称的矩形波。
5.阶跃信号在MATLAB中,单位阶跃信号用stepfun()函数表示,其调用形式为Stepfun(t,t0)其中,t0表示信号发生突变的时候,在t0以前,函数值等于0,t0以后函数值等于1(2).连续时间信号在MATLAB中,离散信号的表示方法与连续信号不同,它无法用符号运算法来表示,而只能采用数值计算法表示,由于MATLAB中元素的个数是有限的,因此,MATLAB无法表示无限序列;另外,在绘制离散信号时必须使用专门绘制离散数据的命令,即stem()函数,而不能用plot()函数。

实验指导书实验1 MATLAB基本操作一、实验目的1.熟悉MATLAB实验环境,练习MATLAB命令、m文件、Simulink的基本操作。
2.利用MATLAB编写程序进行矩阵运算、图形绘制、数据处理等。
3.利用Simulink建立系统的数学模型并仿真求解。
二、实验原理MATLAB环境是一种为数值计算、数据分析和图形显示服务的交互式的环境。
MATLAB有3种窗口,即:命令窗口(The Command Window)、m-文件编辑窗口(The Edit Window)和图形窗口(The Figure Window)。
Simulink 是MATLAB的一个部件,它为MATLAB用户提供了一种有效的对反馈控制系统进行建模、仿真和分析的方式。
而Simulink另外又有Simulink模型编辑窗口。
1.命令窗口(The Command Window)当MATLAB启动后,出现的最大的窗口就是命令窗口。
用户可以在提示符“>>”后面输入交互的命令,这些命令就立即被执行。
在MATLAB中,一连串命令可以放置在一个文件中,不必把它们直接在命令窗口内输入。
在命令窗口中输入该文件名,这一连串命令就被执行了。
因为这样的文件都是以“.m”为后缀,所以称为m文件。
2.m文件编辑窗口(The Edit Window)我们可以用m文件编辑窗口来产生新的m文件,或者编辑已经存在的m文件。
在MATLAB主界面上选择菜单“File/New/M-file”就打开了一个新的m文件编辑窗口;选择菜单“File/Open”就可以打开一个已经存在的m文件,并且可以在这个窗口中编辑这个m文件。
3.图形窗口(The Figure Window)图形窗口用来显示MATLAB程序产生的图形。
图形可以是2维的、3维的数据图形,也可以是照片等。
4.Simulink的启动方式:启动运行Simulink有两种方式:(1)在Command window中,键入simulink,回车。

信号与系统实验教程目录实验一:连续时间信号与系统的时域分析—————-----—--—--—---——--—--————---—-——————————-——6一、实验目的及要求—-——-————-————————-—--——-----——------—--—-—-—-—--——-—--—-——--—---—---------6二、实验原理—-—-———---——————-——-—-—-————-———--—-——-—---——--—-—-—-——-—--———————-———-———-—---—-——61、信号的时域表示方法-—-————-————--—--—————-—--———-——-———-——-——---—--—---—-——-—--—--—--62、用MATLAB仿真连续时间信号和离散时间信号-——-—--—--—----——-—-——--—-——-—-———73、LTI系统的时域描述———-—----—--——----——--—-—----———----—--—-——-—--——--—-———--——--—--11三、实验步骤及内容——-——-——————-———--—-----—-——---—-————-———-——————-——---———-——-—--——--——-—-—15四、实验报告要求—-——-—-————--——-———-———-—-----—-—-——-———-—--——--————-—————---—-——-———-——----—26实验二:连续时间信号的频域分析————---——---—--—--——-———-————-----———————-—————-——--—————27一、实验目的及要求———----——-—--———-——-——-—-----———-27二、实验原理—-—---——--—--—--——-—--———-——————----—-—-—---————-——————-————--——-—--———--—--—-—--—271、连续时间周期信号的傅里叶级数CTFS—--——--—--—--—-——-——-————-—--—-——--—————---——272、连续时间信号的傅里叶变换CTFT————--—--———-—--—-—-—--—--——--———————-—-——————--——283、离散时间信号的傅里叶变换DTFT-—----————-—------—-—-------————------——-—-—-—---284、连续时间周期信号的傅里叶级数CTFS的MATLAB实现-—--——-————--—-—-—-----—295、用MATLAB实现CTFT及其逆变换的计算——--——-——-—-————-—--———---—-——---———--—33三、实验步骤及内容--—--——-—----——----—---———--———--—-—-—--——-—--—-———-———-——--——-———-—-—34四、实验报告要求--—--————---—-————-——————-—————---—--—---——-———--—--——-—----———-—-——-—-——48实验三:连续时间LTI系统的频域分析--———-———-——-—-—---——--———————---——---—----—-—-—---49一、实验目的及要求—----——-——--——————--—————--—-——-——-----————-—-------——-——-—-———-—————----—49二、实验原理—-—--—-—-—-—-—-—-——-———---————————----—-———-—---—---——---——-——-—--————---——--—--——491、连续时间LTI系统的频率响应————————--——-—-—---—-—-—--——-———-————-———---—-—---——-—-492、LTI系统的群延时—--—--—--——-—--——-—-—-——-—------——-—-—---——-———------———--—-——-----—-503、用MATLAB计算系统的频率响应——-—————-—-————---—-—-----———-—---—--—--———--——-—-50三、实验步骤及内容-————-—---——-—-—-——-—----——-----—-—-—-----——-—-—-————-—---———————--——-51四、实验报告要求——————--—-----—--——-——-——--———-——-—-—-——--——-—-—------—--—————--—----—-——58实验四:调制与解调以及抽样与重建---------—————————-——-————-——--—--—--—--———-—————-——--59一、实验目的及要求—-—--——-—-——-—----—--—-———--—--——--—-—--————-——--———-—--—-————----—---—--—59二、实验原理—-—--————-—-———-—-—--——-—-——-—-—-————-———----—-----—--—-———————-----—----——--—--——591、信号的抽样及抽样定理--———---—-—--——-—————-———-—---—---—-—-———-———--—--——-----—--——-592、信号抽样过程中的频谱混叠———--————--——-————-——-—--——---—-—-—---————--—-———---—-———-623、信号重建-————-—-——-—-—-————--—-——--————--———----------——---—---——------——--—-—-———-——--624、调制与解调--——---—-—----—----—-———---—----————-——---———-——--————----—————---———-----—----—-—645、通信系统中的调制与解调仿真—-—---—-———-——-———---—---—-———--————-—--——--—--—--—-————-66三、实验步骤及内容————-—————-———--—-——-—---—------——-------——-———--—--——-—-———-—--—---—-—-66四、实验报告要求--—---—--——-—---——--—--—-—-—--—-——--———-—-———--———--——————---—-——————-—----75实验五:连续时间LTI系统的复频域分析----—-—--—-——----—-—-——-——————————-—--——----——76一、实验目的及要求-———-——---—--—-————----—-——————---—--—-———---———————-—-——-—-——-—————-——-76二、实验原理--—-—-------—-—-—-—-—-------——----——-----—-—---—-—-—-—--—--—--———-—---—-----—-——761、连续时间LTI系统的复频域描述—-—---——-——-—--—————-—----———----—----—-—-—-—---——762、系统函数的零极点分布图—--—-———-——-————--—-——-—---——-—---—--———---—-———-—-—--—-----——-——773、拉普拉斯变换与傅里叶变换之间的关系-—-—--—-—-——-—-—-—--——---—-—---——--———----——-—-784、系统函数的零极点分布与系统稳定性和因果性之间的关系--—-——-——-—---———-—-——-—795、系统函数的零极点分布与系统的滤波特性—--———--——--—---—---———————-—--—--—---—————806、拉普拉斯逆变换的计算———-——-———-—-----———----——-———---—————---——-——-—--———-———-—-—81三、实验步骤及内容-—-------—-—--—---—--———--————--—-————-———---—-————--———--—-—---—-—---——82四、实验报告要求——--—---———--—-—-----——--——-—--——------—-—--—-------——--——--—-—--—-—-—-----87附录:授课方式和考核办法—----—------——-—-—-----—-—--——-—-—-—--—-——----———-—-——-------—-——88实验一信号与系统的时域分析一、实验目的1、熟悉和掌握常用的用于信号与系统时域仿真分析的MA TLAB函数;2、掌握连续时间和离散时间信号的MATLAB产生,掌握用周期延拓的方法将一个非周期信号进行周期信号延拓形成一个周期信号的MATLAB编程;3、牢固掌握系统的单位冲激响应的概念,掌握LTI系统的卷积表达式及其物理意义,掌握卷积的计算方法、卷积的基本性质;4、掌握利用MA TLAB计算卷积的编程方法,并利用所编写的MA TLAB程序验证卷积的常用基本性质;掌握MATLAB描述LTI系统的常用方法及有关函数,并学会利用MATLAB求解LTI系统响应,绘制相应曲线。
Matlab软件在信号与系统辅助教学中的应用作者:王洁丽贾素梅薛芳来源:《现代电子技术》2008年第06期摘要:Matlab是一套功能十分强大的工程计算及数据分析软件,具有友好的可视化编程界面及接近数学表达式的自然化语言。
在信号与系统课程的教学中引入该软件,可以帮助学生完成数值计算、信号与系统分析的可视化建模及仿真调试,通过实例介绍和分析该软件在信号与系统课程教学中的具体应用,引导学生使用智能化教学软件,为接下来的专业课程的学习打下坚实的基础。
关键词:Matlab;信号与系统;辅助教学;可视化建模中图分类号:TP391 文献标识码:B文章编号:1004-373X(2008)06-123-03Application of Matlab in Signal and System Course TeachingWANG Jieili,JIA Sumei,XUE Fang(Handan College,Handan,056005,China)Abstract:Matlab is a kind of engineering computation and data analysis software,which has visual programming interface and natural language of approximate mathematics expression.The software is applied in the course of signal and system,can help students to finish numerical value computation,visual modeling of signal and system analysis and simulation debugging.The practical application in system cource teaching of the software is analyzed.It makes the students use intelligent software in order to study specialized cource.Keywords:Matlab;signal and system;teaching;visual modeling1 引言《信号与系统》是电子信息与通信类专业本科生的一门重要的专业基础课程,有着很强的数学背景[1]。
a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d e0.511.5Linear Simulation ResultsTime (sec)A m p l i t u d e510-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d e510-0.50.51Impulse ResponseTime(sec)A m p l i t u d e函数int1如下:function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf)); tF=tf; for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n); end验证如下:t=[-1:0.01:4]; e=zeros(size(t)); e=(t>-1/2&t<1);[z,zz]=int1(e,t,-1); figure;plot(zz,z);-1-0.500.51 1.52 2.53 3.5400.511.5T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered4-2fsana 函数如下:function F=fsana(t,f,N)omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下:function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数。
1 信号与系统的MATLAB仿真 一、信号生成与运算的实现 1.1 实现)3(sin)()(ttttStfa
)(sin)sin()sin(sin)()(tctttttttStfa
m11.m t=-3*pi:0.01*pi:3*pi; % 定义时间范围向量t f=sinc(t/pi); % 计算Sa(t)函数 plot(t,f); % 绘制Sa(t)的波形 运行结果:
1.2 实现)10()sin()(sin)(ttttctf m12.m t=-10:0.01:10; % 定义时间范围向量t f=sinc(t); % 计算sinc(t)函数 plot(t,f); % 绘制sinc(t)的波形 运行结果:
1.3 信号相加:tttf20cos18cos)( m13.m syms t; % 定义符号变量t f=cos(18*pi*t)+cos(20*pi*t); % 计算符号函数f(t)=cos(18*pi*t)+cos(20*pi*t) ezplot(f,[0 pi]); % 绘制f(t)的波形 运行结果: 2
1.4 信号的调制:tttf50cos)4sin22()( m14.m syms t; % 定义符号变量t f=(2+2*sin(4*pi*t))*cos(50*pi*t) % 计算符号函数f(t)=(2+2*sin(4*pi*t))*cos(50*pi*t) ezplot(f,[0 pi]); % 绘制f(t)的波形 运行结果:
1.5 信号相乘:)20cos()(sin)(ttctf m15.m t=-5:0.01:5; % 定义时间范围向量 f=sinc(t).*cos(20*pi*t); % 计算函数f(t)=sinc(t)*cos(20*pi*t) plot(t,f); % 绘制f(t)的波形 title('sinc(t)*cos(20*pi*t)'); % 加注波形标题 运行结果: 3
二、系统时域的仿真分析 2.1 实现卷积)(*)(thtf,其中:)2()()()],1()([2)(ttthtttf m21.m p=0.01; % 取样时间间隔 nf=0:p:1; % f(t)对应的时间向量 f=2*((nf>=0)-(nf>=1)); % 序列f(n)的值 nh=0:p:2; % h(t)对应的时间向量 h=(nh>=0)-(nh>=2); % 序列h(n)的值 [y,k]=sconv(f,h,nf,nh,p); % 计算y(t)=f(t)*h(t) subplot(3,1,1),stairs(nf,f); % 绘制f(t)的波形 title('f(t)');axis([0 3 0 2.1]); subplot(3,1,2),stairs(nh,h); % 绘制h(t)的波形 title('h(t)');axis([0 3 0 1.1]); subplot(3,1,3),plot(k,y); % 绘制y(t)=f(t)*h(t)的波形 title('y(t)=f(t)*h(t)');axis([0 3 0 2.1]);
子程序 sconv.m % 此函数用于计算连续信号的卷积y(t)=f(t)*h(t) function [y,k]=sconv(f,h,nf,nh,p) % y:卷积积分y(t)对应的非零样值向量 % k:y(t)对应的时间向量 % f:f(t)对应的非零样值向量 % nf:f(t)对应的时间向量 % h:h(t)对应的非零样值向量 % nh:h(t)对应的时间向量 % p:取样时间间隔 y=conv(f,h); % 计算序列f(n)与h(n)的卷积和y(n) y=y*p; % y(n)变成y(t) left=nf(1)+nh(1) % 计算序列y(n)非零样值的起点位置 right=length(nf)+length(nh)-2 % 计算序列y(n)非零样值的终点位置 k=p*(left:right); % 确定卷积和y(n)非零样值的时间向量 运行结果: 4
2.2 实现卷积)(*)(thtf,其中:)()()],2()([2)(tethtttft m22.m p=0.01; % 取样时间间隔 nf=0:p:2; % f(t)对应的时间向量 f=2*((nf>=0)-(nf>=2)); % 序列f(n)的值 nh=0:p:4; % h(t)对应的时间向量 h=exp(-nh); % 序列h(n)的值 [y,k]=sconv(f,h,nf,nh,p); % 计算y(t)=f(t)*h(t) subplot(3,1,1),stairs(nf,f); % 绘制f(t)的波形 title('f(t)');axis([0 6 0 2.1]); subplot(3,1,2),plot(nh,h); % 绘制h(t)的波形 title('h(t)');axis([0 6 0 1.1]); subplot(3,1,3),plot(k,y); % 绘制y(t)=f(t)*h(t)的波形 title('y(t)=f(t)*h(t)');axis([0 6 0 2.1]);运行结果: 5
2.3 设方程 )(2)(6)(5)('''tetytytyt,试求零状态响应)(ty m23.m: yzs=dsolve('D2y+5*Dy+6*y=2*exp(-t)','y(0)=0,Dy(0)=0') ezplot(yzs,[0 8]); 运行结果:
yzs =exp(-t)+exp(-3*t)-2*exp(-2*t) 即:)()2()(32teeetyttt
2.4 已知二阶系统方程)(1)(1)()('''tLCtuLCtuLRtucc 对下列情况分别求)(th,并画出其波形。 a. FCHLR3/1,1,4 b. FCHLR1,1,2 c. FCHLR1,1,1 d. FCHLR1,1,0 m24.m: R=input('电阻R='); % 以交互方式输入电阻R的值 L=input('电感L='); % 以交互方式输入电阻L的值 C=input('电容C='); % 以交互方式输入电阻C的值 b=[1/(L*C)]; a=[1 R/L 1/(L*C)]; impulse(b,a); 运行结果: a. 电阻R=4 电感L=1 电容C=1/3 6
b. 电阻R=2 电感L=1 电容C=1 c. 电阻R=1 电感L=1 电容C=1 7
d. 电阻R=0 电感L=1 电容C=1 8
三、频域仿真分析 3.1 如图所示周期矩形脉冲,试求其幅度谱。 f(t)
-0.50.5t0…………143.54.5-4-4.5-3.5 m31.m: clear all syms t n T tao A T=4;A=1;tao=1; f=A*exp(-j*n*2*pi/T*t); fn=int(f,t,-tao/2,tao/2)/T; % 计算傅立叶系数 fn=simple(fn); % 化简 n=[-20:-1,eps,1:20]; % 给定频谱的整数自变量,eps代表0 fn=subs(fn,n,'n'); % 计算傅立叶系数对应各个n的值 subplot(2,1,1),stem(n,fn,'filled'); % 绘制频谱 line([-20 20],[0 0]); % 在图形中添加坐标线 title('周期矩形脉冲的频谱'); subplot(2,1,2),stem(n,abs(fn),'filled'); % 绘制频谱 title('周期矩形脉冲的幅度谱'); axis([-20 20 0 0.3]); 运行结果: 9
3.2 如图所示三角波信号,即:22,21)(tttf,试求其频谱)(F f(t)
t0-22
1
m32.m: syms t w f ft; % 定义符号变量 f=(1-(abs(t)/2)); % 三角波信号 ft=f*exp(-j*w*t); % 计算被积函数 F=int(ft,t,-2,2); % 计算傅立叶变换F(w) F=simple(F);F % 化简 subplot(2,1,1),ezplot(f,[-2 2]); % 绘制三角波信号 axis([-3 3 0 1.1]);title('三角波信号'); subplot(2,1,2),ezplot(abs(F),[-8:0.01:8]); % 绘制三角波信号的频谱 title('三角波信号的频谱'); 运行结果: F =-(cos(2*w)-1)/w^2
即:)(2)(sin2)2cos(1)(2222aSF
3.3 二阶低通滤波器特性为:020111)(QjH