齿轮系统动力学刚体模型
- 格式:pptx
- 大小:696.75 KB
- 文档页数:10

simpack如何制作齿轮模型
如何制作齿轮动力学模型
欢迎加群191630051制作齿轮模型的难度在于绘制齿轮,我们现在用最简单的方式制作简单的齿轮动力学模型。
1、首先在三维建模软件中制作出想要的齿轮模型,我们直接导入到Simpack 中去,因为Simpack做齿轮外形太复杂,Simpack稍微入门的盆友应该知道,Bodies在运动学模型中的作用就是“好看”。
(导入的步骤不说了,因为我已经制作相关教程了)
2、新建一个参考坐标系(方法略),它和已有参考坐标系的距离也就是齿轮的中心距。
3、Modify第一个Bodies,导入第一个齿轮,它的Joints是齿轮中心和原始坐标系03铰接,并且赋予初速度,设置为Independent。
4、新建一个体,导入第二个齿轮,它的Joints是齿轮中心和新建参考坐标系03铰接,设置为Dependent。
(并通过调节第二个齿轮
的转动角度来使两个齿轮近似啮合)
5、新建一个约束,从一个齿轮的中心到另一个齿轮的中心,我们选择14号约束。
把传动比设为-2,也就是转动方向相反,输入转速是输出转速的2倍。
点击Assembly System观察是否满足运动要求。
6、至此,一个小齿轮带动大齿轮的模型便建立了起来,点击在线积分观看运动情况,虽然传动的啮合不是很准确,但是完全不会影响到计算要求,所以本人认为这是最简单的建立齿轮模型的方法。


机械系统的动力学模型和方程动力学是研究物体运动的规律和原因的科学分支,而机械系统的动力学则是指研究机械系统中各个部件之间相互作用的力学原理和运动规律。
机械系统的动力学模型和方程是描述机械系统运动的数学表示,对于系统的分析和设计有着重要的意义。
一、机械系统的动力学模型机械系统是由各种不同的部件组成的,这些部件之间通过力进行相互作用。
为了研究和描述机械系统的运动规律,我们需要建立相应的动力学模型。
1. 质点模型当机械系统中的部件趋于无限小,可以视为质点时,可以采用质点模型进行描述。
质点模型忽略了物体的形状和结构,只考虑其质量和质心位置。
通过对质点所受外力和力矩进行求解,可以得到系统的运动方程。
2. 刚体模型当机械系统中的部件可以看作刚体时,可以采用刚体模型进行描述。
刚体模型考虑了物体的形状和结构,将其视为不会发生形变的固体。
通过对刚体受力和力矩的分析,可以得到系统的运动方程。
3. 柔性体模型当机械系统中的部件存在形变和弹性时,需要采用柔性体模型进行描述。
柔性体模型考虑了物体的弹性变形和振动,通过弹性力和振动方程的求解,可以得到系统的运动方程。
二、机械系统的动力学方程机械系统的动力学方程是描述系统运动规律的数学方程。
根据牛顿第二定律,可以得到机械系统的动力学方程。
1. 线性动力学方程对于线性系统,动力学方程可以表示为:F = m*a其中,F是物体所受的合外力,m是物体的质量,a是物体的加速度。
2. 旋转动力学方程对于旋转系统,动力学方程可以表示为:M = I*α其中,M是物体所受的合外力矩,I是物体的转动惯量,α是物体的角加速度。
3. 耦合动力学方程对于复杂的机械系统,可以通过将线性动力学方程和旋转动力学方程耦合起来,得到系统的动力学方程。
通过建立机械系统的动力学模型和方程,可以对系统的运动进行研究和分析。
得到系统的运动规律和动态响应,为系统的设计和控制提供依据。
总结:机械系统的动力学模型和方程是研究机械系统运动规律的重要工具。

振 动 与 冲 击第28卷第2期JOURNAL OF V I B RATI O N AND SHOCKVol .28No .22009 刚柔耦合齿轮三维接触动力学建模与振动分析基金项目:云南省应用基础研究基金资助项目(2006E021Q )云南省省院省校合作基金资助项目(2004YX12)云南省教育厅科技研究基金资助项目(5Y0553D )收稿日期:2008-02-13 修改稿收到日期:2008-05-23第一作者姚廷强男,博士生,1979年生通讯作者迟毅林男,教授,博士生导师,1953年生姚廷强,迟毅林,黄亚宇,谭 阳(昆明理工大学机电工程学院,昆明 650093) 摘 要:基于多体动力学理论和迟滞接触动力学方法,提出了刚柔耦合齿轮三维接触动力学模型和动力学分析新方法。
考虑轮齿与轮体间的相对柔性变形,啮合齿对间球-面三维动态接触和齿轮几何参数等因素,通过离散齿廓渐开线获得了齿面的离散接触面,从而建立了齿轮啮合传动动力学模型。
通过数值求解与仿真分析,研究了单侧齿面接触、双侧齿面接触和刚柔耦合特性对齿轮啮合传动特性的影响规律,获得了啮合轮齿全齿面接触冲击力,力矩和角速度等齿轮啮合传动的动态响应特性。
研究表明:新方法和动力学模型更真实地模拟了齿轮啮合传动的齿轮柔性变形和接触冲击等振动响应特性。
该方法和数值计算结果为齿轮啮合传动和齿轮系统动力学研究提供了理论指导和参考数据。
关键词:齿轮系统动力学;接触动力学;刚柔耦合方法;多体动力学;振动分析中图分类号:TP302 文献标识码:A 齿轮传动在实际机械系统中得到了广泛地应用,在机械系统中研究齿轮传动的动力学建模方法将具有重要的工程价值。
由于齿轮啮合传动影响因素众多,如轮齿刚度,啮合刚度,齿侧间隙和几何参数等非线性因素,使得齿轮啮合传动的接触动力学建模具有一定的难度[1-4]。
有限元法被广泛应用于研究单齿对的啮合接触特性[5],但计算效率较低。
在齿轮传动系统中,通常将齿轮啮合接触参数简化为一定数量的弹簧阻尼器连接或齿轮运动副,具有很好的计算效率,但这不是真正意义上的齿轮接触传动,计算结果存在一定的误差[7,8]。

减速器系统动力学多体建模及控制策略减速器系统作为传动装置中至关重要的组成部分,具有将高速输入转矩减速至低速输出的重要功能。
为了实现准确、高效、可靠的工作,需要对减速器系统进行动力学多体建模并设计相应的控制策略。
本文将探讨减速器系统动力学多体建模的方法以及针对不同控制目标的控制策略。
一、减速器系统动力学多体建模减速器系统的动力学行为复杂,因此需要进行多体建模来描述系统的运动特性。
多体建模可以分为两个主要步骤:刚体建模和柔性部件建模。
1. 刚体建模减速器系统中的齿轮、轴承等部件多为刚性材料,可以近似看作刚体。
因此,可以使用欧拉角等方法建立刚体模型,并通过牛顿-欧拉方程描述其运动行为。
同时,需考虑刚体之间的接触、干涉等约束条件,以确保模型的准确度。
2. 柔性部件建模减速器系统中的某些部件,如齿轮轴、弹簧传动等存在一定的柔性。
为了更准确地描述系统的动力学行为,需要考虑柔性部件的挠度和变形。
可以使用有限元法等方法建立柔性部件的模型,并将其与刚体模型进行耦合,实现准确的多体建模。
二、减速器系统控制策略针对不同的控制目标,可以采用不同的控制策略来实现对减速器系统的控制。
以下是几种常见的控制策略:1. 速度控制速度控制是减速器系统中最常见的控制策略之一。
通过对输入速度和输出速度进行测量,并根据速度误差调整控制器输出,可以实现减速器系统的稳定运行。
常用的速度控制方法包括PID控制、模糊控制等。
2. 位置控制当需要精确控制减速器系统输出位置时,可以采用位置控制策略。
通过测量输出位置并与期望位置进行比较,根据位置误差调整控制器输出,实现准确的位置控制。
位置控制常用的方法有PID控制、自适应控制等。
3. 轨迹控制轨迹控制主要针对要求减速器系统输出沿特定轨迹运动的应用。
通过给定期望轨迹,并根据实际运动轨迹进行比较,调整控制器输出,使得减速器系统输出与期望轨迹一致。
轨迹控制可以通过模型预测控制、轨迹跟踪等方法实现。
4. 力控制在一些特殊应用中,需要对减速器系统的输出力进行控制。

齿轮系统动力学的理论体系*王建军 副教授王建军 李润方 摘要 根据对国内外齿轮系统动力学研究成果的系统总结,阐述齿轮系统动力学理论的基本结构体系。
说明齿轮动力学的发展过程;围绕动态激励、模型类型、建模和求解方法以及齿轮系统的固有特性、动态响应和动力稳定性等介绍齿轮系统动力学所涉及的基本问题,讨论该理论的主要工程应用的基础上,提出应进一步研究的方向与重点。
关键词 齿轮系统 动力学性能 理论体系 正问题 反问题中国图书资料分类法分类号 T G132.411 齿轮系统动力学基本理论体系齿轮系统动力学[1]是研究齿轮系统在传递运动和动力过程中的动力学行为的一门科学。
它以齿轮系统为对象,以齿轮副啮合过程的动力学特性为核心,以提高和改善齿轮系统的动力学行为为目的,在充分考虑系统各零部件动态特性的基础上,利用振动力学理论和方法,研究齿轮系统在传递动力和运动中振动、冲击、噪声的基本规律,为设计制造小振动、低噪声、高可靠性、高传动性能的齿轮系统提供理论依据。
齿轮系统是机器最主要的动力和运动传递装置,其力学行为和工作性能对整个机器有重要影响。
因此,齿轮系统动力学近百年来一直受到人们的广泛关注,尤其是近20年来,由于相关力学的理论与实验技术的发展,促进了齿轮系统动力学的深入研究。
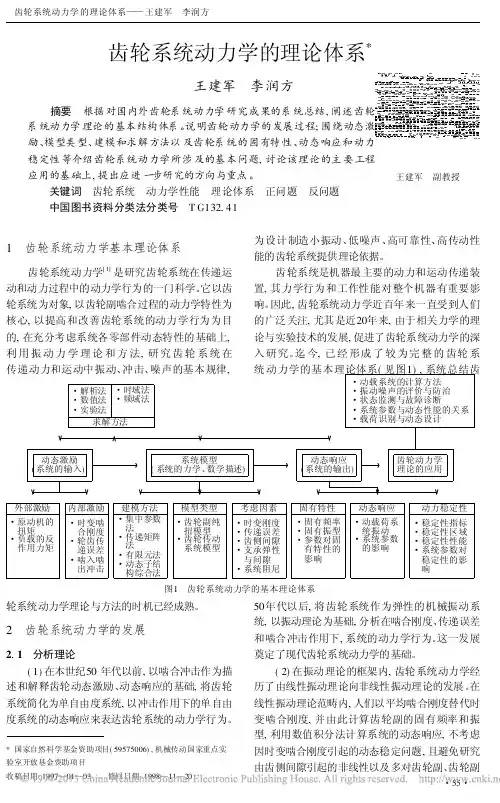
迄今,已经形成了较为完整的齿轮系统动力学的基本理论体系(见图1),系统总结齿图1齿轮系统动力学的基本理论体系・动载系统的计算方法・振动噪声的评价与防治・状态监测与故障诊断・系统参数与动态性能的关系・载荷识别与动态设计齿轮动力学理论的应用动态响应(系统的输出)系统模型(系统的力学、数学描述)动态激励(系统的输入)・稳定性指标・稳定性区域・稳定性性能・系统参数对稳定性的影响动力稳定性・动载荷系统振动・系统参数的影响动态响应・固有频率・固有振型・参数对固有特性的影响固有特性・时变刚度・传递误差・齿侧间隙・支承弹性与间隙・系统阻尼考虑因素・齿轮副纯扭模型・齿轮传动系统模型模型类型・集中参数法・传递矩阵法・有限元法・动态子结构综合法建模方法・时变啮合刚度・轮齿传递误差・啮入啮出冲击内部激励・原动机的扭矩・负载的反作用力矩外部激励求解方法・时域法・频域法・解析法・数值法・实验法*国家自然科学基金资助项目(59575006),机械传动国家重点实验室开放基金资助项目收稿日期:1997—01—03 修回日期:1998—11—20轮系统动力学理论与方法的时机已经成熟。


机械系统动力学建模与分析机械系统动力学建模与分析是研究机械系统在外部作用下的运动规律的一门学科。
它通过建立机械系统的动力学模型,并利用运动学和动力学分析的方法,研究机械系统的运动行为和力学特性,为机械设计、控制和优化提供理论指导和技术支持。
机械系统动力学建模首先需要进行系统分析,确定所研究的机械系统的结构和组成部分。
机械系统一般由刚体、柔性体和质点组成,通过零部件的连接和约束形成整体结构。
然后,根据机械系统的实际工作条件和运动需求,选择适当的动力学模型。
常用的机械系统动力学模型有刚体模型、柔性体模型和混合模型等。
刚体模型是最常用的机械系统动力学模型之一、在刚体模型中,机械系统的各部分被视为刚体,不考虑形变和扭转等因素,只研究刚体的整体运动。
刚体模型适用于描述刚性连接和运动,如摆线机构和齿轮传动等。
利用刚体模型可以建立机械系统的位置、速度和加速度之间的关系,用以描述系统的运动特性。
柔性体模型适用于研究柔性连接和变形的机械系统。
与刚体模型不同,柔性体模型考虑了系统的形变和振动等因素,能够更准确地描述机械系统的振动特性。
柔性体模型根据材料的力学性质,可以采用连续体力学或离散单元法进行建模。
常用的柔性体模型有有限元模型和模态分析模型等。
混合模型是刚体模型和柔性体模型的结合,用于研究既有刚性连接又有柔性变形的机械系统。
在混合模型中,机械系统的各部分既可以视为刚体,也可以视为柔性体,根据实际情况选择合适的模型。
混合模型结合了刚体模型和柔性体模型的优势,既能考虑刚性连接的运动,又能考虑柔性变形的影响,能够更全面地描述机械系统的运动特性。
除了动力学模型的选择,机械系统动力学分析还需要使用运动学和动力学的方法进行分析。
运动学分析研究机械系统的位置、速度和加速度之间的关系,通过建立物体的运动方程,求解系统的运动参数。
动力学分析研究机械系统的力学特性,包括力的作用、力矩的作用、力的平衡和动量守恒等。
通过建立物体的动力学方程,求解系统的运动行为。

机械系统的动力学模型建立与优化研究一、引言机械系统的动力学模型建立与优化研究一直是工程领域的重要课题。
在实际工程中,了解机械系统的动力学行为对于设计、优化和控制都至关重要。
本文将讨论机械系统的动力学模型建立和优化的相关方法和应用。
二、机械系统动力学模型建立1. 质点动力学模型质点动力学模型是机械系统中最简单且常用的模型。
它假设机械系统可以看作一个质点,没有角度和形状的变化。
通过牛顿定律,可以建立质点的运动方程,进而了解系统的运动特性。
这种模型适用于一些简单的机械系统,如自行车等。
2. 刚体动力学模型刚体动力学模型假设机械系统可以看作一个刚体,不仅考虑质点的运动,还考虑刚体的旋转。
对于刚体的运动,可以使用欧拉角或者四元数进行描述。
通过牛顿-欧拉方程,可以建立刚体的运动方程,并得到系统的运动特性。
这种模型适用于一些复杂的机械系统,如汽车、机器人等。
3. 弹性体动力学模型在一些机械系统中,弹性变形是不可忽略的。
为了更准确地描述机械系统的运动行为,需要考虑弹性体的变形和应力分布。
在弹性体动力学模型中,可以使用有限元方法建立有限元模型,通过有限元模型可以得到机械系统的应力和位移分布,进而预测系统的运动特性。
这种模型适用于一些含有弹性材料的机械系统,如弹簧、悬挂系统等。
三、机械系统动力学模型优化机械系统的动力学模型建立只是第一步,如何对模型进行优化是一个更复杂的问题。
在优化过程中,需要考虑多个因素,如系统的性能、效率、稳定性和成本等。
下面介绍两种常见的优化方法。
1. 多目标优化方法多目标优化方法是一种考虑多个目标函数并寻求最优解的方法。
在机械系统的动力学模型优化中,可能存在多个相互矛盾的目标,如提高系统的性能同时降低成本,增加系统的稳定性同时减少功耗等。
使用多目标优化方法可以找到系统在多个目标下的最优解,帮助决策者做出权衡。
2. 参数优化方法参数优化方法是一种通过调整模型参数以达到最优解的方法。
在机械系统的动力学模型中,可能存在一些设计参数,如材料的选择、结构的尺寸等。

XXXX学士学位论文直齿行星齿轮传动动力学分析作者:AAA指导教师:BB班级:CCC班2013年10月27日摘要:行星齿轮被广泛应用于船舶、飞机、汽车、重型机械等许多领域,它的振动和噪音一直以来都是普遍关注的问题。
为了减小其振动和噪音,动力学分析是必不可少的。
本文分析了行星齿轮动力学当中的一些关键性问题,提高了对于行星齿轮传动动态特性的理解。
本文在系杆随动参考坐标系下建立NGW型直齿行星齿轮传动的动力学模型。
把行星齿轮机构划分成几个相互关联的子系统,通过分析各构件间的相对位移关系利用牛顿第二定律推导出系统的运动微分方程。
应用仿真分析软件ADAMS对行星齿轮传动系统模型进行仿真模拟及运动学分析,并应用solidworks软件对行星齿轮传动系统进行三维实体参数化建模。
实现了用虚拟样机来代替实际样机进行验证设计,提高了设计质量和效率。
关键词:行星齿轮,动力学分析,ADAMS,仿真Abstract:Planetary gear noise and vibration are primary concerns in their applications in the transmissions of marine vessels, aircrafts, automobiles, and heavy machinery. Dynamic analysis is essential to the noise and vibration reduction.This work analytically investigates some critical issues and advances the understanding of planetary gear dynamics. This work Developed An analytical dynamic model of NGW spur planetary gear unit. In order to derive the displacement relationships between gears and carrier, divided the planetary gear mechanism into several sub systems. The governing differential equations were obtained by Newton's second law.ADAMS simulation analysis software for planetary gear drive system is applied to simulate and perform dynamic analysis. And solidworks software for planetary gear drive system to build three-dimensional solid parametric modeling is applied. With a virtual prototype instead of the actual prototype for the design verification, the design quality and efficiency is improved.Key word:planetary gear transmissions, dynamic analysis, ADAMS, simulation目录1 绪论 (1)1.1 本文研究的背景及意义 (1)1.2 行星齿轮传动的特点及其应用 (1)1.2.1 行星齿轮传动简介 (2)1.2.2 行星齿轮传动的特点 (2)1.2.3 行星齿轮传动的应用 (2)1.3 齿轮系统动力学概述 (4)1.3.1 动力学概述 (4)1.3.2 齿轮系统动力学研究的目标及内容 (4)1.4 行星齿轮传动动力学研究现状及展望 (5)1.4.1 行星齿轮传动动力学研究现状 (5)1.4.2 行星齿轮传动动力学研究展望 (6)1.5 论文研究的主要内容 (7)1.5.1 直齿行星齿轮传动动力学建模 (7)1.5.2 直齿行星齿轮传动固有特性分析 (8)1.5.3 直齿行星齿轮传动动响应分析 (8)1.6 初始数据 (9)2 直齿行星齿轮传动动力学建模 (10)2.1 数学模型 (10)2.2 动力学微分方程的推导 (11)2.2.1 变形协调条件的推导 (11)2.2.2 子构件运动微分方程的建立 (13)2.2.3 系统运动微分方程的建立 (17)3 相关设计参数的计算 (19)3.1 尺寸参数与质量参数的计算 (19)3.1.1 尺寸系数的计算 (19)3.1.2 质量参数的计算 (20)3.2 载荷计算 (20)3.3 刚度参数的计算 (24)3.3.1 轴承刚度系数的计算方法 (25)3.3.2 齿轮啮合综合刚度的计算方法 (27)3.3.3 刚度参数的计算结果 (31)3.4 轮齿啮合点的计算 (31)4 直齿行星齿轮传动固有特性分析 (32)4.1 ADAMS中动力学模型的建立 (32)4.2 利用ADAMS进行固有特性分析 (32)4.2.1 直齿行星齿轮传动系统的固有频率分析 (33)4.2.2 直齿行星齿轮传动系统的振型分析 (33)4.3 数学模型与仿真模型结果对比 (35)4.4 直齿行星齿轮传动固有特性分析的结论 (36)4.4.1 旋转模式 (36)4.4.2 平移模式 (36)4.4.3 行星模式 (37)5 直齿行星齿轮传动动响应分析 (38)5.1 直齿行星齿轮系统实体模型的建立 (38)5.2 ADAMS与solidworks之间的数据交换 (38)5.3 建立行星齿轮多体动力学模型 (38)5.3.1 ADAMS碰撞力的选择及定义 (39)5.3.2 碰撞参数的确定 (40)5.4 仿真计算 (41)5.4.1 输入输出转速仿真结果及分析 (41)5.4.2 接触力仿真结果及分析 (42)6 全文总结及展望 (47)6.1 全文总结 (47)6.2 展望 (47)致谢参考文献附录1 绪论1.1 本文研究的背景及意义随着科学技术的飞速发展,机械工业也发生着日新月异的变化,特别是近二三十年来机电一体化产品的广泛应用,在机械、航空、航天领域的机电系统正朝着高速、重载、大柔度、高精度和自动化的方向发展,使得人们对设备的动态性能提出了更高的要求。
齿轮系统动⼒学及接触问题摘要齿轮⾮线性接触特性及啮合刚度的研究对于齿轮接触特性的研究,可以采⽤解析法和数值法。
解析法包括材料⼒学计算法和弹性⼒学计算法等,数值法包括接触问题的有限元法和边界元法。
齿轮接触特性计算的解析法把啮合轮齿简化为两圆柱体通过Hertz公式计算接触应⼒及接触变形。
但由于齿轮齿廓曲率半径沿齿⾯变化,加之Hertz公式不能确定齿⾯接触疲劳强度计算中的累积塑性变形,因此其计算结果较为近似往往⽤修正系数(动载系数、齿向载荷分布系数、齿间载荷分配系数等)对接触应⼒进⾏修正。
对于齿轮接触变形的计算公式,G Lundberg、H .Winter、梅泽清彦、寺内喜男等分别采⽤材料⼒学和弹性⼒学⽅法进⾏了推导。
接触问题数值⽅法的研究始于70年代中期,⽽后得到⼴泛应⽤。
0.C. Zienkiewicz、A.Fr ancevilla、N .Okamoto、 J. T. Stadter、T .D .Sachdeva等分别⽤刚度矩阵修正法或间隙单元法研究了⼆维及三维弹性接触问题。
J.Tseng、陈万吉、李润⽅等提出了接触问题有限元混合法。
该⽅法以接触内⼒作为基本未知量,将整个系统总刚度矩阵凝缩到接触边界,形成关于接触内⼒的柔度⽅程,⼤⼤缩短了计算时间。
⽽后,李润⽅、陈万吉、B .C. Lee等将接触问题的表⾯⾮线性和材料⾮线性相藕合。
提出了有摩擦的弹塑性接触有限元混合法。
T.An dersion等提出了⼆维弹性接触问题的边界元法,⽽后逐渐发展到三维接触问题、热弹性问题等。
这些研究成果为齿轮接触特性的数值分析提供了理论基础。
S. M. Vijayakar⽤弹性接触有限元法研究了斜齿轮、锥齿轮、蜗轮蜗杆的接触应⼒。
李润⽅等对轮齿接触特性作了深⼊的研究考虑了轮齿的弹塑性变形、齿⾯摩擦、本体温度等的影响,并对轮齿啮合过程作分析,给出了最佳齿廓修形曲线等重要结论。
C.Gosselin等⽤有限元法分析了直齿轮和锥齿轮接触区的位移和应⼒,并与解析解进⾏了⽐较,两者相差20%以上。