实验模态分析

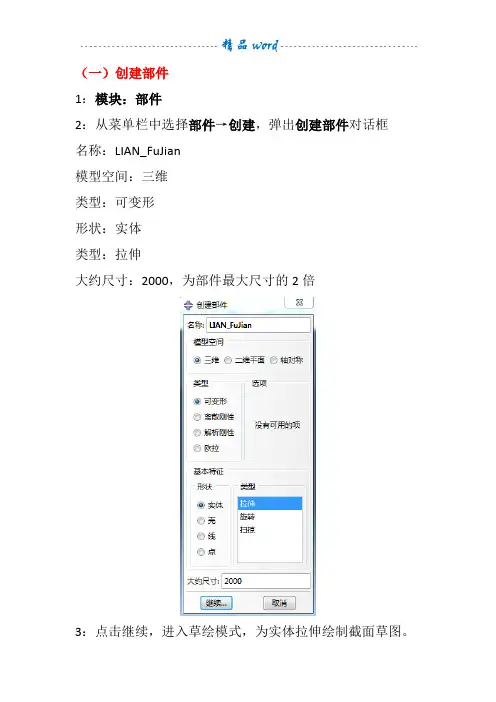
（一）创建部件1：模块：部件2：从菜单栏中选择部件→创建，弹出创建部件对话框名称：LIAN_FuJian模型空间：三维类型：可变形形状：实体类型：拉伸大约尺寸：2000，为部件最大尺寸的2倍3：点击继续，进入草绘模式，为实体拉伸绘制截面草图。

4：点击创建圆工具，绘制2个同心圆。

大圆直径为1000，小圆直径为400。

5：点击创建构造：圆工具，绘制一个直径为700的构造圆。

6：点击创建构造工具，创建2条构造线，一并添加固定约束。

7：点击创建圆工具，以构造圆与竖直构造线的交点为圆心，绘制一个直径为100的圆。

8：点击环形阵列工具，点选刚才创建的圆为要阵列的实体，按下鼠标中键，弹出环形阵列对话框个数：6总角度：360点击确定阵列结果如下：9：在绘图区按下鼠标中键，弹出编辑基本拉伸对话框类型：指定深度深度：200点击确定，第一个部件绘制完成10：创建第二个部件-轴：ZHOU。

（二）装配1：模块：装配2：点击创建实例工具，弹出创建实例对话框创建实例：从部件部件：按住Ctrl选取LIAN_FuJian与ZHOU这2个部件实例类型：非独立（网格在部件上）点击确定，装配体如下2：点击平移实例工具，选择ZHOU为要平移的实例，点击完成。

输入平移向量的起始点（0，0，0），回车；输入平移向量的终点（0，0，100），回车。

再点击确定，平移后的装配体如下3：点击合并/切割实例工具，弹出合并/切割实体对话框。

部件名：ASM运算：合并-几何原始实体：禁用相交边界：删除点击继续，选择待合并的实例，框选整个模型，点击完成。

4：在模型树下删除LIAN_FuJian-1和ZHOU-15：由于在接下来的分析中只需要用到ASM部件，故可以将LIAN_FuJian和ZHOU删除。

模块：部件点击部件管理器工具，选中LIAN_FuJian和ZHOU，删除。

（三）定义材料和截面属性1：模块：属性2：点击创建材料工具，弹出编辑材料对话框名称：Steel通用→密度：7.85e-9力学→弹性→弹性：弹性模量：2.1e5泊松比：0.3点击确定3：单击创建截面工具，弹出创建截面对话框名称：Section-1类别：实体类型：均质点击继续，弹出编辑截面对话框。

结构模态分析实验报告1. 引言在结构工程领域中，结构模态分析是一种重要的分析方法，旨在研究和了解结构的固有特性，包括自然频率、振型和阻尼等。

通过模态分析，我们可以评估结构的稳定性、安全性以及对外界激励的响应能力。

本实验旨在通过模态分析方法对某一结构进行测试和分析，以获取结构的模态参数。

2. 实验设备和方法2.1 实验设备本实验使用的设备包括： - 振动台：用于提供激励力的设备。

- 振动传感器：用于测量结构的振动响应。

- 数据采集系统：用于采集传感器测量到的数据。

2.2 实验方法本实验采用以下步骤进行结构模态分析： 1. 确定实验对象：选择待测试的结构，并对其进行准备，如清洁表面、固定传感器等。

2. 安装传感器：将振动传感器安装在结构的关键位置，以测量结构的振动响应。

3. 准备振动台：调整振动台的参数，如频率、振幅等，以提供适当的激励力。

4. 开始振动测试：启动振动台，通过施加激励力对结构进行振动，并同时采集传感器的数据。

5. 数据分析：利用数据采集系统获取的数据，进行模态分析，计算结构的自然频率、振型等参数。

6.结果分析：根据计算得到的模态参数，对结构的稳定性和响应能力进行评估。

3. 实验结果通过实验和数据分析，我们得到了以下结构的模态参数： - 自然频率1：X Hz - 自然频率2：Y Hz - 自然频率3：Z Hz同时，我们还得到了结构的振型图，描述了结构在不同振动频率下的振动形态。

4. 结果分析根据实验结果，我们可以对结构的稳定性和响应能力进行初步评估。

通过比较得到的自然频率和已知的设计要求，我们可以判断结构是否存在共振现象；通过分析振型图，我们可以了解结构在不同振动频率下的振动特点。

5. 结论本实验通过结构模态分析方法，获取了待测试结构的模态参数，并对其稳定性和响应能力进行了初步评估。

实验结果表明，该结构在给定的激励条件下表现出良好的稳定性和响应能力。

这些结果对于结构的设计和改进具有重要的参考价值。

模态分析方法与步骤下面我将从模态分析的定义、方法、步骤和案例实践等方面进行详细介绍。

一、模态分析的定义模态分析是指通过对系统的不同动态模态（如结构模态、振动模态等）进行分析和评估，以揭示系统的特性、行为和潜在问题。

其目的是为了更好地了解系统的功能、性能、稳定性等，并为系统的优化提供依据。

二、模态分析的方法1.实验方法：通过实际测试和测量，获取系统的模态参数（如固有频率、阻尼比、模态形态等），从而分析系统的动态特性。

2.数值模拟方法：利用数学建模和计算机仿真技术，建立系统的动力学模型，并进行模拟分析，以获取系统的模态响应和模态特性。

3.统计分析方法：通过对大量历史数据或采样数据的分析，探索系统的模态变化规律和概率分布情况。

三、模态分析的步骤1.确定分析目标：明确需要进行模态分析的对象、目的和要求。

例如，是为了定位系统的故障、评估系统的稳定性、优化系统的结构等。

2.数据采集和处理：根据分析目标，确定所需的数据类型和采集方法，例如使用传感器进行采集或获取历史数据。

然后对采集到的数据进行处理，如滤波、时域变换、频域分析等。

3.建立模型：根据已有的数据和系统特性，建立适当的模型。

例如，对其中一结构物进行模态分析时，可以建立结构的有限元模型。

4.分析模态特性：利用实验、仿真或统计方法，分析系统的模态特性，如固有频率、振型等。

可以绘制频谱图、振型图等，以便直观地展示结果。

5.识别问题和改进方案：基于对系统模态特性的分析，识别潜在问题，并提出相应的改进方案。

例如，如果发现其中一模态频率太低，可能意味着系统存在过度振动或共振问题，需要采取相应的措施来改进。

6.验证和优化：对改进方案进行验证和优化，以确保其有效性和可行性。

可以通过迭代分析和实验评估来逐步完善方案。

四、模态分析的案例实践1.桥梁的模态分析：对大跨度桥梁的模态分析可以帮助提前发现潜在的共振问题，并优化桥梁的设计和结构。

例如，可以通过数值模拟方法对桥梁的振动特性进行分析，以确定固有频率和振型，并预测桥梁在不同外界激励下的动态响应。

悬臂梁模态分析实验报告一、实验目的通过对悬臂梁进行模态分析实验，了解悬臂梁在不同振动模态下的固有频率和振型，并验证计算模态分析结果的准确性。

二、实验原理悬臂梁是一种常见的结构形式，其在振动过程中会出现不同的振动模态，每个振动模态对应一个固有频率和振型。

模态分析是通过实验或计算的方法，确定一个结构在振动中的固有频率和振型的过程。

在本实验中，我们选择一根长度为L的悬臂梁，将其固定在一个支撑架上。

在悬臂梁上施加一个外力，使梁发生振动。

利用振动传感器测量悬臂梁不同位置处的振动加速度，并通过信号处理来得到悬臂梁的模态信息。

三、实验器材和仪器1.悬臂梁：长度为L、直径为d的悬臂梁2.支撑架：用来支撑悬臂梁的架子3.外力施加装置：用来在悬臂梁上施加外力的装置4.振动传感器：用来测量悬臂梁不同位置的振动加速度5.信号处理器：用来对振动信号进行处理和分析的设备四、实验步骤1.将悬臂梁固定在支撑架上，并调整支撑架的角度和高度，使悬臂梁处于水平状态。

2.在悬臂梁上选择一个合适的位置，安装振动传感器，并将传感器连接到信号处理器上。

3.利用外力施加装置，在悬臂梁上施加一个单一方向的外力。

4.启动信号处理器，并进行振动信号的采集和处理。

5.分析处理后的振动信号数据，得到悬臂梁的固有频率和振型。

五、实验结果及讨论根据实验数据，我们得到了悬臂梁的固有频率和振型，并与理论计算值进行比较。

整个实验过程中，我们进行了多次实验，分别在不同的外力大小下进行了振动测试。

通过对比实验数据和计算结果，验证了模态分析方法的准确性。

六、实验结论通过模态分析实验，我们成功地确定了悬臂梁在不同振动模态下的固有频率和振型，并验证了计算模态分析结果的准确性。

这对于进一步研究和应用悬臂梁的振动特性具有重要的意义。

七、实验心得通过本次实验，我深刻了解了悬臂梁的振动特性和模态分析的原理和方法。

实验过程中，我学会了如何正确选择和安装振动传感器，以及如何对振动信号进行分析处理。

模态分析的应用及它的试验模态分析模态分析是一种通过分析系统的模态特性来预测和改善系统性能的方法。

它可以应用于各种领域，包括机械工程、土木工程、航空航天工程、电力系统等。

在机械工程中，模态分析可以帮助设计人员了解结构的振动特性，以及在不同条件下结构的自然频率和振型。

这对于避免共振现象、减少结构疲劳和保证结构稳定性非常重要。

模态分析还可以用来优化设计，改善结构的刚度和减轻结构的重量。

在土木工程中，模态分析可以用来评估建筑物、桥梁和其他结构的振动响应。

通过模态分析，可以确定结构的临界风速、车辆通过时的振动响应等，以确保结构的安全性和使用寿命。

在航空航天工程中，模态分析可以帮助设计人员了解飞机、火箭等飞行器的自由振动特性。

通过模态分析，可以确定飞行器的固有振动频率和振动模态，并优化设计以减少结构的振动响应和降低噪音。

在电力系统中，模态分析可以用来评估系统的稳定性和动态响应。

通过模态分析，可以确定系统中存在的低频振荡模态，以及可能导致系统瓦解的致命模态。

这有助于设计人员优化系统的控制策略和改善系统的稳定性。

试验模态分析是通过实验测量来获取结构的模态参数，以进行模态分析的方法。

试验模态分析通常分为激励法和反馈法两种方法。

在激励法中，实验过程中对结构施加激励信号，并通过测量系统的响应信号来获取结构的模态参数。

常用的激励信号包括冲击信号和正弦信号。

通过分析结构响应信号的频谱特性，可以确定结构的自然频率和阻尼比。

在反馈法中，通过测量系统的响应信号，然后根据经验公式或模态参数识别算法，反推出结构的模态参数。

反馈法不需要对结构进行外部激励，因此更加方便实用，但也存在一定的理论假设和误差。

试验模态分析可以用于实际结构的模态识别和评估，因为它可以直接测量结构的实际响应，避免了理论模态分析中的近似和假设。

然而，试验模态分析需要在实际工程环境中进行，受到环境噪声、传感器布置等因素的影响，所以需要合理设计实验方案和选择适当的仪器设备。

一、实验目的1. 通过实验了解梁的模态特性，包括固有频率和振型；2. 掌握梁模态分析的基本方法，包括激振、信号采集、数据处理等；3. 熟悉实验设备的操作和调试，提高实验技能。

二、实验原理梁的模态分析是研究结构振动特性的重要手段。

本实验采用共振法进行梁的模态分析，即通过激振使梁产生振动，通过信号采集和数据处理得到梁的固有频率和振型。

三、实验设备与材料1. 实验设备：激振器、加速度传感器、信号采集系统、数据采集卡、计算机等；2. 实验材料：一根等截面简支梁。

四、实验步骤1. 将梁固定在实验台上，确保梁的支承条件符合简支梁的要求；2. 将加速度传感器粘贴在梁上，用于采集梁的振动信号；3. 连接信号采集系统和数据采集卡，确保信号采集系统与计算机正常连接；4. 开启激振器，进行激振实验；5. 采集梁的振动信号，并对信号进行预处理，如滤波、去噪等；6. 利用信号处理软件对采集到的信号进行频谱分析，得到梁的固有频率和振型。

五、实验结果与分析1. 实验数据（1）梁的几何参数：长度L=1000mm，宽度b=50mm，高度h=100mm；（2）材料参数：弹性模量E=2.06×10^5 MPa，密度ρ=7850 kg/m^3；（3）实验得到的固有频率和振型。

2. 实验结果分析（1）固有频率：根据实验数据，得到梁的前三阶固有频率分别为f1=50Hz、f2=120Hz、f3=180Hz；（2）振型：通过频谱分析，得到梁的前三阶振型如图1所示。

图1 梁的前三阶振型从实验结果可以看出，梁的固有频率和振型与理论计算值基本吻合，说明本实验所采用的模态分析方法具有较高的精度。

六、实验总结1. 通过本次实验，掌握了梁的模态分析基本方法，提高了实验技能；2. 熟悉了实验设备的操作和调试，为今后进行类似实验奠定了基础；3. 实验结果表明，本实验所采用的模态分析方法具有较高的精度，为工程实际提供了参考。

七、实验建议1. 在实验过程中，注意激振器的激振频率应与梁的固有频率接近，以提高实验精度；2. 信号采集时，应确保传感器粘贴牢固，避免信号干扰；3. 在数据处理过程中，注意滤波、去噪等预处理步骤，以提高数据质量；4. 实验过程中，应仔细观察梁的振动现象，以便及时发现问题并进行调整。

第10章 实验模态分析试验模态分析(experimental modal analysis )是利用振动测试、信号处理和参数识别的方法，确定振动结构动态特性的现代试验分析技术。

一个振动结构的动态特性可以用模态来表示，表征结构模态的特征参数是结构的各阶固有频率、固有振型、模态质量、模态刚度和模态阻尼等。

在结构动力分析中，建立用模态参数表示的振动系统的运动方程，并确定其模态参数的过程称为模态分析(modal analysis )。

模态分析存在两个过程，一个是正过程，即根据结构的物理模型和物理参数建立系统的数学模型，通过引入模态参数建立模态方程，其目的是为了使方程解耦简化计算，这就是通常所说的模态分析，也称为理论模态分析，对于复杂结构，从理论上去计算这些模态参数，进行理论模态分析是很困难的。

试验模态分析是模态分析的另一过程，也称为逆过程，它通过对结构的输入激励和输出响应的测试，在物理参数未知的情况下由计算机进行信号处理，通过参数识别找出振动系统的模态参数，建立结构的模态模型，非常直观地了解各阶模态振动的情况，为结构动力分析提供分析参数。

试验模态分析是一种在结构动力分析中应用广泛、发展迅速的理论与实验技术相结合的有效方法。

§10.1 机械阻抗和机械导纳机械阻抗的概念来自于机械振动的电模拟，根据电路中存在的电阻抗相应地引入机械阻抗的概念：机械系统受到简谐激励时激励力的复数力幅与响应的复数振幅之比称为机械阻抗，并将机械阻抗的倒数称为机械导纳。

由于振动系统的响应是用位移、速度和加速度来表示的，故机械阻抗（导纳）有六种形式：位移阻抗（动刚度） /x Z F X = 位移导纳（动柔度） /x Y X F = 速度阻抗 /v Z F V = 速度导纳 /v Y V F = 加速度阻抗（动质量） /a Z F A = 加速度导纳（惯性率） /a Y A F =其中，F 为复数力幅，X 、V 、A 分别为位移、速度和加速度的复数振幅。

2022年春季学期讨论生课程考核（读书报告、讨论报告）考核科目：试验模态分析同学所在院（系）：同学所在学科:学生姓名:学号:学生类别:考核结果阅卷人试验模态分析与参数识别报告模态分析可分为试验模态分析与工作模态分析等。

模态分析的最终目标是识别出系统的模态参数，为结构系统的振动分析、振动故障诊断和预报、结构动力特性的优化设计供应依据。

模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。

这些模态参数可以由计算或试验分析取得，这样一个计算或试验分析过程称为模态分析。

1、模态分析原理模态分析的过程是将线性时不变系统振动微分方程组中的物理坐标变换为模态坐标,使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，坐标变换的变换矩阵为振型矩阵，其每列即为各阶振型。

[M]{X}÷[C]{X}+[K]{X}={F(∕)}⑴其中：[M]—质量矩阵，[K]一刚度矩阵，[C]一粘性阻尼矩阵，{尸⑺}一激励力的列阵。

振动模态是弹性结构固有的、整体的特性。

假如通过模态分析方法搞清晰了结构物在某一易受影响的频率范围内，各阶主要模态的特性，就可能预知结构在此频段内，在外部或内部各种振源作用下实际振动响应，而且一旦通过模态分析知道模态参数并赐予验证，就可以把这些参数用于设计过程，优化系统动态特性，或者讨论把该结构连接到其他结构上时所产生的影响。

方程(1)经傅氏变换，可得频域内的振动方程：(-√ [ M] + j∖∖[q +[ ∕C]) {X(ιv)} = {F(w)}(2)对应于固有频率叼的固有振型或模态向量以幅值最大点为参考点的表达式为：M={X(叫)}∕X(叫)厘。

它们亦即简谐自由振动的主振型，满意以下关系式：([K]^[M])[∣ }z=O(3)此代数方程组的系数行列式等于零，即为特征方程式：[M], [K]为实数对称矩阵，[M] 正定，[K]为非负定，其特征值域和对应的特征向量为实数。

实验模态分析方法与应用概论引言：实验模态分析是一种用于研究结构动力学特性的方法，通过实验测量和数据分析，可以确定结构的固有频率、阻尼比以及模态形态等参数。

实验模态分析方法包括模态参数识别、模态不确定度评估和模型修正三个步骤。

本文将介绍实验模态分析方法的基本原理和常用应用。

一、实验模态分析方法的基本原理1.1模态分析的基本思想1.2模态参数识别在模态参数识别过程中，需要选择合适的激励信号和测量点位置，通过对结构的振动响应信号进行分析，得到结构的固有频率、阻尼比和模态振型等参数。

常用的模态参数识别方法包括傅里叶变换法、自相关法、互谱法和最小二乘法等。

1.3模态形态绘制在模态形态绘制过程中，通常需要在结构上布置加速度传感器或激光测振仪等测量设备，测量结构的振动响应信号。

然后，通过信号处理和数据分析技术，将实际测量的振动响应数据转化为结构的模态振型，并绘制成图像。

二、实验模态分析方法的应用2.1结构健康监测实验模态分析方法可以用于结构健康监测，通过定期对结构进行振动测试和模态分析，可以及时发现结构的损伤和变形等问题，为结构的维护和修复提供参考。

例如，在桥梁结构的健康监测中，可以通过模态分析方法来确定桥梁的固有频率和模态形态，从而判断桥梁的结构安全状况。

2.2结构参数识别实验模态分析方法还可以用于结构参数的识别。

通过对结构在不同工况下的振动响应信号进行测量和分析，可以确定结构的质量、刚度和阻尼等参数。

例如，在机械系统中，可以通过模态分析方法来识别机械系统的转子和轴系的质量和刚度参数，从而评估系统的性能和可靠性。

2.3结构优化设计实验模态分析方法还可以用于结构的优化设计。

通过对不同结构参数和材料的改变进行模态分析和比较，可以评估结构的动力特性，并选择最佳的设计方案。

例如，在汽车工程中，可以通过模态分析方法来优化汽车底盘的结构，提高汽车的悬挂系统和减震器的性能。

总结：实验模态分析方法是一种研究结构动力学特性的重要手段，通过实验测量和数据分析，可以确定结构的固有频率、阻尼比和模态振型等参数。

实验模态分析技术实验报告一、实验内容用锤击激振法测量传递函数，求取驱动桥壳的模态参数。

二、实验目的（1）掌握测量传递函数常用的锤击激振法；（2）测量激振力和加速度响应的时间记录曲线和传递函数；（3）比较原点传递函数和跨点传递函数的特征；（4）识别驱动桥壳的模态参数。

三、实验仪器实验仪器包括力锤、加速度计、电荷放大器、信号采集卡、信号分析记录系统。

其中：（1）力锤用于激励实验对象，本实验使用钢制锤头进行激励；（2）加速度计用于拾取响应信号并转换成为电荷信号；（3）电荷放大器用于将电荷信号放大成电为适合测量的压信号，本实验采用SINOCERA公司生产的YE3822A信号放大器；（4）信号采集卡用于对传感器采集得到的数字信号进行采样，并转化为数字信号，本试样采用DT公司产的DT9837A采集卡；（5）信号分析记录系统包括一台笔记本电脑和相应的应用程序，本实验采用DEWESoft 7.0软件进行振动信号的时间历程测量。

各个仪器与实验对象的安装位置、连接关系如图1所示。

图2~5为实验现场的仪器安装实物图。

力锤加速度计1加速度计2电荷放大器1电荷放大器2电荷放大器3信号采集卡笔记本电脑图1图2图3图4图5四、实验数据采集过程用安装有加速度传感器的力锤敲击实验对象上的某一点。

加速度传感器拾取激励力的信号。

安装在实验对象的某一观测点上的加速度计拾取响应信号，经电荷放大器后输入信号采集系统。

（1）仪器操作要点如下：a)锤子上的加速度传感器信号必须接入信号采集器的第一通道，响应信号依次接入信号采集器的其他通道；b)在信号采集分析系统上设置适当的参数，首先设置采集参数，如实验名（ASCⅡ码）、试验号（数字）、数据路径、结果路径、采样类型（多次触发）、单位类型（可变）、设置工程单位和标定值；c)采样菜单中选用多次触发，设置相应的参数，开始采样。

（2）敲击传感器附近的测点，测量原点传递函数；（3）敲击远离传感器的其他测点，测量跨点传递函数。

模态分析实验报告姓名：学号：任课教师：实验时间：指导老师：实验地点：实验1 传递函数的测量一、实验内容用锤击激振法测量传递函数。

二、实验目的1)掌握锤击激振法测量传递函数的方法；2)测量激励力和加速度响应的时间记录曲线、力的自功率谱和传递函数；3)分析传递函数的各种显示形式（实部、虚部、幅值、对数、相位）及相干函数；4)比较原点传递函数和跨点传递函数的特征；5)考察激励点和响应点互换对传递函数的影响；6)比较不同材料的力锤锤帽对激励信号的影响；三、实验仪器和测试系统1、实验仪器主要用到的实验仪器有：冲击力锤、加速度传感器，LMS LMS-SCADAS Ⅲ测试系统，具体型号和参数见表1-1。

仪器名称型号序列号灵敏度备注数据采集和分析系统LMS-SCADAS Ⅲ比利时力锤2302-10 3164 2.25 mV/N加速度传感器100 mV/g 丹麦B&K表1-1 实验仪器2 、测试系统利用试验测量的激励信号(力锤激励信号)和响应的时间历程信号，运用数字信号处理技术获得频率响应函数(Frequency Response Function, FRF)，得到系统的非参数模型。

然后利用参数识别方法得到系统的模态参数。

测试系统主要完成力锤激励信号及各点响应信号时间历程的同步采集，完成数字信号的处理和参数的识别。

测量分析系统的框图如图1-1所示。

测量系统由振动加速度传感器、力锤和比利时LMS公司SCADAS采集前端及Modal Impact测量分析软件组成。

力锤及加速度传感器通过信号线与SCADAS采集前端相连，振动传感器及力锤为ICP型传感器，需要SCADAS 采集前端对其供电。

SCADAS 采集相应的信号和进行信号处理(如抗混滤波，A/D 转换等)，所测信号通过电缆与电脑完成数据通讯。

力锤力传感器加速度传感器LMS 数据采集分析系统图1-1 测试分析系统框图四、实验数据采集1、振动测试实验台架实验测量的是一段轴，在轴上安装了3个加速度传感器，如图1-2所示，轴由四根弹簧悬挂起来，使得整个测试统的频率很低，基本上不会影响到最终的测试结果。

平板模态分析实验报告引言平板模态分析是一种通过实验手段来研究结构的固有振动特性的方法，通过测定结构在不同频率下的自由振动模态，可以得到结构的固有频率、振型和阻尼特性等参数，为结构的设计与改进提供重要依据。

本实验旨在利用模态分析实验方法，研究一块平板的固有频率和振型分布。

实验目的1. 学习平板模态分析的实验方法和步骤；2. 测定平板的固有频率和振型，并分析其特征。

实验装置与原理1. 装置：实验装置包括平板样品、信号调理器、激励器、振动传感器和数据采集系统等；2. 原理：实验利用激励器对平板样品施加外力，引起平板振动；振动传感器能够测量平板各个位置的振动信号，并通过信号调理器放大和处理后得到相应的振动响应数据；数据采集系统将振动数据以一定频率进行采样存储。

实验步骤1. 将平板样品固定在实验台上，使其边界完全固定；2. 设置合适的激励信号，并将激励器安装在平板的中央位置；3. 在平板的不同位置安装振动传感器，以测量振动响应信号；4. 打开数据采集系统，设置采样频率和数据采样时长；5. 开始采集数据，同时激励器对平板施加外力；6. 根据采集到的振动响应信号，进行数据处理和分析。

实验结果与分析根据实验采集到的数据，可以得到平板的固有频率和振型。

首先，通过采集到的振动响应信号，可以绘制出振动模态频谱图，即频率与振动响应幅值的关系图。

根据频谱图的峰值位置，可以确定平板的固有频率。

同时，根据不同频率下的振动响应信号，可以绘制出平板的振型图，即不同频率下平板的振动节点分布图。

通过观察振型图，可以得到平板不同模态下的振动形态，进一步分析平板的结构特性。

结论利用平板模态分析实验方法，可以得到平板的固有频率和振型分布，为结构的设计和改进提供依据。

实验结果表明，通过实验方法得到的固有频率和振型与理论计算相吻合，验证了实验方法的可靠性。

因此，平板模态分析实验是一种有效的研究结构振动特性的手段。

总结本实验通过平板模态分析实验方法，研究了一个平板的固有频率和振型。