【中小学资料】云南省曲靖市师宗县2018届中考数学横向复习 第六单元 圆 第25讲 与圆有关的计算考点测试题

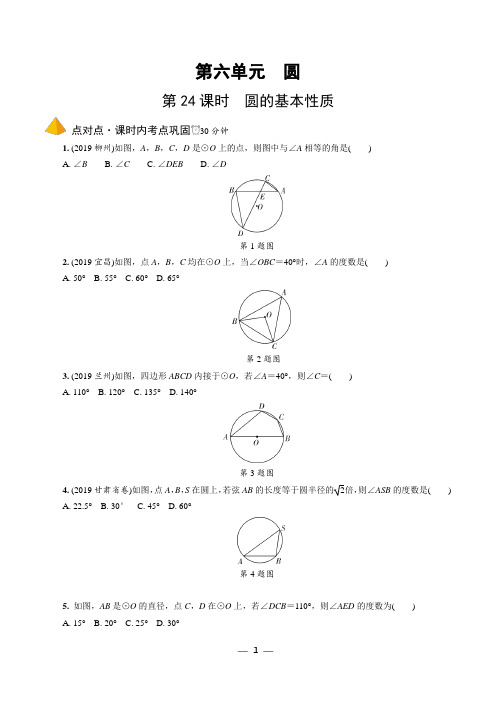
第六单元圆第24课时圆的基本性质点对点·课时内考点巩固30分钟1. (2019柳州)如图，A，B，C，D是⊙O上的点，则图中与∠A相等的角是()A. ∠BB. ∠CC. ∠DEBD. ∠D第1题图2. (2019宜昌)如图，点A，B，C均在⊙O上，当∠OBC＝40°时，∠A的度数是()A. 50°B. 55°C. 60°D. 65°第2题图3. (2019兰州)如图，四边形ABCD内接于⊙O，若∠A＝40°，则∠C＝()A. 110°B. 120°C. 135°D. 140°第3题图4. (2019甘肃省卷)如图，点A，B，S在圆上，若弦AB的长度等于圆半径的2倍，则∠ASB的度数是()A. 22.5°B. 30°C. 45°D. 60°第4题图5.如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB＝110°，则∠AED的度数为()A. 15°B. 20°C. 25°D. 30°第5题图6. (2019西安高新一中模拟)如图，四边形ABCD 内接于⊙O ，AD ∥BC ，∠DAB ＝48°，则∠AOC 的度数是( )A. 48°B. 96°C. 114°D. 132°第6题图7. (2019陕西黑马卷)如图，在⊙O 中，弦AB ∥CD ，连接BC ，OA ，OD .若∠BCD ＝25°，CD ＝OD ，则∠AOD 的度数是( )A. 140°B. 120°C. 110°D. 100°第7题图8. (2019赤峰)如图，AB 是⊙O 的弦，OC ⊥AB 交⊙O 于点C ，点D 是⊙O 上一点，∠ADC ＝30°，则∠BOC 的度数为( )A. 30°B. 40°C. 50°D. 60°第8题图9. (2019贵港)如图，AD 是⊙O 的直径，AB ︵＝CD ︵，若∠AOB ＝40°，则圆周角∠BPC 的度数是( ) A. 40° B. 50° C. 60° D ．70°第9题图10. 如图，△ABC 内接于⊙O ，∠BAC ＝120°，AB ＝AC ，BD 为⊙O 的直径，AD ＝6，则BD 的长为( ) A. 3 B. 2 3 C. 4 3 D. 12第10题图11. 如图，AB 为⊙O 的直径，∠CAB ＝30°，CB ＝3，∠ACB 的平分线CD 交⊙O 于点D ，则弦AD 的长为( )A. 2 3B. 2 2C. 3 3D. 3 2第11题图12. 如图，B 、C 是⊙A 上的两点，AB 的垂直平分线与⊙A 交于E 、F 两点，与线段AC 交于点D ，连接BC 、BD 、BF 、CF .若∠BFC ＝20°，则∠DBC ＝( )A. 30°B. 29°C. 28°D. 20°第12题图13. (2019西工大附中模拟)如图，已知△ABC 内接于⊙O ，EF 为⊙O 的直径，且点F 是弧BC ︵的中点．若∠B ＝40°，∠C ＝60°，则∠AFE 的度数为( )A. 10°B. 20°C. 30°D. 40°第13题图14. (2019西安铁一中模拟)如图，在半径为3的⊙O中，弦BC、DE所对的圆周角分别是∠A、∠F，且∠A＋∠F＝90°.若BC＝4，则DE的长为()A. 13B. 4C. 5D. 2 5第14题图15.在圆内接四边形ABCD中，∠ACB＝∠ACD＝60°，对角线AC、BD交于点E.已知BC＝32，CD ＝22，则线段CE的长为()第15题图A. 32 2B. 7 5C. 62 5D. 22 316. (2019株洲)如图所示，AB为⊙O的直径，点C在⊙O上，且OC⊥AB，过点C的弦CD与线段OB 相交于点E，满足∠AEC＝65°，连接AD，则∠BAD＝________度．第16题图17.(2019安徽)如图，△ABC内接于⊙O，∠CAB＝30°，∠CBA＝45°，CD⊥AB于点D，若⊙O的半径为2，则CD的长为________．第17题图18.已知半径为5的⊙O中，弦AB＝52，弦AC＝5，则∠BAC的度数是________．点对线·板块内考点衔接10分钟1. (2019襄阳)如图，AD是⊙O的直径，BC是弦，四边形OBCD是平行四边形，AC与OB相交于点P，下列结论错误的是()A. AP＝2OPB. CD＝2OPC. OB⊥ACD. AC平分OB第1题图2. (2019西工大附中模拟)如图，已知⊙O的内接五边形ABCDE，连接BE、CE，若AB＝BC＝CE，∠EDC ＝130°，则∠ABE的度数为()A. 25°B. 30°C. 35°D. 40°第2题图3.(2019天水)如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE.若∠D＝80°，则∠EAC的度数为()A. 20°B. 25°C. 30°D. 35°第3题图4.(2019柳州)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片，则这个正方形纸片的边长应为________．5.如图，在矩形ABCD中，AB＝3，BC＝4，O为矩形ABCD的中心，以D为圆心，1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP、OA，则△AOP面积的最大值为________．第5题图点对面·跨板块考点迁移2分钟1. (2019安顺)如图，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，则tan∠OBC 为()第1题图A. 13 B. 22 C.223 D.24参考答案第24课时 圆的基本性质点对点·课时内考点巩固1. D 【解析】在⊙O 中，∵∠A 与∠D 都是BC ︵所对的圆周角，∴∠A ＝∠D .2. A 【解析】∵OB ＝OC ，∴∠OCB ＝∠OBC ＝40°.∴在△OBC 中，∠BOC ＝180°－∠OCB －∠OBC ＝180°－40°－40°＝100°.∴∠A ＝12∠BOC ＝12×100°＝50°.3. D 【解析】∵四边形ABCD 内接于⊙O ，∠A ＝40°，∴∠C ＝180°－∠A ＝140°.4. C 【解析】如解图，设圆心为O ，半径为r ，则AB ＝2r .连接OA 、OB ，则r 2＋r 2＝(2r )2，∴△OAB 为等腰直角三角形，∠AOB ＝90°.∴∠ASB ＝12∠AOB ＝45°.第4题解图5. B 【解析】如解图，连接AC ，∵AB 为直径，∴∠ACB ＝90°，∴∠ACD ＝∠DCB －∠ACB ＝110°－90°＝20°，∴∠AED ＝∠ACD ＝20°.第5题解图6. B 【解析】∵AD ∥BC ，∴∠B ＝180°－∠DAB ＝132°，∵四边形ABCD 内接于⊙O ，∴∠D ＝180°－∠B ＝48°，由圆周角定理得，∠AOC ＝2∠D ＝96°.7. C 【解析】如解图，连接OC ，∵AB ∥CD ，∴∠B ＝∠BCD ＝25°，∴∠AOC ＝50°，∵CD ＝OD ，OD ＝OC ，∴OC ＝OD ＝CD ，∴△COD 为等边三角形，∴∠COD ＝60°，∴∠AOD ＝∠AOC ＋∠COD ＝110°.第7题解图8. D 【解析】∵OC ⊥AB ，∴点C 是AB ︵的中点，即AC ︵＝BC ︵.∴∠BOC ＝∠AOC ＝2∠ADC ＝60°.9. B 【解析】∵AB ︵＝CD ︵，∴∠COD ＝∠AOB ＝40°，∴∠BOC ＝100°，∴∠BPC ＝12∠BOC ＝50°.10. C 【解析】∵∠BAC ＝120°，AB ＝AC ，∴∠BCA ＝12×(180°－120°)＝30°.∴∠D ＝∠BCA ＝30°.∵BD为⊙O 的直径，∴∠BAD ＝90°.在Rt △BAD 中，BD ＝AD cos30°＝632＝4 3. 11. D 【解析】如解图，连接BD ，∵AB 为⊙O 的直径，∴∠ACB ＝∠ADB ＝90°，在Rt △ABC 中，∵∠CAB ＝30°，∴AB ＝2CB ＝6，∵CD 平分∠ACB ，∴∠BCD ＝45°，∵∠BAD ＝∠BCD ＝45°，∴△ABD 为等腰直角三角形，∴AD ＝22AB ＝22×6＝3 2.第11题解图12. A 【解析】∵∠BFC ＝20°，∴∠BAC ＝2∠BFC ＝40°，∵AB ＝AC ，∴∠ABC ＝∠ACB ＝12(180°－40°)＝70°.又∵EF 是线段AB 的垂直平分线，∴AD ＝BD ，∴∠ABD ＝∠BAC ＝40°，∴∠DBC ＝∠ABC －∠ABD ＝70°－40°＝30°.13. A 【解析】如解图，连接OC 、CF .∵∠B ＝40°，∠ACB ＝60°，∴∠BAC ＝80°，∠AFC ＝∠ABC ＝40°，∵点F 是弧BC ︵的中点，∴∠BAF ＝∠CAF ＝40°，∴∠COF ＝2∠CAF ＝80°，∵OF ＝OC ，∴∠OFC ＝12(180°－80°)＝50°，∴∠AFE ＝∠OFC －∠AFC ＝10°.第13题解图14. D 【解析】如解图，连接DO 并延长，交⊙O 于点G ，连接EG 、FG ，则∠DFG ＝∠DEG ＝90°，又∵∠A ＋∠DFE ＝90°，∠GFE ＋∠DFE ＝90°，∴∠A ＝∠GFE .则GE ＝BC ＝4.∵⊙O 的半径为3，∴DG ＝6.在Rt △DEG 中，DE ＝DG 2－GE 2＝62－42＝2 5.第14题解图15. C 【解析】如解图，作BM ⊥AC 于点M ，DN ⊥AC 于点N ，则BM ∥DN ，∴△BME ∽△DNE ，∴MENE ＝BM DN ，∵∠ACB ＝∠ACD ＝60°，∴∠CBM ＝∠CDN ＝30°，∴CM ＝12BC ＝322，CN ＝12CD ＝2，∴BM ＝3CM ＝362，DN ＝3CN ＝6，∴MN ＝CM －CN ＝122，∴ME NE ＝32，∴EN ＝25MN ＝25，∴CE ＝CN ＋EN ＝2＋25＝625.第15题解图16. 20 【解析】∵AB 为⊙O 的直径，点C 在⊙O 上，且OC ⊥AB ，∴∠ADC ＝12∠AOC ＝45°.∵∠AEC＝65°，且∠AEC 是△ADE 的一个外角，∴∠BAD ＝∠AEC －∠ADC ＝20°.17. 2 【解析】如解图，连接OA 、OC ，∵∠CBA ＝45°，∴∠AOC ＝90°.又∵OA ＝OC ＝2，∴AC ＝2 2.在Rt △ACD 中，∠CDA ＝90°，∠CAD ＝30°，∴CD ＝AC ·sin30°＝ 2.第17题解图18. 105°或15° 【解析】如解图，连接OC ，OA ，OB .∵OC ＝OA ＝AC ＝5，∴△OAC 是等边三角形，∴∠CAO ＝60°，∵OA ＝OB ＝5，AB ＝52，∴OA 2＋OB 2＝AB 2，∴△OAB 是等腰直角三角形，∠OAB ＝45°，点C 的位置有两种情况，如解图①时，∠BAC ＝∠CAO ＋∠OAB ＝60°＋45°＝105°；如解图②时，∠BAC ＝∠CAO －∠OAB ＝60°－45°＝15°.综上所述，∠BAC 的度数是105°或15°.第18题解图点对线·板块内考点衔接1. A 【解析】如解图，连接OC .∵四边形OBCD 是平行四边形，OD ＝OB ，∴四边形OBCD 是菱形．∴OD ＝OC ＝CD .∵AD 是⊙O 的直径，∴∠ACD ＝90°.∵CD ∥OB ，∴CD ＝2OP ，OB ⊥AC .故B 、C 选项正确．∵△CBP ≌△COP (HL)，∴BP ＝OP .故D 选项正确．第1题解图2. B 【解析】如解图，连接OA ，OB ，OC ，OE ，∵AB ＝BC ＝CE ，∴AB ︵＝BC ︵＝CE ︵，∠1＝∠2＝∠3，在四边形BCDE 中，∵∠D ＝130°，∴∠CBE ＝50°，∠2＝2∠CBE ＝100°，∴∠1＝∠3＝∠2＝100°，∠AOE ＝360°－3×100°＝60°，∴∠ABE ＝12∠AOE ＝30°.第2题解图3. C 【解析】∵∠AEB ＋∠AEC ＝∠D ＋∠AEC ＝180°，∠D ＝80°，∴∠AEB ＝∠D ＝80°.∵四边形ABCD 是菱形，∴∠B ＝∠D ＝80°，AB ＝BC ，∴∠B ＝∠AEB .∴∠BAE ＝180°－2∠B ＝20°，∠BAC ＝∠ACB ＝12(180°－∠B )＝50°.∴∠EAC ＝∠BAC －∠BAE ＝30°.4. 52 【解析】如解图，四边形ABCD 为正方形，BD 为⊙O 的直径，OA 为半径，则OA ＝OB ＝5，OA ⊥OB ，∴AB ＝OA 2＋OB 2＝52＋52＝5 2.第4题解图5.174【解析】如解图，延长AO 至C 点，过点D 作DF ⊥AC 于点F ，延长FD 交⊙D 于点P ′，连接AP ′，OP ′，要使△AOP 面积最大，则只需AO 边上的高最大，此时P ′满足条件，即P ′F 为△AOP 的AO 边上最大的高．∵DF ＝AD ·CD AC ＝4×342＋32＝125，∴P ′F ＝DF ＋DP ′＝125＋1＝175，AO ＝12AC ＝52，∴△AOP 的最大面积为12AO ·P ′F ＝12×52×175＝174.第5题解图点对面·跨板块考点迁移1. D 【解析】如解图，连接AC 、AO ，得到等腰三角形AOC ，过A 点作AD ⊥OC ，垂足为点D ，∴∠CAD ＝12∠CAO ＝∠OBC ，∵点C 坐标为(0，2)，∴CD ＝OD ＝1，∴在Rt △ACD 中，AD ＝AC 2－CD 2＝32－12＝22，∴tan ∠OBC ＝tan ∠CAD ＝CD AD ＝122＝24.第1题解图第六单元 圆第25课时 与圆有关的位置关系点对点·课时内考点巩固30分钟1. (2019广州)平面内，⊙O 的半径为1，点P 到O 的距离为2，过点P 可作⊙O 的切线的条数为( ) A. 0条 B. 1条 C. 2条 D. 无数条2. (2019重庆B 卷)如图，AB 是⊙O 的直径，AC 是⊙O 的切线，A 为切点，若∠C ＝40°，则∠B 的度数为( )第2题图A. 60°B. 50°C. 40°D. 30° 点对线·板块内考点衔接60分钟1. (2019哈尔滨)如图，P A 、PB 分别与⊙O 相切于A 、B 两点，点C 为⊙O 上一点，连接AC 、BC ，若∠P ＝50°，则∠ACB 的度数为( )A. 60°B. 75°C. 70°D. 65°第1题图2. (2019舟山)如图，已知⊙O 上三点A ，B 、C ，半径OC ＝1，∠ABC ＝30°，切线P A 交OC 延长线于点P ，则P A 的长为( )A. 2B. 3C. 2D. 1 2第2题图3.如图，AB是⊙O的直径，P A切⊙O于点A，连接PO并延长交⊙O于点C，连接AC.若AB＝10，∠P ＝30°，则AC的长度是()A. 5 3B. 5 2C. 5D. 5 2第3题图4. (2019泰安)如图，△ABC是⊙O的内接三角形，∠A＝119°，过点C的圆的切线交BO于点P，则∠P 的度数为()A. 32°B. 31°C. 29°D. 61°第4题图5. (北师九下P92例2题改编)如图，边长为23的等边△ABC的内切圆的半径为()A. 1B. 3C. 2D. 2 3第5题图6. (2019贺州)如图，在△ABC中，O是AB边上的点，以O为圆心，OB为半径的⊙O与AC相切于点D，BD平分∠ABC，AD＝3OD，AB＝12，CD的长是()A. 2 3B. 2C. 3 3D. 4 3第6题图7.如图，AB是⊙O的直径，点C在BA的延长线上，直线CD与⊙O相切于点D，弦DF⊥AB于点E，连接BD.若CD＝BD＝43，则OE的长度为()第7题图A. 3B. 2C. 2 3D. 48. (2018益阳)如图，在圆O中，AB为直径，AD为弦，过点B的切线与AD的延长线交于点C，AD＝DC，则∠C＝________度．第8题图9.(2019南京)如图，P A、PB是⊙O的切线，A、B为切点，点C、D在⊙O上．若∠P＝102°，则∠A ＋∠C＝________°.第9题图10. (2019眉山)如图，在Rt△AOB中，OA＝OB＝42，⊙O的半径为2，点P是AB边上的动点，过点P作⊙O的一条切线PQ(点Q为切点)，则线段PQ长的最小值为________．第10题图11.(2019陕师大附中模拟)如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D.(1)求证：AD平分∠BAC；(2)若BE＝2，BD＝4，求⊙O的半径．第11题图12.如图，MP与⊙O相切于点M，连接PO并延长，交⊙O于点A、B，弦AC∥MP，连接OM、BC、CM.(1)求证：OM∥BC；(2)若∠P＝30°，求证：四边形BCMO为菱形．第12题图13.如图，AB为⊙O的直径，AD、BE为⊙O的弦，延长AD、BE交于点C，且AB＝AC，过点B作⊙O的切线交AC 的延长线于点F .(1)求证：BE ＝CE ；(2)若BF ＝4，CF ＝2，求AD 的长．第13题图14. (2019西安交大附中模拟)如图，在△ABC 中，∠ACB ＝90°，点D 是AB 的中点，以AD 为直径的⊙O 交AC 于点E ，⊙O 的切线EF 交CD 于点F .(1)求证：EF ⊥CD ；(2)若AC ＝10，cos A ＝56，求线段DF 的长．第14题图15. (2019黄冈改编)如图，Rt △ABC 中，∠ACB ＝90°，以AC 为直径的⊙O 交AB 于点D ，过点D 作⊙O 的切线交BC 于点E ，连接OE .(1)求证：△DBE 是等腰三角形；(2)求证：CA ·CE ＝CO ·CB .第15题图16. (2019凉山州)如图，点D 是以AB 为直径的⊙O 上一点，过点B 作⊙O 的切线，交AD 的延长线于点C ，E 是BC 的中点，连接DE 并延长与AB 的延长线交于点F .(1)求证：DF 是⊙O 的切线； (2)若OB ＝BF ，EF ＝4，求AD 的长．第16题图17. 如图，在Rt △ACB 中，∠C ＝90°，D 是AB 上一点，以BD 为直径的⊙O 切AC 于点E ，交BC 于点F ，连接DF .(1)求证：DF ＝2CE ；(2)若BC ＝3，sin B ＝45，求线段BF 的长．第17题图18. (2019新疆)如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D, CE⊥AB于点E.(1)求证：∠BCE＝∠BCD；(2)若AD＝10，CE＝2BE，求⊙O的半径．第18题图参考答案第25课时 与圆有关的位置关系点对点·课时内考点巩固1. C 【解析】根据切线的定义进行判断，过圆外一点可以作两条直线和圆相切．2. B 【解析】∵AC 是⊙O 的切线，∴AB ⊥AC ，∵∠C ＝40°，∴∠B ＝50°. 点对线·板块内考点衔接1. D 【解析】如解图，连接OA 、OB ，∵P A 、PB 分别与⊙O 相切于A 、B 两点，∴OA ⊥P A ，OB ⊥PB ，∴∠OAP ＝∠OBP ＝90°，∴∠AOB ＝180°－∠P ＝180°－50°＝130°，∴∠ACB ＝12∠AOB ＝12×130°＝65°.第1题解图2. B 【解析】如解图，连接OA ，∵∠AOC 与∠ABC 是AC ︵所对的圆心角和圆周角，∴∠AOC ＝2∠ABC ＝60°，∵AP 是⊙O 的切线，∴OA ⊥AP ，∴AP ＝OA ·tan ∠AOC ＝1·tan60°＝ 3.第2题解图3. A 【解析】如解图，连接BC ，∵AP 是⊙O 的切线，∴∠BAP ＝90°.∵∠P ＝30°，∴∠AOP ＝60°.∴∠BOC ＝60°.∵OC ＝OA ，∴∠ACP ＝∠BAC ＝12∠BOC ＝30°.∵AB 是⊙O 的直径，∴∠ACB ＝90°.在Rt △ABC 中，∵∠BAC ＝30°，AB ＝10，∴AC ＝5 3.第3题解图4. A 【解析】如解图，设BP 与⊙O 交于点M ，连接OC ，CM .∵PC 是⊙O 的切线，∴∠OCP ＝90°.∵四边形ABMC 是圆内接四边形，∠A ＝119°，∴∠BMC ＝180°－119°＝61°.∵OC ＝OM ，∴∠OCM ＝∠OMC ＝61°.∴在△COM 中，∠COM ＝58°.∴在△COP 中，∠P ＝180°－∠COM －∠OCP ＝180°－58°－90°＝32°.第4题解图5. A 【解析】如解图，连接OA ，过点O 作OD ⊥AB 于点D ，∵⊙O 是等边三角形ABC 的内切圆，∴OD ⊥AB ，D 为AB 的中点．∵AB ＝23，∴AD ＝12AB ＝ 3.∵在等边△ABC 中，∠CAB ＝60°，∴∠OAD＝30°. ∴tan ∠OAD ＝ODAD. ∴ OD ＝AD ·tan30°＝1.第5题解图6. A 【解析】∵AD 是⊙O 的切线，∴OD ⊥AD .在Rt △AOD 中，AD ＝3OD ，∴tan A ＝OD AD ＝OD3OD ＝33.∴∠A ＝30°.∴∠AOD ＝60°.∵OD ＝OB ，∴∠ODB ＝∠ABD ＝12∠AOD ＝30°.∵BD 平分∠ABC ，∴∠CBD ＝∠ABD ＝30°，∴∠ABC ＝60°，∴∠C ＝90°. 在Rt △ABC 中，sin A ＝BC AB ，AB ＝12，∴BC ＝AB ·sin A ＝12×12＝6. 在Rt △CBD 中，CD ＝BC ·tan ∠CBD ＝6×33＝2 3. 7. B 【解析】如解图，连接OD ，∵直线CD 与⊙O 相切于点D ，∴OD ⊥CD ，∴∠ODC ＝90°，∵CD ＝BD ＝43，∴∠C ＝∠B ，∵OD ＝OB ，∴∠B ＝∠ODB ，∴∠DOE ＝∠B ＋∠ODB ＝2∠B ＝2∠C ，在Rt △OCD 中，∠DOE ＝2∠C ，则∠DOE ＝60°，∠C ＝30°，∴OD ＝CD ·tan C ＝43×33＝4，∵DF ⊥AB ，∴∠DEO ＝90°，在Rt △ODE 中，OE ＝OD ·cos ∠EOD ＝4×12＝2.第7题解图8. 45 【解析】∵AB 为⊙O 的直径，∴∠ADB ＝90°，∵BC 为⊙O 的切线，∴AB ⊥BC ，∴∠ABC ＝90°，∵AD ＝CD ，∴△ABC 为等腰直角三角形，∴∠C ＝45°.9. 219 【解析】如解图，连接AB ，∵P A 、PB 是⊙O 的切线，∴P A ＝PB ，∵∠P ＝102°，∴∠P AB ＝∠PBA ＝12(180°－102°)＝39°，∵∠DAB ＋∠C ＝180°，∴∠P AD ＋∠C ＝∠P AB ＋∠DAB ＋∠C ＝180°＋39°＝219°.第9题解图10. 23 【解析】如解图，连接OQ ，则PQ ＝OP 2－OQ 2，根据题意可知OQ 长为定值，若使得PQ 最小，只要OP 最小即可，当OP ⊥AB 时能取得最小值．∵OA ＝OB ＝42，∴AB ＝8，∴OP ＝4，∴PQ ＝42－22＝2 3.第10题解图11. (1)证明：如解图，连接OD ， ∵BC 是⊙O 的切线， ∴OD ⊥BC ， 又∵AC ⊥BC ， ∴OD ∥AC ， ∴∠2＝∠3； ∵OA ＝OD ， ∴∠1＝∠3， ∴∠1＝∠2， ∴AD 平分∠BAC ；第11题解图(2)解：设⊙O的半径为r，在Rt△BOD中，有OD2＋BD2＝OB2，即r2＋42＝(2＋r)2，解得r＝3.∴⊙O的半径为3.12.证明：(1)∵MP与⊙O相切于点M，∴OM⊥MP，又∵AC∥MP，∴OM⊥AC，又∵AB是⊙O的直径，∴∠ACB＝90°，∴BC⊥AC，∴OM∥BC；(2)∵AC∥MP，∠P＝30°，∴∠BAC＝∠P＝30°，∵∠ACB＝90°，∴AB＝2BC，又∵AB＝2OB，∴BC＝OB＝OM，∵OM∥BC，∴四边形BCMO为平行四边形，又∵OB＝OM，∴四边形BCMO为菱形．13. (1)证明：如解图，连接AE.∵AB＝AC，∴△ABC是等腰三角形．∵AB是⊙O的直径，∴∠AEB＝90°，即AE⊥BC，∴E为BC边的中点，∴BE＝CE；第13题解图(2)解：如解图，连接BD ，设⊙O 的半径为r . ∵BF 为⊙O 的切线， ∴∠ABF ＝90°.在Rt △ABF 中，AB 2＋BF 2＝AF 2， 即(2r )2＋42＝(2r ＋2)2， 解得r ＝32.∴AB ＝AC ＝2r ＝3，AF ＝2r ＋2＝5. ∵AB 是⊙O 的直径， ∴∠ADB ＝∠ABF ＝90°. 又∵∠BAD ＝∠F AB ， ∴Rt △ABD ∽Rt △AFB . ∴AB AF ＝AD AB ，即35＝AD3. ∴AD ＝95.14. (1)证明：如解图，连接OE ， ∵OA ＝OE ， ∴∠A ＝∠OEA ，∵∠ACB ＝90°，点D 是AB 的中点， ∴AD ＝CD ， ∴∠A ＝∠DCA ， ∴∠OEA ＝∠DCA ， ∴OE ∥CD ， ∵EF 为⊙O 的切线， ∴OE ⊥EF ， ∴EF ⊥CD ；第14题解图(2)解：∵cos A ＝56，∴AC AB ＝56， ∵AC ＝10， ∴AB ＝12，∵∠ACB ＝90°，点D 是AB 的中点， ∴AD ＝DC ＝12AB ＝6，由(1)可得，OE ∥CD ，∴AE ＝12AC ，△OEA ∽△DCA ，∴AO AD ＝AE AC ＝12， ∴AE ＝EC ＝12AC ＝5，∵cos A ＝cos ∠DCA ＝CFCE ，∴CF ＝256，∴DF ＝CD －CF ＝6－256＝116.15. 证明：(1)如解图，连接OD 、CD ， ∵DE 是⊙O 的切线， ∴∠ODE ＝90°，在Rt △OCE 和Rt △ODE 中，⎩⎪⎨⎪⎧OC ＝OD OE ＝OE ， ∴Rt △OCE ≌Rt △ODE (HL)， ∴DE ＝CE ， ∴∠ECD ＝∠CDE ， ∵AC 是⊙O 的直径， ∴∠CDA ＝90°， ∴∠CDB ＝90°，∴∠B ＋∠ECD ＝90°，∠CDE ＋∠BDE ＝90°， ∵∠ECD ＝∠CDE ， ∴∠BDE ＝∠B ， ∴BE ＝DE ，∴△DBE 是等腰三角形；第15题解图(2)由(1)可得，BE ＝DE ＝CE ， ∴点E 是BC 的中点， ∴OE 是△ABC 的中位线， ∴OE ∥AB ， ∴△COE ∽△CAB . ∴CO CA ＝CE CB， ∴CA ·CE ＝CO ·CB .16. (1)证明：如解图，连接OD ，BD ， ∵BC 是⊙O 的切线， ∴BC ⊥OB ， ∴∠OBC ＝90°. ∵AB 为⊙O 的直径， ∴∠ADB ＝90°. ∴∠CDB ＝90°. ∵E 是BC 的中点， ∴ED ＝EB ＝12BC ，∴∠EDB ＝∠EBD . ∵OD ＝OB ， ∴∠ODB ＝∠OBD ， ∴∠ODF ＝∠OBC ＝90°， ∴DF ⊥OD .∵OD 是⊙O 的半径， ∴DF 是⊙O 的切线；第16题解图(2)解：由(1)知∠ODF ＝90°，∵OD ＝OB ＝BF ， ∴sin F ＝OD OF ＝12，∴∠F ＝30°，∵∠DOB ＋∠F ＝90°， ∴∠DOB ＝60°， ∴△ODB 是等边三角形， ∴∠OBD ＝60°， ∴tan ∠OBD ＝ADBD ＝3，∴AD ＝3BD . ∵BC ⊥AF ， ∴BE EF ＝sin F ＝12. ∵EF ＝4， ∴BE ＝2，∴BF ＝EF 2－BE 2＝23＝OB ＝DB ， ∴AD ＝3BD ＝6.17. (1)证明：如解图，连接OE 交DF 于点G ， ∵AC 切⊙O 于点E ， ∴∠CEO ＝90°， 又∵BD 为⊙O 的直径， ∴∠DFC ＝∠DFB ＝90°， ∵∠C ＝90°，∴四边形CEGF 为矩形， ∴CE ＝GF ，∠EGF ＝90°， ∴DF ＝2CE ；第17题解图(2)解：在Rt △ABC 中，∵∠C ＝90°，BC ＝3，sin B ＝45，∴AB ＝5，设OE ＝x ，∵OE ∥BC ， ∴△AOE ∽△ABC ，∴OE BC ＝AO AB， ∴x 3＝5－x 5， ∴x ＝158，∴BD ＝2OE ＝154，在Rt △BDF 中，∵∠DFB ＝90°，sin B ＝45，∴cos B ＝35＝BF BD ＝BF154，∴BF ＝94.18. (1)证明：如解图，连接OC ，AC ， ∵AB 是⊙O 的直径， ∴∠ACB ＝90°，∴∠ACO ＋∠OCB ＝90°， 又∵CD 是⊙O 的切线， ∴∠OCD ＝90°， ∴∠OCB ＋∠BCD ＝90°. ∴∠ACO ＝∠BCD . ∵CE ⊥AB ， ∴∠CEB ＝90°， ∴∠BCE ＋∠ABC ＝90°. ∵∠A ＋∠ABC ＝90°， ∴∠BCE ＝∠A . ∵OA ＝OC ，∴∠A ＝∠ACO ＝∠BCD . ∴∠BCE ＝∠BCD ；第18题解图(2)解：如解图，过点B 作BF ⊥CD 于点F ，得△BFD ∽△CED . 由(1)得∵BC 平分∠ECD ，∴BF ＝BE . ∵CE ＝2BE ， ∴BD CD ＝BF CE ＝BE CE ＝12. 即CD ＝2BD .∵∠BCD ＝∠A ，∠CDB ＝∠ADC ， ∴△CBD ∽△ACD ， ∴BD CD ＝CD AD. ∵AD ＝10， ∴BD ＝52，∴AB ＝152，∴OA ＝154.∴⊙O 的半径为154.第六单元 圆第26课时 与圆有关的计算点对点·课时内考点巩固5分钟1. (2019长沙)一个扇形的半径为6，圆心角为120°，则这个扇形的面积是( ) A. 2π B. 4π C. 12π D. 24π2. (2019青海)如图，在扇形AOB 中，AC 为弦，∠AOB ＝140°，∠CAO ＝60°，OA ＝6，则BC ︵的长为( )第2题图A. 4π3 B. 8π3C. 23πD. 2π3. (2019哈尔滨)一个扇形的弧长是11π cm ，半径是18 cm ，则此扇形的圆心角是________度．点对线·板块内考点衔接15分钟1. (2019枣庄)如图，在边长为4的正方形ABCD 中，以点B 为圆心，AB 为半径画弧，交对角线BD 于点E ，则图中阴影部分的面积是(结果保留π)( )A. 8－πB. 16－2πC. 8－2πD. 8－12π第1题图2. (2019绍兴)如图，△ABC 内接于⊙O ，∠B ＝65°，∠C ＝70°.若BC ＝22，则BC ︵的长为( ) A. π B. 2π C. 2π D. 22π第2题图3. (2019青岛)如图，线段AB 经过⊙O 的圆心，AC ，BD 分别与⊙O 相切于点C ，D .若AC ＝BD ＝4，∠A ＝45°，则CD ︵的长度为( )A. πB. 2πC. 22πD. 4π第3题图4. (2019南充)如图，在半径为6的⊙O 中，点A ，B ，C 都在⊙O 上，四边形OABC 是平行四边形，则图中阴影部分的面积为( )A. 6πB. 33πC. 23πD. 2π第4题图5. (2019山西)如图，在Rt △ABC 中，∠ABC ＝90°，AB ＝23，BC ＝2，以AB 的中点O 为圆心，OA 的长为半径作半圆交AC 于点D ，则图中阴影部分的面积为( )A.534－π2 B. 534＋π2C. 23－πD. 43－π2第5题图6. (2019泰安)如图，将⊙O 沿弦AB 折叠，AB ︵恰好经过圆心O ，若⊙O 的半径为3，则AB ︵的长为( ) A. 12π B. π C. 2π D. 3π第6题图7. (2019重庆A 卷)如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，∠ABC ＝60°，AB ＝2.分别以点A ，点C 为圆心，以AO 的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为________．(结果保留π)第7题图8. (全国视野创新题推荐·2019贵阳)如图，用等分圆的方法，在半径为OA 的圆中，画出了如图所示的四叶幸运草，若OA ＝2，则四叶幸运草的周长是________．第8题图点对面·跨板块考点迁移2分钟1. (2019天水)如图，在平面直角坐标系中，已知⊙D 经过原点O ，与x 轴、y 轴分别交于A 、B 两点，B 点坐标为(0，23)，OC 与⊙D 相交于点C ，∠OCA ＝30°，则图中阴影部分的面积为________．(结果保留根号和π)第1题图参考答案第26课时 与圆有关的计算点对点·课时内考点巩固1. C 【解析】∵扇形的半径为6，圆心角为120°，∴S 扇形＝120·π·62360＝12π.2. B 【解析】如解图，连接CO ，∵OC ＝OA ，∠CAO ＝60°，∴△AOC 为等边三角形．∴∠AOC ＝60°，∴∠BOC ＝∠AOB －∠AOC ＝80°，∴BC ︵的长为80×6π180＝8π3.第2题解图3. 110 【解析】设此扇形的圆心角为n °，根据题意得l ＝nπr 180＝nπ·18180＝11π，解得n ＝110. 点对线·板块内考点衔接1. C 【解析】∵正方形ABCD 的边长为4，∴AB ＝4，∠ABD ＝45°.∴S 阴影＝S △ABD －S 扇形ABE ＝12×AB 2－45π×AB 2360＝12×42－45π×42360＝8－2π.2. A 【解析】如解图，连接OB ，OC .∵∠ABC ＝65°，∠ACB ＝70°，∴∠A ＝180°－∠ABC －∠ACB ＝45°，∵∠1＝2∠A ＝90°，OB ＝OC ，∴△OBC 是等腰直角三角形，∵BC ＝22，∴OB ＝OC ＝2，∴BC ︵的长为90×π×2180＝π.第2题解图3. B 【解析】如解图，连接OC ，OD .∵AC ，BD 分别与⊙O 相切于点C ，D ，∴OC ⊥AC ，OD ⊥BD . ∵∠A ＝45°，∴△ACO 是等腰直角三角形，∴AC ＝OC ＝OD ＝4.∵AC ＝BD ＝4，∴△BDO 是等腰直角三角形，∴∠AOC ＝∠BOD ＝45°，∴∠COD ＝90°. ∴CD ︵的长为90π×4180＝2π.第3题解图4. A 【解析】如解图，连接OB ，交AC 于点D .由题意易知四边形OABC 为菱形，∴△OAB 为等边三角形，∴S △OAD ＝S △BCD ，∠AOB ＝60°，∵⊙O 的半径为6.∴S 阴影＝S 扇形AOB ＝60360×π×62＝6π.第4题解图5. A 【解析】如解图，连接OD ，过点D 作DE ⊥AB 于点E .∵在Rt △ABC 中，AB ＝23，BC ＝2，∴S △ABC ＝12AB ·BC ＝2 3.在Rt △ABC 中，∵tan ∠BAC ＝BC AB ＝223＝33，∴∠BAC ＝30°，∴∠BOD ＝60°.∵OA ＝OB ＝OD ＝12AB ＝3，∴S 扇形BOD ＝60·π·OD 2360＝π2.∵DE ＝OD ·sin60°＝32，∴S △AOD ＝12OA ·DE ＝334.∴S 阴影＝S △ABC －S △AOD －S 扇形BOD ＝534－π2.第5题解图6. C 【解析】如解图，过点O 作OM ⊥AB 于点M ，连接AO 、BO ，∵⊙O 的半径为3，∴OM ＝12×3＝32.∵在Rt △AOM 中，OM ＝12OA ，∴∠OAB ＝30°，∵OA ＝OB ，∴∠OBA ＝∠OAB ＝30°，∴∠AOB ＝120°.∴AB ︵的长为120π×3180＝2π.第6题解图7. 23－2π3 【解析】∵四边形ABCD 是菱形，∴AC ⊥BD ，AO ＝CO ，∵∠ABC ＝60°，∴∠BAD ＝∠BCD ＝120°，∵AB ＝2，∴AO ＝1，BO ＝3，∴S 菱形ABCD ＝12AC ·BD ＝2AO ·BO ＝23，S 扇形＝2×120π×12360＝2π3，∴S 阴影＝23－2π3. 8. 42π 【解析】如解图，根据题意可知四叶幸运草的周长是以AB 为直径的4个半圆弧长，∵OA ＝OB ＝2，∠AOB ＝90°，在Rt △AOB 中，AB ＝OA 2＋OB 2＝22＋22＝22，∴AB ︵的长为12×π×22＝2π，∵四叶幸运草的周长为2π×4＝42π.第8题解图点对面·跨板块考点迁移1. 2π－23 【解析】如解图，连接OD 、AB ，∵∠AOB ＝90°，A 、O 、B 在⊙D 上，∴AB 是⊙D 的直径，∵∠OCA ＝30°，∴∠ODA ＝60°，∠ABO ＝30°.∴△AOD 为等边三角形，∴OD ＝OA ＝OB ·tan30°＝23×33＝2.∴S 阴影＝12S ⊙D －S △AOB ＝12π×22－12×2×23＝2π－2 3.第1题解图。

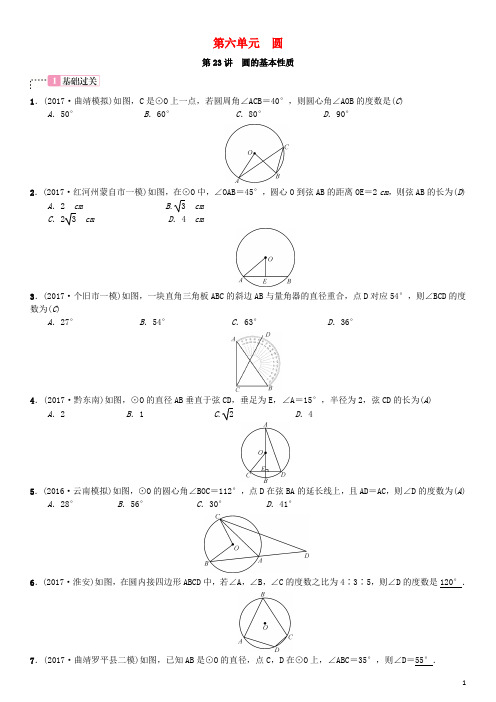
第六单元圆第23讲圆的基本性质1．(2017·曲靖模拟)如图，C是⊙O上一点，若圆周角∠ACB＝40°，则圆心角∠AOB的度数是(C) A．50°B．60°C．80°D．90°2．(2017·红河州蒙自市一模)如图，在⊙O中，∠OAB＝45°，圆心O到弦AB的距离OE＝2 cm，则弦AB的长为(D) A．2 cm B. 3 cmC．2 3 cm D．4 cm3．(2017·个旧市一模)如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应54°，则∠BCD的度数为(C)A．27°B．54°C．63°D．36°4．(2017·黔东南)如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A＝15°，半径为2，弦CD的长为(A) A．2 B．1 C. 2 D．45．(2016·云南模拟)如图，⊙O的圆心角∠BOC＝112°，点D在弦BA的延长线上，且AD＝AC，则∠D的度数为(A) A．28°B．56°C．30°D．41°6．(2017·淮安)如图，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4∶3∶5，则∠D的度数是120°．7．(2017·曲靖罗平县二模)如图，已知AB是⊙O的直径，点C，D在⊙O上，∠ABC＝35°，则∠D＝55°．8．(2017·曲靖一模)如图，⊙O 的半径为4，△ABC 是⊙O 的内接三角形，连接OB ，OC.若∠BAC 和∠BOC 互补，则弦BC 的长度为9．(2016·曲靖模拟)如图，AB 是⊙O 的直径，C ，D ，E 都是⊙O 上的点，则∠1＋∠2＝90°．10．(2016·曲靖模拟)如图，⊙O 是△ABC 的外接圆，AD 是⊙O 的直径．若⊙O 的半径是3，sin B ＝16，则线段AC 的长为1．11．(2013·西双版纳)如图，AB 是⊙O 的直径，点C 在⊙O 上，点P 在线段OA 上运动，设∠PCB＝α，则α的最大值是90°．12．如图，已知AB 是⊙O 的直径，BC 为弦，过圆心O 作OD⊥BC 交弧BC 于点D ，连接DC.若∠DCB＝32°，则∠BAC ＝64°．13．如图，A ，B 是⊙O 上的两点，∠AOB ＝120°，C 是弧AB ︵的中点，求证：四边形OACB 是菱形．证明：连接OC.∵C 是AB ︵的中点，∠AOB ＝120°，∴∠AOC ＝∠BOC＝60°. 又∵OA＝OC ＝OB ，∴△OAC 和△OBC 都是等边三角形． ∴AC ＝OA ＝OB ＝BC. ∴四边形OACB 是菱形．14．如图，点A ，B ，C 在⊙O 上，∠A ＝36°，∠C ＝28°，则∠B＝(C )A ．100°B ．72°C ．64°D ．36°15．(2017·青岛)如图，AB 是⊙O 的直径，点C ，D ，E 在⊙O 上．若∠AED＝20°，则∠BCD 的度数为(B )A ．100°B ．110°C ．115°D ．120°16．(2017·昆明官渡区模拟)如图，⊙O 的半径OD⊥弦AB 于点C ，连接AO 并延长交⊙O 于点E ，连接EC.若AB ＝8，CD ＝2，则EC 的长为(D )A ．2B ．8C .13D ．21317．如图，已知△ABC，以AB 为直径的⊙O 分别交AC 于D ，BC 于E ，连接ED ，若ED ＝EC.(1)求证：AB ＝AC ；(2)若AB ＝4，BC ＝23，求CD 的长．解：(1)证明：∵ED＝EC ，∴∠EDC ＝∠C. ∵∠EDC ＝∠B，∴∠B ＝∠C.∴AB＝AC. (2)连接AE.∵AB 为直径，∴AE ⊥BC. 由(1)知AB ＝AC ， ∴BE ＝CE ＝12BC ＝ 3.又由(1)知∠EDC＝∠B，∠C ＝∠C， ∴△EDC ∽△ABC.∴CE CA ＝CDCB ，即34＝CD 23.∴CD＝32.18．(2017·孝感)已知半径为2的⊙O 中，弦AC ＝2，弦AD ＝22，则∠COD 的度数为30°或150°．。

第4讲 分式1．(2017·武汉)若代数式1a －4在实数范围内有意义，则实数a 的取值范围为(D ) A ．a ＝4 B ．a ＞4C ．a ＜4D ．a ≠42．(2017·昆明市官渡区二模)化简a 2－b 2a 2＋ab 的结果为(B ) A ．－b a B .a －b a C .a ＋b a D ．－b 3．下列分式中，最简分式是(A ) A .x 2－1x 2＋1 B .x ＋1x 2－1C .x 2－2xy ＋y 2x 2－xyD .x 2－362x ＋124．(2017·河北)若3－2x x －1＝( )＋1x －1，则( )中的数是(B ) A ．－1 B ．－2C ．－3D ．任意实数5．当x ＝6，y ＝－2时，代数式x 2－y 2（x －y ）2的值为(D ) A ．2 B .43 C ．1 D .126．(2017·嘉兴)若分式2x －4x ＋1的值为0，则x 的值为2． 7．(2017·徐州)计算：(1＋4x －2)÷x ＋2x 2－4x ＋4. 解：原式＝x －2＋4x －2·（x －2）2x ＋2＝x －2. 8．(2017·楚雄州一模)先化简，再求值：(2x ＋3－13－x )÷x x 2－9，其中x ＝1. 解：原式＝2（x －3）＋（x ＋3）（x ＋3）（x －3）÷x x 2－9＝3（x －1）（x ＋3）（x －3）·（x ＋3）（x －3）x ＝3（x －1）x . 当x ＝1时，原式＝0.9．(2015·曲靖)先化简，再求值：a a 2＋4a ＋4÷(1－2a －4a 2－4)，其中a ＝3－2. 解：原式＝a （a ＋2）2÷a （a －2）（a ＋2）（a －2）＝a （a ＋2）2·a ＋2a＝1a ＋2. 当a ＝3－2时，原式＝33. 10．(2017·昆明市官渡区模拟)先化简，x 2－1x 2－2x ＋1÷x 2＋x x －1＋2x，再从－1，1，和2中选取一个合适的x 值带入求值．2 解：原式＝（x ＋1）（x －1）（x －1）2·x －1x （x ＋1）＋2x ＝1x ＋2x ＝3x .当x ＝2时，原式＝32.11．(2017C 乐山)若a 2－ab ＝0(b≠0)，则aa ＋b ＝(C )A ．0B .12C ．0或12D ．1或212．若a 2＋5ab －b 2＝0，则b a －a b 的值为5．13．(2017·杭州)若m －3m －1·|m|＝m －3m －1，则m ＝－1或3．14．(2017·吉林)某学生化简分式1x ＋1＋2x 2－1出现了错误，解答过程如下：原式＝1（x ＋1）（x －1）＋2（x ＋1）（x －1）(第一步)＝1＋2（x ＋1）（x －1）(第二步)＝3x 2－1.(第三步)(1)该学生解答过程是从第一步开始出错的，其错误原因是分式的基本性质用错；(2)请写出此题正确的解答过程．解：原式＝x －1（x ＋1）（x －1）＋2（x ＋1）（x －1）＝x ＋1（x ＋1）（x －1）＝1x －1.。

第4讲 分式1．(2017·武汉)若代数式1a －4在实数范围内有意义，则实数a 的取值范围为(D ) A ．a ＝4 B ．a ＞4C ．a ＜4D ．a ≠42．(2017·昆明市官渡区二模)化简a 2－b 2a 2＋ab 的结果为(B ) A ．－b a B .a －b a C .a ＋b a D ．－b 3．下列分式中，最简分式是(A ) A .x 2－1x 2＋1 B .x ＋1x 2－1C .x 2－2xy ＋y 2x 2－xyD .x 2－362x ＋124．(2017·河北)若3－2x x －1＝( )＋1x －1，则( )中的数是(B ) A ．－1 B ．－2C ．－3D ．任意实数5．当x ＝6，y ＝－2时，代数式x 2－y 2（x －y ）2的值为(D ) A ．2 B .43 C ．1 D .126．(2017·嘉兴)若分式2x －4x ＋1的值为0，则x 的值为2． 7．(2017·徐州)计算：(1＋4x －2)÷x ＋2x 2－4x ＋4. 解：原式＝x －2＋4x －2·（x －2）2x ＋2＝x －2. 8．(2017·楚雄州一模)先化简，再求值：(2x ＋3－13－x )÷x x 2－9，其中x ＝1. 解：原式＝2（x －3）＋（x ＋3）（x ＋3）（x －3）÷x x 2－9＝3（x －1）（x ＋3）（x －3）·（x ＋3）（x －3）x ＝3（x －1）x . 当x ＝1时，原式＝0.9．(2015·曲靖)先化简，再求值：a a 2＋4a ＋4÷(1－2a －4a 2－4)，其中a ＝3－2. 解：原式＝a （a ＋2）2÷a （a －2）（a ＋2）（a －2）＝a （a ＋2）2·a ＋2a＝1a ＋2. 当a ＝3－2时，原式＝33. 10．(2017·昆明市官渡区模拟)先化简，x 2－1x 2－2x ＋1÷x 2＋x x －1＋2x，再从－1，1，和2中选取一个合适的x 值带入求值．解：原式＝（x ＋1）（x －1）（x －1）2·x －1x （x ＋1）＋2x ＝1x ＋2x ＝3x. 当x ＝2时，原式＝32.11．(2017C 乐山)若a 2－ab ＝0(b≠0)，则a a ＋b ＝(C ) A ．0 B .12 C ．0或12 D ．1或212．若a 2＋5ab －b 2＝0，则b a －a b的值为5． 13．(2017·杭州)若m －3m －1·|m|＝m －3m －1，则m ＝－1或3．14．(2017·吉林)某学生化简分式1x ＋1＋2x 2－1出现了错误，解答过程如下： 原式＝1（x ＋1）（x －1）＋2（x ＋1）（x －1）(第一步) ＝1＋2（x ＋1）（x －1）(第二步) ＝3x 2－1.(第三步) (1)该学生解答过程是从第一步开始出错的，其错误原因是分式的基本性质用错；(2)请写出此题正确的解答过程．解：原式＝x －1（x ＋1）（x －1）＋2（x ＋1）（x －1）＝x ＋1（x ＋1）（x －1） ＝1x －1.。

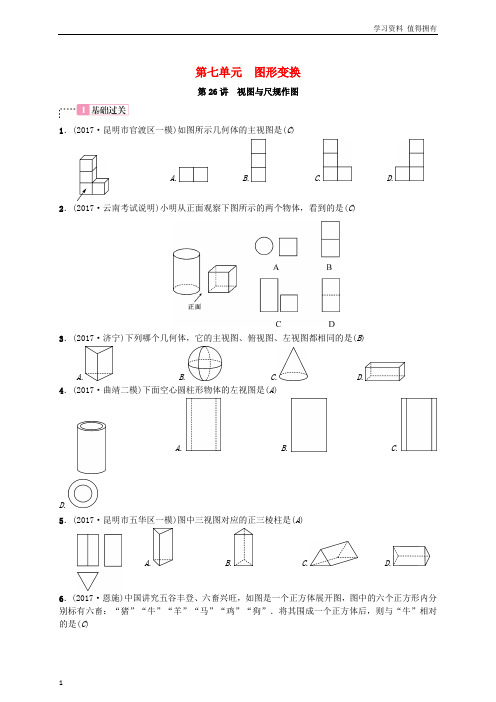
第七单元图形变换第26讲视图与尺规作图1．(2017·昆明市官渡区一模)如图所示几何体的主视图是(C)A.B.C.D. 2．(2017·云南考试说明)小明从正面观察下图所示的两个物体，看到的是(C)3．(2017·济宁)下列哪个几何体，它的主视图、俯视图、左视图都相同的是(B)A.B.C.D.4．(2017·曲靖二模)下面空心圆柱形物体的左视图是(A)A.B.C.D.5．(2017·昆明市五华区一模)图中三视图对应的正三棱柱是(A)A.B.C.D.6．(2017·恩施)中国讲究五谷丰登、六畜兴旺，如图是一个正方体展开图，图中的六个正方形内分别标有六畜：“猪”“牛”“羊”“马”“鸡”“狗”．将其围成一个正方体后，则与“牛”相对的是(C)A ．羊B ．马C ．鸡D ．狗7．(2017·深圳)如图，已知线段AB ，分别以A ，B 为圆心，大于12AB 的长为半径作弧，连接弧的交点得到直线l ，在直线l 上取一点C ，使得∠CAB＝25°，延长AC 至M ，求∠BCM 的度数为(B )A ．40°B ．50°C ．60°D ．70°8．(2017·聊城)如图是由若干小正方体组成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，这个几何体的主视图是(C )A .B .C .D .9．(2017·陕西)如图所示的几何体是由一个长方体和一个圆柱体组成的，则它的主视图是(B )A .B .C .D .10．(2016·河北)如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．步骤1：以C 为圆心，CA 为半径画弧①；步骤2：以B 为圆心，BA 为半径画弧②，交弧①于点D ； 步骤3：连接AD ，交BC 延长线于点H. 下列叙述正确的是(A ) A ．BH 垂直平分线段AD B ．AC 平分∠BAD C ．S △ABC ＝BC·AHD ．AB ＝AD11．如图是由6个棱长均为1的正方体组成的几何体，它的主视图的面积为5．12．如图是一个圆柱体的三视图，由图中数据计算此圆柱体的侧面积为24π．13．如图，已知线段AB ，分别以点A ，B 为圆心，大于线段12AB 的长为半径画弧，相交于点C ，D ，连接AC ，BC ，BD ，CD ，DA.其中AB ＝4，CD ＝5，则四边形ADBC 的面积为10．14．(2016·昆明模拟)如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体(D )A ．主视图改变，左视图改变B ．俯视图不变，左视图不变C．俯视图改变，左视图改变D．主视图改变，左视图不变15．(2017·常德)如图是一个几何体的三视图，则这个几何体是(B)A.B.C.D.16．(2017·凉山)如图是一个几何体的三视图，则该几何体的侧面积是(A)A．213πB．10πC．20πD．413π17．(2017·齐齐哈尔)一个几何体的主视图和俯视图如图所示，若这个几何体最多有a个小正方体组成，最少有b个小正方体组成，则a＋b等于(C)A．10 B．11 C．12 D．13提示：a＝7，b＝5.18．(2017·呼和浩特)如图是某几何体的三视图，根据图中数据，求得该几何体的表面积为(225＋。

第7讲 一元二次方程1．(2017·泰安)一元二次方程x 2－6x －6＝0配方后化为(A )A ．(x －3)2＝15B ．(x －3)2＝3C ．(x ＋3)2＝15D ．(x ＋3)2＝32．(2017·普洱市思茅区校级一模)一元二次方程x 2－4x ＋4＝0的根的情况是(C )A ．有两个不相等的实数根B ．有一个实数根C ．有两个相等的实数根D ．没有实数根3．(2017·苏州)关于x 的一元二次方程x 2－2x ＋k ＝0有两个相等的实数根，则k 的值为(A )A ．1B ．－1C ．2D ．－24．方程x 2＋x －12＝0的两个根为(D )A ．x 1＝－2，x 2＝6B ．x 1＝－6，x 2＝2C ．x 1＝－3，x 2＝4D ．x 1＝－4，x 2＝35．(2017·威海)若1－3是方程x 2－2x ＋c ＝0的一个根，则c 的值为(A )A ．－2B ．43－2C ．3－ 3D ．1＋ 36．(2017·云南考试说明)某商品经过两次降价，每件售价由原来的55元降到了35元．设平均每次降价的百分率为x ，则下列方程中正确的是(C )A ．55(1＋x)2＝35B ．35(1＋x)2＝55C ．55(1－x)2＝35D ．35(1－x)2＝557．(2017·白银)如图，某小区计划在一块长为32 m ，宽为20 m 的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570 m 2.若设道路的宽为x m ，则下面所列方程正确的是(A )A ．(32－2x)(20－x)＝570B ．32x ＋2×20x＝32×32－570C ．(32－x)(20－x)＝32×20－570D ．32x ＋2×20x－2x 2＝5708．(2017·曲靖一模)若关于x 的方程(a －1)x1＋a 2＝1是一元二次方程，则a 的值是－1．9．(2017·泰安)关于x 的一元二次方程x 2＋(2k －1)x ＋(k 2－1)＝0无实数根，则k 的取值范围为k>54． 10．(2017·曲靖模拟)一元二次方程x 2＋mx ＋2m ＝0的两个实根分别为x 1，x 2，若x 1＋x 2＝1，则x 1x 2＝－2．11．(2017·云南模拟)若方程3x 2－5x －2＝0有一根是a ，则6a 2－10a ＝4．12．(2017·曲靖市罗平县一模)用配方法解方程：x 2－x ＝3x ＋5.解：原方程整理，得x 2－4x ＝5.∴x 2－4x ＋4＝5＋4，即(x －2)2＝9.∴x －2＝3或x －2＝－3.解得x ＝5或x ＝－1.13．解方程：3x(x －2)＝2(2－x)．解：3x(x －2)＋2(x －2)＝0.(x －2)(3x ＋2)＝0.∴x 1＝2，x 2＝－23.14．关于x 的一元二次方程x 2＋(2m ＋1)x ＋m 2－1＝0有两个不相等的实数根．(1)求m 的取值范围；(2)写出一个满足条件的m 的值，并求此时方程的根．解：(1)∵原方程有两个不相等实数根，∴Δ＝(2m ＋1)2－4(m 2－1)＝4m ＋5>0.解得m>－54. (2)m ＝1，原方程为x 2＋3x ＝0，即x(x ＋3)＝0.∴x 1＝0，x 2＝－3.(m 取其他值也可以)15．为进一步发展基础教育，自2015年以来，某县加大了教育经费的投入，2015年该县投入教育经费6 000万元，2017年投入教育经费8 640万元，假设该县这两年投入教育经费的年平均增长率相同．(1)求这两年该县投入教育经费的年平均增长率；(2)若该县教育经费的投入还将保持相同的年平均增长率，请你预算2018年该县投入教育经费多少万元． 解：(1)设这两年该县投入教育经费的年平均增长率为x.则6 000(1＋x)2＝8 640.解得x 1＝0.2，x 2＝－2.2(不合题意，舍去)．答：这两年该县投入教育经费的年平均增长率为20%.(2)∵2017年该县投入教育经费8 640万元，且增长率为20%，∴2018年该县投入教育经费y ＝8 640×(1＋0.2)＝10 368(万元)．答：预算2018年该县投入教育经费10 368万元．16．(2017·曲靖市罗平县一模)曲靖市某楼盘准备以每平方米4 000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米3 240元的均价开盘销售．(1)求平均每次下调的百分率；(2)某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.9折销售；②不打折，送两年物业管理费，物业管理费是每平方米每月1.4元，请问哪种方案更优惠？解：(1)设平均每次下调的百分率是x.依题意，得4 000(1－x)2＝3 240.解得x ＝0.1＝10%或x ＝1.9(不合题意，舍去).答：平均每次下调的百分率是10%.(2)方案①优惠：100×3 240×(1－99%)＝3 240(元)；方案②优惠：100×1.4×12×2＝3 360(元)．故选择方案②更优惠．17．(2017·曲靖一模)若k 为整数，且关于x 的方程(x ＋1)2＝1－k 没有实根，则满足条件的k 的值为2．(只需写一个)18．设m ，n 分别为一元二次方程x 2＋2x －2 018＝0的两个实数根，则m 2＋3m ＋n ＝2_016．19．(2017·云南考试说明)如图，张大叔从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1 m的正方形后，剩下的部分刚好能围成一个容积为15 m3的无盖长方体箱子，且此长方体箱子的底面长比宽多2 m．现已知购买这种铁皮每平方米需20元，则张大叔购回这块铁皮共花了多少元？解：设这种箱子的底部宽x m，则长为(x＋2)m.由题意，得x(x＋2)×1＝15.解得x1＝－5(不符合题意，舍去)，x2＝3.x＋2＝3＋2＝5.由长方体展开图知，要购买矩形铁皮的面积为(5＋2)×(3＋2)＝35(m2)．35×20＝700(元)．答：张大叔购回这块矩形铁皮共花了700元．19．(2017·曲靖一模)等腰三角形的边长是方程x2－6x＋8＝0的解，则这个三角形的周长是10或6或12．。

第4讲 分式1．(2017·武汉)若代数式1a －4在实数范围内有意义，则实数a 的取值范围为(D ) A ．a ＝4 B ．a ＞4C ．a ＜4D ．a ≠42．(2017·昆明市官渡区二模)化简a 2－b 2a 2＋ab 的结果为(B ) A ．－b a B .a －b a C .a ＋b a D ．－b 3．下列分式中，最简分式是(A ) A .x 2－1x 2＋1 B .x ＋1x 2－1C .x 2－2xy ＋y 2x 2－xyD .x 2－362x ＋124．(2017·河北)若3－2x x －1＝( )＋1x －1，则( )中的数是(B ) A ．－1 B ．－2C ．－3D ．任意实数5．当x ＝6，y ＝－2时，代数式x 2－y 2（x －y ）2的值为(D ) A ．2 B .43 C ．1 D .126．(2017·嘉兴)若分式2x －4x ＋1的值为0，则x 的值为2． 7．(2017·徐州)计算：(1＋4x －2)÷x ＋2x 2－4x ＋4. 解：原式＝x －2＋4x －2·（x －2）2x ＋2＝x －2. 8．(2017·楚雄州一模)先化简，再求值：(2x ＋3－13－x )÷x x 2－9，其中x ＝1. 解：原式＝2（x －3）＋（x ＋3）（x ＋3）（x －3）÷x x －9＝3（x －1）（x ＋3）（x －3）·（x ＋3）（x －3）x ＝3（x －1）x . 当x ＝1时，原式＝0.9．(2015·曲靖)先化简，再求值：a a 2＋4a ＋4÷(1－2a －4a 2－4)，其中a ＝3－2. 解：原式＝a （a ＋2）2÷a （a －2）（a ＋2）（a －2）＝a （a ＋2）2·a ＋2a＝1a ＋2. 当a ＝3－2时，原式＝33. 10．(2017·昆明市官渡区模拟)先化简，x 2－1x 2－2x ＋1÷x 2＋x x －1＋2x，再从－1，1，和2中选取一个合适的x 值带入求值．2 解：原式＝（x ＋1）（x －1）（x －1）2·x －1x （x ＋1）＋2x ＝1x ＋2x ＝3x .当x ＝2时，原式＝32.11．(2017C 乐山)若a 2－ab ＝0(b≠0)，则aa ＋b ＝(C )A ．0B .12C ．0或12D ．1或212．若a 2＋5ab －b 2＝0，则b a －a b 的值为5．13．(2017·杭州)若m －3m －1·|m|＝m －3m －1，则m ＝－1或3．14．(2017·吉林)某学生化简分式1x ＋1＋2x 2－1出现了错误，解答过程如下：原式＝1（x ＋1）（x －1）＋2（x ＋1）（x －1）(第一步)＝1＋2（x ＋1）（x －1）(第二步)＝3x 2－1.(第三步)(1)该学生解答过程是从第一步开始出错的，其错误原因是分式的基本性质用错；(2)请写出此题正确的解答过程．解：原式＝x －1（x ＋1）（x －1）＋2（x ＋1）（x －1）＝x ＋1（x ＋1）（x －1）＝1x －1.。

第五单元四边形第21讲平行四边形与多边形1．如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是(C)A．AB∥CD B．AB＝CDC．AC＝BD D．OA＝OC2．如图，在▱ABCD中，M是BC延长线上的一点，若∠A＝135°，则∠MCD的度数是(A)A．45°B．55°C．65°D．75°3．(2017·昆明市官渡区模拟)一个正多边形的内角和为1 080°，则这个正多边形的每个外角为(B) A．30°B．45°C．60°D．80°4．(2017·丽水)如图，在▱ABCD中，连接AC，∠ABC＝∠CAD＝45°，AB＝2，则BC的长是(C)A. 2 B．2 C．2 2 D．45．(2017·衡阳)如图，在四边形ABCD中，AB∥CD，要使四边形ABCD是平行四边形，可添加的条件不正确的是(D) A．AB＝CD B．BC∥ADC．∠A＝∠C D．BC＝AD6．(2017·贵阳)如图，在▱ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，若△CED的周长为6，则▱ABCD的周长为(B)A．6 B．12 C．18 D．247．(2017·云南考试说明)如图，在▱ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，则阴影部分的面积为(C) A．3 B．6 C．12 D．248．(2017·曲靖市罗平县三模)若一个多边形的对角线条数为9，则这个多边形的边数为6． 9．(2017·邵阳)如图所示的正六边形ABCDEF ，连接FD ，则∠FDC 的大小为90°．10．(2017·武汉)如图，在▱ABCD 中，∠D ＝100°，∠DAB 的平分线AE 交DC 于点E ，连接BE.若AE ＝AB ，则∠EBC 的度数为30°．11．如图，将▱ABCO 放置在平面直角坐标系xOy 中，O 为坐标原点，若点A 的坐标是(6，0)，点C 的坐标是(1，4)，则点B 的坐标是(7，4)．12．(2017·南京)如图，在▱ABCD 中，点E ，F 分别在AD ，BC 上，且AE ＝CF ，EF ，BD 相交于点O ，求证：OE ＝OF.证明：连接BE 、DF.∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AD ＝BC. ∵AE ＝CF ，∴DE ＝BF.∴四边形BEDF 是平行四边形． ∴OF ＝OE.(提示：或证△DOE≌△BOF 亦可．)13．(2017·曲靖模拟)如图，在▱ABCD 中，对角线AC ，BD 相交成的锐角为60°，若AC ＝6，BD ＝8，求▱ABCD 的面积．(3≈1.73，结果精确到0.1)解：过点A 作AE⊥BD 于点E. ∵四边形ABCD 是平行四边形， ∴OA ＝12AC ＝3.在Rt △AEO 中，∠AOE ＝60°， ∴AE ＝OA·sin 60°＝3×32＝332. ∴S ▱ABCD ＝2S △ABD ＝2×12BD·AE＝2×12×8×332＝123≈20.8.14．如图，E 是▱ABCD 的边CD 的中点，延长AE 交BC 的延长线于点F.(1)求证：△ADE≌△FCE；(2)若∠BAF＝90°，BC ＝5，EF ＝3，求CD 的长．解：(1)证明：∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AB ∥CD.∴∠DAE ＝∠F，∠D ＝∠ECF. ∵E 是▱ABCD 的边CD 的中点， ∴DE ＝CE.在△ADE 和△FCE 中， ⎩⎪⎨⎪⎧∠DAE＝∠F，∠D ＝∠ECF，DE ＝CE ，∴△ADE ≌△FCE(AAS )．(2)∵△ADE≌△FCE，∴AE ＝EF ＝3. ∵AB ∥CD ，∴∠AED ＝∠BAF＝90°. 在▱ABCD 中，AD ＝BC ＝5， ∴DE ＝AD 2－AE 2＝52－32＝4. ∴CD ＝2DE ＝8.15．如图，点O 是△ABC 内一点，连接OB ，OC ，并将AB ，OB ，OC ，AC 的中点D ，E ，F ，G 依次连接，得到四边形DEFG.(1)求证：四边形DEFG 是平行四边形；(2)若M 为EF 的中点，OM ＝3，∠OBC 和∠OCB 互余，求DG 的长度．解：(1)证明：∵D，G 分别是AB ，AC 的中点， ∴DG ∥BC ，DG ＝12BC.∵E ，F 分别是OB ，OC 的中点，∴EF ∥BC ，EF ＝12BC.∴DG＝EF ，DG ∥EF.∴四边形DEFG 是平行四边形． (2)∵∠OBC 和∠OCB 互余，∴∠OBC ＋∠OCB＝90°.∴∠BOC ＝90°. ∵M 为EF 的中点，OM ＝3，∴EF ＝2OM ＝6.又∵四边形DEFG 是平行四边形，∴DG ＝EF ＝6.16．(2017·曲靖二模)如图，在▱ABCD 中，用直尺和圆规作∠BAD 的平分线AG 交BC 于点E ，若BF ＝6，AB ＝4，则AE 的长为(B )A .7B ．27C ．37D ．4717．(2017·昆明市五华区一模)阅读理解：如图1所示，在平面内选一定点O ，引一条有方向的射线ON ，再选定一个单位长度，那么平面上任一点M 的位置可由OM 的长度m 与∠MON 的度数θ确定，有序数对(m ，θ)称为M 点的“极坐标”，这样建立的坐标系称为“极坐标系”．应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA 在射线ON 上，则正六边形的顶点C 的极坐标应记为(A )图1 图2A ．(4，60°)B ．(4，45°)C ．(22，60°)D ．(22，50°)18．如图，四边形ABCD 为平行四边形，∠BAD 的角平分线AE 交CD 于点F ，交BC 的延长线于点E.(1)求证：BE ＝CD ；(2)连接BF ，若BF⊥AE，∠BEA ＝60°，AB ＝4，求▱ABCD 的面积．解：(1)证明：∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AB ＝CD. ∴∠AEB ＝∠DAE.∵AE 是∠BAD 的平分线，∴∠BAE ＝∠DAE.∴∠BAE＝∠AEB. ∴AB ＝B E.∴BE＝CD.(2)∵AB＝BE ，∠BEA ＝60°，∴△ABE 是等边三角形．∴AE＝AB ＝4. ∵BF ⊥AE ，∴AF ＝EF ＝2.∴BF ＝AB 2－AF 2＝42－22＝2 3.∵AD ∥BC ，∴∠D＝∠ECF，∠DAF ＝∠E. 在△ADF 和△ECF 中， ⎩⎪⎨⎪⎧∠D＝∠ECF，∠DAF ＝∠E，AF ＝EF ，∴△ADF ≌△ECF(AAS )．∴S △ADF ＝S △ECF . ∴S ▱ABCD ＝S △ABE ＝12AE·BF＝12×4×23＝4 3.19．(2017·黑龙江)在▱ABCD中，∠A的平分线把BC边分成长度是3和4的两部分，则▱ABCD的周长是(C) A．22 B．20 C．22或20 D．18。

第5讲 二次根式1．(2017·日照)式子a ＋1a －2有意义，则实数a 的取值范围是(C ) A ．a ≥－1 B ．a ≠2 C ．a ≥－1且a≠2 D ．a ＞22．(2017·益阳)下列各式化简后的结果为32的是(C )A . 6B .12C .18D .36 3．(2017·十堰)下列运算正确的是(C )A .2＋3＝ 5B ．22×32＝6 2C .8÷2＝2D ．32－2＝34．计算(515－245)÷(－5)的结果为(A ) A ．5 B ．－5 C ．7 D ．－75．(2017·滨州)下列计算：(1)(2)2＝2；(2)（－2）2＝2；(3)(－23)2＝12；(4)(2＋3)(2－3)＝－1.其中结果正确的个数为(D )A ．1B ．2C ．3D ．4 6．计算：(1)(2017·衡阳)12－3(2)(2017·哈尔滨)27－ (3)(2017·天津)(4＋7)(4＝9； (4)(2016·青岛)32－82＝2．7．(2017·大连)计算：(2＋1)2－8＋(－2)2.解：原式＝3＋22－22＋4＝7.8．(2017·陕西)计算：(－2)×6＋|3－2|－(12)－1.解：原式＝－12＋2－3－2＝－23－3＝－3 3.9．计算：12＋|－3|－(－2 015)0＋(12)－1－3tan 60°.解：原式＝23＋3－1＋2－3×3＝1.10．(2017·枣庄)实数a ，b 在数轴上对应点的位置如图所示，化简|a|＋（a －b ）2的结果是(A )A ．－2a ＋bB ．2a －bC ．－bD ．b11．若a －1＋b 2－4b ＋4＝0，则ab 的值等于(D )A ．－2B ．0C ．1D ．212．(2015·孝感)已知x ＝2－3，则代数式(7＋43)x 2＋(2＋3)x ＋3的值是(C )A ．0B . 3C ．2＋ 3D ．2－ 3 13．(2017·大理模拟)观察下列等式：(1)12－13＝1223； (2)12（13－14）＝1338； (3)13（14－15）＝14415.根据上述各等式反映的规律，请写出第514．计算：(3＋2－1)(3－2＋1)．解：原式＝[3＋(2－1)][3－(2－1)]＝(3)2－(2－1)2＝3－(2－22＋1) ＝3－2＋22－1 ＝2 2.15．(人教八下教材P 16“阅读与思考”变式)(2017·泸州)已知三角形的三边长分别为a 、b 、c ，求其面积问题，中外数学家曾经进行过深入研究，古希腊的几何学家海伦(Heron ，约公元50年)给出求其面积的海伦公式S ＝p （p －a ）（p －b ）（p －c ），其中p ＝a ＋b ＋c2；我国南宋时期数学家秦九韶(约1202～1261)曾提出利用三角形的三边求其面积的秦九韶公式S ＝12a 2b 2－（a 2＋b 2－c 22）2，若一个三角形的三边长分别为2，3，4，则其面积是(B )A .3158B .3154 C .3152 D .152。