当前位置：文档之家 › 编译原理第四讲

编译原理第四讲

  • 格式：pptx
  • 大小：343.20 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

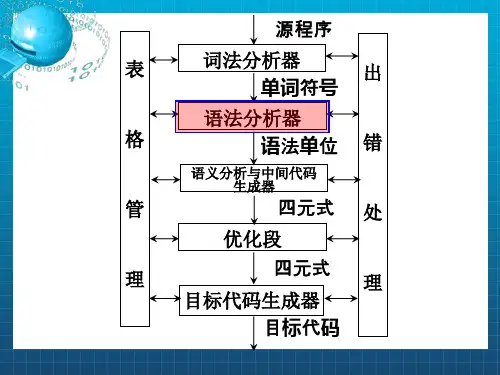
编译原理课件第四章

编译原理课件第四章
为一个句子(合式程序)。
单词符号
语法分
源程序 词法分
语法分 析树 编译程序
析器 取下一单词 析器
后续部分
... 符号表
• 语法分析的方法： • 自下而上分析法(Bottom-up)
• 基本思想：从输入串开始，逐步进行“归约”，
直到文法的开始符号。即从树末端开始，构造语法 树。所谓归约，是指根据文法的产生式规则，把产 生式的右部替换成左部符号。
FIRST( i)∩FOLLOW(A)= i=1,2,...,n
如果一个文法G满足以上条件，则称该文法G为L L(1)文法。
• 对于一个满足上述条件的文法，可以对其输入串进行有效的无回溯的自上而下分析。假 设要用非终结符A进行匹配，面临的输入符号为a，A的所有产生式为 A→ 1 | 2 | … | n 1. 若aFIRST( i)，则指派 i执行匹配任务；
Q→Sab | ab | b • 现在的Q不含直接左递归，把它代入到S的有关候选后，S变成
S→Sabc | abc | bc | c
• 例 考虑文法G(S)
S→Qc|c Q→Rb|b R→Sa|a
• S变成
S→Sabc | abc | bc | c
• 消除S的直接左递归后： S→abcS | bcS | cS S→abcS | Q→Sab |ab | b R→Sa|a
P P
含有左递归的文法将使自上而下的分 析陷入无限循环。
4.3 LL(1)分析法
• 构造不带回溯的自上而下分析算法 • 要消除文法的左递归性 • 克服回溯
4.3.1 左递归的消除
• 直接消除见诸于产生式中的左递归：假定关于非终结符P的规则为 P→P |
其中不以P开头。 我们可以把P的规则等价地改写为如下的非直接左递归形式：

《编译原理教程》第四章语义分析和中间代码生成

《编译原理教程》第四章语义分析和中间代码生成

控制流分析和数据流分析案例
总结词
控制流分析和数据流分析是编译器设计中两种重要的 语义分析技术。
详细描述
在控制流分析案例中，我们以一个具有条件语句和循环 的程序为例，分析其控制流图（Control Flow Graph， CFG）。CFG是一个有向图，用于表示程序中各个基本块 之间的控制流程关系。通过CFG，编译器可以检测到潜 在的程序错误，如死代码和无限循环。在数据流分析案 例中，我们使用数据流方程来跟踪程序中变量的值在执 行过程中的变化。我们以一个简单的程序为例，该程序 包含一个变量在函数调用后被修改的情况。通过数据流 分析，我们可以确定变量的最新值，以便在后续的语义 分析中使用。
定义
三地址代码是一种中间代码形式，它由一系列的三元组操作数和 操作符组成。
特点
三地址代码具有高度规范化，易于分析和优化，且易于转换成目 标代码。
常见形式
常见的三地址代码有三种基本形式，即加法、减法和赋值。
循环优化
定义
循环优化是指在编译过程中，对循环结构进行优化， 以提高目标代码的执行效率。
常见方法
将源程序分解成一个个的词素或标记。
语法分析
根据语言的语法规则，将词素或标记组合成一个个的语句或表达式。
语义分析
对语法分析得到的语句或表达式进行语义检查，确保其语义正确。
中间代码生成
基于语义分析的结果，生成中间代码。
02
语义分析技术
类型检查
类型检查是编译过程中对源代码进行语义分析的重要环节，其主要目的是 确保源代码பைடு நூலகம்类型安全。
常见的循环优化方法包括循环展开、循环合并、循环 嵌套等。
优化效果
通过循环优化，可以减少循环的次数，提高程序的执 行效率。

《编译原理》课件

《编译原理》课件
代码生成
编译器可以将高级语言编写的源代码转换成机器语言或低级语言，以便在特定的硬件平台上运行。编 译器还可以生成可执行文件或动态链接库等二进制文件。
编译器在人工智能领域的应用
机器学习编译器
机器学习编译器可以将机器学习模型转换成可执行代码，以便在嵌入式设备或边缘计算 设备上运行。这种编译器可以优化模型的计算性能和内存占用，提高模型的运行效率。
3
缺点
对于某些复杂文法，可能导致大量的无用推导和 状态爆炸。
自底向上的语法分析
分析步骤
从输入符号序列的最后一个符号开始，逐步向上构建语法树，直 到找到与文法中的某个产生式右部匹配的符号串。
优点
可以充分利用已知信息，避免不必要的推导和状态爆炸。
缺点
对于某些复杂文法，可能导致大量的无用归约和状态爆炸。
04
中间代码生成
中间代码生成的定义和任务
定义
中间代码生成是编译器的一个阶段，将源代码转换成中间代码的过程。
任务
将源代码转换成一种中间表示形式，以便进行后续的优化和目标代码生成。
三地址代码的生成
01
三地址代码是一种中间代码形 式，由一系列的三元式组成。
02
三元式的形式为(op, arg1, arg2)，表示执行一个操作(op) 并产生一个结果，操作数arg1 和arg2来自寄存器、常数或之 前的计算结果。
语义分析
检查AST是否有语义错误，如类型错 误、未定义的变量等。
中间代码生成
将AST转换为中间代码，通常是三地 址代码。
代码优化
对中间代码进行优化，提高执行效 率。
代码生成
将中间代码转换为机器语言代码， 能够在特定硬件上执行。
编译器的分类

编译原理课件第四章

编译原理课件第四章

中间代码生成的过程和方法
过程
中间代码生成是将源代码转换为中间表示形式的过 程，可以使用三地址码等中间代码表示。
方法
中间代码生成可以应用常见的优化技术，如常量折 叠、公共子表达式消除等。
编译优化的基本原理和技术
基本原理
编译优化的基本原理包括消除冗余、提高并行度和改进数据局部性等。
技术
编译优化的常用技术有指令调度、循环优化和内函数等。
编译原理课件第四章
在这一章中，我们将介绍编译原理课件中的第四章内容。我们将探讨编译器 前端和后端的概念，以及它们各自的任务和流程。
编译器前端和后端
1
编译器后端
2
编译器后端负责中间代码生成、代码优 化和目标代码生成等任务。
编译器前端
编译器前端负责词法分析、语法分析和 语义分析等任务。
语法分析器的作用和原理
1 作用
语法分析器用于分析源代码的语法结构，并生成抽象语法树。
2 原理
语法分析器使用文法规则和语法分析算法进行解析，如LL(1)分析和LR分析。
语法制导翻译的概念和实现
概念
语法制导翻译是在语法分析的同时进行翻译，通过 语法规则和语义动作实现。
实现
语法制导翻译可以使用语义动作和符号表等技术来 实现语义分析和中间代码生成。

西安交通大学编译原理课件

西安交通大学编译原理课件

E→E+a|a E⇒E+a ⇒E+a+a ⇒… L(G)={a,a+a,a+a+a,…}
5
上下文无关文法回顾
A→Aa|a A→aA|a
L(G)={an|n为整数，n≥1}
A→Aα|β A→αA|β
A→ε
β不以A开头 L(G)={βαn|n为整数，n≥0}
L(G)={ε,…}
A→Aa|ε A→aA|ε
10
Parse Trees and Abstract Syntax Trees
推导：从开始符号起构造特定句子的一个方法 推导：不能够唯一地表示所推到出的句子的结构
11
上下文无关文法回顾
exp→exp op exp|(exp) | number op →+|-|*
(number – number) * number
15
exp⇒exp op exp ⇒(exp) op exp ⇒(exp op exp) op exp ⇒(number op exp) op exp ⇒(number - exp) op exp ⇒(number - number) op exp ⇒(number - number) * exp ⇒(number - number) * number
typedef struct streenode
{ ExpKind kind;
OpKind op;
struct streenode *lchild, *rchild;
int val;
} StreeNode;
typedef StreeNode *SyntaxTree;
18
Yinliang Zhao （赵银亮）

编译原理课件-词法分析

编译原理课件-词法分析
有窮自動機分為兩類：確定的有窮自動機 (Deterministic Finite Automata)和不確定的有 窮自動 機(Nondeterministic Finite Automata) 。
關於有窮自動機將討論如下內容
確定的有窮自動機DFA 不確定的有窮自動機NFA NFA的確定化 DFA的最小化
VT={a,d} VN={S,A,B}
A B(ad)B B
AdB
正規文法和正規式
對G=(VN,VT,P,S),存在一個 =VT上的正規式R : L(R)=L(G)
AxB AxAy Axy
, By ≈ A=xy ≈ A=xy ≈ A=xy
正規文法和正規式
G[s]:SaA|a AaAadAd
A(ad)A(ad)
=f（Q，b）=Q
Q屬於終態。
得證。
a
Ua b, a
S
b
aQ
b
V
b
DFA M所能接受的符號串的全體記為L(M).
對於任何兩個有窮自動機M和M′，如果L(M)=L(M′)，則 稱M與M′是等價的.
結論：
上一個符號串集V是正規的，當且僅當存在一個上 的確定有窮自動機M，使得V=L(M)。
DFA的確定性表現在轉換函數f:K×Σ→K是一個單值函 數，也就是說，對任何狀態k∈K，和輸入符號a∈Σ， f(k,a)唯一地確定了下一個狀態。從狀態轉換圖來看， 若字母表Σ含有n個輸入字元，那麼任何一個狀態結 點最多有n條弧射出，而且每條弧以一個不同的輸入 字元標記。
狀態
字元
a
S
U
U
Q
V
U
Q
Q
b
V0
V0
Q0
Q

编译原理精选版演示课件.ppt


预测分析表
3
表驱动的预测分析程序模型
khk
4
实现步骤：
（1） 判断文法是否为LL(1)文法。 如果文法中含有左递归，必须先消除 左递归
（2）构造预测分析表 ： Select(A ) （3）列出预测分析过程
khk
5
第6章：自底向上分析方法
自底向上分析方法，也称移进归约分析法
实现思想（是推导的逆过程）：
对输入符号串自左向右进行扫描，并将输入符逐个 移入一个后进先出栈中，边移入边分析，一旦栈顶 符号串形成某个句型的可归约串时，就用该产生式 的左部非终结符代替相应右部的文法符号串，称为 归约。重复这一过程，直到归约到栈中只剩下文法 的开始符号时，则分析成功。
关键问题
khk
6
移进—规约分析（Shift-reduce parsing)
＋
A a
可得 b <. a
由A→( B 且B＋ ( B… 可得 (<. (
＋
B aa…
可得 (<. a
＋
B Aa )
可得 (<. A
khk
18
A(B(Aa) …)
(3) 求> .关系:
A(B…B
＋
Aa
由S→bAb，且A…) 可得 ) > . b
A＋…B 可得 B > . b
khk
88
例1：文法
SaAcBe A b A Ab B d
输入串abbcde#分析
khk
9
归约分析过程（移进归约）：
步骤 1 2 3 4 5 6 7 8 9 10 1kh1k
符号栈 # #a #ab #aA #aAb #aA #aAc #aAcd #aAcB #aAcBe #S

编译原理课件chapter4


三地址代码的生成
总结词
三地址代码是一种常见的中间代码形式，它由一系列的三元 式组成，每个三元式包含一个操作符和两个操作数。
详细描述
三地址代码的生成是编译过程中的一个重要步骤，它通过对 源代码进行语法分析和语义分析，将高级语言转换为一系列 的三元式。这些三元式表示了源代码中的运算和数据传输操 作，可以进一步转换为目标代码。
常见的寄存器分配算法包括基于 图的方法、线性扫描算法和遗传
算法等。
目标代码的生成
01
02
03
04
目标代码的生成通常涉及指令 选择、指令调度和代码优化等
步骤。
指令选择是根据中间代码选择 合适的目标指令的过程，需要 考虑指令集架构、语义等约束
。
指令调度是为了确定指令的执 行顺序，以充分利用处理器资
源并提高指令级并行度。
为了能够处理连续输入的字符流，词 法分析器需要使用一个输入缓冲区来 存储尚未处理的字符。
设计状态转换图
根据正则表达式的规则，可以设计出 一个状态转换图，用于描述如何将输 入的字符转换为相应的词法单元。
词法分析器的实现
编写词法分析器程序
根据状态转换图和输入缓冲区的处理 逻辑，可以编写出相应的词法分析器 程序。
循环展开
将循环体多次执行，减 少循环次数，提高程序
运行效率。
循环优化
通过优化循环结构，减 少循环次数，提高程序
运行效率。
函数内联
将函数调用替换为函数 体中的代码，减少函数
调用的开销。
循环优化
01
02
03
04
循环展开
将循环体多次执行，减少循环 次数，提高程序运行效率。
循环合并
将多个循环合并为一个循环， 减少循环次数，提高程序运行

编译原理 Chapter 4

expression expression + term expression expression – term expression term term term * factor term term / factor term factor factor ( expression ) factor id
码生成 支持语言的演化和迭代
3
语法分析器的作用
• 基本作用
– 从词法分析器获得词法单元的序列，确认该序列是否 可以由语言的文法生成
– 对于语法错误的程序，报告错误信息 – 对于语法正确的程序，生成语法分析树 (简称语法树)
• 通常并不真的生产这棵语法分析树
4
语法分析器的分类
• 通用语法分析器
– 可以对任意文法进行语法分析 – 效率很低，不适合用于编表示形式
– 根结点的标号时文法的开始符号 – 每个叶子结点的标号是非终结符号、终结符号或ε – 每个内部结点的标号是非终结符号 – 每个内部结点表示某个产生式的一次应用
• 内部结点的标号为产生式头，结点的子结点从左到右是产生 式的体
• 树的叶子组成的序列是根的文法符号的一个句型 • 一棵语法分析树可对应多个推导序列，但每颗分
18
词法分析和语法分析的比较
阶段
输入
输出
描述体系
词法分析 源程序符号串 词法单元序列 正则表达式
语法分析 词法单元序列 语法树 上下文无关文法
19
上下文无关文法和正则表达式 (1)
• 上下文无关文法比正则表达式的能力更强
– 所有的正则语言都可以使用文法描述 – 但是一些用文法描述的语言不能用正则表达式描述
| other open_stmt if expr then stmt

《编译原理》课件

了解中间代码生成的概念和它在编译过程中的角色。 学习四元式和三地址码的表示和生成方式，以及中间代码优化的技巧。
六、代码生成
了解目标机器的指令系统和存储结构，以及它们对代码生成的影响。 学习寄存器分配和目标代码生成的基本原理和方法。
七、附录
参考文献提供了进一步学习编译原理的资源。 课程总结将回顾课程中学到的重要知识，并概述关键概念和技术。 问题解答将回答学生在课程学习中提出的问题。 课程评价将收集学生对课程的反馈和评价，以便对将来的课程进行改进。
《编译原理》PPT课件
编译原理PPT课件将带您深入了解编译原理的重要概念和技术。这个课程介绍 了编译原理的意义以及编译过程的概述。
一、引言
课程介绍编译原理的重要性，让您理解为什么编译原理对于软件开发非常关 键。 编译过程的概述将带您了解传统的编译过程中涉及的各个阶段和任务。
二、词法分析
词法分析是编译过程中的第一步，了解词法分析的作用以及它在编译器中的 实现。 掌握正则表达式和有限自动机的概念，这些是实现词法分骤，理解它的作用和不同的语法分析方法。 学习上下文无关文法以及LL(1)语法分析器和LR(1)语法分析器的实现原理。
四、语义分析
语义分析是编译过程中的重要一环，了解它的作用和涉及的任务。 学习语义动作、符号表管理和类型检查，以及如何进行语法制导翻译。
五、中间代码生成
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 通过正则表达式来描述各种词法单元的模式。 • 正则表达式所表示的集合称为正则集
• 正则表达式与正则文法的等价性
正则表达式的非形式化描述
正则表达式及对应正则集的定义（递归）
设∑是一个字母表， ⑴ Φ是∑上的RE，L(Φ)=Φ； ⑵ ε是∑上的RE，L(ε)={ε}； ⑶ 对于a∈∑，a是RE，L(a)={a}； ⑷如果r和s是RE，L(r)=R,L(s)=S，则： r 与 s 的“或（并）” (r|s) 是 RE，L(r|s)=R∪S； r与s的“连接” (rs)是RE，L(rs)=RS； r的闭包(r*)是RE，L(r*)=R*。 ⑸ 只有满足⑴、⑵、⑶、⑷的才是RE。
本节内容
• 有穷自动机
– 带空字符的有穷自动机 – NFA到DFA的转换
• 正则集、正则文法和正则表达式
带ε动作的FA
• 定义：如果FA的弧上允许标记ε，既允许自 动机对ε作状态转移，则称为ε自动机，记为 εNFA或εDFA • 引入ε动作的意义
– 为了把识别各类单词的有穷自动机用ε矢线连接 起来，组成一个单一的εNFA，再把所得到的 εNFA确定化，再据此设计词法分析器
带ε动作的FA
例子
1
f
2
o
3
r
4
ε
0
ε
5
iLeabharlann 6f7带ε动作的FA
a b
s
ε ε
0
s
ε c
1
s
3
s
c
2
NFA到DFA的变换
• NFA具有不确定性，因此通常需要构造一个 等价的DFA，我们把接受同一语言的任何两 个FA称作等价的FA，即：L(M)=L(N)
• 由NFA构造DFA的基本思想 • 算法：子集法
运算的优先级
正则表达式的例子
例：教材 P30
正则表达式的等价
正则文法到正则表达式的转换
正则文法到正则表达式的转换
例3.6，教材p32
NFA到DFA的变换
• 预备知识：
– 状态的ε-闭包ε-closure(q) – 状态集的ε闭包ε-closure(I)
NFA到DFA的变换
• 例子： 教材P28
ε ε 1 ε 4 b 5 ε 2 a 3 ε 6 ε 7 a 8
ε 0
b
9
b
10
ε
• 正则表达式 • 正则集 • 正则文法
正则表达式的作用