二次函数+相似

二次函数典型例题——相似、全等1、如图，已知点A （4，0），O 为坐标原点，P 是线段OA 上任意一点（不含端点O ，A ），过P 、O 两点的二次函数y 1和过P 、A 两点的二次函数y 2的图象开口均向下，它们的顶点分别为B 、C ，射线OB 与AC 相交于点D ．当OD =AD =3时，这两个二次函数的最大值之和等于（ A ）A B C ．3 D ．42、定义：对于抛物线2y ax bx c =++（a 、b 、c 是常数，0a ≠），若2b ac =，则称该抛物线为黄金抛物线．例如：2222y x x =-+是黄金抛物线． ⑴请再写出一个与上例不同的黄金抛物线的解析式；⑵若抛物线2y ax bx c =++（a 、b 、c 是常数，0a ≠）是黄金抛物线，请探究该黄金抛物线与x 轴的公共点个数的情况（说明理由）；⑶将黄金抛物线2222y x x =-+沿对称轴向下平移3个单位.①直接写出平移后的新抛物线的解析式；②设①中的新抛物线与y 轴交于点A ，对称轴与x 轴交于点B ，动点Q 在对称轴上，问新抛物线上是否存在点P ，使以点P 、Q 、B 为顶点的三角形与△AOB 全等？若存在，直接写出所有符合条件的点P 的坐标；若不存在，请说明理由.3、在平面直角坐标系xOy 中，抛物线235y mx x m =+++与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C （0 , 4），D 为OC 的中点. （1）求m 的值；（2）抛物线的对称轴与 x 轴交于点E ，在直线AD 上是否存在点F ，使得以点A 、B 、F 为顶点的三角形与ADE ∆相似？若存在，请求出点F 的坐标，若不存在，请说明理由； （3）在抛物线的对称轴上是否存在点G ，使△GBC 中BC 出点G 的坐标；若不存在，请说明理由．解：（1）抛物线m m mx y +++=532与y 轴交于点C （0 , 4），∴ 5 4.m +=∴ 1.m =-（2）抛物线的解析式为 234y x x =-++.可求抛物线与x 轴的交点A （-1，0），B （4，0）. 可求点E 的坐标3(,0)2.由图知，点F 在x 轴下方的直线AD 上时，ABF ∆是钝角三角形，不可能与ADE ∆相似，所以点F 一定在x 轴上方.此时ABF ∆与ADE ∆有一个公共角，两个三角形相似存在两种情况： ①当AB AEAF AD=时，由于E 为AB 的中点，此时D 为AF 的中点， 可求 F 点坐标为（1，4）. ② 当AB AD AF AE =时，55AF AF =解得过F 点作FH ⊥x 轴，垂足为H .可求F 的坐标为352（，）.(3) 在抛物线的对称轴上存在符合题意的点G .由题意，可知△OBC 为等腰直角三角形，直线BC 为 4.y x =-+ 可求与直线BCy =-x +9或y =-x -1. ∴ 点G 在直线y =-x +9或y =-x -1上. ∵ 抛物线的对称轴是直线23=x , ∴ ⎪⎩⎪⎨⎧+-==.9,23x y x 解得..215,23⎪⎪⎩⎪⎪⎨⎧==y x 或⎪⎩⎪⎨⎧--==.1,23x y x 解得⎪⎪⎩⎪⎪⎨⎧-==.25,23y x ∴ 点G 的坐标为31535(,)-2222或（，）.4、如图，在平面直角坐标系xOy 中，二次函数图象的顶点坐标为C （- 4，且在x 轴上截得的线段AB 的长为6. （1）求二次函数的解析式；（2）在y 轴上确定一点M ，使MA +MC 的值最小，求出点M 的坐标； （3）在x 轴下方的抛物线上，是否存在点N ，使得以N 、A 、B 三点为顶点的三角形与△ABC相似？如果存在，求出点N 的坐标；如果不存在，请说明理由.备用图5、在平面直角坐标系xOy 中，已知抛物线32++=bx ax y 经过（－2，－5）和（5，－12）两点．（1）求此抛物线的解析式；（2）设此抛物线与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于C 点，D 是线段BC 上一点（不与点B 、C 重合），若以B 、O 、D 为顶点的三角形与△BAC 相似，求点D 的坐标；（3）点P 在y 轴上，点M 在此抛物线上，若要使以点P 、M 、A 、B 为顶点的四边形是平行四边形，请你直接写出点M 的坐标．6、已知直线y=kx-3与x 轴交于点A （4，0），与y 轴交于点C ，抛物线234y x mx n =-++经过点A 和点C,动点P 在x 轴上以每秒1个长度单位的速度由抛物线与x 轴的另一个交点B 向点A 运动，点Q 由点C 沿线段CA 向点A 运动且速度是点P 运动速度的2倍.（1）求此抛物线的解析式和直线的解析式； （2）如果点P 和点Q 同时出发，运动时间为t （秒），试问当t 为何值时，以A 、P 、Q为顶点的三角形与△AOC 相似；（3）在直线CA 上方的抛物线上是否存在一点D ，使得△ACD 的面积最大.若存在，求 出点D 的坐标；若不存在，请说明理由．解：（1）∵ 直线y=kx-3过点A （4，0），∴ 0 = 4k -3，解得k=34． ∴ 直线的解析式为 y=34x-3．……………………………………1分 由直线y=34x-3与y 轴交于点C ，可知C(0，-3) ． ∴ 2344304m -⨯+-=，解得 m=154． ∴ 抛物线解析式为23153.44y x x =-+- ………………………2分（2）对于抛物线3x 415x 43y 2-+-=， 令y=0，则03x 415x 432=-+-，解得x 1=1，x 2=4．∴ B(1，0). ………………………………………………3分∴ AB=3，AO=4，OC=3，AC=5，AP=3-t ，AQ=5-2t . ① 若∠Q 1P 1A=90°,则P 1Q 1∥OC （如图1）， ∴ △AP 1Q 1∽△AOC . ∴11AP AQ AO AC =, ∴3t 52t45--=．解得t= 53； ………4分 ② 若∠P 2Q 2A=90°, ∵∠P 2AQ 2 =∠OAC ，∴ △AP 2Q 2∽△AOC. ∴22AP AQ AC AO =, ∴ 3t 52t54--=．解得t=136； ………………5分 备用图综上所述，当t 的值为53或136时，以P 、Q 、A 为顶点的三角形与△AOC 相似． （3）答：存在．过点D 作DF ⊥x 轴，垂足为E ，交AC 于点F （如图2）.∴ S △ADF =12DF ·AE ，S △CDF =12DF ·OE ． ∴ S △ACD = S △ADF + S △CDF =12DF×(AE+OE) =12×4 (DE+EF)=2×(23153x x 3x 3444-+--+)=23x 6x 2-+．…………6分∴ S △ACD =23(x 2)62--+（0<x<4）．又0<2<4且二次项系数023<-，∴ 当x=2时，S △ACD 的面积最大．而当x=2时，y=32．∴ 满足条件的D 点坐标为D (2, 32)． …………………7分7.如图1，已知二次函数232y x bx b =++的图象与x 轴交于A 、B 两点(B 在A 的左侧)，顶点为C ， 点D （1，m ）在此二次函数图象的对称轴上，过点D 作y 轴的垂线，交对称轴右侧的抛物线于E 点．（1）求此二次函数的解析式和点C 的坐标；（2）当点D 的坐标为（1，1）时，连接BD 、BE ．求证：BE 平分ABD ∠；（3）点G 在抛物线的对称轴上且位于第一象限，若以A 、C 、G 为顶点的三角形与以G 、D 、E 为顶点的三角形相似，求点E 的横坐标．解：（1）∵点D （1，m ）在232y x bx b =++图象的对称轴上，∴112b -=． ∴2b =-．∴二次函数的解析式为223y x x =--．………………………………………1分图1 备用图1 备用图2∴C （1，-4）． …………………………………………………………………2分（2）∵D （1，1），且DE 垂直于y 轴， ∴点E 的纵坐标为1，DE 平行于x 轴． ∴DEB EBO ∠=∠．令1y =，则2231x x --=，解得121xx ==∵点E 位于对称轴右侧，∴E (1． ∴D E令0y =，则223=0x x --，求得点A 的坐标为（3,0），点B 的坐标为（-1,0）． ∴BD =∴BD = D E ．……………………………………………………………………3分∴ DEB DBE ∠=∠． ∴ DBE EBO ∠=∠．∴BE 平分ABD ∠．……………………………………………………………4分 （3）∵以A 、C 、G 为顶点的三角形与以G 、D 、E 为顶点的三角形相似，且△GDE 为直角三角形， ∴△ACG 为直角三角形．∵G 在抛物线对称轴上且位于第一象限， ∴90CAG ∠= ．∵A （3,0）C （1，-4），A F C G ⊥,∴求得G 点坐标为（1，1）． ∴AG AC = ∴AC =2 AG .∴GD =2 DE 或 DE =2 GD .设()2, 23E t t t --（t >1） ，1︒.当点D 在点G 的上方时，则DE=t -1，GD = (223t t --)1-=224t t --. i. 如图2，当 GD =2 DE 时， 则有， 224t t --= 2(t -1).图1图3图2解得，=2t 舍负)………………………5分 ii. 如图3，当DE =2GD 时， 则有，t -1=2(224t t --). 解得，127=1=2t t -，.(舍负)…………………6分 2︒. 当点D 在点G 的下方时，则DE=t -1，GD =1- (223t t --)= -2+2+4t t . i. 如图4，当 GD =2 DE 时， 则有， 2+2+4t t -=2（t -1）.解得，=t 舍负) ………………………7分 ii. 如图5，当DE =2 GD 时， 则有，t -1=2（2+2+4t t -）. 解得，123=3=2t t -，.(舍负) …………………8分 综上，E点的横坐标为或72或3.8.在平面直角坐标系中，抛物线32++=bx ax y 与x 轴的两个交点分别为A （-3，0）,B （1，0），顶点为C .(1) 求抛物线的表达式和顶点坐标；(2) 过点C 作CH ⊥x 轴于点H ，若点P 为x 轴上方的抛物线上一动点（点P 与顶点C 不重合），PQ ⊥AC 于点Q ，当△PCQ 与△ACH 相似时，求点P 的坐标. （1）由题意，得9-33030a b a b +=⎧⎨++=⎩解得，⎩⎨⎧-=-=21b a抛物线的解析式为y=-x 2-2x+3 ………………………2分顶点C 的坐标为（-1，4） ………………………3分 （2）①若点P 在对称轴右侧（如图①），只能是△PCQ ∽△CAH ，得∠QCP =∠CAH . 延长CP 交x 轴于M ，∴AM =CM ，∴AM 2=CM 2. 设M （m ，0），则( m +3)2=42+(m +1)2，∴m =2，即M （2，0）. 设直线CM 的解析式为y=k 1x+b 1，图4图5则⎩⎨⎧=+=+-0241111b k b k ， 解之得341-=k ，381=b . ∴直线CM 的解析式3834+-=x y .…………………………………4分 3238342+--=+-x x x ， 解得311=x ，12-=x (舍去). 9201=y . ∴)92031(，P . ………………………………………………5分 ②若点P 在对称轴左侧（如图②），只能是△PCQ ∽△ACH ，得∠PCQ =∠ACH . 过A 作CA 的垂线交PC 于点F ，作FN ⊥x 轴于点N .由△CF A ∽△CAH 得2==AHCH AF CA ， 由△FNA ∽△AHC 得21===CA AF HC NA AH FN . ∴12==FN AN ，, 点F 坐标为（-5,1）.设直线CF 的解析式为y=k 2x+b 2，则⎩⎨⎧=+-=+-1542222b k b k ，解之得419,4322==b k . ∴直线CF 的解析式41943+=x y .……………………………………6分 32419432+--=+x x x ， 解得471-=x ，12-=x (舍去). ∴)165547(，-P . …………………………………7分 ∴满足条件的点P 坐标为)201(，或)557(，-（图①） （图②）。

相似三角形的存在性（作业）例：在平面直角坐标系中，二次函数图象的顶点坐标为C(4，)，且与x轴的两个交点间的距离为6．（1）求二次函数的解析式；（2）在x轴上方的抛物线上，是否存在点Q，使得以Q，A，B为顶点的三角形与△ABC相似？如果存在，请求出点Q的坐标；如果不存在，请说明理由．第一问：研究背景图形【思路分析】①由顶点坐标C(4，可知对称轴为直线_______，利用两个交点间的距离为6，再结合抛物线的对称性可知A(___，___)，B(___，___)．②设交点式__________________，再代入坐标__________可求解出解析式__________________．【过程示范】∵顶点坐标为C(4，又∵抛物线与x设抛物线的解析式为将C (4，代入可得，9a =，∴所求解析式为2y x x =． 第二问：整合信息、分析特征、设计方案 【思路分析】相似三角形存在性问题也是在存在性问题的框架下进行的：①分析特征：先研究定点、动点，其中_________为定点，点__为____________________的动点；则________为目标三角形．进一步研究此三角形，发现其中________________；构造辅助线：____________________________，能够计算出∠BAC =_____°，∠ACB =________°；再考虑研究△QAB ，固定线段为______，并且由于点Q 在x 轴上方的抛物线上，所以△QAB 为______（填“钝角”或“直角”）三角形．②画图求解：先考虑点Q 在抛物线对称轴右侧的情况，此时 ∠ABQ 为钝角，要想使△ABC 与△ABQ 相似，则需要∠ABQ =_____°，且_________．求解时，可根据∠ABQ =_____°，AB =BQ =_____来求出Q 点坐标．同理，考虑点Q 在抛物线对称轴左侧时的情况．③结果验证：考虑点Q 还要在抛物线上，将点Q 代入抛物线解析式验证．【过程示范】存在点Q 使得△QAB 与△ABC 相似．由抛物线对称性可知，AC =BC ，过点C 作CD ⊥x 轴于则AD =3，CD在Rt △ACD 中，tan ∠DAC， ∴∠BAC =∠ABC =30°，∠ACB =120°． ①当△ACB ∽△ABQ 时， ∠ABQ =120°且BQ =AB =6． 过点Q 作QE ⊥x 轴，垂足为E ， 则在Rt △BQE 中，BQ =6，∠QBE =60°， ∴QE =BQ ·sin60°=6=BE =3， ∴E (10，0)，Q 1(10，． 当x =10时，y= ∴点Q 1在抛物线上．②由抛物线的对称性可知，还存在AQ2=AB，此时△Q2AB∽△ACB，点Q2的坐标为(-2，．综上：Q1(10，，Q2(-2，．1.如图，已知抛物线y=x2-1与x轴交于A，B两点，与y轴交于点C，过点A作AP∥CB交抛物线于点P．（1）求A，B，C三点的坐标．（2）在x轴上方的抛物线上是否存在一点M，过点M作MG⊥x轴于点G，使以A，M，G为顶点的三角形与△PCA相似？若存在，请求出点M的坐标；若不存在，请说明理由．2.如图，抛物线y=ax2+b与x轴交于点A，B，且点A的坐标为(1，0)，与y轴交于点C(0，1)．（1）求抛物线的解析式，并求出点B的坐标．（2）过点B作BD∥CA交抛物线于点D，在x轴上点A的左侧是否存在点P，使以P，A，C为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由．3.如图，抛物线经过A(4，0)，B(1，0)，C(0，-2)三点．（1）求抛物线的解析式．（2）P是抛物线上一动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．【参考答案】例题示范： 第一问：① x =4，(1，0)，(7，0)② y =a (x -1)(x -7)，C (4，，2y x x =+ 第二问：①点A ，B ，C ，点Q ，在x 轴上方的抛物线上，△ABC ，CA =CB ，过点C 作CD ⊥AB 于点D ，30，120，AB ，钝角。

专题29二次函数与相似、全等存在性问题题型一相似三角形存在性问题在坐标系中确定点，使得由该点及其他点构成的三角形与其他三角形相似，即为“相似三角形存在性问题”．【相似判定】判定1：三边对应成比例的两个三角形是相似三角形；判定2：两边对应成比例且夹角相等的两个三角形是相似三角形；判定3：有两组角对应相等的三角形是相似三角形．以上也是坐标系中相似三角形存在性问题的方法来源，根据题目给的已知条件选择恰当的判定方法，解决问题【题型分析】通常相似的两三角形有一个是已知的，而另一三角形中有1或2个动点，即可分为“单动点”类、“双动点”两类问题．【思路总结】根据相似三角形的做题经验，可以发现，判定1基本是不会用的，这里也一样不怎么用，对比判定2、3可以发现，都有角相等！所以，要证相似的两个三角形必然有相等角，关键点也是先找到一组相等角．然后再找：思路1：两相等角的两边对应成比例；思路2：还存在另一组角相等．事实上，坐标系中在已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1．一、如何得到相等角？二、如何构造两边成比例或者得到第二组角？搞定这两个问题就可以了．1．如图，在平面直角坐标系中，抛物线C：y＝ax2+bx+c（a≠0）经过点（1，1）和（4，1）．（1）求抛物线C的对称轴．（2）当a＝﹣1时，将抛物线C向左平移2个单位，再向下平移1个单位，得到抛物线C1．①求抛物线C1的解析式．②设抛物线C1与x轴交于A，B两点（点A在点B的右侧），与y轴交于点C，连接BC．点D为第一象限内抛物线C1上一动点，过点D作DE⊥OA于点E．设点D的横坐标为m．是否存在点D，使得以点O，D，E为顶点的三角形与△BOC相似？若存在，求出m的值；若不存在，请说明理由．2．如图，抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，连接BC，与抛物线的对称轴交于点E，顶点为点D．（1）求抛物线的解析式；（2）点P是对称轴左侧抛物线上的一个动点，点Q在射线ED上，若以点P、Q、E为顶点的三角形与△BOC 相似，请直接写出点P的坐标．3．如图，直线y＝﹣x+分别交x轴、y轴于点A，B，过点A的抛物线y＝﹣x2+bx+c与x轴的另一交点为C，与y轴交于点D（0，3），抛物线的对称轴l交AD于点E，连接OE交AB于点F．（1）求抛物线的解析式；（2）求证：OE⊥AB；（3）P为抛物线上的一动点，直线PO交AD于点M，是否存在这样的点P，使以A，O，M为顶点的三角形与△ACD相似？若存在，求点P的横坐标；若不存在，请说明理由．4．如图，在平面直角坐标系xOy中，抛物线y＝﹣x2+x+4与两坐标轴分别相交于A，B，C三点．（1）求证：∠ACB＝90°；（2）点D是第一象限内该抛物线上的动点，过点D作x轴的垂线交BC于点E，交x轴于点F，点G是AC 的中点，若以点C，D，E为顶点的三角形与△AOG相似，求点D的坐标．5．如图，已知二次函数的图象与x轴交于A和B（﹣3，0）两点，与y轴交于C（0，﹣3），对称轴为直线x＝﹣1，直线y＝﹣2x+m经过点A，且与y轴交于点D，与抛物线交于点E，与对称轴交于点F．（1）求抛物线的解析式和m的值；（2）在y轴上是否存在点P，使得以D、E、P为顶点的三角形与△AOD相似，若存在，求出点P的坐标；若不存在，试说明理由；题型二全等三角形存在性问题6．如图，抛物线y＝x2+bx+c经过点（3，12）和（﹣2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．（1）求该抛物线的表达式；（2）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P，点E的坐标．7．如图，抛物线y＝x2+bx+c经过点（﹣2，5）和（2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．（1）求该抛物线的表达式；（2）求出点A，B，C的坐标；（3）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P，D，E为顶点的三角形与△BOC全等，求满足条件的点P，点E的坐标．8．如图，抛物线y＝ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，点D是抛物线的顶点．（1）求抛物线的解析式．（2）直线BC交对称轴于点E，P是坐标平面内一点，请直接写出△PCE与△ACD全等时点P的坐标．9．如图1，抛物线y1＝ax2﹣x+c与x轴交于点A和点B（1，0），与y轴交于点C（0，），抛物线y1的顶点为G，GM⊥x轴于点M．将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2．（1）求抛物线y2的解析式；（2）点P为抛物线y1上一动点，过点P作y轴的平行线交抛物线y2于点Q，点Q关于直线l的对称点为R，若以P，Q，R为顶点的三角形与△AMG全等，求直线PR的解析式．10．如图，抛物线y＝x2+bx+c经过点A（﹣1，0），B（0，﹣2），并与x轴交于点C，点M是抛物线对称轴l 上任意一点（点M，B，C三点不在同一直线上）．（1）求该抛物线所表示的二次函数的表达式；（2）在抛物线上找出两点P1，P2，使得△MP1P2与△MCB全等，并求出点P1，P2的坐标；。

专题4二次函数与相似问题函数中因动点产生的相似三角形问题一般有三个解题途径①求相似三角形的第三个顶点时，先要分析已知三角形的边和角的特点，进而得出已知三角形是否为特殊三角形。

根据未知三角形中已知边与已知三角形的可能对应边分类讨论。

②或利用已知三角形中对应角，在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。

③若两个三角形的各边均未给出，则应先设所求点的坐标进而用函数解析式来表示各边的长度，之后利用相似来列方程求解。

相似三角形常见的判定方法：（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；这是判定三角形相似的一种基本方法．相似的基本图形可分别记为“A”型和“X”型，如图所示在应用时要善于从复杂的图形中抽象出这些基本图形．（2）三边法：三组对应边的比相等的两个三角形相似；（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；（4）两角法：有两组角对应相等的两个三角形相似．判定定理“两边及其夹角法”是常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验．如果已知∠A＝∠D，探求△ABC与△DEF相似，只要把夹∠A和∠D的两边表示出来，按照对应边成比例，分AB DEAC DF=和AB DFAC DE=两种情况列方程．应用判定定理“两角法”解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等．应用判定定理“三边法”解题不多见，根据三边对应成比例列连比式解方程（组）．还有一种情况，讨论两个直角三角形相似，如果一组锐角相等，其中一个直角三角形的锐角三角比是确定的，那么就转化为讨论另一个三角形是直角三角形的问题．【例1】（2022•贵港）如图，已知抛物线y＝﹣x2+bx+c经过A（0，3）和B（，﹣）两点，直线AB与x轴相交于点C，P是直线AB上方的抛物线上的一个动点，PD⊥x轴交AB于点D．（1）求该抛物线的表达式；（2）若PE∥x轴交AB于点E，求PD+PE的最大值；（3）若以A，P，D为顶点的三角形与△AOC相似，请直接写出所有满足条件的点P，点D的坐标．【例2】．（2022•衡阳）如图，已知抛物线y＝x2﹣x﹣2交x轴于A、B两点，将该抛物线位于x轴下方的部分沿x轴翻折，其余部分不变，得到的新图象记为“图象W”，图象W交y轴于点C．（1）写出图象W位于线段AB上方部分对应的函数关系式；（2）若直线y＝﹣x+b与图象W有三个交点，请结合图象，直接写出b的值；（3）P为x轴正半轴上一动点，过点P作PM∥y轴交直线BC于点M，交图象W于点N，是否存在这样的点P，使△CMN与△OBC相似？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．【例3】．（2022•桂林）如图，抛物线y＝﹣x2+3x+4与x轴交于A，B两点（点A位于点B的左侧），与y 轴交于C点，抛物线的对称轴l与x轴交于点N，长为1的线段PQ（点P位于点Q的上方）在x轴上方的抛物线对称轴上运动．（1）直接写出A，B，C三点的坐标；（2）求CP+PQ+QB的最小值；（3）过点P作PM⊥y轴于点M，当△CPM和△QBN相似时，求点Q的坐标．【例4】（2022•玉林）如图，已知抛物线：y＝﹣2x2+bx+c与x轴交于点A，B（2，0）（A在B的左侧），与y轴交于点C，对称轴是直线x＝，P是第一象限内抛物线上的任一点．（1）求抛物线的解析式；（2）若点D为线段OC的中点，则△POD能否是等边三角形？请说明理由；（3）过点P作x轴的垂线与线段BC交于点M，垂足为点H，若以P，M，C为顶点的三角形与△BMH相似，求点P的坐标．1．（2020秋•兴城市期末）如图，抛物线y＝ax2+bx+4经过A（4，0），B（﹣1，0）两点，与y轴交于点C，D为第一象限抛物线上的动点，连接AC，BC，DA，DB，DB与AC相交于点E．（1）求抛物线的解析式；（2）如图1，设△ADE的面积为S1，△BCE的面积为S2，当S1＝S2+5时，求点D的坐标；（3）如图2，过点C作CF∥x轴，点M是直线CF上的一点，MN⊥CF交抛物线于点N，是否存在以C，M，N为顶点的三角形与△BCO相似？若存在，请直接写出点M的坐标，若不存在，请说明理由．2．（2020秋•郴州期末）已知抛物线y＝x2﹣3x+与x轴交于A，B两点（点A在点B的左边）．（1）求A，B两点的坐标；（2）如图1，若点D是抛物线上在第四象限的点，连接DA并延长，交y轴于点P，过点D作DE⊥x轴于点E．当△APO与△ADE的面积比为＝时．求点D的坐标；（3）如图2，抛物线与y轴相交于点F．若点Q是线段OF上的动点，过点Q作与x轴平行的直线交抛物线于M，N两点（点M在点N的左边）．请问是否存在以Q，A，M为顶点的三角形与△QNA相似？若存在，求出点Q的坐标；若不存在，请说明理由．3．（2020秋•长垣市期末）如图1，抛物线y＝x2+bx+c与x轴、y轴分别交于点B（6，0）和点C（0，﹣3）．（1）求抛物线的解析式；（2）点P是直线BC下方抛物线上一动点，其横坐标为m，连接PB、PC，当△PBC的面积为时，求m 值；（3）如图2，点M是线段OB上的一个动点，过点M作x轴的垂线l分别与直线BC和抛物线交于D，E 两点，是否存在以C，D，E为顶点的三角形与△BDM相似，若存在，请直接写出点M的坐标；若不存在，请说明理由．4．（2021秋•邹城市期末）如图，已知抛物线y＝x2+2x的顶点为A，直线y＝x+2与抛物线交于B，C两点．（1）求A，B，C三点的坐标；（2）作CD⊥x轴于点D，求证：△ODC∽△ABC；（3）若点P为抛物线上的一个动点，过点P作PM⊥x轴于点M，则是否还存在除C点外的其他位置的点，使以O，P，M为顶点的三角形与△ABC相似？若存在，请求出这样的P点坐标；若不存在，请说明理由．5．（2021秋•攸县期末）如图，已知直线y＝﹣2x+4分别交x轴、y轴于点A、B，抛物线过A，B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）若抛物线的解析式为y＝﹣2x2+2x+4，设其顶点为M，其对称轴交AB于点N．①求点M和点N的坐标；②在抛物线的对称轴上找一点Q，使|AQ﹣BQ|的值最大，请直接写出点Q的坐标；③是否存在点P，使四边形MNPD为菱形？并说明理由；（2）当点P的横坐标为1时，是否存在这样的抛物线，使得以B、P、D为顶点的三角形与△AOB相似？若存在，求出满足条件的抛物线的解析式；若不存在，请说明理由．6．（2022•禹城市模拟）如图，抛物线经过A（4，0），B（1，0），C（0，﹣2）三点．（1）求出抛物线的解析式；（2）P是抛物线在第一象限上的一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M 为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；＝S△ABC，直接写出点D （3）若抛物线上有一点D（点D位于直线AC的上方且不与点B重合）使得S△DCA的坐标．7．（2022•祥云县模拟）如图，已知抛物线y＝ax2+bx+c过点A（﹣1，0），B（3，0），交y轴于点C（0，3），点M是该抛物线上第一象限内的一个动点，ME垂直x轴于点E，交线段BC于点D，MN∥x轴，交y轴于点N．（1）求抛物线y＝ax2+bx+c的表达式；（2）若四边形MNOE是正方形，求该正方形的边长；（3）连结OD，AC，抛物线上是否存在点M，使得以C，O，D为顶点的三角形与△ABC相似，若存在，请求出点M的坐标，若不存在，请说明理由．8．（2022•松江区校级模拟）如图，抛物线y＝x2﹣bx+c过点B（3，0），C（0，﹣3），D为抛物线的顶点．（1）求抛物线的解析式以及顶点坐标；（2）连接BC，CD，DB，求∠CBD的正切值；（3）点C关于抛物线y＝x2﹣bx+c对称轴的对称点为E点，连接BE，直线BE与对称轴交于点M，在（2）的条件下，点P是抛物线对称轴上的一点，是否存在点P使△CDB和△BMP相似，若存在，求点P坐标，若不存在，请说明理由．9．（2022•平江县一模）如图，抛物线y＝ax2+bx+8与x轴交于A（﹣2，0）和点B（8，0），与y轴交于点C，顶点为D，连接AC，BC，BC与抛物线的对称轴l交于点E．（1）求该抛物线的函数表达式；（2）点P是第一象限内抛物线上的动点，连接PB，PC，设四边形PBOC和△AOC的面积分别为S四边形PBOC ，记S＝S四边形PBOC﹣S△AOC，求S最大值点P的坐标及S的最大值；和S△AOC（3）点N是对称轴l右侧抛物线上的动点，在射线ED上是否存在点M，使得以点M，N，E为顶点的三角形与△BOC相似？若存在，求点M的坐标；若不存在，请说明理由．10．（2022•莱州市一模）如图①，在平面直角坐标系中，抛物线y＝x2+c经过点A（4，3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，﹣2）且垂直于y轴的直线，连接PO．（1）求抛物线的表达式，并求出顶点B的坐标；（2）试证明：经过点O的⊙P与直线l相切；（3）如图②，已知点C的坐标为（1，2），是否存在点P，使得以点P，O及（2）中的切点为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．11．（2022•巩义市模拟）已知，二次函数y＝ax2+bx﹣3的图象与x轴交于A，B两点（点A在点B的左边），与y轴交于C点，点A的坐标为（﹣1，0），且OB＝OC．（1）求二次函数的解析式；（2）当0≤x≤4时，求二次函数的最大值和最小值分别为多少？（3）设点C'与点C关于该抛物线的对称轴对称．在y轴上是否存在点P，使△PCC'与△POB相似，且PC 与PO是对应边？若存在，求出点P的坐标；若不存在，请说明理由．12．（2022•澄迈县模拟）在平面直角坐标系中，抛物线经过点A（﹣2，0），B（﹣3，3）及原点O，顶点为C．（1）求该抛物线的函数表达式及顶点C的坐标；（2）设该抛物线上一动点P的横坐标为t．①在图1中，当﹣3＜t＜0时，求△PBO的面积S与t的函数关系式，并求S的最大值；②在图2中，若点P在该抛物线上，点E在该抛物线的对称轴上，且以A，O，P，E为顶点的四边形是平行四边形，求点P的坐标；③在图3中，若P是y轴左侧该抛物线上的动点，过点P作PM⊥x轴，垂足为M，是否存在点P使得以点P，M，A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．13．（2022•丰南区二模）如图①、②，在平面直角坐标系中，一边长为2的等边三角板CDE恰好与坐标系中的△OAB重合，现将三角板CDE绕边AB的中点G（G点也是DE的中点），按顺时针方向旋转180°到△C′ED的位置．（1）直接写出C′的坐标，并求经过O、A、C′三点的抛物线的解析式；（2）点P在第四象限的抛物线上，求△C′OP的最大面积；（3）如图③，⊙G是以AB为直径的圆，过B点作⊙G的切线与x轴相交于点F，抛物线上是否存在一点M，使得△BOF与△AOM相似？若存在，请求出点M的坐标；若不存在，请说明理由．14．（2022•莱芜区三模）如图，在平面直角坐标系中，一次函数y＝﹣x+3的图象与x轴交于点A，与y轴交于点B，二次函数y＝x2+bx+c的图象经过A和点C（0，﹣3）．（1）求二次函数的表达式；（2）如图1，平移线段AC，点A的对应点D落在二次函数在第一象限的图象上，点C的对应点E落在直线AB上，直接写出四边形ACED的形状，并求出此时点D的坐标；（3）如图2，在（2）的条件下，连接CD，交x轴于点M，点P为直线CD下方抛物线上一个动点，过点P作PF⊥x轴，交CD于点F，连接PC，是否存在点P，使得以点P，C，F为顶点的三角形与△COM相似？若存在，求出线段FP的长度；若不存在，请说明理由．15．（2022•临清市三模）如图，抛物线y＝﹣x2+bx+c的顶点D坐标为（1，4），且与x轴相交于A，B两点（点A在点B的左侧，与y轴相交于点C，点E在x轴上方且在对称轴左侧的抛物线上运动，点F在抛物线上并且和点E关于抛物线的对称轴对称，作矩形EFGH，其中点G，H都在x轴上．（1）求抛物线解析式；（2）设点F横坐标为m，①用含有m的代数式表示点E的横坐标为（直接填空）；②当矩形EFGH为正方形时，求点G的坐标；③连接AD，当EG与AD垂直时，求点G的坐标；（3）过顶点D作DM⊥x轴于点M，过点F作FP⊥AD于点P，直接写出△DFP与△DAM相似时，点F 的坐标．16．（2022•成都模拟）如图①，已知抛物线y＝﹣（x﹣1）2+k交x轴于A，B两点，交y轴于点C，P是抛物线上的动点，且满足OB＝3OA．（1）求抛物线的解析式；（2）若点P在第一象限，直线y＝x+b经过点P且与直线BC交于点E，设点P的横坐标为t，当线段PE 的长度随着t的增大而减小时，求t的取值范围；（3）如图②，过点A作BC的平行线m，与抛物线交于另一点D．点P在直线m上方，点Q在线段AD 上，若△CPQ与△AOC相似，且点P与点O是对应点，求点P的坐标．17．（2022•东莞市校级一模）在平面直角坐标系xOy中，已知抛物线y＝﹣x2+2kx+2k2+1与x轴的左交点为A，右交点为B，与y轴的交点为C，对称轴为直线l，对于抛物线上的两点（x1，y1），（x2，y2）（x1＜k＜x2），当x1+x2＝2时，y1﹣y2＝0恒成立．（1）求该抛物线的解析式；（2）点M是第二象限内直线AC上方的抛物线上的一点，过点M作MN⊥AC于点N，求线段MN的最大值，并求出此时点M的坐标；（3）点P是直线l右侧抛物线上的一点，PQ⊥l于点Q，AP交直线l于点F，是否存在这样的点P，使△PQF与△ACO相似？若存在，请求出点P的坐标，若不存在，请说明理由．18．（2022•碑林区校级模拟）如图，Rt△ABC中，∠ACB＝90°，AB＝8，AC＝4，以AB所在直线为x轴建立平面直角坐标系，若C（0，2）．（1）请直接写出A、B的坐标；（2）求经过A、B、C三点的抛物线表达式；（3）l为抛物线对称轴，P是直线l右侧抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P、D、E为顶点的三角形与△ABC全等，求满足条件的点P，点E的坐标．【例1】（2022•贵港）如图，已知抛物线y＝﹣x2+bx+c经过A（0，3）和B（，﹣）两点，直线AB与x轴相交于点C，P是直线AB上方的抛物线上的一个动点，PD⊥x轴交AB于点D．（1）求该抛物线的表达式；（2）若PE∥x轴交AB于点E，求PD+PE的最大值；（3）若以A，P，D为顶点的三角形与△AOC相似，请直接写出所有满足条件的点P，点D的坐标．【分析】（1）直接利用待定系数法，即可求出解析式；（2）先求出点C的坐标，然后证明Rt△DPE∽Rt△AOC，再由二次函数的最值性质，求出答案；（3）根据题意，可分为两种情况进行分析：当△AOC∽△APD时；当△AOC∽△DAP时；分别求出两种情况的点的坐标，即可得到答案．【解析】（1）将A（0，3）和B（，﹣）代入y＝﹣x2+bx+c，，解得，∴该抛物线的解析式为y＝﹣x2+2x+3；（2）设直线AB的解析式为y＝kx+n，把A（0，3）和B（，﹣）代入，，解得，∴直线AB的解析式为y＝﹣x+3，当y＝0时，﹣x+3＝0，解得：x＝2，∴C点坐标为（2，0），∵PD⊥x轴，PE∥x轴，∴∠ACO＝∠DEP，∴Rt△DPE∽Rt△AOC，∴，∴PE＝PD，∴PD+PE＝PD，设点P的坐标为（a，﹣a2+2a+3），则D点坐标为（a，﹣a+3），∴PD＝（﹣a2+2a+3）﹣（﹣a+3）＝﹣（a﹣）2+，∴PD+PE＝﹣（a﹣）2+，∵﹣＜0，∴当a＝时，PD+PE有最大值为；（3）①当△AOC∽△APD时，∵PD⊥x轴，∠DPA＝90°，∴点P纵坐标是3，横坐标x＞0，即﹣x2+2x+3＝3，解得x＝2，∴点D的坐标为（2，0）；∵PD⊥x轴，∴点P的横坐标为2，∴点P的纵坐标为：y＝﹣22+2×2+3＝3，∴点P的坐标为（2，3），点D的坐标为（2，0）；②当△AOC∽△DAP时，此时∠APG＝∠ACO，过点A作AG⊥PD于点G，∴△APG∽△ACO，∴，设点P的坐标为（m，﹣m2+2m+3），则D点坐标为（m，﹣m+3），则，解得：m＝，∴D点坐标为（，1），P点坐标为（，），综上，点P的坐标为（2，3），点D的坐标为（2，0）或P点坐标为（，），D点坐标为（，1）．【例2】（2022•衡阳）如图，已知抛物线y＝x2﹣x﹣2交x轴于A、B两点，将该抛物线位于x轴下方的部分沿x轴翻折，其余部分不变，得到的新图象记为“图象W”，图象W交y轴于点C．（1）写出图象W位于线段AB上方部分对应的函数关系式；（2）若直线y＝﹣x+b与图象W有三个交点，请结合图象，直接写出b的值；（3）P为x轴正半轴上一动点，过点P作PM∥y轴交直线BC于点M，交图象W于点N，是否存在这样的点P，使△CMN与△OBC相似？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．【分析】（1）令x＝0和翻折的性质可得C（0，2），令y＝0可得点A、B的坐标，利用待定系数法即可求出图象W的解析式；（2）利用数形结合找出当y＝﹣x+b经过点C或者y＝﹣x+b与y＝x2﹣x﹣2相切时，直线y＝﹣x+b与新图象恰好有三个不同的交点，①当直线y＝﹣x+b经过点C（0，2）时，利用一次函数图象上点的坐标特征，即可求出b值；②当y＝﹣x+b与y＝x2﹣x﹣2相切时，联立一次函数解析式和抛物线解析式，利用根的判别式Δ＝0，即可求出b值．综上即可得出结论；（3）先确定△BOC是等腰直角三角形，分三种情况：∠CNM＝90°或∠MCN＝90°，分别画图可得结论．【解析】（1）当x＝0时，y＝﹣2，∴C（0，2），当y＝0时，x2﹣x﹣2＝0，（x﹣2）（x+1）＝0，∴x1＝2，x2＝﹣1，∴A（﹣1，0），B（2，0），设图象W的解析式为：y＝a（x+1）（x﹣2），把C（0，2）代入得：﹣2a＝2，∴a＝﹣1，∴y＝﹣（x+1）（x﹣2）＝﹣x2+x+2，∴图象W位于线段AB上方部分对应的函数关系式为：y＝﹣x2+x+2（﹣1＜x＜2）；（2）由图象得直线y＝﹣x+b与图象W有三个交点时，存在两种情况：①当直线y＝﹣x+b过点C时，与图象W有三个交点，此时b＝2；②当直线y＝﹣x+b与图象W位于线段AB上方部分对应的函数图象相切时，如图1，﹣x+b＝﹣x2+x+2，x2﹣2x+b﹣2＝0，Δ＝（﹣2）2﹣4×1×（b﹣2）＝0，∴b＝3，综上，b的值是2或3；（3）∵OB＝OC＝2，∠BOC＝90°，∴△BOC是等腰直角三角形，如图2，CN∥OB，△CNM∽△BOC，∵PN∥y轴，∴P（1，0）；如图3，CN∥OB，△CNM∽△BOC，当y＝2时，x2﹣x﹣2＝2，x2﹣x﹣4＝0，∴x1＝，x2＝，∴P（，0）；如图4，当∠MCN＝90°时，△OBC∽△CMN，∴CN的解析式为：y＝x+2，∴x+2＝x2﹣x﹣2，∴x1＝1+，x2＝1﹣（舍），∴P（1+，0），综上，点P的坐标为（1，0）或（，0）或（1+，0）．【例3】（2022•桂林）如图，抛物线y＝﹣x2+3x+4与x轴交于A，B两点（点A位于点B的左侧），与y轴交于C点，抛物线的对称轴l与x轴交于点N，长为1的线段PQ（点P位于点Q的上方）在x轴上方的抛物线对称轴上运动．（1）直接写出A，B，C三点的坐标；（2）求CP+PQ+QB的最小值；（3）过点P作PM⊥y轴于点M，当△CPM和△QBN相似时，求点Q的坐标．【分析】（1）由y＝﹣x2+3x+4可得A（﹣1，0），B（4，0），C（0，4）；（2）将C（0，4）向下平移至C'，使CC'＝PQ，连接BC'交抛物线的对称轴l于Q，可知四边形CC'QP是平行四边形，及得CP+PQ+BQ＝C'Q+PQ+BQ＝BC'+PQ，而B，Q，C'共线，故此时CP+PQ+BQ最小，最小值为BC'+PQ的值，由勾股定理可得BC'＝5，即得CP+PQ+BQ最小值为6；（3）由在y＝﹣x2+3x+4得抛物线对称轴为直线x＝﹣＝，设Q（，t），则P（，t+1），M（0，t+1），N（，0），知BN＝，QN＝t，PM＝，CM＝|t﹣3|，①当＝时，＝，可解得Q（，）或（，）；②当＝时，＝，得Q（，）．【解析】（1）在y＝﹣x2+3x+4中，令x＝0得y＝4，令y＝0得x＝﹣1或x＝4，∴A（﹣1，0），B（4，0），C（0，4）；（2）将C（0，4）向下平移至C'，使CC'＝PQ，连接BC'交抛物线的对称轴l于Q，如图：∵CC'＝PQ，CC'∥PQ，∴四边形CC'QP是平行四边形，∴CP＝C'Q，∴CP+PQ+BQ＝C'Q+PQ+BQ＝BC'+PQ，∵B，Q，C'共线，∴此时CP+PQ+BQ最小，最小值为BC'+PQ的值，∵C（0，4），CC'＝PQ＝1，∴C'（0，3），∵B（4，0），∴BC'＝＝5，∴BC'+PQ＝5+1＝6，∴CP+PQ+BQ最小值为6；（3）如图：由在y＝﹣x2+3x+4得抛物线对称轴为直线x＝﹣＝，设Q（，t），则P（，t+1），M（0，t+1），N（，0），∵B（4，0），C（0，4）；∴BN＝，QN＝t，PM＝，CM＝|t﹣3|，∵∠CMP＝∠QNB＝90°，∴△CPM和△QBN相似，只需＝或＝，①当＝时，＝，解得t＝或t＝，∴Q（，）或（，）；②当＝时，＝，解得t＝或t＝（舍去），∴Q（，），综上所述，Q的坐标是（，）或（，）或（，）．【例4】（2022•玉林）如图，已知抛物线：y＝﹣2x2+bx+c与x轴交于点A，B（2，0）（A在B的左侧），与y轴交于点C，对称轴是直线x＝，P是第一象限内抛物线上的任一点．（1）求抛物线的解析式；（2）若点D为线段OC的中点，则△POD能否是等边三角形？请说明理由；（3）过点P作x轴的垂线与线段BC交于点M，垂足为点H，若以P，M，C为顶点的三角形与△BMH相似，求点P的坐标．【分析】（1）把点B（2，0）代入y＝﹣2x2+bx+c中，再由对称轴是直线x＝列方程，两个方程组成方程组可解答；（2）当△POD是等边三角形时，点P在OD的垂直平分线上，所以作OD的垂直平分线与抛物线的交点即为点P，计算OD≠PD，可知△POD不可能是等边三角形；（3）分种情况：①当PC∥x轴时，△CPM∽△BHM时，根据PH的长列方程可解答；②②如图3，△PCM ∽△BHM，过点P作PE⊥y轴于E，证明△PEC∽△COB，可得结论．【解析】（1）由题意得：，解得：，∴抛物线的解析式为：y＝﹣2x2+2x+4；（2）△POD不可能是等边三角形，理由如下：如图1，取OD的中点E，过点E作EP∥x轴，交抛物线于点P，连接PD，PO，∵C（0，4），D是OD的中点，∴E（0，1），当y＝1时，﹣2x2+2x+4＝1，2x2﹣2x﹣3＝0，解得：x1＝，x2＝（舍），∴P（，1），∴OD≠PD，∴△POD不可能是等边三角形；（3）设点P的坐标为（t，﹣2t2+2t+4），则OH＝t，BH＝2﹣t，分两种情况：①如图2，△CMP∽△BMH，∴∠PCM＝∠OBC，∠BHM＝∠CPM＝90°，∴tan∠OBC＝tan∠PCM，∴＝＝＝＝2，∴PM＝2PC＝2t，MH＝2BH＝2（2﹣t），∵PH＝PM+MH，∴2t+2（2﹣t）＝﹣2t2+2t+4，解得：t1＝0，t2＝1，∴P（1，4）；②如图3，△PCM∽△BHM，则∠PCM＝∠BHM＝90°，过点P作PE⊥y轴于E，∴∠PEC＝∠BOC＝∠PCM＝90°，∴∠PCE+∠EPC＝∠PCE+∠BCO＝90°，∴∠BCO＝∠EPC，∴△PEC∽△COB，∴＝，∴＝，解得：t1＝0（舍），t2＝，∴P（，）；综上，点P的坐标为（1，4）或（，）．1．（2020秋•兴城市期末）如图，抛物线y＝ax2+bx+4经过A（4，0），B（﹣1，0）两点，与y轴交于点C，D为第一象限抛物线上的动点，连接AC，BC，DA，DB，DB与AC相交于点E．（1）求抛物线的解析式；（2）如图1，设△ADE的面积为S1，△BCE的面积为S2，当S1＝S2+5时，求点D的坐标；（3）如图2，过点C作CF∥x轴，点M是直线CF上的一点，MN⊥CF交抛物线于点N，是否存在以C，M，N为顶点的三角形与△BCO相似？若存在，请直接写出点M的坐标，若不存在，请说明理由．【分析】（1）运用待定系数法将A（4，0），B（﹣1，0）代入y＝ax2+bx+4，解方程组即可求得答案；（2）根据题意，当S1＝S2+5，即S△ABD＝S△ABC+5，设D（x，y），表示出△ABD和△ABC的面积，列方程求解即可；（3）分情况讨论，列出三角形相似的三种情况，画出相应图形，设M（m，4），则N（m，﹣m2+3m+4），运用相似三角形性质，建立方程求解即可．【解析】（1）∵抛物线y＝ax2+bx+4经过A（4，0），B（﹣1，0）两点，∴，解得：，∴y＝﹣x2+3x+4；（2）∵抛物线y＝﹣x2+3x+4与y轴交于点C，令x＝0，则y＝4，∴C（0，4），∵S1＝S2+5，∴S1+S△AEB＝S2+S△AEB+5，＝S△ABC+5，即S△ABD∵A（4，0），B（﹣1，0），∴AB＝5，设D（x，y），∴×5×y＝×5×4+5，∴y＝6，∴﹣x2+3x+4＝6，解得：x1＝1，x2＝2，∴D1（1，6），D2（2，6）；（3）设M（m，4），则N（m，﹣m2+3m+4），①如图2，△BOC∽△NMC，则＝，∴＝，解得：m＝0（舍去），m＝，经检验，m＝是原方程的解，∴M（，4）；②如图3，△BOC∽△CMN，则＝，∴＝，解得：m＝0（舍去），m＝﹣1，经检验，m＝﹣1是原方程的解，∴M（﹣1，4）；③如图4，△BOC∽△NMC，则＝，∴＝，解得：m＝0（舍去），m＝，经检验，m＝是原方程的解，∴M（，4）；④如图5，△BOC∽△CMN，则＝，∴＝，解得：m＝0（舍去），m＝7，经检验，m＝7是原方程的解，∴M（7，4）；综上所述，点M的坐标为（，4）或（﹣1，4）或（，4）或（7，4）．2．（2020秋•郴州期末）已知抛物线y＝x2﹣3x+与x轴交于A，B两点（点A在点B的左边）．（1）求A，B两点的坐标；（2）如图1，若点D是抛物线上在第四象限的点，连接DA并延长，交y轴于点P，过点D作DE⊥x轴于点E．当△APO与△ADE的面积比为＝时．求点D的坐标；（3）如图2，抛物线与y轴相交于点F．若点Q是线段OF上的动点，过点Q作与x轴平行的直线交抛物线于M，N两点（点M在点N的左边）．请问是否存在以Q，A，M为顶点的三角形与△QNA相似？若存在，求出点Q的坐标；若不存在，请说明理由．【分析】（1）在抛物线解析式中，令y＝0则可求得A、B的坐标；（2）证明△AOP∽△AED，根据相似三角形面积的比等于对应边的比的平方列比例式可得AE＝2，从而得点D的横坐标为3，代入抛物线的解析式可得点D的坐标；（3）如图2所示，若以Q，A，M为顶点的三角形与△QNA相似，有两种情况，但是∠QAM与∠QAN不可能相等，所以最后只存在一种情况：△AQM∽△NQA，列比例式可得结论．【解析】（1）当y＝0时，x2﹣3x+＝0，解得：x1＝1，x2＝5，∴A（1，0），B（5，0）；（2）∵DE⊥x轴，∴∠AED＝90°，∴∠AOP＝∠AED＝90°，∵∠OAP＝∠DAE，∴△AOP∽△AED，∴＝＝，∴＝，∵OA＝1，∴AE＝2，∴OE＝3，当x＝3时，y＝﹣3×3+＝﹣2，∴D（3，﹣2）；（3）如图2，设Q（0，m），当x＝0时，y＝，∴F（0，），∵点Q是线段OF上的动点，∴0≤m≤，当y＝m时，x2﹣3x+＝m，x2﹣6x+5﹣2m＝0，x＝3，∴x1＝3+，x2＝3﹣，∴QM＝3﹣，QN＝3+，在Rt△AOQ中，由勾股定理得：AQ＝，∵∠AQM＝∠AQN，∴当△AQM和△AQN相似只存在一种情况：△AQM∽△NQA，∴，∴AQ2＝NQ•QM，即1+m2＝（3+）（3﹣），解得：m1＝﹣1+，m2＝﹣1﹣（舍），∴Q（0，﹣1+）．3．（2020秋•长垣市期末）如图1，抛物线y＝x2+bx+c与x轴、y轴分别交于点B（6，0）和点C（0，﹣3）．（1）求抛物线的解析式；（2）点P是直线BC下方抛物线上一动点，其横坐标为m，连接PB、PC，当△PBC的面积为时，求m 值；（3）如图2，点M是线段OB上的一个动点，过点M作x轴的垂线l分别与直线BC和抛物线交于D，E 两点，是否存在以C，D，E为顶点的三角形与△BDM相似，若存在，请直接写出点M的坐标；若不存在，请说明理由．【分析】（1）根据点A、B的坐标，利用待定系数法即可求出该抛物线的函数关系式；（2）根据点P是直线BC下方抛物线上一动点，其横坐标为m，表示PH的长，根据三角形的面积列方程解出即可得出结论；（3）先根据两三角形相似判断出∠CED＝∠BMD＝90°或∠DCE＝∠DMB＝90°，进而分两种情况讨论即可得出结论．【解析】（1）把点B（6，0）和点C（0，﹣3）代入得：，解得：，∴抛物线的解析式为；（2）设直线BC的解析式为：y＝ax+n，由点B（6，0）和C（0，﹣3）得：，解得：，∴直线BC的解析式为，如图1，过点P作y轴的平行线交BC于点H，∵点P的坐标为（m，），PH∥y轴，∴点H的坐标为（m，），∴PH＝y H﹣y P＝﹣（）＝﹣，x B﹣x C＝6﹣0＝6，＝PH×6＝（﹣）×6＝﹣＝，∵S△PBC解得：m1＝1，m2＝5，∴m值为1或5；（3）如图2，∵∠CDE＝∠BDM，△CDE与△BDM相似，∴∠CED＝∠BMD＝90°或∠DCE＝∠DMB＝90°，设M（x，0），①当∠CED＝∠BDM＝90°，∴CE∥AB，∵C（0，﹣3），∴点E的纵坐标为﹣3，∵点E在抛物线上，∴x2﹣x﹣3＝﹣3．∴x＝0（舍）或x＝5，∴M（5，0）；②当∠DCE＝∠DMB＝90°，∵OB＝6，OC＝3，∴BC＝＝3，由（2）知直线BC的关系式为y＝x﹣3，∴OM＝x，BM＝6﹣x，DM＝3﹣x，由（2）同理得ED＝﹣+3x，∵DM∥OC，∴，即，∴CD＝，∴BD＝BC﹣CD＝﹣x，∵△ECD∽△BMD，∴，即＝，∴＝x（3﹣x）2，x（6﹣x）（1﹣x）＝0，x1＝0（舍），x2＝6（舍），x3＝1，∴M（1，0）；综上所述：点M的坐标为（5，0）或（1，0）．4．（2021秋•邹城市期末）如图，已知抛物线y＝x2+2x的顶点为A，直线y＝x+2与抛物线交于B，C两点．（1）求A，B，C三点的坐标；（2）作CD⊥x轴于点D，求证：△ODC∽△ABC；（3）若点P为抛物线上的一个动点，过点P作PM⊥x轴于点M，则是否还存在除C点外的其他位置的点，使以O，P，M为顶点的三角形与△ABC相似？若存在，请求出这样的P点坐标；若不存在，请说明理由．【分析】（1）将抛物线配方后可得顶点A的坐标，将抛物线和一次函数的解析式联立方程组，解出可得B 和C的坐标；（2）先根据两点的距离计算AB、BC、AC的长，根据勾股定理的逆定理可得：∠ABC＝90°，最后根据两边的比相等且夹角为90度得两三角形相似；（3）存在，设M（x，0），则P（x，x2+2x），表示OM＝|x|，PM＝|x2+2x|，分两种情况：有＝或＝，根据比例式代入可得对应x的值，计算点P的坐标即可．【解答】（1）解：y＝x2+2x＝（x+1）2﹣1，∴顶点A（﹣1，﹣1）；由，解得：或∴B（﹣2，0），C（1，3）；（2）证明：∵A（﹣1，﹣1），B（﹣2，0），C（1，3），∴AB＝＝，BC＝＝3，AC＝＝2，∴AB2+BC2＝AC2，＝＝，∴∠ABC＝90°，∵OD＝1，CD＝3，∴＝，∴，∠ABC＝∠ODC＝90°，∴△ODC∽△ABC；（3）存在这样的P点，设M（x，0），则P（x，x2+2x），∴OM＝|x|，PM＝|x2+2x|，当以O，P，M为顶点的三角形与△ABC相似时，有＝或＝，由（2）知：AB＝，CB＝3，①当＝时，则＝，当P在第二象限时，x＜0，x2+2x＞0，∴，解得：x1＝0（舍），x2＝﹣，当P在第三象限时，x＜0，x2+2x＜0，∴＝，解得：x1＝0（舍），x2＝﹣，②当＝时，则＝3，同理代入可得：x＝﹣5或x＝1（舍），综上所述，存在这样的点P，坐标为（﹣，﹣）或（﹣，）或（﹣5，15）．5．（2021秋•攸县期末）如图，已知直线y＝﹣2x+4分别交x轴、y轴于点A、B，抛物线过A，B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）若抛物线的解析式为y＝﹣2x2+2x+4，设其顶点为M，其对称轴交AB于点N．①求点M和点N的坐标；②在抛物线的对称轴上找一点Q，使|AQ﹣BQ|的值最大，请直接写出点Q的坐标；③是否存在点P，使四边形MNPD为菱形？并说明理由；（2）当点P的横坐标为1时，是否存在这样的抛物线，使得以B、P、D为顶点的三角形与△AOB相似？若存在，求出满足条件的抛物线的解析式；若不存在，请说明理由．【分析】（1）①函数的对称轴为：x＝﹣＝，故点M（，），即可求解；②设抛物线与x轴左侧的交点为R（﹣1，0），则点A与R关于抛物线的对称轴对称，连接RB并延长交抛物线的对称轴于点Q，则点Q为所求，即可求解；③四边形MNPD为菱形，首先PD＝MN，即（﹣2x2+2x+4）﹣（﹣2x+4）＝，解得：x＝或（舍去），故点P（，1），而PN＝＝≠MN，即可求解；（2）分∠DBP为直角、∠BDP为直角两种情况，分别求解即可．【解析】（1）①函数的对称轴为：x＝﹣＝，故点M（，），当x＝时，y＝﹣2x+4＝3，故点N（，3）；②设抛物线与x轴左侧的交点为R（﹣1，0），则点A与R关于抛物线的对称轴对称，连接RB并延长交抛物线的对称轴于点Q，则点Q为所求，将R、B的坐标代入一次函数表达式：y＝kx+b并解得：直线RB的表达式为：y＝4x+4，当x＝时，y＝6，故点Q（，6）；③不存在，理由：设点P（x，﹣2x+4），则点D（x，﹣2x2+2x+4），MN＝﹣3＝，四边形MNPD为菱形，首先PD＝MN，即（﹣2x2+2x+4）﹣（﹣2x+4）＝，解得：x＝或（舍去），故点P（，1），而PN＝＝≠MN，故不存在点P，使四边形MNPD为菱形；（2）当点P的横坐标为1时，则其坐标为：（1，2），此时点A、B的坐标分别为：（2，0）、（0，4），①当∠DBP为直角时，以B、P、D为顶点的三角形与△AOB相似，则∠BAO＝∠BDP＝α，tan∠BAO＝＝2＝tanα，则sinα＝，PA＝，PB＝AB﹣PA＝2﹣＝，则PD＝＝，故点D（1，）；②当∠BDP为直角时，以B、P、D为顶点的三角形与△AOB相似，则BD∥x轴，则点B、D关于抛物线的对称轴对称，故点D（1，4），综上，点D的坐标为：（1，4）或（1，），将点A、B、D的坐标代入抛物线表达式：y＝ax2+bx+c并解得：y＝﹣2x2+2x+4或y＝﹣x2+3x+4．6．（2022•禹城市模拟）如图，抛物线经过A（4，0），B（1，0），C（0，﹣2）三点．（1）求出抛物线的解析式；（2）P是抛物线在第一象限上的一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M 为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；＝S△ABC，直接写出点D （3）若抛物线上有一点D（点D位于直线AC的上方且不与点B重合）使得S△DCA的坐标．。

抛物线中的相似问题三个解题途径① 求相似三角形的第三个顶点时，先要分析已知三角形的边．和角．的特点，进而得出已知三角形是否为特殊三角形。

根据未知三角形中已知边与已知三角形的可能对应边分类讨论。

②或利用已知三角形中对应角，在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。

③若两个三角形的各边均未给出，则应先设所求点的坐标进而用函数解析式来表示各边的长度，之后利用相似来列方程求解。

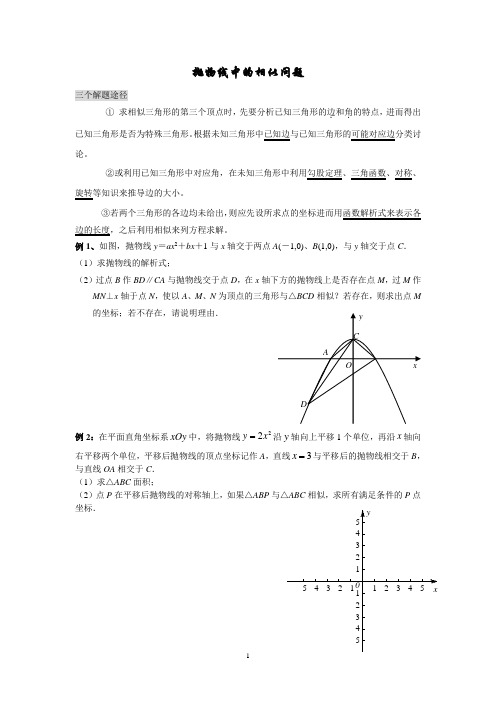
例1、如图，抛物线y ＝ax 2＋bx ＋1与x 轴交于两点A (－1,0)、B (1,0)，与y 轴交于点C ． （1）求抛物线的解析式；（2）过点B 作BD ∥CA 与抛物线交于点D ，在x 轴下方的抛物线上是否存在点M ，过M 作MN ⊥x 轴于点N ，使以A 、M 、N 为顶点的三角形与△BCD 相似？若存在，则求出点M 的坐标；若不存在，请说明理由．例2：在平面直角坐标系xOy 中，将抛物线22y x =沿y 轴向上平移1个单位，再沿x 轴向右平移两个单位，平移后抛物线的顶点坐标记作A ，直线3x =与平移后的抛物线相交于B ，与直线OA 相交于C ． （1）求△ABC 面积；（2）点P 在平移后抛物线的对称轴上，如果△ABP 与△ABC 相似，求所有满足条件的P 点坐标．例3、如图，平面直角坐标系中，点A 、B 、C 在x 轴上，点D 、E 在y 轴上，OA =OD =2，OC =OE =4，DB ⊥DC ，直线AD 与经过B 、E 、C 三点的抛物线交于F 、G 两点，与其对称轴交于M .点P 为线段FG 上一个动点(与F 、G 不重合)，PQ ∥y 轴与抛物线交于点Q . (1)求经过B 、E 、C 三点的抛物线的解析式；(2)是否存在点P ，使得以P 、Q 、M 为顶点的三角形与△AOD 相似？若存在，求出满足条件的点P 的坐标；若不存在，请说明理由；练习题： 练1、（09青海）矩形OABC 在平面直角坐标系中位置如图所示，A C 、两点的坐标分别为(60)A ，，(03)C -，，直线34y x =-与BC 边相交于D 点． （1）求点D 的坐标； （2）若抛物线294y ax x =-经过点A ，试确定此抛物线的表达式； （3）设（2）中的抛物线的对称轴与直线OD 交于点M ，点P 为对称轴上一动点，以P O M 、、为顶点的三角形与OCD △相似，求符合条件的点P 的坐标．练2、、已知抛物线2y ax bx c =++经过0P E ⎫⎪⎪⎝⎭及原点(00)O ，．（1）求抛物线的解析式．（2）过P 点作平行于x 轴的直线PC 交y 轴于C 点，在抛物线对称轴右侧且位于直线PC 下方的抛物线上，任取一点Q ，过点Q 作直线QA 平行于y 轴交x 轴于A 点，交直线PC 于B 点，直线QA 与直线PC 及两坐标轴围成矩形OABC ．是否存在点Q ，使得OPC△与PQB △相似？若存在，求出Q 点的坐标；若不存在，说明理由．（3）如果符合（2）中的Q 点在x 轴的上方，连结OQ ，矩形OABC 内的四个三角形OPC PQB OQP OQA ，，，△△△△之间存在怎样的关系？为什么？练3：如图1，已知抛物线的顶点为A （0，1），矩形CDEF 的顶点C 、F 在抛物线上，D 、E 在x 轴上，CF 交y 轴于点B （2，0），且其面积为8。

二次函数相似综合专题知识要点1．求抛物线的解析式（载体作用，注意利用顶点式隐藏顶点坐标或利用比根式隐藏与x 轴两交点的坐标）．2．结合质点运动，探索两个几何变量之间的函数关系； 3．探索存在问题（面积、线段、角度等）； 4．几何最值、几何定值与几何推理；5．全等、相似、轴对称、旋转、平移、解直角三角形、圆的相关知识的综合运用； 6．注意结合抛物线的图象变换构建存在性问题． 例题解析【例1】已知抛物线y ＝223x x --与x 轴交于A ，B 两点，与y 轴交于点C ．①若抛物线的顶点为M ，求四边形ACMB 的面积； ②在第一象限的抛物线上求点P ，使S △ABP ＝10； ③在第一象限的抛物线上求点P ，使S △ACP ＝10； ④在②的条件下，在抛物线上求点Q ，使S △APQ ＝S △BPQ ；⑤在②的条件下，在抛物线上求点Q ，使S △APQ ∶S △BPQ ＝1∶3．〖练1〗如图，□OABC 中，点A 坐标为（2，0），抛物线y ＝24ax bx ++经过点A ，B ，C三点，交y 轴于点D ． ①求此抛物线的解析式；②P 是抛物线上一点，且△OBP ≌△ODP ，求P 点坐标；③直线MN ∥x 轴，交抛物线于N ，交y 轴于M ，连线段BN ，AM ，BN 交OD 于E ，若AM ∥BN ，求线段MN 的长．第①问图第②问图第③问图【例2】已知△ABC为直角三角形，∠ACB＝90°，AC＝BC，点A，C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B，D．（1）求点A的坐标（用m表示）；（2）求抛物线的解析式；（3）设点Q为抛物线上点P至点B之间的一动点，连结PQ并延长交BC于点E，连结BQ并延长交AC于点F，试证明：FC（AC＋EC）为定值．【例3】如图，在平面直角坐标系中，点O为坐标原点，直与x轴交于点A，过点A的抛物线y＝2ax bx+与直线y＝4x-+交于另一点B，且点B的横坐标为1．（1）求a，b的值；（2）点P是线段AB上一动点（点P不与点A，B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d与t之间函数关系式（不要求写出自变量的取值范围）；（3）在（2）的条件下，当S△ACN＝S△PMN时，连接ON，点Q在线段BP上，过点Q 作QR∥MN交ON于点R，连接MQ，BR，当∠MQR－∠BRN＝45°时，求点R的坐标．〖练2〗已知抛物线C 1：y ＝223x x --与x 轴交于A ，B 两点（A 在B 点左侧），与y 轴交于点C ．（1）求A ，B ，C 三点坐标；（2）将抛物线向右平移2个单位，向上平移3个单位，得到抛物线C 2，将线段AC绕坐标平面内的某点旋转后，得到线段MN ，且MN ⊥AC ，M ，N 点恰好落在抛物线C 2上，如图，求M 点的坐标；（3）设抛物线C 1的顶点为D ，DE ⊥AB 于E ，M 为x 轴下方抛物线C 1上一动点（不与点D 重合），MN ⊥BC 于N ，是否存在这样的点M ，使△MND 与△BED 相似？若存在，求M 点的坐标；若不存在，请说明理由．【例4】在平面直角坐标系xOy 中，已知抛物线y ＝24(2)9x c --+与x 轴交于A ，B 两点（点A 在点B 的左侧），交y 轴的正半轴于点C ，其顶点为M ，MH ⊥x 轴于点H ，MA 交y 轴于为N ，sin ∠MOH． （1）求此抛物线的函数表达式；（2）过H 的直线与y 轴相交于点P ，过O ，M 两点作直线PH 的垂线，垂足分别为E ，F ，若HE HF＝12JF ，求点P 的坐标； （3）将（1）中的抛物线沿y 轴折叠，使点A 落在点D 处，连接MD ，Q 为（1）中的抛物线上一动点，直线NQ 交x 轴于点G ，当Q 点在抛物线上运动时，是否存在点Q ，使△ANG 与△ADM 相似？若存在，求出所有符合条件的直线QG 的解析式；若不存在，请说明理由．〖练3〗抛物线y ＝2(1)4a x --的顶点为D ，与x 轴交于A ，B 两点，与y 轴负半轴交于点C ，对称轴与x 轴交于点H ，且HD ＝AB ． （1）求此抛物线的解析式；（2）若M 为对称轴右侧抛物线上一点，MN ∥x 轴交抛物线于另一点N ，以MN 为斜边的直角三角形的直角顶点在x 轴上，当这个直角三角形的顶点至少有一个时，求M 点纵坐标的取值范围；（3）经过C ，D 两点的直线与x 轴交于E 点，P 为对称轴右侧抛物线上一点，CP交对称轴于点F ，是否存在这样一点P ，使△CDF 与△EAC 相似、若存在，求点P 的坐标；若不存在，请说明理由．【例5】已知抛物线C 1：y ＝2(1)2a x +-的顶点为A ，且经过点B （－2，－1）．（1）求A 点的坐标和抛物线C 1的解析式；（2）如图1，将抛物线C 1向下平移2个单位后得到抛物线C 2，且抛物线C 2与直线AB 相交于C ，D 两点，求S △OAC ∶S △OAD 的值；（3）如图2，若过P （－4，0），Q （0，2）的直线为l ，点E 在（2）中抛物线C 2对称轴右侧部分（含顶点）运动，直线m 过点C 和点E ．问：是否存在直线m，使直线l ，m 与x 轴围成的三角形和直线l ，m 与y 轴围成的三角形相似？若存在，求出直线m 的解析式；若不存在，请说明理由．〖练4〗如图1，抛物线C 1：y ＝2ax bx c ++的顶点为A （1，134-），与y 轴的负半轴交于点B ．（1）求点B 的坐标；（2）如图2，将抛物线C 1向下平移与直线AB 相交于C ，D 两点，若BC ＋AD ＝AB ，求平移后的抛物线C 2的解析式；（3）如图3，在（2）中，设抛物线C 2与y 轴交于G 点，顶点为E ，EF ⊥x 轴于F点，点M （m ，0）是x 轴上一动点，点N 在线段EF 上，若∠MNG ＝90°，请你分析实数m 的变化范围；图1图2图1图3图2【例6】如图，已知抛物线y ＝2x bx c ++与x 轴交于点A （1，0）和点B ，与y 轴交于点C（0，－3）．（1）求抛物线的解析式；（2）如图1，已知点H （0，－1），问在抛物线上是否存在点G （点G 在y 轴的左侧），使得S △GHC ＝S △GHA ？若存在，求出点G 的坐标；若不存在，请说明理由； （3）如图2，抛物线上点D 在x 轴上的正投影为点E （－2，0），F 是OC 的中点，连接DF ，P 为线段BD 上的一点，若∠EPF ＝∠BDF ，求线段PE 的长．〖练5〗如图，抛物线1y ＝22ax ax b -+经过点A （－1，0），C （0，32）两点，与x 轴交于点一点B ．（1）求此抛物线的解析式；（2）若抛物线的顶点为M ，点P 为线段OB 上一动点（不与点B 重合），点Q 在线段MB 上移动，且∠MPQ ＝45°，设线段OP ＝x ，MQ2y ，求2y 与x 的函数关系式，并直接写出自变量x 的取值范围；（3）在同一平面直角坐标系中，两条直线x ＝m ，x ＝n 分别与抛物线交于点E ，G ，与（2）中的函数图象交于点F ，H ，问四边形EFGH 能否为平行四边形？若能，求出m ，n 之间的数量关系；若不能，请说明理由．图1图2【例7】如图1，抛物线y ＝(1)(3)a x x -+交x 轴于A ，B 两点，交y 轴于点C ，OC 2＝3OA ·OB ．（1）求此抛物线的解析式；（2）如图2，点E 为线段OA 上的一点，过点E 且垂直x 轴的直线交抛物线于点F ，若直线AC 将△AEF 分成面积之比为1∶2的两部分，求点E 的坐标；（3）如图3，若直线y ＝12x b +交x 轴于点M ，交y 轴于点N ，将△MON 沿直线MN 折叠，得到△MPN ，点O 的对称点为P ，是否存在这样的b 值，使点P 恰好落在抛物线上？若存在，求出b 的值；若不存在，请说明理由．〖练6〗如图1，抛物线y ＝2(21)4a x ax b --+与x 轴交于A ，B 两点，与y 轴正半轴交于点C ，直线BC 的解析式：y ＝3kx k -，tan ∠OCB ＝1． （1）求此抛物线的解析式；（2）如图2，若y 轴负半轴上点M ，此抛物线上点N ，关于直线AC 对称，求点N的坐标；（3）设D 为该抛物线的顶点，在此抛物线的对称轴上是否存在一点P ，使得△P AD与△ABC 相似、若存在，请求出点P 的坐标；若不存在，请说明理由．备用图【例8】在平面直线坐标系中，抛物线y ＝23ax bx ++交x 轴于A ，B 两点（A 点在B 点左侧），交y 轴于C 点，对称轴为直线x ＝1，sin ∠OCA． （1）求此抛物线的解析式，并求顶点E 的坐标；（2）将（1）中的抛物线向下平移，若平移后，在四边形ABEC 中满足S△BCE＝S △ABC ，求此时直线BC 的解析式；（3）将（1）中的抛物线作适当的平移，若平移后，在四边形ABED 中满足S △BCE＝2S △AOC ，且顶点E 恰好落在直线y ＝43x -+上，求此时抛物线的解析式．〖练7〗如图1，在平面直角坐标系中，直线l ：y ＝3342x --沿x 轴翻折后，与x 轴交于点A ，与y 轴交于点B ，抛物线y ＝22()3x h -与y 轴交于点D ，与直线AB 交于点E ，F （点F 在点E 的右侧）． （1）求直线AB 的解析式；（2）若线段DF ∥x 轴，求抛物线的解析式；（3）如图2，在（2）的条件下，过F 作FH ⊥x 轴于点G ，与直线l 交于点H，在备用图备用图抛物线上是否存在P ，Q 两点（点P 在点Q 的上方），PQ 与AP 交于点M ，与FH 交于点N ，使得直线PQ 既平分△AFH 的周长又平分△AFH 的面积？如果存在，求出P ，Q 的坐标；若不存在，请说明理由．图2图1。

二次函数存在性问题——相似三角形例一、如图，抛物线y=ax2+bx+c（a≠0）经过点A（﹣3，0）、B（1，0）、C（﹣2，1），交y轴于点M．（1）求抛物线的表达式；（2）D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交线段AM于点F，求线段DF长度的最大值，并求此时点D的坐标；（3）抛物线上是否存在一点P，作PN垂直x轴于点N，使得以点P、A、N为顶点的三角形与△MAO相似？若存在，求点P的坐标；若不存在，请说明理由．例二.如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C（1）求抛物线的函数解析式．（2）设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标．（3）P是抛物线上第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P，M，A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．随堂练习1.如图，抛物线21y ax bx =++与x 轴交于A （-1，0）、B （1，0）两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）过点B 作BD ∥CA 与抛物线交于点D ，求四边形ACBD 的面积；（3）M 是x 轴下方抛物线上的一个动点，过M 作MN ⊥x 轴于点N ，是否存在点M ，使以A 、M 、N 为顶点的三角形与△BCD 相似？若存在，请求出点M 的坐标；若不存在，请说明理由．2. 如图，在平面直角坐标系xOy 中，直线y=x+4与坐标轴分别交于A 、B 两点，过A 、B 两点的抛物线为y=﹣x2+bx+c．点D为线段AB上一动点，过点D作CD⊥x 轴于点C，交抛物线于点E．（1）求抛物线的解析式．（2）当DE=4时，求四边形CAEB的面积．（3）连接BE，是否存在点D，使得△DBE和△DAC相似？若存在，求此点D坐标；若不存在，说明理由．3.如图，抛物线y=ax2+b与x轴交于点A、B，且A点的坐标为（1，0），与y轴交于点C（0，1）．（1）求抛物线的解析式，并求出点B坐标；（2）过点B作BD∥CA交抛物线于点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）（3）在x轴上方的抛物线上是否存在点P，过点P作PE垂直于x轴，垂足为点E，使以B、P、E为顶点的三角形与△CBD 相似？若存在请求出P点的坐标；若不存在，请说明理由．4.如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C 和D（3，0）．（1）求直线BD和抛物线的解析式．（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．5. 如图，四边形ABCD是平行四边形，AB=4，OB=2，抛物线过A、B、C三点，与x轴交于另一点D．一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动，运动到点A停止，同时一动点Q从点D出发，以每秒3个单位长度的速度沿DC向点C运动，与点P同时停止．（1）求抛物线的解析式；（2）若抛物线的对称轴与AB交于点E，与x轴交于点F，当点P运动时间t为何值时，四边形POQE是等腰梯形？（3）当t为何值时，以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似？6. 如图，抛物线y=ax2﹣2ax+c（a≠0）交x轴于A、B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G．（1）求抛物线的解析式；（2）抛物线的对称轴l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长；（3）在（2）的条件下，连结PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由．。

学习好资料欢迎下载二次函数压轴专题の相似问题1. 如图，直线 y=-x+3 与 x 轴、y 轴分别相交于点 B、点 C，经过 B、C两点的抛物线 y=ax2+bx+c与 x 轴的另一个交点为 A，顶点为 P，且对称轴是直线 x=2.C(1)求 A 点的坐标；(2)求该抛物线的函数表达式；(3) 连结 AC.请问在 x 轴上是否存在点Q，使得以点 P、B、Q为顶点的三角形与ABC相似，若存在，请求出点Q的坐标；若不存在，请说明理由.OA BP2．（青海省）矩形OABC 在平面直角坐标系中位置如图所示，A、C 两点的坐标分别为A（ 6，0）， C（ 0，－3），直线y＝－3x 与 BC 边相交于 D 点．4（1）求点 D 的坐标；（2）若抛物线y＝ax 2－9x 经过点 A，试确定此抛物线的表达式；4（ 3）设（ 2）中的抛物线的对称轴与直线OD 交于点 M，点 P 为对称轴上一动点，以P、 O、 M 为顶点的三角形与△OCD 相似，求符合条件的点P 的坐标．yAO6x- 3C DB3．（广西北海市）如图，在平面直角坐标中，二次函数图象的顶点坐标为C( 4，－ 3 ) ，且在 x 轴上截得的线段AB 的长为 6．（1）求二次函数的解析式；（2）点 P 在y轴上，且使得△ PAC 的周长最小，求：①点 P 的坐标；②△ PAC 的周长和面积；（ 3）在 x 轴上方的抛物线上，是否存在点Q，使得以Q、 A、 B 三点为顶点的三角形与△ ABC 相似？如果存在，求出点Q 的坐标；如果不存在，请说明理由．y ＝－3x4yO A B xC4．如图，二次函数y1 x 2c的图象经过点D2⑴求 c 的值；93,，与x轴交于A、B两点．2⑵如图①，设点 C 为该二次函数的图象在x 轴上方的一点，直线AC 将四边形ABCD 的面积二等分，试证明线段BD 被直线 AC 平分，并求此时直线AC 的函数解析式；⑶设点 P、Q 为该二次函数的图象在x 轴上方的两个动点，试猜想：是否存在这样的点P、Q，使△ AQP≌△ ABP？如果存在，请举例验证你的猜想；如果不存在，请说明理由．（图②供选用）5、已知：在直角平面坐标系中，二次函数y ax2bx 3(a 0) 的图像与X轴交于A、B两点，点A在点B的左侧，与 Y 轴交于点 C，且 OC=OB=3AO（1）、求二次函数的解析式；（2）、设点 D 是点 C 关于此抛物线对称轴的对称点，直线 AD 、BC 交于点 P，试判断直线 AD 、BC 是否垂直，并证明你的结论；（3）、在（2）的条件下，若点M 、N 分别是射线PC、PD 上的点，问：是否存在这样的点M 、N,使得以点P、M 、 N 为顶点的三角形与△ ACP 全等？若存在，求出点 M 、N 的坐标；若不存在，请说明理由。

一、二次函数性质1. 已知二次函数f(x) = ax^2 + bx + c，其中a、b、c为实数，且a ≠ 0。

若f(x)的对称轴为x = 1，且f(0) = 2，求f(x)的解析式。

2. 设二次函数f(x) = ax^2 + bx + c的图象开口向上，且f(1) = 3，f(1) = 1，求f(x)的解析式。

3. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且f(0) = 1，f(1) = 3，求f(x)的解析式。

4. 设二次函数f(x) = ax^2 + bx + c的图象开口向下，且f(1) = 3，f(1) = 1，求f(x)的解析式。

5. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且f(0) = 1，f(2) = 3，求f(x)的解析式。

二、二次函数图像1. 已知二次函数f(x) = ax^2 + bx + c的图象开口向上，且顶点坐标为(1, 2)，求f(x)的解析式。

2. 设二次函数f(x) = ax^2 + bx + c的图象开口向下，且顶点坐标为(1, 3)，求f(x)的解析式。

3. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且顶点坐标为(0, 1)，求f(x)的解析式。

4. 设二次函数f(x) = ax^2 + bx + c的图象开口向上，且顶点坐标为(2, 3)，求f(x)的解析式。

5. 已知二次函数f(x) = ax^2 + bx + c的图象开口向下，且顶点坐标为(1, 2)，求f(x)的解析式。

三、二次函数图像变换1. 已知二次函数f(x) = x^2的图象，求函数g(x) = (x 1)^2 + 2的图象。

2. 设二次函数f(x) = x^2的图象，求函数g(x) = (x + 2)^2 3的图象。

3. 已知二次函数f(x) = x^2的图象，求函数g(x) = (x 1)^22的图象。