基于矩阵分解的兴趣点推荐

矩阵分解在推荐系统的应用随着互联网的发展和电子商务的兴起，推荐系统逐渐成为用户获取信息和商品的重要途径。

推荐系统的核心目标是根据用户的历史行为和个人偏好，预测和推荐用户可能感兴趣的信息和商品。

为了实现准确的推荐，矩阵分解作为一种常用的方法被广泛应用在推荐系统中。

矩阵分解是一种数学方法，它将一个大的矩阵分解为两个较小的矩阵的乘积。

在推荐系统中，矩阵分解可以被用来对用户和商品之间的关系进行建模。

通过将用户-商品评分矩阵分解为用户特征矩阵和商品特征矩阵，推荐系统可以通过计算用户和商品之间的相似度来预测用户对未知商品的喜好程度。

首先，推荐系统需要收集用户的历史行为数据，例如用户购买记录、评分和点击行为等。

这些数据可以表示为一个稀疏的用户-商品评分矩阵，其中行表示用户，列表示商品，每个元素表示用户对商品的评分或行为。

然后，通过矩阵分解，可以将用户-商品评分矩阵分解为用户特征矩阵和商品特征矩阵。

用户特征矩阵是一个N×K的矩阵，其中N是用户的数量，K是特征的数量。

每一行表示一个用户，每一列表示一个特征。

特征可以是用户的年龄、性别、兴趣爱好等。

同样，商品特征矩阵是一个M×K的矩阵，其中M是商品的数量。

每一行表示一个商品。

通过计算用户特征矩阵和商品特征矩阵之间的相似度，推荐系统可以预测用户对未知商品的评分。

矩阵分解的优势在于它可以充分利用用户和商品之间的隐含关系。

通过分解用户-商品评分矩阵，推荐系统可以挖掘用户和商品的潜在特性，从而更好地理解用户的偏好和商品的特点。

此外，矩阵分解还可以减轻数据稀疏性问题，因为通过用户特征矩阵和商品特征矩阵的乘积，可以填充原始评分矩阵中的缺失值。

矩阵分解在推荐系统中的应用不仅限于常见的商品推荐，还可以扩展到其他领域。

例如，在电影推荐系统中，矩阵分解可以用来为用户推荐适合其口味的电影。

在社交网络中，矩阵分解可以用来预测用户之间的社交关系。

此外，矩阵分解还可以应用在音乐推荐、新闻推荐和广告推荐等多个领域。

基于矩阵分解的协作过滤推荐算法研究近年来，推荐系统成为电商、社交媒体等领域广泛应用的核心技术，它可以帮助用户发现感兴趣的商品、信息和人脉等，提高用户体验和交易额。

其中，基于协作过滤的推荐算法是最为经典和有效的一种。

协作过滤推荐算法的核心思想是利用用户对物品的共同评价信息，从而找到物品之间的相似性，进而预测和推荐用户可能感兴趣的物品。

根据推荐数据的不同类型和结构，协作过滤算法可以分为基于用户的协作过滤、基于物品的协作过滤、基于社交网络的协作过滤等不同形式。

近年来，矩阵分解技术在协作过滤推荐算法中也变得越来越被重视，其核心思想是将原始高维稀疏的评分矩阵转化为低维稠密的用户-物品矩阵，然后利用矩阵分解算法对矩阵进行分解和降维，从而获得用户和物品的特征向量表示，进而进行预测和推荐。

主要的矩阵分解算法有SVD、PMF、NMF、ALS等。

其中，SVD是最为经典和基础的矩阵分解算法，它可以将评分矩阵分解为三个矩阵的乘积，分别表示用户的特征矩阵、物品的特征矩阵和奇异值矩阵。

但是，SVD算法在大规模数据下的计算和内存消耗较大，难以直接应用于工业实践。

因此，研究者们提出了很多优化和改进算法，比如基于梯度下降的PMF算法、基于非负矩阵分解的NMF算法、基于交替最小二乘法的ALS算法等。

值得注意的是，矩阵分解算法在应用中还需要考虑数据稀疏性和冷启动问题。

数据稀疏性指的是评分矩阵中大部分元素缺失，因此需要利用其他信息（比如用户画像、社交网络）进行补全。

冷启动问题指的是新用户和新物品在评分矩阵中没有任何记录，因此需要利用其他信息（比如用户注册信息、商品描述）进行推荐。

此外，矩阵分解算法也有一些应用上的局限性，比如无法处理带时序信息的数据、无法处理不同类型的物品和用户行为等问题。

因此，在实际应用中，需要结合其他推荐算法（如内容-based推荐、混合推荐）进行综合推荐，获得更为准确和多样化的推荐结果。

总之，基于矩阵分解的协作过滤推荐算法在电商、社交媒体、影视等领域有着广泛应用和深远意义，其理论和应用前景也还存在着很多有待探究的问题和挑战，需要研究者们不断进行优化和创新。

矩阵分解算法在推荐系统中的应用研究随着信息时代的来临，互联网上数据源头的增加和用户数量的爆发性增长，传统的推荐算法已经无法满足数据量和用户需求的匹配，导致了推荐效果无法达到理想目标。

矩阵分解算法作为一种有效的推荐算法逐渐得到业界的认可，尤其在推荐系统中得到广泛应用，具有很高的理论研究和实际应用价值。

一、矩阵分解算法的概念和基本原理矩阵分解算法是推荐系统中一种常见的算法，可以将矩阵中的元素分解成两个低维度的矩阵，通过计算两个低维度矩阵之间的乘积得到原矩阵，这种分解方式在推荐系统中可以很好地解决因为高维数据而导致的数据稀疏性问题。

以协同过滤算法为例，矩阵分解算法通过把每个用户对每个商品的评价看作矩阵中的一个元素来实现。

矩阵分解算法的基本原理是将原始数据集分解成两个或多个子集，然后利用子集之间的内部关系或者子集之间的相互关系来推断出其他数据。

利用矩阵分解算法可以将高维稀疏的矩阵分解成低维稠密矩阵，提高了数据分析效率，解决了大规模数据处理时所面临的稀疏性和存储性问题。

二、矩阵分解算法在推荐系统中的应用1. 协同过滤算法协同过滤算法是推荐系统中最常用的算法之一，而矩阵分解算法可以说是协同过滤算法的一种优化算法，可以大幅度提高协同过滤算法的推荐效果。

矩阵分解算法通过将用户对每个商品的评价转换成矩阵形式，然后分解矩阵，通过计算两个低维度矩阵之间的乘积来推荐用户可能喜欢的商品。

2. 基于隐语义模型的推荐算法基于隐语义模型的推荐算法可以提高推荐系统的准确性和效率。

该算法通过分解用户评价矩阵，得到用户和商品的隐向量，通过计算隐向量的相似性，实现对商品的推荐。

该算法可以克服数据稀疏性带来的用户冷启动、数据质量差等问题，实现更高效的推荐。

三、矩阵分解算法的优缺点分析1. 优点（1）矩阵分解算法可以将数据集分解成多个子集，实现高效率的数据处理；（2）矩阵分解算法可以实现低维度向量的计算，减小数据稀疏性带来的影响，提高推荐效果；（3）矩阵分解算法可以解决冷启动问题，实现更快速的推荐。

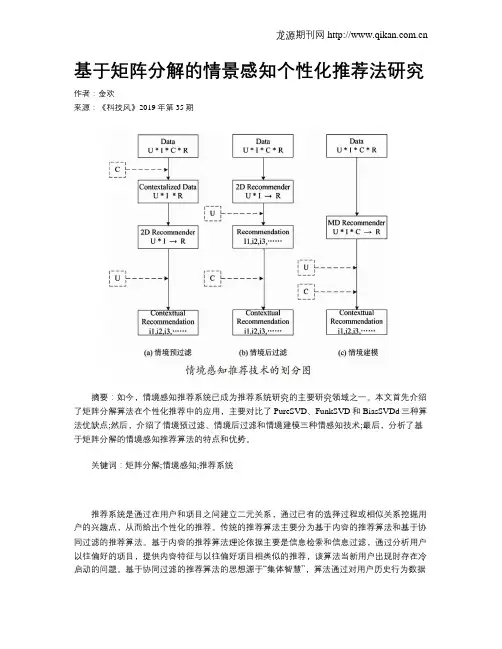
基于矩阵分解的情景感知个性化推荐法研究作者：金欢来源：《科技风》2019年第35期摘要：如今，情境感知推荐系统已成为推荐系统研究的主要研究领域之一。

本文首先介绍了矩阵分解算法在个性化推荐中的应用，主要对比了PureSVD、FunkSVD和BiasSVDd三种算法优缺点;然后，介绍了情境预过滤、情境后过滤和情境建模三种情感知技术;最后，分析了基于矩阵分解的情境感知推荐算法的特点和优势。

关键词：矩阵分解;情境感知;推荐系统推荐系统是通过在用户和项目之间建立二元关系，通过已有的选择过程或相似关系挖掘用户的兴趣点，从而给出个性化的推荐。

传统的推荐算法主要分为基于内容的推荐算法和基于协同过滤的推荐算法。

基于内容的推荐算法理论依据主要是信息检索和信息过滤，通过分析用户以往偏好的项目，提供内容特征与以往偏好项目相类似的推荐，该算法当新用户出现时存在冷启动的问题。

基于协同过滤的推荐算法的思想源于“集体智慧”，算法通过对用户历史行为数据的挖掘发现用户的偏好，基于不同的偏好对用户进行群组划分并推荐品味相似的商品。

协同过滤算法同样也存在冷启动的问题，当没新用户数据时，无法给出较好的推荐。

没有考虑情境的差异，比如不同根据季节的不同，给用户推荐与季节相适应的服饰。

基于以上问题，研究人员提出了基于矩阵分解的情境感知推荐法。

1 矩阵分解算法在个性化推荐中的应用矩阵分解的核心思想是将用户评分矩阵分解为低秩的矩阵，使其乘积尽可能接近原始评分矩阵，使得预测的矩阵与原始矩阵之间的误差平方最小。

奇异值分解（Singular Value Decomposition，以下简称SVD）在机器学习领域得到了广泛的应用，因为它不仅可以用于降维算法中的特征分解，还能用于推荐算法。

如果将m个用户和n个项目对应的评分看做一个矩阵M，本文将用矩阵分解来解决该问题。

1.1 PureSVD算法PureSVD（传统的奇异值分解）在降维中的应用，将用户和项目对应的m×n矩阵M进行SVD分解，通过选择部分较大的奇异值进行降维分解为：Mm×n=Um×k∑k×kVTk×n（1）其中k是矩阵M中的奇异值的个数，一般会小于用户数和项目数。

基于用户信任和兴趣的概率矩阵分解推荐方法彭鹏;米传民;肖琳【期刊名称】《计算机系统应用》【年(卷),期】2017(026)009【摘要】传统协同过滤推荐算法存在数据稀疏性、冷启动、新用户等问题.随着社交网络和电子商务的迅猛发展,利用用户间的信任关系和用户兴趣提供个性化推荐成为研究的热点.本文提出一种结合用户信任和兴趣的概率矩阵分解(STUIPMF)推荐方法.该方法首先从用户评分角度挖掘用户间的隐性信任关系和潜在兴趣标签,然后利用概率矩阵分解模型对用户评分信息、用户信任关系、用户兴趣标签信息进行矩阵分解,进一步挖掘用户潜在特征,缓解数据稀疏性.在Epinions数据集上进行实验验证,结果表明,该方法能够在一定程度上提高推荐精度,缓解冷启动和新用户问题,同时具有较好的可扩展性.%The traditional collaborative filtering recommendation algorithm has such problems as datasparseness,coldstart and new users.With the rapid development of social network and e-commerce,how to provide personalized recommendations based on the trust between users and user interest tag is becoming a hot research topic.In this study,we propose a probability matrix factorization model (STUIPMF) by integrating social trust and user interest.First,we excavate implicit trust relationship between users and potential interest label from the perspective of user rating.Then we use the probability matrix factorization model to conduct matrix decomposition of user ratings information,users trust relationship,user interest labelinformation,and further excavate the user characteristics to ease data sparseness.Finally,we make experiments based on the Epinions dataset to verify the proposed method.The results show that the proposed method can to some extent improve the recommendation accuracy,ease cold-start and new user problems.Meanwhile,the proposed STUIPMF approach also has good scalability.【总页数】9页(P1-9)【作者】彭鹏;米传民;肖琳【作者单位】南京航空航天大学经济与管理学院,南京211100;南京航空航天大学经济与管理学院,南京211100;南京航空航天大学经济与管理学院,南京211100【正文语种】中文【相关文献】1.结合用户组群和隐性信任的概率矩阵分解推荐 [J], 席茜;张凤琴;李小青2.融合信任和基于概率矩阵分解的推荐算法 [J], 田保军; 杨浒昀; 房建东3.基于概率矩阵分解算法的社交网络用户兴趣点个性化推荐 [J], 张敏军;华庆一4.融合用户信任度的概率矩阵分解推荐算法 [J], 陈辉;王锴钺5.融合用户信任度的概率矩阵分解群组推荐算法 [J], 宋玉龙;马文明;刘彤彤因版权原因，仅展示原文概要，查看原文内容请购买。

《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言随着互联网的飞速发展，信息过载问题日益严重，如何从海量数据中快速准确地为用户提供感兴趣的内容成为了亟待解决的问题。

推荐系统作为解决这一问题的有效手段，近年来受到了广泛关注。

其中，基于矩阵分解的推荐算法因其高效性和准确性而备受青睐。

然而，传统的矩阵分解推荐算法在处理用户偏好不确定性、数据稀疏性和冷启动等问题时仍存在一定局限性。

因此，本文旨在研究基于矩阵分解的鲁棒推荐算法，以提高推荐系统的准确性和鲁棒性。

二、矩阵分解推荐算法概述矩阵分解是推荐系统中常用的一种技术，其基本思想是将用户-项目评分矩阵分解为用户和项目的潜在特征矩阵。

通过分析这些潜在特征，可以预测用户对项目的评分，从而进行推荐。

常见的矩阵分解算法包括奇异值分解（SVD）、非负矩阵分解（NMF）等。

这些算法在处理大规模数据时表现出色，但在处理用户偏好不确定性、数据稀疏性和冷启动等问题时仍需改进。

三、鲁棒性矩阵分解推荐算法研究为了解决上述问题，本文提出了一种基于鲁棒性矩阵分解的推荐算法。

该算法在传统矩阵分解的基础上，引入了鲁棒性优化策略，以增强算法对用户偏好不确定性、数据稀疏性和冷启动等问题的处理能力。

1. 鲁棒性优化策略针对用户偏好不确定性问题，我们采用了一种基于加权正则化的方法。

通过引入权重因子，对不同用户的评分进行加权处理，以反映用户偏好的不确定性。

这样，在矩阵分解过程中，算法可以更好地捕捉用户的个性化偏好。

针对数据稀疏性问题，我们采用了融合辅助信息的策略。

通过将辅助信息（如用户社交网络、项目属性等）融入矩阵分解过程，提高算法对稀疏数据的利用能力。

这样，即使面对数据稀疏的情况，算法仍能准确预测用户对项目的评分。

针对冷启动问题，我们采用了协同矩阵分解的方法。

通过将新用户或新项目的潜在特征与已知用户或项目的潜在特征进行协同学习，加速新用户或新项目的特征学习过程。

这样，即使面对冷启动问题，算法也能快速为用户或项目生成准确的推荐。

矩阵分解算法在推荐系统中的应用实践推荐系统是一类重要的信息过滤系统，其目的是通过利用用户历史行为数据，挖掘用户的兴趣模式，并根据这些模式为用户提供个性化的推荐结果。

在推荐系统中，矩阵分解算法是一种常用的方法，通过对用户-物品评分矩阵进行分解，能够有效地捕捉用户和物品之间的潜在关系，从而实现个性化的推荐。

1. 推荐系统概述推荐系统在人们的日常生活中扮演着重要的角色，它们广泛应用于电子商务、社交网络、音乐、电影等领域。

推荐系统的目标是在大量的物品中，根据用户的兴趣，为用户提供个性化的推荐结果，帮助用户发现潜在的兴趣点。

推荐系统通常分为两种类型：协同过滤和内容过滤。

其中，协同过滤是一种通过分析用户之间的关系，为用户进行推荐的方法。

而内容过滤则是基于物品的属性信息为用户进行推荐。

矩阵分解算法主要应用于协同过滤推荐系统中。

2. 矩阵分解算法原理矩阵分解算法的主要思想是将用户-物品评分矩阵分解为两个低秩的矩阵，通过这种方式，可以捕捉到用户和物品之间的潜在关系。

通常使用的矩阵分解算法有奇异值分解（Singular Value Decomposition，简称SVD）和潜在语义索引（Latent Semantic Indexing，简称LSI）。

在矩阵分解算法中，用户-物品评分矩阵被表示为R，矩阵R中的每个元素R[i,j]表示用户i对物品j的评分。

矩阵分解的目标是找到两个低秩矩阵P和Q，使得它们的乘积近似等于原始矩阵R。

具体的目标函数可以表示为：R ≈ P × Q其中，P是一个m×k的矩阵，表示用户和潜在因素之间的关系，Q是一个k×n的矩阵，表示物品和潜在因素之间的关系。

通过最小化目标函数，可以通过优化算法（如梯度下降）来寻找最优的P和Q矩阵。

3. 推荐系统中的应用实践矩阵分解算法在推荐系统中的应用主要包括基于矩阵分解的协同过滤算法和深度矩阵分解算法。

基于矩阵分解的协同过滤算法是推荐系统中最常用的方法之一。

《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言随着互联网技术的飞速发展，信息过载问题日益突出，使得用户难以从海量的数据中筛选出符合自己兴趣的内容。

推荐系统作为解决这一问题的有效手段，被广泛应用于电商、视频、音乐、社交等众多领域。

其中，基于矩阵分解的推荐算法因其实用性和高效性受到了广泛关注。

然而，传统的矩阵分解推荐算法在处理用户和项目的稀疏性、冷启动问题以及动态变化的数据时，其鲁棒性有待提升。

本文针对这些问题，对基于矩阵分解的鲁棒推荐算法进行研究。

二、矩阵分解推荐算法概述矩阵分解是推荐系统中的一种重要技术，其基本思想是将用户-项目评分矩阵分解为用户和项目的隐因子矩阵。

通过这些隐因子矩阵，可以预测用户对项目的评分，从而进行推荐。

传统的矩阵分解算法如SVD、NMF等在处理大规模数据时表现出色，但在处理数据稀疏性、冷启动和动态变化等方面存在不足。

三、鲁棒性在推荐算法中的重要性鲁棒性是评价推荐算法性能的重要指标之一。

在现实应用中，推荐系统的数据往往具有高度的稀疏性、动态性和不确定性。

因此，一个鲁棒的推荐算法应该能够有效地处理这些挑战。

具体来说，鲁棒的推荐算法应具备以下特点：对数据稀疏性的鲁棒性、对冷启动问题的鲁棒性以及对动态变化的鲁棒性。

四、基于矩阵分解的鲁棒推荐算法研究为了解决传统矩阵分解推荐算法在处理稀疏性、冷启动和动态变化等方面的不足，本文提出了一种基于矩阵分解的鲁棒推荐算法。

该算法在传统的矩阵分解基础上，引入了以下改进措施：1. 引入正则化项：通过引入正则化项，可以有效地抑制过拟合现象，提高算法的鲁棒性。

此外，正则化项还可以提高算法对噪声数据的处理能力。

2. 结合时间因素：考虑到用户和项目的动态变化特性，本文在矩阵分解过程中引入了时间因素。

通过考虑用户和项目的时间变化趋势，可以更准确地预测用户对项目的评分。

3. 融合其他信息：除了用户-项目评分信息外，还可以融合其他相关信息如用户的社会网络信息、项目的内容信息等。

基于矩阵分解的推荐系统优化与实现近年来，随着互联网的不断普及和数据量的不断增加，推荐系统成为了各大电商、视频网站等互联网企业业务中不可或缺的一部分。

然而，市场上的推荐系统存在推荐不准确、数据量过大等问题。

为了解决这些问题，推荐系统也不断地进行着优化及创新。

其中，基于矩阵分解的推荐系统成为了一种强有力的推荐算法，被广泛运用于各类推荐场景。

一、什么是基于矩阵分解的推荐系统?矩阵分解即将一个大矩阵拆分成多个小矩阵的过程。

基于矩阵分解的推荐系统，可以将用户和商品的关系表达为一个矩阵。

该矩阵可以被分解为两个小矩阵，通过对这两个小矩阵进行操作，可以得出用户和商品的关系，以及推荐的评分等信息。

具体地说，将用户和商品之间的评分关系表示为一个矩阵，并将此矩阵分解为用户与特征之间的矩阵，以及商品与特征之间的矩阵。

通过这种方式，可以将较大的矩阵分解为两个较小的矩阵，并在此基础上实现推荐。

基于矩阵分解的推荐系统不仅可以提高推荐的准确性，同时也可以通过降维的方式，实现对海量数据的快速处理。

二、基于矩阵分解的推荐系统的优劣势基于矩阵分解的推荐系统拥有以下几个优势：1、提高推荐准确性：基于矩阵分解的推荐系统可以从用户和商品之间的关系中挖掘出更多的信息，进而提高推荐的准确性。

与传统的推荐算法相比，基于矩阵分解的推荐系统能够更好地解决“长尾推荐”问题，提高推荐的全面性和可信度。

2、适用于海量数据的处理：对于互联网企业而言，处理海量数据是一个十分困难的问题。

基于矩阵分解的推荐系统通过降维处理，可以大大降低数据的处理难度，并提高数据的处理速度。

3、可扩展性：基于矩阵分解的推荐系统可以动态地调整特征矩阵的大小，从而让推荐算法能够随着业务的发展和数据规模的变化而自适应。

然而，基于矩阵分解的推荐系统也存在以下几个弊端：1、初期建立阶段需要大量的历史数据：要让基于矩阵分解的推荐系统达到最优的推荐效果，需要使用大量的历史数据进行参考和训练。

这就对互联网企业的数据积累能力提出了较高的要求。

《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言在信息爆炸的时代，如何从海量的数据中为用户提供个性化的推荐成为了互联网服务的关键问题。

推荐算法作为一种有效的手段，已经被广泛应用于各大互联网平台。

其中，基于矩阵分解的推荐算法因其良好的可扩展性和准确性而备受关注。

然而，传统的矩阵分解推荐算法在处理数据稀疏性和噪声干扰时仍存在一定的问题。

因此，本文提出了一种基于矩阵分解的鲁棒推荐算法，以提高推荐系统的准确性和稳定性。

二、矩阵分解推荐算法概述矩阵分解是一种常用的推荐算法技术，其基本思想是将用户-项目评分矩阵分解为用户矩阵和项目矩阵，通过分析这两个矩阵来预测用户对项目的评分。

在传统的矩阵分解推荐算法中，通常采用随机梯度下降等方法进行优化，但这种方法在处理数据稀疏性和噪声干扰时效果并不理想。

三、鲁棒性问题的提出在现实应用中，推荐系统常常面临数据稀疏性和噪声干扰等问题。

数据稀疏性指的是用户对项目的评分数据不足，导致推荐算法难以准确预测用户的偏好；而噪声干扰则是指数据中存在的错误或异常值，这些因素都会影响推荐系统的准确性和稳定性。

因此，如何在处理这些问题的同时保持算法的鲁棒性成为了推荐算法研究的重要方向。

四、基于矩阵分解的鲁棒推荐算法针对上述问题，本文提出了一种基于矩阵分解的鲁棒推荐算法。

该算法在传统的矩阵分解基础上，引入了鲁棒性优化策略，包括数据预处理、正则化项和损失函数优化等方面。

首先，在数据预处理阶段，我们采用了一种基于奇异值分解的降维方法，对原始的用户-项目评分矩阵进行预处理，以降低数据稀疏性对算法的影响。

其次，在正则化项方面，我们引入了L1和L2正则化项，以防止过拟合和提高算法的稳定性。

最后，在损失函数优化方面，我们采用了鲁棒损失函数来处理噪声干扰问题。

五、实验与分析为了验证本文提出的鲁棒推荐算法的有效性，我们进行了大量的实验。

实验结果表明，与传统的矩阵分解推荐算法相比，本文提出的鲁棒推荐算法在处理数据稀疏性和噪声干扰方面具有更好的性能。

矩阵分解技术在推荐系统的应用与效果推荐系统作为一种重要的信息过滤工具，已经广泛应用于电子商务、社交媒体和在线内容平台等各个领域。

众所周知，推荐系统的核心任务是根据用户的历史行为和个人兴趣，为其提供个性化的推荐内容。

为了实现这一目标，矩阵分解技术被广泛应用于推荐系统中，以提高推荐的准确性和个性化程度。

一、矩阵分解技术简介矩阵分解技术是一种将原始推荐数据进行降维的方法，将大规模的用户-项目评分矩阵分解为两个低秩矩阵的乘积。

通过这种方式，可以将高维度的推荐数据转化为低维度的矩阵表示，从而减少数据的稀疏性和计算复杂度。

其中，用户矩阵和项目矩阵分别代表了用户和项目在低维空间中的特征向量。

二、基于矩阵分解的协同过滤推荐算法基于矩阵分解的协同过滤推荐算法通过分析用户和项目在低维度空间中的特征向量，找到相似的用户或项目，并将其作为推荐的依据。

算法的具体流程如下：1. 数据预处理：将用户-项目评分数据转化为评分矩阵，其中空缺的评分值可用0或其他特定值表示。

2. 矩阵分解：采用矩阵分解技术将评分矩阵分解为用户矩阵和项目矩阵。

3. 相似度计算：计算用户或项目之间的相似度，常用的方法有余弦相似度和皮尔逊相似度等。

4. 预测评分：根据相似度计算用户对项目的评分，选取与用户兴趣最相似的项目进行推荐。

5. 推荐结果生成：根据预测评分和推荐策略生成最终的推荐结果。

基于矩阵分解的协同过滤推荐算法具有以下优点：1. 隐性特征表示：通过矩阵分解，将用户和项目的隐性特征表示为低维度的向量，更能捕捉到用户兴趣的隐藏特征，提高了推荐的准确性。

2. 解决数据稀疏性：对于大规模的推荐数据，存在用户评分的稀疏性问题。

而矩阵分解可以通过填补缺失值，减少数据的稀疏性，更好地进行推荐。

3. 可解释性强：矩阵分解将用户和项目表示为低维度的特征向量，这些向量可以很好地解释用户和项目之间的关系，提高了推荐结果的可解释性。

三、矩阵分解技术在推荐系统中的应用1. 个性化推荐：基于矩阵分解的推荐算法可以根据用户的历史行为和兴趣，为其提供个性化的推荐内容，提高用户满意度和购买转化率。

摘要推荐系统是一种基于交互式评分数据的数据挖掘技术，通过深层次地挖掘显式评分数据和隐式反馈数据中具有潜在价值的信息，得到用户和物品的个性化偏好，从而预测用户对物品的喜好程度。

然而，推荐技术在实际应用过程中遇到了一些瓶颈问题，比如数据冷启动，数据稀疏性和动态增量数据。

众所周知，数据稀疏性是推荐系统最为常见的难题之一。

推荐技术是从显式评分数据中深度挖掘出用户的兴趣偏好并进行有效合理的推荐。

然而，由于评分数据的缺失，推荐模型不能最大化地学习用户的兴趣特征，导致评分预测值与真实值存在很大的偏差，从而降低了推荐准确率。

针对数据稀疏性问题，本文开展了一系列的相关研究工作，主要内容如下：1.为了缓解数据稀疏性，本文除了对显式评分数据进行数据挖掘以外，还为推荐模型引入了隐式反馈信息，如社交信息。

由于社交用户的兴趣共享性，模型能够深层次地学习用户的兴趣偏好。

本文利用矩阵分解将显式评分信息和社交信息分别投影到相应的低维特征空间，生成了用户的兴趣偏好和物品的个性化特征并为用户进行推荐。

2.针对模型的准确性，本文在显隐式信息的基础上提出了多种推荐策略，其中包括基于矩阵分解的推荐、基于用户的推荐和基于物品的推荐。

这三种推荐策略分别从用户和物品的潜在因子、用户的社交因子、物品的特征因子的角度进行推荐。

在对显隐式信息进行矩阵分解的同时，本文将这三种推荐策略融合成统一的预测评分机制，共同学习出用户的兴趣偏好和物品的特征。

这种方法有利于改善推荐模型的预测准确性。

3.为了充分地挖掘社交网络信息，本文基于用户行为的方法学习社交用户的个性化偏好并使用特征向量来表示。

接着，利用社交用户的兴趣差异性衡量用户之间的社交关系度，其代表了社交用户之间的兴趣相似性。

最后，将细粒度化的社交信息作为隐式信息嵌入到矩阵分解中，进一步地学习用户的个性化偏好，提高了预测准确性。

关键词：推荐系统，数据稀疏性，矩阵分解，社交网络，协同推荐AbstractThe recommendation system,which is a data mining technology based on interactive rating data,extracts personalized preferences of users and items by means of deeply mining the potential information from explicit and implicit feedback data and predicts the degree that a user is interested in an item.However,there exist some bottlenecks in practical applications of the recommendation technology,such as cold start of data,data sparsity and dynamic incremental data.As is well-known,data sparsity is one of the most common problems in the field of the recommendation system.The recommendation aims to mine the user’s preference for the item from the explicit information and makes reasonable recommendations for users. However,the model cannot learn the user’s interest to the maximum because of the lack of rating information,which leads to a large deviation between the prediction and the true and reduces the accuracy of the recommendation.For the problem of data sparsity,the thesis has carried out a series of the researches.The main work of the thesis is as follows:1.To alleviate data sparsity,the thesis introduces implicit feedback information for the recommendation model,such as social information,in addition to data mining of explicit data.Due to sharing the interest of social users,the model is able to deeply learn the user’s interest preferences.In the thesis,matrix factorization is used to project the explicit information and social information to the corresponding low-dimensional feature space respectively and make the user’s preferences and personalized feature of the item that are used to recommend items for users.2.For the accuracy of the model,the thesis proposes multiple recommendation strategies on the foundation of explicit and implicit information,including matrix factorization for recommendation,user-based recommendation and item-based recommendation.The recommendation strategies make recommendations from the perspective of potential factors of users and items,the user’s social factors and characteristic factors of items.While using matrix factorization to decompose explicit and implicit information,the thesis combines the recommendation strategies into a predictive scoring mechanism to jointly learn the user’s preferences and the characteristics of items. The method is helpful to improve the prediction accuracy of the recommendation model.3.So as to fully mine the social network,the thesis learns the personalized preferences of social users based on the user’s behavior and uses feature vectors to represent them.Then,the difference of the social user’s interests is used to measure the degree of social relationship between users,which represents the similarity of interests between social users.Finally,the fine-grained social information is embedded into the matrix factorization as implicit information to further learn the user’s personalized preferences and improve the accuracy of the model.Keywords:the recommendation system,data sparsity,matrix factorization,the social network,collaborative recommendation目录第1章绪论 (1)1.1研究背景及意义 (1)1.2国内外研究现状 (2)1.2.1基于模型的社交推荐 (3)1.2.2基于内容的社交推荐 (4)1.2.3基于协同过滤的社交推荐 (5)1.2.4基于信任度的社交推荐 (6)1.2.5基于深度学习的社交推荐 (6)1.3本文研究内容 (7)1.4论文章节安排 (8)第2章相关知识介绍 (10)2.1推荐系统 (10)2.1.1推荐系统原理 (10)2.1.2推荐系统的核心体系 (12)2.1.3推荐系统架构 (13)2.2推荐系统常用的推荐策略 (14)2.2.1基于内容的推荐 (14)2.2.2协同过滤推荐 (15)2.2.3基于模型的协同推荐 (18)2.3奇异值分解模型 (20)2.4本章小结 (22)第3章基于矩阵分解的多策略社交推荐 (23)3.1融合社交网络的奇异值分解模型 (23)3.2推荐策略的融合方法 (25)3.3基于矩阵分解的多策略社交推荐模型 (27)3.4基于矩阵分解的多策略社交推荐模型的应用 (33)3.4.1基于矩阵分解的多策略社交推荐算法 (34)3.4.2复杂度分析 (35)3.5案例分析 (36)3.5.1评估指标 (36)3.5.2实验对比模型 (37)3.5.3实验结果分析 (39)3.6本章小结 (40)第4章基于量化社交网络的多策略社交推荐 (41)4.1社交网络 (41)4.2社交网络的量化 (42)4.3基于量化社交网络的多策略社交推荐模型的应用 (45)4.3.1基于量化社交网络的多策略社交推荐算法 (47)4.3.2复杂度分析 (49)4.4案例分析 (49)4.4.1实验数据 (49)4.4.2社交网络量化处理 (50)4.4.3实验分析 (51)4.5本章小结 (53)第5章总结与展望 (54)5.1全文总结 (54)5.2展望 (55)参考文献 (56)致谢 (62)攻读硕士学位期间从事的科研工作及取得的成果 (63)第1章绪论1.1研究背景及意义近年来，随着人工智能的崛起，人类的生活方式发生了翻天覆地的变化，社会正在逐渐迈入大数据互联网时代。

基于矩阵分解的推荐系统算法设计推荐系统是指根据用户历史行为和偏好，为用户推荐个性化的物品或服务。

推荐系统的发展可以追溯到上个世纪90年代末期，当时Amazon推出了一个基于协同过滤的推荐系统，但是由于当时数据量较小，算法效果并不理想。

随着互联网的快速发展和社交网络的兴起，推荐系统也愈发重要和普及。

目前市面上的推荐系统种类繁多，包括基于内容的推荐、基于知识图谱的推荐、基于深度学习的推荐等等。

其中最为经典的算法便是基于矩阵分解的推荐算法。

在进行矩阵分解前，需要先对数据进行预处理，一般是将用户对物品的评分矩阵转化为用户对物品评分的稀疏矩阵。

稀疏矩阵即缺失值较多的矩阵，这是由于用户不会对所有物品都进行评分所导致的。

为了解决这个问题，我们可以采用矩阵分解算法来填补这些缺失值。

矩阵分解是指将一个矩阵分解为多个较小的矩阵的过程。

在推荐系统算法中，我们需要将用户对物品的评分矩阵分解为两个矩阵——一个用户矩阵和一个物品矩阵。

其中，用户矩阵记录了每个用户的偏好，物品矩阵记录了每个物品的属性。

在矩阵分解的过程中，我们需要通过最小化评分预测误差来优化用户矩阵和物品矩阵的值。

实际上，矩阵分解算法最重要的思想就是利用隐式反馈进行优化。

所谓隐式反馈，就是指用户没有对某些物品进行评分，但是我们仍然可以利用其他的间接信息来对这些物品进行评分。

换言之，当用户对某个物品没有评分时，我们便可以推断出这个物品并不是用户的最爱，或者用户并没有去过这个商家等等。

基于矩阵分解的推荐算法还有一个优势就是可以处理海量的数据。

当数据量非常大的时候，通常不可能将整个评分矩阵存储在内存中。

但是在矩阵分解算法中，我们只需要在一些随机样本上进行计算，这样就可以轻松地处理大量的数据了。

基于矩阵分解的推荐算法最初是由Simon Funk在2006年提出的。

此后，Po-Sen Huang等人在2012年提出了一种名为"Probabilistic Matrix Factorization"的改进算法。

《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言随着互联网技术的飞速发展，信息过载问题日益严重，如何从海量数据中为用户提供精准、个性化的推荐服务成为了一个重要的研究方向。

推荐系统作为解决这一问题的有效手段，已经在电商、社交、视频等领域得到了广泛应用。

在众多的推荐算法中，基于矩阵分解的推荐算法以其出色的准确性和稳定性成为了研究的热点。

然而，传统的矩阵分解算法在面对数据稀疏性、用户行为的不稳定性和数据噪声等问题时，推荐性能会受到一定影响。

因此，本文针对这些问题，提出了一种基于矩阵分解的鲁棒推荐算法。

二、相关背景与理论基础在介绍本文提出的鲁棒推荐算法之前，我们首先对相关背景和理论基础进行简要介绍。

1. 推荐系统概述：推荐系统通过分析用户的历史行为和偏好，以及物品之间的关联性，为用户提供个性化的推荐服务。

常见的推荐算法包括协同过滤、内容推荐和混合推荐等。

2. 矩阵分解技术：矩阵分解是推荐系统中的一种常用技术，通过将用户-物品评分矩阵分解为用户和物品的潜在特征矩阵，从而实现对用户和物品的隐式表达。

常见的矩阵分解算法包括奇异值分解（SVD）和梯度下降法等。

三、传统矩阵分解算法的局限性尽管传统的矩阵分解算法在推荐系统中取得了较好的效果，但在实际应用中仍存在一些局限性。

首先，当数据稀疏性较高时，算法的准确性会受到很大影响；其次，用户行为的不稳定性会导致推荐结果的不准确；最后，数据噪声的存在也会对算法的鲁棒性造成挑战。

四、基于矩阵分解的鲁棒推荐算法针对上述问题，本文提出了一种基于矩阵分解的鲁棒推荐算法。

该算法通过引入正则化项和优化损失函数，提高了算法的鲁棒性。

具体步骤如下：1. 数据预处理：对原始数据进行清洗、去噪和归一化处理，以提高数据的可用性和准确性。

2. 引入正则化项：在矩阵分解的过程中，引入正则化项（如L1范数或L2范数），以降低过拟合风险，提高算法的稳定性。

3. 优化损失函数：通过优化损失函数（如均方误差损失函数），使算法在面对数据稀疏性和噪声时具有更好的鲁棒性。

《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言在互联网大数据时代，推荐系统已经成为许多在线平台的核心组成部分，如电商平台、社交媒体、视频网站等。

推荐系统通过分析用户的历史行为和偏好，为用户提供个性化的内容推荐。

其中，基于矩阵分解的推荐算法以其准确性和效率成为一种广泛使用的推荐方法。

然而，随着数据复杂性和多样性的增加，传统的矩阵分解推荐算法面临着一系列挑战，如数据稀疏性、冷启动问题以及噪声干扰等。

因此，本文提出了一种基于矩阵分解的鲁棒推荐算法，旨在解决这些问题并提高推荐系统的性能。

二、矩阵分解推荐算法概述矩阵分解是一种常用的推荐算法，其基本思想是将用户-项目评分矩阵分解为用户矩阵和项目矩阵。

通过优化算法求解这两个矩阵，可以预测用户对项目的评分，从而进行推荐。

矩阵分解的优势在于能够处理大规模数据集，且具有良好的可扩展性。

然而，在实际应用中，由于数据稀疏性和噪声的存在，矩阵分解的准确性会受到一定影响。

三、鲁棒性在推荐算法中的重要性鲁棒性是指算法在面对噪声、异常值、数据缺失等干扰时仍能保持良好性能的特性。

在推荐系统中，鲁棒性尤为重要。

由于用户行为和数据本身的不确定性，推荐系统中常常存在各种噪声和异常值。

这些因素会干扰推荐算法的准确性，导致推荐结果偏离用户真实需求。

因此，提高推荐算法的鲁棒性对于提高推荐系统的性能至关重要。

四、基于矩阵分解的鲁棒推荐算法针对传统矩阵分解推荐算法的不足，本文提出了一种基于矩阵分解的鲁棒推荐算法。

该算法在矩阵分解的基础上，引入了鲁棒性优化策略。

具体而言，该算法通过引入正则化项和损失函数中的鲁棒项来提高算法的鲁棒性。

正则化项可以约束模型的复杂度，防止过拟合；而鲁棒项则可以降低噪声和异常值对模型的影响。

此外，该算法还采用了迭代优化算法来求解优化问题，进一步提高了解的准确性和稳定性。

五、实验与分析为了验证本文提出的鲁棒推荐算法的有效性，我们进行了大量实验。

实验数据集包括电影评分数据集、电商商品购买数据集等。

《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言随着互联网技术的飞速发展，信息过载问题日益严重，推荐系统应运而生，成为解决这一问题的有效手段。

在众多推荐算法中，基于矩阵分解的推荐算法因其准确性和有效性受到了广泛关注。

然而，传统的矩阵分解推荐算法在处理数据稀疏性和用户偏好变化等实际问题时，往往表现出一定的脆弱性。

因此，本文提出了一种基于矩阵分解的鲁棒推荐算法，以提高推荐系统的稳定性和准确性。

二、相关研究概述矩阵分解是推荐系统中的一种常用技术，通过分析用户-项目评分矩阵，提取出用户的潜在特征和项目的潜在特征，从而进行推荐。

近年来，许多研究者对矩阵分解技术进行了深入研究，提出了许多改进的算法。

然而，这些算法在处理数据稀疏性和用户偏好变化等问题时，仍存在一定的局限性。

因此，研究鲁棒的矩阵分解推荐算法具有重要的现实意义。

三、基于矩阵分解的鲁棒推荐算法（一）算法原理本文提出的基于矩阵分解的鲁棒推荐算法，主要思路是在传统的矩阵分解基础上，引入鲁棒性优化方法。

具体来说，通过在损失函数中加入正则化项和约束条件，使得算法在处理数据稀疏性和用户偏好变化等问题时，能够更好地保持稳定性。

同时，通过优化算法的迭代过程，提高算法的收敛速度和准确性。

（二）算法实现1. 数据预处理：对用户-项目评分矩阵进行预处理，包括数据清洗、缺失值填充等操作，以提高数据的完整性和质量。

2. 矩阵分解：采用传统的矩阵分解技术，对用户-项目评分矩阵进行分解，提取出用户的潜在特征和项目的潜在特征。

3. 鲁棒性优化：在损失函数中加入正则化项和约束条件，对算法进行鲁棒性优化。

具体来说，通过调整正则化参数和约束条件，使得算法在处理数据稀疏性和用户偏好变化等问题时，能够更好地保持稳定性。

4. 迭代优化：采用优化算法对损失函数进行迭代优化，直至达到收敛。

（三）算法优势本文提出的基于矩阵分解的鲁棒推荐算法具有以下优势：1. 鲁棒性强：通过引入鲁棒性优化方法，使得算法在处理数据稀疏性和用户偏好变化等问题时，能够更好地保持稳定性。