电力系统低频功率振荡阻尼转矩分析理论与方法(杜文娟,王海风)思维导图

基于PSAT的电力系统低频振荡分析论文定稿

基于PSAT的电力系统低频振荡分析论文定稿LT目录摘要.......................................... 错误!未定义书签。

ABSTRACT....................................... 错误!未定义书签。

第1章绪论. (1)1.1 电力系统低频振荡综述及研究意义 (1)1.1.1 电力系统低频振荡综述 (1)1.1.2 电力系统低频振荡研究意义 (1)1.2 电力系统分析工具PSAT的简要介绍 (2)1.3 本文主要工作 (2)第2章电力系统低频振荡概述 (4)2.1 低频振荡的研究背景 (4)2.2 低频振荡的产生原因 (4)2.3 低频振荡的定义及分类 (4)2.3.1 低频振荡的定义 (4)2.3.2 低频振荡的分类 (5)2.4 低频振荡的机理 (5)2.4.1 基于阻尼转矩的原理 (5)2.4.2 基于强迫振荡的原理 (5)2.4.3 基于强谐振的原理 (6)2.4.4 分岔理论 (6)2.4.5 混沌现象理论 (6)2.5 低频振荡的分析方法 (6)2.5.1特征分析法 (7)2.5.2 时域仿真法 (9)2.5.3 基于正规形理论的方法 (9)2.5.4 基于量测的方法 (10)2.6 低频振荡的抑制措施 (10)2.6.1 一次系统策略 (10)2.6.2 二次系统策略 (10)2.7 本章小结 (12)第3章 PSAT在电力系统分析中的应用 (13)3.1 Matlab中PSAT的概述 (13)3.2 PSAT中主要功能模块介绍 (13)3.2.1 系统模型库及主界面 (13)3.2.2 潮流计算 (14)3.2.3 最优潮流 (14)3.2.4 小信号分析 (15)3.2.5 时域仿真分析 (15)3.3 本章小结 (15)第4章基于PSAT的电力系统低频振荡分析 (16)4.1 模型的建立 (16)4.2 运用PSAT计算潮流解 (19)4.3 计算特征值以及各机组参与因子 (20)4.4 励磁装置对电力系统低频振荡的影响分析 (21)4.4.1 励磁系统对低频振荡影响原理 (21)4.4.2 PSAT对励磁分析结果 (22)4.5 加装PSS对电力系统低频振荡的影响 (22)4.5.1 PSS抑制低频振荡的原理 (22)4.5.2 PSAT对加装PSS分析结果 (23)4.6 本章小结 (24)第5章结论与展望 (25)参考文献 (26)附录 (29)致谢 (55)第1章绪论1.1 电力系统低频振荡综述及研究意义1.1.1 电力系统低频振荡综述电力系统低频振荡的问题是随着电网互联而产生的。

电力系统低频振荡的影响因素研究

电力系统低频振荡的影响因素研究摘要：随着电网的扩大和市场经济的发展，电力行业变得越来越趋于极限，必须充分理解这个问题。

本文阐述了低频振荡在电力系统中的工作原理，并阐述了一般分析方法。

从不同方法的比较分析出发，分析了研究的可能方向。

本文阐述了该课题的基本思路、实践方法、研究领域和难点，展望了未来。

关键词：低频振荡；特征值分析；电力系统阻尼发电厂同步发电机在电力系统初期联网，阻尼绕组尼引起足够的阻尼，抑制振动的发展。

在这一点上，很少出现低频振荡情况。

随着电网规模的增大，还应生产大型电力联系，以改善电网低频振荡问题。

如果不及时抑制，可能导致停电，可能危及系统的稳定和安全运行，甚至可能产生严重后果。

一、慨况由于电力系统的负阻尼，低频振荡通常发生在弱联系、远距离、重负荷的线路中，而低频振荡则更可能发生在高性能励磁系统系统中。

没有阻尼，甚至没有对应于发电机相对摇摆的负阻尼。

功率波动在输电线路中出现，功率波动频率由系统缺乏阻尼或系统负阻尼，系统在0.1-2.0hz范围内增加，通常称为低频振荡(也称为功率和机电振荡)。

一般来说，电力系统的振荡模式可以分为地区和区域，当系统中的低振振荡率非常低(0.1-0.5hz)时，通常将其视为互联系统之间的区域间振荡。

如果振荡大于1Hz，则视为局部或区域振荡。

在振荡模式区域中，振荡频率取决于机组数量。

因此，将阻尼添加到少数强相关机组上将大大增加振动阻尼。

区域振荡模式的振荡频率较低，需要更多机组。

因此，只有关键机组的阻尼才能增加振荡模式下的阻尼。

区域振荡模式下低频振动的抑制显然比区域振荡模式下低频振动的抑制更复杂和困难。

因此，在系统运行期间，它们更容易受到区域振荡模式下低频的影响。

二、低频振荡的振荡机理1.负阻尼。

1969年F.De Mello使用阻尼转矩的概念来研究无噪声单机系统中低频振荡的机理。

应注意的是，由于励磁系统的惯性，随着励磁调节器增益的增加，与转子机械振动相对应的实际根值随着负值逐渐增加。

电力系统低频振荡机理及其控制措施研究

随着互联电力系统规模日益扩大，电力系统的稳定性问题越来越突出。在大区域电网的互联过程中，系统出现了超低频ｆ１ｚ０３ｚ荡现象。低频振荡现象常出现在长距离、０Ｈ一．Ｈ）．￣－重负荷输电线路中。由于互联引发的区域低频振荡问题，已成为威胁互联电网安全稳定运行、制约电网传输能力的重要因素之一。为此，有必要对电力系统低频振荡产生的原因及抑制低频振荡的措施等方面进行分析。
扰动时，扰动被逐渐放大，引起功率的低频振荡。重负荷线路、
现代快速高顶值倍数的励磁系统是造成系统出现负阻尼的主
要原因。（１）
单机无穷大系统中发电机转子运动方程为：
ＴＪ：Ｄ
对于单机无穷大系统，电机采用二阶模型，发转子运动方
程为：
将式（在工作点附近线性化，１）则有：
Ｔ】＋Ｄ＋０ＫＡ８＝
式中：：Ｋ
Ａ＝
。８，。其特征方程为：
（）３
ｌ一ｏＤ∞ Ｔｃ △ Ｊｓ８ｌ ∞
令Ｋ＝
）Ｌ
Ｔ２Ｄ＋＝Ｊ＋Ｋ０
可求得其根为：
＝
ｃｓ其特征根为：０ｏ８，
： ± ，＜ＴＫＤ４ｊ（）８
（）
（５）
二Ｉ：
．
：（ ∈ ；一 ±、＝）４（ ∞＝－ｏｊ
如果系统阻尼为负，Ｄ００＜，时显然为增幅振荡；则＞，【０此
式、一然荡率阻Ｄ零的荡尼形式振荡的基本形式。但是当Ａ＃０时，中Ｉ鲁自振频，尼为时振Ｉ＝／即Ｐ可以得到：

电磁振荡与电磁波(思维导图)

电磁振荡与电磁波LC振荡电路描述频率周期计算公式波长电磁波谱波速真空为光速电路图振荡电路充电电路阻尼振荡振幅逐渐减小解释动力学电容交替充放电电感自感周期性变化能量电场能磁场能转化电场能量电压电荷量磁场能量电流磁感应强度能量损耗焦耳热理想无电阻电磁波辐射理想时忽略电磁波机理麦克斯韦电磁场理论变化的电场产生磁场位移电流变化的磁场产生电场涡旋电场场是物质存在的一种形式粒子与场两种形式电磁波电场和磁场相互激发并非电场和磁场的合称特点横波现象偏振原理E⊥B⊥v波现象衍射干涉反射折射多普勒效应描述真空中波速为c频率周期实验赫兹发现电磁波发射振子接收谐振器与机械波的比较相同点各物理量周期性变化不同点传播不依赖介质波速与频率和介质种类有关应用无线电波发射与接收发射载波(货车)高振荡频率开放电路：地线天线调制(装车)调频FM调幅AM转换其他信号转换为电信号接收调谐(停车)电谐振解调(卸货)调制的逆过程检波(AMJ解调)原理电磁感应天线转换电信号转为其他信号电磁波谱特点和应用无线电波自由电子振荡产生长波中波中短波短波微波X射线原子内层电子跃迁γ射线原子核跃迁红外线可见光紫外线原子外层电子跃迁四大序列以产生机理分类，频率有所重叠序列内以波长分段，不存在重叠。

电力系统低频振荡分析方法探讨

关键词：电力系统；低频振荡；分析方法；Prony 算法；HHT；经验模态分解；在线辨识。
I
华中科技大学硕士学位论文
Abstract
Research on the analysis method for low frequency oscillation of power system is the basis to study the mechanism for low frequency oscillations ．With modern power networks complicated gradually，dynamic non-linear theory grown rapidly，and new equipment and technologies used widespread，the conventional analysis methods have many shortcomings． Therefore ， it is necessary to study new methods of vibration analysis in order to more effectively reveal the mechanism of oscillation of the interconnected system． This paper from the perspective of the analysis explored the issue about low frequency oscillations ． Firstly， system for low frequency oscillations of the main analytical methods are summarized， and pointed out the advantages and disadvantages of various methods and the scope of application．Secondly，Prony algorithm is Proposed in the analysis of low-frequency oscillations ， including the application of its basic principles，common indicators and setting parameters in detail，point ed out that Prony algorithm for low- frequency oscillations in power system analysis have the limitations of non- linear systems research．Thirdly， the Hilbert－ Huang （HHT） algorithm for low- frequency oscillations in nonlinear is introduced． The fault transient information from HHT and extract parameters of models were analyzed the dynamics of low- frequency oscillations and the oscillation characteristics，also between the various models with nonlinear interaction． On this basis ， then based on empirical mode decomposition （ EMD） of the Prony analysis method of low-frequency oscillations is developed． The EMD used as a pre-processing data method， it means that the Prony algorithm could overcome not only difficulty to deal with the shortcomings of non-stationary signals，as well as the problem difficult to select wavelet of small and medium-sized wavelet algorithm， but also to enable them to effectively deal with

基于Prony法的电力系统低频振荡分析与控制

硕士学位论文论文题目基于Prony法的电力系统低频振荡分析与控制作者姓名刘国平指导教师徐政教授学科(专业) 电力系统及其自动化所在学院电气工程学院提交日期二○○四年二月申请浙江大学工学硕士学位论文基于Prony法的电力系统低频振荡分析与控制硕士研究生：刘国平导师：徐政教授申请学位级别：工学硕士学科、专业：电气工程、电力系统及其自动化提交论文日期： 2004 年 2 月 25 日答辩日期：年月日授予学位单位：浙江大学授予学位日期：年月日Analysis and Control of Low-Frequency Electromechanical Oscillations in Power Systems Based on Prony’s MethodbyLiu GuopingSupervised by：Prof. Xu ZhengCollege of Electrical EngineeringZhejiang University, Hangzhou, P. R. ChinaFebruary, 2004浙江大学硕士学位论文摘要基于Prony法的电力系统低频振荡分析与控制摘要本文以基于Prony法的电力系统低频振荡分析与控制为研究内容，主要做了以下工作：1.分析了低频振荡的分类，危害，成因以及典型故障事例，比较了多种能够抑制低频振荡的措施。

简介了本文工作所需要的几种工具软件－PSS/E，Matlab 和SSAT。

2.通过分析特征值法存在的一些不足，引出Prony分析方法。

对其基本原理，常用指标，参数选择进行了详细阐述。

测试了时间长度，采样频率以及Prony 模型阶数对分析结果的影响。

并分析了Prony法推广到多输出信号的情况，阐明了非线性对Prony分析法的影响。

最后，把Prony方法应用到了传递函数的辨识中，为后面阻尼低频振荡的控制器设计打下基础。

3.分析了阻尼低频振荡的控制器选择，主要阐明了PSS，TCSC和直流小信号调制的应用场合。

新能源并网系统宽频振荡分析与抑制

新能源并网系统宽频振荡分析与抑制
读书笔记
01 思维导图
03 精彩摘录 05 目录分析
目录
02 内容摘要 04 阅读感受 06 作者简介
思维导图
本书关键字分析思维导图
系统
提出
系统
宽频
措施
并网
影响
并网
振荡
振荡新能源
实验
分析
抑制
研究
分析
有效
方法
一系列
内容摘要
内容摘要
本书主要对新能源并网系统宽频振荡的问题进行了深入的分析与探讨，提出了一系列有效的抑制方法。本书首先介绍了新能源并网系统宽频振荡的概念和影响，然后详细阐述了宽频振荡的成因和抑制措施。在新能源并网系统中，宽频振荡是一种常见的动态行为，它对系统的稳定性和电能质量产生重要影响。本书结合前人研究成果，综述了新能源并网系统宽频振荡的相关研究现状和不足，以便更好地提出分析和抑制方法。在此基础上，本书采用理论分析和实验研究相结合的方式，对新能源并网系统宽频振荡进行了深入的分析，并提出了一系列有效的抑制措施。本书通过实验验证了所提出的分析和抑制方法的可行性和有效性。实验结果表明，本书所提出的方法可以有效地抑制新能源并网系统宽频振荡的产生，提高系统的稳定性，减少振荡对电能质量的影响。
阅读感受
我还想给这本书打个满分。我认为这本书在内容丰富性、理论深度和实用性方面都做得非常出色。书中的科学知识解释得深入浅出，使得读者可以更好地理解这些复杂的概念。作者对问题的分析也非常透彻，使得读者可以更加全面地了解这个问题的复杂性以及解决方法。这是一本非常值得一读的书，我毫不犹豫地给它打满分。在阅读这本书的过程中，我深深地感受到了科学的魅力和挑战。通过作者的分析和解释，我可以更加深入地理解新能源并网系统宽频振荡的问题，也对我自身的知识和理解有了很大的提升。这本书不仅提供了我需要的科学知识，也激发了我对科学的热爱和追求。我相信这本书也会对其他读者产生类似的影响，让更多的人对这个领域有更深入的理解和研究。

电力系统低频振荡潘学萍精品文档

Yorino N, Sasaki H, Tamura Y, et al. A Generalized Analysis Method of Auto-Parametric Resonance in Power Systems. IEEE Trans on Power Systems, 1989, 4 (3): 1057~1064
2000-10-9
潘学萍，2011年9月30日
xuy
泰勒展开
忽略高阶项
U 可逆
x f (x)
xAxH.O. .T
x Ax
y u1AuΛy
y it u T ix 0 e it y i0 e it
x i t u i 1 y 1 0 e 1 t u i 2 y 2 0 e 2 t u iy n 0 e n t
2000-10-9
潘学萍，2011年9月30日
• 正规形方法
泰勒展开 x f (x)
x

Ax
1 2
xTH 1x xTHnx

H.O.T.
忽略2阶及以上高阶项
x

Ax

1 2

xT
H1x

xT Hnx
xuy U 可逆
y Λy F 2Y
yzh2(z)
忽略3阶及
z Λ zO 3
z Λz
当不存在2
以上高阶项
次谐振时
2000-10-9
潘学萍，2011年9月30日
zj jzj
yj t
zj0ejt
n

n
h2k j z lk0zl0ek lt
k 1l 1
x itnu iz jj0 e jtnu i j n nh 2 k jz lk0 zl0 e k lt

电力系统低频振荡及电力系统稳定器

sin 0
XL
Me K1 K2Eq'
K1

Xq Xd

X
' d
Xe
Iq0U sin0
U cos0
Xq Xe
EQ0
UdG Xq Iq
UdG Ucos0 XL Iq
Iq

U
cos 0
X q X L
K2

Xq
X
' d
电力系统低频振荡及电力系统稳定器
North China Electric Power University
学习目录
一、电力系统低频振荡的基本概念
二、研究低频振荡的同步发电机动态模型
三、计及励磁系统的同步发电机稳定性分析
四、电力系统稳定器PSS
2019-5-31 North China Electric Power University
运行点线性化
Eq'

Eq
(Xd

X
' d
)

I
d
EQ

Eq'
(Xq

X
' d
)

I
d
同步发电机相量图
UqG Eq X d Id
UqG Eq X d Id
运行点线性化
UdG X q Iq
运行点线性化
UdG X q Iq
2019-5-31 North China Electric Power University page4

1 d2TE2Q
K5

1 K6

电路理论思维导图-简单高清脑图_知犀

电阻电路的等效变换
串并联
电阻的串并联电源的串并联
串联电阻相加，并联电导相加
对称电路
对称面通过端口的情况对称面垂直端口的情况
垂直通过对称面的支路的电流为零，可以断开该支路，对称结点是等位点对，可以短接这些等位点
当电路存在垂直于端口的对称面时，对称面上的各结点为等位点，可以短接这些结点
电桥电路
电桥电路图平衡条件
R₁R₃=R₂R₄对臂电阻之积相等 R₁/R₄=R₂/R₃邻臂之比相等
星三角变换
三角to星星to三角
电源变换
戴维南支路（独立电压源＋线性电阻）与诺顿支路互换（独立电流源＋线性电阻）
变换注意事项
戴维南支路与诺顿支路的电阻相等电压源、电流源、电阻三者的值满足类似于欧姆定律的关系电压源与电流源的方向类似于非关联参考方向
理想运放：虚短虚断
运算放大器
叠加定理替代定理戴维南定理和诺顿定理最大功率传输定理特勒根定理互易定理
电路定理
网孔法结点法回路方程
电路分析方程
电路理论
基本定律
基尔霍夫定律
基尔霍夫电流定律KCL 基尔霍夫电压定律KVL
KCL独立性 KVL独立性
有n个结点、b条支路的电路，可以列写n-1个独立的KCL方程电路中任意n-1个结点的KCL方程就是n-1个独立的KCL方程广义结节的KCL方程是被闭合面包围的结点的KCL方程之代数和有n个结点、b条支路的电路，可以列写b-n+1个独立的KVL方程平面电路所有网孔的KVL方程就是b-n+1个独立KVL方程回路的KVL方程是被回路所包含的网孔的KVL方程之代数和
受控电源的电源变换类似，不过要注意控制量转移

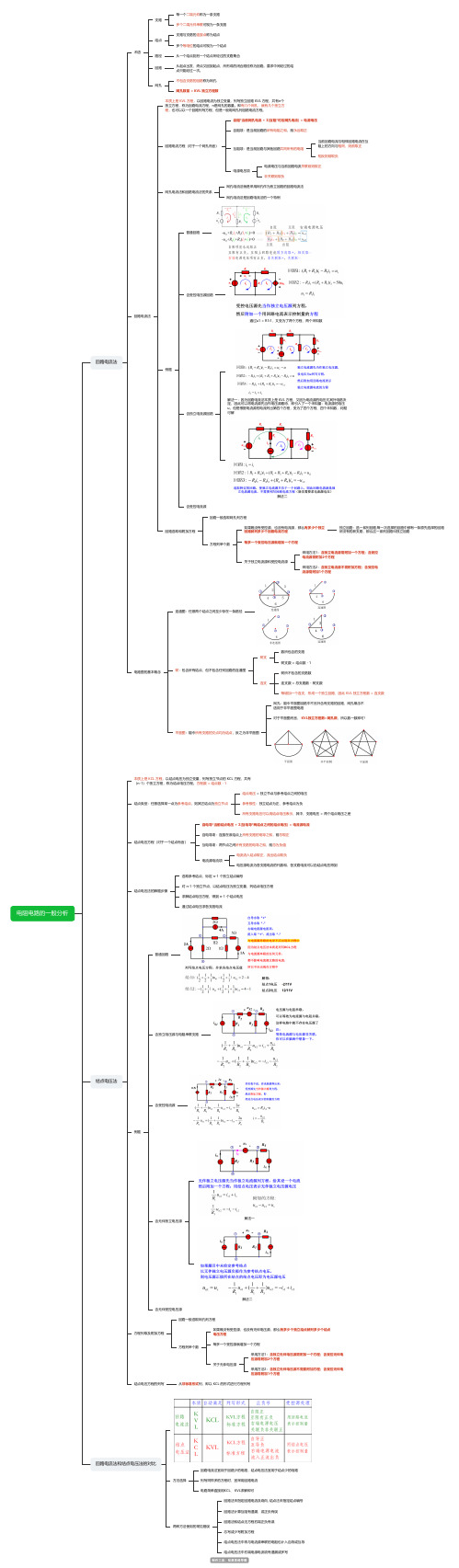
电阻电路的一般分析思维导图

电阻电路的一般分析回路电流法术语支路每一个二端元件称为一条支路多个二端元件串联可视为一条支路结点支路与支路的连接点称为结点多个等电位的结点可视为一个结点路径从一个结点到另一个结点所经过的支路集合回路从起点出发，终点又回到起点，所形成的闭合路径称为回路。

要求中间经过的结点只能经过一次。

网孔不包含支路的回路称为网孔网孔数量 = KVL 独立方程数回路电流法本质上是 KVL 方程，以回路电流为独立变量，列写独立回路 KVL 方程，共有n个独立方程，称为回路电流方程，n是网孔的数量。

即有几个网孔，就有几个独立方程，也可以以一个回路列写方程，但是一般用网孔列回路电流方程。

回路电流方程（对于一个网孔而言）自阻*当前网孔电流 + Σ(互阻*对应网孔电流) = 电源电压自阻项：是当前回路的所有电阻之和，前永远取正互阻项：是当前回路与其他回路共同所有的电阻当前回路电流与相邻回路电流在互阻上的方向与相同，则前取正相反则前取负电源电压项电源电压与当前回路电流关联前则取正非关联则取负网孔电流法和回路电流法的关系网孔电流法就是采用网孔作为独立回路的回路电流法网孔电流法是回路电流法的一个特例例题普通回路含受控电压源回路通过u1 = R1i1，又变为了两个方程、两个未知数含独立电流源回路解法一：因为回路电流法本质上是 KVL 方程，又因为电流源的电压尤其外电路决定，因此可以将电流源先当作电压源看待，即引入了一个未知量：电流源的电压u。

但是根据电流源的电流列出第四个方程，变为了四个方程、四个未知数，问题可解解法二含受控电流源回路选取和附加方程回路一般选取网孔列方程方程列举个数如果既没有受控源，也没有电流源，那么有多少个独立回路就列多少个回路电流方程独立回路：选一系列回路,每一次选择的回路中都有一条原先选择的回路所没有的新支路，那么这一系列回路叫独立回路每多一个受控电压源就增加一个方程关于独立电流源和受控电流源采用方法1：含独立电流源需附加一个方程；含受控电流源需附加2个方程采用方法2：含独立电流源不需附加方程；含受控电流源需附加1个方程电路图的基本概念连通图：任意两个结点之间至少存在一条路径树：包含所有结点，但不包含任何回路的连通图树支数所包含的支路树支数 = 结点数 - 1连支树所不包含的支路数连支数 = 总支路数 - 树支数每增加一个连支，形成一个独立回路，因此 KVL 独立方程数 = 连支数平面图：能令所有支路的交点均为结点，反之为非平面图网孔：能令平面图回路中不另外含有支路的回路，网孔概念不适用于非平面图电路对于平面图而言，KVL独立方程数=网孔数，所以数一数即可！结点电压法本质上是 KCL 方程，以结点电压为独立变量，列写独立节点的 KCL 方程，共有（n-1）个独立方程，称为结点电压方程。

电力系统低频振荡分析方法综述

电力系统低频振荡分析方法综述作者：乔真徐振宇来源：《中国科技博览》2013年第33期摘要：本文介绍了低频振荡的相关概念及产生机理，总结了低频振荡分析方法的相关理论，归纳和对比了现有算法，并对各自的优缺点进行了总结。

关键词：低频振荡；分析方法；低频振荡机理中图分类号：X830.21 引言低频振荡是由发电机转子间的阻尼不足而引起的，属于小扰动稳定范围，其振荡频率一般在0.1～2.5Hz之间。

按低频振荡涉及的范围来分，大致分为局部振荡模式（Local modals）和区域振荡模式（Inter-area modals）两类。

局部振荡模式是电气距离较近的厂站、机组之间的振荡，振荡频率一般在0.7～2.5Hz之间，局限于区域内，易于消除。

区域振荡模式是电气距离较大的两部分机群的振荡，在互联系统中，耦合的两个或多个发电机群间如果联系较薄弱，就会经常发生这种振荡。

由于两部分机群间电气距离较大，其振荡频率一般在0.1～0.7Hz之间。

2 低频振荡的产生机理低频振荡的产生机理主要有3方面：（1）由于调节器的作用，产生附加的负阻尼且系统的特征根发生变化，引起增幅振荡。

（2）由于系统的非线性，在某些特定的运行范围内稳定结构发生变化，导致低频振荡。

（3）当系统的扰动信号和系统的自然频率存在某种特定关系时会导致谐振，当谐振频率较低时表现为低频振荡。

3 低频振荡的分析方法现代电力系统是一个阶数高、非线性强、控制系统难于协调、参数难于确定的动态系统，对电力系统的分析极其困难。

一般认为低频振荡属于功角稳定中小扰动稳定性问题的范畴，进行电力系统低频振荡的分析，主要的方法有非线性理论分析法和线性理论分析法。

3.1线性理论分析法线性理论分析法也称为特征值分析法，其实质为李雅普诺夫线性化方法，是研究低频振荡的经典方法。

线性理论分析法在工作点附近将系统进行线性化，列出线性化之后的系统小扰动状态方程矩阵，求取其特征值来判断系统是否稳定。

特征值的符号反映振荡的收敛与发散，实部可以反映系统的阻尼情况，特征值的大小反映发散或收敛的速度，系统所有特征值的实部不全为负数时系统是不稳定的，特征值的虚部反映振荡角频率的大小。

电力系统低频振荡分析与抑制综述_修改版_3

[17]
难以实现, 同时对于截断误差对分析结果有多大的影响, 仍缺乏严格的数学证明[23]。 1.1.4 基于分岔理论的分析方法电力系统低频振荡问题可用局部分叉理论中的即电力系统低频振荡的稳 Hopf 分叉进行分析[2425]，定极限是与系统的微分方程发生 Hopf 分叉的情况相关的。与传统方法不同，该类方法用局部流形对平衡点附近的特性进行分析，它可以将电力系统中的静、动态稳定问题统一研究。文献[26]以单机无穷大系统为研究对象，得出当发电机励磁参数变化时，系统出现的都是亚临界分岔，解决了以往利用传统分析方法无法解释的一些问题。文献[27]利用复变量构建的一维中心子空间和数值法求出了曲率系数，解决了以往算法只能用于简单系统而不适于多机电力系统的问题，实现了对多机电力系统非线性振荡的分析。 1.2 基于系统实测信号的分析方法 1.2.1 滤波器类方法低频振荡的在线监测和离线分析都要解决的关键问题是振荡模式的辨识，即根据实测数据计算频率、阻尼系数等。文献[28]提出了一种基于滤波器组的低频振荡监测系统，实测数据经滤波器处理后如果幅值越限超过一定的时间就发出振荡告警信号；文献[29]考虑到实际电力系统中负荷波动频率远远大于系统的振荡频率，提出了将负荷的随机波动视为对电力系统的白噪声输入，采用求解 Wiener-Hopf 线性预测方程组的方法来求取振荡信号的频率及阻尼信息，分析结果表明该方法可以用于实时估计电力系统低频振荡的模式信息。 1.2.2 回归分析类方法自回归模型（auto regressive，AR）和滑动平均自回归模型（ auto regressive moving-average ， ARMA）是常用的参数谱估计方法。文献[30]和[31]建立了实测数据的 AR 模型，分别利用奇异值分解和自适应卡尔曼滤波器分析实测数据，估计模型参数，通过极点计算系统特征值和振荡参数；文献[32]建立了实测数据的 ARMA 模型，利用最小二乘方法从实测数据中估计振荡参数；文献 [33] 在文献 [32] 的基础上，建立了实测数据的 ARMAX 模型，采用 R3LS （ robust regularized recursive least-square）算法对本模型进行求解，测

电力系统振荡PPT课件

振荡的处理方式？
由解裂装置有计划的进行解裂，以终止振荡。
放任继电保护装置在震荡中自由动作。该方式是西方一些国家长期的习惯做法。只要是机电保护装置本身没
有问题，在系统震荡中动作导致大面积停电仍然被认为是正确的。该观点的主要根源是这些国家的系统联结较强，但这些观点直接导致了美国几次大停电
调度处理。保持系统的稳定性，留待调度处理，我国处理振荡的成功运行经验。
49.1Hz，负荷损失近380万千瓦。
一、电力系统振荡
振荡的起因？
稳定破坏：静态稳定破坏、暂态稳定破坏。暂态稳定破坏是由短路引起的，短路故障破坏了系统功率的平衡，此时若故障切除慢就可能导致系统失去稳定。
大机组失磁或线路传输功率超过稳定极限等原因造成的稳定破坏为静态稳定破坏。
一、电力系统振荡
电弧压降，当弧电流超过100A时，压降与流过的电流无关。压降一般小于额定相间电压的6%。
二、振荡闭锁与开放
电弧压降与余弦电压的关系
在单侧电源故障，忽略线路阻抗的电阻分量时， . Ucos Uarc
在双侧电源下，电弧中有对侧电源的助增电流，但弧光电压不变。如果线路阻抗的相角较小，例如为75度，则余弦电压将增大到0.26p.u.。为了获得弧光压降，采取补偿的方法。
小结
上述振荡过程中短路故障的识别方法，已经有成熟的运行经验。
另外还有利用测量阻抗变化率、余弦电压变化率及具有浮动门槛的电流突变量的识别方法。
感谢大家
Ucos(90L)U . arc
二、振荡闭锁与开放
振荡中心电压Uz
I
振荡时Ucos等于振荡中心的电压
P
φ
M ΣZ
Q
Uφ M
E M

关于低频振荡分析方法的评述

关于低频振荡分析方法的评述薛禹胜1,2,郝思鹏2,1,刘俊勇3,Zhaoyang DONG 4,Gerard LEDWICH 5(1.国网电力科学研究院/南京南瑞集团公司,江苏省南京市210003;2.东南大学电气工程学院,江苏省南京市210096;3.四川大学电气信息学院,四川省成都市610065;4.U niver sity o f Q ueensland,Austr alia;5.Q ueensland U niv ersity of T echno lo gy ,A ust ralia)摘要:为更好地梳理概念,将低频振荡分析方法分为两大类,即针对系统模型平衡点的特征根方法以及沿着系统受扰轨迹的模式提取方法。

平衡点特征根方法可进一步按采用的系统模型分为确定性的线性化模型、确定性的非线性模型和概率模型。

这类方法与具体扰动无关,但只能反映系统在该平衡点附近的动态行为,故不适用于包含强非线性、变系数、相继故障或有离散控制的系统。

受扰轨迹模式分析方法则从特定扰动下的时间响应曲线中提取振荡信息的时间序列,包括系统模型未知情况下(如实测轨迹)的信号处理法和系统模型已知情况下(如仿真轨迹)的分时段定常线性化法。

在评述各种方法的基础上,提出改进的思路及有望突破的研究方向。

关键词:低频振荡;平衡点特征根;轨迹特征根时间序列;信号处理;保稳降维线性变换;分时段定常线性化中图分类号:TM 712收稿日期:2008 11 05。

国家自然科学基金重大项目(50595413);国家电网公司科技项目(SGK J[2007]98&187)。

0 引言国内外电网多次出现的低频振荡严重危及了电力系统的稳定运行,并引起电力企业和学术界的高度关注[1 2]。

低频振荡是指发电机组转子动能与电网势能之间持久的机电振荡,在机械上表现为互补机群转子相对角的长期摆动,在电气上则表现为该互补机群定子之间的功率振荡。

其振荡频率主要取决于2个机群各自总转动惯量(分别记为M s 和M a )倒数之和的倒数,即M =(M -1s +M -1a )-1。