广西贵港市2017届中考数学总复习 第五单元 四边形 第20讲 平行四边形与多边形试题

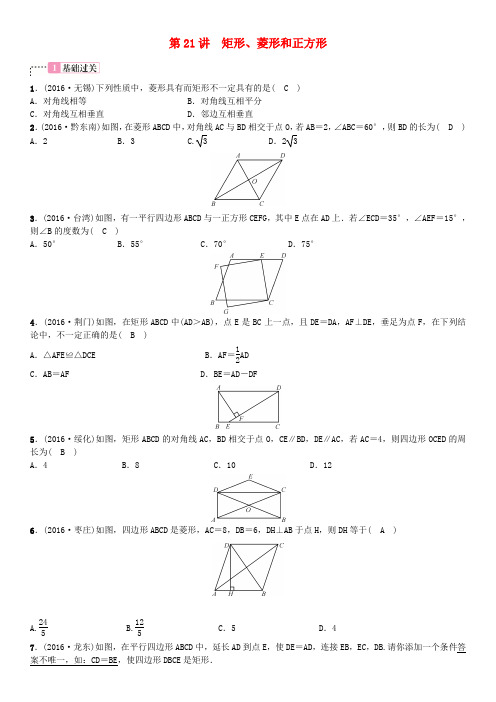
第21讲 矩形、菱形和正方形1．(2016·无锡)下列性质中，菱形具有而矩形不一定具有的是( C ) A ．对角线相等 B ．对角线互相平分 C ．对角线互相垂直 D ．邻边互相垂直 2．(2016·黔东南)如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，若AB ＝2，∠ABC ＝60°，则BD 的长为( D ) A ．2 B ．3 C. 3 D ．2 33．(2016·台湾)如图，有一平行四边形ABCD 与一正方形CEFG ，其中E 点在AD 上．若∠ECD＝35°，∠AEF ＝15°，则∠B 的度数为( C )A ．50°B ．55°C ．70°D ．75°4．(2016·荆门)如图，在矩形ABCD 中(AD ＞AB)，点E 是BC 上一点，且DE ＝DA ，AF ⊥DE ，垂足为点F ，在下列结论中，不一定正确的是( B )A ．△AFE ≌△DCEB ．AF ＝12ADC ．AB ＝AFD ．BE ＝AD －DF5．(2016·绥化)如图，矩形ABCD 的对角线AC ，BD 相交于点O ，CE ∥BD ，DE ∥AC ，若AC ＝4，则四边形OCED 的周长为( B )A ．4B ．8C ．10D ．126．(2016·枣庄)如图，四边形ABCD 是菱形，AC ＝8，DB ＝6，DH ⊥AB 于点H ，则DH 等于( A )A.245 B.125C ．5D ．4 7．(2016·龙东)如图，在平行四边形ABCD 中，延长AD 到点E ，使DE ＝AD ，连接EB ，EC ，DB.请你添加一个条件答案不唯一，如：CD ＝BE ，使四边形DBCE 是矩形．8．(2016·扬州)如图，菱形ABCD 的对角线AC ，BD 相交于点O ，点E 为AD 的中点，若OE ＝3，则菱形ABCD 的周长为24．9．(2016·昆明)如图，E ，F ，G ，H 分别是矩形ABCD 各边的中点，AB ＝6，BC ＝8，则四边形EFGH 的面积是24．10．(2016·青岛)如图，在正方形ABCD 中，对角线AC 与BD 相交于点O ，E 为BC 上一点，CE ＝5，F 为DE 的中点．若△CEF 的周长为18，则OF 的长为3.5．11．(2016·云南)如图，菱形ABCD 的对角线AC 与BD 交于点O ，∠ABC ∶∠BAD ＝1∶2，BE ∥AC ，CE ∥BD. (1)求tan ∠DBC 的值；(2)求证：四边形OBEC 是矩形．解：(1)∵四边形ABCD 是菱形， ∴AD ∥BC ，∠DBC ＝12∠ABC.∴∠ABC ＋∠BAD＝180°. 又∵∠ABC∶∠BAD＝1∶2， ∴∠ABC ＝60°. ∴∠DBC ＝12∠ABC＝30°.∴tan ∠DBC ＝tan30°＝33. (2)证明：∵四边形ABCD 是菱形， ∴AC ⊥BD ，即∠BOC＝90°. ∵BE ∥AC ，CE ∥BD ， ∴BE ∥OC ，CE ∥OB.∴四边形OBEC 是平行四边形，且∠BOC＝90°.∴四边形OBEC 是矩形．12．(2016·遵义)如图，在矩形ABCD 中，延长AB 至E ，延长CD 至F ，BE ＝DF ，连接EF ，与BC ，AD 分别相交于P ，Q 两点．(1)求证：CP ＝AQ ；(2)若BP ＝1，PQ ＝22，∠AEF ＝45°，求矩形ABCD 的面积．解：(1)证明：∵四边形ABCD 是矩形，∴∠A ＝∠ABC＝∠C＝∠ADC＝90°，AB ＝CD ，AD ＝BC ，AB ∥CD ，AD ∥BC. ∴∠E ＝∠F.∵BE ＝DF ，∴AE ＝CF.在△CFP 和△AEQ 中，⎩⎪⎨⎪⎧∠C＝∠A，CF ＝AE ，∠F ＝∠E，∴△CFP ≌△AEQ(ASA)．∴CP ＝AQ.(2)∵AD∥BC，∴∠PBE ＝∠A＝90°. ∵∠AEF ＝45°，∴△BEP ，△AEQ 是等腰直角三角形． ∴BE ＝BP ＝1，AQ ＝AE.∴PE ＝2BP ＝ 2.∴EQ ＝PE ＋PQ ＝2＋22＝3 2. ∴AQ ＝AE ＝3. ∴AB ＝AE －BE ＝2.∵CP ＝AQ ，AD ＝BC ，∴DQ ＝BP ＝1. ∴AD ＝AQ ＋DQ ＝3＋1＝4. ∴S 矩形ABCD ＝AB·AD＝2×4＝8.13．(2016·菏泽)在▱ABCD 中，AB ＝3，BC ＝4，当▱ABCD 的面积最大时，下列结论正确的有( B ) ①AC ＝5；②∠A＋∠C＝180°；③AC⊥BD；④AC＝BD.A ．①②③B ．①②④C ．②③④D ．①③④14．(2016·舟山)如图，矩形ABCD 中，AD ＝2，AB ＝3，过点A ，C 作相距为2的平行线段AE ，CF ，分别交CD ，AB 于点E ，F ，则DE 的长是( D )A. 5B.136 C ．1 D.5615．(2016·张家界)如图，将矩形ABCD 沿GH 对折，点C 落在Q 处，点D 落在E 处，EQ 与BC 相交于点F.若AD ＝8 cm ，AB ＝6 cm ，AE ＝4 cm.则△EBF 的周长是8 cm.16．(2016·株洲)已知正方形ABCD ，BC ＝3，点E ，F 分别是CB ，CD 延长线上的点，DF ＝BE ，连接AE ，AF ，过点A 作AH⊥ED 于H 点．(1)求证：△ADF≌△ABE；(2)若BE ＝1，求tan ∠AED 的值．解：(1)在正方形ABCD 中，∵AD ＝AB ，∠ADC ＝∠ABC＝90°， ∴∠ADF ＝∠ABE＝90°.在△ADF 与△ABE 中，⎩⎪⎨⎪⎧AD ＝AB ，∠ADF ＝∠ABE，DF ＝BE ，∴△ADF ≌△ABE.(2)过点A 作AH⊥DE 于点H ，在Rt △ABE 中，∵AB ＝BC ＝3，BE ＝1， ∴AE ＝10，ED ＝CD 2＋CE 2＝5.∴S △AED ＝12AD·BA＝92，S △ADE ＝12DE·AH＝92.解得AH ＝1.8.在Rt △AHE 中，∵AE ＝10，AH ＝1.8， ∴EH ＝2.6.∴tan ∠AED ＝AH EH ＝1.82.6＝913.17．如图，在正方形ABCD 的边长为2，∠DAC 的平分线交DC 于点E ，点P ，Q 分别是AD 和AE 上的动点，则DQ ＋PQ。

2017 年广西贵港市中考数学试卷一、选择题：本大题共12 个小题，每题 3 分，共36 分 . 在每题给出的四个选项中，只.有一项为哪一项切合题目要求的1． 7 的相反数是（）A． 7B．﹣ 7C．D．﹣）2．数据 3， 2， 4， 2， 5， 3，2 的中位数和众数分别是（A．2，3 B． 4，2 C．3，2 D．2， 23．如图是一个空心圆柱体，它的左视图是（）A．B．C．D．4．以下二次根式中，最简二次根式是（）A．B．C．D．5．以下运算正确的选项是（）A． 3a2+a=3a3 B ． 2a3?（﹣ a2） =2a5 C． 4a6+2a2=2a3D．（﹣ 3a）2﹣a2=8a26．在平面直角坐标系中，点P（ m﹣ 3，4﹣ 2m）不行能在（）A．第一象限 B ．第二象限C．第三象限 D ．第四象限7．以下命题中假命题是（）A．正六边形的外角和等于360°B．位似图形必然相像C．样本方差越大，数据颠簸越小D．方程 x2+x+1=0 无实数根8．从长为 3，5，7，10 的四条线段中随意选用三条作为边，能构成三角形的概率是（）A．B．C．D．19．如图，A，B，C，D 是⊙ O上的四个点， B 是的中点，M是半径OD上随意一点．若∠ BDC=40°，则∠ AMB的度数不行能是（）A．45° B．60° C．75° D．85°10．将以下图的抛物线向右平移 1 个单位长度，再向上平移 3 个单位长度后，获取的抛物线分析式是（）A． y=（ x﹣1）2+1 B． y=（ x+1）2+1 C． y=2（ x﹣ 1）2+1D． y=2（ x+1）2+111．如图，在Rt△ ABC中，∠ ACB=90°，将△ABC绕极点 C 逆时针旋转获取△A'B'C ， M是BC的中点， P 是 A'B' 的中点，连结 PM．若 BC=2，∠BAC=30°，则线段 PM的最大值是（）A．4B． 3C． 2D． 112．如图，在正方形ABCD中， O是对角线 AC与 BD的交点， M是 BC边上的动点（点M不与B，C 重合），CN⊥ DM，CN与 AB交于点 N，连结 OM，ON，MN．以下五个结论：①△ CNB≌△DMC；222②△ CON≌△ DOM；③△ OMN∽△ OAD；④ AN+CM=MN；⑤若 AB=2，则 S△OMN的最小值是，其中正确结论的个数是（）A．2B． 3C．4D．5二、填空题（每题 3 分，满分18 分，将答案填在答题纸上）13．计算：﹣3﹣ 5=．14．中国的领水面积约为370 000km 2，将数370 000用科学记数法表示为．15．如图，AB∥ CD，点E 在AB 上，点 F 在CD上，假如∠CFE：∠ EFB=3： 4，∠ ABF=40°，那么∠BEF的度数为．16．如图，点P 在等边△ ABC的内部，且PC=6，PA=8，PB=10，将线段 PC绕点 C 顺时针旋转60°获取 P'C，连结 AP' ，则 sin ∠ PAP'的值为．17．如图，在扇形长为半径作交OAB中， C 是OB于点 E，若OA的中点，CD⊥OA，CD与交于点D，以OA=4，∠AOB=120°，则图中暗影部分的面积为O为圆心，OC的．（结果保存π）18．如图，过C（ 2，1）作AC∥x轴， BC∥y轴，点A， B 都在直线y= ﹣ x+6上，若双曲线y=（x＞ 0）与△ ABC总有公共点，则k 的取值范围是．三、解答题（本大题共 8小题，共66 分 . 解答应写出文字说明、证明过程或演算步骤. ）19．（ 1）计算： | ﹣ 3|+ （+π）0﹣（﹣）﹣2﹣2cos60°；（2）先化简，在求值：（﹣） +，此中 a=﹣ 2+ ．20．尺规作图（不写作法，保存作图印迹）：已知线段 a 和∠ AOB，点 M在 OB上（以下图）．（1）在 OA边上作点 P，使 OP=2a；（2）作∠ AOB的均分线；（3）过点 M作 OB的垂线．21．如图，一次函数y=2x﹣ 4 的图象与反比率函数y=的图象交于A，B 两点，且点 A 的横坐标为 3．（1）求反比率函数的分析式；（2）求点 B 的坐标．22．在展开“经典阅读”活动中，某学校为认识全校学生利用课外时间阅读的状况，学校团委随机抽取若干名学生，检查他们一周的课外阅读时间，并依据检查结果绘制了以下尚不完整的统计表．依据图表信息，解答以下问题：频次散布表阅读时间频数频次（小时）（人）1≤ x＜ 2180.122≤ x＜ 3a m3≤ x＜ 4450.34≤ x＜ 536n5≤ x＜ 6210.14共计b1（1）填空： a=， b=，m=， n=；（2）将频数散布直方图增补完好（绘图后请标明相应的频数）；（3）若该校由 3000 名学生，请依据上述检查结果，估量该校学生一周的课外阅读时间不足三小时的人数．23．某次篮球联赛初赛阶段，每队有10 场竞赛，每场竞赛都要分出输赢，每队胜一场得2分，负一场得 1 分，积分超出 15分才能获取参赛资格．（1）已知甲队在初赛阶段的积分为18 分，求甲队初赛阶段胜、负各多少场；（2）假如乙队要获取参加决赛资格，那么乙队在初赛阶段起码要胜多少场？24．如图，在菱形ABCD中，点 P 在对角线AC上，且 PA=PD，⊙ O是△ PAD的外接圆．（1）求证： AB是⊙ O的切线；（2）若 AC=8， tan ∠ BAC=，求⊙ O的半径．25．如图，抛物线y=a（ x﹣ 1）（x﹣ 3）与 x 轴交于 A， B 两点，与y 轴的正半轴交于点C，其极点为D．（1）写出 C， D 两点的坐标（用含 a 的式子表示）；（2）设 S△BCD： S△ABD=k，求 k 的值；（3）当△ BCD是直角三角形时，求对应抛物线的分析式．26．已知，在Rt△ ABC中，∠ ACB=90°， AC=4， BC=2， D 是 AC 边上的一个动点，将△ABD 沿 BD所在直线折叠，使点 A 落在点 P 处．（1）如图 1，若点 D 是 AC中点，连结PC．①写出 BP， BD的长；②求证：四边形 BCPD是平行四边形．（2）如图 2，若 BD=AD，过点 P作 PH⊥ BC交 BC的延伸线于点 H，求 PH的长．2017 年广西贵港市中考数学试卷参照答案与试题分析一、选择题：本大题共12 个小题，每题 3 分，共 36 分 . 在每题给出的四个选项中，只有一项为哪一项切合题目要求的.1． 7 的相反数是（）A． 7B．﹣ 7 C．D．﹣【考点】 14：相反数．【剖析】依据一个数的相反数就是在这个数前方添上“﹣”号，求解即可．【解答】解： 7 的相反数是﹣7，应选： B．2．数据 3， 2， 4， 2， 5， 3，2 的中位数和众数分别是（）A．2，3 B． 4，2 C．3，2 D．2， 2【考点】 W5：众数； W4：中位数．【剖析】依据中位数和众数的定义分别进行解答即可．【解答】解：把这组数据从小到大摆列：2， 2， 2， 3， 3， 4， 5，最中间的数是3，则这组数据的中位数是3；2 出现了3 次，出现的次数最多，则众数是2．应选： C．3．如图是一个空心圆柱体，它的左视图是（）A．B．C．D．【考点】 U1：简单几何体的三视图．【剖析】依据从左侧看获取的图形是左视图，可得答案．【解答】解：从左侧看是三个矩形，中间矩形的左右两边是虚线，应选： B．）4．以下二次根式中，最简二次根式是（A． B． C． D．【考点】 74：最简二次根式．【剖析】检查最简二次根式的两个条件能否同时知足，同时知足的就是最简二次根式，不然就不是．【解答】解： A、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故 A 切合题意；B、被开方数含能开得尽方的因数或因式，故 B 不切合题意；C、被开方数含分母，故 C 不切合题意；D、被开方数含能开得尽方的因数或因式，故D不切合题意；应选：A．5．以下运算正确的选项是（）A． 3a2+a=3a3 B ． 2a3?（﹣ a2） =2a5 C． 4a6+2a2=2a3D．（﹣ 3a）2﹣a2=8a2【考点】 49：单项式乘单项式；35：归并同类项；47：幂的乘方与积的乘方．【剖析】运用归并同类项，单项式乘以单项式，幂的乘方等运算法例运算即可．【解答】解： A.3a 2与 a 不是同类项，不可以归并，因此 A 错误；B.2a 3?（﹣ a2） =2×（﹣ 1）a5=﹣ 2a5，因此 B 错误；C.4a 6与 2a2不是同类项，不可以归并，因此C 错误；D．（﹣ 3a）2﹣a2=9a2﹣ a2=8a2，因此 D正确，应选 D．6．在平面直角坐标系中，点P（ m﹣ 3，4﹣ 2m）不行能在（）A．第一象限 B ．第二象限C．第三象限 D ．第四象限【考点】 D1：点的坐标．【剖析】分点P 的横坐标是正数和负数两种状况议论求解．【解答】解：①m﹣ 3＞ 0，即 m＞ 3 时，﹣ 2m＜﹣ 6，4﹣ 2m＜﹣ 2，因此，点P（ m﹣ 3，4﹣ 2m）在第四象限，不行能在第一象限；②m﹣ 3＜ 0，即 m＜ 3 时，﹣ 2m＞﹣ 6，4﹣ 2m＞﹣ 2，点 P（ m﹣ 3， 4﹣ 2m）能够在第二或三象限，综上所述，点 P 不行能在第一象限．应选 A．7．以下命题中假命题是（）A．正六边形的外角和等于360°B．位似图形必然相像C．样本方差越大，数据颠簸越小D．方程 x2+x+1=0 无实数根【考点】 O1：命题与定理．【剖析】依据正确的命题是真命题，错误的命题是假命题进行剖析即可．【解答】解： A、正六边形的外角和等于360°，是真命题；B、位似图形必然相像，是真命题；C、样本方差越大，数据颠簸越小，是假命题；D、方程 x2+x+1=0 无实数根，是真命题；应选： C．8．从长为 3，5，7，10 的四条线段中随意选用三条作为边，能构成三角形的概率是（）A．B．C．D．1【考点】 X6：列表法与树状图法；K6：三角形三边关系．【剖析】列举出全部等可能的状况数，找出能构成三角形的状况数，即可求出所求概率．【解答】解：从长为3， 5， 7， 10 的四条线段中随意选用三条作为边，全部等可能状况有：3， 5， 7； 3， 5， 10； 3， 7，10； 5， 7， 10，共 4 种，此中能构成三角形的状况有：3， 5， 7； 5， 7， 10，共 2 种，则 P（能构成三角形） = = ，应选 B9．如图，A，B，C，D 是⊙ O上的四个点， B 是的中点，M是半径OD上随意一点．若∠ BDC=40°，则∠ AMB的度数不行能是（）A．45° B．60° C．75° D．85°【考点】 M5：圆周角定理；M4：圆心角、弧、弦的关系．【剖析】依据圆周角定理求得∠AOB的度数，则∠AOB的度数必定不小于∠AMB的度数，据此即可判断．【解答】解：∵ B 是的中点，∴∠ AOB=2∠BDC=80°，又∵ M是 OD上一点，∴∠ AMB≤∠ AOB=80°．则不切合条件的只有85°．应选 D．10．将以下图的抛物线向右平移 1 个单位长度，再向上平移 3 个单位长度后，获取的抛物线分析式是（）A． y=（ x﹣1）2+1 B． y=（ x+1）2+1 C． y=2（ x﹣ 1）2+1D． y=2（ x+1）2+1【考点】 H6：二次函数图象与几何变换．【剖析】依据平移规律，可得答案．【解答】解：由图象，得y=2x 2﹣ 2，由平移规律，得y=2（ x﹣ 1）2+1，应选： C．11．如图，在Rt△ ABC中，∠ ACB=90°，将△ABC绕极点 C 逆时针旋转获取△A'B'C ， M是BC的中点， P 是 A'B' 的中点，连结 PM．若 BC=2，∠BAC=30°，则线段 PM的最大值是（）A．4B． 3C．2D．1【考点】 R2：旋转的性质．【剖析】如图连结PC．思想求出PC=2，依据 PM≤ PC+CM，可得 PM≤3，由此即可解决问题．【解答】解：如图连结PC．在 Rt △ ABC中，∵∠ A=30°， BC=2，∴AB=4，依据旋转不变性可知， A′ B′=AB=4，∴A′P=PB′，∴PC= A′B′=2，∵CM=BM=1，又∵ PM≤ PC+CM，即 PM≤ 3，∴PM的最大值为3（此时 P、C、 M共线）．应选 B．12．如图，在正方形ABCD中， O是对角线 AC与 BD的交点， M是 BC边上的动点（点M不与B，C 重合），CN⊥ DM，CN与 AB交于点 N，连结 OM，ON，MN．以下五个结论：①△ CNB≌△DMC；222，其②△ CON≌△ DOM；③△ OMN∽△ OAD；④ AN+CM=MN；⑤若 AB=2，则 S△OMN的最小值是中正确结论的个数是（）A．2B． 3C．4D．5【考点】 S9：相像三角形的判断与性质；KD：全等三角形的判断与性质；LE：正方形的性质．【剖析】依据正方形的性质，挨次判断△ CNB≌△ DMC，△ OCM≌△ OBN，△ CON≌△ DOM，△ OMN ∽△ OAD，依据全等三角形的性质以及勾股定理进行计算即可得出结论．【解答】解：∵正方形ABCD中， CD=BC，∠ BCD=90°，∴∠ BCN+∠DCN=90°，又∵ CN⊥ DM，∴∠ CDM+∠DCN=90°，∴∠ BCN=∠CDM，又∵∠ CBN=∠DCM=90°，∴△ CNB≌△ DMC（ ASA），故①正确；依据△ CNB≌△ DMC，可得 CM=BN，又∵∠ OCM=∠OBN=45°， OC=OB，∴△ OCM≌△ OBN（ SAS），∴OM=ON，∠ COM=∠ BON，∴∠ DOC+∠COM=∠ COB+∠ BPN，即∠ DOM=∠ CON，又∵ DO=CO，∴△ CON≌△ DOM（ SAS），故②正确；∵∠ BON+∠BOM=∠ COM+∠BOM=90°，∴∠ MON=90°，即△MON是等腰直角三角形，又∵△ AOD是等腰直角三角形，∴△ OMN∽△ OAD，故③正确；∵AB=BC，CM=BN，∴BM=AN，222又∵ Rt △ BMN中， BM+BN=MN，222∴AN+CM=MN，故④正确；∵△ OCM≌△ OBN，∴四边形BMON的面积 =△ BOC的面积 =1，即四边形BMON的面积是定值1，∴当△ MNB的面积最大时，△MNO的面积最小，设 BN=x=CM，则 BM=2﹣ x，∴△ MNB的面积 = x（ 2﹣x） =﹣x2+x ，∴当 x=1 时，△ MNB的面积有最大值，此时 S△OMN的最小值是1﹣=，故⑤正确；综上所述，正确结论的个数是 5 个，应选： D．二、填空题（每题 3 分，满分18 分，将答案填在答题纸上）13．计算：﹣ 3﹣ 5=﹣8．【考点】 1A：有理数的减法．【剖析】依占有理数的减法运算法例进行计算即可得解．【解答】解：﹣3﹣ 5=﹣ 8．故答案为：﹣ 8．14．中国的领水面积约为370 000km 2，将数 370 000 用科学记数法表示为3.7 × 105．【考点】 1I ：科学记数法—表示较大的数．【剖析】科学记数法的表示形式为a× 10n的形式，此中1≤ |a| ＜ 10，n 为整数．确立n 的值时，要看把原数变为 a 时，小数点挪动了多少位， n 的绝对值与小数点挪动的位数同样．当原数绝对值大于 10 时， n 是正数；当原数的绝对值小于 1 时， n 是负数．确立 a× 10n（ 1≤|a | ＜ 10， n 为整数）中 n 的值，因为 370 000 有 6 位，因此能够确立 n=6﹣ 1=5．【解答】解： 370 000=3.7 ×105，故答案为： 3.7 × 105．15．如图， AB∥ CD，点 E 在 AB 上，点 F 在 CD上，假如∠ CFE：∠ EFB=3： 4，∠ABF=40°，那么∠ BEF的度数为 60° ．【考点】 JA：平行线的性质．【剖析】先依据平行线的性质，获取∠CFB的度数，再依据∠CFE：∠ EFB=3： 4 以及平行线的性质，即可得出∠BEF的度数．【解答】解：∵AB∥CD，∠ ABF=40°，∴∠ CFB=180°﹣∠ B=140°，又∵∠ CFE：∠ EFB=3： 4，∴∠ CFE= ∠ CFB=60°，∵AB∥ CD，∴∠ BEF=∠CFE=60°，故答案为： 60°．16．如图，点P 在等边△ ABC的内部，且PC=6，PA=8，PB=10，将线段 PC绕点 C 顺时针旋转60°获取 P'C，连结 AP' ，则 sin ∠ PAP'的值为．【考点】 R2：旋转的性质；KK：等边三角形的性质；T7：解直角三角形．【剖析】连结 PP′，如图，先利用旋转的性质得 CP=CP′=6，∠PCP′=60°，则可判断△ CPP′为等边三角形获取 PP′=PC=6，再证明△ PCB≌△ P′CA 获取 PB=P′A=10，接着利用勾股定理的逆定理证明△ APP′为直角三角形，∠ APP′=90°，而后依据正弦的定义求解．【解答】解：连结 PP′，如图，∵线段 PC绕点 C 顺时针旋转60°获取 P'C ，∴CP=CP′=6，∠ PCP′=60°，∴△ CPP′为等边三角形，∴PP′=PC=6，∵△ ABC为等边三角形，∴CB=CA，∠ ACB=60°，∴∠ PCB=∠P′CA，在△ PCB和△ P′CA 中，∴△ PCB≌△ P′CA，∴PB=P′A=10，∵62+82=102，222∴PP′ +AP=P′A，∴△ APP′为直角三角形，∠∴sin ∠PAP′===故答案为．APP′=90°，．17．如图，在扇形OAB中， C 是 OA的中点， CD⊥OA，CD与交于点D，以O为圆心，OC的长为半径作交OB 于点E，若OA=4，∠AOB=120°，则图中暗影部分的面积为π +2．（结果保存π）【考点】 MO：扇形面积的计算；KG：线段垂直均分线的性质．【剖析】连结 OD、 AD，依据点 C为 OA的中点可得∠ CDO=30°，既而可得△ ADO为等边三角形，求出扇形 AOD的面积，最后用扇形 AOB的面积减去扇形 COE的面积，再减去 S 空白ADC即可求出暗影部分的面积．【解答】解：连结O、 AD，∵点 C 为 OA的中点，∴∠ CDO=30°，∠ DOC=60°，∴△ ADO为等边三角形，∴S 扇形AOD==π ，∴S 暗影 =S扇形AOB﹣ S 扇形COE﹣（ S 扇形AOD﹣ S△COD）=﹣﹣（π ﹣× 2×2）=π ﹣π ﹣π +2=π +2 ．故答案为π +2 ．18．如图，过C（ 2，1）作AC∥x轴， BC∥y轴，点A， B 都在直线y= ﹣ x+6上，若双曲线y=（x＞ 0）与△ ABC总有公共点，则k 的取值范围是2≤ k≤9．【考点】 G8：反比率函数与一次函数的交点问题．【剖析】把 C 的坐标代入求出k≥ 2，解两函数构成的方程组，依据根的鉴别式求出k≤9，即可得出答案．【解答】解：当反比率函数的图象过 C 点时，把C的坐标代入得：k=2× 1=2；把 y=﹣ x+6 代入 y= 得：﹣ x+6= ，x2﹣6x +k=0，△=（﹣ 6）2﹣4k=36 ﹣4k ，∵反比率函数y=的图象与△ ABC有公共点，∴36﹣ 4k≥0，k≤ 9，即 k 的范围是 2≤ k≤ 9，故答案为： 2≤ k≤ 9．三、解答题（本大题共 8小题，共66 分 . 解答应写出文字说明、证明过程或演算步骤. ）19．（ 1）计算： | ﹣ 3|+ （+π）0﹣（﹣）﹣2﹣2cos60°；（2）先化简，在求值：（﹣） +，此中 a=﹣ 2+ ．【考点】 6D：分式的化简求值； 2C：实数的运算； 6E：零指数幂； 6F：负整数指数幂；T5：特别角的三角函数值．【剖析】（ 1）依据零指数幂的意义、特别角的锐角三角函数以及负整数指数幂的意义即可求出答案；（2）先化简原式，而后将 a 的值代入即可求出答案．【解答】解：（ 1）原式 =3+1﹣（﹣ 2）2﹣2× =4﹣ 4﹣1=﹣ 1（2）当 a=﹣ 2+原式=+===7+520．尺规作图（不写作法，保存作图印迹）：已知线段 a 和∠ AOB，点 M在 OB上（以下图）．（1）在 OA边上作点 P，使 OP=2a；（2）作∠ AOB的均分线；（3）过点 M作 OB的垂线．【考点】 N3：作图—复杂作图．【剖析】（ 1）在 OA上截取 OP=2a即可求出点P 的地点；（2）依据角均分线的作法即可作出∠AOB的均分线；（3）以 M为圆心，作一圆与射线 OB交于两点，再以这两点分别为圆心，作两个相等半径的圆交于 D 点，连结MD即为 OB的垂线；【解答】解：（ 1）点 P 为所求作；（2） OC为所求作；（3） MD为所求作；21．如图，一次函数y=2x﹣ 4 的图象与反比率函数y=的图象交于A，B 两点，且点 A 的横坐标为 3．（1）求反比率函数的分析式；（2）求点 B 的坐标．【考点】 G8：反比率函数与一次函数的交点问题．【剖析】（ 1）把 x=3 代入一次函数分析式求得 A 的坐标，利用待定系数法求得反比率函数解析式；（2）解一次函数与反比率函数分析式构成的方程组求得 B 的坐标．【解答】解：（ 1）把 x=3 代入 y=2x﹣ 4 得 y=6﹣ 4=2，则 A 的坐标是（ 3， 2）．把（ 3， 2）代入 y=得k=6，则反比率函数的分析式是y=；（2）依据题意得2x﹣ 4=，解得 x=3 或﹣ 1，把 x=﹣ 1 代入 y=2x ﹣ 4 得 y=﹣6，则 B的坐标是（﹣1，﹣ 6）．22．在展开“经典阅读”活动中，某学校为认识全校学生利用课外时间阅读的状况，学校团委随机抽取若干名学生，检查他们一周的课外阅读时间，并依据检查结果绘制了以下尚不完整的统计表．依据图表信息，解答以下问题：频次散布表阅读时间频数频次（小时）（人）1≤ x＜ 2180.122≤ x＜ 3a m3≤ x＜ 4450.34≤ x＜ 536n5≤ x＜ 6210.14共计b1（1）填空： a=30 ， b=150 ， m= 0.2， n= 0.24；（2）将频数散布直方图增补完好（绘图后请标明相应的频数）；（3）若该校由 3000 名学生，请依据上述检查结果，估量该校学生一周的课外阅读时间不足三小时的人数．【考点】 V8：频数（率）散布直方图；V5：用样本预计整体；V7：频数（率）散布表．b=150，再根【剖析】（ 1）依据阅读时间为 1≤ x＜ 2 的人数及所占百分比可得，求出总人数据频次、频数、总人数的关系即可求出 m、 n、 a；（2）依据数据将频数散布直方图增补完好即可；（3）由总人数乘以时间不足三小时的人数的频次即可．【解答】解：（ 1） b=18÷ 0.12=150 （人），∴n=36÷ 150=0.24 ，∴m=1﹣ 0.12 ﹣ 0.3 ﹣0.24 ﹣ 0.14=0.2 ，∴a=0.2 × 150=30；故答案为： 30， 150， 0.2 ， 0.24 ；（2）以下图：（3） 3000×（ 0.12+0.2 ） =960（人）；即估量该校学生一周的课外阅读时间不足三小时的人数为960 人．23．某次篮球联赛初赛阶段，每队有10 场竞赛，每场竞赛都要分出输赢，每队胜一场得2分，负一场得 1 分，积分超出 15分才能获取参赛资格．（1）已知甲队在初赛阶段的积分为18 分，求甲队初赛阶段胜、负各多少场；（2）假如乙队要获取参加决赛资格，那么乙队在初赛阶段起码要胜多少场？【考点】 C9：一元一次不等式的应用； 8A：一元一次方程的应用．【剖析】（ 1）设甲队胜了x 场，则负了（10﹣ x）场，依据每队胜一场得 2 分，负一场得1分，利用甲队在初赛阶段的积分为18 分，从而得出等式求出答案；（2）设乙队在初赛阶段胜 a 场，依据积分超出15 分才能获取参赛资格，从而得出答案．【解答】解：（ 1）设甲队胜了x 场，则负了（10﹣ x）场，依据题意可得：2x+10﹣ x=18，解得： x=8，则 10﹣ x=2，答：甲队胜了8 场，则负了 2 场；（2）设乙队在初赛阶段胜 a 场，依据题意可得：2a+（ 10﹣ a）≥ 15，解得： a≥ 5，答：乙队在初赛阶段起码要胜 5 场．24．如图，在菱形ABCD中，点 P 在对角线AC上，且 PA=PD，⊙ O是△ PAD的外接圆．（1）求证： AB是⊙ O的切线；（2）若 AC=8， tan ∠ BAC=，求⊙ O的半径．【考点】 ME：切线的判断与性质；L8：菱形的性质；T7：解直角三角形．【剖析】（ 1）连结 OP、 OA， OP交 AD于 E，由 PA=PD得弧 AP=弧 DP，依据垂径定理的推理得OP⊥ AD，AE=DE，则∠ 1+∠OPA=90°，而∠ OAP=∠ OPA，因此∠ 1+∠OAP=90°，再依据菱形的性质得∠1=∠2，因此∠2+∠OAP=90°，而后依据切线的判断定理获取直线AB与⊙O相切；（2）连结 BD，交 AC于点 F，依据菱形的性质得 DB与 AC相互垂直均分，则 AF=4，tan ∠ DAC= ，获取 DF=2 ，依据勾股定理获取 AD= =2 ，求得 AE= ，设⊙ O的半径为 R，则 OE=R﹣，OA=R，依据勾股定理列方程即可获取结论．【解答】解：（ 1）连结 OP、 OA， OP交 AD于 E，如图，∵PA=PD，∴弧 AP=弧 DP，∴OP⊥AD，AE=DE，∴∠1+∠OPA=90°，∵OP=OA，∴∠ OAP=∠OPA，∴∠ 1+∠OAP=90°，∵四边形ABCD为菱形，∴∠ 1=∠ 2，∴∠ 2+∠OAP=90°，∴OA⊥ AB，∴直线 AB与⊙ O相切；（2）连结 BD，交 AC于点 F，如图，∵四边形 ABCD为菱形，∴DB与 AC相互垂直均分，∵AC=8， tan ∠ BAC=，∴AF=4， tan ∠ DAC== ，∴DF=2，∴AD==2，∴A E= ，在 Rt △ PAE中， tan ∠ 1==，∴PE=，设⊙ O的半径为R，则 OE=R﹣，OA=R，在 Rt △ OAE中，∵222OA=OE+AE，∴R2=（ R﹣）2+（） 2，∴R=，即⊙ O的半径为．25．如图，抛物线y=a（ x﹣ 1）（x﹣ 3）与 x 轴交于 A， B 两点，与y 轴的正半轴交于点C，其极点为D．（1）写出 C， D 两点的坐标（用含 a 的式子表示）；（2）设 S△BCD： S△ABD=k，求 k 的值；（3）当△ BCD是直角三角形时，求对应抛物线的分析式．【考点】 HF：二次函数综合题．【剖析】（ 1）令 x=0 可求得 C 点坐标，化为极点式可求得D点坐标；（2）令 y=0 可求得 A、B 的坐标，联合 D 点坐标可求得△ABD的面积，设直线CD交 x 轴于点 E，由 C、 D坐标，利用待定系数法可求得直线CD的分析式，则可求得 E 点坐标，从而可表示出△ BCD的面积，可求得k 的值；22（3）由 B、 C、 D 的坐标，可表示出BC、BD 和分别利用勾股定理可获取对于 a 的方程，可求得2CD，分∠ CBD=90°和∠ CDB=90°两种状况，a 的值，则可求得抛物线的分析式．【解答】解：（1）在 y=a（ x﹣ 1）（ x﹣ 3），令 x=0 可得 y=3a，∴C（ 0， 3a），∵y=a（ x﹣1）（ x﹣ 3） =a（ x2﹣4x+3） =a（ x﹣ 2）2﹣a，∴D（ 2，﹣ a）；（2）在 y=a（ x﹣ 1）（ x﹣ 3）中，令 y=0 可解得 x=1 或 x=3，∴A（ 1， 0）， B（ 3，0），∴AB=3﹣ 1=2，∴S△ABD= × 2×a=a，如图，设直线 CD交 x 轴于点 E，设直线 CD分析式为 y=kx+b ，把 C、 D 的坐标代入可得，解得∴直线 CD分析式为y=﹣ 2ax+3a，令 y=0 可解得∴E（，0），∴BE=3﹣=x=，，∴S△BCD=S△BEC+S△BED=××（3a+a）=3a，∴S△BCD： S△ABD=（ 3a）： a=3，∴k=3；（3）∵ B（3， 0）， C（ 0， 3a）， D（ 2，﹣ a），222222222222∴BC=3 +（ 3a）=9+9a ， CD=2 +（﹣ a﹣3a） =4+16a， BD=（ 3﹣ 2） +a =1+a ，∵∠ BCD＜∠ BCO＜90°，∴△ BCD为直角三角形时，只好有∠CBD=90°或∠ CDB=90°两种状况，①当∠ CBD=90°时，则有222222BC+BD=CD，即 9+9a +1+a =4+16a，解得 a=﹣ 1（舍去）或 a=1，此时抛物线分析式为y=x 2﹣ 4x+3；222222（舍去）或 a=，②当∠ CDB=90°时，则有 CD+BD=BC，即 4+16a +1+a =9+9a ，解得 a=﹣此时抛物线分析式为 y=x2﹣2x+；综上可知当△ BCD是直角三角形时，抛物线的分析式为y=x 2﹣ 4x+3 或 y=x2﹣2 x+．26．已知，在 Rt △ ABC中，∠ ACB=90°， AC=4， BC=2， D 是 AC 边上的一个动点，将△ ABD 沿 BD所在直线折叠，使点 A 落在点 P 处．（1）如图 1，若点 D 是 AC中点，连结PC．①写出 BP， BD的长；②求证：四边形BCPD是平行四边形．（2）如图 2，若 BD=AD，过点 P 作 PH⊥ BC交 BC的延伸线于点 H，求 PH的长．【考点】 LO：四边形综合题．【剖析】（ 1）①分别在 Rt △ ABC， Rt △BDC中，求出 AB、BD即可解决问题；②想方法证明 DP∥ BC， DP=BC即可；（2）如图 2 中，作 DN⊥ AB 于 N，PE⊥ AC于 E，延伸 BD交 PA于 M．设 BD=AD=x，则 CD=4﹣ x，在 Rt △ BDC中，可得x2 =（ 4﹣ x）2+22，推出x=，推出DN==，由△BDN∽△BAM，可得=，由此求出AM，由△ ADM∽△ APE，可得=，由此求出AE=，可得EC=AC﹣ AE=4﹣=由此即可解决问题．【解答】解：（ 1）①在∴AB==2，∵AD=CD=2，∴BD==2，Rt △ ABC中，∵BC=2， AC=4，由翻折可知， BP=BA=2．②如图 1 中，∵△ BCD是等腰直角三角形，∴∠ BDC=45°，∴∠ ADB=∠BDP=135°，∴∠ PDC=135°﹣ 45°=90°，∴∠ BCD=∠PDC=90°，∴DP∥ BC，∵ PD=AD=BC=2，∴四边形BCPD是平行四边形．（2）如图 2 中，作 DN⊥ AB于 N， PE⊥AC于 E，延伸 BD交 PA于 M．设 BD=AD=x，则 CD=4﹣ x，222在 Rt △ BDC中，∵ BD=CD+BC，222∴x =（ 4﹣ x） +2 ，∴x=，∵DB=DA， DN⊥ AB，∴BN=AN=，在 Rt △ BDN中， DN= 由△ BDN∽△ BAM，可得==，，∴=，∴A M=2，∴A P=2AM=4，由△ ADM∽△ APE，可得=，∴= ，∴A E= ，∴EC=AC﹣ AE=4﹣=，易证四边形PECH是矩形，∴P H=EC= ．。

广西省贵港市2017年中考数学试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 7的相反数是（ ）A ．7B ．7-C ．17D ．17-2.数据3,2,4,2,5,3,2的中位数和众数分别是 （ ）A ．2,3B ．4,2C ．3,2D ．2,23. 如图是一个空心圆柱体，它的左视图是（ ）A ．B ．C ．D ．4. 下列二次根式中，最简二次根式是（ ）A ．2-B ．12 C.15 D ．2a5. 下列运算正确的是（ ）A ．2333a a a +=B ．()32522a a a -=C. 623422a a a += D ．()22238a a a --=6. 在平面直角坐标系中，点()3,42P m m -- 不可能在（ ）A ．第一象限B ．第二象限 C. 第三象限 D ．第四象限7. 下列命题中假命题是（ ）A ．正六边形的外角和等于360B ．位似图形必定相似C.样本方差越大，数据波动越小 D ．方程210x x ++=无实数根8. 从长为3,5,7,10 的四条线段中任意选取三条作为边，能构成三角形的概率是（ ）A ．14B ．12 C.34D ．1 9. 如图，,,,A B C D 是O 上的四个点，B 是AC 的中点，M 是半径OD 上任意一点，若40BDC ∠= ，则AMB ∠的度数不可能是（ ）A ．45B ．60 C. 75 D ．8510. 将如图所示的抛物线向右平移1个单位长度，再向上平移3个单位长度后，得到的抛物线解析式是 （ ）A ．()211y x =-+B ．()211y x =++C.()2211y x =-+ D ．()2211y x =++11. 如图，在R t A B C ∆中，90ACB ∠= ，将ABC ∆绕顶点C 逆时针旋转得到'',A B C M ∆是BC 的中点，P 是''A B 的中点，连接PM ，若230BC BAC =∠=，，则线段PM 的最大值是 （ ）A ．4B ．3 C.2 D ．112. 如图，在正方形ABCD 中，O 是对角线AC 与BD 的交点，M 是BC 边上的动点（点M 不与,B C 重合），,CN DM CN ⊥与AB 交于点N ，连接,,OM ON MN .下列五个结论：①CNB DMC ∆≅∆ ；②CON DOM ∆≅∆ ；③OMN OAD ∆≅∆ ；④222AN CM MN += ；⑤若2AB =，则OMN S ∆的最小值是12，其中正确结论的个数是 （ ）A ．2B ．3 C. 4 D ．5第Ⅱ卷（共90分）二、填空题（每题3分，满分18分，将答案填在答题纸上）13.计算：35--= ．14.中国的领水面积为2370000km ，把370000用科学记数法表示为 ．15.如图，AB CD ，点E 在AB 上，点F 在CD 上，如果:3:4,40CFE EFB ABF ∠∠=∠= ，那么BEF ∠的度数为 ．16.如图，点P 在等边ABC ∆的内部，且6,8,10PC PA PB ===，将线段PC 绕点C 顺时针旋转60得到'P C ，连接'AP ，则sin 'PAP ∠的值为 ．17. 如图，在扇形OAB 中，C 是OA 的中点，,CD OA CD ⊥ 与AB 交于点D ，以O 为圆心，OC 的长为半径作CE 交OB 于点E ，若4,120OA AOB =∠=，则图中阴影部分的面积为 ．（结果保留π）18. 如图，过()2,1C 作AC x 轴，BC y 轴，点,A B 都在直线6y x =-+上，若双曲线()0k y x x =>与ABC ∆总有公共点，则k 的取值范围是 ．三、解答题 （本大题共8小题，共66分.解答应写出文字说明、证明过程或演算步骤.）19. （1）计算：()201352cos602π-⎛⎫-++--- ⎪⎝⎭； （2）先化简，在求值：21142111a a a a +⎛⎫-+ ⎪-+-⎝⎭ ，其中22a =-+ . 20. 尺规作图（不写作法，保留作图痕迹）：已知线段a 和AOB ∠，点M 在OB 上（如图所示）.（1）在OA 边上作点P ，使2OP a = ；（2）作AOB ∠的平分线；（3）过点M 作OB 的垂线.21. 如图，一次函数24y x =- 的图象与反比例函数k y x= 的图象交于,A B 两点，且点A 的横坐标为3 .（1）求反比例函数的解析式；（2）求点B 的坐标.22. 在开展“经典阅读”活动中，某学校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计表.根据图表信息，解答下列问题：频率分布表阅读时间（小时） 频数 （人） 频率12x ≤< 180.12 23x ≤< a m34x ≤< 450.345x ≤< 36n 56x ≤< 210.14 合计 b 1频数分布直方图（1）填空：a = ，b = ，m = ，n = ；（2）将频数分布直方图补充完整（画图后请标注相应的频数）；（3）若该校由3000名学生，请根据上述调查结果，估算该校学生一周的课外阅读时间不足三小时的人数.23. 某次篮球联赛初赛阶段，每队有10场比赛，每场比赛都要分出胜负，每队胜一场得2分， 负一场得1分，积分超过15分才能获得参赛资格.（1）已知甲队在初赛阶段的积分为18分，求甲队初赛阶段胜、负各多少场；（2）如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？24. 如图，在菱形ABCD 中，点P 在对角线AC 上，且PA PD =，O 是PAD ∆的外接圆.（1）求证：AB 是O 的切线；（2）若28,tan ,2AC BAC =∠=求O 的半径. 25.如图，抛物线()()13y a x x =--与x 轴交于 ,A B 两点，与y 轴的正半轴交于点C ，其顶点为D .（1）写出,C D 两点的坐标（用含a 的式子表示）；（2）设:BCD ABD S S k ∆= ，求k 的值；（3）当BCD ∆是直角三角形时，求对应抛物线的解析式.26. 已知，在Rt ABC ∆中，90,4,2,ACB AC BC D ∠===是AC 边上的一个动点，将ABD ∆沿BD 所在直线折叠，使点A 落在点P 处.（1）如图1，若点D 是AC 中点，连接PC . ①写出,BP BD 的长；②求证：四边形BCPD 是平行四边形.（2）如图2，若BD AD =，过点P 作PH BC ⊥交BC 的延长线于点H ，求PH 的长.随州市2017年初中毕业升学考试数学试题第Ⅰ卷（共30分）一、选择题：本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.2-的绝对值是（ ） A ．2B ．2-C ．12D ．12-2.下列运算正确的是（ ） A ．336a a a +=B ．222()a b a b -=- C ．326()a a -= D ．1226a a a ÷=3.如图是某几何体的三视图，这个几何体是（ ）A ．圆锥B ．长方体C ．圆柱D ．三棱柱4.一组数据2,3,5,4,4的中位数和平均数分别是（ ） A ．4和3.5B ．4和3.6C ．5和3.5D ．5和3.65.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是（ ）A ．两点之间线段最短B ．两点确定一条直线C ．垂线段最短D ．经过直线外一点，有且只有一条直线与这条直线平行6.如图，用尺规作图作AOC AOB ∠=∠的第一步是以点O 为圆心，以任意长为半径画弧①，分别交OA 、OB 于点E 、F ，那么第二步的作图痕迹②的作法是（ ）A ．以点F 为圆心，OE 长为半径画弧B ．以点F 为圆心，EF 长为半径画弧C ．以点E 为圆心，OE 长为半径画弧D ．以点E 为圆心，EF 长为半径画弧7.小明到商店购买“五四青年节”活动奖品，购买20支铅笔和10本笔记本共需110元，但购买30支铅笔和5本笔记本只需85元．设每支铅笔x 元，每本笔记本y 元，则可列方程组（ ）A ．203011010585x y x y +=⎧⎨+=⎩B ．201011030585x y x y +=⎧⎨+=⎩C ．205110301085x y x y +=⎧⎨+=⎩D ．520110103085x y x y +=⎧⎨+=⎩8.在公园内，牡丹按正方形种植，在它的周围种植芍药，如图反映了牡丹的列数()n 和芍药的数量规律，那么当11n =时，芍药的数量为（ ）A ．84株B ．88株C ．92株D ．121株9.对于二次函数223y x mx =--，下列结论错误的是（ ） A ．它的图象与x 轴有两个交点 B ．方程223x mx -=的两根之积为3- C ．它的图象的对称轴在y 轴的右侧D ．x m <时，y 随x 的增大而减小10.如图，在矩形ABCD 中，AB BC <，E 为CD 边的中点．将ADE ∆绕点E 顺时针旋转180︒，点D 的对应点为C ，点A 的对应点为F ，过点E 作ME AF ⊥交BC 于点M ，连接AM 、BD 交于点N .现有下列结论：①AM AD MC =+；②AM DE BM =+；③2DE AD CM =⋅；④点N 为ABM ∆的外心. 其中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个第Ⅱ卷（共90分）二、填空题（每题3分，满分18分，将答案填在答题纸上）11.根据中央“精准扶贫”规划，每年要减贫约11700000人，将数据11700000用科学记数法表示为 ．12.“抛掷一枚质地均匀的硬币，正面向上”是 事件（从“必然”、“随机”、“不可能”中选一个）． 13.如图，已知AB 是O 的弦，半径OC 垂直AB ，点D 是O 上一点，且点D 与点C 位于弦AB 两侧，连接AD 、CD 、OB ，若70BOC ∠=︒，则ADC ∠= 度．14.在ABC ∆中，6AB =，5AC =，点D 在边AB 上，且2AD =，点E 在边AC 上，当AE = 时，以A 、D 、E 为顶点的三角形与ABC ∆相似．15.如图，AOB ∠的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点(3,0)N 是OB 上的一定点，点M 是ON 的中点，30AOB ∠=︒，要使PM PN +最小，则点P 点的坐标为 ．16.在一条笔直的公路上有A 、B 、C 三地，C 地位于A 、B 两地之间．甲车从A 地沿这条公路匀速驶向C 地，乙车从B 地沿这条公路匀速驶向A 地．在甲车出发至甲车到达C 地的过程中，甲、乙两车各自与C地的距离y （km ）与甲车行驶时间()t h 之间的函数关系如图所示．下列结论：①甲车出发2h 时，两车相遇；②乙车出发1.5h 时，两车相距170km ；③乙车出发527h 时，两车相遇；④甲车到达C 地时，两车相距40km .其中正确的是 （填写所有正确结论的序号）．三、解答题 （本大题共9题，共72.解答应写出文字说明、证明过程或演算步骤.）17.计算：2021()(2017)(3)|2|3π---+---. 18.解分式方程：2311xx x x +=--． 19.如图，在平面直角坐标系中，将坐标原点O 沿x 轴向左平移2个单位长度得到点A ，过点A 作y 轴的平行线交反比例函数k y x =的图象于点B ，32AB =.（1）求反比例函数的解析式；（2）若11(,)P x y 、22(,)Q x y 是该反比例函数图象上的两点，且12x x <时，12y y >，指出点P 、Q 各位于哪个象限？并简要说明理由．20.风电已成为我国继煤电、水电之后的第三大电源．风电机组主要由塔杆和叶片组成（如图1），图2是从图1引出的平面图．假设你站在A 处测得塔杆顶端C 的仰角是55︒，沿HA 方向水平前进43米到达山底G 处，在山顶B 处发现正好一叶片到达最高位置，此时测得叶片的顶端D （D 、C 、H 在同一直线上）的仰角是45︒．已知叶片的长度为35米（塔杆与叶片连接处的长度忽略不计），山高BG 为10米，BG HG ⊥，CH AH ⊥，求塔杆CH 的高．（参考数据：tan55 1.4︒≈，tan350.7︒≈，sin550.8︒≈，sin350.6︒≈）21.某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛，初赛后对选手成绩进行了整理，分成5个小组（x 表示成绩，单位：分）．A 组：7580x ≤<；B 组：8085x ≤<；C 组：8590x ≤<；D 组：9095x ≤<；E 组：95100x ≤<，并绘制如图两幅不完整的统计图．请根据图中信息，解答下列问题：（1）参加初赛的选手共有 名，请补全频率分布直方图；（2）扇形统计图中，C 组对应的圆心角是多少度？E 组人数占参赛选手的百分比是多少？（3）学校准备组成8人的代表队参加市级决赛，E 组6名选手直接进入代表队，现要从D 组中的两名男生和两名女生中，随机选取两名选手进入代表队，请用列表或画树状图的方法，求恰好选中一名男生和一名女生的概率．22.如图，在Rt ABC ∆中，90C ∠=︒，AC BC =，点O 在AB 上，经过点A 的O 与BC 相切于点D ，交AB 于点E ．（1）求证：AD 评分BAC ∠；（2）若1CD =，求图中阴影部分的面积（结果保留π）．23.某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．（1）求该种水果每次降价的百分率；（2）从第一次降价的第1天算起，第x 天（x 为正数）的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤，设销售该水果第x （天）的利润为y （元），求y 与x （115x ≤<）之间的函数关系式，并求出第几天时销售利润最大？（3）在（2）的条件下，若要使第15天的利润比（2）中最大利润最多少127.5元，则第15天在第14天的价格基础上最多可降多少元？24.如图，分别是可活动的菱形和平行四边形学具，已知平行四边形较短的边与菱形的边长相等．（1）在一次数学活动中，某小组学生将菱形的一边与平行四边形较短边重合，摆拼成如图1所示的图形，AF 经过点C ，连接DE 交AF 于点M ，观察发现：点M 是DE 的中点．下面是两位学生有代表性的证明思路： 思路１：不需作辅助线，直接证三角形全等； 思路2：不证三角形全等，连接BD 交AF 于点H ．、 ……请参考上面的思路，证明点M 是DE 的中点（只需用一种方法证明）；（2）如图2，在（1）的条件下，当135ABE ∠=︒时，延长AD 、EF 交于点N ，求AMNE的值；（3）在（2）的条件下，若AF k AB =（k 为大于2的常数），直接用含k 的代数式表示AMMF的值．25.在平面直角坐标系中，我们定义直线y ax a =-为抛物线2y ax bx c =++（a 、b 、c 为常数，0a ≠）的“梦想直线”；有一个顶点在抛物线上，另一个顶点在y 轴上的三角形为其“梦想三角形”． 已知抛物线223432333y x x =--+与其“梦想直线”交于A 、B 两点（点A 在点B 的左侧），与x 轴负半轴交于点C ．（1）填空：该抛物线的“梦想直线”的解析式为 ，点A 的坐标为 ，点B 的坐标为 ；（2）如图，点M 为线段CB 上一动点，将ACM ∆以AM 所在直线为对称轴翻折，点C 的对称点为N ，若AMN ∆为该抛物线的“梦想三角形”，求点N 的坐标；。

FH PACBED考数学复习二十——四边形与平行四边形一、中考要求：1．探索并了解多边形的内角和与外角和公式，了解正多边形的概念；掌握多边形的内角和定理与外角和定理；了解n 边形的对角线的条数公式。

2．通过探索平面图形的镶嵌，知道任意一个三角形、四边形或正六边形可以镶嵌平面，并能运用这几种图形进行简单的镶嵌设计。

3．掌握平行四边形的定义、性质和判定方法(从边、角、对角线三个方面);知道平行四边形是中心对称图形，具备不稳定性，4．会用平行四边形的性质与判定解决简单的问题。

二、知识要点：1．一般地，由n 条不在同一直线上的线段 连结组成的平面图形称为n 边形，又称为多边形。

2．如果多边形的各边都 ，各内角也都 ，则称这个多边形为正多边形。

3．连结多边形不相邻的两个顶点的线段叫做多边形的 。

4．n 边形的内角和为 。

正n 边形的一个内角是 。

5．任意多边形的外角和为 。

正n 边形的一个外角是 。

6．从n 边形的一个顶点可引 条对角线，n 边形一共有 条对角线。

7．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个 角时，这几个多边形就能拼成一个平面图形。

两种图形的平面镶嵌：正三角形可以与边长相等的 镶嵌。

8．平行四边形的定义两组对边分别 的四边形叫做平行四边形。

9．平行四边形的性质(1)边： (2)角： (3)对角线： (4)对称性：10．两条平行线间的距离： 11．平行四边形的识别从边考虑⎪⎩⎪⎨⎧ ⎪⎭⎪⎬⎫ 是平行四边形。

从角考虑： (4)两组对角 的四边形是平行四边形。

说说此判定的证明方法：从对角线考虑(5)对角线 的四边形是平行四边形。

三、典例剖析：例1.如图，已知在□ABCD 中，E 、F 是对角线BD 上的两点，BE ＝DF ，点G 、H 分别在BA 和DC 的延长线上，且AG ＝CH ，连接GE 、EH 、HF 、FG ． 求证：四边形GEHF 是平行四边形．例2．如图，在平行四边形ABCD 中，E 、F 分别是边AD 、BC 的中点，AC 分别交BE 、DF 于点M 、N . 给出下列 结论：①△ABM ≌△CDN ；②AM =31AC ；③DN =2NF ； ④S △AMB =21S △ABC .其中正确的结论是 （只填序号）.例3．已知四边形ABCD 的对角线AC 与BD 交于点O ,给出下列四个论断 ① OA ＝OC ② AB ＝CD ③ ∠BAD ＝∠DCB ④ AD ∥BC请你从中选择两个论断作为条件,以“四边形ABCD 为平行四边形”作为结论,完成下列各题： ①构造一个真命题．．．： ； ②构造一个假命题．．．： ， 举反例加以说明 . 例4．如图，在△ABC 中，AB =AC =5，BC =6，动点P 从点A 出发沿AB 向点B 移动，（点P 与点A 、B 不重合），作PD //BC 交AC 于点D ，在DC 上取点E ，以DE 、DP 为邻边作平行四边形PFED ，使点F 到PD 的距离16FH PD =，连接BF ，设AP x =（1）△ABC 的面积等于NMFEDBA(1)两组对边 的四边形 (2)两组对边 的四边形 (3)一组对边 且 的四边形（2）设△PBF 的面积为y ，求y 与x 的函数关系，并求y 的最大值；（3）当BP =BF 时，求x 的值随堂演练：1．图中是一个五角星图案，中间部分的五边形ABCDE 是一个正五边形， 则图中∠ABC 的度数是 .2．如果只用一种正多边形进行镶嵌，那么在下列的正多边形中， 不能镶嵌成一个平面的是（ ）．A ．正三角形B .正方形C .正五边形D .正六边形 3.一个多边形内角和是，则这个多边形是（ ） A ．六边形B ．七边形C ．八边形D ．九边形4．在平行四边形ABCD 中，点1A ，2A ，3A ，4A 和1C ，2C ，3C ，4C 分别是AB 和CD 的五等分点，点1B ，2B 和1D ，2D 分别是BC 和DA 的三等分点，已知四边形4242A B C D 的面积为1，则平行四边形ABCD 的面积为（ ） A ．2B ．35C ．53D ．155．边长为的正六边形的面积等于（ ） A ．B ．C ．D ．6．如图，在周长为20cm 的□ABCD 中，AB ≠AD ，AC 、BD 相交于点O ，OE ⊥BD 交AD 于E ，则△ABE 的周长为7．下列四种边长均为a 的正多边形中，能与边长为a 的正三角形作平面镶嵌的正多边形有1080a 243a 2a 2233a 233a A BCDEABCDOED D 1D 2 AA 1 A 2 A 3 A 4B 1B 2 CC 2 13 4 B（）①正方形②正五边形③正六边形④正八边形A．4种B．3种C．2种D．1种8.如图，在□ABCD中，对角线AC、BD相交于点O，若AC=14，BD=8，AB=10，则△OAB的周长为.9.如图，在平行四边形ABCD中，DB=DC、65=∠A，CE⊥BD于E，则=∠BCE．10. 如图是对称中心为点的正八边形．如果用一个含角的直角三角板的角，借助点（使角的顶点落在点处）把这个正八边形的面积等分．那么的所有可能的值有（）A．2个B．3个C．4个D．5个11. 问题背景（1）如图1，△ABC中，DE∥BC分别交AB，AC于D，E两点，过点E作EF∥AB交BC于点F．请按图示数据填空：四边形DBFE的面积S=，△EFC的面积1S=，△ADE的面积2S=．探究发现（2）在（1）中，若BF a=，FC b=，DE与BC间的距离为h．请证明2124S S S=．拓展迁移（3）如图2，□DEFG的四个顶点在△ABC的三边上，若△ADG、△DBE、△GFC的面积分别为2、5、3，试利用．．（2．）中的结论．．．．求△ABC的面积．O45O O nnB CD GFE图2AB CDFE图1A36214．四边形一条对角线所在直线上的点，如果到这条对角线的两端点的距离不相等，但到另一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点．如图l，点P为四边形ABCD对角线AC所在直线上的一点，PD=PB，PA≠PC，则点P为四边形ABCD的准等距点．(1)如图2，画出菱形ABCD的一个准等距点．(2)如图3，作出四边形ABCD的一个准等距点(尺规作图，保留作图痕迹，不要求写作法)．(3)如图4，在四边形ABCD中，P是AC上的点，PA≠PC，延长BP交CD于点E，延长DP交BC于点F，且∠CDF=∠CBE，CE=CF．求证：点P是四边形AB CD的准等距点．图1中考数学复习作业二十1．如图下面对图形的判断正确的是( )A ．非对称图形B ．既是轴对称图形，又是中心对称图形C ．是轴对称图形，非中心对称图形D ．是中心对称图形，非轴对称图形 2．如图所示，顺次连接矩形ABCD 各边中点，得到菱形EFGH ， 这个由矩形和菱形所组成的图形( ) A ．是轴对称图形但不是中心对称图形 B ．是中心对称图形但不是轴对称图形C ．既是轴对称图形又是中心对称图形D ．没有对称性3．只用下列正多边形地砖中的一种，能够铺满地面的是（ ） A .正十边形 B .正八边形 C .正六边形 D .正五边形4．A 、B 、C 、D 在同一平面内，从①AB ∥CD ；②AB =CD ；③BC ∥AD ；④BC =AD 这四个条件中任选两个，能使四边形ABCD 是平行四边形的选法有 ( )A ．3种B ．4种C ．5种D ．6种5．平行四边形ABCD 中，AB =3，BC =5，∠B 的平分线把长边分成两条线段之比是( )A ．3:2B ．3:1C ．4:2D ．4:16．如果平行四边形的一条边长是4，一条对角线长是10，那么它的另一条对角线的长m 的取值范围是( )A ．6＜m ＜14B ．1＜m ＜9C ．3＜m ＜7D ．2＜m ＜18 7．三角形纸片ABC 中，∠A =65°，∠B =75°，将纸片的一角折叠，使 点C 落在ABC 内(如图)，若∠1=20°，则∠2的度数为。

中考数学总复习《平行四边形的判定与性质》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．如图在四边形ABCD中AB=CD，对角线AC、BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF、CE，若DE=BF，则下列结论不一定正确的是（）A．CF=AE B．OE=OFC．△CDE为直角三角形D．四边形ABCD是平行四边形2．如图四边形ABCD中AB∥CD，∥B＝∥D点E为BC延长线上一点，连接AE，AE交CD于点H，∥DCE的平分线交AE于点G．若AB＝2AD＝10，点H为CD的中点，HE＝6，则AC的值为（）A．9B．√97C．10D．3 √103．如图在Rt∥ABC中∥ACB=90°，分别以AB、AC为腰向外作等腰直角三角形∥ABD和∥ACE，连结DE，CA的延长线交DE于点F,则与线段AF相等的是()A．AC B．AB C．BC D．AB4．如图在菱形ΑΒCD中∠Α=60∘，AD=8，F是ΑΒ的中点．过点F作FΕ⊥ΑD，垂足为Ε．将ΔΑΕF沿点Α到点Β的方向平移，得到ΔΑ′Ε′F ′．设Ρ、Ρ′分别是ΕF、Ε′F ′的中点，当点Α′与点Β重合时，四边形ΡΡ′CD的面积为（）A．28√3B．24√3C．32√3D．32√3−85．下列说法中错误的是()A．平行四边形的对角线互相平分B．对角线互相垂直的四边形是菱形C．菱形的对角线互相垂直D．对角线互相平分的四边形是平行四边形6．如图．若要使平行四边形ABCD成为菱形．则需要添加的条件是（）A．AB=CD B．AD=BC C．AB=BC D．AC=BD7．如图点A是直线l外一点，在l上取两点B，C，分别以A，C为圆心，BC，AB的长为半径作弧，两弧交于点D，分别连接AB，AD，CD，若∥ABC+∥ADC=120°，则∥A的度数是（）A．100°B．110°C．120°D．125°8．如图在∥ABC中AB＝AC＝10，BC＝12，点D是BC上一点，DE∥AC，DF∥AB，则∥BED与∥DFC的周长的和为（）A．34B．32C．22D．209．如图在平面直角坐标系中点A(1,5),B(4,1),C(m,−m),D(m−3,−m+4)，当四边形ABCD 的周长最小时，则m 的值为（）.A．√2B．32C．2D．310．如图分别在四边形ABCD的各边上取中点E，F，G，H，连接EG，在EG上取一点M，连接HM，过F作FN∥HM，交EG于N，将四边形ABCD中的四边形①和②移动后按图中方式摆放，得到四边形AHM′G′和AF′N′E，延长M′G′，N′F′相交于点K，得到四边形MM′KN′．下列说法中错误的是（）A．S四边形MM′KN′=S四边形ABCD B．HM=NFC．四边形MM′KN′是平行四边形D．∠K=∠AHM′11．如图,已知∥ABC与∥CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD 是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤∥AOE与∥COF成中心对称.其中正确的个数为（）A．2B．3C．4D．512．如图P为平行四边形ABCD内一点，过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点，若S四边形AHPE＝3，S四边形PFCG＝5，则S∥PBD为（）A．0.5B．1C．1.5D．2二、填空题13．如图在平行四边形ABCD中点E，F分别在BC，AD上，请添加一个条件，使四边形AECF是平行四边形（只填一个即可）．14．如图在Rt△ABC中AC=2√3，BC=2，点P是斜边AB上任意一点，D是AC的中点，连接PD并延长，使DE=PD.以PE，PC为边构造平行四边形PCQE，则对角线PQ的最小值为.15．如图▱ABCD中∥BAD=120°，E、F分别在CD和BC的延长线上，AE∥BD，EF∥BC，EF=5√3，则AB的长是16．如图在∥ABC中∥ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD= 13BD，连接DM、DN、MN．若AB=6，则DN=．17．若AC＝10，BD＝8，那么当AO＝DO＝时，四边形ABCD是平行四边形。

2017年广西贵港市中考数学试卷一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．7的相反数是（ ）A．7B．﹣7C．D．﹣2．数据3，2，4，2，5，3，2的中位数和众数分别是（ ）A．2，3B．4，2C．3，2D．2，23．如图是一个空心圆柱体，它的左视图是（ ）A．B．C．D．4．下列二次根式中，最简二次根式是（ ）A．B．C．D．5．下列运算正确的是（ ）A．3a2+a=3a3B．2a3•（﹣a2）=2a5C．4a6+2a2=2a3D．（﹣3a）2﹣a2=8a26．在平面直角坐标系中，点P（m﹣3，4﹣2m）不可能在（ ）A．第一象限B．第二象限C．第三象限D．第四象限7．下列命题中假命题是（ ）A．正六边形的外角和等于360°B．位似图形必定相似C．样本方差越大，数据波动越小D．方程x2+x+1=0无实数根8．从长为3，5，7，10的四条线段中任意选取三条作为边，能构成三角形的概率是（ ）A．B．C．D．19．如图，A，B，C，D是⊙O上的四个点，B是的中点，M是半径OD上任意一点．若∠BDC=40°，则∠AMB的度数不可能是（ ）A．45°B．60°C．75°D．85°10．将如图所示的抛物线向右平移1个单位长度，再向上平移3个单位长度后，得到的抛物线解析式是（ ）A．y=（x﹣1）2+1B．y=（x+1）2+1C．y=2（x﹣1）2+1D．y=2（x+1）2+111．如图，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值是（ ）A．4B．3C．2D．112．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是，其中正确结论的个数是（ ）A．2B．3C．4D．5二、填空题（每题3分，满分18分，将答案填在答题纸上）13．计算：﹣3﹣5= ．14．中国的领水面积约为370 000km2，将数370 000用科学记数法表示为 ．15．如图，AB∥CD，点E在AB上，点F在CD上，如果∠CFE：∠EFB=3：4，∠ABF=40°，那么∠BEF的度数为 ．16．如图，点P在等边△ABC的内部，且PC=6，PA=8，PB=10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，则sin∠PAP'的值为 ．17．如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与交于点D，以O为圆心，OC 的长为半径作交OB于点E，若OA=4，∠AOB=120°，则图中阴影部分的面积为 ．（结果保留π）18．如图，过C（2，1）作AC∥x轴，BC∥y轴，点A，B都在直线y=﹣x+6上，若双曲线y=（x＞0）与△ABC总有公共点，则k的取值范围是 ．三、解答题（本大题共8小题，共66分.解答应写出文字说明、证明过程或演算步骤.）19．（1）计算：|﹣3|+（+π）0﹣（﹣）﹣2﹣2cos60°；（2）先化简，在求值：（﹣）+，其中a=﹣2+．20．尺规作图（不写作法，保留作图痕迹）：已知线段a和∠AOB，点M在OB上（如图所示）．（1）在OA边上作点P，使OP=2a；（2）作∠AOB的平分线；（3）过点M作OB的垂线．21．如图，一次函数y=2x﹣4的图象与反比例函数y=的图象交于A，B两点，且点A的横坐标为3．（1）求反比例函数的解析式；（2）求点B的坐标．22．在开展“经典阅读”活动中，某学校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计表．根据图表信息，解答下列问题：频率分布表阅读时间（小时）频数（人）频率1≤x＜2180.12 2≤x＜3a m 3≤x＜4450.3 4≤x＜536n 5≤x＜6210.14合计b1（1）填空：a= ，b= ，m= ，n= ；（2）将频数分布直方图补充完整（画图后请标注相应的频数）；（3）若该校由3000名学生，请根据上述调查结果，估算该校学生一周的课外阅读时间不足三小时的人数．23．某次篮球联赛初赛阶段，每队有10场比赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得1分，积分超过15分才能获得参赛资格．（1）已知甲队在初赛阶段的积分为18分，求甲队初赛阶段胜、负各多少场；（2）如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？24．如图，在菱形ABCD中，点P在对角线AC上，且PA=PD，⊙O是△PAD的外接圆．（1）求证：AB是⊙O的切线；（2）若AC=8，tan∠BAC=，求⊙O的半径．25．如图，抛物线y=a（x﹣1）（x﹣3）与x轴交于A，B两点，与y轴的正半轴交于点C，其顶点为D．（1）写出C，D两点的坐标（用含a的式子表示）；（2）设S△BCD：S△ABD=k，求k的值；（3）当△BCD是直角三角形时，求对应抛物线的解析式．26．已知，在Rt△ABC中，∠ACB=90°，AC=4，BC=2，D是AC边上的一个动点，将△ABD 沿BD所在直线折叠，使点A落在点P处．（1）如图1，若点D是AC中点，连接PC．①写出BP，BD的长；②求证：四边形BCPD是平行四边形．（2）如图2，若BD=AD，过点P作PH⊥BC交BC的延长线于点H，求PH的长．　2017年广西贵港市中考数学试卷参考答案与试题解析一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．7的相反数是（ ）A．7B．﹣7C．D．﹣【考点】14：相反数．【分析】根据一个数的相反数就是在这个数前面添上“﹣”号，求解即可．【解答】解：7的相反数是﹣7，故选：B．2．数据3，2，4，2，5，3，2的中位数和众数分别是（ ）A．2，3B．4，2C．3，2D．2，2【考点】W5：众数；W4：中位数．【分析】根据中位数和众数的定义分别进行解答即可．【解答】解：把这组数据从小到大排列：2，2，2，3，3，4，5，最中间的数是3，则这组数据的中位数是3；2出现了3次，出现的次数最多，则众数是2．故选：C．3．如图是一个空心圆柱体，它的左视图是（ ）A．B．C．D．【考点】U1：简单几何体的三视图．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看是三个矩形，中间矩形的左右两边是虚线，故选：B．4．下列二次根式中，最简二次根式是（ ）A．B．C．D．【考点】74：最简二次根式．【分析】检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．【解答】解：A、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故A符合题意；B、被开方数含能开得尽方的因数或因式，故B不符合题意；C、被开方数含分母，故C不符合题意；D、被开方数含能开得尽方的因数或因式，故D不符合题意；故选：A．5．下列运算正确的是（ ）A．3a2+a=3a3B．2a3•（﹣a2）=2a5C．4a6+2a2=2a3D．（﹣3a）2﹣a2=8a2【考点】49：单项式乘单项式；35：合并同类项；47：幂的乘方与积的乘方．【分析】运用合并同类项，单项式乘以单项式，幂的乘方等运算法则运算即可．【解答】解：A.3a2与a不是同类项，不能合并，所以A错误；B.2a3•（﹣a2）=2×（﹣1）a5=﹣2a5，所以B错误；C.4a6与2a2不是同类项，不能合并，所以C错误；D．（﹣3a）2﹣a2=9a2﹣a2=8a2，所以D正确，故选D．6．在平面直角坐标系中，点P（m﹣3，4﹣2m）不可能在（ ）A．第一象限B．第二象限C．第三象限D．第四象限【考点】D1：点的坐标．【分析】分点P的横坐标是正数和负数两种情况讨论求解．【解答】解：①m﹣3＞0，即m＞3时，﹣2m＜﹣6，4﹣2m＜﹣2，所以，点P（m﹣3，4﹣2m）在第四象限，不可能在第一象限；②m﹣3＜0，即m＜3时，﹣2m＞﹣6，4﹣2m＞﹣2，点P（m﹣3，4﹣2m）可以在第二或三象限，综上所述，点P不可能在第一象限．故选A．7．下列命题中假命题是（ ）A．正六边形的外角和等于360°B．位似图形必定相似C．样本方差越大，数据波动越小D．方程x2+x+1=0无实数根【考点】O1：命题与定理．【分析】根据正确的命题是真命题，错误的命题是假命题进行分析即可．【解答】解：A、正六边形的外角和等于360°，是真命题；B、位似图形必定相似，是真命题；C、样本方差越大，数据波动越小，是假命题；D、方程x2+x+1=0无实数根，是真命题；故选：C．8．从长为3，5，7，10的四条线段中任意选取三条作为边，能构成三角形的概率是（ ）A．B．C．D．1【考点】X6：列表法与树状图法；K6：三角形三边关系．【分析】列举出所有等可能的情况数，找出能构成三角形的情况数，即可求出所求概率．【解答】解：从长为3，5，7，10的四条线段中任意选取三条作为边，所有等可能情况有：3，5，7；3，5，10；3，7，10；5，7，10，共4种，其中能构成三角形的情况有：3，5，7；5，7，10，共2种，则P（能构成三角形）==，故选B9．如图，A，B，C，D是⊙O上的四个点，B是的中点，M是半径OD上任意一点．若∠BDC=40°，则∠AMB的度数不可能是（ ）A．45°B．60°C．75°D．85°【考点】M5：圆周角定理；M4：圆心角、弧、弦的关系．【分析】根据圆周角定理求得∠AOB的度数，则∠AOB的度数一定不小于∠AMB的度数，据此即可判断．【解答】解：∵B是的中点，∴∠AOB=2∠BDC=80°，又∵M是OD上一点，∴∠AMB≤∠AOB=80°．则不符合条件的只有85°．故选D．10．将如图所示的抛物线向右平移1个单位长度，再向上平移3个单位长度后，得到的抛物线解析式是（ ）A．y=（x﹣1）2+1B．y=（x+1）2+1C．y=2（x﹣1）2+1D．y=2（x+1）2+1【考点】H6：二次函数图象与几何变换．【分析】根据平移规律，可得答案．【解答】解：由图象，得y=2x2﹣2，由平移规律，得y=2（x﹣1）2+1，故选：C．11．如图，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值是（ ）A．4B．3C．2D．1【考点】R2：旋转的性质．【分析】如图连接PC．思想求出PC=2，根据PM≤PC+CM，可得PM≤3，由此即可解决问题．【解答】解：如图连接PC．在Rt△ABC中，∵∠A=30°，BC=2，∴AB=4，根据旋转不变性可知，A′B′=AB=4，∴A′P=PB′，∴PC=A′B′=2，∵CM=BM=1，又∵PM≤PC+CM，即PM≤3，∴PM的最大值为3（此时P、C、M共线）．故选B．12．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是，其中正确结论的个数是（ ）A．2B．3C．4D．5【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LE：正方形的性质．【分析】根据正方形的性质，依次判定△CNB≌△DMC，△OCM≌△OBN，△CON≌△DOM，△OMN∽△OAD，根据全等三角形的性质以及勾股定理进行计算即可得出结论．【解答】解：∵正方形ABCD中，CD=BC，∠BCD=90°，∴∠BCN+∠DCN=90°，又∵CN⊥DM，∴∠CDM+∠DCN=90°，∴∠BCN=∠CDM，又∵∠CBN=∠DCM=90°，∴△CNB≌△DMC（ASA），故①正确；根据△CNB≌△DMC，可得CM=BN，又∵∠OCM=∠OBN=45°，OC=OB，∴△OCM≌△OBN（SAS），∴OM=ON，∠COM=∠BON，∴∠DOC+∠COM=∠COB+∠BPN，即∠DOM=∠CON，又∵DO=CO，∴△CON≌△DOM（SAS），故②正确；∵∠BON+∠BOM=∠COM+∠BOM=90°，∴∠MON=90°，即△MON是等腰直角三角形，又∵△AOD是等腰直角三角形，∴△OMN∽△OAD，故③正确；∵AB=BC，CM=BN，∴BM=AN，又∵Rt△BMN中，BM2+BN2=MN2，∴AN2+CM2=MN2，故④正确；∵△OCM≌△OBN，∴四边形BMON的面积=△BOC的面积=1，即四边形BMON的面积是定值1，∴当△MNB的面积最大时，△MNO的面积最小，设BN=x=CM，则BM=2﹣x，∴△MNB的面积=x（2﹣x）=﹣x2+x，∴当x=1时，△MNB的面积有最大值，此时S△OMN的最小值是1﹣=，故⑤正确；综上所述，正确结论的个数是5个，故选：D．二、填空题（每题3分，满分18分，将答案填在答题纸上）13．计算：﹣3﹣5=　﹣8　．【考点】1A：有理数的减法．【分析】根据有理数的减法运算法则进行计算即可得解．【解答】解：﹣3﹣5=﹣8．故答案为：﹣8．14．中国的领水面积约为370 000km2，将数370 000用科学记数法表示为　3.7×105　．【考点】1I：科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．确定a×10n（1≤|a|＜10，n为整数）中n的值，由于370 000有6位，所以可以确定n=6﹣1=5．【解答】解：370 000=3.7×105，故答案为：3.7×105．15．如图，AB∥CD，点E在AB上，点F在CD上，如果∠CFE：∠EFB=3：4，∠ABF=40°，那么∠BEF的度数为　60°　．【考点】JA：平行线的性质．【分析】先根据平行线的性质，得到∠CFB的度数，再根据∠CFE：∠EFB=3：4以及平行线的性质，即可得出∠BEF的度数．【解答】解：∵AB∥CD，∠ABF=40°，∴∠CFB=180°﹣∠B=140°，又∵∠CFE：∠EFB=3：4，∴∠CFE=∠CFB=60°，∵AB∥CD，∴∠BEF=∠CFE=60°，故答案为：60°．16．如图，点P在等边△ABC的内部，且PC=6，PA=8，PB=10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，则sin∠PAP'的值为 ．【考点】R2：旋转的性质；KK：等边三角形的性质；T7：解直角三角形．【分析】连接PP′，如图，先利用旋转的性质得CP=CP′=6，∠PCP′=60°，则可判定△CPP′为等边三角形得到PP′=PC=6，再证明△PCB≌△P′CA得到PB=P′A=10，接着利用勾股定理的逆定理证明△APP′为直角三角形，∠APP′=90°，然后根据正弦的定义求解．【解答】解：连接PP′，如图，∵线段PC绕点C顺时针旋转60°得到P'C，∴CP=CP′=6，∠PCP′=60°，∴△CPP′为等边三角形，∴PP′=PC=6，∵△ABC为等边三角形，∴CB=CA，∠ACB=60°，∴∠PCB=∠P′CA，在△PCB和△P′CA中，∴△PCB≌△P′CA，∴PB=P′A=10，∵62+82=102，∴PP′2+AP2=P′A2，∴△APP′为直角三角形，∠APP′=90°，∴sin∠PAP′===．故答案为．17．如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与交于点D，以O为圆心，OC的长为半径作交OB于点E，若OA=4，∠AOB=120°，则图中阴影部分的面积为　π+2　．（结果保留π）【考点】MO：扇形面积的计算；KG：线段垂直平分线的性质．【分析】连接OD、AD，根据点C为OA的中点可得∠CDO=30°，继而可得△ADO为等边三角形，求出扇形AOD的面积，最后用扇形AOB的面积减去扇形COE的面积，再减去S空白ADC 即可求出阴影部分的面积．【解答】解：连接O、AD，∵点C为OA的中点，∴∠C DO=30°，∠DOC=60°，∴△ADO为等边三角形，∴S扇形AOD==π，∴S阴影=S扇形AOB﹣S扇形COE﹣（S扇形AOD﹣S△COD）=﹣﹣（π﹣×2×2）=π﹣π﹣π+2=π+2．故答案为π+2．18．如图，过C（2，1）作AC∥x轴，BC∥y轴，点A，B都在直线y=﹣x+6上，若双曲线y=（x＞0）与△ABC总有公共点，则k的取值范围是　2≤k≤9　．【考点】G8：反比例函数与一次函数的交点问题．【分析】把C的坐标代入求出k≥2，解两函数组成的方程组，根据根的判别式求出k≤9，即可得出答案．【解答】解：当反比例函数的图象过C点时，把C的坐标代入得：k=2×1=2；把y=﹣x+6代入y=得：﹣x+6=，x2﹣6x+k=0，△=（﹣6）2﹣4k=36﹣4k，∵反比例函数y=的图象与△ABC有公共点，∴36﹣4k≥0，k≤9，即k的范围是2≤k≤9，故答案为：2≤k≤9．三、解答题（本大题共8小题，共66分.解答应写出文字说明、证明过程或演算步骤.）19．（1）计算：|﹣3|+（+π）0﹣（﹣）﹣2﹣2cos60°；（2）先化简，在求值：（﹣）+，其中a=﹣2+．【考点】6D：分式的化简求值；2C：实数的运算；6E：零指数幂；6F：负整数指数幂；T5：特殊角的三角函数值．【分析】（1）根据零指数幂的意义、特殊角的锐角三角函数以及负整数指数幂的意义即可求出答案；（2）先化简原式，然后将a的值代入即可求出答案．【解答】解：（1）原式=3+1﹣（﹣2）2﹣2×=4﹣4﹣1=﹣1（2）当a=﹣2+原式=+===7+520．尺规作图（不写作法，保留作图痕迹）：已知线段a和∠AOB，点M在OB上（如图所示）．（1）在OA边上作点P，使OP=2a；（2）作∠AOB的平分线；（3）过点M作OB的垂线．【考点】N3：作图—复杂作图．【分析】（1）在OA上截取OP=2a即可求出点P的位置；（2）根据角平分线的作法即可作出∠AOB的平分线；（3）以M为圆心，作一圆与射线OB交于两点，再以这两点分别为圆心，作两个相等半径的圆交于D点，连接MD即为OB的垂线；【解答】解：（1）点P为所求作；（2）OC为所求作；（3）MD为所求作；21．如图，一次函数y=2x﹣4的图象与反比例函数y=的图象交于A，B两点，且点A的横坐标为3．（1）求反比例函数的解析式；（2）求点B的坐标．【考点】G8：反比例函数与一次函数的交点问题．【分析】（1）把x=3代入一次函数解析式求得A的坐标，利用待定系数法求得反比例函数解析式；（2）解一次函数与反比例函数解析式组成的方程组求得B的坐标．【解答】解：（1）把x=3代入y=2x﹣4得y=6﹣4=2，则A的坐标是（3，2）．把（3，2）代入y=得k=6，则反比例函数的解析式是y=；（2）根据题意得2x﹣4=，解得x=3或﹣1，把x=﹣1代入y=2x﹣4得y=﹣6，则B的坐标是（﹣1，﹣6）．22．在开展“经典阅读”活动中，某学校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计表．根据图表信息，解答下列问题：频率分布表阅读时间（小时）频数（人）频率1≤x＜2180.12 2≤x＜3a m 3≤x＜4450.3 4≤x＜536n 5≤x＜6210.14合计b1（1）填空：a=　30　，b=　150　，m=　0.2　，n=　0.24　；（2）将频数分布直方图补充完整（画图后请标注相应的频数）；（3）若该校由3000名学生，请根据上述调查结果，估算该校学生一周的课外阅读时间不足三小时的人数．【考点】V8：频数（率）分布直方图；V5：用样本估计总体；V7：频数（率）分布表．【分析】（1）根据阅读时间为1≤x＜2的人数及所占百分比可得，求出总人数b=150，再根据频率、频数、总人数的关系即可求出m、n、a；（2）根据数据将频数分布直方图补充完整即可；（3）由总人数乘以时间不足三小时的人数的频率即可．【解答】解：（1）b=18÷0.12=150（人），∴n=36÷150=0.24，∴m=1﹣0.12﹣0.3﹣0.24﹣0.14=0.2，∴a=0.2×150=30；故答案为：30，150，0.2，0.24；（2）如图所示：（3）3000×（0.12+0.2）=960（人）；即估算该校学生一周的课外阅读时间不足三小时的人数为960人．23．某次篮球联赛初赛阶段，每队有10场比赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得1分，积分超过15分才能获得参赛资格．（1）已知甲队在初赛阶段的积分为18分，求甲队初赛阶段胜、负各多少场；（2）如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？【考点】C9：一元一次不等式的应用；8A：一元一次方程的应用．【分析】（1）设甲队胜了x场，则负了（10﹣x）场，根据每队胜一场得2分，负一场得1分，利用甲队在初赛阶段的积分为18分，进而得出等式求出答案；（2）设乙队在初赛阶段胜a场，根据积分超过15分才能获得参赛资格，进而得出答案．【解答】解：（1）设甲队胜了x场，则负了（10﹣x）场，根据题意可得：2x+10﹣x=18，解得：x=8，则10﹣x=2，答：甲队胜了8场，则负了2场；（2）设乙队在初赛阶段胜a场，根据题意可得：2a+（10﹣a）≥15，解得：a≥5，答：乙队在初赛阶段至少要胜5场．24．如图，在菱形ABCD中，点P在对角线AC上，且PA=PD，⊙O是△PAD的外接圆．（1）求证：AB是⊙O的切线；（2）若AC=8，tan∠BAC=，求⊙O的半径．【考点】ME：切线的判定与性质；L8：菱形的性质；T7：解直角三角形．【分析】（1）连结OP、OA，OP交AD于E，由PA=PD得弧AP=弧DP，根据垂径定理的推理得OP⊥AD，AE=DE，则∠1+∠OPA=90°，而∠OAP=∠OPA，所以∠1+∠OAP=90°，再根据菱形的性质得∠1=∠2，所以∠2+∠OAP=90°，然后根据切线的判定定理得到直线AB与⊙O 相切；（2）连结BD，交AC于点F，根据菱形的性质得DB与AC互相垂直平分，则AF=4，tan∠DAC=，得到DF=2，根据勾股定理得到AD==2，求得AE=，设⊙O的半径为R，则OE=R﹣，OA=R，根据勾股定理列方程即可得到结论．【解答】解：（1）连结OP、OA，OP交AD于E，如图，∵PA=PD，∴弧AP=弧DP，∴OP⊥AD，AE=DE，∴∠1+∠OPA=90°，∵OP=OA，∴∠OAP=∠OPA，∴∠1+∠OAP=90°，∵四边形ABCD为菱形，∴∠1=∠2，∴∠2+∠OAP=90°，∴OA⊥AB，∴直线AB与⊙O相切；（2）连结BD，交AC于点F，如图，∵四边形ABCD为菱形，∴DB与AC互相垂直平分，∵AC=8，tan∠BAC=，∴AF=4，tan∠DAC==，∴DF=2，∴AD==2，∴AE=，在Rt△PAE中，tan∠1==，∴PE=，设⊙O的半径为R，则OE=R﹣，OA=R，在Rt△OAE中，∵OA2=OE2+AE2，∴R2=（R﹣）2+（）2，∴R=，即⊙O的半径为．25．如图，抛物线y=a（x﹣1）（x﹣3）与x轴交于A，B两点，与y轴的正半轴交于点C，其顶点为D．（1）写出C，D两点的坐标（用含a的式子表示）；（2）设S△BCD：S△ABD=k，求k的值；（3）当△BCD是直角三角形时，求对应抛物线的解析式．【考点】HF：二次函数综合题．【分析】（1）令x=0可求得C点坐标，化为顶点式可求得D点坐标；（2）令y=0可求得A、B的坐标，结合D点坐标可求得△ABD的面积，设直线CD交x轴于点E，由C、D坐标，利用待定系数法可求得直线CD的解析式，则可求得E点坐标，从而可表示出△BCD的面积，可求得k的值；（3）由B、C、D的坐标，可表示出BC2、BD2和CD2，分∠CBD=90°和∠CDB=90°两种情况，分别利用勾股定理可得到关于a的方程，可求得a的值，则可求得抛物线的解析式．【解答】解：（1）在y=a（x﹣1）（x﹣3），令x=0可得y=3a，∴C（0，3a），∵y=a（x﹣1）（x﹣3）=a（x2﹣4x+3）=a（x﹣2）2﹣a，∴D（2，﹣a）；（2）在y=a（x﹣1）（x﹣3）中，令y=0可解得x=1或x=3，∴A（1，0），B（3，0），∴AB=3﹣1=2，∴S△ABD=×2×a=a，如图，设直线CD交x轴于点E，设直线CD解析式为y=kx+b，把C、D的坐标代入可得，解得，∴直线CD解析式为y=﹣2ax+3a，令y=0可解得x=，∴E（，0），∴BE=3﹣=∴S△BCD=S△BEC+S△BED=××（3a+a）=3a，∴S△BCD：S△ABD=（3a）：a=3，∴k=3；（3）∵B（3，0），C（0，3a），D（2，﹣a），∴BC2=32+（3a）2=9+9a2，CD2=22+（﹣a﹣3a）2=4+16a2，BD2=（3﹣2）2+a2=1+a2，∵∠BCD＜∠BCO＜90°，∴△BCD为直角三角形时，只能有∠CBD=90°或∠CDB=90°两种情况，①当∠CBD=90°时，则有BC2+BD2=CD2，即9+9a2+1+a2=4+16a2，解得a=﹣1（舍去）或a=1，此时抛物线解析式为y=x2﹣4x+3；②当∠CDB=90°时，则有CD2+BD2=BC2，即4+16a2+1+a2=9+9a2，解得a=﹣（舍去）或a=，此时抛物线解析式为y=x2﹣2x+；综上可知当△BCD是直角三角形时，抛物线的解析式为y=x2﹣4x+3或y=x2﹣2x+．26．已知，在Rt△ABC中，∠ACB=90°，AC=4，BC=2，D是AC边上的一个动点，将△ABD 沿BD所在直线折叠，使点A落在点P处．（1）如图1，若点D是AC中点，连接PC．①写出BP，BD的长；②求证：四边形BCPD是平行四边形．（2）如图2，若BD=AD，过点P作PH⊥BC交BC的延长线于点H，求PH的长．【考点】LO：四边形综合题．【分析】（1）①分别在Rt△ABC，Rt△BDC中，求出AB、BD即可解决问题；②想办法证明DP∥BC，DP=BC即可；（2）如图2中，作DN⊥AB于N，PE⊥AC于E，延长BD交PA于M．设BD=AD=x，则CD=4﹣x，在Rt△BDC中，可得x2=（4﹣x）2+22，推出x=，推出DN==，由△BDN∽△BAM，可得=，由此求出AM，由△ADM∽△APE，可得=，由此求出AE=，可得EC=AC﹣AE=4﹣=由此即可解决问题．【解答】解：（1）①在Rt△ABC中，∵BC=2，AC=4，∴AB==2，∵AD=CD=2，∴BD==2，由翻折可知，BP=BA=2．②如图1中，∵△BCD是等腰直角三角形，∴∠BDC=45°，∴∠ADB=∠BDP=135°，∴∠PDC=135°﹣45°=90°，∴∠BCD=∠PDC=90°，∴DP∥BC，∵PD=AD=BC=2，∴四边形BCPD是平行四边形．（2）如图2中，作DN⊥AB于N，PE⊥AC于E，延长BD交PA于M．设BD=AD=x，则CD=4﹣x，在Rt△BDC中，∵BD2=CD2+BC2，∴x2=（4﹣x）2+22，∴x=，∵DB=DA，DN⊥AB，∴BN=AN=，在Rt△BDN中，DN==，由△BDN∽△BAM，可得=，∴=，∴AM=2，∴AP=2AM=4，由△ADM∽△APE，可得=，∴=，∴AE=，∴EC=AC﹣AE=4﹣=，易证四边形PECH是矩形，∴PH=EC=．。

2017年广西贵港市中考数学试卷一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．7的相反数是（）A．7 B．﹣7 C．D．﹣2．数据3，2，4，2，5，3，2的中位数和众数分别是（）A．2，3 B．4，2 C．3，2 D．2，23．如图是一个空心圆柱体，它的左视图是（）A． B．C． D．4．下列二次根式中，最简二次根式是（）A． B． C．D．5．下列运算正确的是（）A．3a2+a=3a3 B．2a3•（﹣a2）=2a5C．4a6+2a2=2a3D．（﹣3a）2﹣a2=8a26．在平面直角坐标系中，点P（m﹣3，4﹣2m）不可能在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限7．下列命题中假命题是（）A．正六边形的外角和等于360°B．位似图形必定相似C．样本方差越大，数据波动越小D．方程x2+x+1=0无实数根8．从长为3，5，7，10的四条线段中任意选取三条作为边，能构成三角形的概率是（）A．B．C．D．19．如图，A，B，C，D是⊙O上的四个点，B是的中点，M是半径OD上任意一点．若∠BDC=40°，则∠AMB的度数不可能是（）A．45° B．60° C．75° D．85°10．将如图所示的抛物线向右平移1个单位长度，再向上平移3个单位长度后，得到的抛物线解析式是（）A．y=（x﹣1）2+1 B．y=（x+1）2+1 C．y=2（x﹣1）2+1 D．y=2（x+1）2+111．如图，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值是（）A．4 B．3 C．2 D．112．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是，其中正确结论的个数是（）A．2 B．3 C．4 D．5二、填空题（每题3分，满分18分，将答案填在答题纸上）13．计算：﹣3﹣5= ．14．中国的领水面积约为370 000km2，将数370 000用科学记数法表示为．15．如图，AB∥CD，点E在AB上，点F在CD上，如果∠CFE：∠EFB=3：4，∠ABF=40°，那么∠BEF的度数为．16．如图，点P在等边△ABC的内部，且PC=6，PA=8，PB=10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，则sin∠PAP'的值为．17．如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与交于点D，以O为圆心，OC的长为半径作交OB于点E，若OA=4，∠AOB=120°，则图中阴影部分的面积为．（结果保留π）18．如图，过C（2，1）作AC∥x轴，BC∥y轴，点A，B都在直线y=﹣x+6上，若双曲线y=（x＞0）与△ABC总有公共点，则k的取值范围是．三、解答题（本大题共8小题，共66分.解答应写出文字说明、证明过程或演算步骤.）19．（1）计算：|﹣3|+（+π）0﹣（﹣）﹣2﹣2cos60°；（2）先化简，在求值：（﹣）+，其中a=﹣2+．20．尺规作图（不写作法，保留作图痕迹）：已知线段a和∠AOB，点M在OB上（如图所示）．（1）在OA边上作点P，使OP=2a；（2）作∠AOB的平分线；（3）过点M作OB的垂线．21．如图，一次函数y=2x﹣4的图象与反比例函数y=的图象交于A，B两点，且点A的横坐标为3．（1）求反比例函数的解析式；（2）求点B的坐标．22．在开展“经典阅读”活动中，某学校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计表．根据图表信息，解答下列问题：频率分布表阅读时间（小时）频数（人）频率1≤x＜2 18 0.122≤x＜3 a m3≤x＜4 45 0.34≤x＜5 36 n5≤x＜6 21 0.14合计 b 1（1）填空：a= ，b= ，m= ，n= ；（2）将频数分布直方图补充完整（画图后请标注相应的频数）；（3）若该校由3000名学生，请根据上述调查结果，估算该校学生一周的课外阅读时间不足三小时的人数．23．某次篮球联赛初赛阶段，每队有10场比赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得1分，积分超过15分才能获得参赛资格．（1）已知甲队在初赛阶段的积分为18分，求甲队初赛阶段胜、负各多少场；（2）如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？24．如图，在菱形ABCD中，点P在对角线AC上，且PA=PD，⊙O是△PAD的外接圆．（1）求证：AB是⊙O的切线；（2）若AC=8，tan∠BAC=，求⊙O的半径．25．如图，抛物线y=a（x﹣1）（x﹣3）与x轴交于A，B两点，与y轴的正半轴交于点C，其顶点为D．（1）写出C，D两点的坐标（用含a的式子表示）；（2）设S△BCD：S△ABD=k，求k的值；（3）当△BCD是直角三角形时，求对应抛物线的解析式．26．已知，在Rt△ABC中，∠ACB=90°，AC=4，BC=2，D是AC边上的一个动点，将△ABD 沿BD所在直线折叠，使点A落在点P处．（1）如图1，若点D是AC中点，连接PC．①写出BP，BD的长；②求证：四边形BCPD是平行四边形．（2）如图2，若BD=AD，过点P作PH⊥BC交BC的延长线于点H，求PH的长．2017年广西贵港市中考数学试卷参考答案与试题解析一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．7的相反数是（）A．7 B．﹣7 C．D．﹣【考点】14：相反数．【分析】根据一个数的相反数就是在这个数前面添上“﹣”号，求解即可．【解答】解：7的相反数是﹣7，故选：B．2．数据3，2，4，2，5，3，2的中位数和众数分别是（）A．2，3 B．4，2 C．3，2 D．2，2【考点】W5：众数；W4：中位数．【分析】根据中位数和众数的定义分别进行解答即可．【解答】解：把这组数据从小到大排列：2，2，2，3，3，4，5，最中间的数是3，则这组数据的中位数是3；2出现了3次，出现的次数最多，则众数是2．故选：C．3．如图是一个空心圆柱体，它的左视图是（）A． B．C． D．【考点】U1：简单几何体的三视图．【分析】根据从左边看得到的图形是左视图，可得答案．【解答】解：从左边看是三个矩形，中间矩形的左右两边是虚线，故选：B．4．下列二次根式中，最简二次根式是（）A． B． C．D．【考点】74：最简二次根式．【分析】检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．【解答】解：A、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故A符合题意；B、被开方数含能开得尽方的因数或因式，故B不符合题意；C、被开方数含分母，故C不符合题意；D、被开方数含能开得尽方的因数或因式，故D不符合题意；故选：A．5．下列运算正确的是（）A．3a2+a=3a3 B．2a3•（﹣a2）=2a5C．4a6+2a2=2a3D．（﹣3a）2﹣a2=8a2【考点】49：单项式乘单项式；35：合并同类项；47：幂的乘方与积的乘方．【分析】运用合并同类项，单项式乘以单项式，幂的乘方等运算法则运算即可．【解答】解：A.3a2与a不是同类项，不能合并，所以A错误；B.2a3•（﹣a2）=2×（﹣1）a5=﹣2a5，所以B错误；C.4a6与2a2不是同类项，不能合并，所以C错误；D．（﹣3a）2﹣a2=9a2﹣a2=8a2，所以D正确，故选D．6．在平面直角坐标系中，点P（m﹣3，4﹣2m）不可能在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】D1：点的坐标．【分析】分点P的横坐标是正数和负数两种情况讨论求解．【解答】解：①m﹣3＞0，即m＞3时，﹣2m＜﹣6，4﹣2m＜﹣2，所以，点P（m﹣3，4﹣2m）在第四象限，不可能在第一象限；②m﹣3＜0，即m＜3时，﹣2m＞﹣6，4﹣2m＞﹣2，点P（m﹣3，4﹣2m）可以在第二或三象限，综上所述，点P不可能在第一象限．故选A．7．下列命题中假命题是（）A．正六边形的外角和等于360°B．位似图形必定相似C．样本方差越大，数据波动越小D．方程x2+x+1=0无实数根【考点】O1：命题与定理．【分析】根据正确的命题是真命题，错误的命题是假命题进行分析即可．【解答】解：A、正六边形的外角和等于360°，是真命题；B、位似图形必定相似，是真命题；C、样本方差越大，数据波动越小，是假命题；D、方程x2+x+1=0无实数根，是真命题；故选：C．8．从长为3，5，7，10的四条线段中任意选取三条作为边，能构成三角形的概率是（）A．B．C．D．1【考点】X6：列表法与树状图法；K6：三角形三边关系．【分析】列举出所有等可能的情况数，找出能构成三角形的情况数，即可求出所求概率．【解答】解：从长为3，5，7，10的四条线段中任意选取三条作为边，所有等可能情况有：3，5，7；3，5，10；3，7，10；5，7，10，共4种，其中能构成三角形的情况有：3，5，7；5，7，10，共2种，则P（能构成三角形）==，故选B9．如图，A，B，C，D是⊙O上的四个点，B是的中点，M是半径OD上任意一点．若∠BDC=40°，则∠AMB的度数不可能是（）A．45° B．60° C．75° D．85°【考点】M5：圆周角定理；M4：圆心角、弧、弦的关系．【分析】根据圆周角定理求得∠AOB的度数，则∠AOB的度数一定不小于∠AMB的度数，据此即可判断．【解答】解：∵B是的中点，∴∠AOB=2∠BDC=80°，又∵M是OD上一点，∴∠AMB≤∠AOB=80°．则不符合条件的只有85°．故选D．10．将如图所示的抛物线向右平移1个单位长度，再向上平移3个单位长度后，得到的抛物线解析式是（）A．y=（x﹣1）2+1 B．y=（x+1）2+1 C．y=2（x﹣1）2+1 D．y=2（x+1）2+1【考点】H6：二次函数图象与几何变换．【分析】根据平移规律，可得答案．【解答】解：由图象，得y=2x2﹣2，由平移规律，得y=2（x﹣1）2+1，故选：C．11．如图，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值是（）A．4 B．3 C．2 D．1【考点】R2：旋转的性质．【分析】如图连接PC．思想求出PC=2，根据PM≤PC+CM，可得PM≤3，由此即可解决问题．【解答】解：如图连接PC．在Rt△ABC中，∵∠A=30°，BC=2，∴AB=4，根据旋转不变性可知，A′B′=AB=4，∴A′P=PB′，∴PC=A′B′=2，∵CM=BM=1，又∵PM≤PC+CM，即PM≤3，∴PM的最大值为3（此时P、C、M共线）．故选B．12．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是，其中正确结论的个数是（）A．2 B．3 C．4 D．5【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LE：正方形的性质．【分析】根据正方形的性质，依次判定△CNB≌△DMC，△OCM≌△OBN，△CON≌△DOM，△OMN ∽△OAD，根据全等三角形的性质以及勾股定理进行计算即可得出结论．【解答】解：∵正方形ABCD中，CD=BC，∠BCD=90°，∴∠BCN+∠DCN=90°，又∵CN⊥DM，∴∠CDM+∠DCN=90°，∴∠BCN=∠CDM，又∵∠CBN=∠DCM=90°，∴△CNB≌△DMC（ASA），故①正确；根据△CNB≌△DMC，可得CM=BN，又∵∠OCM=∠OBN=45°，OC=OB，∴△OCM≌△OBN（SAS），∴OM=ON，∠COM=∠BON，∴∠DOC+∠COM=∠COB+∠BPN，即∠DOM=∠CON，又∵DO=CO，∴△CON≌△DOM（SAS），故②正确；∵∠BON+∠BOM=∠COM+∠BOM=90°，∴∠MON=90°，即△MON是等腰直角三角形，又∵△AOD是等腰直角三角形，∴△OMN∽△OAD，故③正确；∵AB=BC，CM=BN，∴BM=AN，又∵Rt△BMN中，BM2+BN2=MN2，∴AN2+CM2=MN2，故④正确；∵△OCM≌△OBN，∴四边形BMON的面积=△BOC的面积=1，即四边形BMON的面积是定值1，∴当△MNB的面积最大时，△MNO的面积最小，设BN=x=CM，则BM=2﹣x，∴△MNB的面积=x（2﹣x）=﹣x2+x，∴当x=1时，△MNB的面积有最大值，此时S△OMN的最小值是1﹣=，故⑤正确；综上所述，正确结论的个数是5个，故选：D．二、填空题（每题3分，满分18分，将答案填在答题纸上）13．计算：﹣3﹣5= ﹣8 ．【考点】1A：有理数的减法．【分析】根据有理数的减法运算法则进行计算即可得解．【解答】解：﹣3﹣5=﹣8．故答案为：﹣8．14．中国的领水面积约为370 000km2，将数370 000用科学记数法表示为 3.7×105．【考点】1I：科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．确定a×10n（1≤|a|＜10，n为整数）中n的值，由于370 000有6位，所以可以确定n=6﹣1=5．【解答】解：370 000=3.7×105，故答案为：3.7×105．15．如图，AB∥CD，点E在AB上，点F在CD上，如果∠CFE：∠EFB=3：4，∠ABF=40°，那么∠BEF的度数为60°．【考点】JA：平行线的性质．【分析】先根据平行线的性质，得到∠CFB的度数，再根据∠CFE：∠EFB=3：4以及平行线的性质，即可得出∠BEF的度数．【解答】解：∵AB∥CD，∠ABF=40°，∴∠CFB=180°﹣∠B=140°，又∵∠CFE：∠EFB=3：4，∴∠CFE=∠CFB=60°，∵AB∥CD，∴∠BEF=∠CFE=60°，故答案为：60°．16．如图，点P在等边△ABC的内部，且PC=6，PA=8，PB=10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，则sin∠PAP'的值为．【考点】R2：旋转的性质；KK：等边三角形的性质；T7：解直角三角形．【分析】连接PP′，如图，先利用旋转的性质得CP=CP′=6，∠PCP′=60°，则可判定△CPP′为等边三角形得到PP′=PC=6，再证明△PCB≌△P′CA得到PB=P′A=10，接着利用勾股定理的逆定理证明△APP′为直角三角形，∠APP′=90°，然后根据正弦的定义求解．【解答】解：连接PP′，如图，∵线段PC绕点C顺时针旋转60°得到P'C，∴CP=CP′=6，∠PCP′=60°，∴△CPP′为等边三角形，∴PP′=PC=6，∵△ABC为等边三角形，∴CB=CA，∠ACB=60°，∴∠PCB=∠P′CA，在△PCB和△P′CA中，∴△PCB≌△P′CA，∴PB=P′A=10，∵62+82=102，∴PP′2+AP2=P′A2，∴△APP′为直角三角形，∠AP P′=90°，∴sin∠PAP′===．故答案为．17．如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与交于点D，以O为圆心，OC的长为半径作交OB于点E，若OA=4，∠AOB=120°，则图中阴影部分的面积为π+2．（结果保留π）【考点】MO：扇形面积的计算；KG：线段垂直平分线的性质．【分析】连接OD、AD，根据点C为OA的中点可得∠CDO=30°，继而可得△ADO为等边三角形，求出扇形AOD的面积，最后用扇形AOB的面积减去扇形COE的面积，再减去S空白ADC即可求出阴影部分的面积．【解答】解：连接O、AD，∵点C为OA的中点，∴∠C DO=30°，∠DOC=60°，∴△ADO为等边三角形，∴S扇形AOD==π，∴S阴影=S扇形AOB﹣S扇形COE﹣（S扇形AOD﹣S△COD）=﹣﹣（π﹣×2×2）=π﹣π﹣π+2=π+2．故答案为π+2．18．如图，过C（2，1）作AC∥x轴，BC∥y轴，点A，B都在直线y=﹣x+6上，若双曲线y=（x＞0）与△ABC总有公共点，则k的取值范围是2≤k≤9 ．【考点】G8：反比例函数与一次函数的交点问题．【分析】把C的坐标代入求出k≥2，解两函数组成的方程组，根据根的判别式求出k≤9，即可得出答案．【解答】解：当反比例函数的图象过C点时，把C的坐标代入得：k=2×1=2；把y=﹣x+6代入y=得：﹣x+6=，x2﹣6x+k=0，△=（﹣6）2﹣4k=36﹣4k，∵反比例函数y=的图象与△ABC有公共点，∴36﹣4k≥0，k≤9，即k的范围是2≤k≤9，故答案为：2≤k≤9．三、解答题（本大题共8小题，共66分.解答应写出文字说明、证明过程或演算步骤.）19．（1）计算：|﹣3|+（+π）0﹣（﹣）﹣2﹣2cos60°；（2）先化简，在求值：（﹣）+，其中a=﹣2+．【考点】6D：分式的化简求值；2C：实数的运算；6E：零指数幂；6F：负整数指数幂；T5：特殊角的三角函数值．【分析】（1）根据零指数幂的意义、特殊角的锐角三角函数以及负整数指数幂的意义即可求出答案；（2）先化简原式，然后将a的值代入即可求出答案．【解答】解：（1）原式=3+1﹣（﹣2）2﹣2×=4﹣4﹣1=﹣1（2）当a=﹣2+原式=+===7+520．尺规作图（不写作法，保留作图痕迹）：已知线段a和∠AOB，点M在OB上（如图所示）．（1）在OA边上作点P，使OP=2a；（2）作∠AOB的平分线；（3）过点M作OB的垂线．【考点】N3：作图—复杂作图．【分析】（1）在OA上截取OP=2a即可求出点P的位置；（2）根据角平分线的作法即可作出∠AOB的平分线；（3）以M为圆心，作一圆与射线OB交于两点，再以这两点分别为圆心，作两个相等半径的圆交于D点，连接MD即为OB的垂线；【解答】解：（1）点P为所求作；（2）OC为所求作；（3）MD为所求作；21．如图，一次函数y=2x﹣4的图象与反比例函数y=的图象交于A，B两点，且点A的横坐标为3．（1）求反比例函数的解析式；（2）求点B的坐标．【考点】G8：反比例函数与一次函数的交点问题．【分析】（1）把x=3代入一次函数解析式求得A的坐标，利用待定系数法求得反比例函数解析式；（2）解一次函数与反比例函数解析式组成的方程组求得B的坐标．【解答】解：（1）把x=3代入y=2x﹣4得y=6﹣4=2，则A的坐标是（3，2）．把（3，2）代入y=得k=6，则反比例函数的解析式是y=；（2）根据题意得2x﹣4=，解得x=3或﹣1，把x=﹣1代入y=2x﹣4得y=﹣6，则B的坐标是（﹣1，﹣6）．22．在开展“经典阅读”活动中，某学校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计表．根据图表信息，解答下列问题：频率分布表阅读时间（小时）频数（人）频率1≤x＜2 18 0.122≤x＜3 a m3≤x＜4 45 0.34≤x＜5 36 n5≤x＜6 21 0.14合计 b 1（1）填空：a= 30 ，b= 150 ，m= 0.2 ，n= 0.24 ；（2）将频数分布直方图补充完整（画图后请标注相应的频数）；（3）若该校由3000名学生，请根据上述调查结果，估算该校学生一周的课外阅读时间不足三小时的人数．【考点】V8：频数（率）分布直方图；V5：用样本估计总体；V7：频数（率）分布表．【分析】（1）根据阅读时间为1≤x＜2的人数及所占百分比可得，求出总人数b=150，再根据频率、频数、总人数的关系即可求出m、n、a；（2）根据数据将频数分布直方图补充完整即可；（3）由总人数乘以时间不足三小时的人数的频率即可．【解答】解：（1）b=18÷0.12=150（人），∴n=36÷150=0.24，∴m=1﹣0.12﹣0.3﹣0.24﹣0.14=0.2，∴a=0.2×150=30；故答案为：30，150，0.2，0.24；（2）如图所示：（3）3000×（0.12+0.2）=960（人）；即估算该校学生一周的课外阅读时间不足三小时的人数为960人．23．某次篮球联赛初赛阶段，每队有10场比赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得1分，积分超过15分才能获得参赛资格．（1）已知甲队在初赛阶段的积分为18分，求甲队初赛阶段胜、负各多少场；（2）如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？【考点】C9：一元一次不等式的应用；8A：一元一次方程的应用．【分析】（1）设甲队胜了x场，则负了（10﹣x）场，根据每队胜一场得2分，负一场得1分，利用甲队在初赛阶段的积分为18分，进而得出等式求出答案；（2）设乙队在初赛阶段胜a场，根据积分超过15分才能获得参赛资格，进而得出答案．【解答】解：（1）设甲队胜了x场，则负了（10﹣x）场，根据题意可得：2x+10﹣x=18，解得：x=8，则10﹣x=2，答：甲队胜了8场，则负了2场；（2）设乙队在初赛阶段胜a场，根据题意可得：2a+（10﹣a）≥15，解得：a≥5，答：乙队在初赛阶段至少要胜5场．24．如图，在菱形ABCD中，点P在对角线AC上，且PA=PD，⊙O是△PAD的外接圆．（1）求证：AB是⊙O的切线；（2）若AC=8，tan∠BAC=，求⊙O的半径．【考点】ME：切线的判定与性质；L8：菱形的性质；T7：解直角三角形．【分析】（1）连结OP、OA，OP交AD于E，由PA=PD得弧AP=弧DP，根据垂径定理的推理得OP⊥AD，AE=DE，则∠1+∠OPA=90°，而∠OAP=∠OPA，所以∠1+∠OAP=90°，再根据菱形的性质得∠1=∠2，所以∠2+∠OAP=90°，然后根据切线的判定定理得到直线AB与⊙O相切；（2）连结BD，交AC于点F，根据菱形的性质得DB与AC互相垂直平分，则AF=4，tan∠DAC=，得到DF=2，根据勾股定理得到AD==2，求得AE=，设⊙O的半径为R，则OE=R﹣，OA=R，根据勾股定理列方程即可得到结论．【解答】解：（1）连结OP、OA，OP交AD于E，如图，∵PA=PD，∴弧AP=弧DP，∴OP⊥AD，AE=DE，∴∠1+∠OPA=90°，∵OP=OA，∴∠OAP=∠OPA，∴∠1+∠OAP=90°，∵四边形ABCD为菱形，∴∠1=∠2，∴∠2+∠OAP=90°，∴OA⊥AB，∴直线AB与⊙O相切；（2）连结BD，交AC于点F，如图，∵四边形ABCD为菱形，∴DB与AC互相垂直平分，∵AC=8，tan∠BAC=，∴AF=4，tan∠DAC==，∴DF=2，∴AD==2，∴AE=，在Rt△PAE中，tan∠1==，∴PE=，设⊙O的半径为R，则OE=R﹣，OA=R，在Rt△OAE中，∵OA2=OE2+AE2，∴R2=（R﹣）2+（）2，∴R=，即⊙O的半径为．25．如图，抛物线y=a（x﹣1）（x﹣3）与x轴交于A，B两点，与y轴的正半轴交于点C，其顶点为D．（1）写出C，D两点的坐标（用含a的式子表示）；（2）设S△BCD：S△ABD=k，求k的值；（3）当△BCD是直角三角形时，求对应抛物线的解析式．【考点】HF：二次函数综合题．【分析】（1）令x=0可求得C点坐标，化为顶点式可求得D点坐标；（2）令y=0可求得A、B的坐标，结合D点坐标可求得△ABD的面积，设直线CD交x轴于点E，由C、D坐标，利用待定系数法可求得直线CD的解析式，则可求得E点坐标，从而可表示出△BCD的面积，可求得k的值；（3）由B、C、D的坐标，可表示出BC2、BD2和CD2，分∠CBD=90°和∠CDB=90°两种情况，分别利用勾股定理可得到关于a的方程，可求得a的值，则可求得抛物线的解析式．【解答】解：（1）在y=a（x﹣1）（x﹣3），令x=0可得y=3a，∴C（0，3a），∵y=a（x﹣1）（x﹣3）=a（x2﹣4x+3）=a（x﹣2）2﹣a，∴D（2，﹣a）；（2）在y=a（x﹣1）（x﹣3）中，令y=0可解得x=1或x=3，∴A（1，0），B（3，0），∴AB=3﹣1=2，∴S△ABD=×2×a=a，如图，设直线CD交x轴于点E，设直线CD解析式为y=kx+b，把C、D的坐标代入可得，解得，∴直线CD解析式为y=﹣2ax+3a，令y=0可解得x=，∴E（，0），∴BE=3﹣=∴S△BCD=S△BEC+S△BED=××（3a+a）=3a，∴S△BCD：S△ABD=（3a）：a=3，∴k=3；（3）∵B（3，0），C（0，3a），D（2，﹣a），∴BC2=32+（3a）2=9+9a2，CD2=22+（﹣a﹣3a）2=4+16a2，BD2=（3﹣2）2+a2=1+a2，∵∠BCD＜∠BCO＜90°，∴△BCD为直角三角形时，只能有∠CBD=90°或∠CDB=90°两种情况，①当∠CBD=90°时，则有BC2+BD2=CD2，即9+9a2+1+a2=4+16a2，解得a=﹣1（舍去）或a=1，此时抛物线解析式为y=x2﹣4x+3；②当∠CDB=90°时，则有CD2+BD2=BC2，即4+16a2+1+a2=9+9a2，解得a=﹣（舍去）或a=，此时抛物线解析式为y=x2﹣2x+；综上可知当△BCD是直角三角形时，抛物线的解析式为y=x2﹣4x+3或y=x2﹣2x+．26．已知，在Rt△ABC中，∠ACB=90°，AC=4，BC=2，D是AC边上的一个动点，将△ABD 沿BD所在直线折叠，使点A落在点P处．（1）如图1，若点D是AC中点，连接PC．①写出BP，BD的长；②求证：四边形BCPD是平行四边形．（2）如图2，若BD=AD，过点P作PH⊥BC交BC的延长线于点H，求PH的长．【考点】LO：四边形综合题．【分析】（1）①分别在Rt△ABC，Rt△BDC中，求出AB、BD即可解决问题；②想办法证明DP∥BC，DP=BC即可；（2）如图2中，作DN⊥AB于N，PE⊥AC于E，延长BD交PA于M．设BD=AD=x，则CD=4﹣x，在Rt△BDC中，可得x2=（4﹣x）2+22，推出x=，推出DN==，由△BDN∽△BAM，可得=，由此求出AM，由△ADM∽△APE，可得=，由此求出AE=，可得EC=AC﹣AE=4﹣=由此即可解决问题．【解答】解：（1）①在Rt△ABC中，∵BC=2，AC=4，∴AB==2，∵AD=CD=2，∴BD==2，由翻折可知，BP=BA=2．②如图1中，∵△BCD是等腰直角三角形，∴∠BDC=45°，∴∠ADB=∠BDP=135°，∴∠PDC=135°﹣45°=90°，∴∠BCD=∠PDC=90°，∴DP∥BC，∵PD=AD=BC=2，∴四边形BCPD是平行四边形．（2）如图2中，作DN⊥AB于N，PE⊥AC于E，延长BD交PA于M．设BD=AD=x，则CD=4﹣x，在Rt△BDC中，∵BD2=CD2+BC2，∴x2=（4﹣x）2+22，∴x=，∵DB=DA，DN⊥AB，∴BN=AN=，在Rt△BDN中，DN==，由△BDN∽△BAM，可得=，∴=，∴AM=2，∴AP=2AM=4，由△ADM∽△APE，可得=，∴=，∴AE=，∴EC=AC﹣AE=4﹣=，易证四边形PECH是矩形，∴PH=EC=．。