半导体PN结物理特性实验智能化数据处理系数的制作
- 格式:doc
- 大小:470.50 KB
- 文档页数:26

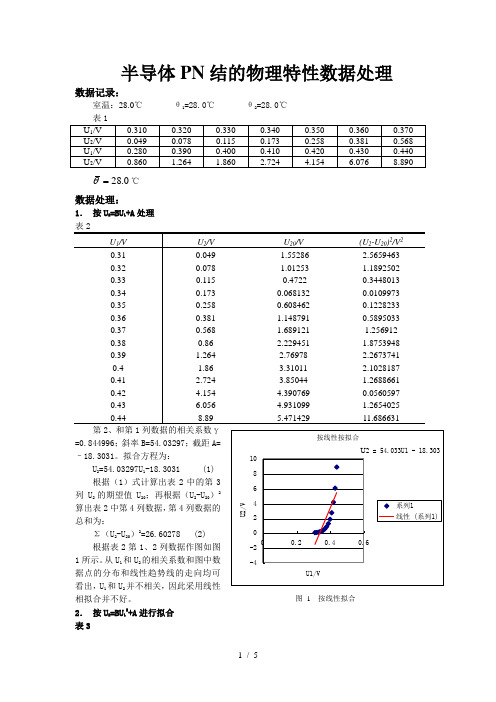
半导体PN 结的物理特性数据处理数据记录:室温:28.0℃ θ1=28.0℃ θ2=28.0℃0.28=θ℃ 数据处理:1. 按U 2=BU 1+A 处理 表2第2、和第1列数据的相关系数γ=0.844996;斜率B=54.03297;截距A=–18.3031。
拟合方程为:U 2=54.03297U 1-18.3031 (1) 根据(1)式计算出表2中的第3列U 2的期望值U 20;再根据(U 2-U 20)2算出表2中第4列数据,第4列数据的总和为:Σ(U 2-U 20)2=26.60278 (2) 根据表2第1、2列数据作图如图1所示。
从U 1和U 2的相关系数和图中数据点的分布和线性趋势线的走向均可看出,U 1和U 2并不相关,因此采用线性相拟合并不好。
2. 按U 2=BU 12+A 进行拟合 表3图 1 按线性拟合表3第2、和第3列数据的相关系数γ=0.8675393;斜率B=73.881948;截距A=–8.550421。
拟合方程为:U 2=73.881948U 12-8.550421 (3) 根据(3)式计算出表3中的第4列U 2的期望值U 20;再根据(U 2-U 20)2算出表3中第5列数据,第5列数据的总和为:Σ(U 2-U 20)2=23.011569 (4)根据表3第3、2列数据作图如图1所示。
从U 12和U 2的相关系数和图中数据点的分布和线性趋势线的走向均可看出,U 12和U 2并不相关,因此采用幂函数拟合并不好。
3.按U 2=AU 1B进行拟合对表4的第1、2列数据取对数构成表4中的第3、4列。
图 2 按幂函数拟合表4第4、和第3列数据的相关系数γ=0.999223;斜率B=14.7826;截距A=14.21027。
拟合方程为: LNU 2=14.7826LNU 1+14.21027 (5)(5)式可写为:LNU 2=LNU 114。
786+Lne 14。
2107于是有 U 2=1484022×U 114。

半导体PN 结的物理特性实验报告姓名:陈晨 学号:12307110123 专业:物理学系 日期:2013年12月16日 一、引言半导体PN 结是电子技术中许多元件的物质基础具有广泛应用,因此半导体PN 结的伏安特性是半导体物理学的重要内容。
本实验利用运算放大器组成电流-电压变换器的方法精确测量弱电流,研究PN 结的正向电流I ,正向电压U ,温度T 之间的关系。
本实验桶过处理实验数据得到经验公式,验证了正向电流与正向电压的指数关系,正向电流与温度的指数关系以及正向电压与温度的线性关系,并由此与计算玻尔兹曼常数k 与0K 时材料的禁带宽度E ,加深了对半导体PN 节的理解。
二、实验原理 1、 PN 结的物理特性(1)PN 结的定义:若将一块半导体晶体一侧掺杂成P 型半导体,即有多余电子的半导体,另一侧掺杂成N 型半导体,即有多余空穴的半导体,则中间二者相连的接触面就称为PN 结。
(2)PN 结的正向伏安特性:根据半导体物理学的理论,一个理想PN 结的正向电流I 与正向电压U 之间存在关系 ①,其中I S 为反向饱和电流,k 为玻尔兹曼常数,T 为热力学温度,e 为电子电量。
在常温(T=300K )下和实验所取电压U的范围内, 故①可化为 ②,两边取对数可得 。
(3)当温度T 不变时作lnI-U 图像并对其进行线性拟合,得到线性拟合方程的斜率为e/kT ,带入已知常数e 和T ,便得玻尔兹曼常数k 。
2、反向饱和电流I s(1)禁带宽度E :在固体物理学中泛指半导体或是绝缘体的价带顶端至传导带底端的能量差距。
对一个本征半导体而言,其导电性与禁带宽度的大小有关,只有获得足够能量的电子才能从价带被激发,跨过禁带宽度跃迁至导带。
(2)根据半导体物理学的理论,理想PN 结的反向饱和电流Is 可以表示为③,代入②得 ,其中I 0为与结面积和掺杂浓度等有关的常数,γ取决于少数载流子迁移率对温度的关系,通常取γ=3.4,k 为玻尔兹曼常数,T 为热力学温度.E 为0K时材料的禁带宽度。


专业:应用物理题目:PN 结特性(1)研究 PN 结正向压降随温度变化的基本规律。
(2)学习用 PN 结测温的方法。
(3)学习一种测量玻尔兹曼常数的方法。
DH-PN-2 型PN 结正向特性综合实验仪、DH-SJ 温度传感实验装置PN 结正向电流IF 和压降VF之间存在如下近似关系其中q 为电子电荷;k 为玻尔兹曼常数;T 为热力学温度;Is为反向饱和电流,它是一个和PN 结材料的禁带宽度以及温度等有关的系数其中 C 是与结面积、掺杂浓度等有关的常数; r 对温度的关系(通常取 r=3.4); V g (0)为 0K 时 联立二式可得是常数,其数值取决于少数载流子迁移率 PN 结材料的导带底和价带顶的电势差。
Vl 随温度线性变化, Vnl 为非线性变化,若忽略非线性部份,误差分析如下温度由 T 1 变为 T 时,正向电压由 V F1 变为 V F 时,正向电压理论值与忽略非线性部份值得 偏差为当温度变化范围较小时,该偏差可忽略(通过改变温度与I F 也可改善线度),令 I F =常数, 则正向压降只随温度升高线性下降,这就是 PN 结测温的依据。
1. 实验系统检查与连接关闭 DH-SJ 型温度传感器实验装置上的“加热电流”、“风扇电流”开关,接上加热电源 线。
插好 Pt100 温度传感器和 PN 结温度传感器,两者连接均为直插式。
PN 结引出线分 别插入 PN 结正向特性综合试验仪上的+V 、-V 和+I 、-I 。
打开电源开关,温度传感器实验装置上将显示出室温 T R ,记录下起始温度 T R 。
2. 玻尔兹曼常数 k 的测定测得 PN 结 I ~V 关系,求出玻尔兹曼常数 k 。
将 PN 结正向特性综合试验仪上的电流量 程置于适当档位,调整电流调节旋钮以改变正向电流 I F 输出示值,观察记录相应的正向电 压 V F 值读数。
3. 至少完成对一种 PN 结材料的 V ~T 曲线的测量及数据处理(1)测定 V ~T 关系曲线 选择合适的正向电流 I F (如 I F =50µA ,普通选小于 100μA 的 值,以减小自身热效应),并保持不变。

半导体PN 结物理特性实验智能化数据处理系数的制作实验13 半导体PN 结的物理特性【实验目的】(1)测量半导体PN 结电流与电压关系。
(2)测定PN 结温度传感器的灵敏度和玻尔兹曼常数。
【实验原理】PN 结伏安特性及玻尔兹曼常数测量由半导体物理学可知,PN 结的正向电流—电压关系满足:)1e(0-=kTU I I (13.1)式中,I 是通过PN 结的正向电流,I 0是反向饱和电流,在温度恒定时,I 为常数,T 是热力学温度,e 是电子的电荷量,U 为PN 结正向压降。
由于在常温T=300K 时,kT /e ≈0.026V ,而PN 结正向压降约为0.1V 的数量级,则1e >>kTU exp ,(13.1)式括号内 -1项完全可以忽略,于是有:kTUI I e0= (13.2)也即PN 结正向电流随正向电压按指数规律变化。
若测得PN 结I-U 关系值,则利用(13.1)式可以求出e /kT 。
在测得温度T 后,就可以得到e /k 常数,把电子电量作为已知值代入,即可求得玻尔兹曼常数k 。
在实际测量中,二极管的正向I -U 关系虽然能较好满足指数关系,但求得的常数k 往往偏小。
这是因为通过二极管电流不只是扩散电流,还有其它电流。
一般它包括三个部分:(1)扩散电流,它严格遵循(13.2)式;(2)耗尽层符合电流,它正比于kTeU 2e;(3)表面电流,它是由Si 和SiO 2界面中杂质引起的,其值正比于mkTeU e ,一般m >2。
因此,为了验证(13.2)式及求出准确的e /k 常数,不宜采用硅二极管,而采用硅三极管接成共基极线路,因为此时集电极与基极短接,集电极电流中仅仅是扩散电流。
复合电流主要在基极出现,测量集电极电流时,将不包括它。
本实验中选取性能良好的硅三极管(TIP31型),实验中又处于较低的正向偏置,这样表面电流影响也完全可以忽略,所以此时集电极图10.3 PN 结扩散电源与结电压关系测量线路图2.弱电流测量过去实验中10-6A ~ 10-11A 量级弱电流采用光点反射式检流计测量,该仪器灵敏度较高约10-9A/分度,但有许多不足之处。
成都信息工程学院物理实验报告姓名: 蔡青 专业: 班级: 学号: 实验日期: 2007-9-1下午 实验教室: 5102-1 指导教师: 【实验名称】 PN 结物理特性综合实验 【实验目的】1. 在室温时,测量PN 结电流与电压关系,证明此关系符合波耳兹曼分布规律2. 在不同温度条件下,测量玻尔兹曼常数3. 学习用运算放大器组成电流-电压变换器测量弱电流4. 测量PN 结电压与温度关系,求出该PN 结温度传感器的灵敏度5. 计算在0K 温度时,半导体硅材料的近似禁带宽度 【实验仪器】半导体PN 结的物理特性实验仪 资产编号:××××,型号:××× 【实验原理】1.PN 结的伏安特性及玻尔兹曼常数测量 PN 结的正向电流-电压关系满足:]1)/[exp(0-=kT eU I I (1)当()exp /1eU kT >>时,(1)式括号内-1项完全可以忽略,于是有:0exp(/)I I eU kT = (2)也即PN 结正向电流随正向电压按指数规律变化。
若测得PN 结I U -关系值,则利用(1)式可以求出/e kT 。
在测得温度T 后,就可以得到/e k ,把电子电量e 作为已知值代入,即可求得玻尔兹曼常数k 。
实验线路如图1所示。
2、弱电流测量LF356是一个高输入阻抗集成运算放大器,用它组成电流-电压变换器(弱电流放大器),如图2所示。
其中虚线框内电阻r Z 为电流-电压变换器等效输入阻抗。
运算放大器的输入电压0U 为:00i U K U =- (3)式(3)中i U 为输入电压,0K 为运算放大器的开环电压增益,即图2中电阻f R →∞时的电压增益(fR 称反馈电阻)。
因而有:0(1)i i s ffU U U K I R R -+==(4)由(4)式可得电流-电压变换器等效输入阻抗x Z 为1i f f x sU R R Z I K K ==≈+ (5)由(3)式和(4)式可得电流-电压变换器输入电流s I 与输出电压0U 之间的关系式,即:图1 PN 结扩散电源与结电压关系测量线路图图2 电流-电压变换器i s frU UI Z R ==-(6)只要测得输出电压0U 和已知f R 值,即可求得s I 值。
半导体PN结的物理特性实验目的与要求1、学会用运算放大器组成电流-电压变换器的方法测量弱电流。
2、研究PN结的正向电流与电压之间的关系。
3、学习通过实验数据处理求得经验公式的方法。
实验原理PN 结的物理特性测量由半导体物理学中有关PN 结的研究,可以得出PN 结的正向电流一电压关系满足(1)式中I是通过PN 结的正向电流,I0是不随电压变化的常数,T 是热力学温度,e 是电子的电荷量,U 为PN 结正向压降. 由于在常温(300 K)下,KT/e =0,026 V,而PN 结正向压降约为十分之几伏,则e eU/kT>>l,(1)式括号内-1 项完全可以忽略,于是有(2)即PN 结正向电流随正向电压按指数规律变化. 若测得PN 结I-U关系值,则利用(2)式可以求出e/kT. 在测得温度T 后,就可以得到e/k 常数,然后将电子电量作为已知值代入,即可求得玻尔兹曼常数k。
在实际测量中,为了提高测量玻尔兹曼常数的正确性,利用集成运算放大器组成的电流-电压变换器输人阻抗极小的特点,常用半导体三极管的集电极c与基极b短接(共基极)来代替PN结进行测量. 具体线路如图下实验仪器PN结实验仪、TIP31型三极管、恒温装置1 、直流电源和数字电压表,包括—15 V——0——+ 15V直流电源、1.5 V直流电源、0——2 V三位半数字电压表、四位半数字电压表.2、LF356 集成运算放大器,它的各引线脚如2脚、3 脚、4 脚、6 脚、7 脚由学生用棒针引线连接;待测样品TIP31型三极管的e、b、c 三电极可以从机壳右面接线柱接入3、不诱钢保温杯組合,它包括保温杯、内盛少量油的玻璃试管、搅拌器水银温度计等. (实验时,开始保温杯内为适量室温水,然后根据实验需要加一些热水,以改变槽内水的温度; 测量时应搅拌水,待槽内水温恒定时,进行测量)实验内容一、必做部分:1、在室温(保温杯加入适量的自来水,为什么?)下,测量PN结正向电流与电压的关系。
PN结的I-V特性的有限差分法的数值仿真路小龙(四川大学物理科学与技术学院微电子2012222020045)摘要:本文选取电注入条件下的非平衡PN结为研究对象。
从器件内部载流子和电场的分布情况以及状态和运动出发,依据器件的几何结构及杂质分布,在小注入条件,突变耗尽层条件,通过耗尽层的电子空穴电流为常量条件,波尔兹曼边界条件下建立严格的物理模型,并选取有限差分法进行运算得到器件的性能参数图。
通过这种方法能深刻理解器件内部的工作原理、能定量分析器件性能参数与设计参数之间的关系。
关键词:PN结,内部电场,数值计算,有限差分法1869年阴极射线管的发明成为了电子技术的发展起点,1904年真空电子二极管的诞生打开了电子技术的发展的大门,在这之后真空电子三极管,半导体PN结和其他半导体器件的发展为快速发展的电子信息技术奠定了基础,人们的生活随着这些半导体技术和微电子技术发展发生了天翻地覆的变化。
从早期的收音机、电话到现在的电脑手机等,都能感受到微电子技术带给人们生活上的极大便利。
自从IC芯片的诞生以来,其发展基本上遵循了因特尔公司创始人之一的摩尔1965年预言的摩尔定律。
芯片上可容纳的晶体管数目每18个月便可增加一倍,即芯片集成度18个月翻一番。
随着晶体管数目的增加,晶体管的尺寸越来越小,导致晶体管的电流电压方程变的越来越复杂,研发一种新的芯片的成本越来越高,为了节约成本提高效率,在芯片投产之前都要进行大量的计算机仿真,以确保电路功能的准确性和稳定性。
有很多著名公司也致力于电子技术自动化软件的研发,如Cadences,Synopsys等。
本文通过分析半导体二极管的原理,建立相应的物理器件模型,并对其电流电压关系进行数值计算,使二极管器件的计算机仿真成为一种可能。
一、物理模型和数学模型半导体的导电性能介于导体和绝缘体之间,我们通常选择硅(Si)作为现代半导体器件的主体材料,没有经过掺杂的纯净的半导体的导电能很差。
半导体PN 结物理特性实验智能化数据处理系数的制作实验13 半导体PN 结的物理特性【实验目的】(1)测量半导体PN 结电流与电压关系。
(2)测定PN 结温度传感器的灵敏度和玻尔兹曼常数。
【实验原理】PN 结伏安特性及玻尔兹曼常数测量由半导体物理学可知,PN 结的正向电流—电压关系满足:)1e(0-=kTU I I (13.1)式中,I 是通过PN 结的正向电流,I 0是反向饱和电流,在温度恒定时,I 为常数,T 是热力学温度,e 是电子的电荷量,U 为PN 结正向压降。
由于在常温T=300K 时,kT /e ≈0.026V ,而PN 结正向压降约为0.1V 的数量级,则1e >>kTU exp ,(13.1)式括号内 -1项完全可以忽略,于是有:kTUI I e0= (13.2)也即PN 结正向电流随正向电压按指数规律变化。
若测得PN 结I-U 关系值,则利用(13.1)式可以求出e /kT 。
在测得温度T 后,就可以得到e /k 常数,把电子电量作为已知值代入,即可求得玻尔兹曼常数k 。
在实际测量中,二极管的正向I -U 关系虽然能较好满足指数关系,但求得的常数k 往往偏小。
这是因为通过二极管电流不只是扩散电流,还有其它电流。
一般它包括三个部分:(1)扩散电流,它严格遵循(13.2)式;(2)耗尽层符合电流,它正比于kTeU 2e;(3)表面电流,它是由Si 和SiO 2界面中杂质引起的,其值正比于mkTeU e ,一般m >2。
因此,为了验证(13.2)式及求出准确的e /k 常数,不宜采用硅二极管,而采用硅三极管接成共基极线路,因为此时集电极与基极短接,集电极电流中仅仅是扩散电流。
复合电流主要在基极出现,测量集电极电流时,将不包括它。
本实验中选取性能良好的硅三极管(TIP31型),实验中又处于较低的正向偏置,这样表面电流影响也完全可以忽略,所以此时集电极图10.3 PN 结扩散电源与结电压关系测量线路图2.弱电流测量过去实验中10-6A ~ 10-11A 量级弱电流采用光点反射式检流计测量,该仪器灵敏度较高约10-9A/分度,但有许多不足之处。
如十分怕震,挂丝易断;使用时稍有不慎,光标易偏出满度,瞬间过载引起引丝疲劳变形产生不回零点及指示差变大。
使用和维修极不方便。
近年来,集成电路与数字化显示技术越来越普及。
高输入阻抗运算放大器性能优良,价格低廉,用它组成电流-电压变换器测量弱电流信号,具有输入阻抗低,电流灵敏度高。
温漂小、线性好、设计制作简单、结构牢靠等优点,因而被广泛应用于物理测量中。
LF356是一个高输入阻抗集成运算放大器,用它组成电流-电压变换器(弱电流放大器),如图13.4所示。
其中虚线框内电阻Z r 为电流-电压变换器等效输入阻抗。
由图13.4可,运算放大器的输入电压U 0为:U k U -=图13.4 电流-电压变换器式(13.3)中U i 为输入电压,K 0为运算放大器的开环电压增益,即图13.4中电阻∞→f R 时的电压增益,R f 称反馈电阻。
因为理想运算放大器的输入阻抗∞→i r ,所以信号源输入电流只流经反馈网络构成的通路。
因而有:f f i s R K I Ui R U U I )(00+=-=(13.4)由式(13.4)可得电流—电压变换器等效输入阻抗Z r 为01K R K R I U Z f f s ir ≈+==(13.5)由式(13.3)和式(13.4)可得电流—电压变换器输入电流I s 输出电压U 0之间得关系式,即: ff s R K U R K K U I )/11()1(00000+-=+=(13.6)由(13.6)式只要测得输出电压U 0和已知R f 值,即可求得I S 值。
以高输入阻抗集成运算放大器LF356为例来讨论Z r 和I S 值得大小。
对LF356运放的开环增益K 0=2×105,输入阻抗r i ≈1012Ω。
若取R f 为1.00M Ω,则由(5)式可得: 51021101.0056=⨯+⨯=r Z (Ω)若选用四位半量程200mV 数字电压表,它最后一位变化为0.01mV ,那么用上述电流—电压变换器能显示最小电流值为:A 101101V 1001.0)(1163min⨯=Ω⨯⨯=-s I 由此说明,用集成运算放大器组成电流-电压变换器测量弱电流,具有输入阻抗小、灵敏度高的优点。
3.PN 结的结电压be U 与热力学温度T 关系测量。
当PN 结通过恒定小电流(通常电流I =1 000μA ),由半导体理论可得be U 与T 近似关系:go be U ST U +=(13.5)式中3.2-≈S mV/℃为PN 结温度传感器灵敏度。
由go U 可求出温度0K 时半导体材料的近似禁带宽度00g g qU E =。
硅材料的0g E 约为1.20eV 。
【实验内容】一、be c U I -关系测定,并进行曲线拟合求经验公式,计算玻尔兹曼常数。
(1U U be =) (1)实验线路如图10.3所示。
图中U 1为三位半数字电压表,U 2为四位半数字电压表,TIP31型为带散热板的功率三极管,调节电压的分压器为多圈电位器,为保持PN 结与周围环境一致,把TIP31型三极管浸没在盛有变压器油干井槽中。
变压器油温度用铂电阻进行测量。
(2)在室温情况下,测量三极管发射极与基极之间电压U 1和相应电压U 2。
在常温下U 1的值约从0.3V 至0.42V 范围每隔0.01V 测一点数据,约测10多数据点,至U 2值达到饱和时(U 2值变化较小或基本不变),结束测量。
在记数据开始和记数据结束都要同时记录变压器油的温度θ,取温度平均值-θ。
3.改变干井恒温器温度,待PN 结与油温湿度一致时,重复测量U 1和U 2的关系数据,并与室温测得的结果进行比较。
4.曲线拟合求经验公式:运用最小二乘法,将实验数据分别代入线性回归、指数回归、乘幂回归这三种常用的基本函数(它们是物理学中最常用的基本函数),然后求出衡量各回归程序好坏的标准差δ。
对已测得的U 1和U 2各对数据,以U 1为自变量,U 2作因变量,分别代入: (1)线性函数U 2=aU 1+b ; (2)乘幂函数U 2=aU 1b ; (3)指数函数12e bU a U =。
求出各函数相应的a 和b 值,得出三种函数式,究竟哪一种函数符合物理规律必须用标准差来检验。
办法是:把实验测得的各个自变量U 1分别代入三个基本函数,得到相应因变量的预期值U 2*,并由此求出各函数拟合的标准差: ∑=-=ni i i n U U 12*]/)([δ式中n 为测量数据个数,U i 为实验测得的因变量,U i *为将自变量代入基本函数的因变量预期值,最后比较哪一种基本函数为标准差最小,说明该函数拟合得最好。
5.计算e /k 常数,将电子的电量作为标准差代入,求出玻尔兹曼常数并与公认值进行比较。
二、T U be -关系测定,求PN 结温度传感器灵敏度S ,计算硅材料0K 时近似禁带宽度0g E 值。
图10.5 图10.6(1)实验线路如图10.5所示,测温电路如图10.6所示。
其中数字电压表V 2通过双刀双向开关,既作测温电桥指零用,又作监测PN 结电流,保持电流I =100μA 用。
(2)通过调节图5电路中电源电压,使上电阻两端电压保持不变,即电流I =100μA 。
同时用电桥测量铂电阻T R 的电阻值,通过查铂电阻值与温度关系表,可得恒温器的实际湿度。
从室温开始每隔5℃-10℃测一定be U 值(即V 1)与温度θ(℃)关系,求得T U be -关系。
(至少测6点以上数据)3.用最小二乘法对T U be -关系进行直线拟合,求出PN 结测温灵敏度S 及近似求得温度为0K 时硅材料禁带宽度0g E 。
【实验数据】1.be c U I -关系测定,曲线拟合求经验公式,计算玻尔兹曼常数。
室温条件下:1θ = ℃,2θ = ℃,-θ= ℃表13.11 2 3 4 5 6 7 U 1/V U 2/V U 1/V U 2/V以U 1为自变量,U 2为因变量,分别进行线性函数、乘幂函数和指数函数的拟合,结果填入表13.2中。
表13.2线性回归b aU U +=12 乘幂回归b aU U 12=指数回归1e 2bU a U = n U 1/V U 2/V U 2*/V(U 2-U 2*)2/V 2U 2*/V (U 2-U 2*)2/V 2U 2*/V (U 2-U 2*)2/V 21 2345 678 9 10111213 14δ r a 、b计算玻尔兹曼常数: 由表13.2数据得k /e =bT = CK/J则k/e ek == J/K 将结果与玻尔兹曼公认值进行比较。
2.电流I =100μA 时,T U be -关系测定,求PN 结温度传感器的灵敏度S ,计算0K 进硅材料的近似禁带宽度0g E 。
表13.3 T U be -关系测定序号 Ω/T Rθ/℃T /K be U /V1 23 4 5 6 7 8 9 10 11用计算器对T U be -数据进行直线拟合得: (1)斜率,即传感器灵敏度S = mV/K (2)截距0g U = V (0K 温度)(3)相关系数r =(4) 禁带宽度eU E g =0= 电子伏特,将此结果与硅在0K 温度时禁带宽度公认值0g E =1.205eV 相比较。
【注意事项】1.数据处理时,对扩散电流太小(起始状态)及扩散电流接近或达到饱和时的数据,在处理数据时删去,因为这些数据可能偏离公式(13.2)。
2.必须观测恒温装置上温度计读数,待TIP31三极管温度处于恒定时(即处于热平衡时),才能记录U 1和U 2数据。
(3)用本装置做实验,TIP31型三极管温度可采用的范围为0 ~ 50℃。
若要在 -120℃ ~ 0℃温度范围内做实验,必须有低温恒温装置。
(4)由于各公司的运算放大器(LF356)性能有些差异,在换用LF356时,有可能同台仪器达到饱和电压U 2值不相同。
(5)本仪器电源具有短路自动保护,运算放大器若 15V 接反或地线漏接,本仪器也有保护装置,一般情况集成电路不易损坏。
请勿将二极管保护装置拆除。
【参考文献】[1] 沈元华, 陆申龙. 基础物理实验[M]. 北京: 高等教育出版社. 2003: 193-196 [2] 吕斯骅, 段家忯. 基础物理实验[M]. 北京: 高等教育出版社. 2003: 307 [3] 徐华伟, 谭春光, 朱亚辉等.低温半导体PN 结的物理特性及玻尔兹曼常数的测量[J].物理实验. 1999, 12(2):1-3 [4] 陆申龙, 曹正东. 低温条件下半导体材料禁带宽度的测量[J]. 大学物理. 15(10) 1996: 37-39 [5] 陈水桥. PN 结正向压降温度特性的研究和应用[J]. 物理实验. 20(7) 2000: 7-93.1 界面设计3.2 智能按钮制作(a)直线拟合to handle mouseentertext of field field90="实验数据都输入了吗?输入好了就单击计算" endto handle mouseleavetext of field field90="返回"endto handle buttonclick--6420,1905::15,0;6420,8835::0,0;13420,8835::0.28,0.48local x[20]local y[20]x0=6420;y0=8835-2310scalex=(13420-6420)/(0.48-0.28);scaley=(8835-1905-2310)/(0-15);n=20;step i from 101 to 120x[i-100]=0;y[i-100]=0;if (text of field ("field"&i)=null)nn=i-100if nn<nn=nn-1;endelsex[i-100]=text of field ("field"&i)y[i-100]=text of field ("field"&(i+100))endend-- text of field field90=x0+scalex*(x[1]-0.28)&","&y0+scaley*y[1]&","&x0+scalex*(x[2]-0.28)&","&y0+scaley *y[2]step i from 1 to n-1set vertices of line ("line"&i) to x0+scalex*(x[i]-0.28),y0+scaley*y[i],x0+scalex*(x[i+1]-0.28),y0+scaley*y[i+1]end--直线拟合sumx=0;sumy=0;sumxy=0;sumxx=0;step i from 1 to nsumx=sumx+x[i]sumy=sumy+y[i]sumxy=sumxy+x[i]*y[i]sumxx=sumxx+x[i]*x[i]endk=(n*sumxy-sumx*sumy)/(n*sumxx-(sumx)^2)b=sumy/n-k*sumx/nxx1=0.3;xx2=0.48yy1=k*xx1+b;yy2=k*xx2+bset vertices of angledline angledline1 to x0+scalex*(xx1-0.28),y0+scaley*yy1,x0+scalex*(xx2-0.28),y0+scaley*yy2sum1=0step i from 1 to nsum1=sum1+(y[i]-k*x[i]-b)^2;endif (k*1000 mod 1)<0.5text of field field91=((k*1000 div 1)+0)/1000elsetext of field field91=((k*1000 div 1)+1)/1000endif (b*1000 mod 1)<0.5text of field field92=((b*1000 div 1)+0)/1000elsetext of field field92=((b*1000 div 1)+1)/1000endtext of field field93=((sum1*1000 div 1)+1)/1000end(b)指数拟合to handle mouseentertext of field field90="实验数据都输入了吗?输入好了就单击计算" endto handle mouseleavetext of field field90="返回"endto handle buttonclick--6420,1905::15,0;6420,8835::0,0;13420,8835::0.28,0.48local x[20]local y[20]local xx[20]local yy[20]local yyy[20]x0=6420;y0=8835-2310scalex=(13420-6420)/(0.48-0.28);scaley=(8835-1905-2310)/(0-15);n=20;step i from 101 to 120x[i-100]=0;y[i-100]=0;if (text of field ("field"&i)=null)nn=i-100if nn<nn=nn-1;endelsex[i-100]=text of field ("field"&i)y[i-100]=text of field ("field"&(i+100))endend--text of field field90=log(y[13],2.718)step i from 1 to n-1set vertices of line ("line"&i) to x0+scalex*(x[i]-0.28),y0+scaley*y[i],x0+scalex*(x[i+1]-0.28),y0+scaley*y[i+1]end--指数拟合sumx=0;sumy=0;sumxy=0;sumxx=0;step i from 1 to nxx[i]=log(x[i],2.718);yy[i]=log(y[i],2.718);sumx=sumx+xx[i]sumy=sumy+yy[i]sumxy=sumxy+xx[i]*yy[i]sumxx=sumxx+xx[i]*xx[i]endk=(n*sumxy-sumx*sumy)/(n*sumxx-(sumx)^2)b=sumy/n-k*sumx/nbb=k;aa=exp(b);sum1=0;step i from 1 to nsum1=sum1+(y[i]-aa*x[i]^bb)^2;endsum11=sqrt(sum1/n);if (aa*1000 mod 1)<0.5text of field field91=((aa*1000 div 1)+0)/1000 elsetext of field field91=((aa*1000 div 1)+1)/1000 endif (bb*1000 mod 1)<0.5text of field field92=((bb*1000 div 1)+0)/1000 elsetext of field field92=((bb*1000 div 1)+1)/1000 endstep i from n+1 to 20x[i]=x[n];y[i]=y[n];end--text of field field90=sum1if (sum11*1000 mod 1)<0.5text of field field93=((sum11*1000 div 1)+0)/1000 elsetext of field field93=((sum11*1000 div 1)+1)/1000 endnnn=15step i from 1 to 20xx[i]=x0+scalex*(x[i]-0.28);yyy[i]=aa*x[i]^bb;yy[i]=y0+scaley*yyy[i];end-- text of field field93="u21="&aa*x[1]^bb&","&"u22="&aa*x[2]^bb&","&"u23="&aa*x[3]^bb&","&"u24="& aa*x[4]^bb&","&"u25="&aa*x[5]^bb&","&"u26="&aa*x[6]^bb&","&"u27="&aa*x[7]^bb&"," &"u28="&aa*x[8]^bb&","&"u29="&aa*x[9]^bb&","&"u210="&aa*x[10]^bb&","&"u211="&aa *x[11]^bb&","&"u212="&aa*x[12]^bb&","&"u213="&aa*x[13]^bb&","&"u214="&aa*x[14]^bb &","&"u215="&aa*x[15]^bb&","&"u216="&aa*x[16]^bb&","&"u217="&aa*x[17]^bbset vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7];pause nnn; set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8];p ause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15]; pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15], xx[16],yy[16];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15], xx[16],yy[16],xx[17],yy[17];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15], xx[16],yy[16],xx[17],yy[17],xx[18],yy[18];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15], xx[16],yy[16],xx[17],yy[17],xx[18],yy[18],xx[19],yy[19];pause nnn;end(c)e指数拟合to handle mouseentertext of field field90="实验数据都输入了吗?输入好了就单击计算"endto handle mouseleavetext of field field90="返回"endto handle buttonclick--6420,1905::15,0;6420,8835::0,0;13420,8835::0.28,0.48local x[20]local y[20]local xx[20]local yy[20]local yyy[20]x0=6420;y0=8835-2310scalex=(13420-6420)/(0.48-0.28);scaley=(8835-1905-2310)/(0-15);n=20;step i from 101 to 120x[i-100]=0;y[i-100]=0;if (text of field ("field"&i)=null)nn=i-100if nn<nn=nn-1;endelsex[i-100]=text of field ("field"&i)y[i-100]=text of field ("field"&(i+100))endend--text of field field90=log(y[13],2.718)step i from 1 to n-1set vertices of line ("line"&i) to x0+scalex*(x[i]-0.28),y0+scaley*y[i],x0+scalex*(x[i+1]-0.28),y0+scaley*y[i+1]end----直线拟合----sumx=0;sumy=0;sumxy=0;sumxx=0;----step i from 1 to n-- sumx=sumx+x[i]-- sumy=sumy+y[i]-- sumxy=sumxy+x[i]*y[i]-- sumxx=sumxx+x[i]*x[i]----k=(n*sumxy-sumx*sumy)/(n*sumxx-(sumx)^2)--b=sumy/n-k*sumx/n----xx1=0.3;xx2=0.48--yy1=k*xx1+b;yy2=k*xx2+b---- set vertices of angledline angledline1 to x0+scalex*(xx1-0.28),y0+scaley*yy1,x0+scalex*(xx2-0.28),y0+scaley*yy2----sum1=0--step i from 1 to n-- sum1=sum1+(y[i]-k*x[i]-b)^2;--end--指数拟合sumx=0;sumy=0;sumxy=0;sumxx=0;step i from 1 to nxx[i]=x[i];yy[i]=log(y[i],2.718);sumx=sumx+xx[i]sumy=sumy+yy[i]sumxy=sumxy+xx[i]*yy[i]sumxx=sumxx+xx[i]*xx[i]endk=(n*sumxy-sumx*sumy)/(n*sumxx-(sumx)^2)b=sumy/n-k*sumx/nbb=k;aa=exp(b);--if (bb*1000 mod 1)<0.5-- text of field field91=((bb*1000 div 1)+0)/1000--else-- text of field field91=((bb*1000 div 1)+1)/1000--endif (aa div 1)>0if (aa*1000 mod 1)<0.5text of field field91=((aa*1000 div 1)+0)/1000elsetext of field field91=((aa*1000 div 1)+1)/1000endif (aa*10 div 1)>0if (aa*10000 mod 1)<0.5text of field field91=((aa*10000 div 1)+0)/10000elsetext of field field91=((aa*10000 div 1)+1)/10000endelseif (aa*100 div 1)>0if (aa*100000 mod 1)<0.5text of field field91=((aa*100000 div 1)+0)/100000elsetext of field field91=((aa*100000 div 1)+1)/100000endelseif (aa*1000 div 1)>0if (aa*1000000 mod 1)<0.5text of field field91=((aa*1000000 div 1)+0)/1000000elsetext of field field91=((aa*1000000 div 1)+1)/1000000endelseif (aa*10000 div 1)>0if (aa*10000000 mod 1)<0.5text of field field91=((aa*10000000 div 1)+0)/10000000elsetext of field field91=((aa*10000000 div 1)+1)/10000000endelseif (aa*100000 div 1)>0if (aa*100000000 mod 1)<0.5text of field field91=((aa*100000000 div 1)+0)/100000000elsetext of field field91=((aa*100000000 div 1)+1)/100000000endelseif (aa*1000000 div 1)>0if (aa*1000000000 mod 1)<0.5text of field field91=((aa*1000000000 div 1)+0)/1000000000elsetext of field field91=((aa*1000000000 div 1)+1)/1000000000endelseif (aa*10000000 div 1)>0if (aa*10000000000 mod 1)<0.5text of field field91=((aa*10000000000 div 1)+0)/10000000000elsetext of field field91=((aa*10000000000 div 1)+1)/10000000000endelseif (aa*100000000 div 1)>0if (aa*100000000000 mod 1)<0.5text of field field91=((aa*100000000000 div 1)+0)/100000000000elsetext of field field91=((aa*100000000000 div 1)+1)/100000000000endelseif (aa*1000000000 div 1)>0if (aa*1000000000000 mod 1)<0.5text of field field91=((aa*1000000000000 div 1)+0)/1000000000000elsetext of field field91=((aa*1000000000000 div 1)+1)/1000000000000endelseif (aa*10000000000000 mod 1)<0.5text of field field91=((aa*10000000000000 div 1)+0)/10000000000000elsetext of field field91=((aa*10000000000000 div 1)+1)/10000000000000endendendendendendendendendendendif (bb*1000 mod 1)<0.5text of field field92=((bb*1000 div 1)+0)/1000elsetext of field field92=((bb*1000 div 1)+1)/1000endsum1=0step i from 1 to nsum1=sum1+(y[i]-aa*exp(x[i]*bb))^2;endsum11=sqrt(sum1/n)step i from n+1 to 20x[i]=x[n];y[i]=y[n];endif (sum11*1000 mod 1)<0.5text of field field93=((sum11*1000 div 1)+0)/1000elsetext of field field93=((sum11*1000 div 1)+1)/1000endnnn=15step i from 1 to 20xx[i]=x0+scalex*(x[i]-0.28);yyy[i]=aa*exp(x[i]*bb);yy[i]=y0+scaley*yyy[i];endset vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7];pause nnn; set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8];p ause nnn;set vertices of angledline angledline1 toxx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15]; pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15], xx[16],yy[16];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15], xx[16],yy[16],xx[17],yy[17];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15], xx[16],yy[16],xx[17],yy[17],xx[18],yy[18];pause nnn;set vertices of angledline angledline1 to xx[1],yy[1],xx[2],yy[2],xx[3],yy[3],xx[4],yy[4],xx[5],yy[5],xx[6],yy[6],xx[7],yy[7],xx[8],yy[8],x x[9],yy[9],xx[10],yy[10],xx[11],yy[11],xx[12],yy[12],xx[13],yy[13],xx[14],yy[14],xx[15],yy[15], xx[16],yy[16],xx[17],yy[17],xx[18],yy[18],xx[19],yy[19];pause nnn;-- text of field field90=yyy[1]&","&yyy[2]&","&yyy[3]&","&yyy[4]&","&yyy[5]&","&yyy[6]&","&yyy[7]&", "&yyy[8]&","&yyy[9]&","&yyy[10]&","&yyy[11]&","&yyy[12]&","&yyy[13]&","&yyy[14]&", "&yyy[15]&","&yyy[16]&","&yyy[17]&","&yyy[18]&","&yyy[19]&","&yyy[20]End(d)禁带宽度to handle mouseentertext of field field90="实验数据都输入了吗?输入好了就单击计算" endto handle mouseleavetext of field field90="返回"endto handle buttonclick--6420,1905::15,0;6420,8835::0,0;13420,8835::0.28,0.48local x[20]local y[20]local z[20]local xx[20]local yy[20]local yyy[20]x0=6420;y0=8835-2310scalex=(13420-6420)/(360-280);scaley=(8835-1905-2310)/(0.4-0.8);n=20;step i from 101 to 120x[i-100]=0;y[i-100]=0;if (text of field ("field"&i)=null)nn=i-100if nn<nn=nn-1;endelsey[i-100]=text of field ("field"&i)z[i-100]=text of field ("field"&(i+100))x[i-100]=z[i-100]+273.15text of field ("field"&(i+200))=x[i-100]endendtext of field field90=(x0+scalex*(x[1]-280))&","&(y0+scaley*(y[1]-0.4))if n<3show field field100elsestep i from 1 to n-1set vertices of line ("line"&i) to x0+scalex*(x[i]-280),y0+scaley*(y[i]-0.4),x0+scalex*(x[i+1]-280),y0+scaley*(y[i+1]-0.4)end----直线拟合sumx=0;sumy=0;sumxy=0;sumxx=0;step i from 1 to nsumx=sumx+x[i]sumy=sumy+y[i]sumxy=sumxy+x[i]*y[i]sumxx=sumxx+x[i]*x[i]endk=(n*sumxy-sumx*sumy)/(n*sumxx-(sumx)^2)b=sumy/n-k*sumx/nxx1=298;xx2=340;yy1=k*xx1+b;yy2=k*xx2+b;set vertices of angledline angledline1 to x0+scalex*(xx1-280),y0+scaley*(yy1-0.4),x0+scalex*(xx2-280),y0+scaley*(yy2-0.4)text of field field92=b;if k>0if (k div 1)>0if (k*1000 mod 1)<0.5text of field field91=((k*1000 div 1)+0)/1000elsetext of field field91=((k*1000 div 1)+1)/1000endelseif (k*10 div 1)>0if (k*10000 mod 1)<0.5text of field field91=((k*10000 div 1)+0)/10000elsetext of field field91=((k*10000 div 1)+1)/10000endelseif (k*100 div 1)>0if (k*100000 mod 1)<0.5text of field field91=((k*100000 div 1)+0)/100000elsetext of field field91=((k*100000 div 1)+1)/100000endelseif (k*1000 div 1)>0if (k*1000000 mod 1)<0.5text of field field91=((k*1000000 div 1)+0)/1000000elsetext of field field91=((k*1000000 div 1)+1)/1000000endelseif (k*10000 div 1)>0if (k*10000000 mod 1)<0.5text of field field91=((k*10000000 div 1)+0)/10000000elsetext of field field91=((k*10000000 div 1)+1)/10000000endelseif (k*100000 div 1)>0if (k*100000000 mod 1)<0.5text of field field91=((k*100000000 div 1)+0)/100000000elsetext of field field91=((k*100000000 div 1)+1)/100000000endelseif (k*1000000 div 1)>0if (k*1000000000 mod 1)<0.5text of field field91=((k*1000000000 div 1)+0)/1000000000elsetext of field field91=((k*1000000000 div 1)+1)/1000000000endelseif (k*10000000 div 1)>0if (k*10000000000 mod 1)<0.5text of field field91=((k*10000000000 div 1)+0)/10000000000elsetext of field field91=((k*10000000000 div 1)+1)/10000000000endelseif (k*100000000 div 1)>0if (k*100000000000 mod 1)<0.5text of field field91=((k*100000000000 div 1)+0)/100000000000elsetext of field field91=((k*100000000000 div 1)+1)/100000000000endelseif (k*1000000000 div 1)>0if (k*1000000000000 mod 1)<0.5text of field field91=((k*1000000000000 div 1)+0)/1000000000000elsetext of field field91=((k*1000000000000 div 1)+1)/1000000000000endelseif (k*10000000000000 mod 1)<0.5text of field field91=((k*10000000000000 div 1)+0)/10000000000000elsetext of field field91=((k*10000000000000 div 1)+1)/10000000000000endendendendendendendendendendendelsek=-kif (k div 1)>0if (k*1000 mod 1)<0.5text of field field91=((k*1000 div 1)+0)*(-1)/1000elsetext of field field91=((k*1000 div 1)+1)*(-1)/1000endelseif (k*10 div 1)>0if (k*10000 mod 1)<0.5text of field field91=((k*10000 div 1)+0)*(-1)/10000elsetext of field field91=((k*10000 div 1)+1)*(-1)/10000endelseif (k*100 div 1)>0if (k*100000 mod 1)<0.5text of field field91=((k*100000 div 1)+0)*(-1)/100000elsetext of field field91=((k*100000 div 1)+1)*(-1)/100000endelseif (k*1000 div 1)>0if (k*1000000 mod 1)<0.5text of field field91=((k*1000000 div 1)+0)*(-1)/1000000elsetext of field field91=((k*1000000 div 1)+1)*(-1)/1000000endelseif (k*10000 div 1)>0if (k*10000000 mod 1)<0.5text of field field91=((k*10000000 div 1)+0)*(-1)/10000000elsetext of field field91=((k*10000000 div 1)+1)*(-1)/10000000endelseif (k*100000 div 1)>0if (k*100000000 mod 1)<0.5text of field field91=((k*100000000 div 1)+0)*(-1)/100000000text of field field91=((k*100000000 div 1)+1)*(-1)/100000000endelseif (k*1000000 div 1)>0if (k*1000000000 mod 1)<0.5text of field field91=((k*1000000000 div 1)+0)*(-1)/1000000000elsetext of field field91=((k*1000000000 div 1)+1)*(-1)/1000000000endelseif (k*10000000 div 1)>0if (k*10000000000 mod 1)<0.5text of field field91=((k*10000000000 div 1)+0)*(-1)/10000000000elsetext of field field91=((k*10000000000 div 1)+1)*(-1)/10000000000endelseif (k*100000000 div 1)>0if (k*100000000000 mod 1)<0.5text of field field91=((k*100000000000 div 1)+0)*(-1)/100000000000elsetext of field field91=((k*100000000000 div 1)+1)*(-1)/100000000000endelseif (k*1000000000 div 1)>0if (k*1000000000000 mod 1)<0.5text of field field91=((k*1000000000000 div 1)+0)*(-1)/1000000000000elsetext of field field91=((k*1000000000000 div 1)+1)*(-1)/1000000000000endelseif (k*10000000000000 mod 1)<0.5text of field field91=((k*10000000000000 div 1)+0)*(-1)/10000000000000elsetext of field field91=((k*10000000000000 div 1)+1)*(-1)/10000000000000endendendendendendendendendendendbb=b;if (bb*1000 mod 1)<0.5text of field field92=((bb*1000 div 1)+0)/1000 elsetext of field field92=((bb*1000 div 1)+1)/1000 endendend4 结论直线拟合方差最大为47.695;。