圆中考经典题型

中考数学压轴题之新定义经典题型【01】.在平面直角坐标系xOy 中，C 的半径为r ，P 是与圆心C 不重合的点，点P 关于O 的反称点的定义如下：若在射线CP 上存在一点P ¢，满足2CP CP r ¢+=，则称P ¢为点P 关于C 的反称点，下图为点P 及其关于C 的反称点P ¢的示意图。

的示意图。

(1)(1)当当O 的半径为1时。

时。

①分别判断点(2,1)M ，3(,0)2N ，(1(1,,3)T 关于O 的反称点是否存在，若存在？在？求其坐标；求其坐标；②点P 在直线2y x =-+上，若点P 关于O 的反称点P ¢存在，且点P ¢不在x 轴上，求点P 的横坐标的取值范围；的横坐标的取值范围； (2)(2)当当C 的圆心在x 轴上，轴上，半径为半径为1，直线3233y x =-+与x 轴，轴，y y 轴分别交于点A ，B ，若线段AB 上存在点P ，使得点P 关于C 的反称点P ¢在C 的内部，求圆心C 的横坐标的取值范围。

的横坐标的取值范围。

yPOCx1 1【02】.在平面直角坐标系xOy 中，点P 的坐标为()11,x y ，点Q 的坐标为()22,x y ，且12x x ¹，12y y ¹，若,P Q 为某个矩形的两个顶点，为某个矩形的两个顶点，且该矩形的边均与某条坐标轴且该矩形的边均与某条坐标轴垂直，则称该矩形为点P Q ，的“相关矩形”的“相关矩形”..下图为点,P Q 的“相关矩形”的示意图意图. .（1）已知点A 的坐标为()10，，①若点B 的坐标为()31，，求点,A B 的“相关矩形”的面积；的“相关矩形”的面积；②点C 在直线3x =上，若点,A C 的“相关矩形”为正方形，求直线AC 的表达式；式；（2）O ⊙的半径为2，点M 的坐标为(),3m .若在O ⊙上存在一点N ，使得点,M N的“相关矩形”为正方形，求m 的取值范围的取值范围. .【03】对于平面直角坐标系xOy 中的点P 和⊙C ，给出如下定义：若存在过点P 的直线l 交⊙C 于异于点P 的A ，B 两点，在P ，A ，B 三点中，位于中间的点恰为以另外两点为端点的线段的中点时，则称点P 为⊙C 的相邻点，直线l 为⊙C 关于点P 的相邻线的相邻线. . （1）当⊙O 的半径为1时，时， ○1分别判断在点D （，14），E （0，-3），F （4，0）中，是⊙O 的相邻点有____________________；；○2请从○1中的答案中，任选一个相邻点，在图1中做出⊙O 关于它的一条相邻线，并说明你的作图过程相邻线，并说明你的作图过程. .○3点P 在直线3y x =-+上，若点P 为⊙O 的相邻点，求点P 横坐标的取值范围；范围；（2）⊙C 的圆心在x 轴上，半径为1，直线3233y x =-+与x 轴，y 轴分别交于点M ，N ，若线段．．MN 上存在⊙C 的相邻点P ，直接写出圆心C 的横坐标的取值范围．范围．21备用图1备用图2 图1【04】定义：y 是一个关于x 的函数，若对于每个实数x ，函数y 的值为三数2+x ，12+x ，205+-x 中的最小值，则函数y 叫做这三数的最小值函数.（1）画出这个最小值函数的图象，并判断点A （1， 3）是否为这个）是否为这个最小值函数图象上的点；图象上的点；（2）设这个最小值函数图象的最高点为B ，点A （1, 3），动点M （m ，m ）.①直接写出△ABM 的面积，其面积是的面积，其面积是 ； ②若以M 为圆心的圆经过B A ,两点，写出点M 的坐标；的坐标；③以②中的点M 为圆心，以2为半径作圆为半径作圆. . 在此圆上找一点P ，使22PA PB +的值最小，直接写出此最小值的值最小，直接写出此最小值. .【05】在平面直角坐标系xOy 中，对于点P 和图形W ,如果线段OP 与图形W 无公共点，则称点P 为关于图形W 的“阳光点”；如果线段OP 与图形W 有公共点，则称点P 为关于图形W 的“阴影点”． （1）如图1，已知点()13A ，，()11B ，，连接AB①在()11,4P ，()21,2P ，()32,3P ，()42,1P 这四个点中，关于线段AB 的“阳光点”是；是；②线段11A B AB P ；11A B 上的所有点都是关于线段AB 的“阴影点”，且当线段11A B 向上或向下平移时，都会有11A B 上的点成为关于线段AB 的“阳光点”．若11A B 的长为4，且点1A 在1B 的上方，则点1A 的坐标为的坐标为_________________________________________________________；； （2）如图2，已知点()13C ，，C e 与y 轴相切于点D ．若E e 的半径为32，圆心E 在直线343l y x =-+：上，且E e 上的所有点都是关于C e 的“阴影点”，求圆心E 的横坐标的取值范围；的横坐标的取值范围；（3）如图3，M e 的半径是3，点M 到原点的距离为5．点N 是M e 上到原点距离最近的点，点Q 和T 是坐标平面内的两个动点，且M e 上的所有点都是关于NQT D 的“阴影点”，直接写出NQT D 的周长的最小值．的周长的最小值．图1 图2 图3yxB A OyxCOD yx11O【06】给出如下规定：在平面直角坐标系xOy 中，对于点P （x ，y ），以及两个无公共点的图形1W 和2W ，若在图形1W 和2W 上分别存在点M （1x ，1y ）和N （2x ，2y ），使得P 是线段MN 的中点，则称点M 和N 被点P “关联”，并称点P 为图形1W 和2W 的一个“中位点”，此时P ，M ，N 三个点的坐标满足122x x x +=，122y yy +=．（1）已知点(0,1),(4,1),(3,1),(3,2)A B C D --，连接AB ，CD ．①对于线段AB 和线段CD ，若点A 和C 被点P “关联”，则点P 的坐标为____________________；； ②线段AB 和线段CD 的一个“中位点”是1(2,)2Q -，求这两条线段上被点Q “关联”的两个点的坐标；“关联”的两个点的坐标；（2）如图1，已知点R （－（－2,02,02,0）和抛物线）和抛物线1W ：22y x x =-，对于抛物线1W 上的每一个点M ，在抛物线2W 上都存在点N ，使得点N 和M 被点R “关联”，请在图1中画出符合条件的抛物线2W ；（3）正方形EFGH 的顶点分别是(4,1),(4,1),(2,1),(2,1)E F G H ------，⊙T 的圆心为(3,0)T ，半径为1．请在图2中画出由正方形EFGH 和⊙T 的所有“中位点”组成的图形（若涉及平面中某个区域时可以用阴影表示），并直接写出该图形的面积．并直接写出该图形的面积．图1 图2R【06】在平面直角坐标系中，⊙C 的半径为r ，P 是与圆心C 不重合的点，点P 关于⊙C 的限距点的定义如下：若为直线PC 与⊙C 的一个交点，满足，则称为点P 关于⊙C 的限距点，右图为点P 及其关于⊙C 的限距点的示意图．的示意图． （1）当⊙O 的半径为1时．时．①分别判断点M ，N ，T 关于⊙O 的限距点是否存在？若存在，求其坐标；在？若存在，求其坐标；②点D 的坐标为（的坐标为（2,02,02,0）），DE ，DF 分别切⊙O 于点E ，点F ，点P 在△DEF 的边上的边上..若点P 关于⊙O 的限距点存在，求点的横坐标的取值范围；取值范围；（2）保持（）保持（11）中D ，E ，F 三点不变，点P 在△DEF 的边上沿E →F →D →E的方向的方向运动，⊙C 的圆心C 的坐标为（1,01,0）），半径为r .请从下面两个问题中任选一个作答一个作答. .温馨提示：答对问题1得2分，答对问题2得1分，两题均答不重复计分.问题1问题2若点P 关于⊙C 的限距点存在，且随点P 的运动所形成的路径长为，则r 的最小值为的最小值为______________________________．． 若点P 关于⊙C 的限距点不存在，则r 的取值范围为的取值范围为________. ________.xOy P ¢2r PP r ¢££P ¢P¢(3,4)5(,0)2(1,2)P ¢P ¢P ¢P ¢r p P¢【07】对于某一函数给出如下定义：若存在实数p ，当其自变量的值为p 时，其函数值等于p ，则称p 为这个函数的不变值. 在函数存在不变值时，该函数的最大不变值与最小不变值之差q 称为这个函数的不变长度.特别地，当函数只有一个不变值时，其不变长度q 为零为零..例如，下图中的函数有0，1两个不变值，其不变长度q 等于1.（1）分别判断函数1y x =-，1y x=，2y x =有没有不变值？如果有，直接写出其不变长度；其不变长度；（2）函数22y x bx =-.①若其不变长度为零，求b 的值；的值；②若13b ££，求其不变长度q 的取值范围；的取值范围；（3）记函数22()y x x x m =-³的图象为1G ，将1G 沿x=m 翻折后得到的函数图象记为2G .函数G 的图象由 1G 和2G 两部分组成，若其不变长度q 满足03q ££，则m 的取值范围为的取值范围为 . .【08】P 是⊙O 内一点，过点P 作⊙O 的任意一条弦AB ，我们把P A PB ×的值称为点P 关于⊙O 的“幂值”．（1）⊙O 的半径为5，OP = 3．①如图1，若点P 恰为弦AB 的中点，则点P 关于⊙O 的“幂值”为________________；； ②判断当弦AB 的位置改变时，点P 关于⊙O 的“幂值”是否为定值，若是定值，证明你的结论；若不是定值，求点P 关于⊙O 的“幂值”的取值范围．的取值范围．（2）若⊙O 的半径为r ，OP = d ，请参考（，请参考（11）的思路，用含r 、d 的式子表示点P 关于⊙O 的“幂值”或“幂值”的取值范围的“幂值”或“幂值”的取值范围________________________；； （3）在平面直角坐标系xOy 中，⊙O 的半径为4，若在直线33y x b =+上存在点P ，使得点P 关于⊙O 的“幂值”为1313，，请写出b 的取值范围的取值范围________________________．．图1POBAO备用图备用图【09】在平面直角坐标系xOy 中，中，图形图形W 在坐标轴上的投影长度定义如下：设点),(11y x P ，),(22y x Q 是图形W 上的任意两点．若21x x -的最大值为m ，则图形W 在x 轴上的投影长度m l x =；若21y y -的最大值为n ，则图形W 在y 轴上的投影长度n l y =．如图，图形W 在x 轴上的投影长度213=-=xl ；在y 轴上的投影长度404=-=y l ．（1）已知点)3,3(A ，)1,4(B ．如图1所示，若图形W 为△OAB ，则=xl ，=y l ．（2）已知点)0,4(C ，点D 在直线26y x =-+上，若图形W 为△OCD ．当y x l l =时，求点D 的坐标．的坐标．（3）若图形W 为函数2x y =）（b x a ££的图象，其中0a b £<．当该图形．当该图形满足1£=y x l l 时，请直接写出a 的取值范围．的取值范围．x yO BA 1234123x y O 1231234图1【10】.在平面直角坐标系xOy 中，对图形W 给出如下定义：若图形W 上的所有点都在以原点为顶点的角的内部或边界上，在所有满足条件的角中，其度数的最小值称为图形的坐标角度，例如，下图中的矩形ABCD 的坐标角度是9090°．°．°．（1）已知点)3,0(-A ，)1,1(--B ，在点)0,2(C ，)0,1(-D ，)2,2(-E 中，选一点，使得以该点及点A ，B 为顶点的三角形的坐标角度为9090°，则满足条件°，则满足条件的点为的点为 ； （2）将函数2ax y =)31(££a 的图象在直线1=y 下方的部分沿直线1=y 向上翻折，求所得图形坐标角度m 的取值范围；的取值范围；（3）记某个圆的半径为r ，圆心到原点的距离为l ，且)1(3-=r l ，若该圆的，若该圆的坐标角度°££°9060m ．直接写出满足条件的r 的取值范围．的取值范围． O xy D C B A –1–2–312312345。

中考数学必考经典题型题型一 先化简再求值命题趋势由河南近几年的中考题型可知，分式的化简求值是每年的考查重点，几乎都 以解答题的形式出现，其中以除法和减法形式为主，要求对分式化简的运算法则及分式有意义的条件熟练掌握。

例：先化简，再求值： ( 1 + x +1 1 ) ÷ x -1 x 2 - x x 2 - 2x +1, 其中 x =-1. 分析：原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，将 x 的值带入计算即可求值。

题型二阴影部分面积的相关计算命题趋势近年来的中考有关阴影面积的题目几乎每年都会考查到，而且不断翻新，精 彩纷呈．这类问题往往与变换、函数、相似等知识结合，涉及到转化、整体等数学思想方法，具有很强的综合性。

例如图 17，记抛物线 y ＝－x 2＋1 的图象与 x 正半轴的交点为A ，将线段 OA 分成n 等份．设分点分别为 P 1，P 2，…，P n －1，过每个分点作 x 轴的垂线，分别与抛物线交于点 Q 1，Q 2，…，Q n －1，再记直角三角形 OP 1Q 1，P 1P 2Q 2，…的面积分别为 S 1，S 2，…，这样就有 S 1＝ n 2 -1 2n 3 ，S 2＝ n 2 - 42n 3…；记Ｗ＝S 1＋S 2＋…＋S n －1，当 n 越来越大时，你猜想 W 最接近的常数是()(A) 23 (B) 12(C) 13(D) 14分析 如图 17，抛物线 y ＝－x 2＋1 的图象与 x 正半轴的交点为A(1，0)，与 y 轴的交点为 8(0，1)．设抛物线与 y 轴及 x 正半轴所围成的面积为 S ，M(x ，y )在图示抛物线上，则OM 2 = x 2 + y 223 3 2 从 而 = (1 - y ) + y 2⎛ 1 ⎫23 ＝ y - ⎪ + ． ⎝ ⎭ 4由 0≤y32≤1， 得 ≤OM ≤1．4这段图象在图示半径为 11个圆 面积之间，即4 、1 的两个 圆所夹的圆环内，所以 S 在图示两 243 1＜S ＜ π．164显然，当 n 的值越大时，W 的值就越来越接近抛物线与 y 轴和 x 正半轴所围成的面积的一半，所以3 1＜W ＜ π．328与其最接近的值是，故本题应选 C ．题型三 解直角三角形的实际应用命题趋势解直角三角形的应用是中考的必考内容之一，它通常以实际生活为背景，考 查学生运用直角三角形知识建立数学模型的能力，解答这类问题的方法是运用 “遇斜化直”的数学思想，即通过作辅助线(斜三角形的高线)把它转化为直角三角形问题，然后根据已知条件与未知元素之间的关系，利用解直角三角形的知识， 列出方程来求解。

中考数学经典几何模型之胡不归最值模型(解析版)在数学中，经典几何模型是考试中经常出现的题型之一。

其中，胡不归最值模型是一种常见的最值问题。

这类问题通常涉及到形如“PA+kP”的式子，可以分为两类问题：胡不归问题和阿氏圆问题。

胡不归问题的故事源于一个少年外出求学，得知父亲病危后，他立即赶回家。

虽然他所在的位置到家的路上有一片砂石地，但他仍然义无反顾地走了这条路。

当他到家时，父亲已经去世了，他深感悔恨并痛哭流涕。

邻居告诉他，父亲在临终前一直念叨着“胡不归？胡不归？……”（“胡”同“何”）。

这个故事启发我们思考如何求解“PA+kP”型问题中的最值。

以胡不归问题为例，我们需要求解一个动点P在直线MN 外的运动速度为V1，在直线MN上运动的速度为V2，且V1<V2，A、B为定点，点C在直线MN上，确定点C的位置使得AC+BC的值最小，即求BC+kAC的最小值。

为了解决这个问题，我们可以构造射线AD使得sin∠DAN=k，即CH=kAC。

这样，我们可以将问题转化为求BC+CH最小值，过B点作BH⊥AD交MN于点C，交AD于H点，此时BC+CH取到最小值，即BC+kAC最小。

在解决“PA+kP”型问题时，关键是构造与kP相等的线段，将“PA+kP”型问题转化为“PA+PC”型。

而这里的P必须是一条方向不变的线段，方能构造定角利用三角函数得到kP的等线段。

举个例子，如图所示，在△ABC中，AB=AC=10，tanA=2，BE⊥AC于点E，D是线段BE上的一个动点，则CD+BD的最小值为5.这个问题的关键在于处理“CD+BD”的式子，考虑tanA=2，△ABE三边之比为1:2:5，sin ABE⊥AB交AB于H点，则DH=BD/5.通过构造HD，我们可以将问题转化为求CD+CH的最小值，其中CH=kAC，k=sin∠DAN=BD/5.过B点作BH⊥AD交MN于点C，交AD于H点，此时BC+CH取到最小值，即CD+BD的最小值为5.综上所述，胡不归最值模型是一类常见的最值问题。

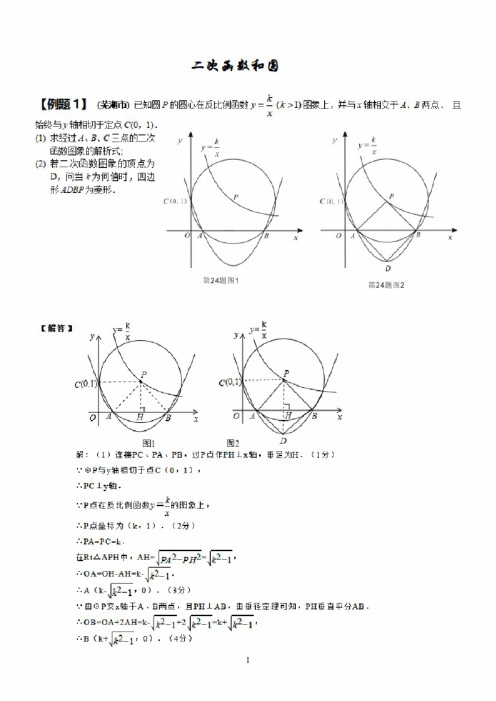
【仲烦1】（我市）已知圆P的圆心在反比例函数y=-（A：>1）上，并与工轴相交于X、3两点.且x始终与］轴相切于定点C（0,1）.⑴求经过三点的二次匣1数图象的解析式；（2）若二次函教图象的顶点为D,问当上为何值时'四边形也站尹为菱形.【耕音】解：（1）连接PC、PAx PB，谊P点ffPHXx轴.垂足为H・（1分）与y轴相切于点C（0, 1），.-.PC±y^.•.•P点在反比例函数》二占的囹象上，X•.•P点坐标为（k,1）.（2分）•.•PAU.在RtAAPH中，AH=厨2_尸於后一1，•'•A(k-90 ).(3分)•.•由。

P交x轴于A、B两点，且PHJLAB，由垂径击理可知，PH垂直平分AB.AOB=OA+2AH=k•••B3小2_1，0）.《4分〉故过A、B两点的抛物线的对称轴为PH所在的直钱斛析式为x=k.可设该抛物线解析式为y=a<x-k）2+h.（5分）又二.抛物线过C（。

，1），B（k-^2_r0），[ak^-^h=1•3|—?昭得a=l，h=1-k^.（7分）•.•抛物线解析式为y=心）2+1上2.（B分）（2）由<1）知抛物线顶点D坐标为（k,l-k2>•・•DH-k2-l.若四边形ADBP为装形.则必有PH=DH.（10分）VPH=1，.•-k2-l=l.又">1,（11分）•・•当k取以时，PD与AB互相垂直平分，则四边形ADBP为菱形•（12分）3【百麒2]翎南省韶关市）25.如图6,在平面直角坐标系中旭边形OABC是矩形,。

虹4应=2,直线），=-"：与坐标轴交于D、E。

设M是加的中点，P是线段DE上的动点.（1）求M、D两点的坐标；<2）当P在什么位置时，PA=PB?求出此时P点的坐标j<3）过P作PH1BC,垂足为H,当以PM为直径的OF与BC相切于点N时，求梯形PHBH的面积.图6【分析】(1)因为四边形OABC是逅形，0A=4,AB=2»直线>=r-?与坐标轴交于D、E，M是AB的中点2.所以令y=0,即司术出D的坐标，而AM-1.印以M(4,1)；(2)因为PA=PB.断以P是AB的香直平分线和直线ED的交点，而AE的中垂线是y=l，断以P的纵坐标为1，令直线ED的解析式中的y=l，求出的x的值即为相应的P的横坐标；(3〉可设P(x，y>，连将PN、MN、NF，因为点P在y・x-：上，所以P《x，粮据蹦意可2得PNlMNi FN±BCi F是圈心，又因N是钱段HB的中点，HN-NB-—»PH-2-(-x*-)t2 2 2BM=1,利用直径对的圆周角是直甬可得到ZHPX-ZHNP=ZHNP-ZBNM=90°•所以ZHPN=ZB取ph ir£x+| NM,又因ZPHN-ZB-900-所以可得到R tAPNH<^RtANMB•所以—•A2=—^，这BM BN—4-x1—样牧可得到关于X的方程，解之即可求出X的值，而饬求面招的四边形是一个直角梯形，南以Spg=也皿滋或"医号)("6+应)=.21_色叵.2 2 24满答】俄；《1)M", 1),D《9,0)；(2分)2(2)V PA=PB>•七点P在线段AB的中毒线上，•.•点P的纵坐标是I，3又•:点P在尸-X-—上，2・.•点P的坐标为(【，1)?(4分)（3）设P（x，y），连接PN、MN、NF，3点P lSy=・x+-上，匕3・'・P（x ,-w+—），2依题意知：PN«LMN>FN^BC,F是圆心，・'・N是线段HB的中点，HN=NB=±M，PH=2.2口，BM=1，<6分）22HPN-ZHNP=NHNP-ZBNM=90°，NHPN=ZBNN1，又ZPHN=ZB=90°5RtAPNH^RtANMBs:HN_PH•'两南，4-x x*.."F=二，-等」22，（8分）x?-12x+14=0»朋得；x-6-j22（^-*>^舍去），k=6-皿=些罕=空也艾竺=一*孕屈，（9分）2【例题31（||-4省白银等7市新课程）28.在直角坐标系中>0A的丰径为4,圆心A曜标为（2, 0），S与X轴交于E、尸两点，与），轴交于（7、D两点，过点（7作0X的切线时，交x轴于点3.（1）求直线C5的解析式：（2）若抛物线.件履7）日€的顶点在直线3C上,与x轴的交点恰为点E、已求该抛物线的解析式J（3）试判断点C是否在抛物线上？（4）在抛物线上是否存在三个点，由它构成的三角形与A4OC相似？直接与出两组这样的点•4［分析】(1>SHAC.根撮区］的李径求出AC. W1B点人的坐麻求出0A，燃后利用勾腹定理列式求出0C・从而得到点C的坐标，再求出ZCAO=60=.然后粮掘直有三甬形两锐角互余米出NB=30。

中考数学10道经典题型分析跟大家分享一下近期初三数学总复习的一些好的题目，相信总有一款题目你会感兴趣。

第1题、第2题：阿氏圆的经典题目。

这是最值经常见的题目，确定动点的运动轨迹，构造母子相似三角形解决线段的系数，三点共线时距离最短。

具体技巧请参加题目解答与分析。

经典题目1：阿氏圆经典题目。

经典题目2：阿氏圆问题。

第3题：费马点问题。

费马点问题也是最值问题最常见的题型，三线线段之和最短，通过旋转构造全等三角形，实现线段的转换（移到同一直线上），四点共圆时，线段之和最短。

经典题目3：胡不归问题。

第4题：胡不归问题。

胡不归问题同样的线段最值常见问题，AB+kCD的最值问题，首先要解决其中一条线段的K值，阿氏圆通常采用构造母子相似三角形来解决这个问题，而胡不归通常采用三角函数来解决这个问题。

这道综合题还是很不错的，值得练一练。

经典题目4：胡不归问题。

第5，6题：二次函数中的a,b,c问题。

在选择题中，这也算是比较有点难度的问题了，而且考试的频率往往非常高，需要熟练掌握。

基本的技巧我已经在下面列出了。

经典题目5：二次函数多结论问题。

经典题目7：二次函数多结论问题。

第7题：相似三角形综合题目。

这是一次模拟测验的倒数第2题，三角形综合题。

这道题比较好，是因为它不只一种解法，尤其是在第3问中，有不同的作辅助线的方法，有点意思。

经典题目7：三角形综合题。

第8题：中考压轴题模拟题。

这是深圳南山区联考模拟卷的压轴题，最后一问其实并不难，根据题意不难理解，动点的运动轨迹是某个圆的一段弧，在同一个圆中，同弧（弦）所对的圆周角相等，从而可以确定动点的运动轨迹，三点共线时，由距离最短。

具本思路和过程可参照下面答案。

经典题目8：中考压轴题目。

第9题：平行四边形的存在性问题。

这道题目真的很不错，弄懂这道题目，平行四边形的存在性问题就基本弄懂了。

我在参考答案中列举了三种常见的方法，其中包括点的坐标平移法，中点坐标（平行四边形对角顶点坐标之间的关系要熟练掌握）等。

经典几何模型之隐圆”“圆来如此简单”————段廉洁一.名称由来在中考数学中，有一类高频率考题，几乎每年各地都会出现，明明图形中没有出现“圆”，但是解题中必须用到“圆”的知识点，像这样的题我们称之为“隐圆模型”。

正所谓：有“圆”千里来相会，无“圆”对面不相逢。

“隐圆模型”的题的关键突破口就在于能否看出这个“隐藏的圆”。

一旦“圆”形毕露，则答案手到擒来！二.模型建立【模型一：定弦定角】【模型二：动点到定点定长（通俗讲究是一个动的点到一个固定的点的距离不变）】【模型三：直角所对的是直径】【模型四：四点共圆】三．模型基本类型图形解读【模型一：定弦定角的“前世今生”】【模型二：动点到定点定长】【模型三：直角所对的是直径】【模型四：四点共圆】四．“隐圆”破解策略牢记口诀：定点定长走圆周，定线定角跑双弧。

直角必有外接圆，对角互补也共圆。

五．“隐圆”题型知识储备六．“隐圆”典型例题【模型一：定弦定角】1.（2017威海）如图1，△ABC为等边三角形，AB=2，若P为△ABC内一动点，且满足∠PAB=∠ACP，则线段PB长度的最小值为__________。

简答：因为∠PAB=∠PCA，∠PAB+∠PAC=60°，所以∠PAC+∠PCA=60°，即∠APC=120°。

因为AC定长、∠APC=120°定角，故满足“定弦定角模型”，P在圆上，圆周角∠APC=120°，通过简单推导可知圆心角∠AOC=60°，故以AC为边向下作等边△AOC，以O为圆心，OA 为半径作⊙O，P在⊙O上。

当B、P、O三点共线时，BP最短（知识储备一：点圆距离），此时BP32.如图1所示，边长为2的等边△ABC的原点A在x轴的正半轴上移动，∠BOD=30°，顶点A在射线OD上移动，则顶点C到原点O的最大距离为__________。

简答：因为∠AOB =30°（定角），AB =2（定弦），故A 、B 、O 三点共圆，圆心角为60°，故以AB 为边向O 方向作等边△ABQ ，∠AQB =60°为圆心角，Q 为圆心，以QA 为半径作⊙Q （如图2），由知识储备二可知当OC ⊥AB 时，OC 距离最大，OC =OQ +QH +HC =2+3+3=2+23【思考：若∠BOD =45°呢？（提示：需要构造倍角模型）】3.如图1，点A 是直线y =-x 上的一个动点，点B 是x 轴上的动点，若AB =2，则△AOB 面积最大值为（）A.2B .12+C .12-D .22简答：因为AB =2（定弦），∠AOB =135°（定角），因为∠AOB 是圆周角，故圆心角为90°，以AB 为斜边向上方作等腰直角△QAB ，则Q 为圆心（如图2），由“知识储备二”可知，当OQ ⊥AB 时，此时△OAB 的高OH 最大，面积最大。

中考必考——数学动点经典例题分析动态几何问题已经成为中考试题的一大热点题型．这类试题以运动的点、线段、变化的角、图形的面积为基本条件，给出一个或多个变量，要求确定变量与其他量之间的关系，或变量在一定条件为定值时，进行相关的几何计算和综合解答。

下面是几个例题及分析(2000年·上海)如图1在半径为6,圆心角为90的扇形OAB 的弧AB上有一个动点P,PH⊥OA垂足为⊥OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO、GP、GH中有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH= x,G=y求y关于x的函数解析式，并写出函数的定义域(即自变量x 的取值范围)(3)如果⊥PGH是等腰三角形试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变于是线段GO、GP、GH中,有长度保持不变的线段，这条线段是GH=2/3 M=2/3.120P=2.(2)在Rt⊥POH中，OH=√OP2−PH2=√36−x2⊥MH=12OH=12√36−x2在Rt⊥POH中MP=√PH2+MH2=12√36+3x21.分析:此题为点动题，因此，1)搞清动点所走的路线及速度，这样就能求出相应线段的长;2)分析在运动中点的几种特殊位置由题意知，点P 为动点，所走的路线为: ABC 速度为1cm/s。

而t=2s，故可求出AP 的值，进而求出⊥APE 的面积2.分析:两点同时运动，点P 在前，点Q在后，速度相等，因此两点距出发点A的距离相差总是2cm.P在AB边上运动后，又到BC边上运动因此PM、N 截平行四边形ABCD 所得图形不同.故分两种情况:(1)⊥当P、Q 都在AB 上运动时,PM、N 截平行四边形ABCD 所得的图形永远为直角梯形.此时0≤t≤6.⊥当P在BC上运动，而Q在A 边上运动时，画出相应图形，所成图形为六边形DFOBPG,不规则图形面积用割补法.此时6<t≤8.可以尝试自己解答一下吆！以上是数学动点例题及解析，你学会如何解答此类问题了么？。

专题21 最值问题中的阿氏圆模型【模型展示】1、一般将含有k 的线段两端点分别与圆心O 相连，即连接OB 、OP ；2、计算出线段OP 与OB 及OP 与OA 的线段比，找到线段比为k 的情况3、连接AC ，与圆O 的交点即为点P4、将图2中△BPO 单独提取出，如图4，△PCO△△BPO （母子型相似模型）（构造出△PCO△△BPO ，就可以得到OC/OP=OP/OB ，进而推出OP²=OB·OC ，即“半径的平方＝原有线段×构造线段”，确定C 的位置后，连接AC ，求出AC 的长度“阿氏圆”即可破解）“PA+k·PB”型的最值【题型演练】 一、单选题1．如图，在Rt △ABC 中，△ACB ＝90°，CB ＝7，AC ＝9，以C 为圆心、3为半径作△C ，P半径r（圆心）构造的点（定点）（动点）B O P C为△C上一动点，连接AP、BP，则13AP＋BP的最小值为（）A．7B．C．4D．【答案】B【详解】思路引领：如图，在CA上截取CM，使得CM＝1，连接PM，PC，BM．利用相似三角形的性质证明MP13=P A，可得13AP+BP＝PM+PB≥BM，利用勾股定理求出BM即可解决问题．答案详解：如图，在CA上截取CM，使得CM＝1，连接PM，PC，BM．△PC＝3，CM＝1，CA＝9，△PC2＝CM•CA，△PC CM CA CP=，△△PCM＝△ACP，△△PCM△△ACP，△13 PM PCPA AC==，△PM13=P A，△13AP+BP＝PM+PB，△PM+PB≥BM，在Rt△BCM中，△△BCM＝90°，CM＝1，BC＝7，△BM=△13AP +BP△13AP +BP 的最小值为 故选：B ．二、填空题2．如图，在ABC 中，90,2B AB CB ∠=︒==，以点B 为圆心作圆B 与AC 相切，点P 为圆B 上任一动点，则PA +的最小值是___________．【分析】作BH △AC 于H ，取BC 的中点D ，连接PD ，如图，根据切线的性质得BH 为△B的半径，再根据等腰直角三角形的性质得到BH 12=AC =△BPD △△BCP 得到PD =，所以P A +＝P A +PD ，而P A +PD ≥AD （当且仅当A 、P 、D 共线时取等号），从而计算出AD 得到P A PC 的最小值． 【详解】解：作BH △AC 于H ，取BC 的中点D ，连接PD ，如图， △AC 为切线， △BH 为△B 的半径， △△ABC ＝90°，AB ＝CB ＝2， △AC＝△BH 12=AC = △BP△PB BC =BD BP =，而△PBD＝△CBP，△△BPD△△BCP，△PD PBPC BC==△PD=，△P A+＝P A+PD，而P A+PD≥AD（当且仅当A、P、D共线时取等号），而AD=△P A+PD即P A PC【点睛】本题考查了切线的性质：圆的切线垂直于经过切点的半径．解决问题的关键是利用相似比确定线段PD=．也考查了等腰直角三角形的性质．3．如图，已知正方ABCD的边长为6，圆B的半径为3，点P是圆B上的一个动点，则12 PD PC-的最大值为_______．【答案】15 2【分析】如图，连接BP，在BC上取一点M，使得BM=32，进而证明BPM BCP△∽△,则在点P 运动的任意时刻，均有PM =12PC ，从而将问题转化为求PD -PM 的最大值．连接PD ，在△PDM 中，PD -PM ＜DM ，故当D 、M 、P 共线时，PD -PM =DM 为最大值，勾股定理即可求得DM ．【详解】如图，连接BP ，在BC 上取一点M ，使得BM =32，31232BM BP ==，3162BP BC ==BM BPBP BC∴= PBM CBP ∠=∠∴BPM BCP △∽△12MP BM PC BP ∴== 12MP PC ∴=12PD PC PD MD ∴-=-在△PDM 中，PD -PM ＜DM ，当D 、M 、P 共线时，PD -PM =DM 为最大值，四边形ABCD是正方形90C∴∠=︒在Rt CDM中，152 DM===故答案为：152．【点睛】本题考查了圆的性质，相似三角形的性质与判定，勾股定理，构造12PC是解题的关键．4．如图，边长为4的正方形，内切圆记为△O，P是△OA＋PB的最小值为________．【答案】A＋PB P A PB）PB即可解答．【详解】解：设△O半径为r，OP＝r ＝12BC ＝2，OB ＝取OB 的中点I ，连接PI ， △OI＝IB△OP OI ==，OB OP ==， △OP OB OI OP= ，△O 是公共角， △△BOP △△POI ，△PI OI PB OP ==，△PI PB ，△AP PB ＝AP ＋PI ，△当A 、P 、I 在一条直线上时，＋PB 最小， 作IE △AB 于E ， △△ABO ＝45°，△IE ＝BE ＝2BI ＝1， △AE ＝AB −BE ＝3， △AI△APPB 最小值＝AI ，A ＋PB P A PB ），A ＋PB ．故答案是【点睛】本题是“阿氏圆”问题，解决问题的关键是构造相似三角形．5．【新知探究】新定义：平面内两定点A, B ，所有满足PAPB=k ( k 为定值)的P 点形成的图形是圆，我们把这种圆称之为“阿氏圆”，【问题解决】如图，在△ABC 中，CB = 4 ，AB= 2AC ，则△ABC 面积的最大值为_____．【答案】16 3【分析】以A为顶点，AC为边，在△ABC外部作△CAP=△ABC，AP与BC的延长线交于点P，证出△APC△△BPA，列出比例式可得BP=2AP，CP=12AP，从而求出AP、BP和CP，即可求出点A的运动轨迹，最后找出距离BC最远的A点的位置即可求出结论．【详解】解：以A为顶点，AC为边，在△ABC外部作△CAP=△ABC，AP与BC的延长线交于点P，△△APC=△BPA，AB= 2AC△△APC△△BPA，△12 AP CP AC BP AP AB===△BP=2AP，CP=12AP △BP－CP=BC=4△2AP－12AP=4解得：AP=8 3△BP=163，CP=43，即点P为定点△点A的轨迹为以点P为圆心，83为半径的圆上，如下图所示，过点P作BC的垂线，交圆P于点A1，此时A1到BC的距离最大，即△ABC的面积最大S△A1BC=12BC·A1P=12×4×83=163即△ABC面积的最大值为16 3故答案为：163．【点睛】此题考查的是相似三角形的判定及性质、确定点的运动轨迹和求三角形的面积，掌握相似三角形的判定及性质、圆的定义和三角形的面积公式是解决此题的关键． 6．如图，在Rt ABC 中，AB ＝AC ＝4，点E ，F 分别是AB ，AC 的中点，点P 是扇形AEF 的EF 上任意一点，连接BP ，CP ，则12BP +CP 的最小值是_____．【分析】在AB 上取一点T ，使得AT ＝1，连接PT ，P A ，CT ．证明PAT BAP ∽，推出PTPB＝AP AB＝12，推出PT ＝12PB ，推出2PB +CP ＝CP +PT ，根据PC +PT ≥TC ，求出CT 即可解决问题．【详解】解：在AB 上取一点T ，使得AT ＝1，连接PT ，P A ，CT ．△P A ＝2．AT ＝1，AB ＝4， △P A 2＝4 AT •AB ， △PA AT ＝ABPA， △△P AT ＝△P AB ， △PAT BAP ∽，△PTPB＝APAB＝12，△PT＝12PB，△12PB+CP＝CP+PT，△PC+PT≥TC，在Rt ACT中，△△CAT＝90°，AT＝1，AC＝4，△CT△12PB+PC△12PB+PC【点睛】本题考查等腰直角三角形的性质，三角形相似的判定与性质，勾股定理的应用，三角形的三边关系，圆的基本性质，掌握以上知识是解题的关键．7．如图，已知正方形ABCD的边长为4，△B的半径为2，点P是△B上的一个动点，则PD﹣12PC的最大值为_____．【答案】5【详解】分析: 由PD−12PC＝PD−PG≤DG，当点P在DG的延长线上时，PD−12PC的值最大，最大值为DG＝5．详解: 在BC上取一点G，使得BG＝1，如图，△221PBBG==，422BCPB==，△PB BC BG PB=，△△PBG＝△PBC，△△PBG△△CBP，△12 PG BGPC PB==，△PG＝12PC，当点P在DG的延长线上时，PD−12PC的值最大，最大值为DG5．故答案为5点睛:学会构建相似三角形解决问题，学会用转化的思想思考问题，把问题转化为两点之间线段最短解决，题目比较难，属于中考压轴题．8．如图，在△ABC中，△ACB=90°，BC=12，AC=9，以点C为圆心，6为半径的圆上有一个动点D.连接AD、BD、CD，则2AD+3BD的最小值是________.【答案】【分析】如下图，在CA上取一点E，使得CE=4，先证△DCE△△ACD，将23AD转化为DE，从而求得23AD BD+的最小距离，进而得出2AD+3BD的最小值．【详解】如下图，在CA 上取一点E ，使得CE=4△AC=9，CD=6，CE=4 △CD AC CE CD= △△ECD=△ACD△△DCE△△ACD △69ED DC AD AC == △ED=23AD 在△EDB 中，ED+DB≥EB△ED+DB 最小为EB ，即ED+DB=EB △23AD DB EB +=在Rt△ECB 中，△23AD DB +=△2AD+3DB=故答案为：【点睛】本题考查求最值问题，解题关键是构造出△DCE△△ACD ．三、解答题9．如图1，在RT △ABC 中，△ACB ＝90°，CB ＝4，CA ＝6，圆C 的半径为2，点P 为圆上一动点，连接AP ，BP ，求：△12AP BP +， △2AP BP +， △13AP BP +， △3AP BP +的最小值．【答案】△；△ 【分析】△在CB 上取点D ，使1CD =，连接CP 、DP 、AD ．根据作图结合题意易证DCP PCB ~，即可得出12PD BP =，从而推出12AP BP AP PD +=+，说明当A 、P 、D 三点共线时，AP PD +最小，最小值即为AD 长．最后在Rt ACD 中，利用勾股定理求出AD 的长即可； △由122()2AP BP AP BP +=+，即可求出结果； △在CA 上取点E ，使23CE =，连接CP 、EP 、BE ．根据作图结合题意易证ECP PCA ~，即可得出13EP AP =，从而推出13AP BP EP BP +=+，说明当B 、P 、E 三点共线时，EP BP +最小，最小值即为BE 长．最后在Rt BCE △中，利用勾股定理求出BE 的长即可；△由133()3AP BP AP BP +=+，即可求出结果．【详解】解：△如图，在CB 上取点D ，使1CD =，连接CP 、DP 、AD ．△1CD =，2CP =，4CB =，△12CD CP CP CB ==． 又△DCP PCB ∠=∠，△DCP PCB ~， △12PD BP =，即12PD BP =， △12AP BP AP PD +=+，△当A 、P 、D 三点共线时，AP PD +最小，最小值即为AD 长．△在Rt ACD 中，AD△12AP BP +； △△122()2AP BP AP BP +=+， △2AP BP +的最小值为2=△如图，在CA 上取点E ，使23CE =，连接CP 、EP 、BE ．△23CE =，2CP =，6CA =， △13CE CP CP CA ==． 又△ECP PCA ∠=∠，△ECP PCA ~， △13EP AP =，即13EP AP =， △13AP BP EP BP +=+，△当B 、P 、E 三点共线时，EP BP +最小，最小值即为BE 长．△在Rt BCE △中，BE =△13AP BP + △△133()3AP BP AP BP +=+，△3AP BP +的最小值为3= 【点睛】本题考查圆的基本性质，相似三角形的判定和性质，勾股定理．正确的作出辅助线，并且理解三点共线时线段最短是解答本题的关键．10．如图，Rt △ABC ，△ACB ＝90°，AC ＝BC ＝2，以C 为顶点的正方形CDEF （C 、D 、E 、F 四个顶点按逆时针方向排列）可以绕点C 自由转动，且CD AF ，BD（1）求证：△BDC △△AFC（2）当正方形CDEF 有顶点在线段AB 上时，直接写出BD 的值；（3）直接写出正方形CDEF 旋转过程中，BD AD 的最小值．【答案】（1）见解析；（21或；（3【分析】（1）利用SAS ，即可证明△FCA △△DCB ；（2）分两种情况当点D ，E 在AB 边上时和当点E ，F 在边AB 上时，讨论即可求解；（3）取AC 的中点M ．连接DM ，BM ．则CM ＝1，可证得△DCM △△ACD ，可得DMAD ，从而得到当B ，D ，M 共线时，BD AD 的值最小，即可求解． 【详解】（1）证明： △四边形CDEF 是正方形，△CF ＝CD ，△DCF ＝△ACB ＝90°，△△ACF ＝△DCB ，△AC ＝CB ，△△FCA △△DCB （SAS ）；（2）解：△如图2中，当点D ，E 在AB 边上时，△AC ＝BC ＝2，△ACB ＝90°，△sin 45AC AB ==︒△CD △AB ，△AD ＝BD ＝sin 45AC =⨯︒=△BD AD ＝1==； △如图3中，当点E ，F 在边AB 上时．BD＝CF ＝sin 452BC ⨯︒== AD，△BD AD =综上所述，BD 1 （3）如图4中．取AC 的中点M ．连接DM ，BM ．则CM ＝1，△CDCM ＝1，CA ＝2，△CD 2＝CM •CA ， △CD CA ＝CM CD， △△DCM ＝△ACD ，△△DCM △△ACD ，△DM AD ＝CD AC△DM ，△BD AD ＝BD +DM ，△当B ，D ，M 共线时，BD AD 的值最小，最小值BM =【点睛】本题主要考查了相似三角形的判定和性质，全等三角形的判定和性质，正方形的性质，锐角三角函数，熟练掌握相关知识点是解题的关键．11．如图，点A 、B 在O 上，且OA ＝OB ＝6，且OA △OB ，点C 是OA 的中点，点D 在OB 上，且OD ＝4，动点P 在O 上．求2PC ＋PD 的最小值．【答案】【分析】连接OP ，在射线OA 上截取AE =6，连接PE ．由题意易证OPC OEP ，即得出2PE PC =，从而得出2PC PD PE PD +=+，由此可知当P 、D 、E 三点共线时，PE PD +最小，最小值为DE 的长，最后在Rt OED △中利用勾股定理求出DE 的长即可．【详解】如图，连接OP ，在射线OA 上截取AE =6，连接PE ．△C 是OA 的中点， △1122OC OA OP ==．△在△OPC 和△OEP 中，12COP POE OC OP OP OE ∠=∠⎧⎪⎨==⎪⎩， △OPC OEP ， △1=2PC PE ，即2PE PC =， △2PC PD PE PD +=+，.△当P 、D 、E 三点共线时，PE PD +最小，最小值即为DE 的长，如图，在Rt OED △中，DE =，△2PC PD +的最小值为【点睛】本题考查同圆半径相等、三角形相似的判定和性质和勾股定理等知识．正确作出辅助线并理解当P 、D 、E 三点共线时，PE PD +最小，最小值为DE 的长是解答本题的关键．12．婆罗摩芨多是公元7世纪古印度伟大的数学家，他在三角形、四边形、零和负数的运算规则，二次方程等方面均有建树，他也研究过对角线互相垂直的圆内接四边形，我们把这类对角线互相垂直的圆内接四边形称为“婆氏四边形”．（1）若平行四边形ABCD 是“婆氏四边形”，则四边形ABCD 是．（填序号）△矩形；△菱形；△正方形（2）如图1，Rt ABC 中，△BAC =90°，以AB 为弦的△O 交AC 于D ，交BC 于E ，连接DE 、AE 、BD ，AB =6，3sin 5C =，若四边形ABED 是“婆氏四边形”，求DE 的长． （3）如图2，四边形ABCD 为△O 的内接四边形，连接AC ，BD ，OA ，OB ，OC ，OD ，已知△BOC +△AOD =180°．△求证：四边形ABCD 是“婆氏四边形”；△当AD +BC =4时，求△O 半径的最小值．【答案】（1）△；（2）3；（3）△见解析；【分析】（1）根本圆内接四边形对角互补和平行四边形对角相等可得△ABC =△ADC =90°，从而可证明四边形ABCD 为矩形，再根据对角线互相垂直的矩形是正方形即可判断；（2）根据垂径定理和圆周角定理可得AD =DE ，△DEB =△DEC =90°，设AD =DE =m ，则DC =8-m ，EC =10-6=4，在Rt △DEC 中解直角三角形即可；（3）△根据圆周角定理即可得出90DCA BDC ∠+∠=︒，从而可得△CED =90°，继而证明结论；△作OM ，ON 分别垂直与AD ，BC ，证明△OAM △△BON ，设ONAM n ，则2AD n =，42BC n ，2BN n ，在Rt △BON 中，根据勾股定理和二次函数的性质即可得出半径的最小值．【详解】解：（1）如下图，△平行四边形ABCD 为△O 的内接四边形， △△ABC =△ADC ，△ABC +△ADC =180°， △△ABC =△ADC =90°， △平行四边形ABCD 为矩形， △四边形ABCD 是“婆氏四边形”， △AC △BD ，△矩形ABCD 为正方形， 故答案为：△；（2）△△BAC =90°，AB =6，3sin 5C =， △10sin ABBC C==，8AC ==,BD 为直径，△△BED =△DEC =90°，△四边形ABED 是“婆氏四边形”， △AE △BD ，△AD =DE ，AB =BE =6，设AD =DE =m ，则DC =8-m ，EC =10-6=4， 在Rt △EDC 中，根据勾股定理,222DE EC DC +=,即2224(8)m m +=-，解得3m =，即DE =3；（3）△设AC ，BD 相交于点E 如图所示△12DCA AOD ∠=∠，12BDC BOC ∠=∠，△BOC +△AOD =180°， △()111809022DCA BDC AOD BOC ∠+∠=∠+∠=⨯︒=︒， △△CED =90°， 即AC △BD ，又△四边形ABCD 是△O 的内接四边形， △四边形ABCD 是“婆氏四边形”；△如下图，作OM ，ON 分别垂直与AD ，BC ， △12AM AD =，12BN BC =，△AMO =△BNO =90°， △△AOM +△OAM =90°， △OA =OB =OC =OD ， △12AOMAOD ,12BON BOC ， △△BOC +△AOD =180°， △+=90AOM BON ， △=OAM BON ， 在△OAM 和△BON 中△90=AMO BNO OAM BON OA OB ∠=∠=︒⎧⎪∠∠⎨⎪=⎩△△OAM △△BON （AAS ）， △12ONAMAD ， △AD +BC =4 设ONAM n ，则2AD n =，42BC n ，2BN n ，在Rt △BON 中，22222(2)2(1)2OBON BN n nn ，当1n=△O【点睛】本题考查圆周角定理、垂径定理、圆内接四边形的性质、勾股定理、正方形的判定定理、二次函数的性质等．（1）中能正确证明出四边形的一个角是90°是解题关键；（2）中能正确表示出Rt △EDC 的三个边是解题关键；（3）中△正确利用圆周角定理是解题关键；△正确作出辅助线构造全等三角形是解题关键．13．阅读以下材料，并按要求完成相应任务．阿波罗尼斯（ApolloniusofPerga ），古希腊人（公元前262~190年），数学家，写了八册圆锥曲线论著，其中有七册流传下来，书中详细讨论了圆锥曲线的各种性质，阿波罗尼斯圆是他的论著中一个著名的问题．一动点P 与两定点A ，B的距离之比等于定比m n :，则点P 的轨迹是以定比:(:1)m n m n ≠内分和外分线段AB 的两个分点的连线为直径的圆，这个圆称为阿波罗尼斯圆，简称“阿氏圆”．如图1，点A ，B 为两定点，点P PA mPB n=，点M 在线段AB 上，点N 在AB 的延长线上且1MA NA m m MB NB n n ⎛⎫==≠ ⎪⎝⎭，则点P 的运动轨迹是以MN 为直径的圆． 下面是“阿氏圆”的证明过程（部分）： 过点B 作//BD AP 交PM 的延长线于点D ． △A ABD ∠=∠，APM BDM ∠=∠． △APM BDM △∽△． △PA MA BD MB =． 又△MA m PAMB n PB==， △PA PA BD PB=． △BD BP．△BPD BDP ∠=∠． △APD BPD ∠=∠．如图2，在图1（隐去MD ，BD ）的基础上过点B 作//BE PN 交AP 于点E ，可知NA PANB PE=，…… 任务：（1）判断PN 是否平分BPC ∠，并说明理由；（2）请根据上面的部分证明及任务（1）中的结论，完成“阿氏圆”证明的剩余部分； （3）应用：如图3，在平面直角坐标系xOy 中，(2,0)A -，(1,0)B ，2PA PB =，则点P 所在圆的圆心坐标为________．【答案】（1）PN 平分BPC ∠．理由见解析；（2）点P 的运动轨迹是以MN 为直径的圆，见解析；（3）(2,0)【分析】（1）利用相似三角形的判定及性质仿照图1的证明即可得证；（2）根据90°的圆周角所对的弦是直径即可证得点P 的运动轨迹是以MN 为直径的圆； （3）结合题目所给的材料分别求得AB 的内分点和外分点的坐标，进而可求得点P 所在圆的圆心坐标．【详解】解：（1）PN 平分BPC ∠．理由如下： △NA m PA NB n PB ==，NA PA NB PE =， △PA PA PB PE=． △PB PE =． △PEB PBE ∠=∠． △//BE PN ，△PEB CPN ∠=∠，PBE BPN ∠=∠． △BPN CPN ∠=∠， 即PN 平分BPC ∠．（2）△12APM BPM APB ∠=∠=∠，12BPN CPN BPC ∠=∠=∠， 且180APB BPC ∠+∠=︒， △1902MPN APC ∠=∠=︒． △MN 为直径．△点P 的运动轨迹是以MN 为直径的圆． （3）△(2,0)A -，(1,0)B ， △AB ＝3，且AO ＝2OB ，△2PA PB =，△点O 为AB 的内分点，当点C 为AB 的外分点时，CA ＝2CB ， △CB ＝AB ＝3， △OC ＝OB+BC ＝4， △点C 的坐标为（4，0），△点P 所在圆的圆心坐标为（2，0）．【点睛】本题考查了相似三角形的判定及性质，直径的判定，熟练掌握相似三角形的判定及性质是解决本题的关键．14．如图1，抛物线24y ax bx =+-与x 轴交于A B 、两点，与y 轴交于点C ，其中点A 的坐标为()1,0-，抛物线的对称轴是直线32x =．(1)求抛物线的解析式；(2)若点P 是直线BC 下方的抛物线上一个动点，是否存在点P 使四边形ABPC 的面积为16，若存在，求出点P 的坐标若不存在，请说明理由；(3)如图2，过点B 作BF BC ⊥交抛物线的对称轴于点F ，以点C 为圆心，2为半径作C ，点Q 为C FQ +的最小值．【答案】(1)234y x x =-- (2)()1,6P 或()3,4【分析】（1）根据点A 的坐标为()1,0-，抛物线的对称轴是直线32x =．待定系数法求二次函数解析式即可，（2）先求得直线BC 解析式，设()2,34P m m m --，则(),4Q m m -，过点P 作PQ 轴交直线BC 于点Q ，根据ABCBCPABPC S S S=+四边形等于16建立方程，解一元二次方程即可求得m 的值，然后求得P 的坐标， （3）在CB上取2CE =，过点E 作EG OC ⊥，构造CQE CBQ ∽，则当,,F Q E 三点共线时，取得最小值，最小值为FE ，勾股定理解直角三形即可． （1）解：△抛物线24y ax bx =+-与x 轴交于A B 、两点，与y 轴交于点C ，点A 的坐标为()1,0-，抛物线的对称轴是直线32x =， △()0,4C -， 32240ba ab ⎧-=⎪⎨⎪--=⎩， 解得13a b =⎧⎨=-⎩，∴抛物线解析式为：234y x x =--，（2）当0y =，即2340x x --=， 解得121,4x x =-=，()4,0B ∴， ()0,4C -，设直线BC 解析式为y kx b =+，440bk b -=⎧⎨+=⎩， 解得14k b =⎧⎨=-⎩，∴直线BC 解析式为4y x =-，设()2,34P m m m --，过点P 作PQ 轴交直线BC 于点Q ，则(),4Q m m -，ABCBCPABPC S SS=+四边形()()22114144344281022m m m m m =⨯+⨯+--++⨯=-++， 四边形ABPC 的面积为16，∴22810m m -++16=，解得121,3m m ==，()1,6P ∴或()3,4，（3）如图，过点B 作BF BC ⊥交抛物线的对称轴于点F ，以点C 为圆心，2为半径作C ，32x =是抛物线的对称轴，35422F y =-=35,22F ⎛⎫∴ ⎪⎝⎭()()4,0,0,4B C ，4,4OB OC ∴==，BC ∴=45OBC ∠=︒，BF BC ⊥， 45FBO ∴∠=︒，在CB 上取CE =过点E 作EG OC ⊥，交y 轴于点G ，交抛物线对称轴于点H ，则CG =1sin 452EG =︒=，31122EH =-= 6FH ∴=，2,CQ CE BC ===22CE CQ CQ BC ∴====，QCE BCQ ∠=∠， CQE CBQ ∴∽，EQ CQ BQ CB ∴==QE ∴=，FQ +FE ≥，当,,F Q E 三点共线时，取得最小值，最小值为FE ，EG FG ⊥EF ∴=FQ + 【点睛】本题考查了二次函数综合，相似三角形的性质与判定，掌握二次函数的性质与相似三角形的性质与判定是解题的关键．15．如图1所示，△O 的半径为 r ，点 A 、B 都在△O 外，P 为△O 上的动点， 已知 r ＝k ·OB ．连接 P A 、PB ，则当“P A ＋k ·PB ”的值最小时，P 点的位置如何确定？【答案】见解析【详解】1：连接动点至圆心0（将系数不为1的线段两端点分别与圆心相连接），即连接OP、OB；2：计算连接线段OP、OB长度；3：计算两线段长度的比值kOPOB=；4：在OB上截取一点C，使得OC OPOP OB=构建母子型相似：5：连接AC，与圆0交点为P，即AC线段长为P A＋K*PB的最小值．本题的关键在于如何确定“k·PB”的大小，（如图2）在线段OB上截取OC使OC＝k·r，则可说明△BPO与△PCO相似，即k·PB＝PC．△本题求“P A＋k·PB”的最小值转化为求“P A＋PC”的最小值，即A、P、C三点共线时最小（如图3），时AC线段长即所求最小值．16．问题提出：如图△，在Rt ABC△中，90C=∠，4CB=，6CA=，△C的半径为2，P 为圆上一动点，连接AP、BP，求12AP BP+的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图△，连接CP，在CB上取一点D，使1CD=，则12CD CPCP CB==．又PCD BCP∠=∠，所以PCD△BCP．所以12PD CD BP CP ==． 所以12PD PB =，所以12AP BP AP PD +=+． 请你完成余下的思考，并直接写出答案：12AP BP +的最小值为________； （2）自主探索：在“问题提出”的条件不变的前提下，求13AP BP +的最小值；（3）拓展延伸：如图△，已知在扇形COD 中，90COD ∠=，6OC =，3OA =，5OB =，P 是CD 上一点，求2PA PB +的最小值．【答案】（1（2（3）13． 【分析】（1）根据题意可知最小值为AD 长度，利用勾股定理即可求出AD 长度． （2）连接CP ，在CA 上取一点D ，使23CD =，即可证明PCD △ACP △，得到13PD AP =，即13AP BP PD BP +=+，所以13AP BP +的最小值为BD 长度，利用勾股定理即可求出BD 长度．（3）延长OC 到E ，使6CE =，连接PE ，OP ，即可证明OAP △△OPE ，得到2EP PA =，即2PA PB EP PB +=+，所以2PA PB +的最小值为BE 长度，利用勾股定理即可求出BE 长度．【详解】（1）根据题意可知，当A 、P 、D 三点共线时，12AP BP +最小，最小值AD ==．（2）连接CP ，在CA 上取一点D ，使23CD =， 则有13CD CP CP CA ==，△PCD ACP ∠=∠， △PCD △ACP △，得13PD CD AP CP ==， △13PD AP =，故13AP BP PD BP +=+， 仅当B 、P 、D 三点共线时，13AP BP +的最小值BD ==（3）延长OC 到E ，使6CE =，连接PE ，OP ，则12OA OP OP OE ==，△AOP POE ∠=∠， △OAP △△OPE ，△12OA OP AP OP OE EP ===， △2EP PA =，△2PA PB EP PB +=+， 仅当E 、P 、B 三点共线时，13EP PB BE +=，即2PA PB +的最小值为13．【点睛】本题考查圆的综合，勾股定理，相似三角形的判定和性质．根据阅读材料的思路构造出PCD △ACP △和OAP △△OPE 是解题的关键．本题较难．17．如图1，在平面直角坐标系中，直线y ＝﹣5x+5与x 轴，y 轴分别交于A ，C 两点，抛物线y ＝x 2+bx+c 经过A ，C 两点，与x 轴的另一交点为B（1）求抛物线解析式及B 点坐标；（2）若点M 为x 轴下方抛物线上一动点，连接MA 、MB 、BC ，当点M 运动到某一位置时，四边形AMBC 面积最大，求此时点M 的坐标及四边形AMBC 的面积；（3）如图2，若P 点是半径为2的△B 上一动点，连接PC 、PA ，当点P 运动到某一位置时，PC+12PA 的值最小，请求出这个最小值，并说明理由．【答案】（1）y ＝x 2﹣6x+5， B （5，）；（2）当M （3，﹣4）时，四边形AMBC 面积最大，最大面积等于18；（3）PC+12PA .【分析】（1）由直线y ＝﹣5x+5求点A 、C 坐标，用待定系数法求抛物线解析式，进而求得点B 坐标．（2）从x 轴把四边形AMBC 分成△ABC 与△ABM ；由点A 、B 、C 坐标求△ABC 面积；设点M 横坐标为m ，过点M 作x 轴的垂线段MH ，则能用m 表示MH 的长，进而求△ABM 的面积，得到△ABM 面积与m 的二次函数关系式，且对应的a 值小于0，配方即求得m 为何值时取得最大值，进而求点M 坐标和四边形AMBC 的面积最大值． （3）作点D 坐标为（4，0），可得BD ＝1，进而有12BD BP BP AB ==，再加上公共角△PBD ＝△ABP ，根据两边对应成比例且夹角相等可证△PBD△△ABP ，得PD PA等于相似比12，进而得PD ＝12AP ，所以当C 、P 、D 在同一直线上时，PC+12PA ＝PC+PD ＝CD 最小．用两点间距离公式即求得CD 的长．【详解】解：（1）直线y＝﹣5x+5，x＝0时，y＝5△C（0，5）y＝﹣5x+5＝0时，解得：x＝1△A（1，0）△抛物线y＝x2+bx+c经过A，C两点△10005b cc++=⎧⎨++=⎩解得：65bc=-⎧⎨=⎩△抛物线解析式为y＝x2﹣6x+5当y＝x2﹣6x+5＝0时，解得：x1＝1，x2＝5△B（5，0）（2）如图1，过点M作MH△x轴于点H△A（1，0），B（5，0），C（0，5）△AB＝5﹣1＝4，OC＝5△S△ABC＝12AB•OC＝12×4×5＝10△点M为x轴下方抛物线上的点△设M（m，m2﹣6m+5）（1＜m＜5）△MH＝|m2﹣6m+5|＝﹣m2+6m﹣5△S△ABM＝12AB•MH＝12×4（﹣m2+6m﹣5）＝﹣2m2+12m﹣10＝﹣2（m﹣3）2+8△S四边形AMBC＝S△ABC+S△ABM＝10+[﹣2（m﹣3）2+8]＝﹣2（m﹣3）2+18△当m＝3，即M（3，﹣4）时，四边形AMBC面积最大，最大面积等于18（3）如图2，在x轴上取点D（4，0），连接PD、CD△BD＝5﹣4＝1△AB＝4，BP＝2△12 BD BP BP AB==△△PBD＝△ABP △△PBD△△ABP△12== PD PD AP BP△PD＝12AP△PC+12PA＝PC+PD△当点C、P、D在同一直线上时，PC+12PA＝PC+PD＝CD最小△CD△PC+12PA【点睛】此题主要考查二次函数综合，解题的关键是熟知二次函数的性质、圆的性质及相似三角形的判断与性质.18．如图，抛物线2y ax bx c=++与x轴交于A0)，B两点（点B在点A的左侧），与y轴交于点C，且3OB OA==，OAC∠的平分线AD交y轴于点D，过点A且垂直于AD 的直线l交y轴于点E，点P是x轴下方抛物线上的一个动点，过点P作PF x⊥轴，垂足为F，交直线AD于点H．（1）求抛物线的解析式；（2）设点P的横坐标为m，当FH HP=时，求m的值；（3）当直线PF为抛物线的对称轴时，以点H为圆心，12HC为半径作H，点Q为H上的一个动点，求14AQ EQ+的最小值．【答案】（1）y 13=x 2﹣3；（2）（3．【分析】对于（1），结合已知先求出点B 和点C 的坐标，再利用待定系数法求解即可； 对于（2），在Rt△OAC 中，利用三角函数的知识求出△OAC 的度数，再利用角平分线的定义求出△OAD 的度数，进而得到点D 的坐标；接下来求出直线AD 的解析式，表示出点P ，H ，F 的坐标，再利用两点间的距离公式可完成解答；对于（3），首先求出△H 的半径，在HA 上取一点K ，使得HK=14，此时K （15-8）；然后由HQ2=HK·HA ，得到△QHK△△AHQ ，再利用相似三角形的性质求出KQ=14AQ ，进而可得当E 、Q 、K 共线时，14AQ+EQ 的值最小，据此解答.【详解】（1）由题意A 0），B （﹣0），C （0，﹣3），设抛物线的解析式为y ＝a （x （x ，把C （0，﹣3）代入得到a 13=，△抛物线的解析式为y 13=x 2﹣3．（2）在Rt△AOC 中，tan△OAC OCOA==△△OAC ＝60°． △AD 平分△OAC ，△△OAD ＝30°，△OD ＝OA •tan30°＝1，△D （0，﹣1），△直线AD 的解析式为y =﹣1，由题意P （m ，13m 2m ﹣3），H （m ﹣1），F （m ，0）．△FH ＝PH ，△1=﹣1﹣（13m 2m ﹣3）解得m =，△当FH ＝HP 时，m 的值为（3）如图，△PF 是对称轴，△F （0），H （2）．△AH △AE ，△△EAO ＝60°，△EO ＝3，△E （0，3）．△C （0，﹣3），△HC =2，AH ＝2FH ＝4，△QH 12=CH ＝1，在HA 上取一点K ，使得HK 14=，此时K （158-）． △HQ 2＝1，HK •HA ＝1，△HQ 2＝HK •HA ，△HQ KHAH HQ=． △△QHK ＝△AHQ ，△△QHK △△AHQ ，△14KQ HQ AQ AH ==，△KQ 14=AQ ，△14AQ +QE ＝KQ +EQ ，△当E 、Q 、K 共线时，14AQ +QE 的值最小，最小值． 【点睛】本题考查了相似三角形对应边成比例、两边成比例且夹角相等的两个三角形相似、待定系数法求二次函数的表达式、二次函数的图象与性质、数轴上两点间的距离公式，熟练掌握该知识点是本题解题的关键.19．阅读以下材料，并按要求完成相应的任务. 已知平面上两点A B 、，则所有符合0(PAk k PB=>且1)k ≠的点P 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆. 阿氏圆基本解法：构造三角形相似.【问题】如图1，在平面直角坐标中，在x 轴，y 轴上分别有点()(),0,0,C m D n ，点P 是平面内一动点，且OP r =，设OPk OD=，求PC kPD +的最小值.阿氏圆的关键解题步骤：第一步：如图1，在OD 上取点M ，使得::OM OP OP OD k ==；第二步：证明kPD PM =；第三步：连接CM ，此时CM 即为所求的最小值. 下面是该题的解答过程(部分)：解：在OD 上取点M ，使得::OM OP OP OD k ==， 又,POD MOP POM DOP ∠=∠∴.任务：()1将以上解答过程补充完整.()2如图2，在RtABC 中，90,4,3,ACB AC BC D ∠=︒==为ABC 内一动点，满足2CD =，利用()1中的结论，请直接写出23AD BD +的最小值.【答案】（1（2. 【分析】 △ 将PC+kPD 转化成PC+MP ，当PC+kPD 最小，即PC+MP 最小，图中可以看出当C 、P 、M 共线最小，利用勾股定理求出即可；△ 根据上一问得出的结果，把图2的各个点与图1对应代入，C 对应O,D 对应P ，A 对应C ，B 对应M ，当D 在AB 上时23AD BD +为最小值，所以23AD BD + =【详解】解()1:,MP PD k MP kPD =∴=∴，PC kPD PC MP ∴+=+，当PC kPD +取最小值时，PC MP +有最小值，即,,C P M 三点共线时有最小值，利用勾股定理得CM =()223AD BD +， 提示：4AC m ==，2433CD kr ==，23AD BD ∴+=【点睛】此题主要考查了新定义的理解与应用，快速准确的掌握新定义并能举一反三是解题的关键. 20．数学概念如图△，AE 是△ABC 的角平分线，D 是直线BC 上一点，如果点D 满足DA ＝DE ，那么点D 叫做△ABC 的边BC 上的“阿氏点”．概念理解（1）在图△中，利用直尺和圆规作△ABC 的边BC 上的“阿氏点”，用字母D 表示（不写作法，保留作图痕迹）； 性质探究（2）在（1）中，求证：△DAB △△DCA ； 知识运用（3）如图△，四边形ABCD 内接于△O ，对角线AC 、BD 相交于点E ，以D 为圆心，DA 为半径的圆恰好经过点C ，且与BD 交于点F ． △求证：点D 是△ABE 的边BE 上的“阿氏点”； △若BE 52=，DE ＝2，AE ＝3，则△D 和△O 的半径长分别为 ， ．【答案】（1）见详解；（2）见详解；（3）△见详解；△3．【分析】（1）根据题意，作△BAC的角平分线，交BC于点E，作AE的垂直平分线，交直线BC于点D，连接AD，即可得到答案．（2）由DA＝DE，得到△AED=△EAD，然后证明△B=△CAD，即可得到结论成立；（3）△连接AF，由DA=DF=DC，则△AFD=△FAD，△ABD=△CAD，然后得到△BAF=△FAC，即可得到结论成立；△由（2）可知，易证△DAB△△DEA，则DA DBDE DA，即可求出DA的长度；作DG△AC，则点G是AC的中点，连接OG，OA，由垂径定理，得到OG△AC，然后求出AC的长度，然后得到DG的长度，利用勾股定理，即可求出OA的长度．【详解】解：（1）如图：根据题意，作△BAC的角平分线，交BC于点E，作AE的垂直平分线，交直线BC于点D，连接AD．（2）如（1）图，△DA＝DE，△△AED=△EAD，△△AED=△B+△BAE，△EAD=△EAC+△CAD，又AE平分△BAC，△△BAE=△EAC，△△B=△CAD，△△ADC=△CDA，△△DAB△△DCA；（3）证明：△连接AF，如图：△DA=DF=DC，△△AFD=△FAD，△ABD=△CAD，△△AFD=△ABD+△BAF，△FAD=△CAD+△FAC，△△BAF=△FAC，△AF平分△BAE，在△ABE中，AF平分△BAE，DF=DA，△点D是△ABE的边BE上的“阿氏点”；△由（2）可知，△△ABD=△CAD，△ADE=△EDA，△△DAB△△DEA，△DA DBDE DA=，即5222DADA+=，△3DA=（负值已舍去）；如图，作DG△AC，连接OG，OA，△DA=DC，△点G是AC的中点，由垂径定理，则OG△AC，易证△AED△△BEC，△AE DEBE CE=，即3252CE=，△53CE =， △514333AC AE CE =+=+=， △111472233AG AC ==⨯=， 在△ADG 中，利用勾股定理，则DG ===，在Rt△AOG 中，设OA=OD=r ，则OG=r 由勾股定理，得222OG AG OA +=，△2227(()3r r +=，解得：r =△△D 和△O 的半径长分别为3故答案为：3 【点睛】本题考查了相似三角形的判定和性质，垂径定理，圆周角定理，勾股定理，以及作图的基本步骤，解题的关键是熟练掌握题意，掌握所学的知识对题目进行分析，正确作出辅助线，从而进行解题．。

沪教版初中数学中考总复习知识点梳理重点题型（常考知识点）巩固练习中考总复习：圆的有关概念、性质与圆有关的位置关系—知识讲解（提高）【考纲要求】1. 圆的基本性质和位置关系是中考考查的重点，但圆中复杂证明及两圆位置关系中证明会有下降趋势，不会有太复杂的大题出现；2.中考试题中将更侧重于具体问题中考查圆的定义及点与圆的位置关系，对应用、创新、开放探究型题目，会根据当前的政治形势、新闻背景和实际生活去命题，进一步体现数学来源于生活，又应用于生活．【知识网络】【考点梳理】考点一、圆的有关概念及性质1．圆的有关概念圆、圆心、半径、等圆；弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧；三角形的外接圆、三角形的内切圆、三角形的外心、三角形的内心、圆心角、圆周角．要点诠释：等弧：在同圆或等圆中，能够互相重合的弧叫做等弧．2．圆的对称性圆是轴对称图形，任何一条直径所在直线都是它的对称轴，圆有无数条对称轴；圆是以圆心为对称中心的中心对称图形；圆具有旋转不变性．3．圆的确定不在同一直线上的三个点确定一个圆．要点诠释：圆心确定圆的位置，半径确定圆的大小．4．垂直于弦的直径垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．要点诠释：在图中(1)直径CD，(2)CD⊥AB，(3)AM＝MB，(4)，(5)．若上述5个条件有2个成立，则另外3个也成立．因此，垂径定理也称“五二三定理”．即知二推三．注意：(1)(3)作条件时，应限制AB不能为直径．5．圆心角、弧、弦之间的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量也相等．6．圆周角圆周角定理在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论1 在同圆或等圆中，相等的圆周角所对的弧也相等．推论2 半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径．要点诠释：圆周角性质的前提是在同圆或等圆中．7.圆内接四边形（1）定义: 圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．考点二、与圆有关的位置关系1．点和圆的位置关系设⊙O的半径为r，点P到圆心的距离OP＝d，则有：点P在圆外d＞r；点P在圆上d＝r；点P在圆内d＜r．要点诠释：圆的确定：①过一点的圆有无数个，如图所示．②过两点A、B的圆有无数个，如图所示．③经过在同一直线上的三点不能作圆．④不在同一直线上的三点确定一个圆．如图所示．2．直线和圆的位置关系（1）切线的判定切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线．(会过圆上一点画圆的切线)（2）切线的性质切线的性质定理圆的切线垂直于过切点的半径．（3）切线长和切线长定理切线长经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长．切线长定理从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．要点诠释：直线l是⊙O的切线，必须符合两个条件：①直线l经过⊙O上的一点A；②OA⊥l．（4）三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆.（5）三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 三角形的内心到三边的距离都相等.要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即 (S为三角形的面积，P为三角形的周长，r为内切圆的半径).3．圆和圆的位置关系(1)基本概念两圆相离、相切、外离、外切、相交、内切、内含的定义．(2)请看下表：要点诠释：①相切包括内切和外切，相离包括外离和内含．其中相切和相交是重点．②同心圆是内含的特殊情况．③圆与圆的位置关系可以从两个圆的相对运动来理解．④“R-r”时，要特别注意，R＞r．考点三、与圆有关的规律探究1．和圆有关的最长线段和最短线段了解和圆有关的最长线段与最短线段，对有关圆的性质的了解极为重要，下面对有关问题进行简单论述．(1)圆中最长的弦是直径．如图①，AB是⊙O的直径，CD为非直径的弦，则AB＞CD，即直径AB是最长的弦．过圆内一点最短的弦，是与过该点的直径垂直的弦，如图②，P是⊙O内任意一点，过点P作⊙O的直径AB，过P作弦CD⊥AB于P，则CD是过点P的最短的弦．(2)圆外一点与圆上一点的连线中，最长的线段与最短的线段都在过圆心的直线上．如图所示，P在⊙O外，连接PO交⊙O于A，延长PO交⊙O于B，则在点P与⊙O上各点连接的线段中，PB最长，PA最短．(3)圆内一点与圆上一点的连线中，最长的线段与最短的线段也都在过圆心的直线上．如图所示，P为⊙O内一点，直径过点P，交⊙O于A、B两点，则PB最长、PA最短．2．与三角形内心有关的角(1)如图所示，I是△ABC的内心，则∠BIC．(2)如图所示，E是△ABC的两外角平分线的交点，．(3)如图所示，E是△ABC内角与外角的平分线的交点，．(4)如图所示，⊙O是△ABC的内切圆，D、E、F分别为切点，则∠DOE＝180°－∠A．(5)如图所示，⊙O是△ABC的内切圆，D、E、F为切点，．(6)如图所示，⊙O是△ABC的内切圆，D、E、F为切点，P为上一点，则．【典型例题】类型一、圆的性质及垂径定理的应用1．已知：如图所示，⊙O中，半径OA＝4，弦BC经过半径OA的中点P，∠OPC＝60°，求弦BC的长．【思路点拨】要用好60°角，构造直角三角形．在圆中常用的是作出弦的弦心距，由弦心距，半弦长及半径构成直角三角形．【答案与解析】解：过O作OM⊥BC于M，连接OC．在Rt△OPM中，∠OPC＝60°，OP，∴PM＝1，OM＝．在Rt△OMC中，BC＝2MC＝．【总结升华】圆的半径、弦长的一半、弦心距三条线段组成一个直角三角形，其中一个锐角为弦所对圆心角的一半，可充分利用它们的关系解决有关垂径定理的计算问题．2．如图所示，在⊙O中，弦AB与CD相交于点M，，连接AC．(1)求证：△MAC是等腰三角形；(2)若AC为⊙O直径，求证：AC2＝2AM·AB．【思路点拨】(1)证明∠MCA＝∠MAC；(2)证明△AOM∽△ABC．【答案与解析】证明：(1) ∵，∴∠MCA＝∠MAC．∴△MAC是等腰三角形．(2)连接OM．∵AC为⊙O直径，∴∠ABC＝90°．∵△MAC是等腰三角形，OA＝OC，∴MO⊥AC．∴∠AOM＝∠ABC＝90°．∵∠MAO＝∠CAB，∴△AOM∽△ABC，∴，∴AO·AC＝AM·AB，∴AC2＝2AM·AB．【总结升华】本题考查的是圆周角定理，涉及到全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的判定与性质及三角形内角和定理，涉及面较广，难度适中．举一反三：【变式】如图所示，在⊙O中，AB＝2CD，则( )A． B．C． D．与的大小关系无法确定【答案】解：要比较与的大小有两种思路．(1)把的一半作出来，比较与的大小；(2)把作出来，比较与的大小．如图所示，作OE⊥AB，垂足为E，交于F．则，且．∵AB＝2CD．∴AE＝CD．在Rt△AFE中，AF＞AE＝CD．∴AF＞CD．∴，即．答案A.【高清课堂：圆的有关概念、性质及与圆有关的位置关系 ID:412074 经典例题2】3．已知：如图所示，△ABC内接于⊙O，BD⊥半径AO于D．(1)求证：∠C＝∠ABD；(2)若BD＝4.8，sinC＝，求⊙O的半径．【思路点拨】过O作OE⊥AB于E，连接BO，再由垂径定理及三角函数进行证明与求解.【答案与解析】解法一：(1)过O作OE⊥AB于E，连接BO(如图所示)，则．又∵ BD⊥AO，∴∠ABD+∠BAD＝90°．∵∠AOE+∠BAD＝90°，∴∠ABD＝∠AOE＝∠C．（2）在Rt△ABD中，，∴．设AD＝4k，则AB＝5k，BD＝3k＝4.8，k＝1.6．∴AB＝8，AE＝4．∵，∴．∴OA＝5．解法二：（1）延长AO交⊙O于C′．（如图所示）∴∠C′＝∠C．∵AC′为⊙O的直径，∴∠ABC′＝90°．∴∠C′+∠BAD＝90°．∵∠BAD+∠ABD＝90°，∴∠ABD＝∠C′＝∠C．（2）在Rt△BDC′中，，∴．在Rt△ABC′中，∵，∴设AB＝4k，则AC′＝5k，BC′＝3k＝6．∴k＝2．∴．【总结升华】解决圆周角的问题中常用的方法有两种：一是把圆周角转化为同弧所对圆心角的一半的角；二是将圆周角的顶点移动到使其一边经过圆心．类型二、圆的切线判定与性质的应用4．（2014秋•兴化市月考）如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE．（1）求证：AC平分∠DAB；（2）求证：△PCF是等腰三角形；（3）若AC=8，BC=6，求线段BE的长．【思路点拨】（1）根据切线的性质可得结论；（2）连接OE，根据圆周角定理得∠ACB=90°，进而可推导得出△PCF是等腰三角形；（3）先在Rt△ACB中，根据勾股定理计算出AB=10，最终算得BE的值．【答案与解析】（1）证明：∵PD为⊙O的切线，∴OC⊥DP，∵AD⊥DP，∴OC∥AD，∴∠DAC=∠OCA，∵O A=OC，∴∠OAC=∠OCA，∴∠OAC=∠DAC，∴AC平分∠DAB；（2）证明：∵AB为⊙O的直径，∴∠ACB=90°，∵CE平分∠ACB，∴∠BCE=45°，∴∠BOE=2∠BCE=90°，∴∠OFE+∠OEF=90°，而∠OFE=∠CFP，∴∠CFP+∠OEF=90°，∵OC⊥PD，∴∠OCP=90°，即∠OCF+∠PCF=90°，而∠OCF=∠OEF，∴∠PCF=∠CFP，∴△PCF是等腰三角形；（3）解：在Rt△ACB中，∵AC=8，BC=6，∴AB==10，∴OB=5，∵∠BOE=90°，∴△BOE为等腰直角三角形，∴BE=OB=5．【总结升华】本题考查了切线的性质，圆周角定理和等腰三角形的判定．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．举一反三：【变式】（2015•毕节市）如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，AC=FC．（1）求证：AC是⊙O的切线；（2）已知圆的半径R=5，EF=3，求DF的长．【答案】（1）证明：连结OA、OD，如图，∵D为BE的下半圆弧的中点，∴OD⊥BE，∴∠D+∠DFO=90°，∵AC=FC，∴∠CAF=∠CFA，∵∠CFA=∠DFO，∴∠CAF=∠DFO，而OA=OD，∴∠OAD=∠ODF，∴∠OAD+∠CAF=90°，即∠OAC=90°，∴OA⊥AC，∴AC是⊙O的切线；（2）解：∵圆的半径R=5，EF=3，∴OF=2，在Rt△ODF中，∵OD=5，OF=2，∴DF==．类型三、切线的性质与等腰三角形、勾股定理综合运用5．如图所示，⊙O是Rt△ABC的外接圆，AB为直径，∠ABC＝30°，CD是⊙O的切线，ED⊥AB于F．(1)判断△DCE的形状；(2)设⊙O的半径为1，且，求证△DCE≌△OCB．【思路点拨】（1）由于AB是直径，那么∠ACB=90°，而∠ABC=30°，易求∠BAC=60°，结合OA=OC，易证△AOC 是正三角形，于是∠OCD=60°，结合CD是切线，易求∠DCE=30°，在Rt△AEF中，易求∠E=30°，于是∠DCE=∠E，可证△CDE为等腰三角形；（2）在Rt△ABC中，由于∠A=60°，AB=2，易求AC=AO=1，利用勾股定理可求BC=，CE=AE-AC=，那么BC=CE，而∠OBC=∠OCB=∠DCE=∠DEC=30°，从而可证△OBC≌△DCE．【答案与解析】解：(1)∵∠ABC＝30°，∴∠BAC＝60°．又∵OA＝OC，∴△AOC是正三角形．∵CD是切线，∴∠OCD＝90°．∴∠DCE＝180°-60°＝90°－30°．∴∠DCE＝∠DEC而ED⊥AB于F，∴∠CED＝90°－∠BAC＝30°．故△CDE为等腰三角形．(2)证明：在△ABC中，∵AB＝2，AC＝AO＝1，∴BC＝．，∴．又∵∠AEF＝30°，∴AE＝2AF＝．∴CE＝AE－AC＝＝BC．而∠OCB＝∠ACB－∠ACO＝30°＝∠ABC，故△CDE≌△COB．【总结升华】本题考查了切线的性质、等边三角形的判定和性质、等腰三角形的判定、勾股定理、全等三角形的判定和性质．解题的关键是证明△AOC是正三角形．举一反三：【变式】如图所示，PQ＝3，以PQ为直径的圆与一个以5为半径的圆相切于点P，正方形ABCD的顶点A、B在大圆上，小圆在正方形的外部且与CD切于点Q，则AB＝________．【答案】解：连接PQ并延长交AB于E，设大圆的圆心为O，连接OA．设AB＝2x，则AE＝x，OB＝2x-2．在Rt△OAE中，OA＝5，∵OA2＝OE2+AE2，即52＝(2x-2)2+x2，∴x＝3．∴AB＝6．答案：66．如图所示，⊙O的直径AB＝4，点P是AB延长线上的一点，PC切⊙O于点C，连接AC．PM平分∠APC 交AC于M．(1)若∠CPA＝30°，求CP的长及∠CMP的度数；(2)若点P在AB的延长线上运动，你认为∠CMP的大小是否发生变化？若变化，说明理由；若不变化，请求出∠CMP的度数；(3)若点P在直径BA的延长线上，PC切⊙O于点C，那么∠CMP的大小是否变化？请直接写出你的结论．【思路点拨】（1）作辅助线，连接OC，根据切线的性质知：OC⊥PC，由∠CPO的值和OC的长，可将PC的长求出；（2）通过角之间的转化，可知：∠CMP=（∠COP+∠CPO），故∠CMP的值不发生变化．【答案与解析】解:(1)连接OC，则∠OCP＝90°．∵ OA＝OC，∴∠COP＝2∠CAP＝60°．∴ CP＝OC·tan60°＝AB·tan60°＝，∴ CP＝．∵ PM平分∠CPA，∴．∴∠CMP＝30°+15°=45°.(2)设∠CPA＝α，∵ PM平分∠CPA，∴∠MPA＝∠CPA．∵∠OCP＝90°，∴∠COP＝90°-α．又∵ OA＝OC，∴∠CAP＝．∴∠CMP＝∠CAP+∠MPA．（3）∠CMP的大小没有变化∵∠CMP=∠A+∠MPA=∠COP+∠CPO=（∠COP+∠CPO）=×90°=45°．【总结升华】解第(2)小题时，引用“设∠CPA＝α”这一方法，用代数方法计算得出结论，降低了解题的难度．本题主要考查切线的性质及对直角三角形性质的运用．举一反三：【变式】如图所示，AB是⊙O的直径，C是的中点，CD⊥AB于D，CD与AE相交于F．(1)求证：AC2＝AF·AE；(2)求证：AF＝CF．【答案】证明：(1)如图所示，连接CE，延长CD交⊙O于G，连接AG．∵AB是⊙O直径，CD⊥AB，∴．∴∠2＝∠3．又∵∠1＝∠1，∴△AFC∽△ACE．∴．∴ AC2＝AF·AE．(2)由(1)得．又∵C是的中点，∴．∴∠2＝∠1．∴AF＝CF．。