高一数学上学期第11周双休练习

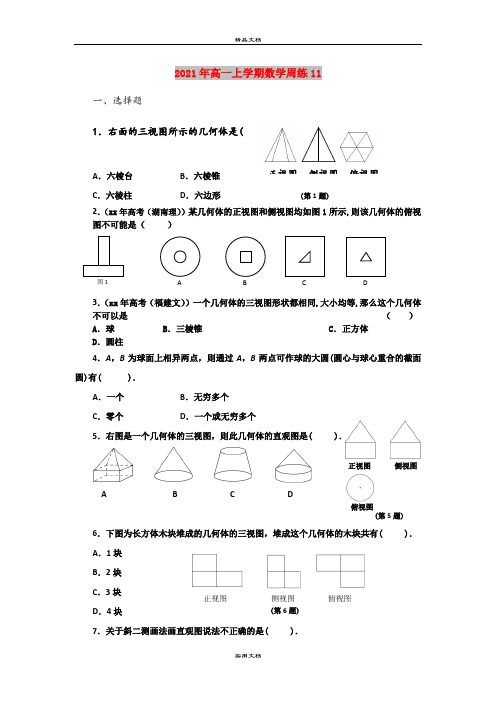
2021年高一上学期数学周练11一、选择题1．右面的三视图所示的几何体是( )．A ．六棱台B ．六棱锥C ．六棱柱D ．六边形 (第1题)2．（xx 年高考（湖南理））某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是（ ）3．（xx 年高考（福建文））一个几何体的三视图形状都相同,大小均等,那么这个几何体不可以是 （ ）A ．球B ．三棱锥C ．正方体D ．圆柱4．A ，B 为球面上相异两点，则通过A ，B 两点可作球的大圆(圆心与球心重合的截面圆)有( )．A ．一个B ．无穷多个C ．零个D ．一个或无穷多个5．右图是一个几何体的三视图，则此几何体的直观图是( )． )．A B C D6．下图为长方体木块堆成的几何体的三视图，堆成这个几何体的木块共有( )．A ．1块B ．2块C ．3块D ．4块 7．关于斜二测画法画直观图说法不正确的是( )．正视图 侧视图俯视图(第5题)正视图 俯视图 侧视图 (第6题)A 图1BC DA．在实物图中取坐标系不同，所得的直观图有可能不同B．平行于坐标轴的线段在直观图中仍然平行于坐标轴C．平行于坐标轴的线段长度在直观图中仍然保持不变D．斜二测坐标系取的角可能是135°8．如图，下列几何体各自的三视图中，有且仅有两个视图相同的是()．A．①②B．①③C．①④D．②④9．一正方体的各顶点都在同一球面上，用过球心的平面去截这个组合体，截面图不能是()．A B C D10．如果一个三角形的平行投影仍然是一个三角形，则下列结论正确的是()．A．原三角形的内心的平行投影还是投影三角形的内心B．原三角形的重心的平行投影还是投影三角形的重心C．原三角形的垂心的平行投影还是投影三角形的垂心D．原三角形的外心的平行投影还是投影三角形的外心11.如图所示为一平面图形的直观图,则此平面图形可能是( )12.给出下列命题：①如果一个几何体的三视图是完全相同的，则这个几何体是正方体;AC B A C11 正视图 B B A A 3 侧视图 A BC 1 ②如果一个几何体的正视图和俯视图都是矩形，则这个几何体是长方体；③如果一个几何体的三视图都是矩形，则这个几何体是长方体；④如果一个几何体的正视图和侧视图都是等腰梯形，则这个几何体是圆台。

贵州省贵阳市清镇2017-2018学年高一数学上学期周练试题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（贵州省贵阳市清镇2017-2018学年高一数学上学期周练试题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为贵州省贵阳市清镇2017-2018学年高一数学上学期周练试题的全部内容。

贵州省贵阳市清镇2017-2018学年高一数学上学期周练试题16。

今年我市参加中考的人数大约有41300人，将41300用科学记数法表示为（ )A ．413×102 B ． 41。

3×103C ． 4。

13×104D ． 0.413×10317.若x ＞y ，则下列式子中错误的是（ ） A ．x ﹣3＞y ﹣3 B ．＞C ． x+3＞y+3D ． ﹣3x ＞﹣3y18。

右图是某几何体的三视图,该几何体是 A.圆锥 B 。

圆柱 C 。

正三棱柱 D 。

正三棱锥19.在等腰三角形、平行四边形、直角梯形和圆中既是轴对称图形又是中心对称 图形的是（ ）A ．等腰三角形B ．平行四边形C ．直角梯形D ．圆 20。

升旗时，旗子的高度h (米)与时间t （分）的函数图像大致为( ）21。

如图是一个正方体展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是（ )A ．我B ． 中C ． 国D ．梦22.已知直线y=kx+b,若k+b=﹣5，kb=6，那么该直线不经过（ ) A ．第一象限 B ．第二象限C ． 第三象限D ． 第四象限23．有四张质地相同的卡片，它们的背面相同，其中两张的正面印有“粽子”的图案，另外两张的正面印有“龙舟”的图案，现将它们背面朝上，洗均匀后排列在桌面，任意翻开两张,那th Ot h Ot h Oth OABCD么两张图案一样的概率是A ．错误!B ．错误!C ．错误!D ．错误!24．某单位向一所希望小学赠送1080件文具，现用A 、B 两种不同的包装箱进行包装，已知每个B 型包装箱比A 型包装箱多装15件文具,单独使用B 型包装箱比单独使用A 型包装箱可少用12个。

2021年高一上学期11月周练数学试卷含答案一、 填空题(本大题共14小题，每小题5分，共70分)1．集合A ＝{0,2，a }，B ＝{1，a 2}，若A ∪B ＝{0,1,2,4,16}，则a 的值为________________．2．设函数f (x )＝⎩⎨⎧1－2x 2x ≤1x 2＋3x －2 x >1，则f (1f 3)的值为________．3．若函数y ＝f (x )的定义域是[0,2]，则函数g (x )＝f 2xx －1的定义域是________．4．三个数a ＝0.32，b ＝log 20.3，c ＝20.3之间的大小关系是________．5． 若函数f (x )唯一的一个零点同时在区间(0,16)、(0,8)、(0,4)、(0,2)内，那么下列命题中正确的是________．(填序号)①函数f (x )在区间(0,1)内有零点；②函数f (x )在区间(0,1)或(1,2)内有零点；③函数f (x )在区间[2,16)内无零点；④函数f (x )在区间(1,16)内无零点．6．已知0<a <1，则方程a |x |＝|log a x |的实根个数是________．7．函数f(x)＝x2－2ax＋1有两个零点，且分别在(0,1)与(1,2)内，则实数a 的取值范围是________．8．设2a＝5b＝m，且1a＋1b＝2，则m＝________.9．设函数f(x)满足：①y＝f(x＋1)是偶函数；②在[1，＋∞)上为增函数，则f(－1)与f(2)的大小关系是________．10．已知log a 12>0，若≤1a，则实数x的取值范围为______________．11．计算：0.25×(－12)－4＋lg 8＋3lg 5＝________.12．直线y＝1与曲线y＝x2－||x＋a有四个交点，则a的取值范围为________________．13．已知关于x的函数y＝log a(2－ax)在[0,1]上是减函数，则a的取值范围是________．14．已知函数f(x)是定义在R上的奇函数，当x>0时，f(x)＝1－2－x，则不等式f(x)<－12的解集是________．二、解答题(本大题共6小题，共90分)15．(14分)已知函数f(x)＝的定义域为集合A，函数g(x)＝－1的值域为集合B，且A∪B＝B，求实数m的取值范围．16．(14分)已知f(x)＝x＋ax2＋bx＋1是定义在[－1,1]上的奇函数，试判断它的单调性，并证明你的结论．17．(14分)已知集合A＝{x∈R|ax2－3x＋2＝0，a∈R}．(1)若A是空集，求a的取值范围；(2)若A中只有一个元素，求a的值，并把这个元素写出来；(3)若A中至多只有一个元素，求a的取值范围．18．(16分)我市有甲，乙两家乒乓球俱乐部，两家设备和服务都很好，但收费方式不同．甲家每张球台每小时5元；乙家按月计费，一个月中30小时以内(含30小时)每张球台90元，超过30小时的部分每张球台每小时2元．某公司准备下个月从这两家中的一家租一张球台开展活动，其活动时间不少于15小时，也不超过40小时．(1)设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40)，在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40)，试求f(x)和g(x)；(2)选择哪家比较合算？为什么？19．(16分)已知f(x)是定义在R上的奇函数，当x≥0时，f(x)＝a x－1.其中a>0且a≠1.(1)求f(2)＋f(－2)的值；(2)求f(x)的解析式；(3)解关于x的不等式－1<f(x－1)<4，结果用集合或区间表示．20．(16分)若非零函数f(x)对任意实数a，b均有f(a＋b)＝f(a)·f(b)，且当x<0时，f(x)>1；(1)求证：f(x)>0；(2)求证：f(x)为减函数；(3)当f(4)＝116时，解不等式f(x2＋x－3)·f(5－x2)≤14.丰县修远双语学校高一数学第一学期周练试卷参考答案1．4解析 ∵A ∪B ＝{0,1,2，a ，a 2}，又∵A ∪B ＝{0,1,2,4,16}， ∴⎩⎨⎧a ＝4，a 2＝16，即a ＝4.否则有⎩⎨⎧a ＝16a 2＝4矛盾．2.127128解析 ∵f (3)＝32＋3×3－2＝16，∴1f 3＝116， ∴f (1f 3)＝f (116)＝1－2×(116)2＝1－2256＝127128. 3．[0,1)解析 由题意得：⎩⎨⎧0≤2x ≤2x ≠1，∴0≤x <1.4．b <a <c解析 20.3>20＝1＝0.30>0.32>0＝log 21>log 20.3. 5．③解析 函数f (x )唯一的一个零点在区间(0,2)内，故函数f (x )在区间[2,16)内无零点．6．2解析 分别画出函数y ＝a |x |与y ＝|log a x |的图象，通过数形结合法，可知交点个数为2.7．1<a <54解析 ∵f (x )＝x 2－2ax ＋1，∴f (x )的图象是开口向上的抛物线．由题意得：⎩⎨⎧f0>0，f1<0，f2>0.即⎩⎨⎧1>0，1－2a ＋1<0，4－4a ＋1>0，解得1<a <54.8.10解析 由2a ＝5b ＝m 得a ＝log 2m ，b ＝log 5m ， ∴1a ＋1b＝log m 2＋log m 5＝log m 10.∵1a ＋1b＝2，∴log m 10＝2，∴m 2＝10，m ＝10.9．f (－1)>f (2)解析 由y ＝f (x ＋1)是偶函数，得到y ＝f (x )的图象关于直线x ＝1对称，∴f (－1)＝f (3)．又f (x )在[1，＋∞)上为单调增函数， ∴f (3)>f (2)，即f (－1)>f (2)． 10．(－∞，－3]∪[1，＋∞) 解析 由log a 12>0得0<a <1.由≤1a得≤a －1，∴x 2＋2x －4≥－1，解得x ≤－3或x ≥1.11.7解析 原式＝0.25×24＋lg 8＋lg 53＝(0.5×2)2×22＋lg(8×53)＝4＋lg 1 000＝7.12．1＜a ＜54解析 y ＝⎩⎨⎧x 2－x ＋a ，x ≥0，x 2＋x ＋a ，x ＜0，作出图象，如图所示．此曲线与y 轴交于(0，a )点，最小值为a －14，要使y ＝1与其有四个交点，只需a －14＜1＜a ，∴1＜a ＜54.13．(1,2)解析 依题意，a >0且a ≠1， ∴2－ax 在[0,1]上是减函数，即当x ＝1时，2－ax 的值最小，又∵2－ax 为真数， ∴⎩⎨⎧a >12－a >0，解得1<a <2.14．(－∞，－1)解析当x>0时，由1－2－x<－1 2，(12)x>32，显然不成立．当x<0时，－x>0.因为该函数是奇函数，所以f(x)＝－f(－x)＝2x－1.由2x－1<－12，即2x<2－1，得x<－1.又因为f(0)＝0<－12不成立，所以不等式的解集是(－∞，－1)．15．解由题意得A＝{x|1<x≤2}，B＝(－1，－1＋31＋m]．由A∪B＝B，得A⊆B，即－1＋31＋m≥2，即31＋m≥3，所以m≥0.16．解∵f(x)＝x＋ax2＋bx＋1是定义在[－1,1]上的奇函数，∴f(0)＝0，即0＋a02＋0＋1＝0，∴a＝0.又∵f(－1)＝－f(1)，∴－12－b＝－12＋b，∴b＝0，∴f(x)＝xx2＋1.∴函数f (x )在[－1,1]上为增函数． 证明如下：任取－1≤x 1<x 2≤1，∴x 1－x 2<0，－1<x 1x 2<1，∴1－x 1x 2>0.∴f (x 1)－f (x 2)＝x 1x 21＋1－x 2x 22＋1＝x 1x 22＋x 1－x 21x 2－x 2x 21＋1x 22＋1＝x 1x 2x 2－x 1＋x 1－x 2x 21＋1x 22＋1＝x 1－x 21－x 1x 2x 21＋1x 22＋1<0，∴f (x 1)<f (x 2)，∴f (x )为[－1,1]上的增函数．17．解 (1)要使A 为空集，方程应无实根，应满足⎩⎨⎧ a≠0Δ<0，解得a>98. (2)当a ＝0时，方程为一次方程，有一解x ＝23； 当a≠0，方程为一元二次方程，使集合A 只有一个元素的条件是Δ＝0，解得a ＝98，x ＝43. ∴a ＝0时，A ＝{23}；a ＝98时，A ＝{43}． (3)问题(3)包含了问题(1)、(2)的两种情况，∴a ＝0或a≥98. 18．解 (1)f (x )＝5x,15≤x ≤40；g (x )＝⎩⎨⎧ 90， 15≤x ≤3030＋2x ， 30<x ≤40.(2)①当15≤x ≤30时，5x ＝90，x ＝18，即当15≤x <18时，f (x )<g (x )；当x ＝18时，f (x )＝g (x )；当18<x ≤30时，f (x )>g (x )．②当30<x ≤40时，f (x )>g (x )，∴当15≤x <18时，选甲家比较合算；当x ＝18时，两家一样合算；当18<x ≤40时，选乙家比较合算．19．解 (1)∵f (x )是奇函数，∴f (－2)＝－f (2)，即f (2)＋f (－2)＝0.(2)当x <0时，－x >0，∴f (－x )＝a －x －1.由f (x )是奇函数，有f (－x )＝－f (x )，∵f (－x )＝a －x －1，∴f (x )＝－a －x ＋1(x <0)．∴所求的解析式为f (x )＝⎩⎨⎧ a x －1 x ≥0－a －x ＋1 x <0.(3)不等式等价于⎩⎨⎧ x －1<0－1<－a－x ＋1＋1<4 或⎩⎨⎧ x －1≥0－1<a x －1－1<4， 即⎩⎨⎧ x －1<0－3<a －x ＋1<2或⎩⎨⎧ x －1≥00<a x －1<5.当a >1时，有⎩⎨⎧ x <1x >1－log a 2或⎩⎨⎧ x ≥1x <1＋log a 5，注意此时log a 2>0，log a 5>0， 可得此时不等式的解集为(1－log a 2,1＋log a 5)． 同理可得，当0<a <1时，不等式的解集为R .综上所述，当a >1时，不等式的解集为(1－log a 2,1＋log a 5)；当0<a <1时，不等式的解集为R .20．(1)证明 f (x )＝f (x 2＋x 2)＝f 2(x2)≥0， 又∵f (x )≠0，∴f (x )>0.(2)证明设x1<x2，则x1－x2<0，又∵f(x)为非零函数，∴f(x1－x2)＝f x1－x2·f x2f x2＝f x1－x2＋x2f x2＝f x1f x2>1，∴f(x1)>f(x2)，∴f(x)为减函数．(3)解由f(4)＝f2(2)＝116，f(x)>0，得f(2)＝14.原不等式转化为f(x2＋x－3＋5－x2)≤f(2)，结合(2)得：x＋2≥2，∴x≥0，故不等式的解集为{x|x≥0}．39052 988C 颌29676 73EC 珬[22170 569A 嚚b36904 9028 逨26997 6975 極@33779 83F3 菳35118 892E 褮31824 7C50 籐20468 4FF4 俴xB。

2021高一数学周末训练卷（解析版）1. 如图，U 为全集，M 、P 、S 是U 的三个子集，则阴影部分所表示的集合是（ ）A ．()M P S ⋂⋂B ．()M P S ⋂⋃C ．)()S C P M U ⋂⋂（ D ．)()S C P M U ⋃⋂（ 【答案】C 【详解】图中的阴影部分是： M∩P 的子集，不属于集合S ，属于集合S 的补集,即是C U S 的子集则阴影部分所表示的集合是（M∩P ）∩(∁U S). 故选C ．2．对于集合A ，B ，定义{|,}A B x x A x B -=∈∉，()()⊕=--A B A B B A .设{}1,2,3,4,5,6M =，{}4,5,6,7,8,9,10N =，则M N ⊕中元素的个数为（ ）.A ．5B ．6C ．7D ．8【答案】C 【详解】由已知{}{}1,2,3,7,8,9,10M N N M -=-=， ∴()(){1,2,3,7,8,9,10}MN M N N M ⊕=-⋃-=.故选：C.3．设甲是乙的必要条件；丙是乙的充分但不必要条件，那么（ ） A ．丙是甲的充分条件，但不是甲的必要条件 B ．丙是甲的必要条件，但不是甲的充分条件 C ．丙是甲的充要条件D ．丙不是甲的充分条件，也不是甲的必要条件 【答案】A【详解】甲是乙的必要条件，所以乙是甲的充分条件，即乙⇒甲； 丙是乙的充分但不必要条件，则丙⇒乙，乙⇒丙，显然丙⇒甲，甲⇒丙，即丙是甲的充分条件，但不是甲的必要条件，故选A4．设集合{}260A x x x =+-=，{}10B x mx =+=，则B 是A 的真子集的一个充分不．．．必要．．的条件是 A ．11,23m ⎧⎫∈-⎨⎬⎩⎭B ．0m ≠C ．110,,23m ⎧⎫∈-⎨⎬⎩⎭D ．10,3m ⎧⎫∈⎨⎬⎩⎭【答案】D 【详解】{}{}26023A x x x =+-==-，,若0m =,则B φ= ,B A,若12m =-,则{}2B =A, 若13m =,则{}3B =-A,B ∴A 的一个充分不必要条件是10,3m ⎧⎫∈⎨⎬⎩⎭.5．在下列三个结论中，正确的有（ ） ①x 2>4是x 3<－8的必要不充分条件；②在ABC 中，AB 2＋AC 2＝BC 2是ABC 为直角三角形的充要条件； ③若a ，b ∈R ，则“a 2＋b 2≠0”是“a ，b 不全为0”的充要条件. A ．①② B ．②③ C ．①③ D ．①②③【答案】C 【详解】①，x 2>4即2x >或2x <-，x 3<－8即2x <-，因为2x >或2x <-成立时，2x <-不一定成立，所以x 2>4是x 3<－8的不充分条件；因为2x <-成立时，2x >或2x <-一定成立，所以x 2>4是x 3<－8的必要条件.即x 2>4是x 3<－8的必要不充分条件.所以该命题正确.②， AB 2＋BC 2＝AC 2成立时，ABC 为直角三角形一定成立；当ABC 为直角三角形成立时，AB 2＋BC 2＝AC 2不一定成立，所以在ABC 中，AB 2＋AC 2＝BC 2是ABC 为直角三角形的充分不必要条件，所以该命题错误.③,即判断“0,0a b ==”是“a 2＋b 2=0”的什么条件，由于a 2＋b 2=0即0,0a b ==，所以“0,0a b ==”是“a 2＋b 2=0”的充要条件，所以“a 2＋b 2≠0”是“a ，b 不全为0”的充要条件，所以该命题正确. 故选：C.6. 下列结论错误的是（ ）A ．命题“若x 2－3x －4＝0，则x ＝4”的逆否命题为“若x ≠4，则x 2－3x －4≠0”B ．“x ＝4”是“x 2－3x －4＝0”的充分条件C ．命题“若m >0，则方程x 2＋x －m ＝0有实根”的逆命题为真命题D ．命题“若m 2＋n 2＝0，则m ＝0且n ＝0”的否命题是“若m 2＋n 2≠0，则m ≠0或n ≠0” 【答案】C 【详解】解：命题“若2340x x --=，则4x =”的逆否命题为“若4x ≠，则2340x x --≠”，故A 正确； “2340x x --=” ⇔ “4x =或1x =”，故“4x =”是“2340x x --=”的充分不必要条件，故B 正确；对于C ，命题“若0m >，则方程20x x m +-=有实根”的逆命题为命题“若方程20x x m +-=有实根，则0m >，方程20x x m +-=有实根时，1144m m ∆=+⇒-，故C 错误． 命题“若220m n +=，则0m =且0n =”的否命题是“若220m n +≠．则0m ≠或0n ≠”，故正确；故选：C ．7．已知a ，b ∈R ，则“0≤a ≤1且0≤b ≤1”是“0≤ab ≤1”的 A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A 【详解】若“0≤a ≤1且0≤b ≤1”，则“0≤ab ≤1”．当a ＝－1，b ＝－1时，满足0≤ab ≤1，但不满足0≤a ≤1且0≤b ≤1， ∴“0≤a ≤1且0≤b ≤1”是“0≤ab ≤1”成立的充分不必要条件．故选A.8．如果对于任意实数[],x x 表示不超过x 的最大整数，那么“[][]=x y ”是“1x y -<成立”的( )． A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】A 【解析】若“[][]x y =”，设[][]x a y a x a b y a c ===+=+，，， 其中[01b c ∈，，） 1x y b c x y ∴-=-∴-＜ 即“[][]x y =”成立能推出“[]1x y -<”成立反之，例如 1.2 2.1x y ==， 满足[]1x y -<但[][]12x y ==，，即[]1x y -<成立，推不出[][]x y =故“[][]x y =”是“|x-y|＜1”成立的充分不必要条件 故选A9.若“2340x x -->”是“223100x ax a -->”的必要不充分条件，则实数a 的取值范围是（ ） A ．635⎡⎤-⎢⎥⎣⎦，B ．425⎡⎤-⎢⎥⎣⎦，C ．(][)635-∞-+∞，， D ．][425⎛⎫-∞-+∞ ⎪⎝⎭，， 【答案】D将2340x x -->的解集记为A ，223100x ax a -->的解集记为B .由题意2340x x -->是223100x ax a -->的必要不充分条件可知B 是A 的真子集.2340x x -->，解得{|4A x x =>或1}x <-,223100x ax a -->,则()()520x a x a -+>,（1）当0a ≥时，{|2B x x a =<-或5}x a >,则5421a a ≥⎧⎨-≤-⎩（等号不能同时成立），解得45a ≥.（2）当0a <时，{|5B x x a =<或2}x a >- ,则2451a a -≥⎧⎨≤-⎩（等号不能同时成立），解得2a ≤-.由（1）（2）可得45a ≥或2a ≤-. 故选：D .10.若实数a ，b 满足a≥0，b≥0，且ab=0，则称a 与b 互补，记φ（a ，b ）=﹣a﹣b 那么φ（a ，b ）=0是a 与b 互补的（ ） A ．必要不充分条件 B ．充分不必要的条件 C ．充要条件 D ．既不充分也不必要条件【答案】C 【解析】试题分析：由φ（a ，b ）＝0得22a b +－a －b ＝０且0,0a b ≥≥；所以φ（a ，b ）＝0是a 与b 互补的充分条件；再由a 与b 互补得到：0,0a b ≥≥，且ab ＝0；从而有，所以φ（a ，b ）＝0是a 与b 互补的必要条件；故得φ（a ，b ）＝0是a 与b 互补的充要条件；故选Ｃ．11．已知不等式()()120a x x x x -->的解集为A ，不等式()()120b x x x x --≥的解集为B ，其中a 、b 是非零常数，则“0ab <”是“A B R =”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既非充分也非必要条件【答案】A 【详解】（1）若0a >，0b >.①若12x x =，不等式()()120a x x x x -->即为()210x x ->，则{}1A x x x =≠，不等式()()120b x x x x --≥即为()210x x -≥，得B R =，A B ⊆，AB B R ==；②若12x x ≠，不妨设12x x <，不等式()()120a x x x x -->即为()()120x x x x -->，则()()12,,A x x =-∞+∞，不等式()()120b x x x x --≥即为()()120x x x x --≥，得(][)12,,B x x =-∞+∞，A B ⊆，则AB B R =≠；（2）同理可知，当0a <，0b <时，A B ⊆，A B B ⋃=不一定为R ； （3）若0a >，0b <.①若12x x =，不等式()()120a x x x x -->即为()210x x ->，则{}1A x x x =≠，不等式()()120b x x x x --≥即为()210x x -≤，则{}1B x =，此时，AB R =；②若12x x ≠，不妨设12x x <，不等式()()120a x x x x -->即为()()120x x x x -->，则()()12,,A x x =-∞+∞，不等式()()120b x x x x --≥即为()()120x x x x --≤，则[]12,B x x =，此时，A B R =；（4）同理，当0a <，0b >时，A B R =.综上所述，“0ab <”是“A B R =”的充分不必要条件.故选A.13.设p ：|x ﹣1|≤1，q ：x 2﹣（2m +1）x +（m ﹣1）（m +2）≤0．若p 是q 的充分不必要条件，则实数m 的取值范围是_____． 【答案】[0，1]由11x -≤得111x -≤-≤，得02x ≤≤.由2(21)(1)(2)0x m x m m -++-+≤，得[(1)][(2)]0x m x m ---+≤， 得12m x m -≤≤+， 若p 是q 的充分不必要条件，则1022m m -≤⎧⎨+≥⎩，得10m m ≤⎧⎨≥⎩，得01m ≤≤，即实数m 的取值范围是[0,1]. 故答案为：[0,1]14.已知:40p k -<<，:q 函数21y kx kx =--的值恒为负，则p 是q 的______条件. 【答案】充分不必要当40k -<<时，k 0<且24(4)0k k k k ∆=+=+<， 所以函数21y kx kx =--的值恒为负；反过来，函数21y kx kx =--的值恒为负不一定有40k -<<，如当0k =时，函数21y kx kx =--的值恒为负.所以p 是q 的充分不必要条件 故答案为：充分不必要15．设集合{}1,2,3,4,5I =，若非空集合A 同时满足①A I ⊆，②()min A A ≤（其中A 表示A 中元素的个数，()min A 表示集合A 中最小元素），称集合A 为I 的一个好子集，I 的所有好子集的个数为______. 【答案】12 【详解】由题意可知，()min A 的取值为1、2、3、4、5. （1）当()min 1A =时，1A ≤，则{}1A =；（2）当()min 2A =时，2A ≤，则符合条件的集合A 有：{}2、{}2,3、{}2,4、{}2,5，共4个；（3）当()min 3A =时，3A ≤，则符合条件的集合A 有：{}3、{}3,4、{}3,5、{}3,4,5，共4个；（4）当()min 4A =时，4A ≤，则符合条件的集合A 有：{}4、{}4,5，共2个；（5）当()min 5A =时，5A ≤，则符合条件的集合A 为{}5. 综上所述，I 的所有好子集的个数为1442112++++=. 故答案为12.16．Q 是有理数集，集合{},,,0M x x a a b Q x ==∈≠，在下列集合中：①}x M ∈；②1x M x ⎧⎫∈⎨⎬⎩⎭；③{}1212,x x x M x M +∈∈；④{}1212,x x x M x M ∈∈.与集合M 相等的集合序号是______. 【答案】①②④ 【解析】 【分析】利用集合的定义以及集合相等的定义进行验证，即可得出结论. 【详解】对于①中的集合，x M ∈，设x a =，a Q ∈，b Q ，)2a b ==+，则2b Q ∈，①中的集合与集合M 相等；对于②中的集合，x M ∈，设x a =，a Q ∈，b Q ，且a 、b 不同时为零.则2212a x a b ===-222a Q a b∈-，222bQ a b-∈-，②中的集合与集合M 相等；对于③中的集合，取1x a =，2x a =-，a Q ∈，bQ ，则120x x M +=∉，③中的集合与集合M 不相等；对于④中的集合，设111x a =，222x a =，其中1a 、2a 、1b 、2b Q ∈，则()()()(121122*********x x a a a a b b a b a b =+=+++12122a a b b Q +∈，1221a b a b Q +∈，④中的集合与集合M 相等.因此，集合M 相等的集合序号是①②④. 故答案为：①②④.17.设集合{|01}A x x a =≤+≤，{|10}B x a x =-≤≤，其中a ∈R ，求A B ．【答案】0a <或1a >时，AB =∅；0a =或1a =时，{0}A B =102a <<时，{|0}A B x a x =-≤≤112a ≤<时，{|10}A B x a x =-≤≤ 【详解】当10a ->即1a >时，B =∅时，AB =∅；当10a -=即1a =时，{|10}A x x =-≤≤，{0}B =，则{0}A B =当10a -<即1a <时，10a -> 若0a ->即0a <时，如下图所示，AB =∅.若0a -=即0a =时，如下图所示，{|01}A x x =≤≤,{|10}B x x =-≤≤，则{0}A B =若10a a -<-<即102a <<时，如下图所示，{|0}A B x a x =-≤≤.若1a a -≤-即112a ≤<时，如下图所示，{|10}A B x a x =-≤≤.综上所述：0a <或1a >时，AB =∅；0a =或1a =时，{0}A B =102a <<时，{|0}A B x a x =-≤≤112a ≤<时，{|10}A B x a x =-≤≤ 18．已知下列三个方程：24430x ax a +-+=，()2210x a x a +-+=，2220x ax a +-=至少有一个方程有实根，求实数a 的取值范围．【答案】32a ≤-或1a >- 【详解】先求使三个方程都没有实根的实数a 的取值范围：由()()()()()21222234443014024120a a a a a a ⎧∆=--+<⎪⎪∆=--<⎨⎪∆=-⨯⨯-<⎪⎩得2224430321020a a a a a a ⎧+-<⎪+->⎨⎪+<⎩解得：312a -<<- ∴至少有一个方程有实根，求实数a 的取值范围：32a ≤-或1a >-19．已知函数f(x)=x 2−2x,g(x)=ax −1，若∀x 1∈[−1,2],∃x 2∈[−1,2]，使得f(x 1)=g(x 2)，求a 的取值范围. 【答案】详见解析 【解析】若∀x 1∈[−1,2],∃x 2∈[−1,2]，使得f(x 1)=g(x 2)，即g(x)在[−1,2]上的值域要包含f(x)在[−1,2]上的值域，又在[−1,2]上f(x)∈[−1,3].①当a <0时，g(x)=ax −1单调递减，此时{g(−1)≥3g(2)≤−1， 解得a ≤−4；②当a =0时，g(x)=−1，显然不满足题设；③当a >0时，g(x)=ax −1单调递增，此时{g(2)≥3g(−1)≤−1， 解得a ≥2.综上，∀x 1∈[−1,2],∃x 2∈[−1,2]，使得f(x 1)=g(x 2)，a 的取值范围为(−∞,−4]∪[2,+∞).20.已知命题：“{}11x x x ∀∈-≤≤，都有不等式2x x m --<0成立”是真命题. （1）求实数m 的取值集合B ；（2）设不等式(3)(2)0x a x a ---<的解集为A ，若x A ∈是x B ∈的充分不必要条件，求实数a 的取值范围.【答案】（1）(2,)+∞；（2）2[,)3+∞.【详解】（1）命题：“{}11x x x ∀∈-≤≤，都有不等式2x x m --<0成立”是真命题， 得2x x m --<0在11x -≤≤时恒成立，∴2max ()m x x >-，得2m >，即{}2(2,)B m m =>=+∞. （2）不等式(3)(2)0x a x a ---<，①当32a a >+，即1a >时，解集{}23A x a x a =+<<，若x A ∈是x B ∈的充分不必要条件，则A 是B 的真子集，∴22a +≥，此时1a >；②当32a a =+，即1a =时，解集A φ=，满足题设条件；③当32a a <+，即1a <时，解集{}32A x a x a =<<+，若x A ∈是x B ∈的充分不必要条件，则A 是B 的真子集， 32a ∴≥，此时213a ≤<. 综上①②③可得2[,)3a ∈+∞ 21．设命题p ：对任意[]0,1x ∈，不等式2223x m m -≥-恒成立；命题q ：存在[]1,1x ∈-，使得不等式210x x m --+≤成立.（1）若p 为真命题，求实数m 的取值范围；（2）若命题p 、q 有且只有一个是真命题，求实数m 的取值范围.【答案】（1）12m ≤≤（2）1m <或524m <≤ 【详解】（1）对于命题p ：对任意[]0,1x ∈，不等式2223x m m -≥-恒成立， 而[]0,1x ∈，有()min 222x -=-，223m m ∴-≥-，12m ∴≤≤， 所以p 为真时，实数m 的取值范围是12m ≤≤；（2）命题q ：存在[]1,1x ∈-，使得不等式210x x m -+-≤成立， 只需()2min 10x x m -+-≤，而22151()24x x m x m -+-=-+-，2min 5(1)4x x m m ∴-+-=-+，504m ∴-+≤，54m ≤， 即命题q 为真时，实数m 的取值范围是54m ≤， 依题意命题,p q 一真一假， 若p 为假命题， q 为真命题，则1254m m m ⎧⎪⎨≤⎪⎩或，得1m <； 若q 为假命题， p 为真命题，则1254m m ≤≤⎧⎪⎨>⎪⎩，得524m <≤， 综上，1m <或524m <≤.。

注：尊敬的各位读者，本文是笔者教育资料系列文章的一篇，由于时间关系，如有相关问题，望各位雅正。

希望本文能对有需要的朋友有所帮助。

如果您需要其它类型的教育资料，可以关注笔者知识店铺。

由于部分内容来源网络，如有部分内容侵权请联系笔者。

高一数学周练（第11周）班别： 姓名： 学号：1、下列函数与x y =有相同图象的一个函数是（ ）A ．2x y = B ．x x y 2= C ．)10(log ≠>=a a a y x a 且 D ．x a a y log = 2、函数1)(2-+=x x x f 的最小值是_________________3、 函数32)(2--=mx x x f 当[)+∞-∈,2x 时是增加的，当()2,-∞-∈x 时是减少的，则)1(f ＝ 4、函数23)(-=x x f 中，且[]3,1-∈x 则)(x f 的值域为（） A.)25,1(- B.⎥⎦⎤⎢⎣⎡-25,35 C.[]7,3- D.⎥⎦⎤⎢⎣⎡-7,35 5、设{}{}34|,|,<>=≤≤==x x x A C b x a x A R U U 或 则___________,__________==b a6、下列判断正确的是（ ）A ．函数22)(2--=x x x x f 是奇函数 B．函数()(1f x x =- C．函数()f x x = D ．函数1)(=x f 既是奇函数又是偶函数7、有以下四个结论，其中正确的是（ ）0)10lg(lg )1(=，0)lg(ln )2(=e ，10lg 10)3(==x x ，则若2,ln )4(e x x e ==则若A.)3)(1(B.)4)(2(C.)2)(1(D.)4)(3( 8、比较大小：3.07.1 1.39.0 3.0log 4.0 3.0log 5.0 9、函数()1,01≠>=-a a a y x 的图像过定点，则定点的坐标为10、函数y =的定义域是 ；11、如果二次函数)3(2+++=m mx x y 有两个不同的零点，则m 的取值范围是（ ）A ．()6,2-B ．[]6,2-C ．{}6,2-D ．()(),26,-∞-+∞12、设()833-+=x x f x ,用二分法求方程()2,10833∈=-+x x x 在内近似解的过程中得()()(),025.1,05.1,01<><f f f 则方程的根落在区间（ ）A ．(1,1.25)B ．(1.25,1.5)C ．(1.5,2)D ．不能确定13、计算：（1）(log )log log 2222545415-++；（2）213121322716125⎥⎥⎦⎤⎢⎢⎣⎡++14、解方程（1）21293-+=x x （2）()()x x x ++-=-3log )1(log 13log 22215、用4M 长的合金条做一个“日”字形的窗户，当窗户的长和宽各为多少时，透过光线最多可以关注笔者知识店铺。

高一数学第11周周末作业班级 姓名一、选择题1．若函数()y f x =是函数3x y =的反函数，则1()2f 的值为（ ）A ．3log 2-B ．2log 3-C ．19D2．下列各组函数中，表示同一函数的是（ ）A ．xx x y x y +=+=21与 B ．x x g x x x f ==)()()(22与 CD ．()()log t a f x x g t a ==与 3．函数1()4x f x a-=+（0a >，且1a ≠）的图像过一定点，则该定点坐标是（ ） A ．（5，1） B ． （1，4） C ．（1，5） D ．（4，1）4．若函数223()(1)mm f x m m x +-=--是幂函数且在(0,)+∞是递减的，则m = （ ） A ．1- B ．2C ．1-或2D ．3 5．已知函数()=y f x 的定义域为[1,5]-，则函数(35)=-y f x 的定义域为（ ）AC ．[810]-,D ．[810]， 6．已知函数()()()f x x a x b =-- (其中a b >)的图像如左图所示，则函数()x g x a b=+的图象是（ ）7．已知52log 2a =， 1.12b =，0.812c -⎛⎫= ⎪⎝⎭，则a 、b 、c 的大小关系是（ ） A ．c b a << B ．a c b << C ．a b c << D ．b c a <<8．已知(),1(4)2,12x a x f x a x x ⎧≥⎪=⎨-+<⎪⎩是R 上的增函数，则实数a 的取值范围为（ ）A ．(1,)∞＋B ．(1,8)C ．(4,8)D ．[4,8)二、填空题（本大题共4小题，每小题5分，共20分）9.若函数()f x =的定义域为R ，则实数a 的取值范围是 .10．若偶函数()y f x =在(,0]-∞上递增，则不等式(ln )(1)f x f >的解集是 .三、解答题（本大题共6小题，满分10+12+12+12+12+12=70分）11．计算：（1（2）1.0lg 10lg 5lg 2lg 125lg 8lg --+12．已知函数()log (1)log (3)(01)a a f x x x a =-++<<．求函数()f x 的定义域13．已知函数22(),21x x a a f x a R ⋅-+=∈+. （1）试判断f (x )的单调性，并证明你的结论；（2）若f (x )为定义域上的奇函数，求函数f (x )的值域．。

学年度第二学期高一数学周末练习卷（九）第11周 命题：时间：_______ 高一____班 姓名___________一．选择题：本大题共12小题，每小题5分，共60分． 在每小题给出的四个选项中，只有一选项是符合题目要求的．1．若,a b R ∈，则下列恒成立的不等式是 ( )A. 2a b+≥2b a a b +≥ C. 22222a b a b ++⎛⎫≥ ⎪⎝⎭D ．()114a b a b ⎛⎫++≥ ⎪⎝⎭ 2. 下面对算法描述正确的一项是 ()A ．算法只能用自然语言来描述B ．算法只能用图形方式来表示C ．同一问题可以有不同的算法D ．同一问题的算法不同，结果必然不同 3. 对赋值语句的描述正确的是 ()①可以给变量提供初值 ②将表达式的值赋给变量 ③可以给一个变量重复赋值 ④不能给同一变量重复赋值A ．①②③B ．①②C ．②③④D ．①②④4. 下列给出的赋值语句中正确的是 () A ．4=M B ．M=-M C ．B=A=3 D ．x+y=05．已知8220,0=++>>xy y x y x ，，则y x 2+的最小值是 ( )A ．3B ．4 C.29 D.211 6．已知42,31<-<<+<-b a b a ，则b a 32+的取值范围是 ( ) A ．⎪⎭⎫ ⎝⎛-27,213 B ．⎪⎭⎫ ⎝⎛-21,27 C ．⎪⎭⎫⎝⎛-213,27 D ．⎪⎭⎫⎝⎛-213,29 7. 如果执行下边的程序框图，输入正整数N (N ≥2)和实数a 1，a 2，…，a N ，输出A ，B ，则( )A ．A ＋B 为a 1，a 2，…，a N 的和 B.A ＋B 2为a 1，a 2，…，a N 的算术平均数C ．A 和B 分别是a 1，a 2，…，a N 中最大的数和最小的数D ．A 和B 分别是a 1，a 2，…，a N 中最小的数和最大的数8．某程序框图如图所示，则该程序运行后输出的B 等于 ( ) A ．15 B ．29 C ．31 D ．639．已知关x 的不等式21<++ax x 的解集为P ，若P ∉1，则实数a 的取值范围为 ( )A ．(][)+∞⋃-∞-,01,B ．[]0,1-C ．()()+∞⋃-∞-,01,D ．(]0,1-10. 上面程序执行后的结果是 （ ） A.12 B.13 C.14 D.1511．设直角三角形两直角边的长分别为b a ,，斜边长为c ，斜边上的高为h ，则44b a +和44h c +的大小关系是 ( )A ． 4444h c b a +<+ B ．4444h c b a +>+ C ．4444h c b a +=+ D ．不能确定12．已知函数()⎩⎨⎧≥--<+=）0(1)0(1x x x x x f 则不等式()31)1(≤-++x f x x 的解集是 ( )A ．{}3-≥x xB ．{}1≥x xC ．{}13-≤≤x xD ．{}31-≤≥x x x ， 二．填空题：本大题共4小题，每小题5分，共20分．13. 用“秦九韶算法”计算多项式12345)(2345+++++=x x x x x x f ，当2=x 时的值的过程中，要经过 次乘法运算和 次加法运算。

2021年高三上学期周练（11.11）数学试题 含答案一、选择题1．设全集，2{|ln(2)},{|2}A x Z y x B x x x =∈=-=≤，则（ ）A ．B ．C ．D ．2．设 ，则的大小关系是（ ）A ．B ．C ．D ．3．在复平面内与复数所对应的点关于实轴对称的点为，则对应的复数为（ ）A ．B ．C ．D ．4．已知命题“”是假命题，给出下列四个结论：①命题“”是真命题；②命题“”是假命题；③命题“”是假命题；④命题“”是真命题.其中正确的结论为（ ）A 、①③B 、②③C 、①④D 、②④5．已知()522100121031...x x a a x a x a x -+=++++，则（ ）A ．B ．C ．D ．6．（xx 春•凉州区校级期末）设f （x ）=，则f （5）的值为（ ）A ．8B ．9C ．10D ．117．为圆上的一个动点，平面内动点满足且 (为坐标原点)，则动点运动的区域面积为（ ）A. B. C. D.8．中，分别为的重心和外心，且，则的形状是（ ）A ．锐角三角形B ．钝角三角形C ．直角三角形D ．上述均不是9．以为端点的线段的垂直平分线方程是（Ａ）3x-y-8=0 （B ）3x+y+4=0 （C ）3x-y+6=0 （D ） 3x+y+2=010．已知函数在区间上是的减函数，则的范围是（ ）A ．B ．C ．D ．11．已知，当取最小值时，的值等于（ ）A ．B ．－C ．19D ．12．椭圆的离心率为（ ）A ．B ．C ．D ．二、填空题13．已知复数（是虚数单位），则 ．14．是的方程的解，则这三个数的大小关系是 ．15．函数是上的增函数，且(sin )(cos )(sin )(cos )f f f f ωωωω+->-+，其中为锐角，并且使得函数在上单调递减，则的取值范围是 ．16．已知点A(x ，lgx1)，B(x2，lgx2)是函数f(x)＝lgx 的图象上任意不同两点，依据图象可知，线段AB 总是位于A ，B 两点之间函数图象的下方，因此有结论＜lg ()成立．运用类比思想方法可知，若点A(x1,2x1)，B(x2,2x2) 是函数g(x)＝2x 的图象上的不同两点，则类似地有__________成立．三、解答题17．已知数列满足，．（1）证明数列是等差数列；（2）求数列的通项公式．18．选修4-1：几何证明选讲如图所示，在中，是的角平分线，的外接圆交于点.（1）证明：；（2）若，求的值.19．已知函数f （x ）对任意的a ，b ∈R ，都有f （a+b ）=f （a ）+f （b ）﹣1，且当x ＞0时，（1）判断并证明f（x）的单调性；（2）若f（4）=3，解不等式f（3m2﹣m﹣2）＜2．20．如图，菱形与正三角形的边长均为2，它们所在平面互相垂直，平面，且．（1）求证：平面；（2）若，求钝二面角的余弦值．21．已知顶点在单位圆上的△，角，，所对的边分别是，，，且．（1）求的值；（2）若，求的取值范围．22．已知数列{an}是公差为正数的等差数列，其前n项和为Sn，且a2·a3＝15，S4＝16．（1）求数列{an}的通项公式；（2）数列{bn}满足b1＝a1，①求数列{bn}的通项公式；②是否存在正整数m，n（m≠n），使得b2，bm，bn成等差数列？若存在，求出m，n的值；若不存在，请说明理由．BADCC AABBB11．A12．A13．14．15．16．17．解：（1）证明：由已知可得：，两边同除以，整理可得，∴数列是以2为首项，1为公差的等差数列．（2）解：由（1）可得，∴数列的通项公式．18．解：（1）证明：延长至，连接，使得.因为，所以，又，所以又因为是的角平分线，故，则∽，所以，又，所以.（2）解：∵是的角平分线，，∴，所以，由圆的割线定理得，，∴，，∴. 19．解：f（a+b）=f（a）+f（b）﹣1，令a=b=0，∴f（0）=f（0）+f（0）﹣1，∴f（0）=1，令a=x，b=﹣x，∴f（0）=f（x）+f（﹣x）﹣1，∴f（﹣x）=2﹣f（x），令x1＜x2，则x2﹣x1＞0，∴f（x2﹣x1）=f（x2）+f（﹣x1）﹣1=f（x2）+2﹣f（x1）﹣1＞1，∴f（x2）＞f（x1），故函数在R上单调递增；（2）f（4）=2f（2）﹣1=3，∴f（2）=2，∴f（3m2﹣m﹣2）＜f（2），∴3m 2﹣m ﹣2＜2，∴﹣1＜m ＜．20．解：（1）如图，过点作于，连接．∴，可证得四边形为平行四边形．∴平面． （2）连接．由（1），得为中点，又，为等边三角形，∴．分别以为轴建立如图所示的空间直角坐标系．则(1,0,0),(2,3,3),(0,0,3),(0,3,0)B F E A -， (3,3,3),(1,3,0),(1,0,3)BF BA BE =-=-=-．设平面的法向量为．由，得，令，得．设平面的法向量为．由，得，令，得．∴．故二面角的余弦值是．21．解：（1）因为，由正弦得，，所以．因为，且，所以．（2）由，得，由，得，，所以224sin 2sin 4sin 2sin()3sin 33b c B C B B B B π-=-=--=． 因为，所以，即，所以．22．解：（1）设数列{a n }的公差为d ，则d ＞0． 由a 2·a 3＝15，S 4＝16，得解得或（舍去）所以a n ＝2n －1．（2）①因为b 1＝a 1，所以1111111()(21)(21)22121n n n n b b a a n n n n ++-===--+-+ 即,……累加得： 所以 也符合上式．故②假设存在正整数m 、n （m ≠n ），使得b 2，b m ，b n 成等差数列，则b 2＋b n ＝2b m ． 又，所以即化简得：当n ＋1＝3，即n ＝2时，m ＝2，（舍去）； 当n ＋1＝9，即n ＝8时，m ＝3，符合题意． 所以存在正整数m ＝3，n ＝8，使得b 2，b m ，b n 成等差数列．20222 4EFE 仾23878 5D46 嵆d26026 65AA 斪39868 9BBC 鮼 28259 6E63 湣h*p36742 8F86 辆 24602 601A 怚31300 7A44 穄。