下载文档原格式
2 微积分实验2.1 基础训练1. 已知)cos(mx e y nx=，利用符号运算函数求y ''. 编写函数文件返回求导结果（1个参数）. 解：function d=myfun syms m n xy=exp(n*x)*cos(m*x); d = diff(y,x,2);2. 已知函数22xa ae y x +=，求解该函数在x =5处的一阶导数值.编写本问题的函数文件第一行格式如下（函数名、文件名自己设定）： function r=myfun %变量r 存储导数值 解：function r=myfun syms a xy=a*exp(x)/sqrt(a^2+x^2); f=diff(y,x); r=subs(f,x,5);3. 使用符号工具箱计算函数211xy +=的6阶麦克劳林多项式. 要求编写一个function 文件返回该结果. 解：function f=fun syms xf = taylor(1/(1+x^2),x, 'order',7); f = simplify(f);4. 求不定积分dx x x ⎰2ln 和定积分dx xex ⎰∞-12。
syms xint(log(x)^2*x) f=x*exp(-x^2);int(f,x,1,inf)5. 求解方程组求下列联立方程的解⎪⎪⎩⎪⎪⎨⎧=+++=++-=-++=+-+159326282310262113654d z y x d z y x d z y x d z y x .编程调用solve 函数求解方程组；编写函数返回4个参数：依次为x ，y ，z ，d 所得结果。
编写本问题的函数文件第一行格式如下（函数名、文件名自己设定）： function [x,y,z,d]=myfun % x,y,z,d 为题目所求的解 解：function [x,y,z,d]=myfun % x,y,z,d 为题目所求的解[x,y,z,d]=solve('4*x+5*y-6*z+3*d=11','2*x+6*y+2*z-d=10',... '3*x-2*y+8*z+2*d=6','x+2*y+3*z+9*d=15')2.2 实验任务问题来源全国数学建模竞赛1997年A 题 一件产品由若干零件组装而成，标志产品性能的某个参数取决于这些零件的参数。
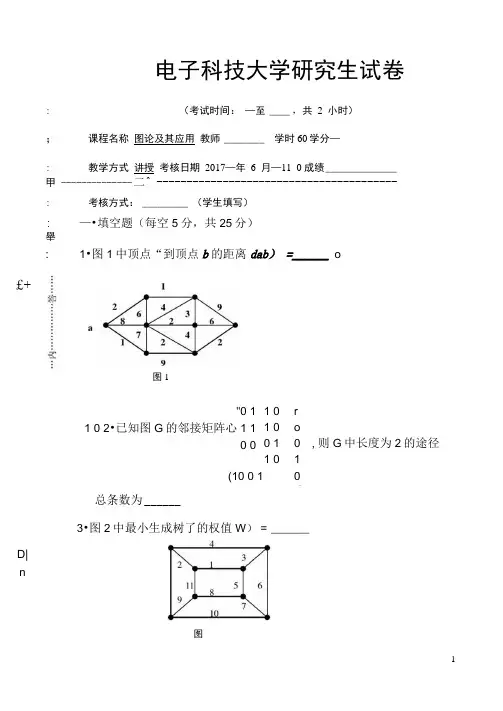
电子科技大学研究生试卷: （考试时间： —至 ____ ，共_2_小时）； 课程名称 图论及其应用 教师 ________ 学时60学分—: 教学方式 讲授 考核日期_2017—年_6_月—11_0 成绩 ______________甲 -------------- 二^ ---------------------------------------- : 考核方式： _________ （学生填写）: —•填空题（每空5分，共25分）舉: 1•图1中顶点“到顶点b 的距离dab ） = ______ o总条数为 ______ 3•图2中最小生成树了的权值W ） = ______£+"0 1 1 0 2•已知图G 的邻接矩阵心1 1 0 0 1 0 1 0 0 1 1 0 (10 0 1 ro0 1丿,则G 中长度为2的途径D|n£+图1图4•图3的最优欧拉环游的权值为5.树叶带权分别为1,245,6,8的最优二元树权值为W(T)=________ 。
二・单项选择(每题3分，共15分)1・关于图的度序列，下列说法正确的是()(A) 对任意一个非负整数序列来说，它都是某图的度序列;(B) 如果非负整数序列K归…心满足「为偶数则它一定是图序/-I列；(C) 若图G度弱于图H ,则图G的边数小于等于图H的边数；(D) .如果图G的顶点总度数大于或等于图H的顶点总度数，则图G度优于图H o2・关于图的割点与割边，下列说法正确的是()(A) 有割边的图一定有割点；(B) 有割点的图一定有割边；(C) 有割边的简单图一定有割点;(D) 割边不在图的任一圈中。
3•设k(G) , 2(G) , 5(G)分别表示图G的点连通度，边连通度和最小度。
下面说法错误的是()(A) 存在图G ,使得狀G)= 5(G) = 2(G)；(B) 存在图G ,使得k(G)<A(G)<3(G)；(C) 设G是n阶简单图，若J(G)> J ,则G连通,且A(G)=J(G);(D) 图G是£连通的，则G的连通度为44•关于哈密尔顿图，下列命题错误的是()(A) 彼得森图是非哈密尔顿图;(B) 若图G的闭包是哈密尔顿图，则其闭包一定是完全图；(C) 若图G的闭包是完全图，则图G是哈密尔顿图；(D) 设G是三阶以上简单图，若G中任意两个不邻接点“与I，,满足,则G是哈密尔顿图。
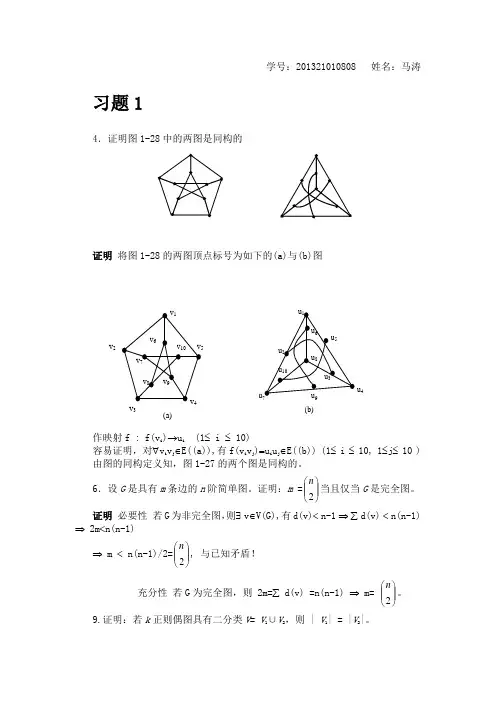
学号：201321010808 姓名：马涛习题14．证明图1-28中的两图是同构的证明 将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明，对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知，图1-27的两个图是同构的。
6．设G 是具有m 条边的n 阶简单图。
证明：m =⎪⎪⎭⎫⎝⎛2n 当且仅当G 是完全图。
证明 必要性 若G 为非完全图，则∃ v ∈V(G),有d(v)< n-1 ⇒ ∑ d(v) < n(n-1) ⇒ 2m <n(n-1)⇒ m < n(n-1)/2=⎪⎪⎭⎫⎝⎛2n , 与已知矛盾！充分性 若G 为完全图，则 2m=∑ d(v) =n(n-1) ⇒ m= ⎪⎪⎭⎫⎝⎛2n 。
9.证明：若k 正则偶图具有二分类V = V 1∪V 2，则 | V 1| = |V 2|。
(a)v 1v 2 v 3 v 4v 5 v 6v 7v 8 v 9v 10 u 1 u 2u 3u 4u 5 u 6 u 7 u 8 u 9 u 10 (b)证明 由于G 为k 正则偶图，所以，k | V 1 | =m = k | V 2 | ⇒ ∣V 1∣= ∣V 2 ∣。
12.证明：若δ≥2，则G 包含圈。
证明 只就连通图证明即可。
设V(G)=｛v 1,v 2,…,v n ｝,对于G 中的路v 1v 2…v k ,若v k 与v 1邻接，则构成一个圈。
若v i1v i2…v in 是一条路，由于δ≥ 2，因此，对v in ，存在点v ik 与之邻接，则v ik ⋯v in v ik 构成一个圈 。
17.证明：若G 不连通，则G 连通。
证明 对)(,_G V v u ∈∀,若u 与v 属于G 的不同连通分支，显然u 与v 在_G 中连通；若u 与v 属于g 的同一连通分支，设w 为G 的另一个连通分支中的一个顶点，则u 与w ，v 与w 分别在_G 中连通，因此，u 与v 在_G 中连通。
习题1： 4,5,11,12,17,184．证明 将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明，对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知，图1-28的两个图是同构的。
5.分析：四个顶点的简单图最少边数为 0，最多边数为 6，所以可按边数进行枚举。
11.证明 由于7个顶点的简单图的最大度不会超过6，因此序列(7,6,5,4,3,3,2)不是图序列；(6,6,5,4,3,3,1)是图序列⇔（5，4，3，2，2，0）是图序列，然（5，4，2，2，0）不是图序列，所以(6,6,5,4,3,3,1) 不是图序列。
12.证明 只就连通图证明即可。
设V(G)=｛v 1,v 2,…,v n ｝,对于G 中的路v 1v 2…v k ,(a)v 1v 2v 3v 4 v 5 v 6v 7v 8 v 9v 10 u 1 u 2 u 3 u 4u 5 u 6u 7 u 8 u 9u 10(b)若v k 与v 1邻接，则构成一个圈。
若v i1v i2…v in 是一条路，由于δ≥ 2，因此，对v in ，存在点v ik 与之邻接，则v ik ⋯v in v ik 构成一个圈 。
17.证明 对)(,_G V v u ∈∀,若u 与v 属于G 的不同连通分支，显然u 与v 在_G 中连通；若u 与v 属于g 的同一连通分支，设w 为G 的另一个连通分支中的一个顶点，则u 与w ，v 与w 分别在_G 中连通，因此，u 与v 在_G 中连通。
18.证明: 因为e 只能属于G 的某一个连通分支,所以只需考虑G 是连通图的情况. 若G − e 仍然连通,则ω(G) = 1 = ω(G − e) < 2 = ω(G) + 1. 若G − e 不连通,则ω(G) = 1 < 2 = ω(G − e) = ω(G) + 1.习题2: 1,9,161. 证明 设是非平凡树T 中一条最长路，若则与在中的邻接点只能有一个，否则，若与除了中顶点之外的其他顶点相连，则可以继续延长，这与是最长路是相矛盾的。
习题三：● 证明：e 是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2，使对任意u ∈V 1及v ∈V 2, G 中的路（u ，v ）必含e .证明：充分性: e 是G 的割边，故G −e 至少含有两个连通分支，设V 1是其中一个连通分支的顶点集，V 2是其余分支的顶点集，对12,u V v V ∀∈∀∈，因为G 中的u,v 不连通，而在G 中u 与v 连通，所以e 在每一条(u,v)路上，G 中的(u,v)必含e 。
必要性：取12,u V v V ∈∈，由假设G 中所有(u,v)路均含有边e ，从而在G −e 中不存在从u 与到v 的路，这表明G 不连通，所以e 是割边。
● 3.设G 是阶大于2的连通图，证明下列命题等价：（1） G 是块（2） G 无环且任意一个点和任意一条边都位于同一个圈上；（3） G 无环且任意三个不同点都位于同一条路上。
（1）→（2）：G 是块，任取G 的一点u ，一边e ，在e 边插入一点v ，使得e 成为两条边，由此得到新图G 1，显然G 1的是阶数大于3的块，由定理，G 中的u,v 位于同一个圈上，于是G 1中u 与边e 都位于同一个圈上。
（2）→（3）：G 无环，且任意一点和任意一条边都位于同一个圈上，任取G 的点u ，边e ，若u 在e 上，则三个不同点位于同一个闭路，即位于同一条路，如u 不在e 上，由定理，e 的两点在同一个闭路上，在e 边插入一个点v ，由此得到新图G 1，显然G 1的是阶数大于3的块，则两条边的三个不同点在同一条路上。
（3）→（1）：G 连通，若G 不是块，则G 中存在着割点u ，划分为不同的子集块V 1, V 2, V 1, V 2无环，12,x v y v ∈∈，点u 在每一条(x,y)的路上，则与已知矛盾，G 是块。
●7.证明：若v 是简单图G 的一个割点，则v 不是补图G̅的割点。
证明：v 是单图G 的割点，则G −v 有两个连通分支。
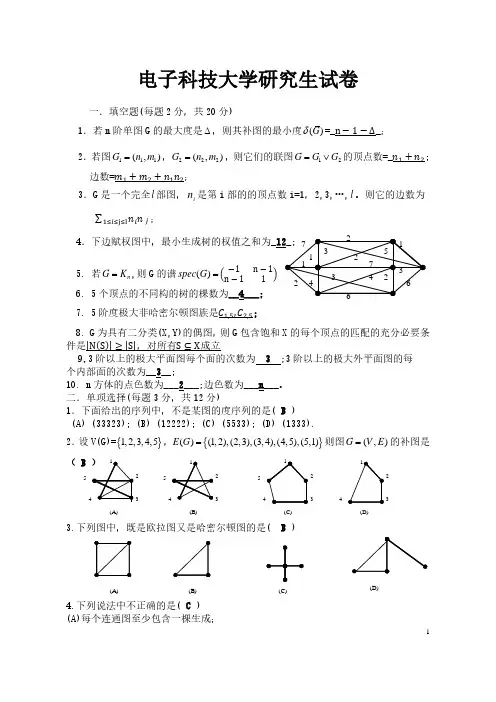
电子科技大学研究生试卷一．填空题(每题2分，共20分)1．若n 阶单图G 的最大度是∆，则其补图的最小度()G δ=_n −1−∆_； 2．若图111(,)G n m =，222(,)G n m =，则它们的联图12G G G =∨的顶点数=_nn 1+nn 2;边数=mm 1+mm 2+nn 1nn 2；3．G 是一个完全l 部图，i n 是第i 部的的顶点数i=1，2,3,…,l 。
则它的边数为∑nn ii nn jj 1≤ii≤j≤l ；4．下边赋权图中，最小生成树的权值之和为5. 若n G K =,则G 的谱()spec G =�−1n −1n −116. 5个顶点的不同构的树的棵数为__4___;7. 5阶度极大非哈密尔顿图族是CC 1,5,CC 2,5;8. G 为具有二分类(X,Y)的偶图，则G 包含饱和X 的每个顶点的匹配的充分必要条件是|N (S )|≥|S |，对所有S ⊆X 成立9.3阶以上的极大平面图每个面的次数为 3 ;3阶以上的极大外平面图的每 个内部面的次数为__3__;10. n 方体的点色数为___2___;边色数为___n ___。
二．单项选择(每题3分，共12分)1．下面给出的序列中，不是某图的度序列的是( B ) (A) (33323); (B) (12222); (C) (5533); (D) (1333).2．设V(G)={}1,2,3,4,5，{}()(1,2),(2,3),(3,4),(4,5),(5,1)E G =则图(,)G V E =的补图是（ B3.下列图中，既是欧拉图又是哈密尔顿图的是( B )4.下列说法中不正确的是( C ) (A)每个连通图至少包含一棵生成；(B) 2 3 5 (A) 2 35(B)23 5 (C) 234(D)(C)(D) (A)1(B)k 正则偶图(k>0)一定存在完美匹配； (C)平面图(*)*G G ≅,其中*G 表示G 的对偶图； (D)完全图2n K 可一因子分解。
图论及其应用第二次作业要求：1、交电子档给助教【助教给每个班设置邮箱，助教设置提交回复】；2、第7章授课结束前均可以提交；3、希望能够独立完成。
1．判断图4-43所示的四个图是否可以一笔画。
上面四个图都是连通图，看是否能一笔画成问题本质上看图是否存在欧拉迹；连通图有欧垃迹当且仅当G 最多有两个奇点。
（a ）不可以 有4个奇点（b ）可以 一个奇点（c ）可以 两个奇点（d ）可以 没有奇点2.（1）画一个有欧拉闭迹和哈密尔顿圈的图；（2）画一个有欧拉闭迹但没有哈密尔顿圈的图；(3) 画一个有哈密尔顿圈但没有欧拉闭迹的图；（4）画一个既没有欧拉闭迹也没有哈密尔顿圈的图。
3. 设n 阶无向简单图G 有m 条边。
证明：若m ≥⎪⎪⎭⎫ ⎝⎛-21n +2，则G 是哈密尔顿图。
(b) (c) (d ) 图4-43证明：G 是H 图。
若不然，因为G 是无向简单图，则n ≥3，由定理1：若G 是n ≥3的非单图，则G 度弱于C m,n 。
于是有：2,1()()(2)(1)(1)21111(1)(2)(1)(21) 1.222m n E G E C m n m n m m n n n m m m n m ⎡⎤≤=+---+-⎣⎦--⎛⎫⎛⎫=+-------≤+ ⎪ ⎪⎝⎭⎝⎭ 这与条件矛盾！所以G 是H 图。
4. 在图4-45中，哪些图是哈密尔顿图？哪些图中有哈密尔顿路？(a)非哈密尔顿图，没有哈密尔顿路(b)哈密尔顿图 （abcdejhfiga)(c)哈密尔顿图 （kjdhbagciefk)(d)非哈密尔顿图 有哈密尔顿路（hjaidebcgf)(e)不是哈密尔顿图，因为有割点a ，有哈密尔顿路（jaibcedkgfh ）5. 证明：若G 没有奇点，则存在边不重的圈C 1, C 2,…, C m ，使得，E (G ) = E (C 1)∪E (C 2)∪…∪E (C m )。
证明：将G 中孤立点除去后的图记为G 1，则G 1也没有奇点，且δ（G 1)，则G 1含圈C 1，在去掉()11G E C -的孤立点后，得图G 2，显然G 2仍无奇度点，且δ（G 2）≥ 2，从而G 2含圈C 1，如此重复下去，直到圈C m ，且G m －E (C m )全为孤立点为止，于是得到E (G ) = E (C 1)∪E (C 2)∪…∪E (C m )。
e （a ）（b ） e （c ） h（d ） 图4-45 （e ）6. 证明：若G 有2k ＞0个奇点，则存在k 条边不重的迹Q 1, Q 2,…, Q k ，使得，E (G ) = E (Q 1)∪E (Q 2)∪…∪E (Q k )。
证明：不失一般性，只就G 是连通图进行证明。
设G=(n,m)是连通图。
令v 1，v 2，...v k ，v k+1，...，v 2k 是G 的所有奇度点。
在v i 与v i+k 间连新边e i 得图G *(1≤i ≤k)。
则G *是欧拉图，因此，由Fleury 算法得欧拉环游C,在C 中删去e i （1≤i ≤k ），得k 条边不重的迹Q i （1≤i ≤k ）;E (G ) = E (Q 1)∪E (Q 2)∪…∪E (Q k )7. 证明：若（1）G 不是二连通图，或者（2）G 是具有二分类（X ,Y ）的偶图，这里|X |≠|Y |，则G 是非哈密尔顿图。
证明：（1）因为G 不是二连通图，则G 不连通或者存在割点v ，有()2w G v -≥，由相关定理得：若G 是Hamilton 图，则对于v(G)的任意非空顶点集S ，有：()w G v S -< ，则该定理得逆否命题也成立，所以可得：若G 不是二连通图，则G 是非Hamilton 图。
（2）因为G 是具有二分类（X ,Y ）的偶图，又因为|X |≠|Y |，在这里假设|X |≦|Y |，则有()w G X Y X -=>，也就是说：对于v(G)的非空顶点集S ，有：()w G S S -<成立，则可以得出G 是非Hamilton 图。
8、证明：若G 有哈密尔顿路，则对于V 的每个真子集S ，有ω(G –S )≤|S |+1。
证明：G 有H 图，设C 是G 的H 圈，则对V(G)的任意非空子集S ，容易知道：()()||G S C S S ωω-≤-≤，必然有：()||1G S S ω-≤+。
9．对下列问题给出一个好算法：（1）构作一个图的闭包；（2）若某图的闭包是完全图，求该图的哈密尔顿圈。
（1）构作一个图的闭包：根据图的闭包定义，构作一个图的闭包，可以通过不断在度和大于等于n 的非邻接顶点对间添边得到。
据此设计算法如下：图的闭包算法：1） 令G0=G ，k=0;2） 在Gk 中求顶点u0与v0，使得：00()()max{()()|uv ()}k k k k G G G G k d u d v d u d v E G +=+∉ 3） 如果00()()k k G G d u d v n +≥则转4）；否则，停止，此时得到G 的闭包。
4） 令100,1k k G G u v k k +=+=+，转2）。
复杂性分析：在第k 次循环里，找到点u 0与v 0，要做如下运算：（a ）找到所有不邻接点对---需要n(n-1)/2次比较运算；（b ）（b ）计算不邻接点对度和---需要做n(n-1)/2-m(G)次加法运算；（c ）选出度和最大的不邻接点对---需要n(n-1)/2-m(G)次比较运算。
所以，总运算量为：211(1)2(1)m(G)()22n n n n O n ⎛⎫-+--= ⎪⎝⎭所以，上面的闭包算法是好算法。
（2）若某图的闭包是完全图，求该图的H 圈。
方法：采取边交换技术把闭包中的一个H 圈逐步转化为G 的一个H 圈。
该方法是基于如下一个事实：在闭包算法中，100k k G G u v +=+，0u 与0v 在G k 中不邻接，且度和大于等于n ，如果在G k+1中有H 圈C k+1如下：100120(,,,...,,)k n G u v v v u +-= 我们有如下断言：在G k+1上，1,i i v v +∃使得001,()i i k u v v v E G +∈若不然，设0()k G d u r =那么在G k 中，至少有r 个顶点与v 0,则0()(1)k G d v n r n r ≤--<-这样与u 0，v 0在G k 中度和大于等于n 矛盾！ 上面结论表明：可以从C k+1中去掉u 0v 0而得到新的H 圈，实现H 圈的变交换。
由此，我们设计算法如下：1） 在闭包构造中，将加入的边依次加入次序记为(1)i e i N ≤≤，这里，N=n(n-1)/2-m(G).在G N 中任意取出一个H 圈C N ，令k=N;2） 若e k 不在C k 中，令11,k k k k k G G e C C --=-=；否则转3）； 3） 设00k k e u v C =∈，令1k k k G G e -=-；求C k 中两个相邻点u 与v 使得u 0，v 0，u ，v 依次排列在C k 上且有：001,()k uu vv E G -∈，令10000{,}{u ,}k k C C u v uv u vv -=-+4） 若k=1,转5）；否则，令k=k-1,转2）；5） 停止。
C 0为G 的H 圈。
复杂性分析：一共进行N 次循环，每次循环运算量主要在3），找满足要求的邻接顶点u 与v,至多n-3次判断。
所以总运算量：N(n-3)，属于好算法。
10．（1）证明：每个k 方体都有完美匹配（2k ≥）；（2）求2,n n n K K 和中不同的完美匹配的个数。
(1) 证明每个k 方体都是k 正则偶图。
事实上，由k 方体的构造：k 方体有2k 个顶点，每个顶点可以用长度为k 的二进制码来表示，两个顶点连线当且仅当代表两个顶点的二进制码只有一位坐标不同。
如果我们划分k 方体的2k 个顶点，把坐标之和为偶数的顶点归入X ，否则归入Y 。
显然，X 中顶点互不邻接，Y 中顶点也如此。
所以k 方体是偶图。
又不难知道k 方体的每个顶点度数为k,所以k 方体是k 正则偶图。
由推论：k 方体存在完美匹配。
(2) 我们用归纳法求K2n 和Kn,n 中不同的完美匹配的个数。
K2n 的任意一个顶点有2n-1种不同的方法被匹配。
所以K2n 的不同完美匹配个数等于(2n-1)K2n-2,如此推下去，可以归纳出K2n 的不同完美匹配个数为：(2n-1)!!同样的推导方法可归纳出K n, n 的不同完美匹配个数为：n!11．证明：一棵树最多只有一个完美匹配。
证明：若不然，设M1与M2是树T 的两个不同的完美匹配，那么M1ΔM2≠Φ,容易知道：T[M1ΔM2]每个非空部分顶点度数为2，即它存在圈，于是推出T 中有圈，矛盾。
12．对每1k >,找出一个没有完美匹配的k 正则简单图的例子。
证明：设K 为奇数，作G 如下：取2k-1个顶点1221,,...,k v v v - ，在奇脚标顶点和偶脚标顶点之间两两连以外边，再连接13572523,,...,k k v v v v v v --边，所得图记为0G ，显然除0G 除21k v -外其余顶点的度均为k ，而21k v -的度为k-1，取k 个两两不相交的0G 的拷贝和一个新顶点0v ，并把每个0G 拷贝中对应于21k v -的顶点与0v 相连以边。
最后所得的图记为G ，显然G 是k-正则的简单图。
又由于0G 含2k-1个顶点，则G 的顶点数为：k*（2k-1）+1。
所以如果G 有一个完美匹配M 的话，则2*(21)11|M|=22k k k k -+-=- 。
假设M 是G 的一个完美匹配，则其边应来自k 个独立的0G ，和跟0v 相关联的一条边。
而每个0G ，其包含的顶点数为2k-1，所以0G 能提供给M 的边最多为k-1条，k 个这样的0G 能提供给M 的边最多为k*（k-1），因此M 最多包含的边为k*（k-1）+1<k 2-(k-1)/2,因此G 不可能有完美匹配当k 为偶数时，取G=K k+1,则G 的顶点数为k+1,显然G 的顶点数为奇数，所以G 无完美匹配。
13．证明63n K -有一个3－因子分解。
证明：K6n-2= K 2(3n-1) , 所以，可以分解为6n-3个边不重的1因子之和。
而任意3个1因子可以并成一个3因子。
所以，共可以并成2n-1个3因子。
即K6n-2可以分解为2n-1个3因子的和。
14．给出分4,4K 为生成林的一个最小分解。
证明：首先将其分解为4条路112...i i i i i i n i n P x y x y y x -+--+= 脚标按模4计算。
