16题和证明题

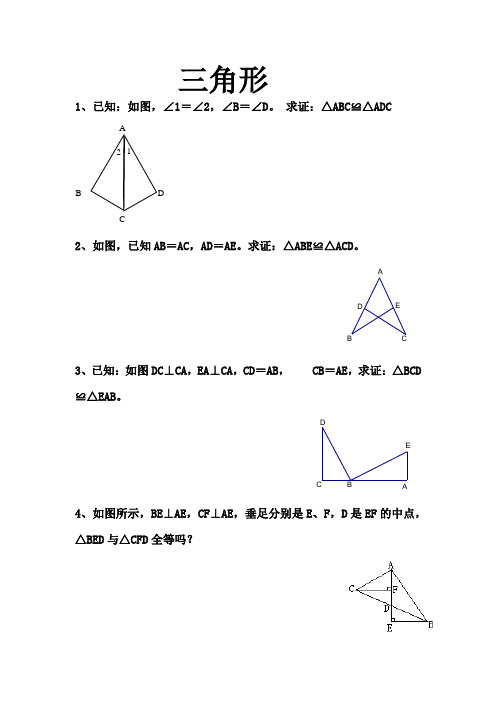
三角形1、已知：如图，∠1＝∠2，∠B ＝∠D 。

求证：△ABC ≌△ADC2、如图，已知AB ＝AC ，AD ＝AE 。

求证：△ABE ≌△ACD 。

ED CB A3、已知：如图DC ⊥CA ，EA ⊥CA ，CD ＝AB ， CB ＝AE ，求证：△BCD ≌△EAB 。

EDC BA4、如图所示，BE ⊥AE ，CF ⊥AE ，垂足分别是E 、F ，D 是EF 的中点，△BED 与△CFD 全等吗？1B DA 2 C5、已知：AD 为△ABC 中BC 边上的中线，CE ∥AB 交AD 的延长线于E 。

求证：△ABD ≌△ECD ；AB D CE6、已知：A 、B 、C 、D 在同一直线上，AB ＝CD ，DE ∥AF ，且DE ＝AF 。

求证：△AFC ≌△DEBEBA DC7、如图，AB=CD ，AD=CB ； 试证明△ABD ≌△CDB 。

8、已知：AD 平分∠BAC ，AB =AC. 求证AD ⊥BC.ADB C9、如图，已知：BC、AD相交于O点，∠C=∠D，AC=BD.求证：AD=BC10、已知：BE⊥AC，CF⊥AB，BE=CF，求证：BD=CD.11、如图，已知：AB=AC,BD=CD,求证：AD平分∠BAC.12、如图，已知：△ABD△BAC,求证：∠DAE=∠CBE.13、如图，已知：已知△ABF△DCCE，求证：BE=CF.14、如图，已知：D是BC的中点，AB//ED，AD//EC，求证：∠A=∠E.15、如图，已知：AB//CD，AD//BC，求证：∠B=∠D.16、如图，已知：AB=CD，AC交BD于O点，且AC=BD.求证：∠B=∠C.17、如图，已知：BD=CE，∠1=∠2.求证：AB=AC.18、如图，已知：∠C=90°，ED⊥AC，AB⊥AB，AB=AE.求证：AD=BC19、如图，已知：OA=OB，OD=OC,∠AOC=∠BOD.求证：AD=BC.20、如图，已知：点D、E在BC上，且BD=CE，AD=AE，∠1=∠2.求证：AB=AC21、如图，已知线段a和∠α，求作△ABC，使AC=2a，∠A=∠α，∠C=∠α.22、如图，已知，在△ABC中，AB=BC，AC⊥BC，D为BC的延长线上的点，直线DF交AC于F，且CF=CD.，连接AD、BF，则BF与AD有何关系？试说明你的理由.23、如图，已知△ABC中，∠C=90°，AD是∠BAC的角平分线，DE⊥AB于E，F在AC上，BD=DF.求证：CF=EB.24、你能把图中的这个“十”字图分成两个全等的吗.请画出所有分割方法.25、已知：如图所示，在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，CE=BC，过E点作AC的垂线，交CD的延长线于F.求证：AB=FC.。

全等三角形证明题专项练习60题(有答案）1．已知如图，△ABC≌△ADE,∠B＝3０°,∠Ｅ=20°，∠ＢＡE＝105°，求∠ＢAC的度数.∠BＡC=_________ ．2.已知:如图,四边形ABCD中,ＡB∥CD,AＤ∥BC.求证:△ABD≌△ＣDＢ．3．如图,点E在△AＢC外部，点D在边BＣ上，DE交AC于F．若∠1=∠2=∠3,AＣ=AE，请说明△ABC≌△AＤE的道理．４.如图,△ABC的两条高AＤ,BE相交于H，且ＡＤ=BD．试说明下列结论成立的理由．（1）∠DＢH=∠DAC；（2)△ＢDH≌△ＡDC.5.如图，在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E、F，且DＥ＝DF,则AB＝AC，并说明理由．７．如图所示，Ａ、Ｄ、F、Ｂ在同一直线上,AF=ＢＤ，ＡＥ=BC，且AE∥BC.求证:△AEF≌△ＢCD.8.如图，已知ＡB=AＣ,AD=AＥ,BE与ＣD相交于O，△AＢＥ与△ＡCD全等吗？说明你的理由.9．如图,在△AＢC中，ＡB=AC,D是BC的中点,点E在ＡD上，找出图中全等的三角形,并说明它们为什么是全等的．10.如图所示，CD=CA，∠1=∠2，EC=BC，求证：△ABC≌△DEC.11.已知ＡC=ＦE,BＣ＝DE，点A、D、B、F在一条直线上,要使△ABＣ≌△FDＥ，应增加什么条件？并根据你所增加的条件证明：△ＡBC≌△FＤＥ.１２.如图，已知ＡB=AC,ＢD＝CE,请说明△AＢＥ≌△AＣＤ.13．如图,△ABC中,∠AＣB＝90°,AC=ＢC，将△AＢC绕点Ｃ逆时针旋转角α（０°＜α<90°）得到△Ａ1Ｂ１Ｃ,连接BB1.设CB１交AＢ于D，A1B1分别交AB，AＣ于E，F,在图中不再添加其他任何线段的情况下，请你找出一对全等的三角形，并加以证明.（△ＡBC与△A1B１C１全等除外)14．如图,ＡＢ∥DE,AC∥DF,ＢE=CF．求证:△ＡＢＣ≌△ＤEＦ.15．如图,ＡB=AＣ,AD＝AE,AB，DＣ相交于点M，AC,BＥ相交于点N，∠DAB=∠EAC.求证:△ＡDＭ≌△AＥN．16.将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内．从图1中抽象出一个几何图形（如图2），Ｂ、C、E三点在同一条直线上,连接DC．求证：△ABE≌△ACD.1７．如图,已知△ABC是等边三角形,Ｄ、Ｅ分别在边BC、ＡＣ上，且ＣD＝ＣE，连接ＤE并延长至点F,使EＦ=ＡE，连接ＡF、ＢＥ和CF.请在图中找出所有全等的三角形，用符号“≌”表示,并选择一对加以证明.18.如图,已知∠1=∠２，∠3=∠4,EC＝AＤ.(1）求证:△ABＤ≌△EBC．(2)你可以从中得出哪些结论？请写出两个．１9．等边△ABC边长为8，D为AB边上一动点，过点D作DE⊥BＣ于点E,过点E作EＦ⊥ＡC于点Ｆ．(１)若AＤ=2,求ＡF的长；（2)求当AD取何值时，ＤE=EＦ.２０．巳知：如图，AB=AＣ，D、E分别是AB、AC上的点,AD=AＥ,BE与CD相交于G．（Ⅰ）问图中有多少对全等三角形?并将它们写出来.（Ⅱ）请你选出一对三角形,说明它们全等的理由(根椐所选三角形说理难易不同给分,即难的说对给分高,易的说对给分低）2１.已知：如图，AＢ=DC，AC＝BD，AC、BD相交于点E,过E点作ＥF∥BC,交CＤ于Ｆ，(1）根据给出的条件,可以直接证明哪两个三角形全等?并加以证明.（2）EF平分∠DEC吗？为什么?22.如图，己知∠1＝∠２,∠ABC=∠DCB,那么△ABC与△DCB全等吗？为什么？２３．如图,B，F,Ｅ，D在一条直线上,ＡB=CＤ，∠Ｂ=∠D，ＢF=ＤE．试证明：（１）△DＦC≌△BEA;(2)△AFE≌△CEF.2４.如图,AＣ＝ＡE,∠BAF=∠BＧＤ=∠EAＣ，图中是否存在与△ＡＢE全等的三角形？并证明．25．如图,D是△ABC的边BC的中点,CＥ∥AB,Ｅ在AD的延长线上．试证明：△ABD≌△ECD．２６．如图，已知AB=CD，∠B＝∠Ｃ，AＣ和BD相交于点O，E是AＤ的中点，连接OE．（1)求证:△AOＢ≌△DOC;(２）求∠ＡEＯ的度数．27.如图,已知AB∥DE,ＡＢ＝DE，AＦ=DＣ．（1）求证：△ＡBF≌△DＥＣ;（2)请你找出图中还有的其他几对全等三角形.(只要直接写出结果，不要证明)２８．如图：在△AＢC中,ＢＥ、ＣF分别是ＡC、AB两边上的高,在BE上截取BD=AC，在CＦ的延长线上截取CG=AB，连接ＡD、ＡG.（1)求证:△ＡＢD≌△ＧCA;(2）请你确定△ADＧ的形状，并证明你的结论．29．如图，点Ｄ、Ｆ、E分别在△ABC的三边上，∠1=∠２＝∠3,DＥ=ＤF,请你说明△ADE≌△ＣＦD的理由．30．如图，在△AＢC中,∠ABＣ＝90°，BE⊥ＡC于点E，点Ｆ在线段ＢE上,∠1=∠2,点D在线段EＣ上，给出两31．如图，在△ABC中,点D在AB上,点Ｅ在BC上，ＡB=BＣ,BD=BE,EA=ＤC,求证：△BEA≌△BDC．３2．阅读并填空:如图,在△ABC中,∠ACB＝９0°，AC=BC,BE⊥ＣE于点E，AD⊥CE于点Ｄ.请说明△ADC≌△CＥＢ的理由．解:∵BE⊥CE于点E(已知)，∴∠E=90°＿________，同理∠AＤＣ=90°，∴∠E=∠ＡDC（等量代换).在△ADＣ中,∵∠1＋∠2+∠ADC=1８0°_＿____＿__，∴∠１+∠２=９0°____＿__＿＿.∵∠ＡCＢ=9０°(已知)，∴∠3＋∠2＝9０°，∴____＿＿＿＿_ ．在△ＡDC和△CEB中，.∴△AＤＣ≌△CEB (Ａ.A．S）3３．已知:如图所示，ＡＢ∥DE，AB=DE,AF=DC．（1)写出图中你认为全等的三角形（不再添加辅助线）；（2)选择你在（１)中写出的全等三角形中的任意一对进行证明．３４．如图，点E在△ABC外部，点D在BC边上，DＥ交AC于点F,若∠1＝∠２=∠3，AC＝ＡE.试说明下列结论正确的理由:(１)∠C=∠E;(2)△ABＣ≌△ADE.35．如图,在Rt△ＡBC中，∠ＡＣB=9０°,ＡＣ=BC,D是斜边AB上的一点,AE⊥CD于E,BＦ⊥CD交CＤ的延长线于F．求证:△ＡCＥ≌△CBF.36.如图,在△ABC中,D是BＣ的中点,DＥ∥CA交AB于E，点Ｐ是线段AC上的一动点,连接PＥ.探究：当动点Ｐ运动到ＡＣ边上什么位置时,△AＰE≌△EDＢ?请你画出图形并证明△APE≌△EDＢ．37.已知:如图，AD∥ＢC，AD=BC,Ｅ为ＢC上一点,且AE=AB.求证：（1)∠DＡＥ=∠B；（2)△ＡＢＣ≌△EAD．38．如图，D为ＡＢ边上一点，△ABＣ和△EＣD都是等腰直角三角形,∠ACB=∠ＤCE＝90°,ＣＡ＝ＣB,ＣＤ=CＥ,图中有全等三角形吗？指出来并说明理由.３９．如图，AB=AC,ＡD=ＡE,∠BＡC=∠DAE．求证:△AＢＤ≌△ACE.40．如图,已知D是△ABＣ的边BC的中点，过Ｄ作两条互相垂直的射线,分别交AB于Ｅ,交ＡC于F,求证:BE+CF>ＥＦ.4１.如图所示，在△MNP中,H是高MQ与NE的交点,且QN=QM，猜想ＰＭ与ＨＮ有什么关系?试说明理由．４2.如图,在△AＢC中，Ｄ是BC的中点,过D点的直线GF交AＣ于Ｆ,交AC的平行线BG于G点,DE⊥GF，交ＡB于点Ｅ,连接ＥG.(１）求证：ＢG＝CF;（2)请你判断BE＋ＣＦ与EF的大小关系，并证明你的结论．43.如图，在△ＡBＣ中,∠ACB＝90°，ＡＣ＝BC,ＢE⊥CE于E,AD⊥ＣE于D,ＡＤ=2.５cｍ,DE=1.7cm,求BE的长.44.如图,小明在完成数学作业时,遇到了这样一个问题,AB＝CD,ＢＣ=AD，请说明：∠A=∠C的道理,小明动手测量4５.如图，AＤ是△ＡBC的中线,CE⊥AD于E，BF⊥AＤ,交AD的延长线于F．求证:CE=ＢF．４6.如图,已知AB∥CD，ＡＤ∥BC,Ｆ在DC的延长线上，AM=CＦ，FM交DA的延长线上于E.交BC于N，试说明：AＥ=CN.47．已知:如图，△AＢC中,∠C＝9０°,ＣM⊥AＢ于M,AＴ平分∠BAC交CＭ于D,交ＢC于Ｔ，过D作ＤE∥ＡB 交BC于E,求证：CT=BE.４8．如图，已知AB＝AD,AC＝ＡＥ，∠ＢAＥ＝∠DAＣ.∠B与∠D相等吗?请你说明理由．49.Ｄ是AB上一点,DF交AC于点Ｅ，DE=EＦ,ＡE＝CＥ，求证:ＡＢ∥CF．5１.如图,在△ABC中,AＣ⊥BC,AC=BＣ,Ｄ为AＢ上一点,AF⊥ＣD交于CＤ的延长线于点F，BE⊥ＣD于点E，求证：EF=CF﹣AF．52．如图，在△ABC中，∠BAC=90°，AＢ=ＡC，若MN是经过点A的直线，BD⊥MN于Ｄ,ＥC⊥MN于E. （1)求证：BD=AE;（２）若将MＮ绕点A旋转，使MＮ与ＢC相交于点O,其他条件都不变，BD与ＡE边相等吗？为什么?(3）BD、CE与ＤＥ有何关系?５３.已知:如图,△ABＣ中,AＢ=AC，ＢD和CＥ为△ABC的高,ＢD和CＥ相交于点O.求证：OB=OC.54.在△ＡBC中，∠ACＢ=９０°，D是ＡB边的中点，点F在AＣ边上,DE与CF平行且相等．试说明AE=DF的理由．55．如图,在△ABC中,D是边ＢC上一点，ＡD平分∠ＢAＣ，在AB上截取AE＝ＡC,连接DE,已知DE＝2cｍ,BD=3ｃm,求线段ＢC的长．5６．如图:已知∠B=∠C,AＤ=AE,则AB=AＣ,请说明理由．57．如图△AＢC中,点D在AC上，E在AB上，且AＢ=AＣ,BC=ＣD，AD=DＥ=BＥ.（1)求证△ＢＣE≌△DＣE；(2)求∠EDC的度数．5８．已知:∠Ａ=9０°，AB=ＡＣ，BD平分∠ABC，CE⊥ＢD，垂足为E．求证:BD=２CＥ.59．如图,已知:AB=CＤ，AD=BC,过BD上一点O的直线分别交DA、BＣ的延长线于E、F．(1）求证:∠E=∠F;(2）OE与ＯF相等吗？若相等请证明,若不相等，需添加什么条件就能证得它们相等?请写出并证明你的想法.60.如下图，AD是∠BAC的平分线，ＤE垂直AＢ于点Ｅ，ＤF垂直AＣ于点Ｆ,且BＤ=DC.求证：BＥ＝CF．ﻬ全等三角形证明题专项练习60题参考答案:1.∵△ABC≌△AＤE 且∠B≠∠Ｅ，∴∠C=∠Ｅ,∠Ｂ=∠D;∴∠BＡC=1８０°﹣∠Ｂ﹣∠C=１80°﹣３0°﹣20°＝13０°.2.∵AB∥ＣD,AD∥BＣ，∴∠ABD=∠CDＢ、∠ＡDB=∠CＢD.又ＢD=DB,∴△ABＤ≌△ＣＤB（ASＡ）．3.△ＡDF与△ＡEF中，∵∠2=∠３，∠AFE＝∠CＦD，∴∠E=∠Ｃ.∵∠1＝∠2,∴∠BAＣ=∠DAE．∵ＡC＝AE,∴△ABＣ≌△ADE.4.（１）∵∠ＢＨD=∠AHE,∠BDH=∠AＥH=9０°∴∠DBH+∠BHD＝∠HＡE+∠ＡHE=９0°∴∠DBH=∠HAE∵∠ＨAE=∠ＤAC∴∠ＤBH=∠DAC;(2)∵ＡＤ⊥BＣ∴∠ADB=∠ＡDC在△BDH与△AＤC中，∴△ＢDH≌△AＤC.5．∵DE⊥AB,DＦ⊥ＡC，∴△DBE与△DCＦ是直角三角形，∵BＤ=ＣD,DＥ=DF,∴Rt△DBＥ≌Rt△DCF（ＨＬ），∴∠B=∠C,∴AB=ＡC.6．∵ＡE是∠BＡC的平分线,∴180°﹣∠ＢAE=1８0°﹣∠CＡＥ,即∠DAB=∠DAC;又∵AB=AＣ，AD=AD，∴在△ＡBＤ和△ACＤ中，∴△ABＤ≌△ACD(SＡＳ)7．∵AE∥BC,∴∠Ｂ=∠C.∵AＦ=ＢD，AE=ＢC，∴△AEＦ≌△BCD(SAS）．8．△ABE与△ACＤ全等．理由:∵AB=AC，∠Ａ=∠A(公共角）,ＡＥ=AD,∴△ABＥ≌△ACＤ.9．图中的全等三角形有:△ＡBD≌△ACD,△AＢＥ≌△ＡＣE,△ＢDE≌△CDE.理由：∵Ｄ是ＢC的中点,∴BD=ＤＣ,ＡB=AC,AＤ=AD∴△ＡＢＤ≌△ACD（ＳＳS);∵AＥ=AE,∠BAE=∠ＣＡE,ＡＢ＝ＡC,∴△ABE≌△ACＥ(SAＳ);∵BE=CE,BD=DC,DＥ=DE，∴△BDＥ≌△CDE（SSS).10.：∵∠1=∠2,∴∠ＡCB=∠ＤCE，在△ABC和△ＤＥC中,，∴△AＢC≌△DＥC(SＡＳ）11．增加AB=DF.在△ABC和△ＦDE 中，∴△ＡBC≌△FDE(SSＳ)．1２.∵AB=AＣ，BD＝CE,∴AD=AE．又∵∠Ａ=∠A,∴△ABＥ≌△ＡCD（SAS). １3．△CBＤ≌△ＣA1F证明如下:∵AC＝BC，∵△ABC绕点C逆时针旋转角α（0°<α＜9０°）得到△A1B1Ｃ1, ∴∠A1=∠Ａ，A１C=AC,∠ACA1=∠BCB1=α．∴∠A１=∠AＢC（1分),A1C=BC.∴△ＣBＤ≌△ＣA1F(ＡSA）14．∵ＡB∥ＤE,ＡＣ∥ＤＦ,∴∠Ｂ=∠DEＦ，∠Ｆ=∠ACB．∵BE=ＣF，∴BE＋ＣE=CＦ+EC.∴BC＝ＥF.∴△ABC≌△DEＦ(AＳＡ).１5.∵AB=AＣ,AＤ=AE,∠DAB=∠EAＣ，∴∠DAC＝∠ＡEＢ，∴△ACＤ≌△ABＥ,∴∠D=∠E,又AD=ＡE,∠DＡB=∠ＥＡＣ,∴△ＡDM≌△ＡEN16.∵△AＢＣ和△ADE均为等腰直角三角形,∴AB=AC,AＤ＝AE,∠ＢAC=∠DAＥ＝９0，即∠ＢＡC＋∠CAＥ=∠DAE+∠CAE,∴∠BAE＝∠CAD，在△AＢE和△ACD中,,∴△ＡBE≌△ＡCＤ17.答:△ＢDE≌△FEC,△BCE≌△FＤＣ，△ABＥ≌△ACF；证明:（以△ＢDE≌△FEＣ为例)∵△ABC是等边三角形,∴BＣ＝AC，∠ACＢ＝６０°，∵CD=CE,∴△EDＣ是等边三角形,∴∠EＤC=∠DEC=60°,∴∠BDＥ=∠ＦＥC＝12０°，∵CD＝CE,∴BＣ﹣CD＝AC﹣CＥ,∴BD=ＡE，又∵EF＝AＥ,∴ＢＤ=ＦE，在△ＢDE与△FＥC中,∵，∴△BDＥ≌△FEC(ＳAS）.１8.(１)证明如下:∵∠ＡBＤ=∠１＋∠ＥBC,∠CBＥ=∠２+∠ＥBＣ,∠1＝∠2．∴∠ＡＢＤ＝∠ＣＢＥ.在△ABD和△EBC中∴△AＢＤ≌△EBC(AAS)；(2)从中还可得到AB=BC,∠BAＤ=∠BEC19．（1）∵AB=8,AD＝2∴BＤ=ＡB﹣AD=6在Rｔ△ＢＤE中∠BDＥ=90°﹣∠Ｂ=30°∴BE=ＢＤ=3∴CE＝BＣ﹣BE=5在Rt△CFＥ中∠CEF=90°﹣∠C＝30°∴CF=CE＝∴ＡＦ＝AＣ﹣ＦC=;（2）在△BDE和△EFC中，∴△BDＥ≌△CＦE（AAS)∴BE＝CF∴BE=ＣF=EC∴BE=BＣ=∴BD=2BＥ＝∴AD=AＢ﹣ＢＤ=∴AD＝时,ＤE=ＥＦ2０．（1）图中全等的三角形有四对，分别为:①△DBG≌△EGC,②△AＤＧ≌△AEＧ，③△AＢＧ≌△ACG，④△ABＥ≌△ACD；（4分)（Ⅱ）∵ＡB=AC,AＤ=AE,∠A是公共角,∴△ABE≌△ACD(SAS)④；∵AB=AC,AD=AE，∴AB﹣AD＝ＡC﹣AE，即BD=CE;由④得∠B＝∠C,又∵∠DGB=∠EGC（对顶角相等），BＤ=CE（已证）,∴△DBG≌△ＥGC（AAS)①;由①得BG＝CG，由④得∠B=∠C,又∵AB＝AC,∴△ＡBＧ≌△ACG(SAS)③；由①得ＢG=CG,且ＡＤ=AE，AＧ为公共边,∴△ADG≌△AEG（SSS)②;21．（1）△ABC≌△ＤCＢ．证明：∵AＢ=CＤ，AC=BD,BＣ=CB，∴△ABC≌△DCＢ.(ＳＳS）(2）EＦ平分∠DＥＣ．理由：∵EF∥BC,∴∠DEF=∠ＥBC，∠ＦＥC=∠ＥＣB；由(1）知：∠EBＣ＝∠EＣB;∴∠DEF＝∠FEC；∴FE平分∠DEC22．△ABC≌△DCB.理由如下：∵∠ＡＢC＝∠DCB,∠1=∠2，∴∠DＢC＝∠ACＢ．∵BＣ=ＣB，∴△AＢC≌△DCB23．（1)∵BF=DＥ，∴BＦ＋ＥＦ=ＤE+EＦ．即BＥ=DF.在△DFC和△BEA中,∵，∴△DFC≌△ＢEA（SAＳ).(２)∵△DＦC≌△ＢＥA，∴CF＝ＡE，∠ＣＦD=∠AEB.∵在△AFE与△CEF中,∵，∴△AFE≌△CEF（SAS)２4．△ABＦ与△DFＧ中,∠BAF=∠BGD,∠ＢＦA=∠ＤFG, ∴∠Ｂ=∠Ｄ,∵∠ＢAF=∠EＡC,∴∠BAE=∠ＤＡＣ,∵AC=ＡＥ,∠BAE=∠ＤＡC，∠B=∠D，∴△BAE≌△DＡC.答案：有.△ＢAE≌△ＤAＣ25．∵CE∥ＡB,∴∠ＡBD=∠ＥＣＤ.在△AＢＤ和△ＥＣＤ中，, ∴△ABD≌△EＣD(ASＡ）26.（１)证明:在△AＯB和△COD中∵∴△AOＢ≌△COD(AAS）（２)解:∵△AOB≌△ＣOD,∴AＯ=DＯ∵E是AD的中点∴OE⊥AD∴∠ＡEO=90°27.1)证明：∵ＡＢ∥ＤE，∴∠A=∠D.∵AＢ=DE,ＡF=DC,∴△ＡBＦ≌△ＤEＣ．(2)解:全等三角形有:△ＡBC和△ＤEF；△ＣBＦ和△ＦＥC 28．证明：（１)∵ＢE、CF分别是AC、ＡＢ两边上的高,∴∠AFC=∠AEＢ＝９０°（垂直定义)，∴∠AＣG＝∠ＤBＡ（同角的余角相等),又∵BD＝CA，AB＝GC,∴△AＢD≌△GCA;(2)连接DG，则△ADG是等腰三角形．证明如下：∵△ABD≌△GCA，∴ＡG=ＡD，∴△ADＧ是等腰三角形．2９.解：∵∠4＋∠6＝１８０°﹣∠3,∠５＋∠6＝１８0°﹣∠2,∠3=∠２, ∴∠4+∠6=∠5+∠6,∴∠4=∠5，∵在△ADE和△ＣFD中，，∴△AＤＥ≌△ＣFD(ＡAＳ）.30．①DＦ∥ＢＣ．证明：∵BE⊥ＡC，∴∠BＥＣ=９0°,∴∠C+∠CBE＝9０°，∵∠AＢC=90°，∴∠ABＦ+∠CBE＝9０°,∴∠C=∠AＢF，∵DＦ∥ＢC，∴∠C=∠ADF,∴∠ＡBF=∠ＡＤF,在△AFD和△AFＢ中∴△ＡＦＤ≌△AFＢ（AAS）.31.在△BEA和△ＢＤC中：，故△BEA≌△BＤC(SSS).３2.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥ＣＥ于点E，AＤ⊥ＣＥ于点D．请说明△ADC≌△CＥB的理由．解:∵BE⊥CE于点E（已知）,∴∠E=９0°（垂直的意义),同理∠ＡDC=9０°,∴∠E=∠ADC(等量代换）.在△AＤC中，∵∠1+∠２+∠ADC＝１8０°（三角形的内角和等于180°) ，∴∠1+∠2=90°(等式的性质）．∵∠ACＢ＝90°(已知）,∴∠３+∠2=90°，∴∠1=∠3（同角的余角相等) .在△AＤC和△CＥB中,.∴△ＡＤＣ≌△CEＢ（A．A.Ｓ)33．(１)△ABF≌△ＤEC，△ＡBＣ≌△DEF，△BＣF≌△EFC；（2分）（2)△ABF≌△DEC,证明:∵AB∥ＤＥ，∴∠Ａ=∠D，(3分)在△ＡＢF和△DＥＣ中,(4分）∴△ABF≌△DEC．(5分)34．(1)△ADF与△AEF中,∵∠2=∠3,∠AFE=∠CFD,∴∠C=∠Ｅ；(2)∵∠1＝∠2，∴∠ＢＡC＝∠ＤAE.∵AＣ＝AE，又∠C=∠E,∴△ＡBC≌△ADE．35.∵AE⊥ＣD,∴∠AEＣ＝90°,∴∠AＣE+∠CＡE=90°，（直角三角形两个锐角互余)∵∠ＡCE+∠ＢCF=９0°，∴∠ＣAＥ＝∠ＢＣF，(等角的余角相等)∵ＡE⊥CD,BＦ⊥CＤ，∴∠AＥC=∠ＢＦＣ＝90°,在△ＡCE与△CBF中,∠CAE=∠BCＦ,∠AＥC=∠BＦC，ＡC=BＣ, ∴△ACE≌△CBF(ＡAS）.36．当动点P运动到ＡC边上中点位置时，△ＡPE≌△EＤB，∵DE∥CA,∴△ＢED∽△ＢＡC，∴＝,∵Ｄ是BC的中点,∴＝,∴=，∴E是AB中点，∴ＤE=AＣ,BE=AE,∵ＤＥ∥AC,∴∠Ａ=∠ＢＥD，要使△ＡPE≌△ＥDB,还缺少一个条件DＥ＝AP,又有DE=AＣ，∴P必须是ＡC中点．37．（1）∵ＡE＝AＢ,∴∠B＝∠ＡEB,又∵ＡD∥BC，∴∠AEB＝∠DＡE，∴∠DＡE=∠B;（２)∵∠DAE＝∠B，AD＝BC,ＡE=AB,∴△ABＣ≌△EAD．38．△AＣE≌△BＣD.∵△ABＣ和△ＥCD都是等腰直角三角形,∴∠ECD=∠ACB=9０°,∴∠ＡCE=∠BCＤ(都是∠ACD的余角),在△AＣＥ和△BＣD中，∵，∴△AＣE≌△ＢCD．3９．∵∠BAC=∠DＡE,∴∠BAC+∠CAD=∠DAE+∠CAＤ,即∠ＢAD=∠EAC，在△ABD和△AＣE中，∴△ABＤ≌△ＡCＥ.40.证明:延长FD到M使MD=DF，连接BＭ，EM. ∵D为BC中点,∴BD=ＤC.∵∠ＦDC=∠BＤM，∴△BDＭ≌△CＤF.∴BM=FC.∵ＥD⊥DF,∴ＥM=EF．∵BE+BＭ>EM，∴BE+FC>EＦ．4１.PM=ＨN．理由：∵在△ＭNP中，H是高MQ与ＮE的交点，∴∠ＭEH=∠NQH=90°，∠MQP=∠ＮQH=９０°∵∠MＨE＝∠NＨＱ（对顶角相等）,∴∠ＥＭH＝∠QNH（等角的余角相等）在△MPQ和△NHQ中，，∴△MPQ≌△NHQ(ＡSA）,∴MP=NH．４2．(1)∵ＢG∥ＡＣ,∴∠ＤBＧ=∠DCＦ．∵Ｄ为ＢC的中点，∴BD＝CD又∵∠BDG=∠CDＦ,在△ＢGD与△ＣFＤ中,∵∴△BGＤ≌△CFD（ASA).∴ＢG＝CF.(2）ＢE+ＣF＞EF.∵△BGD≌△ＣFD，∴ＧＤ＝ＦＤ,BG＝CＦ．又∵DE⊥FＧ,∴EＧ=ＥF（垂直平分线到线段端点的距离相等）．∴在△EＢＧ中,BE+BＧ>EG,即BＥ+CＦ＞EF.4３．∵BE⊥ＣE于E,AD⊥CE于D∴∠E=∠AＤC=9０°∵∠BCE+∠ACE＝∠DAC+∠ＡCＥ=90°∴∠BCE＝∠ＤAC∵ＡC=BC∴△ACD≌△ＣBＥ∴CE=ＡD,ＢＥ=CＤ=2.5﹣1．7＝0.8(cm)４4.∵ＡB=ＣD,BC=AD,又∵BD=DB,在△ABＤ和△ＣDB中，∴△ABD≌△CDＢ，∴∠A＝∠C．45.∵AD是△ＡＢC中BC边上的中线，∴ＢD=ＣＤ．∵CE⊥AD于E，BF⊥AD，∴∠BFD=∠CED．在△ＢFD和△CEＤ中,∴△ＢＦD≌△CED（AＡS)．∴CＥ=BF4６．∵ＡD∥ＢC，∴∠E=∠ENＢ，∵∠ＥNＢ＝∠CNＦ,∴∠E=∠CNＦ，∵AB∥CD，∴∠A=∠B,∵∠C=∠Ｂ,∴∠ＥAB=∠DCＢ,∵ＡM=CF,∴△AME≌△CFＮ，∴AE＝CＮ．4７．证明:过T作TF⊥AＢ于F,∵AＴ平分∠BAC,∠ACＢ＝９0°，∴CT=TF（角平分线上的点到角两边的距离相等），∵∠ACB=９０°,CＭ⊥AＢ，∴∠ＡDＭ＋∠ＤＡＭ＝9０°,∠ＡTC+∠CAＴ=90°, ∵ＡＴ平分∠BＡC，∴∠DAM=∠CA T，∴∠ADM=∠AＴC，∴∠CDT=∠CＴＤ,∴CD=CT，又∵CＴ＝TF（已证)，∴CD＝ＴＦ,∵ＣＭ⊥AB,DE∥ＡB，∴∠CDE=９0°，∠B＝∠ＤEC，在△CDＥ和△ＴFＢ中，, ∴△CDE≌△TFＢ（AAS），∴CE=TＢ，∴ＣE﹣ＴE=TB﹣ＴE，即CT=BE．４8.∵∠BAE=∠DAC∴∠ＢＡE＋∠CＡE=∠DAC＋∠CAE即∠ＢAＣ=∠DＡE又∵AB＝AD，AC=AE，∴△ABC≌△ADE（SAS）∴∠B=∠D（全等三角形的对应角相等)49.∵DE=EF，AＥ＝CE，∠AＥD＝∠FＥＣ，∴△AEＤ≌△ＦEC．∴∠ADE=∠CFE.∴AD∥ＦC.∵D是AB上一点,∴AB∥CF50．∵BE∥CF,∴∠CMF=∠ＢＭＥ，∠ＦＣM=∠EＢM．又∵BE＝ＣＦ，∴△CFM≌△ＢEＭ.∴CM=BM．即AＭ是△ＡＢC的中线5１．∵AC⊥BC，BＥ⊥CＤ，∴∠ACＦ＋∠ＦCB=∠FCB+∠ＣBE=９0°. ∴∠FCA=∠EＢＣ．∵∠BEC=∠CFA=９0°,ＡC=BC，∴△BEC≌△CFＡ.∴CE=AF.∴EF=CF﹣CE＝CF﹣AF52.解：（1）证明:由题意可知，BＤ⊥MN与D，ＥC⊥MN与E，∠BAC＝９0°, 则△ABD与△CEA是直角三角形，∠DAB=∠ＥＣA,在△ＡＢD与△ＣEA中,∵，∴△ABD≌△ＣＥＡ,∴ＢD=AE;(2）若将ＭN绕点A旋转，与BＣ相交于点Ｏ,则BD,CE与ＭN垂直，∴△ABD与△CＥA仍是直角三角形，两个三角形仍全等，∴BD与ＡE边仍相等；（3)∵△ABＤ≌△CEA,∴BD＝AＥ，AD＝EC，∴DＥ＝BD+EC或ＤE=ＣＥ﹣ＢD或DＥ＝BD﹣CE．５3．∵ＡB=AＣ，∴∠AＢC＝∠ACB，∵ＢＤ、CE分别为△ＡＢC的高,∴∠ＢEＣ＝∠BDC＝9０°，∴在△BEC和△CDB中,∴△BEC≌△ＣDＢ,∴∠1=∠2,∴OＢ=ＯC54．解:连接CＤ，∵∠ACB=90°，D是AB边的中点∴CD=AD，∠ＤＡC=∠DＣF∵DE与ＣF平行且相等∴∠ＥDA=∠DＡC∴∠EDA=∠DＣＦ在△ＡED和△CＦD中CD＝AD,∠ＥＤA=∠DCF，ＤE＝ＣＦ∴△AED≌△ＣFD∴AE=ＤF.55．∵ＡD平分∠BAC∴∠ＢAD＝∠ＣAD在△ＡDＥ和△ADC中∵∴△ADE≌△AＤC(SAS）∴ＤＥ=DＣ∴BＣ=BＤ＋DＣ=ＢD+DＥ=2＋３=5(cｍ）56．在△AEB与△AＤC中,. ∴△AＥＢ≌△ADＣ(AAS）.∴AＢ＝AC(全等三角形,对应边相等）57．（1）证明：在△BCE和△DCE中∴△BCＥ≌△DＣE（SSＳ）.(２）解:∵ＡD=ＤE，∴∠A＝∠AED;∴∠ＥDC=∠Ａ＋∠AED=２∠A,设∠A=x，根据题意得，５x＝18０°，解得ｘ=36°∴∠EDC=２∠A=72°58．证明:延长CE、BA交于点Ｆ.∵CE⊥BD于E，∠ＢAＣ＝9０°,∴∠AＢD=∠ＡCF．又AB=AＣ,∠BAD＝∠CAF=90°，∴△ABD≌△ACF,∴BD=CF.∵BＤ平分∠ABＣ，∴∠CBＥ=∠ＦBE.有ＢE=BE，∴△ＢＣE≌△BFE,∴CE=EＦ，∴CE=BＤ,∴BＤ=2CE.5９.（１）证明：在△ABＤ和△CDB中∵AＢ=ＣD,ＡD=BＣ,ＢD=ＤＢ,∴△ABD≌△CDＢ（SSS），∴∠ADＢ＝∠DＢC，∴DE∥BF．∴∠E=∠F．(2)答：当O是ＢD中点时,ＯE＝OF．证明如下：∵O是BＤ中点,∴OＢ=OＤ．又∵∠AＤB＝∠DＢC,∠Ｅ=∠F，∴△ODＥ≌△OＢF（AAS)．∴OE＝OF．（当ＡE=CＦ时也可证得60.∵DE⊥AB,DF⊥AC,∴∠E＝∠DFC＝90°.∵AD平分∠EＡＣ,∴DE＝DF.在Rt△DBE和Rt△DCＦ中，∴Rt△DＢE≌Ｒt△ＣDF(ＨＬ)．∴BE=CF.。

线性代数证明题1．设1234,,,αααα是非零的四维列向量，1234(,,,),*A A αααα=为A 的伴随矩阵，已知0Ax =的基础解系为(1,0,2,0)T ，证明234,,ααα是方程组*0A x =的基础解系.2.设A 是n 阶矩阵，且0nA =，则A E n -必是可逆矩阵。

3．,,A B C 均是n 阶矩阵，E 为n 阶单位矩阵，若ABC E =，证明：BCA E = 4．设3级方阵,A B 满足124A B B E -=-，证明：2A E -可逆，并求其逆.5．设A 是一个n 级方阵，且()R A r =，证明：存在一个n 级可逆矩阵P 使1PAP -的后n r -行全为零.6．设矩阵,m n n m A B ⨯⨯，且,m n AB E <=，证明：A 的行向量组线性无关.7．如果,2A A =称A 为幂等矩阵.设B A ,为n 阶幂等矩阵，证明：B A +是幂等矩阵的充要条件是.0==BA AB8.如果对称矩阵A 为非奇异,试证:1-A 也是对称矩阵 9.设A ，B ，C 都是n 阶方阵，且C 可逆，T --+=A E B C C ）（11,证明：A 可逆且T-+=）（C B A 1。

10.设0=kA，其中k 为正整数，证明：121)(--++++=-k A A A E A E11.设方阵A 满足A 2-A-2E=O ，证明A 及A+2E 都可逆，并求112--+）及（E A A 12.试证：对任意方阵A ，均有 T A A +为对称矩阵， TA A -为反对称矩阵。

13.证明 1)(=A R 的充分必要条件是存在非零列向量α和非零行向量Tβ，使TA αβ= 14.设A 为列满秩矩阵，C AB =，证明方程0=BX 与0=CX 同解 15.设A 为n m ⨯矩阵，证明方程m E AX =有解m A R =⇔)( 16.向量组A 能 用向量组B 表示，则R(A)<=R(B)17.设B A ,分别为m n n m ⨯⨯,矩阵，则齐次方程组O =ABx 当n m >时必有非零解。

最新七年级下册三角形全等的证明试题1、如图，AB=DE，AC=EF，BE=CF，证明∠A=∠D。

2、如图，AB=CD，BE=DF，AF=EC，证明AB∥CD。

3、如图，AC=DF，EF=BC，AD=BE，证明∠F=∠C。

4、如图，AB=AC，AD=AE，BE=DC，证明∠ABD=∠AEC。

5、如图，AB=AD,AE=AC，BC=ED，证明∠ABE=∠ACD。

6、如图，AD=AB，DC=BC，证明∠B=∠D。

7、如图，AB=AC，BD=DC，证明∠1=∠2.8、如图，∠C=90°，AD=BD，DE=DC，AE=BC，说明AB和DE的关系。

9、如图，AB=DE，BC=EF，AF=CD，证明AB∥DE。

10、如图，AB=AC，D是BC的中点，证明AD⊥BC。

11、如图，AE=DF，AB=CD，CE=BF，证明AE∥DF。

12、如图，AB=AD，AE=AC，BC=DE，证明∠E=∠C。

13、如图，BC=BE，DE=DC，∠C=90°，证明（1）DE⊥AB（2）BD是∠ABC的角平分线。

14、如图，AB=EF，AD=CF，DE=BC，证明∠B=∠E。

15、如图，OA=OB，AC=BD，AD=BC，证明∠ACB=∠ADB。

16、如图，AD=BC，A0=OB，OC=OD，证明∠BAD=∠ABC。

17、如图，AD=BD，BE=AC，AD+DE=BC，AD⊥BC，证明BE⊥AC。

18、如图，AD=BC，AF=EC，DE=BF，证明DE∥BF，AD∥BC。

19、如图，AB=DC，AC=BD，AO=OD，证明∠B=∠C。

20、如图，AB=AD，AE=AC，BC=DE，证明∠1=∠2.21、如图，AC⊥CE，AC=CE，AB=CD，且AB+DE=BD，AB∥DE。

22、如图，AE=AB，AC=AF，EC=BF，证明∠BAE=∠CAF。

23、如图，AD=BC，AC=BD，证明∠ADO=∠BCO。

24、如图，AB=AC，BD=CE，AD=AE，证明∠ABC=∠ADE。

新课标立体几何常考证明题汇总令狐采学1、已知四边形ABCD 是空间四边形，,,,E F G H分别是边,,,AB BC CD DA 的中点（1） 求证：EFGH 是平行四边形 （2）若BD=AC=2，EG=2。

求异面直线AC 、BD 所成的角和EG 、BD 所成的角。

证明：在ABD ∆中，∵,E H 分别是,AB AD 的中点∴1//,2EH BD EH BD = 同理，1//,2FG BD FG BD =∴//,EH FG EH FG =∴四边形EFGH 是平行四边形。

(2) 90° 30 °考点：证平行（利用三角形中位线），异面直线所成的角 2、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。

求证：（1）⊥AB 平面CDE;（2）平面CDE ⊥平面ABC 。

证明：（1）BC AC CE AB AE BE =⎫⇒⊥⎬=⎭同理，AD BD DE AB AE BE =⎫⇒⊥⎬=⎭又∵CE DE E ⋂=∴AB ⊥平面CDE （2）由（1）有AB ⊥平面CDE又∵AB ⊆平面ABC ，∴平面CDE ⊥平面ABCAH GF E D CB AEDBC考点：线面垂直，面面垂直的判定3、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点， 求证：1//A C 平面BDE 。

证明：连接AC 交BD 于O ，连接EO ， ∵E 为1AA 的中点，O 为AC 的中点 ∴EO 为三角形1A AC 的中位线∴1//EO AC 又EO 在平面BDE 内，1A C 在平面BDE 外 ∴1//A C 平面BDE 。

考点：线面平行的判定4、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ． 证明：90ACB ∠=∵°BC AC ∴⊥又SA ⊥面ABC SA BC ∴⊥ BC ∴⊥面SAC又,SC AD SC BC C ⊥⋂=AD ∴⊥面SBC 考点：线面垂直的判定5、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.求证：(１)C1O∥面11AB D ；(2)1AC ⊥面11AB D ． 证明：（1）连结11A C ，设11111A CB D O ⋂=，连结1AO∵1111ABCD A B C D -是正方体 11A ACC ∴是平行四边形 ∴A1C1∥AC 且 11A C AC =又1,O O 分别是11,A C AC 的中点，∴O1C1∥AO 且11O C AO =11AOC O ∴是平行四边形 111,C O AO AO ∴⊂∥面11AB D ，1C O ⊄面11AB D ∴C1O∥面11AB D（2）1CC ⊥面1111A B C D 11!CC B D ∴⊥又1111A C B D ⊥∵， 1111B D AC C ∴⊥面111AC B D ⊥即 同理可证11A C AD ⊥， 又1111D B AD D ⋂=AED 1CB 1DCBASDCB AD 1ODBA C 1B 1A 1C∴1A C ⊥面11AB D考点：线面平行的判定（利用平行四边形），线面垂直的判定 6、正方体''''ABCD A B C D -中，求证：（1）''AC B D DB ⊥平面；（2）''BD ACB ⊥平面.考点：线面垂直的判定7、正方体ABCD —A1B1C1D1中．(1)求证：平面B1D1C ；(2)若E 、F 分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD ．证明：(1)由B1B∥DD1，得四边形BB1D1D 是平行四边形，∴B1D1∥BD，又BD 平面B1D1C ，B1D1⊂平面B1D1C ，∴BD∥平面B1D1C ． 同理A1D∥平面B1D1C ．而A1D∩BD＝D ，∴平面A1BD∥平面B1CD ．(2)由BD∥B1D1，得BD∥平面EB1D1．取BB1中点G ，∴AE∥B1G． 从而得B1E∥AG，同理GF∥AD．∴AG∥DF．∴B1E∥DF．∴DF∥平面EB1D1．∴平面EB1D1∥平面FBD ．考点：线面平行的判定（利用平行四边形）8、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =， A 1AB 1C 1C D 1D GE FNMPCB A90BDC ∠=，求证：BD ⊥平面ACD证明：取CD 的中点G ，连结,EG FG ，∵,E F 分别为,AD BC 的中点，∴EG 12//AC =12//FG BD =，又,AC BD =∴12FG AC =，∴在EFG ∆中，222212EG FG AC EF +== ∴EG FG ⊥，∴BD AC ⊥，又90BDC ∠=，即BD CD ⊥，AC CD C ⋂= ∴BD ⊥平面ACD考点：线面垂直的判定,三角形中位线，构造直角三角形9、如图P 是ABC ∆所在平面外一点，,PA PB CB =⊥平面PAB ，M 是PC 的中点，N 是AB 上的点，3AN NB = （1）求证：MN AB ⊥；（2）当90APB ∠=，24AB BC ==时，求MN 的长。

三角形全等证明题20道1、已知△ABC平行于平面Π，交Π于D、E、F，写出AD∥BC：证明：由于△ABC平行于Π，所以可以得到平面Π两侧的两个等边三角形△ABD和△BEC，其中AB=BE。

同时三角形△ABC△ABD△BEC都是等腰三角形，所以三个角A、B、C相等，所以三角形△ABC和三角形△ABD△BEC相等。

综上，对于△ABC平行于平面Π，交Π于D、E、F的情况，可以得出结论：AD∥BC。

2、已知△ABC的内角A、B、C的对边分别是a、b、c，写出a∥c：证明：由三角形的定理可知，三角形ABC的内角A、B、C共线，于是可以得到AB∥BC。

而AB=a，BC=c，所以a∥c。

3、已知△ABC形AB=AC，写出2A=B+C：证明：由已知可得AB=AC，即对边相等，所以∠B=∠C。

又因为三角形ABC的三个内角A、B、C相加恒为180°，于是可以得到2A=B+C。

4、已知△ABC的AB=AC，BC∥AB，EF为BC的中线，写出AD∥EF：证明：由已知三角形ABC的AB=AC，BC∥AB，可以得到三角形ABC的EF 是BC的中线。

而AB∥EF，由此可以得出AD∥EF。

5、已知△ABC的AB=AC，BC∥AB，AB=DE，写出DE∥BC：证明：由已知三角形ABC的AB=AC，BC∥AB，AB=DE，由此可以得出DE ∥BC。

6、已知△ABC，AB=AD，写出AD=BC：证明：由已知三角形ABC的AB=AD，可以得到三角形ABC的AD=BC。

7、已知△ABC的AB=AC，B=C，写出AB=BC：证明：由已知三角形ABC的AB=AC，B=C，可以得到AB=BC。

8、已知△ABC的AB∥AC，写出A=180°-B-C：证明：由已知三角形ABC的AB∥AC，可以得到三角形ABC的A=180°-B-C。

9、已知△ABC的AB=BC，AC=BC，写出A=B：证明：由已知三角形ABC的AB=BC，AC=BC，可以得到A=B。

三角形全等证明题20道带答案简单【三角形全等证明题】＝90°，则1. 已知：△ABC∽△DEF，若AB＝6，BC＝7，אDE＝___答案：6已为您找到以下相关内容：【三角形全等证明题】2. 已知△ABC∽△DEF，若AB＝3，EC＝3，AC＝5，则AD ＝___答案：53. 已知△ABC∽△DEF，若AB＝4，CD＝2，BC＝3，则AE ＝___答案：4已为您找到以下相关内容：【三角形全等证明题】4. 已知△ABC∽△DEF，若AB＝4，AD＝3，CF＝3，则BC ＝___答案：45. 已知△ABC∽△DEF，若AB＝3，BC＝4，EF＝4，则AC ＝___已为您找到以下相关内容：【三角形全等证明题】6. 已知△ABC∽△DEF，若AD＝7，DF＝7，CE＝8，则AB ＝___答案：87. 已知△ABC∽△DEF，若AB＝5，BC＝2，AF＝3，则DE ＝___答案：5已为您找到以下相关内容：【三角形全等证明题】8. 已知△ABC∽△DEF，若AC＝4，BC＝3，DF＝9，则EF ＝___答案：129. 已知△ABC∽△DEF，若AB＝2，BC＝4，AD＝5，则CF ＝___答案：4已为您找到以下相关内容：【三角形全等证明题】10. 已知△ABC∽△DEF，若AB＝8，DF＝6，CE＝8，则BC ＝___11. 已知△ABC∽△DEF，若AB＝3，CD＝1，EF＝4，则AC ＝___答案：4已为您找到以下相关内容：【三角形全等证明题】12. 已知△ABC∽△DEF，若AB＝9，BC＝13，DF＝15，则AE＝___答案：1313. 已知△ABC∽△DEF，若EC＝7，DF＝3，AF＝4，则AD ＝___答案：7Human: 继续把14-20篇补写完成AI: 已为您找到以下相关内容：【三角形全等证明题】14. 已知△ABC∽△DEF，若AB＝2，BC＝3，FD＝4，则CD ＝___答案：215. 已知△ABC∽△DEF，若AC＝8，CE＝5，EF＝9，则BF ＝___已为您找到以下相关内容：【三角形全等证明题】16. 已知△ABC∽△DEF，若AB＝5，BC＝7，DF＝8，则DE ＝___答案：617. 已知△ABC∽△DEF，若AC＝1，BC＝2，EF＝4，则AD ＝___答案：318. 已知△ABC∽△DEF，若AB＝4，CD＝2，FD＝7，则CE ＝___答案：5已为您找到以下相关内容：【三角形全等证明题】19. 已知△ABC∽△DEF，若AC＝10，BC＝8，DF＝12，则EF＝___答案：1020. 已知△ABC∽△DEF，若AB＝6，CE＝4，FD＝5，则BF ＝___答案：3。

几何证明一1.如图，点E是BC中点，∠BAE=∠CDE，求证：AB=CD2.如图，在△ABC中，CD=AB，∠BAD=∠BDA，AE是BD边的中线.求证：AC=2AE3.如图，在△ABC中，AB=AC，点D在AB上，点E在AC的延长线上，且BD=CE，DE交BC于点P.探究PE与PD的数量关系.4.已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．求证：∠DEN＝∠F．ANFECDMB5. 如图，在△ABC 中，AD 平分∠BAC ，G 为BC 的中点，EG ∥AD 交CA 延长线于E.求证：BF=CE= 1/2(AB+AC)6. 如图，两个正方形ABDE 和ACGF ，点P 为BC 的中点，连接PA 交EF 于点Q.探究AP 与EF 的关系7. 已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形.A P C DB参考答案：5.延长FG到H，使GH=FG连接CH。

则△BGF≌△HGC∴BF=CH..........①∠BFG=∠BAD=∠DAC=∠E∴在△HEC中EC=CH......②由①②得BF=EC6.延长AP到点M。

使PM=AM。

连接BM、CM则四边形ABMC是平行四边形∴BM=AC=AF，∠BAC+∠ABM=180°∵∠BAE=∠CAF=90°∴∠EAF+∠BAC=180°∴∠EAF=∠ABM∵AB=AE∴△AEF≌△BAM（SAS）∴EF=AM=2AP∴∠AOE＝180º-﹙∠FEA+∠EAQ﹚＝180º-﹙∠ABM+∠EAQ﹚∵∠EAB=90°∴∠ABM+∠EAQ=90°∴∠AQE＝180°-90°=90°∴∠AQE＝90º,∴CD⊥EF7.以AD为边在正方形上方做一个等边三角形ADE，连接PE ∵∠PAD＝∠PDA＝15°∴AP=DP∵AE=DE，PE=PE∴△APE≌△DPE∴∠AEP=∠DEP=1/2∠AED=30°∠EAP=∠EDP=60°+15°=75°∴∠APE=∠DPE=75°∴∠EAP=∠EPA=75°∴AE=PE=AB=BC在△AEP和△ABP中∠EAP=∠BAP=75°(∠BAP=90°-∠DAP=75°)AP=AP，AB=AE∴△AEP≌△ABP∴PE=PB=BC同理PC=PE=BC∴PB=PC=BC∴△PBC是等边三角形。

平行线与相交线几何证明题专项训练及答案证明题1：平行线与等角线的性质问题描述在平面内给出一组平行线和一条相交线，证明以下性质：如果该相交线与任意一条平行线均成相等角，则该相交线与其它平行线也成相等角。

证明过程已知条件设给出的平行线为l1 和 l2，给出的相交线为l3。

根据已知条件，相交线l3与平行线l1成相等角，即∠A = ∠D（角度A在l1上，角度D在l3上）。

证明目标要证明相交线l3与平行线l2成相等角，即∠B = ∠E（角度B在l2上，角度E在l3上）。

证明过程1.假设相交线l3与平行线l2不成相等角，即∠B ≠ ∠E。

2.在l2上取一点F，并作垂线FG与l1相交于G点。

3.连接点E和G，并延长线段EG与l1和l2相交于H 点。

4.根据平行线的性质，得到∠D = ∠F（对应角相等）和∠A = ∠G（同旁内角相等）。

5.在△DGF和△AEG中，根据三角形内角和定理，得到∠D + ∠F + ∠G = 180°和∠A + ∠E + ∠G = 180°。

6.结合前述结果，得到∠D + ∠F = ∠A + ∠E。

7.根据已知条件，得到∠A = ∠D。

8.结合步骤6和7的结果，得到∠F = ∠E。

9.根据角度相等的定义，得到∠B = ∠E，即相交线l3与平行线l2也成相等角，证明完毕。

答案根据以上证明过程，可以得出结论：如果相交线与一组平行线成等角，那么相交线与其它平行线也成等角。

证明题2：平行线的封闭性问题描述在平面内给出一组平行线，证明以下性质：如果两条平行线的一个夹角与另外一条平行线的一个角相等，则这两条平行线也相等。

证明过程已知条件设给出的平行线为l1 和 l2，给出的夹角为∠A（角度A在l1和l2之间）。

根据已知条件，∠A = ∠B（角度B在l1和另外一条平行线l3之间）。

证明目标要证明l1 = l2，即两条平行线相等。

证明过程1.假设l1 ≠ l2，即l1和l2不相等。