北师大版八年级数学(上)第六单元测试卷

北师大版八年级（上）第二单元达标测试卷(二)数 学（考试时间：100分钟 满分：120分）学校： 班级： 考号： 得分：一、选择题（本大题共12小题，每小题3分，共36分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．在下列实数中，属于无理数的是（ ）A ．53B C ．3.14D22π，0．其中无理数出现的频率为（ ） A ．0.2B ．0.4C ．0.6D ．0.83．若Rt ABC 的两边长a ，b 满足()240a -=，则第三边的长是（ ）A ．5B C ．5或7D ．54．若27a ab m +=+，29b ab m +=-．则a b +的值为（ ） A ．4±B ．4C ．2±D ．252b +4＝4b ，则20152016•a b 的值是（ ） A ．12B ．12-C ．2D ．﹣26．下列等式正确的是（ ）A 3=-B 712± C 4= D ．32=- 7．下列说法中正确的是（ ）A ．81的平方根是9B 4CD ．64的立方根是4±8 ） A ．4和5之间B ．5和6之间C ．6和7之间D ．7和8之间91最接近的是（ ）A ．0.4B ．0.6C ．0.8D ．110．若用我们数学课本上采用的科学计算器进行计算，其按键顺序如图，则输出结果应为（ ）A ．8B ．4C ．12D ．1411．估计)301182） A ．0和1 B ．1和2C ．2和3D ．3和4123236x y z +++=x 、y 、z 为有理数．则xyz ＝（ ）A ．34B ．56 C ．712D ．1318二、填空题（本大题共6小题，每小题3分，共18分）1311163-⎛⎫-= ⎪⎝⎭__________． 14．一个正数a 的两个平方根是21b -和4b +，则a b +的立方根为_______． 155x +x 53x a没有实数根，那么a 的取值范围是__．16．已知a 、b 是相邻的两个正整数，且a ＜11﹣1＜b ，则a +b 的值是_____． 17．已知：1502222a b c -==ab ＋c ＝________． 18．若实数,x y 满足22425x y x y +-=-x yx y+-_________ 三、解答题（本大题共6小题，共66分，解答应写出文字说明、演算步骤或推理过程） 19．把下列各数分别填入相应的集合里．3.14、0.121121112…、2113⎛⎫- ⎪⎝⎭、|6|-、-2011、22-、13π、20% 无理数集合：{}… 负整数集合：{}… 分数集合： {}…正数集合： {}…20．我们规定：a ≥b 时，a ★b =a -b ；当a < b 时，a ★b =a 2-b 2． （1）求5★3的值；（2）若m > 0，化简（m +3）★（2m +3）； （3）若x ★3=7，求x 的值； 21．计算：（1）217110.5395⎛⎫-÷⨯- ⎪⎝⎭（2）()()22231532732-+---⨯+-22．对于一个实数m （m 为非负实数），规定其整数部分为a ，小数部分为b ，例如：当3m =时，则3a =，0b =；当 4.5m =时，则4a =，0.5b =．（1）当m π=时，b = ；当11=m 时，a = ； （2）若5a =，630=-b ，则m = ； （3）当97=+m 时，求-a b 的值．23．实数a ，b ，c ，d ，e 在数轴上的位置如图所示．a 是最小的自然数，b 是最大的负整数，c 和d 是互为相反数，e 表示的数是7．（1）用“＞”或“＜”填空：b 0，c e ，b +c 0； （2）求代数式：|b ﹣e |+|d +c |×2019+2020a的值． 24．已知线段a ，b ，c ，且线段a ，b 满足|a 48＋（b 322＝0 （1）求a ，b 的值；（2）若a ，b ，c 是某直角三角形的三条边的长度，求c 的值．参考答案三、选择题（本大题共12小题，每小题3分，共36分。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、如图，在边长为1的正方形ABCD中，将射线AC绕点A按顺时针方向旋转度（< ≤）得到射线AE，点M是点D关于射线AE的对称点，则线段CM长度的最小值为（）A. B.0.5 C.1 D.2、勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的，已知∠BAC=90°，AB=6，AC=8，点D、E、F、G、H、I都在矩形KLMJ的边上，则矩形KLMJ的周长为（）A.40B.44C.84D.883、“用长分别为5cm、12cm、13cm的三条线段可以围成直角三角形”这一事件是( )A.必然事件B.不可能事件C.随机事件D.以上都不是4、菱形的两条对角线的分别为60cm和80cm，那么边长是（）A.100cmB.80cmC.60cmD.50cm5、三角形三边长分别是3，4，5，则它的最短边上的高为（）A.3B.2.4C.4D.4.86、一根竹子高9尺，折断后竹子顶端落在离竹子底端3尺处，折断处离地面高度是（）A.3尺B.4尺C.5尺D.6尺7、如图，正方形ABCD的对角线交于点O ，以AD为边向外作Rt△ADE ，∠AED＝90°，连接OE ， DE＝6，OE＝，则另一直角边AE的长为（）.A. B.2 C.8 D.108、如图①所示，有一个由传感器A控制的灯，要装在门上方离地高4.5m的墙上，任何东西只要移至该灯5m及5m以内时，灯就会自动发光．请问一个身高1.5m的学生要走到离墙多远的地方灯刚好发光？（）A.4米B.3米C.5米D.7米9、如图，由四个全等的直角三角形和一个小正方形拼成一个大正方形.设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）2=21，大正方形的面积为13.则小正方形的面积为（）A.3B.4C.5D.610、如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD=12，BE=2，则⊙O的半径为（）A.8B.10C.16D.2011、下列命题不成立的是A.三个角的度数之比为1:3:4的三角形是直角三角形B.三个角的度数比为1：：2的三角形是直角三角形C.三边长度比为1：：的三角形是直角三角形D.三边长度之比为：：2的三角形是直角三角形12、三角形的三边为a、b、c，由下列条件不能判断它是直角三角形的是（）A.a:b:c =13∶5∶12B.a 2-b 2=c 2C.a 2=(b+c)(b-c) D.a:b:c=8∶16∶1713、如图，已知Rt△ABC中，∠C＝90°，BC=3, AC=4，则sinA的值为（）．.A. B. C. D.14、如图，∠ACB=90°，CD是斜边上的高，AC=3，BC=4，则CD的长为（）A.1.6B.2.4C.2D.2.115、下列长度的三条线段能组成直角三角形的是( )A.2，3，4B.4，6，8C.6，8，10D.5，11，12二、填空题(共10题，共计30分)16、将等腰直角△ABC按如图方法放置在数轴上，点A和C分别对应的数是﹣2和1．以点A为圆心，AB长为半径画弧，交数轴的正半轴于点D，则点D对应的实数为________．17、一根高9m的旗杆在离地4m高处折断，折断处仍相连，此时在3.9m远处耍的身高为1m的小明________危险.（填有或无）18、如图，正方形ABCD的顶点C，A分别在x轴，y轴上，BC是菱形BDCE的对角线．若BC=6，BD=5，则点D的坐标是________．19、我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的三角形，如图所示，已知，则的长度是________.20、菱形的面积为24，其中的一条对角线长为6，则此菱形的周长为________.21、已知菱形的周长为，两条对角线的和为6，则菱形的面积为________22、如图所示的一块地，已知AD=4米，CD=3米，∠ADC=90°，AB=13米，BC=12米，这块地的面积为________m223、已知a、b、c是△ABC三边的长，且满足关系式，则△ABC的形状为________24、如图，在高3米，坡面线段AB长为5米的楼梯表面铺地毯，已知楼梯宽1.5米，地毯售价为40元/平方米，若将楼梯表面铺满地毯，则至少需________元．25、如图，已知以点A(0，1)、C(1，0)为顶点的△ABC中，∠BAC=60°，∠ACB=90°，在坐标系内有一动点P（不与A重合），以P、B、C为顶点的三角形和△ABC全等，则P点坐标为________.三、解答题(共5题，共计25分)26、在 Rt△ABC 中，∠C＝90°，∠A、∠B、∠C 的对边分别为a、b、c．若a∶c＝15∶17，b＝24，求a.27、有一块直角三角形的绿地，量得两直角边长分别为6m和8m，现在要将绿地扩充成等腰三角形，且扩充部分是以8m为直角边的直角三角形，求扩充后等腰三角形绿地的周长.28、小锤和豆花要测量校园里的一块四边形场地ABCD(如图所示)的周长，其中边BC上有水池及建筑遮挡，没有办法直接测量其长度。

第二章实数测试题一、选择题(每题3分，共30分)1．有一组数如下：－π，13，|－2|，4，7，39，0.808008…(相邻两个8之间0的个数逐次加1)．其中无理数有( )A ．4个B ．5个C ．6个D ．7个2．下列说法中，正确说法的个数是( ) ①－64的立方根是－4； ②49的算术平方根是±7； ③127的立方根是13； ④116的平方根是14. A ．1 B ．2 C ．3 D ．43．下列各组数中，互为相反数的一组是( )A ．－3与3－27 B ．－3与（－3）2 C ．－3与－13D .||－3与34．下列各式计算正确的是( )A .2＋3＝ 5B ．43－33＝1C ．23×33＝6 3D .27÷3＝35．下列各式中，无论x 为任何数都没有意义的是( )A .－7xB .－1999x3C .－0.1x2－1D .3－6x2－56．若a ＝15，则实数a 在数轴上的对应点P 的大致位置是( )图17．如图2是一数值转换机，若输出的结果为－32，则输入的x的值为( )图2A．－4B．4C．±4D．±58．若a，b均为正整数，且a>7，b>320，则a＋b的最小值是( )A．6 B．5 C．4 D．39．实数a，b在数轴上所对应的点的位置如图3所示，且||a>||b，则化简a2－||a＋b 的结果为( )图3A．2a＋b B．－2a＋bC．b D．2a－b10．已知x＝2－3，则代数式(7＋4 3)x2＋(2＋3)x＋3的值是( )A．2＋ 3 B．2－ 3 C．0 D．7＋4 3请将选择题答案填入下表：第Ⅱ卷 (非选择题 共70分)二、填空题(每题3分，共18分) 11．计算：252－242＝________．图412．如图4，正方形ODBC 中，OC ＝1，OA ＝OB ，则数轴上点A 表示的数是________． 13．用计算器计算并比较大小：39________7.(填“＞”“＝”或“＜”) 14．若|x －y|＋y －2＝0，则xy －3的值是________．15．若规定一种运算为a ★b ＝2(b －a)，如3★5＝2×(5－3)＝22，则2★3＝________．16．设a ，b 为非零实数，则a |a|＋b2b所有可能的值为________． 三、解答题(共52分)17．(6分)实数a ，b 在数轴上所对应的点的位置如图5所示，试化简：a2－b2－（a －b ）2.图518．(6分)计算：(1)()－62－25＋（－3）2；(2)50×8－6×32；(3)(3＋2－1)(3－2＋1)．19．(6分)已知a ，b 互为相反数，c ，d 互为倒数，x 是2的平方根，求5（a ＋b ）a2＋b2－2cd＋x 的值．20.(6分)如果a 是100的算术平方根，b 是125的立方根，求a2＋4b ＋1的平方根．21．(6分)某中学要在操场的一块长方形土地上进行绿化，已知这块长方形土地的长为510 m ，宽为415 m .(1)求该长方形土地的面积(精确到0.1 m 2)；(2)如果绿化该长方形土地每平方米的造价为180元，那么绿化该长方形土地所需资金约为多少元？22．(6分)如图6所示，某地有一地下工程，其底面是正方形，面积为405 m2，四个角是面积为5 m2的小正方形渗水坑，根据这些条件如何求a的值？与你的同伴进行交流．图6下面是小康提供的解题方案，根据解题方案请你完成本题的解答过程：①设大正方形的边长为x m，小正方形的边长为y m，那么根据题意可列出关于x的方程为__________，关于y的方程为__________；②利用平方根的意义，可求得x＝________(取正值，结果保留根号)，y＝________(取正值，结果保留根号)；③所以a＝x－2y＝____________＝__________(结果保留根号)；④答：________________________．23．(8分)如图7，在Rt△OA1A2中，∠A1＝90°，OA1＝A1A2＝1，以OA2为直角边向外作直角三角形，…，使A1A2＝A2A3＝A3A4＝…＝A n－1A n＝1.(1)计算OA2和OA3的长；(2)猜想OA75的长(结果化到最简)；(3)请你用类似的思路和方法在数轴上画出表示－3和10的点．图724．(8分)先阅读材料，再回答问题：因为(2－1)(2＋1)＝1，所以12＋1＝2－1；因为(3－2)(3＋2)＝1，所以13＋2＝3－2；因为(4－3)(4＋3)＝1，所以14＋3＝4－ 3.依次类推，你会发现什么规律？请用你发现的规律计算式子12＋1＋13＋2＋…＋1100＋99的值．答案1．A 2.B 3.B 4.D 5．C 6．B 7.C 8.A 9.C 10．A 11．7 12．－213．＜ 14.1215.6－2 16．±2，017．解：由数轴易知a ＜0，b ＞0，|a |＜|b |， 所以原式＝－a －b －(b －a )＝－2b . 18．解：(1)原式＝6－5＋3＝4.(2)原式＝5 2×2 2－3 22＝20－3＝17. (3)(3＋2－1)(3－2＋1)＝[]3＋（2－1）[]3－（2－1） ＝3－(2－1)2＝3－3＋2 2 ＝2 2.19．解：由题意知a ＋b ＝0，cd ＝1，x ＝±2. 当x ＝2时，原式＝－2＋2＝0； 当x ＝－2时，原式＝－2－2＝－2 2， 故原式的值为0或－2 2.20．[解析] 先根据算术平方根、立方根的定义求得a ，b 的值，再代入所求代数式即可计算．解：因为a 是100的算术平方根，b 是125的立方根， 所以a ＝10，b ＝5，所以a2＋4b＋1＝121，所以a2＋4b＋11＝11，所以a2＋4b＋11的平方根为±11.21．[解析] (1)根据这块长方形土地的长为5 10 m，宽为415 m，直接得出面积即可；(2)利用绿化该长方形土地每平方米的造价为180元，即可求出绿化该长方形土地所需资金．解：(1)该长方形土地的面积为510×415＝100 6≈244.9(m2)．(2)因为绿化该长方形土地每平方米的造价为180元，所以180×244.9＝44082(元)．答：绿化该长方形土地所需资金约为44082元．22．解：①x2＝405 y2＝5②9 55③9 5－2 57 5④a的值为7 523．解：(1)OA2＝12＋12＝2，OA3＝()22＋12＝3.(2)OA75＝75＝5 3.(3)如图所示：24．解：规律：当n是正整数时，1n＋1＋n＝n＋1－n，故12＋1＋13＋2＋…＋1100＋99＝(2－1)＋(3－2)＋…＋(100－99)＝100－1＝9.。

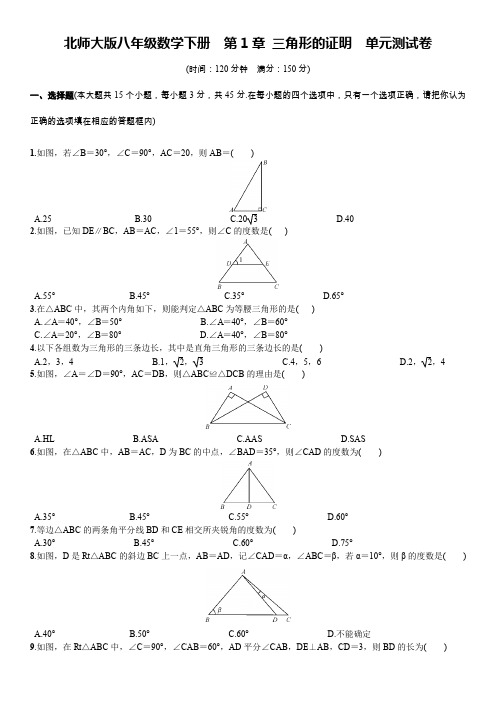
北师大版八年级数学下册第1章三角形的证明单元测试卷(时间：120分钟满分：150分)一、选择题(本大题共15个小题，每小题3分，共45分.在每小题的四个选项中，只有一个选项正确，请把你认为正确的选项填在相应的答题框内)1.如图，若∠B＝30°，∠C＝90°，AC＝20，则AB＝( )A.25B.30C.20 3D.402.如图，已知DE∥BC，AB＝AC，∠1＝55°，则∠C的度数是( )A.55°B.45°C.35°D.65°3.在△ABC中，其两个内角如下，则能判定△ABC为等腰三角形的是( )A.∠A＝40°，∠B＝50°B.∠A＝40°，∠B＝60°C.∠A＝20°，∠B＝80°D.∠A＝40°，∠B＝80°4.以下各组数为三角形的三条边长，其中是直角三角形的三条边长的是( )A.2，3，4B.1，2， 3C.4，5，6D.2，2，45.如图，∠A＝∠D＝90°，AC＝DB，则△ABC≌△DCB的理由是( )A.HLB.ASAC.AASD.SAS6.如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝35°，则∠CAD的度数为( )A.35°B.45°C.55°D.60°7.等边△ABC的两条角平分线BD和CE相交所夹锐角的度数为( )A.30°B.45°C.60°D.75°8.如图，D是Rt△ABC的斜边BC上一点，AB＝AD，记∠CAD＝α，∠ABC＝β，若α＝10°，则β的度数是( )A.40°B.50°C.60°D.不能确定9.如图，在Rt△ABC中，∠C＝90°，∠CAB＝60°，AD平分∠CAB，DE⊥AB，CD＝3，则BD的长为( )A.1.5B.3C.6D.910.用反证法证明“直角三角形中的两个锐角不能都大于45°”，第一步应假设这个直角三角形中( )A.每一个锐角都小于45°B.有一个锐角大于45°C.有一个锐角小于45°D.每一个锐角都大于45°11.如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，那么下列各条件中，不能使Rt△ABC≌Rt△A′B′C′的是( )A.AB＝A′B′＝5，BC＝B′C′＝3B.AB＝B′C′＝5，∠A＝∠B′＝40°C.AC＝A′C′＝5，BC＝B′C′＝3D.AC＝A′C′＝5，∠A＝∠A′＝40°12.观察下列命题的逆命题：①有两边相等的三角形是等腰三角形；②到角的两边的距离相等的点在这个角的平分线上；③直角三角形的两个锐角互余；④全等三角形的面积相等.其中逆命题为假命题的个数是( )A.1B.2C.3D.413.如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E.如果∠BAC＝60°，∠ACE＝24°，那么∠BCE 的大小是( )A.24°B.30°C.32°D.36°14.如图，直角三角形纸片的两直角边长分别为6，8，按如图那样折叠，使点A与点B重合，折痕为DE，则S△BCE∶S△BDE ＝( )A.2∶5B.14∶25C.16∶25D.4∶2115.如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论错误的是( )A.△BPQ是等边三角形B.△PCQ是直角三角形C.∠APB＝150°D.∠APC＝135°二、填空题(本大题共5个小题，每小题5分，共25分)16.在直角三角形中，其中一个锐角是22°，则另外一个锐角是.17.如图，某失联客机从A地起飞，飞行1 000 km到达B地，再折返飞行1 000 km到达C地后在雷达上消失，已知∠ABC＝60°，则失联客机消失时离起飞地A地的距离为km.18.如图，O为数轴原点，A，B两点分别对应－3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为.19.如图，已知△ABC的周长是22，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝3，△ABC的面积是.20.如图，在等腰△ABC中，AB＝AC，∠BAC＝54°，∠BAC的平分线与AB的垂直平分线交于点O，点C沿EF 折叠后与点O重合，则∠OEC的度数是.三、解答题(本大题共7个小题，各题分值见题号后，共80分)21.(本题8分)一个机器零件的形状如图所示，在Rt△ABC中，∠BAC＝30°，BC＝2.5 cm，BD＝13 cm，AD＝12 cm，求△ABD的面积.22.(本题8分)在加快城镇建设中，有两条公路OA和OB交会于O点，在∠AOB的内部有蔬菜基地C和D，现要修建一个蔬菜转运站P，使转运站P到两条公路OA，OB的距离相等，且到两个蔬菜基地C，D的距离也相等，用尺规作出蔬菜转运站P的位置.(要求：不写作法，保留作图痕迹.)23.(本题10分)如图，点P为△ABC的BC边上一点，且PC＝2PB，∠ABC＝45°，∠APC＝60°，CD⊥AP，连接BD，求∠ABD的度数.24.(本题12分)如图，∠AOB＝60°，OC平分∠AOB，C为角平分线上一点，过点C作CD⊥OC，垂足为C，交OB于点D，CE∥OA交OB于点E.(1)判断△CED的形状，并说明理由；(2)若OC＝3，求CD的长.25.(本题12分)如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线于点P，PD⊥AB于D，PE⊥AC于E.(1)求证：BD＝CE；(2)若AB＝6 cm，AC＝10 cm，求AD的长.26.(本题14分)如图，在△ABC中，MP，NO分别垂直平分AB，AC.(1)若BC＝10 cm，试求出△PAO的周长；(2)若AB＝AC，∠BAC＝110°，试求∠PAO的度数；(3)在(2)中，若无AB＝AC的条件，你能求出∠PAO的度数吗？若能，请求出来；若不能，请说明理由.27.(本题16分)如图，△ABC中，AB＝BC＝AC＝12 cm，现有两点M，N分别从点A，B同时出发，沿三角形的边运动，已知点M的速度为1 cm/s，点N的速度为2 cm/s.当点N第一次到达点B时，M，N同时停止运动.(1)点M，N运动几秒后，M，N两点重合？(2)点M，N运动几秒后，可得到等边三角形△AMN?(3)当点M，N在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时M，N运动的时间.参考答案一、选择题(本大题共15个小题，每小题3分，共45分.在每小题的四个选项中，只有一个选项正确，请把你认为正确的选项填在相应的答题框内)1.如图，若∠B＝30°，∠C＝90°，AC＝20，则AB＝(D)A.25B.30C.20 3D.402.如图，已知DE∥BC，AB＝AC，∠1＝55°，则∠C的度数是(A)A.55°B.45°C.35°D.65°3.在△ABC中，其两个内角如下，则能判定△ABC为等腰三角形的是(C)A.∠A＝40°，∠B＝50°B.∠A＝40°，∠B＝60°C.∠A＝20°，∠B＝80°D.∠A＝40°，∠B＝80°4.以下各组数为三角形的三条边长，其中是直角三角形的三条边长的是(B)A.2，3，4B.1，2， 3C.4，5，6D.2，2，45.如图，∠A＝∠D＝90°，AC＝DB，则△ABC≌△DCB的理由是(A)A.HLB.ASAC.AASD.SAS6.如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝35°，则∠CAD的度数为(A)A.35°B.45°C.55°D.60°7.等边△ABC的两条角平分线BD和CE相交所夹锐角的度数为(C)A.30°B.45°C.60°D.75°8.如图，D是Rt△ABC的斜边BC上一点，AB＝AD，记∠CAD＝α，∠ABC＝β，若α＝10°，则β的度数是(B)A.40°B.50°C.60°D.不能确定9.如图，在Rt△ABC中，∠C＝90°，∠CAB＝60°，AD平分∠CAB，DE⊥AB，CD＝3，则BD的长为(C)A.1.5B.3C.6D.910.用反证法证明“直角三角形中的两个锐角不能都大于45°”，第一步应假设这个直角三角形中(D)A.每一个锐角都小于45°B.有一个锐角大于45°C.有一个锐角小于45°D.每一个锐角都大于45°11.如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，那么下列各条件中，不能使Rt△ABC≌Rt△A′B′C′的是(B)A.AB＝A′B′＝5，BC＝B′C′＝3B.AB＝B′C′＝5，∠A＝∠B′＝40°C.AC＝A′C′＝5，BC＝B′C′＝3D.AC＝A′C′＝5，∠A＝∠A′＝40°12.观察下列命题的逆命题：①有两边相等的三角形是等腰三角形；②到角的两边的距离相等的点在这个角的平分线上；③直角三角形的两个锐角互余；④全等三角形的面积相等.其中逆命题为假命题的个数是(A)A.1B.2C.3D.413.如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E.如果∠BAC＝60°，∠ACE＝24°，那么∠BCE 的大小是(C)A.24°B.30°C.32°D.36°14.如图，直角三角形纸片的两直角边长分别为6，8，按如图那样折叠，使点A与点B重合，折痕为DE，则S△BCE∶S△BDE ＝(B)A.2∶5B.14∶25C.16∶25D.4∶2115.如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论错误的是(D)A.△BPQ是等边三角形B.△PCQ是直角三角形C.∠APB＝150°D.∠APC＝135°二、填空题(本大题共5个小题，每小题5分，共25分)16.在直角三角形中，其中一个锐角是22°，则另外一个锐角是68__°.17.如图，某失联客机从A地起飞，飞行1 000 km到达B地，再折返飞行1 000 km到达C地后在雷达上消失，已知∠ABC＝60°，则失联客机消失时离起飞地A地的距离为1__000km.18.如图，O 为数轴原点，A ，B 两点分别对应－3，3，作腰长为4的等腰△ABC ，连接OC ，以O 为圆心，CO 长为半径画弧交数轴于点M ，则点M19.如图，已知△ABC 的周长是22，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于点D ，且OD ＝3，△ABC 的面积是33.20.如图，在等腰△ABC 中，AB ＝AC ，∠BAC ＝54°，∠BAC 的平分线与AB 的垂直平分线交于点O ，点C 沿EF 折叠后与点O 重合，则∠OEC 的度数是108__°.三、解答题(本大题共7个小题，各题分值见题号后，共80分)21.(本题8分)一个机器零件的形状如图所示，在Rt △ABC 中，∠BAC ＝30°，BC ＝2.5 cm ，BD ＝13 cm ，AD ＝12 cm ，求△ABD 的面积.解：∵Rt △ABC 中，∠BAC ＝30°，BC ＝2.5 cm ， ∴AB ＝2BC ＝5 cm.∵52＋122＝132，即AB 2＋AD 2＝BD 2， ∴△ABD 是直角三角形.∴S △ABD ＝12AB·AD ＝12×5×12＝30(cm 2).22.(本题8分)在加快城镇建设中，有两条公路OA 和OB 交会于O 点，在图中∠AOB 的内部有蔬菜基地C 和D ，现要修建一个蔬菜转运站P ，使转运站P 到两条公路OA ，OB 的距离相等，且到两个蔬菜基地C ，D 的距离也相等，用尺规作出蔬菜转运站P 的位置.(要求：不写作法，保留作图痕迹.)解：如图所示.23.(本题10分)如图，点P 为△ABC 的BC 边上一点，且PC ＝2PB ，∠ABC ＝45°，∠APC ＝60°，CD ⊥AP ，连接BD ，求∠ABD 的度数.解：∵∠APC ＝60 °，CD ⊥AP ， ∴∠PCD ＝90 °－∠APC ＝90 °－60 °＝30 °. ∴PC ＝2PD.∵PC ＝2PB ，∴PB ＝PD. ∴∠PBD ＝∠PDB.又∵∠APC ＝∠PBD ＋∠PDB ，∴∠PBD ＝12∠APC ＝12×60 °＝30 °.∵∠ABC ＝45 °，∴∠ABD ＝∠ABC －∠PBD ＝45 °－30 °＝15 °.24.(本题12分)如图，∠AOB ＝60°，OC 平分∠AOB ，C 为角平分线上一点，过点C 作CD ⊥OC ，垂足为C ，交OB 于点D ，CE ∥OA 交OB 于点E.(1)判断△CED 的形状，并说明理由； (2)若OC ＝3，求CD 的长.解：(1)△CED 是等边三角形.理由如下： ∵OC 平分∠AOB ，∠AOB ＝60 °，∴∠AOC ＝∠COE ＝30 °. ∵CE ∥OA ，∴∠AOC ＝∠COE ＝∠OCE ＝30 °，∠CED ＝60 °. ∵CD ⊥OC ，∴∠OCD ＝90 °. ∴∠EDC ＝60 °.∴△CED 是等边三角形.(2)∵△CED 是等边三角形，∴CD ＝CE ＝ED. 又∵∠COE ＝∠OCE ，∴OE ＝EC. ∴CD ＝ED ＝OE.设CD ＝x ，则OD ＝2x.在Rt △OCD 中，根据勾股定理得：x 2＋9＝4x 2，解得x ＝ 3. 则CD ＝ 3.25.(本题12分)如图，△ABC 的外角∠DAC 的平分线交BC 边的垂直平分线于点P ，PD ⊥AB 于D ，PE ⊥AC 于E. (1)求证：BD ＝CE ；(2)若AB ＝6 cm ，AC ＝10 cm ，求AD 的长.解：(1)证明：连接BP ，CP.∵点P 在BC 的垂直平分线上，∴BP ＝CP. ∵AP 是∠DAC 的平分线，∴DP ＝EP ，在Rt △BDP 和Rt △CEP 中，⎩⎪⎨⎪⎧BP ＝CP ，DP ＝EP ，∴Rt △BDP ≌Rt △CEP (HL )，∴BD ＝CE.(2)在Rt △ADP 和Rt △AEP 中，⎩⎪⎨⎪⎧AP ＝AP ，DP ＝EP ，∴Rt △ADP ≌Rt △AEP (HL )，∴AD ＝AE.∵AB ＝6 cm ，AC ＝10 cm ，∴6＋AD ＝10－AE ， 即6＋AD ＝10－AD.解得AD ＝2 cm.26.(本题14分)如图，在△ABC 中，MP ，NO 分别垂直平分AB ，AC.(1)若BC ＝10 cm ，试求出△PAO 的周长； (2)若AB ＝AC ，∠BAC ＝110°，试求∠PAO 的度数；(3)在(2)中，若无AB ＝AC 的条件，你能求出∠PAO 的度数吗？若能，请求出来；若不能，请说明理由.解：(1)∵MP ，NO 分别垂直平分AB ，AC ， ∴AP ＝BP ，AO ＝CO.∴△PAO 的周长为AP ＋PO ＋AO ＝BO ＋PO ＋OC ＝BC. ∵BC ＝10 cm ，∴△PAO 的周长为10 cm.(2)∵AB ＝AC ，∠BAC ＝110 °，∴∠B ＝∠C ＝12×(180 °－110 °)＝35 °.由(1)知AP ＝BP ，AO ＝CO. ∴∠BAP ＝∠B ＝35 °，∠CAO ＝∠C ＝35 °. ∴∠PAO ＝∠BAC －∠BAP －∠CAO ＝110 °－35 °－35 °＝40 °. (3)能.理由如下： ∵∠BAC ＝110 °，∴∠B ＋∠C ＝180 °－110 °＝70 °.由(1)知AP ＝BP ，AO ＝CO.∴∠BAP ＝∠B ，∠CAO ＝∠C.∴∠PAO ＝∠BAC －∠BAP －∠CAO ＝∠BAC －(∠B ＋∠C )＝110 °－70 °＝40 °.27.(本题16分)如图，△ABC 中，AB ＝BC ＝AC ＝12 cm ，现有两点M ，N 分别从点A ，B 同时出发，沿三角形的边运动，已知点M 的速度为1 cm /s ，点N 的速度为2 cm /s .当点N 第一次到达点B 时，M ，N 同时停止运动.(1)点M ，N 运动几秒后，M ，N 两点重合？(2)点M ，N 运动几秒后，可得到等边三角形△AMN?(3)当点M ，N 在BC 边上运动时，能否得到以MN 为底边的等腰三角形AMN ？如存在，请求出此时M ，N 运动的时间.解：(1)设点M ，N 运动x 秒后，M ，N 两点重合，x ×1＋12＝2x ，解得x ＝12.(2)设点M ，N 运动t 秒后，可得到等边三角形△AMN ，如图1，AM ＝t ×1＝t ，AN ＝AB －BN ＝12－2t.∵三角形△AMN 是等边三角形，∴t ＝12－2t ，解得t ＝4.∴点M ，N 运动4秒后，可得到等边三角形△AMN.(3)当点M ，N 在BC 边上运动时，可以得到以MN 为底边的等腰三角形.由(1)知，12秒时M ，N 两点重合，恰好在C 处.如图2，假设△AMN 是以MN 为底边的等腰三角形，∴AN ＝AM.∴∠AMN ＝∠ANM.∴∠AMC ＝∠ANB.∵AB ＝BC ＝AC ，∴△ACB 是等边三角形.∴∠C ＝∠B.在△ACM 和△ABN 中，⎩⎪⎨⎪⎧∠C ＝∠B ，∠AMC ＝∠ANB ，AC ＝AB ， ∴△ACM ≌△ABN (AAS ).∴CM ＝BN.设当点M ，N 在BC 边上运动时，M ，N 运动的时间y 秒时，△AMN 是等腰三角形.∴CM ＝y －12，NB ＝36－2y ，由CM ＝NB ，得y －12＝36－2y ，解得y ＝16.故假设成立.∴当点M ，N 在BC 边上运动时，能得到以MN 为底边的等腰三角形AMN ，此时M ，N 运动的时间为16秒.。

北师大版八年级上册数学第四章《一次函数》单元测试卷（含答案）一、选择题(每题3分，共30分)1．下列两个变量之间不存在函数关系的是( )A．圆的面积S和半径r B．某地一天的气温T与时间t C．某班学生的身高y与学生的学号x D．一个正数的平方根与这个数2．一个正比例函数的图象经过点(－2，－4)，则它的表达式为( )A．y＝－2x B．y＝2x C．y＝－12x D．y＝12x3．【教材P88习题T4改编】正比例函数y＝x的图象向上平移2个单位长度，所得函数为( )A．y＝x＋2 B．y＝x－2 C．y＝2x D．y＝x 24．一次函数y＝mx＋n的图象如图所示，则关于x的方程mx＋n＝0的解为( ) A．x＝3B．x＝－3C．x＝4D．x＝－45．已知点P(a，－3)在一次函数y＝2x＋9的图象上，则a的值为( ) A．－3 B．－6 C．15 D．36．关于函数y＝－x2－1，下列说法错误的是( )A．当x＝2时，y＝－2B．y随x的增大而减小C．若(x1，y1)，(x2，y2)为该函数图象上两点，x1>x2，则y1＞y2D．图象经过第二、三、四象限7．【教材P98复习题T3变式】弹簧挂上物体后会伸长，测得一弹簧的长度y(cm)与所挂物体质量x(kg)间有如下关系(其中x≤12)．下列说法不正确的是( )A．x与y都是变量，且x是自变量B．弹簧不挂物体时的长度为10 cmC．物体质量每增加1 kg，弹簧长度增加0.5 cmD．所挂物体质量为7 kg，弹簧长度为14.5 cm8．若直线y＝－3x＋m与两坐标轴所围成的三角形的面积是6，则m的值为( ) A．6 B．－6 C．±6 D．±39．【教材P99复习题T8变式】已知一次函数y＝kx＋b，y随着x的增大而减小，且kb＞0，则这个函数的大致图象是( )10．【2020·铜仁】如图，在长方形ABCD中，AB＝3，BC＝4，动点P沿折线BCD 从点B开始运动到点D，设点P运动的路程为x，△ADP的面积为y，那么y与x 之间的函数关系的图象大致是( )二、填空题(每题3分，共24分)11．【2021·黑龙江】在函数y ＝1x －5中，自变量x 的取值范围是__________．12．若函数y ＝(m ＋1)x |m |是关于x 的正比例函数，则m ＝________． 13．直线y ＝3x ＋1与y 轴的交点坐标是__________．14．点⎝ ⎛⎭⎪⎫－12，m 和点(2，n )在直线y ＝2x ＋1上，则m 与n 的大小关系是__________．15．拖拉机油箱中有54 L 油，拖拉机工作时，每小时平均耗油6 L ，则油箱里剩下的油量Q (L)与拖拉机的工作时间t (h)之间的函数关系式是________________(写出自变量的取值范围)．16．【教材P 90习题T 2改编】一次函数y ＝－2x ＋m 的图象经过点P (－2，3)，且与x 轴、y 轴分别交于点A ，B ，则△AOB 的面积是________．17．如图，过A 点的一次函数的图象与正比例函数y ＝2x 的图象相交于点B ，则这个一次函数的表达式是____________．(第17题) (第18题)18．甲、乙两地之间是一条直路，在全民健身活动中，赵明阳跑步从甲地往乙地，王浩月骑自行车从乙地往甲地，两人同时出发，王浩月先到达目的地，两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示，下列说法：①两人出发1小时后相遇；②赵明阳跑步的速度为8 km/h；③王浩月到达目的地时两人相距10 km；④王浩月比赵明阳提前1.5 h到目的地．其中错误的序号是________．三、解答题(每题11分，共66分)19．已知y－2与x成正比例，且x＝2时，y＝4.(1)求y与x之间的函数关系式；(2)若点M(m，3)在这个函数的图象上，求点M的坐标．20．已知一次函数y＝(m－3)x＋m－8中，y随x的增大而增大．(1)求m的取值范围；(2)如果这个一次函数又是正比例函数，求m的值；(3)如果这个一次函数的图象经过第一、三、四象限，试写一个m的值，不用写理由．21．如图，一次函数y＝2x＋b的图象与x轴交于点A(2，0)，与y轴交于点B.(1)求b的值，(2)若直线AB上的点C在第一象限，且S△AOC＝4，求点C的坐标．22．如图，一次函数y＝kx＋5的图象与y轴交于点B，与正比例函数y＝32x的图象交于点P(2，a)．(1)求k的值；(2)求△POB的面积．23．水龙头关闭不紧会持续不断地滴水，小明用可以显示水量的容器做实验，并根据实验数据绘制出容器内盛水量y(L)与滴水时间t(h)之间的函数关系图象(如图)．请结合图象解答下面的问题：(1)容器内原有水多少升？(2)求y与t之间的函数表达式，并计算在这种滴水状态下一天的滴水量是多少升．24．某通信公司推出①②两种通信收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的收费金额y (元)与通信时间x (分钟)之间的函数关系如图所示．(1)有月租费的收费方式是________(填“①”或“②”)，月租费是________元； (2)分别求出①②两种收费方式中，收费金额y (元)与通信时间x (分钟)之间的函数表达式；(3)请你根据用户通信时间的多少，给出经济实惠的选择建议．参考答案一、1．D 2．B 3．A 4．D 5．B 6．C 7．D 8．C 9．B 10．D二、11．x ≠5 12．1 13．(0，1) 14．m ＜n15．Q ＝54－6t (0≤t ≤9) 16．14 17．y ＝－x ＋3 18．③三、19．解：(1)设y －2＝kx (k ≠0)．把x ＝2，y ＝4代入，得k ＝1.故y 与x 之间的函数关系式是y ＝x ＋2. (2)因为点M (m ，3)在这个函数的图象上， 所以3＝m ＋2，解得m ＝1.所以点M 的坐标为(1，3)．20．解：(1)因为一次函数y ＝(m －3)x ＋m －8中，y 随x 的增大而增大，所以m －3＞0. 所以m ＞3.(2)因为这个一次函数是正比例函数， 所以m －8＝0，即m ＝8. (3)答案不唯一，如m ＝4.21．解：将A (2，0)的坐标代入y ＝2x ＋b ，得2×2＋b ＝0，解得b ＝－4.(2)因为S △AOC ＝4，点A (2，0)， 所以OA ＝2.所以12OA ·y c ＝4，解得y c ＝4.把y ＝4代入y ＝2x －4，得2x －4＝4， 解得x ＝4.所以点C 的坐标为(4，4)．22．解：(1)把点P (2，a )的坐标代入y ＝32x ，得a ＝3，所以点P 的坐标为(2，3)．把点P (2，3)的坐标代入y ＝kx ＋5，得2k ＋5＝3， 解得k ＝－1.(2)由(1)知一次函数表达式为y ＝－x ＋5. 把x ＝0代入y ＝－x ＋5，得y ＝5，所以点B的坐标为(0，5)．所以S△POB＝12×5×2＝5.23．解：(1)根据图象可知，当t＝0时，y＝0.3，即容器内原有水0.3 L.(2)设y与t之间的函数表达式为y＝kt＋b.将点(0，0.3)，(1.5，0.9)的坐标分别代入，得b＝0.3，1.5k＋b＝0.9，解得k＝0.4.所以y与t之间的函数表达式为y＝0.4t＋0.3.当t＝24时，y＝0.4×24＋0.3＝9.9，所以在这种滴水状态下一天的滴水量是9.9－0.3＝9.6(L)．24．解：(1)①；30(2)记有月租费的收费金额为y1(元)，无月租费的收费金额为y2(元)，则设y1＝k1x＋30，y2＝k2x.将点(500，80)的坐标代入y1＝k1x＋30，得500k1＋30＝80，所以k1＝0.1，则y1＝0.1x＋30.将点(500，100)的坐标代入y2＝k2x，得500k2＝100，所以k2＝0.2，则y2＝0.2x.所以①②两种收费方式中，收费金额y(元)与通信时间x(分钟)之间的函数表达式分别为y1＝0.1x＋30，y2＝0.2x.(3)当收费相同，即y1＝y2时，0.1x＋30＝0.2x，解得x＝300.结合图象，可知当通信时间少于300分钟时，选择收费方式②更实惠；当通信时间超过300分钟时，选择收费方式①更实惠；当通信时间等于300分钟时，选择收费方式①②一样实惠．。

第六单元 比的认识 （单元测试）-2024-2025学年六年级上册数学北师大版一、单选题(共5题；共15分)1．（3分）把5：8的前项加10，要使比值不变，后项应该加上（ ）。

A ．10B ．16C ．24D ．202．（3分）在一个比中，前项是8，比值是，后项是（ ）。

A ．B ．6C ．D ．3．（3分）将甲班人数的 调入乙班后，两班人数相等，原来甲、乙两班的人数比是（ ）。

A ．4：3B ．5：3C ．5：4D ．3：44．（3分）甲数比乙数多，甲数：乙数=（ ）。

A ．4：1B ．4：3C ．5：1D ．5：45．（3分）六（2）班男生人数是女生人数的。

下列说法错误的是（ ）A ．女生人数与男生人数的比是5：2B ．女生人数比男生人数多C ．男生人数比女生人数少D ．男生人数占全班人数的二、判断题(共5题；共15分)6．（3分）把30克盐溶解在120克水中，盐与盐水的质量比是1：4。

（ ）7．（3分）4∶9的后项加上18，要使比值不变，前项应乘3。

（ ）8．（3分）甲、乙两数的比是4：5，乙、丙两数的比是7：8，则甲、丙两数的比是4：8。

（ ）9．（3分）含盐率是20%，盐与水的比是2：10 。

（ ）10．（3分）a 是b 的9倍（a 、b 均不为0），b 和a 的比是9：1。

（ ）三、填空题(共7题；共21分)11．（3分） 100米短跑测试，平平用了12秒，杨杨用了14秒，那么杨杨和平平的速度比是 。

12．（3分）大圆的半径与小圆的直径相等，那么大小两个圆的周长比是　　，它们的面积比是 。

13．（3分）建筑工地配制一种混凝土，所需水泥、黄沙和石子的质量比是2∶3∶5，现工地上三种材料都有24吨，当黄沙全部用完时，水泥还剩 吨，石子需要添加 吨。

14．（3分） 大小两个圆半径的比是 3：2，它们的周长之比是 。

面积之比是　　。

343321632318142535352715．（3分）两个相同的瓶子装滴酒精溶液，一个瓶中酒精与水的体积之比是3：1，另一个瓶中酒精与水的体积之比是4：1。

北师大版八年级下册数学第六单元平行四边形测试题及答案（一）一、选择题1．如图，在▱ABCD中，∠DAB的平分线交CD于点E，交BC的延长线于点G，∠ABC的平分线交CD于点F，交AD的延长线于点H，AG与BH交于点O，连接BE，下列结论错误的是（）A．BO=OH B．DF=CE C．DH=CG D．AB=AE2．如图，在▱ABCD中，连结AC，∠ABC=∠CAD=45°，AB=2，则BC的长是（）A．B．2C．2D．43．如图，六边形ABCDEF的内角都相等，∠DAB=60°，AB=DE，则下列结论成立的个数是（）①AB∥DE；②EF∥AD∥BC；③AF=CD；④四边形ACDF是平行四边形；⑤六边形ABCDEF既是中心对称图形，又是轴对称图形．A．2B．3C．4D．54．如图，已知凸五边形ABCDE的边长均相等，且∠DBE=∠ABE+∠CBD，AC=1，F则BD必定满足（）A．BD＜2B．BD=2C．BD＞2D．以上情况均有可能5．如图，Rt△ABC中，∠ACB=90°，斜边AB=9，D为AB的中点，为CD上一点，且CF=CD，过点B作BE∥DC交AF的延长线于点E，则BE的长为（）A．6B．4C．7D．126．从六边形的一个顶点出发，可以画出m条对角线，它们将六边形分成n个三角形．则m、n的值分别为（）A．4，3B．3，3C．3，4D．4，47．一个多边形的内角和是外角和的2倍，则这个多边形是（）A．四边形B．五边形C．六边形D．八边形8．在下列条件中，不能判定四边形为平行四边形的是（）A．一组对边平行，另一组对边相等B．一组对边平行且相等C．两组对边分别平行D．对角线互相平分9．如图，△ABC的面积是12，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是（）F G HA．4.5B．5C．5.5D．610．如图为互相垂直的两直线将四边形ABCD分成四个区域的情形，若∠A=100°，∠B=∠D=85°，∠C=90°，则根据图中标示的角，判断下列∠1，∠2，∠3的大小关系，何者正确（）A．∠1=∠2＞∠3B．∠1=∠3＞∠2C．∠2＞∠1=∠3D．∠3＞∠1=∠2 11．如图，已知▱ABCD的四个内角的平分线分别相交于点E、、、，连接AC．若EF=2，FG=GC=5，则AC的长是（）A．12B．13C．D．二、填空题12．在平行四边形ABCD中，∠B+∠D=200°，则∠A=．13．如图，在△ABC中，∠BAC=90°，AB=4，AC=6，点D、E分别是BC、AD的中点，AF∥BC交CE的延长线于F．则四边形AFBD的面积为．14．如图，△ABC中，D，E分别是AB，AC的中点，连线DE．若DE=3，则线段BC的长等于．15．如图所示的正六边形ABCDEF，连结FD，则∠FDC的大小为．三、解答题16．如图，延长▱ABCD的边AD到F，使DF=DC，延长CB到点E，使BE=BA，分别连结点A、E和C、F．求证：AE=CF．17．如图，点B、E、C、F在一条直线上，AB=DF，AC=DE，BE=FC,(1)求证：△ABC≌△DFE；(2)连接AF、BD，求证：四边形ABDF是平行四边形．18．△ABC的中线BD、CE相交于O，F，G分别是BO、CO的中点，求证：EF∥DG，且EF=DG．19．(1)解不等式组：(2)如图，已知正五边形ABCDE，AF∥CD交DB的延长线于点F，交DE的延长线于点G．求∠G的度数．20．如图，四边形ABCD的对角线AC⊥BD于点E，AB=BC，F为四边形ABCD外一点，且∠FCA=90°，∠CBF=∠DCB．(1)求证：四边形DBFC是平行四边形；(2)如果BC平分∠DBF，∠F=45°，BD=2，求AC的长．21．如图，四边形ABCD是平行四边形，E、F是对角线BD上的两点，∠1=∠2．(1)求证：DE=BF；(2)求证：四边形AECF是平行四边形．22．如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．(1)求证：四边形BCED是平行四边形；(2)已知DE=2，连接BN，若BN平分∠DBC，求CN的长．答案一、选择题1.D2.C3.D4.A5.A6.C7.C8.A9.A10.D11.B二、填空题12.80°13.1214.615.90°三、解答题16．如图，延长▱ABCD的边AD到F，使DF=DC，延长CB到点E，使BE=BA，分别连结点A、E和C、F．求证：AE=CF．【考点】L5：平行四边形的性质．【专题】解答题【分析】根据平行四边形的性质可得AD=BC，AD∥BC，再证出BE=DF，得出AF=EC，进而可得四边形AECF是平行四边形，从而可得AE=CF．【解答】证明：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴AF∥EC，∵DF=DC，BE=BA，∴BE=DF，∴AF=EC，∴四边形AECF是平行四边形，∴AE=CF．【点评】此题主要考查了平行四边形的性质和判定，关键是掌握平行四边形对边平行且相等，一组对边平行且相等的四边形是平行四边形．17．如图，点B、E、C、F在一条直线上，AB=DF，AC=DE，BE=FC,(1)求证：△ABC≌△DFE；(2)连接AF、BD，求证：四边形ABDF是平行四边形．【考点】L6：平行四边形的判定；KD：全等三角形的判定与性质．【专题】解答题【分析】(1)由SSS证明△ABC≌△DFE即可；(2)连接AF、BD，由全等三角形的性质得出∠ABC=∠DFE，证出AB∥DF，即可得出结论．【解答】证明：(1)∵BE=FC，∴BC=EF，在△ABC和△DFE中，，∴△ABC≌△DFE（SSS）；(2)解：连接AF、BD，如图所示：由(1)知△ABC≌△DFE，∴∠ABC=∠DFE，∴AB∥DF，∵AB=DF，∴四边形ABDF是平行四边形．【点评】本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定；熟练掌握平行四边形的判定方法，证明三角形全等是解决问题的关键．18．△ABC的中线BD、CE相交于O，F，G分别是BO、CO的中点，求证：EF∥DG，且EF=DG．【考点】KX：三角形中位线定理．【专题】解答题【分析】利用三角形中线的性质、中位线的定义和性质证得四边形EFGD的对边DE∥GF，且DE=GF=BC；然后由平行四边形的判定﹣﹣对边平行且相等的四边形是平行四边形，继而证得结论．【解答】证明：连接DE，FG，∵BD、CE是△ABC的中线，∴D，E是AB，AC边中点，∴DE∥BC，DE=BC，同理：FG∥BC，FG=BC，∴DE∥FG，DE=FG，∴四边形DEFG是平行四边形，∴EF∥DG，EF=DG．【点评】本题考查了三角形中位线定理、平行四边形的判定．平行四边形的判定：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；一组对边平行，一组对角相等的四边形是平行四边形19．(1)解不等式组：(2)如图，已知正五边形ABCDE，AF∥CD交DB的延长线于点F，交DE的延长线于点G．求∠G的度数．【考点】L3：多边形内角与外角；CB：解一元一次不等式组；JA：平行线的性质．【专题】解答题【分析】(1)根据不等式的解法即可得到结论；(2)根据五边形ABCDE是正五边形，得到∠DCB=∠EDC=108°，DC=BC根据等腰三角形的性质得到∠CDB=36°，求得∠GDB=72°，根据平行线的性质即可得到结论．【解答】解：(1)，解不等式①，得x≤2，解不等式②，得x＜﹣1，不等式组的解集为x＜﹣1；(2)∵五边形ABCDE是正五边形，∴∠DCB=∠EDC=108°，DC=BC，∴∠CDB=36°，∴∠GDB=72°，∵AF∥CD，∴∠CDB=∠F=36°，∴∠G=72°．【点评】本题考查了不等式的解法，多边形的内角和外角，平行线的性质，正确的识别图形是解题的关键．20．如图，四边形ABCD的对角线AC⊥BD于点E，AB=BC，F为四边形ABCD外一点，且∠FCA=90°，∠CBF=∠DCB．(1)求证：四边形DBFC是平行四边形；(2)如果BC平分∠DBF，∠F=45°，BD=2，求AC的长．【考点】L7：平行四边形的判定与性质；KF：角平分线的性质．【专题】解答题【分析】(1)由这一点就证出BD∥CF，CD∥BF，即可得出四边形DBFC是平行四边形；(2)由平行四边形的性质得出CF=BD=2，由等腰三角形的性质得出AE=CE，作CM ⊥BF于F，则CE=CM，证出△CFM是等腰直角三角形，由勾股定理得出CM= CF=，得出AE=CE=，即可得出AC的长．【解答】(1)证明：∵AC⊥BD，∠FCA=90°，∠CBF=∠DCB．∴BD∥CF，CD∥BF，∴四边形DBFC是平行四边形；(2)解：∵四边形DBFC是平行四边形，∴CF=BD=2，∵AB=BC，AC⊥BD，∴AE=CE，作CM⊥BF于F，∵BC平分∠DBF，∴CE=CM，∵∠F=45°，∴△CFM是等腰直角三角形，∴CM=∴AE=CE=∴AC=2CF=，．，【点评】本题考查了平行四边形的判定与性质、等腰三角形的性质、等腰直角三角形的判定与性质、勾股定理；熟练掌握平行四边形的判定与性质是解决问题的关键．21．如图，四边形ABCD是平行四边形，E、F是对角线BD上的两点，∠1=∠2．(1)求证：DE=BF；(2)求证：四边形AECF是平行四边形．【考点】L7：平行四边形的判定与性质；KD：全等三角形的判定与性质．【专题】解答题【分析】(1)通过全等三角形△CDE≌△ABF的对应边相等证得DE=BF；(2)根据平行四边形的判定定理：对边平行且相等的四边形是平行四边形证得结论．【解答】(1)证明：如图：∵四边形ABCD是平行四边形，∴CD=AB，CD∥AB，∴∠3=∠4，∵∠1=∠3+∠5，∠2=∠4+∠6，∠1=∠2∴∠5=∠6在△CDE与△ABF中，，∴△CDE≌△ABF（ASA），∴DE=BF；(2)证明：∵∠1=∠2，∴CE∥AF．又∵由(1)知，△CDE≌△ABF，∴CE═AF，∴四边形AECF是平行四边形．【点评】本题考查了全等三角形的判定与性质、平行四边形的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．22．如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．(1)求证：四边形BCED是平行四边形；(2)已知DE=2，连接BN，若BN平分∠DBC，求CN的长．【考点】L7：平行四边形的判定与性质．【专题】解答题【分析】(1)由已知角相等，利用对顶角相等，等量代换得到同位角相等，进而得出DB与EC平行，再由内错角相等两直线平行得到DE与BC平行，即可得证；(2)由角平分线得到一对角相等，再由两直线平行内错角相等，等量代换得到一对角相等，再利用等角对等边得到CN=BC，再由平行四边形对边相等即可确定出所求．【解答】(1)证明：∵∠A=∠F，∴DE∥BC，∵∠1=∠2，且∠1=∠DMF，∴∠DMF=∠2，∴DB∥EC，则四边形BCED为平行四边形；(2)解：∵BN平分∠DBC，∴∠DBN=∠CBN，∵EC∥DB，∴∠CNB=∠DBN，∴∠CNB=∠CBN，∴CN=BC=DE=2．【点评】此题考查了平行四边形的判定与性质，熟练掌握平行四边形的判定与性质是解本题的关键．。

第一章单元测试卷一、选择题(每题3分,共30分)1.由下列线段a,b,c组成的三角形,不是直角三角形的是( )A.a=3,b=4,c=5B.a=1,b=错误!未找到引用源。

,c=错误!未找到引用源。

C.a=9,b=12,c=15D.a=错误!未找到引用源。

,b=2,c=错误!未找到引用源。

2.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=90°3.下列四个命题中,假命题是( )A.“等边对等角”与“等角对等边”是互逆定理B.等边三角形是锐角三角形C.角平分线上的点到角两边的距离相等D.真命题的逆命题是真命题4.下列能判定三角形是等腰三角形的是( )A.有两个角为30°,60°B.有两个角为40°,80°C.有两个角为20°,100°D.有两个角为50°,80°5.已知等腰三角形的两条边长分别是7和3,则第三条边的长是( )A.7或3B.7C.4D.36.如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处,若∠B=65°,则∠BDF等于( )A.65°B.50°C.60°D.57.5°7.下列两个三角形中,一定全等的是( )A.有一个角是40°,腰相等的两个等腰三角形B.两个等边三角形C.有一个角是100°,底相等的两个等腰三角形D.有一条边相等,有一个内角相等的两个等腰三角形8.如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC 于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN 的长为 ( )A.4 cmB.3 cmC.2 cmD.1 cm9.如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为( )A.4错误!未找到引用源。

2020-2021学年北师大新版八年级上册数学《第1章勾股定理》单元测试卷一．选择题1．如图所示是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案，现在有五种正方形纸片，面积分别是2，3，4，5，6，选取其中三块（可重复选取），按如图所示方式组成图案，使所围成的三角形是直角三角形，则选取的三块纸片的面积不可以是（）A．3，4，5B．2，2，4C．3，3，6D．2，4，62．在Rt△ABC中，∠C＝90°．若a＝6，b＝8，则c的值是（）A．10B．2C．2D．4.83．如图，在Rt△ABC中，∠C＝90°，AB＝2，AC＝1，则BC的长度为（）A．5B．3C．D．4．“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形，如图，其直角三角形的两条直角边的长分别是2和4，则小正方形与大正方形的面积比是（）A．1：2B．1：4C．1：5D．1：105．下列几组数能作为直角三角形三边长的是（）A．3，4，6B．1，1，C．5，12，14D．，2，5 6．下列各组数中，是勾股数的是（）A．7，8，9B．6，8，11C．5，12，14D．3，4，57．如图，在Rt△ABC中，∠C＝90°，AB＝10，BC＝8．点P是边AC上一动点，过点P 作PQ∥AB交BC于点Q，D为线段PQ的中点，当BD平分∠ABC时，AP的长度为（）A．B．C．D．8．《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺，问折高者几何？意思是一根竹子，原高一丈（一丈＝10尺），一阵风将竹子折断，某竹梢恰好抵地，抵地处离竹子底部6尺远，则折断处离地面的高度是（）A．5.3尺B．6.8尺C．4.7尺D．3.2尺9．丽丽想知道学校旗杆的高，她发现旗杆顶端上的绳子垂直到地面还多2米，当她把绳子的下端拉开离旗杆6米后，发现下端刚好接触地面，则旗杆的高为（）A．4米B．8米C．10米D．12米10．如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为12cm，在容器内壁离容器底部4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，且离容器上沿4cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为15cm，则该圆柱底面周长为（）cm．A．9B．10C．18D．20二．填空题11．直角三角形的两直角边是3和4，则斜边是12．如图，在△ABC中，AB＝5，AC＝4，BC＝3，分别以点A、点B为圆心，大于AB的长为半径画弧，两弧相交于点M，N，作直线MN交AB于点O，连接CO，则CO的长为．13．如图，在3×3的正方形网格中，每个小正方形边长为1，点A，B，C均为格点，以点A为圆心，AB长为半径作弧，交格线于点D，则CD的长为．14．面积为48的等腰三角形底边上的高为6，则腰长为．15．如图，正方形ABCD是由四个全等的直角三角形围成的，若CF＝5，AB＝13，则EF 的长为．16．如图所示的网格是正方形网格，点A，B，C，D是网格线交点，则△ABC的面积与△ADB的面积大小关系为：S△ABC S△ADB（填“＞”“＝”或“＜”）．17．观察下列各组勾股数，并寻找规律：①4，3，5；②6，8，10；③8，15，17；④10，24，26……请根据你发现的规律写出第⑦组勾股数：．18．如图是高空秋千的示意图，小明从起始位置点A处绕着点O经过最低点B．最终荡到最高点C处，若∠AOC＝90°，点A与点B的高度差AD＝1米，水平距离BD＝4米，则点C与点B的高度差CE为米．19．如图，甲、乙两艘客轮同时离开港口C，各自沿一固定方向航行，甲客轮每小时航行16nmile，乙客轮每小时航行12nmile，它们离开港口一个半小时后分别位于点A、B处，且相距30nmile．如果知道甲客轮沿着北偏西45°方向航行，则乙客轮的航行方向可能是．20．如图，如果一只蚂蚁从圆锥底面上的点B出发，沿表面爬到母线AC的中点D处，则最短路线长为．三．解答题21．如图，已知△ABC中，AB＝AC，BD⊥AC于D，BD＝3，BC＝，求AB的长．22．阅读下列材料，解决所提的问题：勾股定理a2+b2＝c2本身就是一个关于a，b，c的方程，我们知道这个方程有无数组解，满足该方程的正整数解（a，b，c）通常叫做勾股数组．关于勾股数组的研究我国历史上有非常辉煌的成就，根据我国古代数学书《周髀算经》记载，在约公元前1100年，人们就已经知道“勾广三、股修四、径隅五”（古人把较短的直角边称为勾，较长的直角边称为股，而斜边则为弦），即知道了勾股数组（3，4，5）．类似地，还可以得到下列勾股数组：（3，4，5），（5，12，13），（7，24，25），（9，40，41），…等等，这些数组也叫做毕达哥拉斯勾股数组．上述勾股数组的规律，可以用下面表格直观表示：勾股数组各组数的和和的另一表示法和与最小数的差股弦3，4，5123×412﹣3＝95，12，13305×630﹣5＝257，24，25567×856﹣7＝499，40，41909×1090﹣9＝81………………观察分析上述勾股数组，可以看出它们具有如下特点：特点1：最小的勾股数的平方等于另两个勾股数的和；特点2：．…学习任务：（1）请你再写出上述勾股数组的一个特点：；（2）如果n表示比1大的奇数，则上述勾股数组可以表示为（n，，）（3）请你证明（2）的结论．23．如图（1）是用硬板纸做成的两个全等的直角三角形，两直角边的长分别为a和b，斜边长为c，请你开动脑筋，将它们拼成一个能证明勾股定理的图形．（1）画出拼成的这个图形的示意图，并用这个图形证明勾股定理；（2）假设图（1）中的直角三角形有若干个，你能运用图（1）中所给的直角三角形拼出另一种能证明勾股定理的图形吗？请画出拼后的示意图（无需证明）24．如图，已知CD＝4，AD＝3，∠ADC＝90°，BC＝12，AB＝13．（1）求AC的长．（2）求图中阴影部分图形的面积．25．如图是5×6的网格．（1）如图（1），A，B，C是网格中的三个格点（即小正方形的顶点），判断AC与BC 的数量和位置关系，直接写出结论，不需要说明理由；（2）如图（2），求∠1+∠2的度数（要求：画出示意图并给出推导过程）．26．如图，每小个正方形的边长都是1，每个小正方形的顶点称格点，△ABC的顶点都是在格点上．（1）求△ABC的周长；（2）求△ABC的面积．27．如图所示，在△ABC中，AB＝5，AC＝13，BC边上的中线AD＝6，求BC的长．参考答案与试题解析一．选择题1．解：由题意可得，三角形各边的平方是对应的各个正方形的面积，∵所围成的三角形是直角三角形，∴斜边对应的正方形的面积＝两直角边对应的正方形的面积和，又∵3+4≠5，2+2＝4，3+3＝6，2+4＝6，∴选取的三块纸片的面积不可以是3，4，5，故选：A．2．解：在Rt△ABC中，∠C＝90°，a＝6，b＝8，由勾股定理得：c＝＝＝10，故选：A．3．解：在Rt△ABC中，∠C＝90°，AB＝2，AC＝1，由勾股定理得，BC＝＝＝，故选：D．4．解：∵直角三角形的两条直角边的长分别是2和4，∴小正方形的边长为2，根据勾股定理得：大正方形的边长＝＝2，∴＝＝＝．故选：C．5．解：A、32+42≠62，不符合勾股定理的逆定理，不是直角三角形，不符合题意；B、12+12≠（）2，不符合勾股定理的逆定理，不是直角三角形，不符合题意；C、52+122≠142，不符合勾股定理的逆定理，不是直角三角形，不符合题意；D、（）2+（2）2＝52，符合勾股定理的逆定理，是直角三角形，符合题意；故选：D．6．解：A、∵72+82≠92，∴这组数不是勾股数．不符合题意；B、∵62+82≠112，∴不是勾股数，不符合题意；C、∵52+122≠14，∴这组数不是勾股数．不符合题意；D、∵32+42＝52，∴是勾股数，符合题意．故选：D．7．解：设BQ＝x，在Rt△ABC中，∠C＝90°，AB＝10，BC＝8，由勾股定理得：AC＝＝＝6，∵BD平分∠ABC，∴∠QBD＝∠ABD，∵PQ∥AB，∴∠QDB＝∠ABD，∴∠QBD＝∠QDB，∴QD＝BQ＝x，∵D为线段PQ的中点，∴QP＝2QD＝2x，∵PQ∥AB，∴△CPQ∽△CAB，∴＝＝，即＝＝，解得：x＝，CP＝，∴AP＝CA﹣CP＝，故选：B．8．解：设竹子折断处离地面x尺，则斜边为（10﹣x）尺，根据勾股定理得：x2+62＝（10﹣x）2．解得：x＝3.2，∴折断处离地面的高度为3.2尺，故选：D．9．解：设旗杆的高为xm，则绳子的长为（x+2）m．根据题意得：x2+62＝（x+2）2，解得x＝8．故旗杆的高为8米．故选：B．10．解：如图：将圆柱展开，EG为上底面圆周长的一半，作A关于E的对称点A'，连接A'B交EG于F，则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF 的长，即AF+BF＝A'B＝15cm，延长BG，过A'作A'D⊥BG于D，∵AE＝A'E＝DG＝4cm，∴BD＝12cm，Rt△A'DB中，由勾股定理得：A'D＝＝9cm，∴则该圆柱底面周长为18cm．故选：C．二．填空题11．解：在直角三角形中，三边边长符合勾股定理，已知两直角边为3、4，则斜边边长＝＝5，故答案为5．12．解：∵AB＝5，AC＝4，BC＝3，∴AB2＝AC2+BC2，∴∠ACB＝90°，由作图可知：MN是AB的垂直平分线，∴O是AB的中点，∴CO＝AB＝，故答案为：．13．解：连接AB，AD，如图所示：∵AD＝AB＝＝2，∴DE＝＝，∴CD＝3﹣．故答案为：3﹣．14．解：如图所示：△ABC中，AB＝AC，AD是底边BC上的高，则BC•AD＝48，BD＝CD，即BC×6＝48，∴BC＝16，∴BD＝BC＝8，∴AB＝＝＝10，故答案为：10．15．解：如图，∵正方形ABCD是由四个全等的直角三角形围成的，∴AH＝BE＝CG＝DF，AE＝BG＝CF＝DH，∴EG＝GF＝GH＝HE，∴四边形EGFH为菱形，∵△ABE为直角三角形，∴∠AEB＝∠GEH＝90°，∴四边形EGFH为正方形，∵四边形ABCD为正方形，∴CD＝AB＝13，在Rt△CDF中，∠DFC＝90°，CF＝5，根据勾股定理得，DF＝12，∴GF＝DF﹣DH＝GC﹣FC＝7，在△GEF中，GE＝GF＝7，∠EGF＝90°，根据勾股定理得，EF＝＝7．故答案为：7．16．解：∵AB2＝8，BC2＝2，AC2＝10，∴AB2+BC2＝AC2，∴△ABC是直角三角形，∴S△ABC ＝××2＝2，S△ABD＝×2×2＝2，∴S△ABC ＝S△ABD，故答案为：＝．17．解：观察前4组数据的规律可知：第一个数是2（n+1）；第二个是：n（n+2）；第三个数是：（n+1）2+1．所以第⑦组勾股数：16，63，65．故答案为：16，63，65．18．解：作AF⊥BO于F，CG⊥BO于G，∵∠AOC＝∠AOF+∠COG＝90°，∠AOF+∠OAF＝90°，∴∠COG＝∠OAF，在△AOF与△OCG中，，∴△AOF≌△OCG（AAS），∴OG＝AF＝BD＝4米，设AO＝x米，在Rt△AFO中，AF2+OF2＝AO2，即42+（x﹣1）2＝x2，解得x＝8.5．则CE＝GB＝OB﹣OG＝8.5﹣4＝4.5（米）．故答案为：4.5．19．解：AC的长度为：16×1.5＝24（n mile），BC的长度为：12×1.5＝18（n mile），∵302＝242+182，∴AB2＝AC2+BC2，∴△ABC是直角三角形，∠ACB＝90°，∵甲客轮沿着北偏西45°方向航行，∴乙客轮的航行方向可能是北偏东45°，故答案为：北偏东45°．20．解：如图将圆锥侧面展开，得到扇形ABB′，则线段BF为所求的最短路线．设∠BAB′＝n°．∵，∴n＝120，即∠BAB′＝120°．∵E为弧BB′中点，∴∠AFB＝90°，∠BAF＝60°，Rt△AFB中，∠ABF＝30°，AB＝6∴AF＝3，BF＝＝3，∴最短路线长为3．故答案为：3．三．解答题21．解：设AB＝AC＝x，∵BD⊥AC，∴∠BDC＝90°，∴CD＝＝1，∴AD＝x﹣1，在Rt△BDA中，BD2+AD2＝AB2，即32+（x﹣1）2＝x2，解得，x＝5，即AB＝5．22．解：特点2，答案不唯一：如：最小的勾股数是奇数，另外两个勾股数是两个连续的正整数，故答案为：答案不唯一：如：最小的勾股数是奇数，另外两个勾股数是两个连续的正整数；（1）上述勾股数组的一个特点：最小的勾股数与比它大1的整数的乘积等于各个勾股数的和，故答案为：最小的勾股数与比它大1的整数的乘积等于各个勾股数的和；（2）如果n表示比1大的奇数，则上述勾股数组可以表示为（n2，，），故答案为：；；（3）证明：n2+（）2＝n2+＝＝（）2，则（n2，，）是勾股数组．23．解：（1）如图所示，是梯形；由上图我们根据梯形的面积公式可知，梯形的面积＝（a+b）（a+b）．从上图我们还发现梯形的面积＝三个三角形的面积，即ab+ab+c2．两者列成等式化简即可得：a2+b2＝c2；（2）画边长为（a+b）的正方形，如图，其中a、b为直角边，c为斜边．24．解：（1）在Rt△ADC中，∠ADC＝90°，由勾股定理，得：AC＝＝＝5；（2）∵AC2+BC2＝52+122＝132＝AB2，∴△ABC是直角三角形，∴图中阴影部分图形的面积＝S △ABC ﹣S △ACD ＝×5×12﹣×3×4＝30﹣6＝24． 25．解：（1）AC ＝BC 且AC ⊥BC ．理由：如图（1），∵CD ＝BE ，∠ADC ＝∠CEB ＝90°，AD ＝CE ， ∴△ACD ≌△CBE （SAS ），∴AC ＝CB ，∠ACD ＝∠CBE ，又∵∠CBE +∠BCE ＝90°，∴∠ACD +∠BCE ＝90°，∴∠ACB ＝180°﹣90°＝90°，∴AC ⊥BC ；（2）如图（2），作△ABC ，△DEF ，∵BC ＝FE ，∠ABC ＝∠DFE ，AB ＝DF ，∴△ABC ≅△DFE （SAS ），∴∠ACB ＝∠DEF ＝∠2．由图，结合勾股定理，得 ，，AD ＝5，∴AC 2+DC 2＝5+20＝25＝AD 2，∴△ACD 是直角三角形，且∠ACD ＝90°．∵∠2+∠ACD +∠1＝180°，∴∠1+∠2＝180°﹣∠ACD ＝180°﹣90°＝90°． 26．解：（1）由勾股定理得：，，， ∴△ABC 的周长＝； （2）由（1）可知，AC 2+AB 2＝（）2+（）2＝20，BC 2＝（2）2＝20， ∴AC 2+AB 2＝BC 2，∴△ABC 是直角三角形，∠BAC ＝90°，∴．27．解：延长AD到E使AD＝DE，连接CE，在△ABD和△ECD中，∴△ABD≌△ECD，∴AB＝CE＝5，AD＝DE＝6，AE＝12，在△AEC中，AC＝13，AE＝12，CE＝5，∴AC2＝AE2+CE2，∴∠E＝90°，由勾股定理得：CD＝＝，∴BC＝2CD＝2，答：BC的长是2．。