当前位置：文档之家 › 浅谈团队管理中的纳什均衡.pptx

浅谈团队管理中的纳什均衡.pptx

  • 格式：pptx
  • 大小：466.99 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

《博弈论与信息经济学》纳什均衡的应用 PPT

《博弈论与信息经济学》纳什均衡的应用 PPT

s p 8ln 2 4 ln 3 2 ln 2 4 ln 3 6 ln 2 ln 81 ln 64 2 ln 9 8 0
s p
Q

p1 s1
p2 ln y 3 ln y s2 2 ln y 4 2 ln
N

N
n

2 ln
n

2
N ln y 1
si

pi

2 ln

N
1

ln
n
，两期的消费量为：y1

y 2
，y2

y 2
11
博弈论与信息经济学
2020/3/2
c.个人最优解于社会最优解的比较
Q



p s

2 ln
4ln

y
y 3 ln y 6 4 4 ln y 8ln 2
2
ln

y
3 y
6 4 ln
y 4 ln 3 2 ln 2
由需求函数得：D1 D2
p1, p1,
p2 p2

x 1
x，由于：cc12

p1 tx
p2 t 1
x
cu1uuuucuur2 x


p2

p1

t

2t ，
代入需求函数：D1 D2

p1, p1,
p2 p2





p

N
n

2 ln Y

N
n

第二节 纳什均衡

第二节 纳什均衡

通俗的讲，就是给定你的最优选择，我会选择能 够使我最优的选择，或者说，我选择在给定你的选择 的情况下我的最优选择，你选择了给定我选择情况下 你的最优选择。这种均衡最后到底均衡在哪一点，由 具体情况决定。在存在帕累托改善的情况下，可能会 达到帕累托最优。
在本例中，B企业选择了生产高度白酒，A企业选 择生产低度白酒是一种均衡；B企业选择了生产低度白 酒，A企业选择生产高度白酒也是一种均衡。由于在B 企业选择生产高度白酒，A企业选择生产低度白酒的时 候，A、B两企业的收益都比B企业选择生产低度白酒， A企业选择生产高度白酒时的收益要高，存在着帕累托 改善，因此最后可能会达到帕累托最优，即B企业选择 生产高度白酒，A企业选择生产低度白酒。
二、无纳什均衡的例子 实际上，纳什均衡也是一种特殊情况，并不是所 有的博弈都会产生纳什均衡。例如：在足球比赛中， 罚点球的时候，守门员和罚球者也构成一个博弈，双 方的收益矩阵如下图所示：
守门员
左中右
左 -1，1 1，-1 1，-1
点
球
中 1，-1 -1，1 1，-1
者
右 1，-1 1，-1 -1，1
由于在b企业选择生产高度白酒a企业选择生产低度白酒的时候ab两企业的收益都比b企业选择生产低度白酒a企业选择生产高度白酒时的收益要高存在着帕累托改善因此最后可能会达到帕累托最优即b企业选择生产高度白酒a企业选择生产低度白酒
第二节 纳什均衡
一、举例 假定A、B两个企业都生产白酒，白酒分为高度和低 度两种。报酬矩阵如图所示：
同样，当罚球者判断守门员将向右扑球时，罚 球者将向左或中发球；当罚球者判断守门员将向右 扑球时，罚球者将向右或中发球；当罚球者判断守 门员将向中扑球时，罚球者将向左或右发球。此时 果守门员也选择 了右，罚球者将得 -1，守门员将得 +1；如果守门员 选择了左或者中，罚球者将得 +1，守门员将得 -1。

纳什均衡

纳什均衡

纳什均衡在政治学中的应用
选举策略：候选人在竞选活动中的决策和策略选择 政治谈判：国家间在谈判过程中的策略选择和利益平衡 国际关系：国家间在合作与竞争中的决策和策略选择 政治制度设计：政治制度设计中的决策和策略选择，如选举制度、议会制度等
纳什均衡在管理学中的应用
战略决策：企业在市场竞争中，通过纳什均衡分析，制定最优策略。 组织结构：纳什均衡理论可以帮助企业优化组织结构，提高管理效率。 激励机制：纳什均衡理论在企业激励机制设计中，可以指导企业制定有效的激励措施。 谈判与合作：纳什均衡理论在企业谈判与合作中，可以帮助企业实现利益最大化。
纳什均衡的应用
博弈论：纳什均衡是博弈论的核心概念，用于分析各种博弈问题 经济学：纳什均衡在经济学中广泛应用，如市场均衡、价格均衡等 政治学：纳什均衡在政治学中用于分析政治博弈，如选举、谈判等 社会学：纳什均衡在社会学中用于分析社会现象，如群体行为、社会规范等
纳什均衡的求解方法
第二章
纳什均衡的求解条件
纳什均衡
目录
CONTENTS
01 纳什均衡的概念 02 纳什均衡的求解方法 03 纳什均衡与博弈论 04 纳什均衡的局限性
05 纳什均衡纳什均衡的定义
纳什均衡是指在 一个博弈中，每 个参与者的策略 都是对其他参与 者策略的最优反 应。
纳什均衡是博弈 论中的一个重要 概念，由约翰·纳 什提出。
纳什均衡的求解步骤
确定博弈的 参与者和策 略集
建立支付矩 阵，表示参 与者在不同 策略下的收 益
计算每个参 与者的最佳 反应策略
检查是否存 在纳什均衡， 即每个参与 者的策略都 是对其他参 与者策略的 最佳反应
如果存在纳 什均衡，则 求解得到均 衡策略；如 果不存在， 则重新调整 策略集或支 付矩阵，重 复步骤3-4。

多重纳什均衡课件

多重纳什均衡课件

例如，在双寡头市场中，两个企业可能采用不同 的混合策略组合，如企业A采用高价和低产的混合 策略，企业B采用低价和高产的混合策略。
此外，如果企业之间采用相同的混合策略组合， 也可能形成多个纳什均衡点。例如，两个企业都 采用高价和低产的混合策略或都采用低价和高产 的混合策略。
04
多重纳什均衡的经济学意义
纳什均衡
在非合作博弈中，如果每个参与者在给定其他参与者策略的 前提下，选择自己的最优策略，那么所有参与者的策略组合 就构成一个纳什均衡。
多重纳什均衡
当存在多个纳什均衡时，这些均衡被称为多重纳什均衡。
多重纳什均衡的存在性条件
博弈的策略空间和参与者的数量
01
当博弈的策略空间和参与者的数量较大时，多重纳什均衡存在
的可能性增加。
博弈的支付函数
02
支付函数的非线性程度和分布情况也会影响多重纳什均衡的存
在性。
博弈的规则和约束条件
03
博弈的规则和约束条件也会对多重纳什均衡的存在性产生影响。
多重纳什均衡的求解方法
直观判断法
对于一些简单的博弈， 可以通过直观判断来找
出多重纳什均衡。
迭代法
通过迭代计算的方法， 可以找出多重纳什均衡。
这种方法通常适用于较 小的博弈。
线性规划法
通过线性规划的方法， 可以找出多重纳什均衡。
这种方法通常适用于较 大的博弈。
概率方法
通过概率方法，可以找 出多重纳什均衡。这种 方法通常适用于具有随
机性的博弈。
03
多重纳什均衡的实例分析
价格竞争中的多重纳什均衡
价格竞争中的多重纳什均衡是指在价格竞争中，企业 之间可能存在多个纳什均衡点，这些均衡点反映了不

纳什均衡理论 优质课件

纳什均衡理论 优质课件
来源及定义 经典案例 重要影响
假设有n个局中人参与博弈，给定其他人策略 的条件下，每个局中人选择自己的纳什均衡。个 人最优策略可能依赖于也可能不依赖于他人的战 略，从而使自己利益最大化。所有局中人策略构 成一个策略组合。纳什均衡指的是这样一种战略 组合，这种策略组合由所有参与人最优策略组成。 即在给定别人策略的情况下，没有人有足够理由 打破这种均衡。纳什均衡，从实质上说，是一种 非合作博弈状态。纳什均衡达成时，并不意味着 博弈双方都处于不动的状态，在顺序博弈中这个 均衡是在博弈者连续的动作与反应中达成的。
关于案例，显然最好的策略是双方都抵赖，结 果是大家都只被判1年。但是由于两人处于隔离 的情况，首先应该是从心理学的角度来看，当 事双方都会怀疑对方会出卖自己以求自保，因 此都会从利己的目的出发进行选择。这两个人 都会有这样一个盘算过程：假如他坦白，如果 我抵赖，得坐10年监狱，如果我坦白最多才8年； 假如他要是抵赖，如果我也抵赖，我就会被判 一年，如果我坦白就可以被释放，而他会坐10 年牢。综合以上几种情况考虑，不管他坦白与 否，对我而言都是坦白了划算。两个人都会动 这样的脑筋，最终，两个人都选择了坦白，结 果都被判8年刑期。
当对手知道了你的 决定之后，就能做 出对自己最有利的 决定。
——纳什均衡理论
假设有两个小偷A和B联合犯事、私入民宅被 警察抓住。警方将两人分别置于不同的两个 房间内进行审讯。对每一个犯罪嫌疑人，警 方给出的政策是：如果一个犯罪嫌疑人坦白 了罪行，交出了赃物，于是证据确凿，两人 都被判有罪。如果另一个犯罪嫌疑人也作了 坦白，则两人各被判刑8年；如果另一个犯罪 嫌人没有坦白而是抵赖，则以妨碍公务罪 （因已有证据表明其有罪）再加刑2年，而坦 白者有功被减刑8年，立即释放。如果两人都 抵赖，则警方因证据不足不能判两人的偷窃 罪，但可以私入民宅的罪名将两人各判入狱1 年。

引言纳什均衡NashEquilibrium反应函数法.ppt

引言纳什均衡NashEquilibrium反应函数法.ppt

的利润分别为6，18和12，再作其它产量组合时亦会有不同的
结果。
最稳定的产量组合，是一个纳什均衡
表12-2 三厂商离散产量组合对应价格和利润
m1
m2
m3
p
π1
π2
π3
3
9
6
2
6
18
12
3
8
6
3
9
24
18
5
5
6
4
20
20
24
5
5
5
5
按博弈方式
非合作博弈 合作博弈
完全理性 有限理性
博弈分类
按博弈人数
二人博弈
二人零和博弈 二人非零和博弈
多人博弈
按博弈状态
静态博弈 动态博弈
完全信息静态博弈 不完全信息静态博弈 完全信息动态博弈 不完全信息动态博弈
Page 18
12.1.3 博弈的结构和分类
【例12-2】1943年2月，日本统帅山本五十六大将计划 由南太平洋新不列颠群岛的拉包尔出发，3天穿过俾 斯麦海，开往新几内亚的莱城，支援困守的日军。有 两条路线：北线和南线。
Two person finite non-zero-sum game
12.1 引 言
12.1.1 博弈论概述
博弈论（game theory）亦称对策论，是研究具有 对抗或竞争性质现象的数学理论和方法，它既是数 学、也是运筹学的一个重要分支。
博弈行为是博弈论中一个重要的概念。博弈行为 是指具有竞争或对抗性质的行为，在这类行为中， 参加斗争或竞争的各方各自具有不同的利益和目标， 各方需考虑对手的各种可能的行动方案，如何采取 行动以及与对手互动对自己最为有利 。

第二讲 纳什均衡 PPT课件

第二讲 纳什均衡 PPT课件
二、情侣博弈的结论：纳什均衡 （三）分类 2.普通纳什均衡 （1）均衡战略与非均衡战略无差异 （2）参与人单独改变策略后，支付可
能不变
2020年1月5日
博弈论第二章
12
第二讲纳什均衡
第三节 纳什均衡
三、寻找纳什均衡的方法
团队合作
（一）严格劣势策略反复消去法
乙

工作 偷懒
工作
6,6
+1，-1
+1，-1 +1，-1
博弈论第二章 第二讲纳什均衡
-1，+1
+1，-1 +3，-3
37
博弈论第二章
33
第二讲纳什均衡
第三节 纳什均衡
四、纳什均衡在微观经济学中的应用： 古诺模型
1.博弈三要素 （3）支付
i (q1, q2 ) (a q1 q2 ) qi ciqi
2020年1月5日
博弈论第二章
34
第二讲纳什均衡
第三节 纳什均衡
四、古诺模型
2.企业i的目标： max i
二、情侣博弈结论：纳什均衡 （一）表述 若存在一个策略组合（足球，足球），
当参与人单独改变策略后，支付下降， 此策略组合为纳什均衡。 ——博弈各方相互作用的稳定结局
2020年1月5日
博弈论第二章
9
第二讲纳什均衡
第三节 纳什均衡
二、情侣博弈的结论：纳什均衡 （二）定义
给定G=｛S1，…,Sn;u1,…,un｝, s*=(s*1,…,sn*) 对于所有i和si∈Si，有： ui(si*,s-i*)≥ ui(si’,s-i*)
2020年1月5日
博弈论第二章
23
第二讲纳什均衡

《纳什均衡四川大学》PPT课件

《纳什均衡四川大学》PPT课件

找自己的策略 使得si 自 S己i 的收益
最Pi大(s1,，s2,但是, sn局) 中人
单方面不能找到自i 己的最佳策略，其结果是相互影响的，是由策
略组合
决定的。s 这(就s1,是s2,一个, s有n ) 相互影响的多人决策
问题。有人可能这样设想：是否有一个局外人，将 个局中人的
收益最大作n 为 个目标的多目标规划问n题，即求：
即
bij
bij
并在 下划线。当 不唯一时，均在下面划线。
7
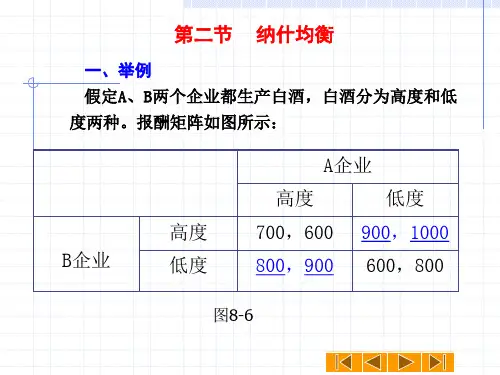
猜钱币游戏
《博弈论及其应用》 （汪贤 裕）
《博弈论‹及#› 其应用》 （汪贤裕）
8
完全信息静态博弈三要素
局中人集合N {1,2,, n}
i 局中人集合即博弈参加人的集合。若给定局中人 ，则记 i N \ {i}
策略集 S i
每个局中人 i(i 有N一) 个策略集Si ，策略集Si ， 可以是有限集，也可以是无限集，
b1n
b2n
bmn
《博弈论及其应用》 （汪贤 裕）
《博弈论‹及#› 其应用》 （汪贤裕）
30
双矩阵博弈称呼的由来（补充2）
(a11,b11)
(aij , bij )mn
(a21
,
b21
)
(am1 , bm1 )
(a12,b12 ) (a22,b22 )
(am2,bm2 )
(a1n,b1n )
若 s s1, s2,是重, sn复剔除占优均衡，但不是纯策略纳什均衡点。则有
t (i) 和Si t (i,) si , 使i 得N
Pi (s || si ) Pi (s || t (i) )（2.2.2）
s 那么在局中人 在i 对 t的(i)剔除过程中应有对任意的策略组合 满足

F-博弈论专题-4-2纳什均衡多重性ppt课件

F-博弈论专题-4-2纳什均衡多重性ppt课件
（六）创新发展面向小微企业和“三农”的金融产品与服务， 探索建立多层次金融服务体系。鼓励温州辖区内各银行机构 加大对小微企业的信贷支持。支持发展面向小微企业和“三 农”的融资租赁企业。建立小微企业融资综合服务中心。
10
（七）培育发展地方资本市场。依法合规开展非上市公司 股份转让及技术、文化等产权交易。
（十一）完善地方金融管理体制，防止出现监管真空，防 范系统性风险和区域性风险。建立金融业综合统计制度， 加强监测预警。
（十二）建立金融综合改革风险防范机制。清晰界定地方 金融管理的职责边界，强化和落实地方政府处置金融风险 和维护地方金融稳定的责任。
11
创业者的机会！
12
二、风险上策均衡
考虑、顾忌博弈方、其他博弈方可能发生错误等时，帕 累托上策均衡并不一定是最优选择，需要考虑：风险上策均 衡。下面就是两个例子。
网友微评：这年头工作经验比学历更重要！
2
多重纳什均衡博弈的分析
帕累托上策均衡 风险上策均衡 聚点均衡
回顾麦琪的礼物——合理均衡
3
一、帕累托上策均衡
（鹰鸽博弈）
这个博弈中有两个纯策略 纳什均衡，（战争，战争） 和（和平，和平），显然
国 家
战争
1 和平
后者帕累托优于前者，所
以，（和平，和平）是本
城市博弈（城市分组相同）、时间博弈 （报出相同的时间）是聚点均衡的典型例 子
14
焦点效应
在某些存在多个Nash均衡的博弈中，往往 会出现这样的现象：所有的参与人都会相 互预期博弈中某一特定的均衡将会出现， 从而选择执行这个特定的均衡。
15
焦点效应
2005年诺贝尔经济学奖获得者Schelling 对这种现象进行了详尽的探讨并且证明： 在一个具有多重均衡的博弈中，趋向于将 参与人的注意力集中到一个均衡的任何事 情，都可能使参与人全都预期并随之实行 这个均衡，就像一个自行应验的预言一样。

第二章 纳什均衡 《博弈论与经济》 PPT课件

第二章 纳什均衡 《博弈论与经济》 PPT课件

▪ G的纳什均衡可由以下划线法求得。
▪ 1.对局中人1的每个策略i (i 1,2,, m) ，寻找局中人2的最
优反应。若最优反应为
j
，即 bij
max
k 1,2,,n
bik
，则在支付矩
阵元素 bij 下划一短线。
▪ 2.对局中人2的每个策略 j ( j 1,2,, n) ，寻找局中人1的
最优反应，若最优反应为 i
▪ 考虑由商店A, B构成的市场，A与B分别销售不同品牌的商 品，进行价格竞争。假设生产的单位成本为零。消费者 分为两类, n A ( 0)个消费者偏好于产品A，nB ( 0)个消费者 偏好于产品B。A,B两种品牌价格分别为 PA , PB 。设消费 者可从A或B处购买单位商品。
▪ 用 0表示由于购买不喜欢的产品所付出的厌恶成本，假 设消费者具有如下的效用函数
按 等待
等按待
(5,1) (9,1)
4，4
(0, 0)
▪ 严格纳什均衡为大猪“按”，小猪“等待”。
▪ 例2.7 在例1.8中的大堤维护博弈中，支付矩阵为
维护
不维护
不维维护护 （(1
4,4) 0,1 4)
（(1140，,1100)）
▪ 利用划线法可得纳什均衡（维护，维护），（不维护， 不维护）。
▪ 为了保护生命财产的安全，政府可以立法，如果参与人
第2章 纳什均衡
2.1 纳什均衡的定义
▪ 纳什均衡是博弈论中最重要的概念，各种非合作博弈模型的均衡概念都是建 立在纳什均衡基础之上的。
▪ 纳什均衡是个策略组合 s* (si*, s*i ) ，它满足两个要求。
▪
1.对每个局中人 i N
，能够预期到对手采用策略组合s

第二讲纳什均衡ppt课件

第二讲纳什均衡ppt课件
• 上策均衡不是普遍存在的，所以该方法失效 • 失效原因：
13
囚 坦白 徒
1 不坦白
囚徒 2
坦白
不坦白
-3， -3
0， -6
-6， 0
-1， -1
两个罪犯的得益矩阵
14
严格下策反复消去法
• 严格下策：不管其它博弈方的策略如何变化，给一个博弈方带来的收益总 是比另一种策略给他带来的收益小的策略
• 思路： – 任何理性的博弈方都不可能选择严格下策 – 把不可能选择的严格下策先排除掉－－排除法，从而留下较好的策略
的最佳对策，也即 ui (si*, si*1, si*, si*1,...sn*) ui (si*, si*1, sij , si*1,...sn*)
对任意 si j Si 都成立，则称 (si*, sn* ) 为 G 的一个纳什
均衡
24
纳什均衡的一致预测性质
•一致预测：
– 如果所有博弈方都预测一个特定博弈结果会出现，所有博弈方都不会 利用该预测或者这种预测能力，选择与预测结果不一致的策略，即没 有哪个博弈方有偏离这个预测结果的愿望，因此预测结果会成为博弈 的最终结果
R1
100，100 0，0
50，101
R2
50，0 1，1
60，0
R3
0，300 0，0 200，200
26
纳什均衡：举例
• 广告博弈
战略
企业2
做广告 不做广告
企业1
做广告 4，4 15，1 不做广告 1，15 10，10
• 纳什均衡：（做广告，做广告）
27
上次的作业
• 画出田忌赛马的得益矩阵 • 画出猜硬币博弈的得益矩阵 • 画出石头、剪子、布的得益矩阵 • 能否用我们今天的几种方法得到均衡解？ • 你觉得它们的最佳应对策略是什么？

4 纳什均衡

4 纳什均衡
在竞选的时候，两党互相攻击越来越厉害， 而实际政治纲领却越来越靠近。等到一个政党 因为攻击另一个政党获胜取代对对手上台以后， 选民发现，新政府较老政府并没有多少实质的 改变。
精选可编辑ppt
14
假设：选民的政治态度从 0到 1排列，越往左代 表越支持劳工阶层，越往右代表越支持企业主 的利益。如下图所示：
三家都在中点是否是一个稳定的纳什均衡？ 若三家都不在一起，各据一点，能否存在一种
情况为纳什均衡？
精选可编辑ppt
17
结论： 当三家杂货铺为选址而竞争，他们会转来
转去跳个不停：只要三家不在一块儿，单独在 最旁边的一家就要往中间挤；而一旦挤到一块 儿，马上又有动机要偏离，就这样转个不停。
实际生活中存在着往中间挤和转个不停的行为， 如：
精选可编辑ppt
26
生活中具有后动优势的例子 帆船比赛：
1983年，美洲杯帆船赛决赛前4轮后， “自由女神号”在这项以7比4胜的比赛 中暂时以3胜1负的成绩领先，也就是只 要再赢一局，他们就可彻底打败对手 “澳大利亚二号”。
第5轮比赛开始了，“澳大利亚二号” 起步违规，不得不撤回，重新起步，故 “自由女神号”在比赛一开始又获得了 37秒的优势。
若甲认为乙选左与右的可能性是一半对一 半，则甲选“上”支付为：９×１／２＋０× １／２＝４.５；选“下”支付为８×１／２ ＋７×１／２＝７.５，所以，甲会选“下”。
实例：猎人捉兔还是捉鹿的博弈
用考试作弊编故事
精选可编辑ppt
32
关于风险厌恶的统计
究竟应取具有支付优势的ＮＥ还是取具有风险优
势的ＮＥ呢？
精选可编辑ppt
12
（2）商业中心区的形成
在城市街道上，我们常见到一些地

02-博弈中的纳什均衡与一致预期PPT课件

02-博弈中的纳什均衡与一致预期PPT课件
❖ (3)second-order CKR: (1)+(2)+每个人知道（2）
❖ nth-order CKR: R(b)C(b)R(b)……C(b)R is rational,
报考北大研究生？
.
你知道其他的人的 想法？
10
重复剔除与理性共识
❖ 重复剔除不仅要求每个人是理性的，而且要求每个人知道其 他人是理性的，每个人知道每个人知道每个人是理性的，如 此等等，即理性是“共同知识”（共识）
敌不动，我不动
❖ 例如：乒乓球，生气
.
15
纳什均衡的作用：一致预期
❖ 一致预期：基于信念的选择是合理的；支持 选择的信念是正确的；
❖ 预期的自我实现：如何所有人认为这个结果 会出现，这个结果就会出现。预期是自我实 现的，预期不会错误。如果你认为我预期你 将选择X，你就真的会选择X。
当你知道这样的纳什均衡结果将来会存在，你 会作怎样的当期决策？
甲乙
··1/2
图1 商业位置博弈
.
24
❖ 所以给定甲在1/2处设店，乙在紧靠甲的 左边或右边设店是最优的。反过来，给 定乙在接近1/2处设店，甲的最优选择也 是在1/2附近设店。这样，甲和乙挤在1/2 处设店就是纳什均衡，这就是商业中心 区的形成原理。
❖ 例如：电视台节目；禁娱、禁广告插播、 禁广告植入？
❖ 政策的猛烈炮火，使地产股俨然成为了 近期A股市场的“炮灰”。失守3000点的沪深 股市，地产股悲剧持续演绎。继4月19日房地 产指数下跌7.58%以后，昨日(4月20日)，该指 数再度下跌2.91%。无论是招、保、万、金等 传统的四大天王，还是先前基金青睐的二三 线城市地产股，二级市场上都遭遇了前所未 有的持续打压。

静态博弈及纳什均衡的相关案例ppt课件

静态博弈及纳什均衡的相关案例ppt课件

1 2 q3
20
公地悲剧—— N人囚徒困境
•
对于所有牧民：
q1

R1 (q2
,
q3
)

48

1 2
q2

1 2
q3
q2

R2 (q1,
q3 )

48

1 2
q1

1 2
q3
11 q3 R1(q1, q2 ) 48 2 q1 2 q2
• 均衡解： q1* q2* q3* 24
略空间为Si ={ A，B，C }。
得票最多的项目将被选中，如果没有任何项目得 到多数票，项目A被选中。
36
三人投票博弈
不同项目当选时参与人的支付函数如下：
u1(A)=u2(B)=u3(C)= 2 u1(B)=u2(C)=u3(A)= 1 u1(C)=u2(A)=u3(B)= 0
请找出该博弈的纳什均衡。
3 q3[100 (q1 q2 q3)] 4q3
19
公地悲剧—— N人囚徒困境
• 对于牧民1：
• 目标函数： max 1 q1[100 (q1 q2 q3)] 4q1
1
q1
100
(2q1

q2

q3 )

4

0
•
反应函数：
q1
1 48 2 q2

* 1


* 2


* 3

576
Q* 72 * 1728
21
公地悲剧—— N人囚徒困境
情形2：私人牧场上 支付： private Q(100 Q) 4Q
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

• 11、夫学须志也，才须学也，非学无以广才，非志无以成学。20.6.2912:01:3512:01Jun-2029-Jun-20
• 12、越是无能的人，越喜欢挑剔别人的错儿。12:01:3512:01:3512:01Monday, June 29, 2020
• 13、志不立，天下无可成之事。20.6.2920.6.2912:01:3512:01:35June 29, 2020
责，而且在兢兢业业的做好本职工作的同时， 给团队其他岗位或人员以有益的帮助或指导， 而且不以利益获得为前提的认识选择，则该 成员也会做出类似选择，其结果所有团队成 员则会努力学习，提高技能，尽职尽责，分 工协作，实现团队优势最大化。
群体决策与个人决策
在团队建设过程中，一个不可回避的问题 是关系到与团队生存与发展有着密切的关系 的各种各样的决策事项所采用的决策方式， 而决策方式的产生和形成则取决于其多次决 策的正误检验，其本质仍然是决策过程
动的情况下，没有人会主动改变自己的策略 以便获得更大利益。在团队管理中，如果团 队成员之间的选择是在非完全信息对称的情 况下做出的，则团队建设就很有可能遇到纳 什均衡。下面我们试分析之。
企业文化与个人追求
企业文化是作为一个组织的企业内部的全 体员工的共同价值观和道德准则，共同的精 神追求和行为规范，从人本逻辑上来讲，企 业文化则是企业家文化，而企业家文化的形 成和确定，则必然打上企业家个人的价值取 向烙印，即企业家自己的所谓最有利的选
Thank You!
• 9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。20. 6.2920.6.29Monday, June 29, 2020
• 10、人的志向通常和他们的能力成正比例。12:01:3512:01:3512:016/29/2020 12:01:35 PM
平均主义，则每一个团队及其成员则会在这 种给定选择中，彼此的最佳选择就是追求不 劳而获，减少劳动量，甚至是高效能人才的 大量流失和闲置，其结果是企业目标的落空。
团队精神与团队冲突团队
精神要求团队每个成员的行为能够积聚团 队的整体优势，形成合力，解决问题，向团 队目标迈进，而团队冲突则是由于团队成员 在交往中产生意见与分歧，出现分歧，对抗 导致彼此间关系紧张的局面，如果团队成员 都能把团队精神视作其他成员的行为出发
点和落脚点，那么该成员则也会做好他的最 佳选择－－做团队精神的捍卫者和实践者， 从而达成每一个成员的最佳选择；相反如果 团队成员认为其他成员完全站在对抗和竞争 的立场上与之对话，那么该成员也必然会站 在同样的立场上做出选择，其结果导致团队 冲突升级，如果在冲突升级过程中没有任何 成员做出重新的以团队精神为导向的选择， 那么团队精神就会沦为乌有，团队也会走向 解体。
团队建设或管理中，两种决策方式并不是截 然对立的，有时甚至是并存的，即使在这种 情况下，纳什均衡现象依然可能发生，只不 过表现得更加隐蔽和复杂罢了。
小知识：
纳什平衡 （Nash equilibrium ），是由 经济学家J. 纳什提出的，是指：非合作对策 中所有对策人都根据各自的信息选择策略， 力图使自己的目标函数值达到最大的一种平 衡解。

• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
择。而团队成员在某种特定的企业文化氛围 里边也有着每个人的追求，即所谓的他所做 的对自己最有利的选择，如果团队成员的选 择与企业家的选择是一致的，这构成一种合 作均衡，否则，团队成员的选择与企业的选 择不同甚至完全相反，这就形成了纳什均衡。 如在市场经济条件下，一家企业文化的价值 追求体系是效率公平，则每一个团队在这种 特定选择中，彼此的最佳选择就是追求效益 最大化，更快更好地完成团队目标，其结果 是企业目标的顺利实现；相反如果一家企业 文化的价值追求体系是伦理公平，讲求
职责分工与利益分配
在团队管理中，进行岗位的职责分工并
进行相对应的利益分配是团队打造的基本要 求。从资源配置的角度看：讲究的是合适的 人在合适的时间做合适的事情，其本质仍然 是合作均衡和纳什均衡的问题。团队成员会 假定其他成员在特定能力、时间和劳动量及 利益分配收获的情况下的工作态度、道德水 准和努力程度。如果一成员认为其他成员在 同样岗位上选择职责过多，劳动强度过大， 而利益收获不足的认识，那么该成员也会选 择同样的看法和认识，最终必然导致职责缺 失，管理漏洞和工作缺位而妨害团队优势的 形成甚至团队目标的完成；相反如果某成员 做出团队其他成员不但承担了大量的工作职
的合作均衡和纳什均衡。个人决策，顾名思 义是团队成员的个体做出决定的行为，而群 体决策是群体成员共同对问题进行分析、探 讨、争论和沟通，最终消除分歧达成共识的 过程。如果团队其他成员选择认为团队某个 成员一贯做出正确的决策，那么个人决策就 会成为团队成员的共同选择，相反如果团队 成员不选择团队某成员能够做出一贯的正确 决策，则团队成员则会倾向于群体决策的选 择，而个人决策和群体决策什么时候导致合 作均衡，什么情况下带来纳什均衡不是一个 理论问题而是一个实践问题，并且在现实的
浅谈团队管理中的纳什均衡
2006年7月
众所周知，团队就是由每一位个体员工和 管理者个体组成的一个共同体，该共同体能 够集中每个个体的知识、智慧和技能优势， 促进个体之间的高度互补与工作协调，并形 成团队优质，解决问题，实现共同目标，而 纳什均衡则是指定博弈、对策和游戏中的一 种情形，一种给定博弈、对策和游戏对手的 最佳选择，自己的最佳选择，即每个人都从 利己的角度出发做出最佳选择，选择对自己 最有利的策略，而不考虑社会福利或其他对 手的利益，这种策略组合由所有局中人的最 佳策略组合构成，在缺乏有效外力推