高中数学课件精选--随机变量的方差

2．3.2 离散型随机变量的方差1．问题导航(1)离散型随机变量的方差及标准差的定义是什么？(2)方差具有哪些性质？两点分布与二项分布的方差分别是什么？ (3)如何计算简单离散型随机变量的方差？ 2．例题导读(1)例4求随机变量的均值和方差、标准差，请试做教材P 68练习1题． (2)例5是均值和方差的实际应用，请试做教材P 68练习3题．1．方差、标准差的定义及方差的性质 (1)方差及标准差的定义：设离散型随机变量X 的分布列为①方差D (X )＝∑n i ＝1(x i －E (X ))2p i . ②标准差为________D （X ）．(2)方差的性质：D (aX ＋b )＝________a 2D (X )． 2．两个常见分布的方差(1)若X 服从两点分布，则D (X )＝________p (1－p )． (2)若X ～B (n ，p )，则D (X )＝________np (1－p )．1．判断(对的打“√”，错的打“×”)(1)离散型随机变量的方差越大，随机变量越稳定．( ) (2)若a 是常数，则D (a )＝0.( )(3)离散型随机变量的方差反映了随机变量偏离于期望的平均程度．( ) 答案：(1)× (2)√ (3)√2．一批产品中，次品率为13，现连续抽取4次，其次品数记为X ，则D (X )的值为( )A.43B.83C.89D ．1答案：C3．如果X 是离散型随机变量，E (X )＝6，D (X )＝0.5，X 1＝2X －5，那么E (X 1)和D (X 1)分别是( )A ．E (X 1)＝12，D (X 1)＝1B ．E (X 1)＝7，D (X 1)＝1C ．E (X 1)＝12，D (X 1)＝2 D ．E (X 1)＝7，D (X 1)＝2 答案：D4．已知随机变量X ________.答案：3.561．方差与标准差的作用随机变量的方差与标准差一样，都是反映随机变量的取值的稳定与波动、集中与离散程度的，方差越小，取值越集中，稳定性越高，波动性越小；反之，方差越大，取值越不集中，稳定性越差，波动性越大．2．随机变量的方差与样本方差的关系随机变量的方差是总体的方差，它是一个常数，样本的方差则是随机变量，是随样本的变化而变化的．对于简单随机样本，随着样本容量的增加，样本的方差越来越接近于总体的方差．求离散型随机变量的方差袋中有20个大小相同的球，其中记上0号的有10个，记上n 号的有n 个(n ＝1，2，3，4)．现从袋中任取一球，ξ表示所取球的标号．求ξ的分布列、均值和方差；[解] 由题意得，ξ的所有可能取值为0，1，2，3，4，P (ξ＝0)＝1020＝12，P (ξ＝1)＝120，P (ξ＝2)＝220＝110，P (ξ＝3)＝320，P (ξ＝4)＝420＝15.故ξ的分布列为所以E (ξ)＝0×12＋1×120＋2×110＋3×320＋4×15＝1.5，D (ξ)＝(0－1.5)2×12＋(1－1.5)2×120＋(2－1.5)2×110＋(3－1.5)2×320＋(4－1.5)2×15＝2.75.[互动探究] 在本例条件下，若η＝aξ＋b ，E (η)＝1，D (η)＝11，试求a ，b 的值． 解：由D (aξ＋b )＝a 2D (ξ)＝11，E (aξ＋b )＝aE (ξ)＋b ＝1，及E (ξ)＝1.5，D (ξ)＝2.75，得2.75a 2＝11，1.5a ＋b ＝1，解得a ＝2，b ＝－2或a ＝－2，b ＝4.1．求离散型随机变量X 的均值、方差的步骤： (1)理解X 的意义，写出X 的所有可能的取值； (2)求X 取每一个值的概率； (3)写出随机变量X 的分布列；(4)由均值、方差的定义求E (X )，D (X )．2．对于变量间存在关系的方差，在求解过程中应注意方差性质的应用，如D (aξ＋b )＝a 2D (ξ)，这样处理既避免了求随机变量η＝aξ＋b 的分布列，又避免了繁杂的计算，简化了1．(1)已知随机变量ξ若E (ξ)＝23，则D (ξ)的值为________．解析：由分布列的性质，得 12＋13＋p ＝1，解得p ＝16. ∵E (ξ)＝0×12＋1×13＋16x ＝23，∴x ＝2.D (ξ)＝⎝⎛⎭⎫0－232×12＋⎝⎛⎭⎫1－232×13＋⎝⎛⎭⎫2－232×16＝1527＝59. 答案：59(2)甲、乙两人进行定点投篮游戏，投篮者若投中，则继续投篮，否则由对方投篮，第一次由甲投篮；已知每次投篮甲、乙命中的概率分别为13，34.在前3次投篮中，乙投篮的次数为ξ，求ξ的分布列、期望．解：乙投篮的次数ξ的取值为0，1，2.P (ξ＝0)＝13×13＝19；P (ξ＝1)＝13×23＋23×14＝718.P (ξ＝2)＝23×34＝12.故ξ的分布列为E (ξ)＝0×19＋1×718＋2×12＝2518，D (ξ)＝(0－2518)2×19＋(1－2518)2×718＋(2－2518)2×12＝149324.两点分布与二项分布的方差一出租车司机从某饭店到火车站途中有六个交通岗，假设他在各交通岗遇到红灯这一事件是相互独立的，并且概率是13.(1)求这位司机遇到红灯数ξ的期望与方差；(2)若遇上红灯，则需等待30 s ，求司机总共等待时间η的期望与方差． [解] (1)易知司机遇上红灯次数ξ服从二项分布，且ξ～B (6，13)，故E (ξ)＝6×13＝2，D (ξ)＝6×13×(1－13)＝43.(2)由已知η＝30ξ，故E (η)＝30E (ξ)＝60(s)，D (η)＝900D (ξ)＝1 200.解决此类问题的第一步是判断随机变量ξ服从什么分布，第二步代入相应的公式求解．若ξ服从两点分布，则D (ξ)＝p (1－p )；若ξ服从二项分布，即ξ～B (n ，p )，则D (ξ)＝np (1－p )．2．(1)(2015·高考广东卷)已知随机变量X 服从二项分布B (n ，p )．若E (X )＝30，D (X )＝20，则p ＝________．解析：由E (X )＝30，D (X )＝20，可得⎩⎪⎨⎪⎧np ＝30，np （1－p ）＝20，解得p ＝13.答案：13(2)在某地举办的射击比赛中，规定每位射手射击10次，每次一发．记分的规则为：击中目标一次得3分；未击中目标得0分；并且凡参赛的射手一律另加2分．已知射手小李击中目标的概率为0.8，求小李在比赛中得分的数学期望与方差．解：用ξ表示小李击中目标的次数，η表示他的得分，则由题意知ξ～B(10，0.8)，η＝3ξ＋2.因为E(ξ)＝10×0.8＝8，D(ξ)＝10×0.8×0.2＝1.6，所以E(η)＝E(3ξ＋2)＝3E(ξ)＋2＝3×8＋2＝26(分)，D(η)＝D(3ξ＋2)＝32×D(ξ)＝9×1.6＝14.4.均值、方差的综合应用甲、乙两名射手在一次射击中得分为两个相互独立的随机变量X与Y，且X，Y 的分布列如下：(1)求a，b的值；(2)计算X，Y的期望与方差，并以此分析甲、乙技术状况．[解](1)由离散型随机变量的分布列的性质可知a＋0.1＋0.6＝1，得a＝0.3.同理0.3＋b＋0.3＝1，得b＝0.4.(2)E(X)＝1×0.3＋2×0.1＋3×0.6＝2.3，E(Y)＝1×0.3＋2×0.4＋3×0.3＝2，D(X)＝(1－2.3)2×0.3＋(2－2.3)2×0.1＋(3－2.3)2×0.6＝0.81，D(Y)＝(1－2)2×0.3＋(2－2)2×0.4＋(3－2)2×0.3＝0.6.由于E(X)＞E(Y)，说明在一次射击中，甲的平均得分比乙高，但D(X)＞D(Y)，说明甲得分的稳定性不如乙，因此甲、乙两人技术水平都不够全面，各有优势与劣势．离散型随机变量的期望反映了离散型随机变量取值的平均水平，而方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度．因此在实际决策问题中，需先运算均值，看一下谁的平均水平高，然后再计算方差，分析一下谁的水平发挥相对稳定，当然不同的模型要求不同，应视情况而定．3．甲、乙两个野生动物保护区有相同的自然环境，且野生动物的种类和数量也大致相试评定这两个保护区的管理水平．解：甲保护区违规次数ξ的数学期望和方差分别为E (ξ)＝0×0.3＋1×0.3＋2×0.2＋3×0.2＝1.3；D (ξ)＝(0－1.3)2×0.3＋(1－1.3)2×0.3＋(2－1.3)2×0.2＋(3－1.3)2×0.2＝1.21.乙保护区的违规次数η的数学期望和方差分别为E (η)＝0×0.1＋1×0.5＋2×0.4＝1.3； D (η)＝(0－1.3)2×0.1＋(1－1.3)2×0.5＋(2－1.3)2×0.4＝0.41.因为E (ξ)＝E (η)，D (ξ)＞D (η)，所以两个保护区内每个季度发生的违规事件的平均次数相同，但甲保护区的违规事件次数相对分散和波动性大，乙保护区的违规事件次数更集中和稳定，说明乙保护区的管理水平较好．试求D (X )和D (2X －1)．[解] E (X )＝0×0.2＋1×0.2＋2×0.3＋3×0.2＋4×0.1＝1.8，所以D (X )＝(0－1.8)2×0.2＋(1－1.8)2×0.2＋(2－1.8)2×0.3＋(3－1.8)2×0.2＋(4－1.8)2×0.1＝1.56.所以D (2X －1)＝4D (X )＝4×1.56＝6.24.[错因与防范] (1)解答本例易将方差的性质用错，即D (aZ ＋b )＝aD (Z )＋b . (2)解决此类问题方法，应利用公式E (aX ＋b )＝aE (X )＋b ，D (aX ＋b )＝a 2D (X )，将求E (aX ＋b )，D (aX ＋b )的问题转化为求E (X )，D (X )的问题，从而可以避免求aX ＋b 的分布列的繁琐的计算，解题时可根据两者之间的关系列出等式，进行相关计算．4．已知随机变量X ～B (100，0.2)，那么D (4X ＋3)的值为( ) A ．64 B ．256 C ．259 D ．320解析：选B.由X ～B (100，0.2)知n ＝100，p ＝0.2， 由公式得D (X )＝np (1－p )＝100×0.2×0.8＝16， 因此D (4X ＋3)＝42D (X )＝16×16＝256.1．设一随机试验的结果只有A 和A ，且P (A )＝m ，令随机变量ξ＝⎩⎪⎨⎪⎧1，A 发生，0，A 不发生，则ξ的方差D (ξ)等于( )A ．mB ．2m (1－m )C ．m (m －1)D ．m (1－m ) 解析：选D.随机变量ξ∴E (ξ)＝0×(1－m )＋1×m ＝m .∴D (ξ)＝(0－m )2×(1－m )＋(1－m )2×m ＝m (1－m )．2．已知随机变量X ＋Y ＝8，若X ～B (10，0.6)，则E (Y )，D (Y )分别是( ) A ．6和2.4 B ．2和2.4 C ．2和5.6 D ．6和5.6解析：选B.由已知随机变量X ＋Y ＝8，所以有Y ＝8－X . 因此，求得E (Y )＝8－E (X )＝8－10×0.6＝2， D (Y )＝(－1)2D (X )＝10×0.6×0.4＝2.4.3．有两台自动包装机甲与乙，包装质量分别为随机变量X 1，X 2，已知E (X 1)＝E (X 2)，D (X 1)>D (X 2)，则自动包装机________的质量较好．解析：因为E (X 1)＝E (X 2)，D (X 1)>D (X 2)，故乙包装机的质量稳定． 答案：乙4．若随机变量X 的分布列为：(1)求m 的值；(2)求E (X )和D (X )．解：(1)由随机变量分布列的性质，得0.1＋0.2＋0.4＋m ＋0.1＝1，解得m ＝0.2.(2)E (X )＝－2×0.1＋(－1)×0.2＋0×0.4＋1×0.2＋2×0.1＝0，D (X )＝(－2－0)2×0.1＋(－1－0)2×0.2＋(0－0)2×0.4＋(1－0)2×0.2＋(2－0)2×0.1＝1.2.[A.基础达标]1．下列说法正确的是( )A ．离散型随机变量ξ的数学期望E (ξ)反映了ξ取值的概率的平均值B ．离散型随机变量ξ的方差D (ξ)反映了ξ取值的平均水平C ．离散型随机变量ξ的数学期望E (ξ)反映了ξ取值的平均水平D ．离散型随机变量ξ的方差D (ξ)反映了ξ取值的概率的平均值解析：选C.由离散型随机变量的数学期望与方差的定义可知，C 正确．故选C. 2．设X ～B (n ，p )，若D (X )＝4，E (X )＝12，则n 和p 分别为( ) A ．18和23B ．16和12C ．20和13D ．15和14解析：选A.∵X ～B (n ，p )，∴⎩⎪⎨⎪⎧np ＝12，np （1－p ）＝4，解得p ＝23，n ＝18.3．已知X 的分布列如下表所示，则下列式子：①E (X )＝－13；②D (X )＝2327；③P (X ＝0)＝13.其中正确的有( )A.0个 B ．1个 C ．2个D ．3个解析：选C.E (X )＝(－1)×12＋0×13＋1×16＝－13，D (X )＝(－1＋13)2×12＋(0＋13)2×13＋(1＋13)2×16＝59，故只有①③正确． 4．设随机变量ξ的分布列为P (ξ＝k )＝C k n (23)k ·(13)n －k ，k ＝0，1，2，…，n ，且E (ξ)＝24，则D (ξ)的值为( ) A ．8B ．12 C.29D ．16解析：选A.由题意可知ξ～B (n ，23)，∴23n ＝E (ξ)＝24.∴n ＝36. ∴D (ξ)＝n ×23×(1－23)＝29×36＝8.5．(2015·滨州高二期末检测)若随机变量X 的分布列为：P (X ＝m )＝13，P (X ＝n )＝a ，若E (X )＝2，则D (X )的最小值等于( )A ．0B ．2C ．4D ．无法计算解析：选A.依题意有a ＝1－13＝23，所以E (X )＝13m ＋23n ＝2，即m ＋2n ＝6.又D (X )＝13(m－2)2＋23(n －2)2＝2n 2－8n ＋8＝2(n －2)2，所以当n ＝2时，D (X )有最小值为0.6．(2014·高考浙江卷)随机变量ξ的取值为0，1，2.若P (ξ＝0)＝15，E (ξ)＝1，则D (ξ)＝________．解析：设P (ξ＝1)＝a ，P (ξ＝2)＝b ，则⎩⎪⎨⎪⎧15＋a ＋b ＝1，a ＋2b ＝1，解得⎩⎨⎧a ＝35，b ＝15，所以D (ξ)＝15＋35×0＋15×1＝25.答案：257．(2015·扬州高二检测)设一次试验成功的概率为p ，进行100次独立重复试验，当p ＝________时，成功次数的标准差的值最大，其最大值为________．解析：由独立重复试验的方差公式可以得到 D (ξ)＝np (1－p )≤n (p ＋1－p 2)2＝n4，等号在p ＝1－p ＝12时成立，所以D (ξ)max ＝100×12×12＝25,D （ξ）max ＝25＝5.答案：1258．随机变量ξ的分布列如下，其中a ，b ，c 成等差数列．若E (ξ)＝53，则D (ξ)的值为________．解析：因为a ，b ，c 成等差数列，所以a ＋c ＝2b .又因为a ＋b ＋c ＝1，所以b ＝13.又因为E (ξ)＝a ＋2b ＋3c ＝53，所以a ＝12，b ＝13，c ＝16，所以ξ的分布列为所以D (ξ)＝(1－53)2×12＋(2－53)2×13＋(3－53)2×16＝59.答案：599．设在12个同类型的零件中有2个次品，抽取3次进行检验，每次抽取1个，并且取出不再放回，若以ξ表示取出次品的个数，求ξ的分布列、期望值及方差．解：ξ的可能值为0，1，2，P (ξ＝0)＝C 02C 310C 312＝611；P (ξ＝1)＝C 12C 210C 312＝922；P (ξ＝2)＝C 22C 110C 312＝122.∴ξ的分布列为∴E (ξ)＝0×611＋1×922＋2×122＝12，D (ξ)＝(0－12)2×611＋(1－12)2×922＋(2－12)2×122＝322＋988＋988＝1544.10．为防止风沙危害，某地决定建设防护绿化带，种植杨树、沙柳等植物．某人一次种植了n 株沙柳，各株沙柳成活与否是相互独立的，成活率为p ，设ξ为成活沙柳的株数，数学期望E (ξ)＝3，标准差D （ξ）＝62. (1)求n ，p 的值并写出ξ的分布列；(2)若有3株或3株以上的沙柳未成活，则需要补种，求需要补种沙柳的概率．解：因为每一株沙柳成活率均为p ，种植了n 株沙柳，相当于做n 次独立重复试验，因此ξ服从二项分布ξ～B (n ，p )．(1)由E (ξ)＝np ＝3，D (ξ)＝np (1－p )＝32，得1－p ＝12，从而n ＝6，p ＝12.ξ的分布列为：(2)记“需要补种沙柳”为事件A ，则P (A )＝P (ξ≤3)， 得P (A )＝1＋6＋15＋2064＝2132.[B.能力提升]1．有甲、乙两名学生，经统计，他们在解答同一份数学试卷时，各自的成绩在80分、90分、100分的概率分布列大致如下表所示：甲：乙：试分析两名学生的成绩水平．解：∵E (X )＝80×0.2＋90×0.6＋100×0.2＝90，D (X )＝(80－90)2×0.2＋(90－90)2×0.6＋(100－90)2×0.2＝40，E (Y )＝80×0.4＋90×0.2＋100×0.4＝90，D (Y )＝(80－90)2×0.4＋(90－90)2×0.2＋(100－90)2×0.4＝80， ∵E (X )＝E (Y )，D (X )＜D (Y )，∴甲生与乙生的成绩均值一样，甲的方差较小，因此甲生的学习成绩较稳定．2．如表，左边为四大名著，右边为名著作者，一位小学语文教师为了激发学生阅读名著的热情，在班内进行名著和其作者的连线游戏，作为奖励，参加连线的同学每连对一个奖励一朵小红花．假定一名小学生对四大名著没有了解，只是随机地连线，试求该学生得到小红花数X 的分布列及其均值、方差．解：可能为0个，1个，2个，4个．P (X ＝0)＝9A 44＝924，P (X ＝1)＝C 14×2A 44＝824， P (X ＝2)＝C 24×1A 44＝624，P (X ＝4)＝1A 44＝124. 故X 的分布列为：∴E (X )＝0×924＋1×824＋2×624＋4×124＝1， D (X )＝924×(0－1)2＋824×(1－1)2＋624×(2－1)2＋124×(4－1)2＝9＋0＋6＋924＝1. 3．某学校为高二年级开展第二外语选修课，要求每位同学最多可以选报两门课程．已知有75%的同学选报法语课，有60%的同学选报日语课．假设每个人对课程的选报是相互独立的，且各人的选报相互之间没有影响．(1)任选1名同学，求其选报过第二外语的概率；(2)任选3名同学，记ξ为3人中选报过第二外语的人数，求ξ的分布列、期望和方差． 解：设事件A ：选报法语课；事件B ：选报日语课．由题设知，事件A 与B 相互独立，且P (A )＝0.75，P (B )＝0.6.(1)法一：任选1名同学，该同学一门课程都没选报的概率是P 1＝P (A －B －)＝P (A )·P (B )＝0.25×0.4＝0.1.所以该人选报过第二外语的概率是P 2＝1－P 1＝1－0.1＝0.9.法二：任选1名同学，该同学只选报一门课程的概率是P 3＝P (AB )＋P (AB )＝0.75×0.4＋0.25×0.6＝0.45，该人选报两门课程的概率是P 4＝P (AB )＝0.75×0.6＝0.45.所以该同学选报过第二外语的概率是P 5＝P 3＋P 4＝0.45＋0.45＝0.9.(2)因为每个人的选报是相互独立的，所以3人中选报过第二外语的人数ξ服从二项分布B (3，0.9)，P (ξ＝k )＝C k 3×0.9k ×0.13－k ，k ＝0，1，2，3， 即ξ的分布列是ξ的期望是E(ξ)＝(或ξ的期望是E(ξ)＝3×0.9＝2.7)，ξ的方差是D(ξ)＝3×0.9×(1－0.9)＝0.27.。

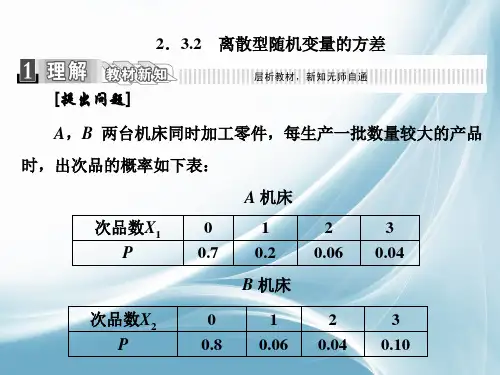
导入新课复习回顾1 .离散型随机变量 X 的均值 均值反映了离散型随机变量取值的平均水平.2 . 两种特殊分布的均值（1）若随机变量X 服从两点分布，则EX=p.（2）若X~B(n ，p) ，则EX=np.ni ii=1EX =x p数学期望是离散型随机变量的一个特征数，它反映了离散型随机变量取值的平均水平，表示了随机变量在随机实验中取值的平均值，所以又常称为随机变量的平均数、均值.今天，我们将对随机变量取值的稳定与波动、集中与离散的程度进行研究.2.3.2离散型随机变量的方差教学目标知识与技能（1）了解离散型随机变量的方差、标准差的意义；（2）会根据离散型随机变量的分布列求出方差或标准差.过程与方法了解方差公式“D(aξ+b)=a2Dξ”，以及“若ξ~Β(n，p)，则Dξ=np(1-p)”，并会应用上述公式计算有关随机变量的方差 .情感、态度与价值观承前启后，感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值.教学重难点重点离散型随机变量的方差、标准差.难点比较两个随机变量的期望与方差的大小，从而解决实际问题 .思考要从两名同学中挑选出一名，代表班级参加射击比赛. 根据以往的成绩记录，第一名同学击中目标靶的环数X1的分布列为X1 5 6 7 8 9 10P 0.03 0.09 0.20 0.31 0.27 0.10第二名同学击中目标靶的环数X2的分布列为X2 5 6 7 8 9P 0.01 0.05 0.20 0.41 0.33根据已学知识，可以从平均中靶环数来比较两名同学射击水平的高低，即通过比较X1和X2的均值来比较两名同学射击水平的高低. 通过计算E(X1)=8，E(X2)=8，发现两个均值相等，因此只根据均值不能区分这两名同学的射击水平.思考除平均中靶环数外，还有其他刻画两名同学各自射击特点的指标吗？图(1)(2)分别表示X 1和X 2的分布列图. 比较两个图形，可以发现，第二名同学的射击成绩更集中于8环，即第二名同学的射击成绩更稳定. O 5 6 7 10 9 8 P 1X 0.10.20.30.40.5O 5 6 7 9 8 P 2X 0.1 0.2 0.3 0.4 0.5 (1) (2) 怎样定量刻画随机变量的稳定性?1.方差设离散型随机变量X 的分布列为知识要点X x 1 x 2 … x i … x n Pp 1p 2…p i…p n则(x i -E(X))2描述了x i (i=1，2，…，n)相对于均值E(X)的偏离程度.为这些偏离程度的加权平均，刻画了随机变量 X 与其均值 EX 的平均偏离程度.我们称 DX 为随机变量 X 的方差(variance). 其算术平方根 为随机变量X 的标准差(standard deviation). 记为 n2i ii=1DX =(x -EX)p DX σX 随机变量的方差和标准差都反映了随机变量取值偏离于均值的平均程度.方差或标准差越小，则随机变量偏离于均值的平均程度越小.说明：随机变量集中的位置是随机变量的均值；方差或标准差这种度量指标是一种加权平均的度量指标.思考随机变量的方差与样本的方差有何联系与区别?随机变量的方差是常数，而样本的方差是随着样本的不同而变化的，因此样本的方差是随机变量.对于简单随机样本，随着样本容量的增加，样本方差越来越接近总体方差，因此常用样本方差来估计总体方差.现在，可以用两名同学射击成绩的方差来刻画他们各自的特点，为选派选手提供依据.由前面的计算结果及方差的定义，得∑102DX=(i-8)P(X=i)=1.50,11i=5∑92DX=(i-8)P(X=i)=0.8222i=5因此第一名同学的射击成绩稳定性较差，第二名同学的射击成绩稳定性较好，稳定于8环左右.知识要点2.几点重要性质（1）若X服从两点分布，则D(X)=p(1-p); （2）若X~B(n，p)，则D(X)=np(1-p); （3）D(aX+b)=a2D(X).例题1A、B两台机床同时加工零件，每生产一批数量较大的产品时，出次品的概率如下表所示：0 1 2 3次品数ξ1概率P 0.7 0.2 0.06 0.040 1 2 3次品数ξ1概率P 0.8 0.06 0.04 0.10问哪一台机床加工质量较好？解：Eξ1=0×0.7+1×0.2+2×0.06+3×0.04=0.44, Eξ2=0×0.8+1×0.06+2×0.04+3×0.10=0.44. 它们的期望相同，再比较它们的方差Dξ1=(0-0.44)2×0.7+(1-0.44)2×0.2+(2-0.44)2 ×0.06+(3-0.44)2×0.04=0.6064,Dξ2=(0-0.44)2×0.8+(1-0.44)2×0.06+(2-0.44)2 ×0.04+(3-0.44)2×0.10=0.9264.∴Dξ1< Dξ2 故A 机床加工较稳定、质量较好.例题2有甲乙两个单位都愿意聘用你，而你能获得如下信息：/元1200 1400 1600 1800 甲单位不同职位月工资X10.4 0.3 0.2 0.1获得相应职位的概率P1乙单位不同职位月工资X/元1000 1400 1800 220020.4 0.3 0.2 0.1获得相应职位的概率P2根据工资待遇的差异情况，你愿意选择哪家单位？解：根据月工资的分布列，利用计算器可算得1EX =12000.4 + 1 4000.3 + 16000.2 + 18000.1 =1400⨯⨯⨯⨯2221DX = (1200-1400) 0. 4 + (1400-1400 )0.3 + (1600 -1400 )0.2⨯⨯⨯2+(1800-1400) 0. 1= 40 000⨯2EX =1 0000.4 +1 4000.3 + 1 8000.2 + 22000.1 = 1400⨯⨯⨯⨯2222DX = (1000-1400)0. 4+(1 400-1400)0.3 + (1800-1400)0.2⨯⨯⨯2+ (2200-1400 )0.l = 160000 .⨯分析：因为 ，所以两家单位的工资均值相等，但甲单位不同职位的工资相对集中，乙单位不同职位的工资相对分散.这样，如果你希望不同职位的工资差距小一些，就选择甲单位；如果你希望不同职位的工资差距大一些，就选择乙单位.1212EX =EX ,DX <DX例题3有同寝室的四位同学分别写一张贺年卡，先集中起来，然后每人去拿一张，记自己拿自己写的贺年卡的人数为X.（1）求随机变量的概率分布；（2）求X的数学期望和方差.4411689P(X =4)==,P(X =3)=0,P(X =2)=,P(X =1)=,P(X =0)=A 242424249861E(X)=0+1+2+30+4=124242424⨯⨯⨯⨯⨯222229861V(X)=(0-1)+(1-1)+(2-1)+(3-1)0+(4-1)=124242424⨯⨯⨯⨯⨯解：（1）因此X 的分布列为（2） X 0 1 23 4 P 9/24 8/24 6/24 0 1/24例题3有一庄家为吸引顾客玩掷骰子游戏，以便自己轻松获利，以海报形式贴出游戏规则：顾客免费掷两枚骰子，把掷出的点数相加，如果得2或12，顾客中将30元；如果得3或11，顾客中将20元；如果得4或10，顾客中将10元；如果得5或9，顾客应付庄家10元；如果得6或8，顾客应付庄家20元；如果得7，顾客应付庄家30元．试用数学知识解释其中的道理.解 :设庄家获利的数额为随机变量，根据两枚骰子的点数之和可能的结果以及游戏规则可得随机变量的概率分布为：X -30 -20 -10 10 20 30 P 2/36 4/36 6/36 8/36 10/36 6/36 246810665 E(X)=(-30)+(-20)+(-10)+10+20+30=⨯⨯⨯⨯⨯⨯3636363636369因此，顾客每玩36人次，庄家可获利约260元，但不确定顾客每玩36人次一定会有些利润；长期而言，庄家获利的均值是这一常数，也就是说庄家一定是赢家.1.熟记方差计算公式课堂小结n 2i i i=1DX =(x -EX)p 2=E(X-EX)22=EX -(EX)2. 三个重要的方差公式（1）若 X 服从两点分布，则 （2）若 ，则 X ~B(n,p)DX =np(1-p)DX =p(1-p)2(3)D(aX +b)=a DX3.求离散型随机变量X的方差、标准差的一般步骤：①理解X 的意义，写出X 可能取的全部值；②求X取各个值的概率，写出分布列；③根据分布列，由期望的定义求出EX；④根据方差、标准差的定义求出、σXDX高考链接1. （2005年天津）某公司有5万元资金用于投资开发项目，如果成功，一年后可获利12%，一旦失败，一年后将丧失全部资金的50%，下表是过去200例类似项目开发的实施结果：投资成功投资失败192次8次则该公司一年后估计可获收益的期望是_____（元）.[答案]4760提示：分布列为ξ0.6 -2.5P 192/200 8/192故1928Eξ=0.6-2.5=4760()200200元⨯⨯2.（2002年天津）甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下（单位：5t/hm2）表所示：品种第一年第二年第三年第四年第五年甲9.8 9.9 10.1 10 10.2 乙9.4 10.3 10.8 9.7 9.8则其中产量比较稳定的小麦品种是_______．[答案]甲种3.（2004年湖北）某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成400万元的损失．现有甲、乙两种相互独立的预防措施可供采用，单独采用甲、乙预防措施所需的费用分别为45万元和30万元，采用相应预防措施后此突发事件不发生的概率分别为0.9和0.85，若预防方案允许甲、乙两种预防措施单独采用，联合采用或不采用，请确定预防方案使总费用最少.（总费用=采取预防措施的费用＋发生突发事件损失的期望值）[解析]①不采用预防措施时，总费用即损失期望值为400×0.3=120（万元）；②若单独采取措施甲，则预防措施费用为45万元，发生突发事件的概率为1－0.9=0.1，损失期望值为400×0.l=40（万元），所以总费用为45＋40=85（万元）；③若单独采取预防措施乙，则预防措施费用为30万元，发生突发事件的概率为1－0.85=0.15，损失期望值为400×0.15=60（万元），所以总费用为30＋60=90（万元）；继续④若联合采取甲、乙两种预防措施，则预防措施费用为45＋30=75（万元），发生突发事件的概率为(1－0.9)(1－0.85)=0.015，损失期望值为400×0.015=6（万元），所以总费用为75＋6=81（万元）．综合①、②、③、④，比较其总费用可知，应选择联合采取甲、乙两种预防措施，可使总费用最少．1.填空课堂练习（1）已知x~B(100,0.5),则Ex=___,Dx=____,sx=___. E(2x-1)=____, D(2x-1)=____, s(2x-1)=_____. 50 25 59910010（1）已知随机变量x 的分布列如上表,则E x 与D x 的值为( )A. 0.6和0.7B. 1.7和0.3C. 0.3和0.7D. 1.7和0.21（2）已知x~B(n ，p)，E x =8，D x =1.6，则n ， p 的值分别是（ ）A ．100和0.08；B ．20和0.4；C ．10和0.2；D ．10和0.8 2.选择 √ x1 2 P 0.3 0.7√3.解答题（1）一盒中装有零件12个，其中有9个正品，3个次品，从中任取一个，如果每次取出次品就不再放回去，再取一个零件，直到取得正品为止．求在取得正品之前已取出次品数的期望.分析：涉及次品率；抽样是否放回的问题．本例采用不放回抽样，每次抽样后次品率将会发生变化，即各次抽样是不独立的．如果抽样采用放回抽样，则各次抽样的次品率不变，各次抽样是否抽出次品是完全独立的事件.解：设取得正品之前已取出的次品数为ξ，显然ξ所有可能取的值为0，1，2，3①当ξ=0时，即第一次取得正品，试验停止，则P （ξ=0）= ②当ξ=1时，即第一次取出次品，第二次取得正品，试验停止，则P （ξ=1）= 43129=449119123=⨯③当ξ=2时，即第一、二次取出次品，第三次取得正品，试验停止，则P （ξ=2）= ④当ξ=3时，即第一、二、三次取出次品，第四次取得正品，试验停止，则 P （ξ=3）= 所以，Eξ= 3299=121110220⨯⨯32191=1211109220⨯⨯⨯399130+1+2+3=44422022010⨯⨯⨯⨯继续（2）有一批数量很大的商品的次品率为1%，从中任意地连续取出200件商品，设其中次品数为ξ，求Eξ，Dξ分析：涉及产品数量很大，而且抽查次数又相对较少的产品抽查问题．由于产品数量很大，因而抽样时抽出次品与否对后面的抽样的次品率影响很小，所以可以认为各次抽查的结果是彼此独立的．解答本题，关键是理解清楚：抽200件商品可以看作200次独立重复试验，即ξ~B（200，1%），从而可用公式：Eξ=np，Dξ=npq(这里q=1-p)直接进行计算.解：因为商品数量相当大，抽200件商品可以看作200次独立重复试验，所以ξ~ B（200，1%）因为Eξ=np，Dξ=npq，这里n=200，p=1%，q=99%，所以,Eξ=200×1%=2,Dξ=200×1%×99%=1.98.习题解答1. E(X)=0×0.1+1×0.2+2×0.4+3×0.2+4×0.1=2. D(X)=(0-2)2×0.1+(1-2)2×0.2+(2-2)2×0.4+(3- 2)2×0.2+(4-2)2×0.1=1.2.D(X) 1.095.2. E(X)=c×1=c，D(X)=(c-c)2×1=0.3. 略.。

离散型随机变量的期望与方差知识集结知识元离散型随机变量的期望与方差知识讲解1．离散型随机变量的期望与方差【知识点的知识】1、离散型随机变量的期望数学期望：一般地，若离散型随机变量ξ的概率分布为x1x2…x n…P p1p2…p n…则称Eξ＝x1p1+x2p2+…+x n p n+…为ξ的数学期望，简称期望．数学期望的意义：数学期望离散型随机变量的一个特征数，它反映了离散型随机变量取值的平均水平．平均数与均值：一般地，在有限取值离散型随机变量ξ的概率分布中，令p1＝p2＝…＝p n，则有p1＝p2＝…＝p n＝，Eξ＝（x1+x2+…+x n）×，所以ξ的数学期望又称为平均数、均值．期望的一个性质：若η＝aξ+b，则E（aξ+b）＝aEξ+b．2、离散型随机变量的方差；方差：对于离散型随机变量ξ，如果它所有可能取的值是x1，x2，…，x n，…，且取这些值的概率分别是p1，p2，…，p n…，那么，称为随机变量ξ的均方差，简称为方差，式中的Eξ是随机变量ξ的期望．标准差：Dξ的算术平方根叫做随机变量ξ的标准差，记作．方差的性质：．方差的意义：（1）随机变量的方差的定义与一组数据的方差的定义式是相同的；（2）随机变量的方差、标准差也是随机变量的特征数，它们都反映了随机变量取值的稳定与波动、集中与离散的程度；（3）标准差与随机变量本身有相同的单位，所以在实际问题中应用更广泛．例题精讲离散型随机变量的期望与方差例1.在某公司的一次投标工作中，中标可以获利12万元，没有中标损失成本费0.5万元、若中标的概率为0.6，设公司盈利为X万元，则D（X）=（）A．7B．31.9C．37.5D．42.5例2.设随机变量ξ服从分布B（n，p），且E（ξ）=1.2，D（ξ）=0.96，则（）A．n=6，p=0.2B．n=4，p=0.3C．n=5，p=0.24D．n=8，p=0.15例3.已知A，B两个不透明盒中各有形状、大小都相同的红球、白球若干个．A盒中有m个红球与10-m个白球，B盒中有10-m个红球与m个白球（0<m<10），若从A，B盒中各取一个球，ξ表示所取的2个球中红球的个数，则当Dξ取到最大值时，m的值为（）A．3B．5C．7D．9当堂练习单选题练习1.随机变量ξ的分布列如表，且E（ξ）=1.1，则D（ξ）=（）A．0.36B．0.52C．0.49D．0.68练习2.在某公司的一次投标工作中，中标可以获利12万元，没有中标损失成本费0.5万元、若中标的概率为0.6，设公司盈利为X万元，则D（X）=（）A．7B．31.9C．37.5D．42.5练习3.设随机变量ξ服从分布B（n，p），且E（ξ）=1.2，D（ξ）=0.96，则（）A．n=6，p=0.2B．n=4，p=0.3C．n=5，p=0.24D．n=8，p=0.15练习4.已知A，B两个不透明盒中各有形状、大小都相同的红球、白球若干个．A盒中有m个红球与10-m个白球，B盒中有10-m个红球与m个白球（0<m<10），若从A，B盒中各取一个球，ξ表示所取的2个球中红球的个数，则当Dξ取到最大值时，m的值为（）A．3B．5C．7D．9解答题练习1.'为了积极支持雄安新区建设，某投资公司计划明年投资1000万元给雄安新区甲、乙两家科技企业，以支持其创新研发计划，经有关部门测算，若不受中美贸易战影响的话，每投入100万元资金，在甲企业可获利150万元，若遭受贸易战影响的话，则将损失50万元；同样的情况，在乙企业可获利100万元，否则将损失20万元，假设甲、乙两企业遭受贸易战影响的概率分别为0.6和0.5．（1）若在甲、乙两企业分别投资500万元，求获利1250万元的概率；（2）若在两企业的投资额相差不超过300万元，求该投资公司明年获利约在什么范围内？'练习2.'某蛇养殖基地因国家实施精准扶贫，大力扶持农业产业发展，拟扩大养殖规模．现对该养殖基地已经售出的王锦蛇的体长（单位：厘米）进行了统计，得到体长的频数分布表如下：若王锦蛇、乌梢蛇成年母蛇的购买成本分别为650元/条、600元/条，每条母蛇平均可为养殖场获得1200元/年的销售额，且每条蛇的繁殖年限均为整数，将每条蛇的繁殖年限的频率看作概率，以每条蛇所获得的毛利润（毛利润=总销售额-购买成本）的期望值作为购买蛇类的依据，试问：应购买哪类蛇？'练习3.'中央政府为了应对因人口老龄化而造成的劳动力短缺等问题，拟定出台“延迟退休年龄政策”．为了了解人们]对“延迟退休年龄政策”的态度，责成人社部进行调研．人社部从网上年龄在15～65岁的人群中随机调查100人，调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下：（2）若以45岁为分界点，从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动．现从这8人中随机抽2人①抽到1人是45岁以下时，求抽到的另一人是45岁以上的概率．②记抽到45岁以上的人数为x，求随机变量x的分布列及数学期望．'练习4.'已知甲、乙两名工人在同样条件下每天各生产100件产品，且每生产1件正品可获利20元，生产1件次品损失30元，甲、乙两名工人100天中出现次品件数的情况如表所示．（1）将甲每天生产的次品数记为x（单位：件），日利润记为y（单位：元），写出y与x的函数关系式；（2）如果将统计的100天中产生次品量的频率作为概率，记X表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和，求随机变量X的分布列和数学期望．'练习5.'“回文数”是指从左到右与从右到左读都一样的正整数，如22，121，3553等．显然2位“回文数”共9个：11，22，33，…，99．现从9个不同2位“回文数”中任取1个乘以4，其结果记为X；从9个不同2位“回文数”中任取2个相加，其结果记为Y．（1）求X为“回文数”的概率；（2）设随机变量ξ表示X，Y两数中“回文数”的个数，求ξ的概率分布和数学期望E（ξ）．'。

7.3.2 离散型随机变量的方差学习目标 1.理解取有限个值的离散型随机变量的方差及标准差的概念.2.能计算简单离散型随机变量的方差，并能解决一些实际问题.3.掌握方差的性质以及两点分布的方差的求法，会利用公式求它们的方差．知识点一 离散型随机变量的方差、标准差 设离散型随机变量X 的分布列如表所示．X x 1 x 2 … x n Pp 1p 2…p n我们用X 所有可能取值x i 与E (X )的偏差的平方(x 1－E (X ))2，(x 2－E (X ))2，…，(x n －E (X ))2，关于取值概率的加权平均，来度量随机变量X 取值与其均值E (X )的偏离程度．我们称D (X )＝(x 1－E (X ))2p1＋(x 2－E (X ))2p 2＋…＋(x n －E (X ))2p n ＝∑i ＝1n(x i －E (X ))2p i 为随机变量X 的方差(variance)，有时也记为Var (X )，并称D (X )为随机变量X 的标准差(standard deviation)，记为σ(X )．知识点二 离散型随机变量方差的性质 1．设a ，b 为常数，则D (aX ＋b )＝a 2D (X )． 2．D (c )＝0(其中c 为常数)．1．离散型随机变量的方差越大，随机变量越稳定．( × ) 2．若a 是常数，则D (a )＝0.( √ )3．离散型随机变量的方差反映了随机变量取值偏离于均值的平均程度．( √ ) 4．若a ，b 为常数，则D (ax ＋b )＝a D (x ).( × )一、求离散型随机变量的方差例1 袋中有20个大小相同的球，其中记上0号的有10个，记上n 号的有n 个(n ＝1,2,3,4)．现从袋中任取一球．ξ表示所取球的标号． (1)求ξ的分布列、均值和方差；(2)若η＝aξ＋b ，E (η)＝1，D (η)＝11，试求a ，b 的值． 解 (1)ξ的分布列为则E (ξ)＝0×12＋1×120＋2×110＋3×320＋4×15＝1.5.D (ξ)＝(0－1.5)2×12＋(1－1.5)2×120＋(2－1.5)2×110＋(3－1.5)2×320＋(4－1.5)2×15＝2.75.(2)由D (η)＝a 2D (ξ)，得a 2×2.75＝11，得a ＝±2. 又由E (η)＝aE (ξ)＋b ，得1.5a ＋b ＝1，所以当a ＝2时，由1＝2×1.5＋b ，得b ＝－2； 当a ＝－2时，由1＝－2×1.5＋b ，得b ＝4.所以⎩⎪⎨⎪⎧ a ＝2，b ＝－2或⎩⎪⎨⎪⎧a ＝－2，b ＝4即为所求．反思感悟 (1)求离散型随机变量方差的步骤 ①理解随机变量X 的意义，写出X 的所有取值； ②求出X 取每个值的概率； ③写出X 的分布列； ④计算E (X )； ⑤计算D (X )．(2)线性关系的方差计算：若η＝aξ＋b ，则D (η)＝a 2D (ξ)． 跟踪训练1 已知随机变量ξ的分布列如下表：(1)求E (ξ)，D (ξ)，D (ξ)； (2)设η＝2ξ＋3，求E (η)，D (η)．解 (1)E (ξ)＝(－1)×12＋0×13＋1×16＝－13，D (ξ)＝⎝⎛⎭⎫－1＋132×12＋⎝⎛⎭⎫0＋132×13＋⎝⎛⎭⎫1＋132×16＝59，D (ξ)＝53. (2)E (η)＝2E (ξ)＋3＝73，D (η)＝4D (ξ)＝209.二、方差的应用例2有甲、乙两种建筑材料，从中各取等量样品检查它们的抗拉强度如下：其中，ξA，ξB分别表示甲、乙两种材料的抗拉强度，在使用时要求抗拉强度不低于120，试比较甲、乙两种建筑材料的稳定程度(哪一个的稳定性较好)．解E(ξA)＝110×0.1＋120×0.2＋125×0.4＋130×0.1＋135×0.2＝125.E(ξB)＝100×0.1＋115×0.2＋125×0.4＋130×0.1＋145×0.2＝125.D(ξA)＝0.1×(110－125)2＋0.2×(120－125)2＋0.4×(125－125)2＋0.1×(130－125)2＋0.2×(135－125)2＝50.D(ξB)＝0.1×(100－125)2＋0.2×(115－125)2＋0.4×(125－125)2＋0.1×(130－125)2＋0.2×(145－125)2＝165.由此可见E(ξA)＝E(ξB)，D(ξA)<D(ξB)，故两种材料的抗拉强度的均值相等，其稳定程度材料乙明显不如材料甲，即甲的稳定性较好．反思感悟均值、方差在决策中的作用(1)均值：均值反映了离散型随机变量取值的平均水平，均值越大，平均水平越高．(2)方差：方差反映了离散型随机变量取值的离散波动程度，方差越大越不稳定．(3)在决策中常结合实际情形依据均值、方差做出决断．跟踪训练2甲、乙两个野生动物保护区有相同的自然环境，且候鸟的种类和数量也大致相同，两个保护区每个季度发现违反保护条例的事件次数的分布列分别为试评定这两个保护区的管理水平．解甲保护区内违反保护条例的次数X的均值和方差分别为E(X)＝0×0.3＋1×0.3＋2×0.2＋3×0.2＝1.3，D(X)＝(0－1.3)2×0.3＋(1－1.3)2×0.3＋(2－1.3)2×0.2＋(3－1.3)2×0.2＝1.21.乙保护区内违反保护条例的次数Y的均值和方差分别为E (Y )＝0×0.1＋1×0.5＋2×0.4＝1.3，D (Y )＝(0－1.3)2×0.1＋(1－1.3)2×0.5＋(2－1.3)2×0.4＝0.41.因为E (X )＝E (Y )，D (X )>D (Y )，所以两个保护区内每个季度发现违反保护条例的事件的平均次数相同，但甲保护区内违反保护条例的事件次数相对分散且波动较大，乙保护区内违反保护条例的事件次数更加集中和稳定，相对而言，乙保护区的管理更好一些． 三、分布列、均值、方差的综合应用例3 甲、乙两人进行定点投篮游戏，投篮者若投中，则继续投篮，否则由对方投篮；第一次由甲投篮，已知每次投篮甲、乙命中的概率分别为13，34.(1)求第三次由乙投篮的概率；(2)在前3次投篮中，乙投篮的次数为X ，求X 的分布列、均值及标准差． 解 (1)P ＝13×23＋23×34＝1318.(2)由题意，得X 的所有可能取值为0,1,2， P (X ＝0)＝13×13＝19.P (X ＝1)＝13×23＋23×14＝718，P (X ＝2)＝23×34＝12.故X 的分布列为E (X )＝0×19＋1×718＋2×12＝2518，D (X )＝⎝⎛⎭⎫0－25182×19＋⎝⎛⎭⎫1－25182×718＋⎝⎛⎭⎫2－25182×12＝149324. ∴σ(X )＝D (X )＝14918. 反思感悟 处理综合问题的方法第一步：确定事件间的关系，是互斥、对立还是相互独立．第二步：要依据事件间的关系，选择相应的概率公式，计算相应事件的概率． 第三步：列分布列，并计算均值及方差．跟踪训练3 有三张形状、大小、质地完全相同的卡片，在各卡片上分别写上0,1,2，现从中任意抽取一张，将其上数字记作x ，然后放回，再抽取一张，其上数字记作y ，令X ＝xy ，求： (1)X 所取各值的分布列；(2)随机变量X 的均值与方差．解 (1)由题意知，随机变量X 的可能取值为0,1,2,4.“X ＝0”是指两次取的卡片上至少有一次为0，其概率为P (X ＝0)＝1－23×23＝59，“X ＝1”是指两次取的卡片上都标着1，其概率为P (X ＝1)＝13×13＝19，“X ＝2”是指两次取的卡片上一个标着1，另一个标着2，其概率为P (X ＝2)＝2×13×13＝29，“X ＝4”是指两次取的卡片上都标着2，其概率为P (X ＝4)＝13×13＝19.则X 的分布列为X 0 1 2 4 P59192919(2)E (X )＝0×59＋1×19＋2×29＋4×19＝1，D (X )＝(0－1)2×59＋(1－1)2×19＋(2－1)2×29＋(4－1)2×19＝169.1．设随机变量X 的方差D (X )＝1，则D (2X ＋1)的值为( ) A ．2 B ．3 C ．4 D ．5 答案 C解析 D (2X ＋1)＝4D (X )＝4×1＝4.2．有甲、乙两种水稻，测得每种水稻各10株的分蘖数据，计算出样本均值E (X 甲)＝E (X 乙)，方差分别为D (X 甲)＝11，D (X 乙)＝3.4.由此可以估计( ) A ．甲种水稻比乙种水稻分蘖整齐 B ．乙种水稻比甲种水稻分蘖整齐 C ．甲、乙两种水稻分蘖整齐程度相同 D ．甲、乙两种水稻分蘖整齐程度不能比较 答案 B3．(多选)下列说法中错误的是( )A ．离散型随机变量X 的均值E (X )反映了X 取值的概率的平均值B ．离散型随机变量X 的方差D (X )反映了X 取值的平均水平C ．离散型随机变量X 的均值E (X )反映了X 取值的平均水平D ．离散型随机变量X 的方差D (X )反映了X 取值的概率的平均值答案 ABD解析 E (X )反映了X 取值的平均水平，D (X )反映了X 取值的离散程度．4．已知离散型随机变量X 的分布列如下表所示，若E (X )＝0，D (X )＝1，则a ＝________，b ＝________.X －1 0 1 2 Pabc112答案512 14解析 由题意知⎩⎪⎨⎪⎧ a ＋b ＋c ＝1112，－a ＋c ＋16＝0，a ＋c ＋13＝1，解得⎩⎪⎨⎪⎧a ＝512，b ＝14，c ＝14.5．随机变量ξ的取值为0,1,2.若P (ξ＝0)＝15，E (ξ)＝1，则D (ξ)＝________.答案 25解析 设P (ξ＝1)＝a ，P (ξ＝2)＝b ， 则⎩⎪⎨⎪⎧15＋a ＋b ＝1，a ＋2b ＝1，解得⎩⎨⎧a ＝35，b ＝15，所以D (ξ)＝15＋35×0＋15×1＝25.1．知识清单：(1)离散型随机变量的方差、标准差． (2)离散型随机变量的方差的性质． 2．方法归纳：转化化归． 3．常见误区：方差公式套用错误．1．随机变量X 的方差，反映其取值的( )A ．平均水平B ．分布规律C ．波动大小D ．最大值和最小值答案 C2．(多选)已知X 的分布列为则( ) A ．E (X )＝2912B ．D (X )＝121144C ．D (X )＝179144D ．E (X )＝1712答案 AC解析 ∵E (X )＝1×14＋2×13＋3×16＋4×14＝2912，∴D (X )＝⎝⎛⎭⎫1－29122×14＋⎝⎛⎭⎫2－29122×13＋⎝⎛⎭⎫3－29122×16＋⎝⎛⎭⎫4－29122×14＝179144. 3．由以往的统计资料表明，甲、乙两名运动员在比赛中的得分情况为现有一场比赛，应派哪位运动员参加较好( ) A ．甲 B ．乙 C ．甲、乙均可 D ．无法确定答案 A解析 ∵E (X 1)＝E (X 2)＝1.1，D (X 1)＝1.12×0.2＋0.12×0.5＋0.92×0.3＝0.49， D (X 2)＝1.12×0.3＋0.12×0.3＋0.92×0.4＝0.69， ∴D (X 1)<D (X 2)，即甲比乙得分稳定， 故派甲运动员参加较好．4．设随机变量X 的概率分布列为P (X ＝k )＝p k (1－p )1－k (k ＝0,1)，则E (X )，D (X )的值分别是( ) A ．0和1 B ．p 和p 2 C ．p 和1－pD ．p 和(1－p )p答案 D解析 由X 的分布列知，P (X ＝0)＝1－p ，P (X ＝1)＝p ， 故E (X )＝0×(1－p )＋1×p ＝p ，易知X 服从两点分布，∴D (X )＝p (1－p )．5．已知随机变量X 的分布列为P (X ＝k )＝13，k ＝1,2,3，则D (3X ＋5)等于( )A ．6B ．9C ．3D ．4 答案 A解析 E (X )＝1×13＋2×13＋3×13＝2，∴D (X )＝13×[(1－2)2＋(2－2)2＋(3－2)2]＝23，∴D (3X ＋5)＝9D (X )＝9×23＝6.6．已知随机变量X 的分布列如表所示：则a ＝________，D (X )＝________. 答案 0.5 3.56解析 根据随机变量分布列的性质，知0.4＋0.1＋a ＝1，所以a ＝0.5， E (X )＝0.4＋0.3＋2.5＝3.2，D (X )＝2.22×0.4＋0.22×0.1＋1.82×0.5＝3.56.7．已知离散型随机变量X 的可能取值为x 1＝－1，x 2＝0，x 3＝1，且E (X )＝0.1，D (X )＝0.89，则对应x 1，x 2，x 3的概率p 1，p 2，p 3分别为________，________，________. 答案 0.4 0.1 0.5 解析 由题意知，⎩⎪⎨⎪⎧－p 1＋p 3＝0.1，1.21p 1＋0.01p 2＋0.81p 3＝0.89，p 1＋p 2＋p 3＝1，解得⎩⎪⎨⎪⎧p 1＝0.4，p 2＝0.1，p 3＝0.5.8．若随机事件A 在1次试验中发生的概率为p (0<p <1)，用随机变量X 表示A 在1次试验中发生的次数，则方差D (X )的最大值为________，此时p ＝________.答案 14 12解析 随机变量X 的所有可能的取值是0,1，并且P (X ＝1)＝p ，P (X ＝0)＝1－p . 从而E (X )＝0×(1－p )＋1×p ＝p ， D (X )＝(0－p )2×(1－p )＋(1－p )2·p ＝p －p 2 ＝－⎝⎛⎭⎫p －122＋14. ∵0<p <1，∴当p ＝12时，D (X )取最大值，最大值是14.9．甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ与η，且ξ，η的分布列为(1)求a ，b 的值；(2)计算ξ，η的均值与方差，并以此分析甲、乙的技术状况．解 (1)由离散型随机变量的分布列的性质可知a ＋0.1＋0.6＝1，∴a ＝0.3. 同理0.3＋b ＋0.3＝1，b ＝0.4.(2)E (ξ)＝1×0.3＋2×0.1＋3×0.6＝2.3， E (η)＝1×0.3＋2×0.4＋3×0.3＝2，D (ξ)＝(1－2.3)2×0.3＋(2－2.3)2×0.1＋(3－2.3)2×0.6＝0.81， D (η)＝(1－2)2×0.3＋(2－2)2×0.4＋(3－2)2×0.3＝0.6.由于E (ξ)>E (η)，说明在一次射击中，甲的平均得分比乙高，但D (ξ)>D (η)，说明甲得分的稳定性不如乙，因此甲、乙两人技术水平都不够全面，各有优劣． 10．已知X 的分布列为(1)求X 2的分布列； (2)计算X 的方差；(3)若Y ＝4X ＋3，求Y 的均值和方差．解 (1)由分布列的性质，知12＋14＋a ＝1，故a ＝14，从而X 2的分布列为X 2 0 1 P1434(2)由(1)知a ＝14，所以X 的均值E (X )＝(－1)×12＋0×14＋1×14＝－14.故X 的方差D (X )＝⎝⎛⎭⎫－1＋142×12＋⎝⎛⎭⎫0＋142×14＋⎝⎛⎭⎫1＋142×14＝1116. (3)因为Y ＝4X ＋3，所以E (Y )＝4E (X )＋3＝2， D (Y )＝42D (X )＝11.11．设随机试验的结果只有A 发生和A 不发生，且P (A )＝m ，令随机变量X ＝⎩⎪⎨⎪⎧1，A 发生，0，A 不发生，则X 的方差D (X )等于( ) A ．m B ．2m (1－m ) C ．m (m －1) D ．m (1－m )答案 D解析 显然X 服从两点分布，∴D (X )＝m (1－m )． 12．(多选)已知随机变量X 的分布列是X 1 2 3 P13ab若E (X )＝116，则( )A ．a ＝12B ．b ＝16C ．D (X )＝1736D ．D (X )＝2318答案 ABC解析 由题意得a ＋b ＝23.①由E (X )＝13＋2a ＋3b ＝116，②得2a ＋3b ＝32，联立①②，得a ＝12，b ＝16.所以D (X )＝⎝⎛⎭⎫1－1162×13＋⎝⎛⎭⎫2－1162×12＋⎝⎛⎭⎫3－1162×16＝1736.故选ABC. 13．已知随机变量ξ的分布列为ξ m n P13a若E (ξ)＝2，则D (ξ)的最小值等于( ) A ．0 B ．2 C ．4 D ．无法计算 答案 D解析 由题意得a ＝1－13＝23，所以E (ξ)＝13m ＋23n ＝2，即m ＋2n ＝6.又D (ξ)＝13×(m －2)2＋23×(n －2)2＝2(n －2)2，当n ＝2时，D (ξ)取得最小值，此时m ＝2，不符合题意，故D (ξ)无法取得最小值．14．若X 是离散型随机变量，P (X ＝x 1)＝23，P (X ＝x 2)＝13，且x 1<x 2，又已知E (X )＝43，D (X )＝29，则x 1＋x 2的值为________． 答案 3解析 由已知得 ⎩⎨⎧x 1·23＋x 2·13＝43，⎝⎛⎭⎫x 1－432·23＋⎝⎛⎭⎫x 2－432·13＝29，即⎩⎪⎨⎪⎧2x 1＋x 2＝4，2⎝⎛⎭⎫x 1－432＋⎝⎛⎭⎫x 2－432＝23，解得⎩⎨⎧x 1＝53，x 2＝23或⎩⎪⎨⎪⎧x 1＝1，x 2＝2， 又x 1<x 2，所以⎩⎪⎨⎪⎧x 1＝1，x 2＝2，所以x 1＋x 2＝3.15．编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位，每位学生坐一个座位，设与座位编号相同的学生的人数是ξ，则E (ξ)＝________，D (ξ)＝________. 答案 1 1解析 ξ的所有可能取值为0,1,3，ξ＝0表示三位同学全坐错了，有2种情况，即编号为1,2,3的座位上分别坐了编号为2,3,1或3,1,2的学生，则P (ξ＝0)＝2A 33＝13；ξ＝1表示三位同学只有1位同学坐对了， 则P (ξ＝1)＝C 13A 33＝12；ξ＝3表示三位同学全坐对了，即对号入座， 则P (ξ＝3)＝1A 33＝16.所以ξ的分布列为E (ξ)＝0×13＋1×12＋3×16＝1.D (ξ)＝13×(0－1)2＋12×(1－1)2＋16×(3－1)2＝1.16．A ，B 两个投资项目的利润率分别为随机变量X 1和X 2，根据市场分析，X 1和X 2的分布列分别如下表：(1)在A ，B 两个投资项目上各投资100万元，Y 1和Y 2分别表示投资项目A 和B 所获得的利润，求方差D (Y 1)，D (Y 2)；(2)将x (0≤x ≤100)万元投资项目A ，(100－x )万元投资项目B ，f (x )表示投资项目A 所得利润的方差与投资项目B 所得利润的方差的和．求f (x )的最小值，并指出x 为何值时，f (x )取得最小值．解 (1)根据题意，知Y 1和Y 2的分布列分别如下表：从而E (Y 1)＝5×0.8＋10×0.2＝6，D (Y 1)＝(5－6)2×0.8＋(10－6)2×0.2＝4，E (Y 2)＝2×0.2＋8×0.5＋12×0.3＝8，D (Y 2)＝(2－8)2×0.2＋(8－8)2×0.5＋(12－8)2×0.3＝12.(2)f (x )＝D ⎝⎛⎭⎫x 100Y 1＋D ⎝⎛⎭⎫100－x 100Y 2＝⎝⎛⎭⎫x 1002D (Y 1)＋⎝⎛⎭⎫100－x 1002D (Y 2)＝41002[x 2＋3(100－x )2] ＝12 500(4x 2－600x ＋30 000) ＝1625(x －75)2＋3， 当x ＝75时，f (x )取得最小值3.高考数学：试卷答题攻略一、“六先六后”，因人因卷制宜。