当前位置：文档之家 › 钢结构设计轴心受力构件截面强度计算

钢结构设计轴心受力构件截面强度计算

  • 格式：doc
  • 大小：526.50 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

钢结构设计原理 第四章-轴心受力构件

钢结构设计原理 第四章-轴心受力构件

因此，失稳时杆件的整个截面都处于加载的过 程中，应力-应变关系假定遵循同一个切线模量 Et，此时轴心受压杆件的屈曲临界力为：
N cr ,t

2 Et I
2 二、实际的轴心受压构件的受力性能
在钢结构中，实际的轴压杆与理想的直杆受力性能之间差别很大，实 际上，轴心受压杆的屈曲性能受许多因素影响，主要的影响因素有：
一、理想轴压构件的受力性能 理想轴压构件是指满足下列4个条件： o杆件本身绝对直杆； o材料均质且各向同性； o无荷载偏心且在荷载作用之前无初始应力； o杆端为两端铰接。 在轴心压力作用下，理想的压杆可能发生三种形式的屈曲： 弯曲屈曲、扭转屈曲、弯扭屈曲——见教科书P97图4–6 轴心受压构件具体以何种形式失稳，主要取决于截面的形式 和尺寸、杆的长度以及杆端的支撑条件。
l N 2 EI 对一无残余应力仅存在初弯曲的轴压杆，杆件中点截面边缘开始 式中 N l2 NE 屈服的条件为：
0
1
经过简化为：
N N vm v0 v0 fy v m v0 v 1 1 N NE A W N N v0 N E fy A W NE N
An—构件的净截面面积_
N fy r f R An
P94式4-2
（1）当轴力构件采用普通螺栓连接时 螺栓为并列布置：
n1 n2 n3
按最危险的截面Ⅰ-Ⅰ 计算，3个截面净截面面积 相同，但 Ⅰ-Ⅰ截面受力最大。
N n
Ⅰ-Ⅰ：N Ⅱ-Ⅱ：N-Nn1/n Ⅲ-Ⅲ：N-N(n1+n2)/n
Ⅰ Ⅱ Ⅲ
2 2
从上面两式我们可以看出，绕不同轴屈曲时，不仅临界力不同，且残余 应力对临界应力的影响程度也不同。因为k1，所以残余应力对弱轴的 影响比对强轴的影响严重的多。

钢结构轴心受力构件计算

钢结构轴心受力构件计算

钢结构轴心受力构件计算3.1 轴心受力构件概述在钢结构中，轴心受力构件的应用十分广泛，如桁架、塔架和网架、网壳等杆件体系。

这类结构的节点通常假设为铰接，当无节间荷载作用时，杆件只受轴向力（轴向拉力或轴向压力）的作用，称为轴心受力构件（轴心受拉构件或轴心受压构件）。

图3-1所示为轴心受力构件在工程上应用的一些实例。

图3-1 轴心受力构件在工程中的应用（a）桁架；（b）塔架；（c）网架轴心受力构件常用的截面形式可分为实腹式和格构式两大类。

（1）实腹式构件制作简单，与其他构件的连接也比较方便，常用的截面形式很多，可直接选用轧制型钢截面，如圆钢、钢管、角钢、工字钢、H 型钢、T 型钢等[图3-2（a）]；也可选用由型钢或钢板组成的组合截面[图3-2（b）]；在轻型结构中则可采用冷弯薄壁型钢截面[图3-2（c）]。

以上这些截面中，截面紧凑（如圆钢）或对两主轴刚度相差悬殊者（如单槽钢、工字钢），一般适用于轴心受拉构件，而受压构件通常采用较为开展、组成板件宽而薄的截面。

（2）格构式构件[图3-2（d）]容易使压杆实现两主轴方向的稳定性。

这种构件的刚度大、抗扭性好，用料较省。

格构式截面一般由两个或多个型钢肢件组成，肢件之间采用缀条或缀板连成整体，缀条和缀板统称为缀材。

图3-2 轴心受力杆件的截面形式（a）轧制型钢截面；（b）焊接实腹式组合截面；（c）冷弯薄壁型钢截面；（d）格构式截面3.2 轴心受力构件的强度及刚度轴心受拉构件的设计除根据结构用途、构件受力大小和材料供应情况选用合理的截面形式外，还要对所选截面进行强度和刚度验算。

强度要求就是使构件截面上的最大正应力不超过钢材的强度设计值，刚度要求就是使构件的长细比不超过容许长细比。

轴心受压构件在设计时，除使所选截面满足强度和刚度要求外，还应使其满足构件整体稳定性和局部稳定性的要求。

整体稳定性要求是使构件在设计荷载作用下不致发生屈曲而丧失承载能力；局部稳定性要求一般是使组成构件的板件宽厚比不超过规定限值，以保证板件不会屈曲，或者使格构式构件的分肢不发生屈曲。

钢结构设计计算公式及计算用表

钢结构设计计算公式及计算用表

钢结构设计计算公式及计算用表为保证承重结构的承载能力和防止在一定条件下出现脆性破坏，应根据结构的重要性、荷载特征、结构形式、应力状态、连接方法、钢材厚度和工作环境等因素综合考虑，选用合适的钢材牌号和材性。

承重结构的钢材宜釆用Q235钢、Q345钢、Q390钢和Q420钢，其质量应分别符合现行国家标准《碳素结构钢》GB/T700和《低合金高强度结构钢》GB/T 1591的规定。

当釆用其他牌号的钢材时，尚应符合相应有关标准的规定和要求。

对Q235钢宜选用镇静钢或半镇静钢。

承重结构的钢材应具有抗拉强度、伸长率、屈服强度和硫、磷含量的合格保证，对焊接结构尚应具有碳含量的合格保证。

焊接承重结构以及重要的非焊接承重结构的钢材还应具有冷弯试验的合格保证。

对于需要验算疲劳的焊接结构的钢材，应具有常温冲击韧性的合格保证。

当结构工作温度等于或低于0°C但高于-20°C时，Q233钢和Q345钢应具有O°CC冲击韧性的合格保证；对Q390钢和Q420钢应具有-20°C冲击韧性的合格保证。

当结构工作温度等于或低于-20€时，对Q235钢和Q345钢应具有-20°C冲击韧性的合格保证；对Q390钢和Q420钢应具有-40°C冲击韧性的合格保证。

对于需要验算疲劳的非焊接结构的钢材亦应具有常温冲击韧性的合格保证，当结构工作温度等于或低于-20°C时，对Q235钢和Q345钢应具有0°C 冲击韧性的合格保证；对Q390钢和Q420钢应具有-20°C冲击韧性的合格保证。

当焊接承重结构为防止钢材的层状撕裂而釆用Z向钢时，其材质应符合现行国家标准《厚度方向性能钢板》GB/T 5313的规定。

钢材的强度设计值（材料强度的标准值除以抗力分项系数），应根据钢材卑度或直径按表1采用。

钢铸件的强度设计值应按表2采用。

连接的强度设计值应按表3〜5采用。

注：表中厚度系指计算点的钢材厚度，对轴心受力构件系指截面中较尽板件的厚度。

钢结构强度稳定性计算书

钢结构强度稳定性计算书

钢结构强度稳定性计算书计算依据：1、《钢结构设计规范》GB50017-2003一、构件受力类别：轴心受压构件。

二、强度验算：1、轴心受压构件的强度，可按下式计算：σ = N/A n≤ f式中N──轴心压力,取N= 10 kN；A n──净截面面积,取A n= 298 mm2；轴心受压构件的强度σ= N / A n = 10×103 / 298 = 33.557 N/mm2；f──钢材的抗压强度设计值，取f= 205 N/mm2；由于轴心受压构件强度σ= 33.557 N/mm2≤承载力设计值f=205 N/mm2,故满足要求！2、摩擦型高强螺栓连接处的强度，按下面两式计算，取最大值：σ = (1-0.5n1/n)N/A n≤ f式中N──轴心压力,取N= 10 kN；A n──净截面面积,取A n= 298 mm2；f──钢材的抗压强度设计值，取f= 205 N/mm2；n──在节点或拼接处，构件一端连接的高强螺栓数目,取n = 4；n1──所计算截面(最外列螺栓处)上高强螺栓数目；取n1 = 2；σ= (1-0.5×n1/n)×N/A n=(1-0.5×2/4)×10×103/298=25.168 N/mm2；σ = N/A ≤ f式中N──轴心压力,取N= 10 kN；A──构件的毛截面面积，取A= 354 mm2；σ=N/A=10×103/354=28.249 N/mm2；由于计算的最大强度σmax = 28.249 N/mm2≤承载力设计值=205 N/mm2,故满足要求！3、轴心受压构件的稳定性按下式计算：N/φA n≤ f式中N──轴心压力,取N= 10 kN；l──构件的计算长度,取l=5000 mm；i──构件的回转半径,取i=23.4 mm；λ──构件的长细比, λ= l/i= 5000/23.4 = 213.675；[λ]──构件的允许长细比,取[λ]=250 ；构件的长细比λ= 213.675 ≤[λ] = 250，满足要求；φ──轴心受压构件的稳定系数, λ=l/i计算得到的构件柔度系数作为参数查表得φ=0.165；A n──净截面面积,取A n= 298 mm2；f──钢材的抗压强度设计值，取f= 205 N/mm2；N/(φA n)=10×103/(0.165×298)=203.376 N/mm2；由于σ= 203.376 N/mm2≤承载力设计值f=205 N/mm2,故满足要求！。

钢结构课件 轴心受力构件的强度及截面选择

钢结构课件 轴心受力构件的强度及截面选择
37
对于闭口截面
It 4A2 /
ds t
闭合截面的循环剪力流
截面面积相同的两种截面
It≈1:500 , ≈30:1
38
约束扭转: 翘曲变形受到约束的扭转
悬臂工字梁的约束扭转
39
扭转剪应力分布
上翼缘的内力
MT Ms M
其中 Ms GIt GIt
M Vf h EI
23
F E
(a) 弹性工作阶段OE：疲劳计算、冷弯薄壁型钢 (b) 弹塑性工作阶段EC：一般受弯构件 (c) 塑性工作阶段CF：塑性铰 (d) 应变硬化阶段FD：一般不利用
24
a a
σ
fy
xx
fy
fy
M e Wn f y
M p Wpn f y
Wn — 梁净截面模量 Wpn — 梁塑性净截面模量
Q235，截面无削弱，计算长度为12.2m，承受静力荷载设计值
为900kN，要求验算此拉杆的强度。
y
【解】：
1、截面特性计算：查附表得
x
x
截面面积 ：An = 2×28.91 = 57.82cm2
回转半径： ix = 3.83cm， iy = 5.41cm
y
2、强度验算
= N / An = 900/57.82×10 = 155.7 < f = 215 N/mm2， 满足
2
§3.1 轴心受力构件的强度及截面选择
定义：构件只承受轴心力的作用。
承受轴心压力时称为轴心受压构件。 承受轴心拉力时称为轴心受拉构件。
N
N
N
N
3
§3.1 轴心受力构件的强度及截面选择
3.1.1 轴心受力构件的应用和截面形式（了解）

钢结构设计规范·轴心受力构件和拉弯、压弯构件的计算·拉弯构件和压弯构

钢结构设计规范·轴心受力构件和拉弯、压弯构件的计算·拉弯构件和压弯构

4.1.1在主平面内受弯的实腹构件(考虑腹板屈曲后强度者参见本规范第4.4.1条)，其抗弯强度应按下列规定计算:`(M_x)/(γ_xW_(nx))+(M_y)/(γ_xW_(ny))≤f`（4.1.1）式中M x、M y——同一截面处绕x轴和y轴的弯矩(对工字形截面：x轴为强轴，y轴为弱轴);Wｎｘ、Wｎｙ——对x轴和y轴的净截面模量;γx、γy——截面塑性发展系数;对工字形截面γy=1.20;对箱形截面，γX=Y y=1.05;对其他截面，可按表5.2.1采用;f——钢材的抗弯强度设计值。

当梁受压翼缘的自由外伸宽度与其厚度之比大于13`sqrt(235//f_y)`而不超过15`sqrt(235//f_y)`时，γx=1.0。

f y应取为钢材牌号所指屈服点。

对需要计算疲劳的梁，宜取γx=γy=1.0。

4.1.2在主平面内受弯的实腹构件(考虑腹板屈曲后强度者参见本规范第4.4.1条)，其抗剪强度应按下式计算:`τ=(VS)/(It_w)`(4.1.2)式中V——计算截面沿腹板平面作用的剪力;S——计算剪应力处以上毛截面对中和轴的面积矩;I——毛截面惯性矩;t w——腹板厚度;fv——钢材的抗剪强度设计值。

4.1.3当梁上翼缘受有沿腹板平面作用的集中荷载、且该荷载处又未设置支承加劲肋时，腹板计算高度上边缘的局部承压强度应按下式计算:`σ_c=(varphiF)/(t_wl_z)≤f`(4.1.3-1)式中F——集中荷载，对动力荷载应考虑动力系数;ψ——集中荷载增大系数;对重级.工作制吊车梁ψ=1. 35;对其他梁，ψ=1.0；l z——集中荷载在腹板计算高度上边缘的假定分布长度，按下式计算:l2=a+5h y+2h R ( 4.1.3-2 )a——集中荷载沿梁跨度方向的支承长度，对钢轨上的轮压可取50mm;h y——自梁顶面至腹板计算高度上边缘的距离;h R——轨道的高度，对梁顶无轨道的梁h R=0;f——钢材的抗压强度设计值。

2.2轴心受力构件设计

2.2轴心受力构件设计

x 1
y
肢件
1
截面的虚实轴：与肢件腹板相交的主轴为实轴，否则 是虚轴，图4-20a、b、c、d。
a)
x
y
b)
x
y
c)
x y
d)
x y
图4－7 格构式柱的截面型 式
对轴心受力构件截面形式的要求：
1）能提供强度所需要的截面面积； 2）制作简便；便于和相邻构件连接； 3）截面宽大而壁厚较薄，以满足刚度要求。
N f An
式中
N——构件的轴心拉力或压力设计值； An——构件的净截面面积； f ——钢材的抗拉或抗压强度设计值。
§5-2 轴心受力构件的强度和刚度
5.2.1 强度计算
轴心受力构件强度承载力以截面平均应力达到钢 材屈服应力为极限 对有削弱的截面，虽然存在应力集中现象，但应 力高峰区会率先屈服使应力塑性重分布，最终达 到均匀分布
双向 ix ， iy 接近， 经济性好，截面 增加加工焊接工 作量 组合灵活，便于 自动焊
加工量较少，材 料单价较低
用材增多，截面 形式、尺寸均受 限制，连接复杂
ix 和 iy 相同或接近 （矩形管），回 圆管单价较高， 转半径大，抗压 与其它构件连接 时相对较繁 稳定性好，用材 省，抗扭刚度大
4.3.2. 截面选择
轴心受力构件的设计：
承载能力的极限状态：
轴心受拉构件—强度控制 轴心受压构件—强度和稳定控制
正常使用的极限状态：
通过保证构件的刚度——限制其长细比
二、轴心受力构件的强度及刚度
2.1 轴心受力构件的强度
轴心受力构件在轴心力作用下，截面内会产生均匀的 拉或压应力，规范规定轴心受力构件的强度应以净截面的 平均应力不超过钢材的屈服强度为准则。轴心受力构件的 强度计算公式：

第四章轴心受力构件公式整理

第四章轴心受力构件公式整理
当 b1 t 0.56 l 0 y b 1 时：
2 2 l b1 0yt 3 .7 1 t 52.7b14
( 4 30a )
yz
( 4 30b )
④、单轴对称的轴心受压构件在绕非对称轴以外的任意轴失稳时 ，应按弯扭屈曲计算其稳定性。
当计算等边角钢构件绕平行轴（u轴)稳 定时，可按下式计算换算长细比，并按b类 截面确定 值：
钢结构
2014-2015-2
一、强度计算（承载能力极限状态）
N f An
N—轴心拉力或压力设计值； An—构件的净截面面积； f—钢材的抗拉强度设计值。
( 4 1)
适用于fy/fu≤0.8的情况；轴心受压构件，当截面无削 弱时，强度不必计算。
二、刚度计算（正常使用极限状态）
保证构件在运输、安装、使用时不会产生过大变形。
( 4 41)
式中： 构件两方向长细比较大 值，当 30时 , 取 30；当 100时，取 100。
B、箱形截面翼缘板
b 235 13 t fy b0 235 40 t fy
( 4 42 ) ( 4 43)
b0 t
( 4 27b )
B、等边双角钢截面，图（b）
b
y
b
当 b t 0.58 l 0 y b时：
4 0 . 475 b yz y 1 2 2 l0 y t 当 b t 0.58 l 0 y b时：
y

（b）
( 4 28a )
yz
y
（C）
( 4 29a )
yz
b2 5 .1 t
2 2 l0 t 1 y 4 17 . 4 b 2

第五章轴心受力构件_钢结构

第五章轴心受力构件_钢结构
12 250 8 250 12
21. 焊接组合工字形截面轴心受压柱，如图所示，轴心压力设计值 N＝ 2000 kN 。 柱 计 算 长 度 l 0 x 6m ， l 0 y 3m ， 钢 材 为 Q345 钢 ， f 315 N/mm 2 ，翼缘为焰切边，截面无削弱。试验算该柱的安全性。
1
20.9
[28a
1
300
20.9
300
图 5-2
12. 设某工业平台承受轴心压力设计值Ｎ=5000KN，柱高 8m，两端铰接。要求设计焊接工字形截
面组合柱。
l1
13. 试设计一桁架的轴心压杆，拟采用两等肢角钢相拼的Ｔ型截面，角钢间距为 12mm，轴心压
力设计值为 380KN，杆长 lox 3.0m ， loy 2.47 m ，Ｑ235 钢材。
－ 10 × 160
I18
b 94mm ， A=30.6 cm
, I x 1660cm
, I y 122cm
,
上、下翼缘焊接钢板
rx 7.36 cm, ry 2.0 cm）
附表 1 长细比 f y / 235 稳定系 数
a 类截面 b 类截面 c 类截面
轴心受压构件稳定系数 40 0.941 0.899 0.839 110 0.563 0.493 0.419 50 0.916 0.856 0.775 115 0.527 0.464 0.399 60 0.883 0.807 0.709 120 0.494 0.437 0.379 70 0.839 0.751 0.643 130 0.434 0.387 0.342 80 0.783 0.688 0.578 140 0.383 0.345 0.309 85 0.750 0.655 0.547 150 0.339 0.308 0.280

轴心受力构件

轴心受力构件

轴心受力构件设计轴心受拉构件时需进行强度和刚度的验算，设计轴心受压构件时需进行强度、整体稳定、局部稳定和刚度的验算。

一、轴心受力构件的强度和刚度1．轴心受力构件的强度计算轴心受力构件的强度是以截面的平均应力达到钢材的屈服点为承载力极限状态f A N n ≤=σ (1) 式中 N ——构件的轴心拉力或压力设计值；n A ——构件的净截面面积；f ——钢材的抗拉强度设计值。

采用高强度螺栓摩擦型连接的构件，验算最外列螺栓处危险截面的强度时，按下式计算：f A N n≤='σ (2) 'N =)5.01(1n n N - (3)式中 n ——连接一侧的高强度螺栓总数；1n ——计算截面(最外列螺栓处)上的高强度螺栓数；0.5——孔前传力系数。

采用高强度螺栓摩擦型连接的拉杆，除按式(2)验算净截面强度外，还应按下式验算毛截面强度f A N ≤=σ (4)2．轴心受力构件的刚度计算轴心受力构件的刚度是以限制其长细比保证][λλ≤ (5) 式中 λ——构件的最大长细比；[λ]——构件的容许长细比。

二、 轴心受压构件的整体稳定1．理想轴心受压构件的屈曲形式理想轴心受压构件可能以三种屈曲形式丧失稳定：①弯曲屈曲 双轴对称截面构件最常见的屈曲形式。

②扭转屈曲 长度较小的十字形截面构件可能发生的扭转屈曲。

③弯扭屈曲 单轴对称截面杆件绕对称轴屈曲时发生弯扭屈曲。

2．理想轴心受压构件的弯曲屈曲临界力若只考虑弯曲变形，临界力公式即为著名的欧拉临界力公式，表达式为N E =22l EI π=22λπEA (6) 3．初始缺陷对轴心受压构件承载力的影响实际工程中的构件不可避免地存在初弯曲、荷载初偏心和残余应力等初始缺陷，这些缺陷会降低轴心受压构件的稳定承载力。

1）残余应力的影响当轴心受压构件截面的平均应力p f >σ时，杆件截面内将出现部分塑性区和部分弹性区。

由于截面塑性区应力不可能再增加，能够产生抵抗力矩的只是截面的弹性区，此时的临界力和临界应力应为：N cr =22l EI e π=22lEI π·I I e (7) cr σ=22λπE ·I I e (8) 式中 I e ——弹性区的截面惯性矩(或有效惯性矩)；I ——全截面的惯性矩。

轴心受力构件和拉弯、压弯构件的计算

轴心受力构件和拉弯、压弯构件的计算

v v1 v2
v''
1
M
x
/ EI
x
Nv / EI x
dv2 dz
1V
1
dM dz
x
1Nv '
v2'' 1Nv''
其中 1 ——单位剪力作用下剪切角变形
v'' v1'' v2'' Nv / EI x 1Nv''
v''
N
v 0
EIx (1 1N )
稳定平衡方程的解
Ncr
2EIx
框架柱的计算长度
第5.3.4条：单厂阶形柱的计算长度
考虑折减——荷载较大的柱失稳时会受到低荷载柱的支承作用； ——考虑厂房的空间作用； ——对多跨厂房，如刚性屋盖或设屋盖纵向水平支撑――则将柱顶视作不动铰支座。
单阶柱
（1）下段柱的计算长度系数 2 ：
当柱上端和横梁铰接时，按柱上端为自由的单阶柱的数值乘以折减系数（整体作用）
1、受压时保证单构件稳定 2、受拉是保证均匀传力 3、分支距离近，填板刚度大，
可视作实腹截面
轴压构件的抗剪验算
第5.1.6条：
第5.1.7条：
1.此时如按柱剪力验算支撑，不十 分恰当，因为该剪力可视作轴压构 件的偶然剪力。
当撑杆的作用是支撑一系列柱 时，就完全不对了 2.原理：带支撑压杆的挠度增量及 支撑构件的轴向变形，根据变形协 调条件推导其轴力； 3.此支撑力不与其他作用产生的轴 力叠加，而是取较大值； 4.一道支撑架在同一方向所支撑的 柱不宜超过8根。
λ
多条柱子曲线 （200多条）
影响因素： 截面形式、尺寸 残余应力分布 初偏心、初弯曲、初扭曲

钢结构基本原理第三章 构件截面承载力 强度

钢结构基本原理第三章 构件截面承载力 强度

第三章 构件截面承载力--强度钢结构承载能力分3个层次截面承载力：材料强度、应力性质及其在截面上分布属强度问题。

构件承载力：构件最大截面未到强度极限之前因丧失稳定而失稳，取决于构件整体刚度，指稳定承载力。

结构承载力：与失稳有关。

3.1 轴心受力构件的强度及截面选择3.1.1 轴心受力构件的应用及截面形式主要用于承重钢结构，如平面、空间桁架和网架等。

轴心受力截面形式：1）热轧型钢截面2）冷弯薄壁型钢截面3）型钢和钢板连接而成的组合截面（实腹式、格构式）（P48页）对截面形式要求：1）提供强度所需截面积2）制作简单3）与相邻构件便于连接4）截面开展而壁厚较薄，满足刚度要求（截面积决定了稳定承载力，面积大整体刚度大，构件稳定性好）。

3.1.2 轴心受拉构件强度由εσ-关系可得：承载极限是截面平均应力达到抗拉强度u f ，但缺少安全储备，且y f 后变形过大，不符合继续承载能力，因此以平均应力y f ≤为准则，以孔洞为例。

规范：轴心受力构件强度计算：规定净截面平均应力不应超过钢材强度设计值f A N n ≤=/σN ：轴心拉力设计值； An ：构件净截面面积；R y f f γ/=: 钢材抗拉强度设计值 R γ:构件抗力分项系数Q235钢078.1=R γ，Q345，Q390，Q420111.1=R γ49页孔洞理解见书例题P493.1.3 轴心受压构件强度原则上与受拉构件没有区别，但一般情况下，轴心受压构件的承载力由稳定性决定，具体见4章。

3.1.4 索的受力性能和强度计算钢索广泛用于悬索结构，张拉结构，桅杆和预应力结构，一般为高强钢丝组成的平行钢丝束，钢绞线，钢丝绳等。

索是一种柔性构件，内力不仅与荷载有关，而且与变形有关，具有很强几何非线性，但我们通常采用下面的假设：1）理想柔性，不能受压，也不能抗弯。

2）材料符合虎克定理。

在此假设下内力与位移按弹性阶段进行计算。

加载初期（0-1）存在少量松弛变形，主要部分（1-2）线性关系，接近强度极限（2-3）明显曲线性质（图见下）实际工程对钢索预拉张，形成虚线应力—应变关系，很大范围是线性的高强度钢丝组成钢索初次拉伸时应力—应变曲线钢索强度计算采用容许应力法：k f A N k k //maxk N ：钢索最大拉力标准值 A ：钢索有效截面积k f :材料强度标准值 k ：安全系数2.5-3.03.2 梁的类型和强度3.2.1 梁类型按制作方法：型钢梁：热轧型钢梁（工字梁、槽钢、H 型钢）。

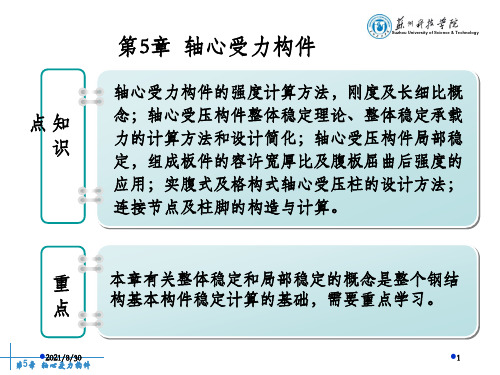
《钢结构设计原理》苏州科技学院教材配套第5章轴心受力构件

《钢结构设计原理》苏州科技学院教材配套第5章轴心受力构件
绕非对称轴： x lox ix
Suzhou University of Science & Technology
y
x
x
绕对称轴y轴: 一般为弯扭屈曲，其临界力低
y
于弯曲屈曲，以换算长细比λyz代替λy
1
yz
1 2
2y
2z
2y 2z 2 4 1 e02
i02
2y 2z
2
2021/8/30
19
第5章 轴心受力构件
3. 初偏心的影响
Suzhou University of Science & Technology
由于构造、杆件截面尺寸、加工、安装等原因，作用于杆端的 轴心压力实际上不可避免的会偏离截面的形心而造成初偏心。
2021/8/30
20
第5章 轴心受力构件
4. 杆端约束的影响
Suzhou University of Science & Technology
四边简支板单向均匀受压时的临界力为：
σ cr
χkπ 2 12(1
E υ2
)(
t b
)2
四边简支单向均匀受压薄板的屈曲
式中：k 屈曲系数，k mb
a
2
a mb
v 0.3 —材料的泊松比
χ — 嵌固系数或弹性约束系数，大于1.0
2021/8/30
31
第5章 轴心受力构件
箱形截面：
h0
tw
Suzhou University of Science & Technology
(c)
tw
b0 tw
(d)
D
tt
b0 /t或h0 /tw 40 235 /f y

轴心受力构件的强度和刚度计算

轴心受力构件的强度和刚度计算

轴心受力构件的强度和刚度计算1.轴心受力构件的强度计算轴心受力构件的强度是以截面的平均应力达到钢材的屈服应力为承载力极限状态。

轴心受力构件的强度计算公式为Na= — <f(4-1)式中：N—构件的轴心拉力或压力设计值；A” --- 构件的净截面面积；f——钢材的抗拉强度设计值。

对于釆用高强度螺栓摩擦型连接的构件，验算净截面强度时一部分剪力己由孔前接触面传递。

因此，验算最外列螺栓处危险截面的强度时，应按下式计算：N' 、0- = —</ (4-2)N' = NQ_0.5±)(4-3)n式中：H—连接一侧的高强度螺栓总数；卩——计算截面(最外列螺栓处)上的高强度螺栓数；0.5——孔前传力系数。

采用高强度螺栓摩擦型连接的拉杆，除按式(4-2)验算净截面强度外，还应按下式验算毛截面强度Na = — < f(4-4)A '式中：A——构件的毛截面面积。

2.轴心受力构件的刚度计算为满足结构的正常使用要求，轴心受力构件应具有一定的刚度，以保证构件不会在运输和安装过程中产生弯曲或过大的变形，以及使用期间因自重产生明显下挠，还有在动力荷载作用下发生较大的振动。

轴心受力构件的刚度是以限制其长细比來保证的，即式中：0—轴心受压构件的整体稳定系数，0=字。

整体稳定系数0值应根据构件的截面分类和构件的长细比查表得到。

构件长细比几应按照下列规定确定：（1）截面为双轴对称或极对称的构件At =】0x / （r A = f oy /f y式中 W —构件对主轴x 和y 的计算长度;构件截面对主轴x 和y 的回转半径。

双轴对称十字形截面构件，厶或心取值不得小于5.07b/t （其中b/t 为悬伸板 件宽厚比）。

（2）截面为单轴对称的构件以上讨论柱的整定稳定临界力时，假定构件失稳时只发生弯曲而没有扭转， 即所谓弯曲屈曲。

对于单轴对称截面，绕对称轴失稳时，在弯曲的同时总伴随着 扭转，即形成弯扭屈曲。

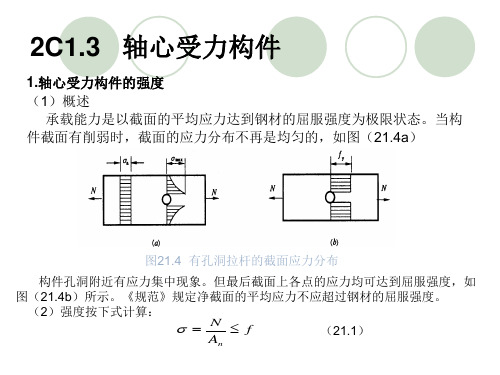
建筑结构——轴心受力构件计算

建筑结构——轴心受力构件计算

求出初选截面面积及回转 ixT和iyT 。
A N
f
ixT
l0 x
（21.9） (21.10)
ixT
l0 x
（21.11）
b.根据 A，ixT和iyT 在型钢表中选一适当的型钢截面。
(2) 组合截面 如果在型钢表中不能够找到比较适当的规格时，可采用组合截面。
a. 初定截面轮廓尺寸 h ixT
1
b iyT
表21.1
表21.2
（4）屈曲分析 a. 如（图21.7）所示两 端 铰支的理想细长压杆，当N力较小时，杆件只有
轴心压缩变形，杆轴保持平直。这时如有外力F干扰，使它微弯，当F力撤去 后，杆件又恢复原来的直线状态，这时杆件处于稳定的平衡状态。
b. 随着N力逐渐加大到某一数值时，如有外力F干扰，杆件微弯，撤除 F力后，杆件仍保持微弯状态，不再恢复到原来的直线状态。这种平衡状态 叫随遇平衡。
l0
2EI l
l0 l , 称为计算长度系数。其值见表21.3
（21.5）
表21.3
1.实际轴心受压构件的实用计算方法
（1）柱子曲线
轴心受压杆件失稳时临界应力与cr 长细比
之间的关系曲线称为
柱子曲线，《钢结构设计规范》将柱子曲线归纳为a,b,c,d四组。 详见表21.4
（本表只列出常用的a、b、c三种类型）。
2C1.3 轴心受力构件
1.轴心受力构件的强度 （1）概述
承载能力是以截面的平均应力达到钢材的屈服强度为极限状态。当构 件截面有削弱时，截面的应力分布不再是均匀的，如图（21.4a）
图21.4 有孔洞拉杆的截面应力分布
构件孔洞附近有应力集中现象。但最后截面上各点的应力均可达到屈服强度，如
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

钢结构设计轴心受力构件截面强度计算7.1.1 轴心受拉构件，当端部连接及中部拼接处组成截面的各板件都由连接件直接传力时，其截面强度计算应符合下列规定：1 除采用高强度螺栓摩擦型连接者外，其截面强度应采用下列公式计算：2 采用高强度螺栓摩擦型连接的构件，其毛截面强度计算应采用式（7.1.1-1），净截面断裂应按下式计算：3 当构件为沿全长都有排列较密螺栓的组合构件时，其截面强度应按下式计算：式中：N——所计算截面处的拉力设计值(N)；f——钢材的抗拉强度设计值(N／mm2)；A——构件的毛截面面积(mm2；A n——构件的净截面面积，当构件多个截面有孔时，取最不利的截面(mm2)；f u——钢材的抗拉强度最小值(N／mm2)；n——在节点或拼接处，构件一端连接的高强度螺栓数目；n1——所计算截面(最外列螺栓处)高强度螺栓数目。

7.1.2 轴心受压构件，当端部连接及中部拼接处组成截面的各板件都由连接件直接传力时，截面强度应按本标准式(7.1.1-1)计算。

但含有虚孔的构件尚需在孔心所在截面按本标准式(7.1.1-2)计算。

7.1.3 轴心受拉构件和轴心受压构件，当其组成板件在节点或拼接处并非全部直接传力时，应将危险截面的面积乘以有效截面系数η，不同构件截面形式和连接方式的η值应符合表7.1.3的规定。

表7.1.3 轴心受力构件节点或拼接处危险截面有效截面系数条文说明7.1.1 原规范在条文说明中给出了式(7.1.1-1)和式(7.1.1-2)，并指出“如果今后采用屈强比更大的钢材，宜用这两个公式来计算，以确保安全”。

当前，屈强比高于0.8的Q460钢已开始采用，为此，用这两个公式取代了净截面屈服的计算公式。

对于Q235和Q345钢，用这两个公式可以节约钢材。

当沿构件长度有排列较密的螺栓孔时，应由净截面屈服控制，以免变形过大。

7.1.2 轴压构件孔洞有螺栓填充者，不必验算净截面强度。

7.1.3 有效截面系数是考虑了杆端非全部直接传力造成的剪切滞后和截面上正应力分布不均匀的影响。

第一章7.2 轴心受压构件的稳定性计算7.2.1 除可考虑屈服后强度的实腹式构件外，轴心受压构件的稳定性计算应符合下式要求：式中：φ——轴心受压构件的稳定系数(取截面两主轴稳定系数中的较小者)，根据构件的长细比(或换算长细比)、钢材屈服强度和表7.2.1-1、表7.2.1-2的截面分类，按本标准附录D采用。

表7.2.1-1 轴心受压构件的截面分类(板厚t＜40mm)注：1 a*类含义为Q235钢取b类，Q345、Q390、Q420和Q460钢取a类；b*类含义为Q235钢取c类，Q345、Q390、Q420和Q460钢取b类；2 无对称轴且剪心和形心不重合的截面，其截面分类可按有对称轴的类似截面确定，如不等边角钢采用等边角钢的类别；当无类似截面时，可取c类。

表7.2.1-2 轴心受压构件的截面分类(板厚t≥40mm)7.2.2 实腹式构件的长细比λ应根据其失稳模式，由下列公式确定：1 截面形心与剪心重合的构件：1) 当计算弯曲屈曲时，长细比按下列公式计算：式中：l0x、l0y——分别为构件对截面主轴x和y的计算长度，根据本标准第7.4节的规定采用(mm)；i x、i y——分别为构件截面对主轴x和y的回转半径(mm)。

2) 当计算扭转屈曲时，长细比应按下式计算，双轴对称十字形截面板件宽厚比不超过15εk者，可不计算扭转屈曲。

式中：I0、I t、I w——分别为构件毛截面对剪心的极惯性矩(m m4)、自由扭转常数(m m4)和扇性惯性矩(m m6)，对十字形截面可近似取I w＝0；I w——扭转屈曲的计算长度，两端铰支且端截面可自由翘曲者，取几何长度l；两端嵌固且端部截面的翘曲完全受到约束者，取0.5l(mm)。

2 截面为单轴对称的构件：1) 计算绕非对称主轴的弯曲屈曲时，长细比应由式(7.2.2-1)、式(7.2.2-2)计算确定。

计算绕对称主轴的弯扭屈曲时，长细比应按下式计算确定：式中：y s——截面形心至剪心的距离(mm)；i0——截面对剪心的极回转半径，单轴对称截面i20＝y2s＋i2x＋i2y(mm)；λz——扭转屈曲换算长细比，由式(7.2.2-3)确定。

2) 等边单角钢轴心受压构件当绕两主轴弯曲的计算长度相等时，可不计算弯扭屈曲。

塔架单角钢压杆应符合本标准第7.6节的相关规定。

3) 双角钢组合T形截面构件绕对称轴的换算长细比λyz可按下列简化公式确定：图7.2.2-1 双角钢组合T形截面b-等边角钢肢宽度；b1-不等边角钢长肢宽度；b2-不等边角钢短肢宽度3 截面无对称轴且剪心和形心不重合的构件，应采用下列换算长细比：式中：N xyz——弹性完善杆的弯扭屈曲临界力，由式(7.2.2-15)确定(N)；x s、y s——截面剪心的坐标(mm)；i0——截面对剪心的极回转半径(mm)；N x、N y、N z—分别为绕x轴和y轴的弯曲屈曲临界力和扭转屈曲临界力(N)；E、G——分别为钢材弹性模量和剪变模量(N／m m2)。

4 不等边角钢轴心受压构件的换算长细比可按下列简化公式确定(图7.2.2-2)：7.2.3 格构式轴心受压构件的稳定性应按本标准式(7.2.1)计算，对实轴的长细比应按本标准式(7.2.2-1)或式(7.2.2-2)计算，对虚轴[图7.2.3(a)]的x轴及图7.2.3(b)、图7.2.3(c)的x轴和y轴应取换算长细比。

换算长细比应按下列公式计算：1 双肢组合构件[图7.2.3(a)]：图7.2.2-2 不等边角钢注：v轴为角钢的弱轴，b1为角钢长肢宽度图7.2.3 格构式组合构件截面式中：λx——整个构件对x轴的长细比；λ1——分肢对最小刚度轴1-1的长细比，其计算长度取为：焊接时，为相邻两缀板的净距离；螺栓连接时，为相邻两缀板边缘螺栓的距离；A1x——构件截面中垂直于x轴的各斜缀条毛截面面积之和(m m2)。

2 四肢组合构件[图7.2.3(b)]：式中：λy——整个构件对y轴的长细比；A1y——构件截面中垂直于y轴的各斜缀条毛截面面积之和(m m2)。

3 缀件为缀条的三肢组合构件[图7.2.3(c)]：式中：A1——构件截面中各斜缀条毛截面面积之和(mm2)；θ——构件截面内缀条所在平面与x轴的夹角。

7.2.4 缀件面宽度较大的格构式柱宜采用缀条柱，斜缀条与构件轴线间的夹角应为40°～70°。

缀条柱的分肢长细比λ1不应大于构件两方向长细比较大值λmax的0.7倍，对虚轴取换算长细比。

格构式柱和大型实腹式柱，在受有较大水平力处和运送单元的端部应设置横隔，横隔的间距不宜大于柱截面长边尺寸的9倍且不宜大于8m。

7.2.5 缀板柱的分肢长细比λ1不应大于40εk，并不应大于λmax的0.5倍，当λmax＜50时，取λmax＝50。

缀板柱中同一截面处缀板或型钢横杆的线刚度之和不得小于柱较大分肢线刚度的6倍。

7.2.6 用填板连接而成的双角钢或双槽钢构件，采用普通螺栓连接时应按格构式构件进行计算；除此之外，可按实腹式构件进行计算，但受压构件填板间的距离不应超过40i，受拉构件填板间的距离不应超过80i。

i为单肢截面回转半径，应按下列规定采用：1 当为图7.2.6(a)、图7.2.6(b)所示的双角钢或双槽钢截面时，取一个角钢或一个槽钢对与填板平行的形心轴的回转半径；2 当为图7.2.6(c)所示的十字形截面时，取一个角钢的最小回转半径。

受压构件的两个侧向支承点之间的填板数不应少于2个。

图7.2.6 计算截面回转半径时的轴线示意图7.2.7 轴心受压构件剪力V值可认为沿构件全长不变，格构式轴心受压构件的剪力V应由承受该剪力的缀材面(包括用整体板连接的面)分担，其值应按下式计算：7.2.8 两端铰支的梭形圆管或方管状截面轴心受压构件(图7.2.8)的稳定性应按本标准式(7.2.1)计算。

其中A 取端截面的截面面积A1，稳定系数φ应根据按下列公式计算的换算长细比λe确定：式中：l0——构件计算长度(mm)；i1——端截面回转半径(mm)；γ——构件楔率；D2、b2——分别为跨中截面圆管外径和方管边长(mm)；D1、b1——分别为端截面圆管外径和方管边长(mm)。

图7.2.8 梭形管状轴心受压构件7.2.9 钢管梭形格构柱的跨中截面应设置横隔。

横隔可采用水平放置的钢板且与周边缀管焊接，也可采用水平放置的钢管并使跨中截面成为稳定截面。

两端铰支的三肢钢管梭形格构柱应按本标准式(7.2.1)计算整体稳定。

稳定系数φ应根据下列公式计算的换算长细比λ0确定：N cr,s应按下列公式计算：N cr,a应按下列公式计算：η1、η2应按下列公式计算：式中：A s——单根分肢的截面面积(m m2)；N cr、N cr,s、N cr,a—分别为屈曲临界力、对称屈曲模态与反对称屈曲模态对应的屈曲临界力(N)；I0、I m、I1——分别为钢管梭形格构柱柱端、1／4跨处以及跨中截面对应的惯性矩(图7.2.9)(m m4)；K v,s、K v,a——分别为对称屈曲与反对称屈曲对应的截面抗剪刚度(N)；η1、η2——与截面惯性矩有关的计算系数；b0、b m、b1——分别为梭形柱柱端、1／4跨处和跨中截面的边长(mm)；l s0——梭形柱节间高度(mm)；I d、I s——横缀杆和弦杆的惯性矩(m m4)；A s——单个分肢的截面面积(m m2)；E——材料的弹性模量(N／m m2)。

图7.2.9 钢管梭形格构柱条文说明7.2.1 式(7.2.1)改用轴心压力设计值与构件承载力之比的表达式，有别于截面强度的应力表达式，使概念明确。

热轧型钢的残余应力峰值和钢材强度无关，它的不利影响随钢材强度的提高而减弱，因此，对屈服强度达到和超过345MPa的b／h＞0.8的H型钢和等边角钢的稳定系数φ可提高一类采用。

板件宽厚比超过本标准第7.3.1条规定的实腹式构件应按本标准式(7.3.3-1)计算轴心受压构件的稳定性。

7.2.2 本条对原规范第5.1.2条进行了局部修改。

截面单轴对称构件换算长细比的计算公式(7.2.2-4)和单、双角钢的简化公式，都来自弹性稳定理论，这些公式用于弹塑性范围时偏于保守，原因是当构件进入非弹性后其弹性模量下降为E t＝τE，但剪切模量G并不和E同步下降，在构件截面全部屈服之前可以认为G 保持常量。

计算分析和试验都表明，等边单角钢轴压构件当两端铰支且没有中间支点时，绕强轴弯扭屈曲的承载力总是高于绕弱轴弯曲屈曲承载力，因此条文明确指出这类构件无须计算弯扭屈曲，并删去了原公式(5.1.2-5)。

双角钢截面轴压构件抗扭刚度较强，对弯扭屈曲承载力的影响较弱，仍保留原来的弹性公式，只是表达方式上作了改变。